DOI:10.32604/iasc.2023.028368

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.028368 |  |
| Article |
Evaluating Partitioning Based Clustering Methods for Extended Non-negative Matrix Factorization (NMF)
1Guru Gobind Singh Indraprastha University, Delhi, India
2Bhagwan Parshuram Institute of Technology, Delhi, India
*Corresponding Author: Neetika Bhandari. Email: bneetika3116@gmail.com
Received: 08 February 2022; Accepted: 12 April 2022
Abstract: Data is humongous today because of the extensive use of World Wide Web, Social Media and Intelligent Systems. This data can be very important and useful if it is harnessed carefully and correctly. Useful information can be extracted from this massive data using the Data Mining process. The information extracted can be used to make vital decisions in various industries. Clustering is a very popular Data Mining method which divides the data points into different groups such that all similar data points form a part of the same group. Clustering methods are of various types. Many parameters and indexes exist for the evaluation and comparison of these methods. In this paper, we have compared partitioning based methods K-Means, Fuzzy C-Means (FCM), Partitioning Around Medoids (PAM) and Clustering Large Application (CLARA) on secure perturbed data. Comparison and identification has been done for the method which performs better for analyzing the data perturbed using Extended NMF on the basis of the values of various indexes like Dunn Index, Silhouette Index, Xie-Beni Index and Davies-Bouldin Index.
Keywords: Clustering; CLARA; Davies-Bouldin index; Dunn index; FCM; intelligent systems; K-means; non-negative matrix factorization (NMF); PAM; privacy preserving data mining; Silhouette index; Xie-Beni index
Data is present in huge volumes today. This data can be collected in different forms and from various industries like healthcare, defense, education, law, banking, stock market and more. These industries use Artificial Intelligence (AI) systems to analyze the collected data as it helps in making important decisions. AI systems are intelligent machines which use data mining methods to resolve various problems. These systems process large datasets to quickly produce desirable results in a trustworthy manner. The intelligent systems rely on data mining and machine learning for their intelligent behaviour. AI systems are being used largely in various fields like finance, stocks, healthcare, education, physics, banking and many more to shape and process the gathered data to produce valuable information [1,2].
But before applying data analysis, it is required to ensure that this data is secure. The original data from the industries contains sensitive data and can be exploited to impose threats of privacy of individuals if harnessed in the wrong manner. It is very important to provide security to the sensitive data against unauthorized users and malicious access. To ensure privacy of data various measures have been proposed and can be taken. Privacy Preserving Data Mining (PPDM) [3–5] allows to make the sensitive critical data secure whilst maintaining its utility. Various PPDM methods exist which have their own characteristics, advantages and disadvantages [6,7]. One of these methods is Perturbation based PPDM techniques in which data is distorted before Data Mining to make it secure. The authors in [8] have proposed a perturbation based PPDM method Extended NMF and compared it with NMF based on various privacy measures. The results concluded that Extended NMF provides better privacy to data than NMF alone.
Once the data has been made secure, it can be used to extract useful knowledge and information which can be beneficial to industries and can help to make important decisions. The original raw data is not useful if it is not analyzed. This is done by Data Mining [9,10]. Data Mining is the process to efficiently extract beneficial information from the original data collected from different sources. Many data mining techniques exist which can be used to uncover knowledge in desired forms and patterns. Clustering is one of the most widely used Data Mining techniques which allows to group similar data points together. Clustering is a very useful unsupervised learning method which is used in intelligent systems as part of preprocessing step to help and make the supervised learning process more efficient and reliable [2,11]. Clustering methods can be classified into different types. Partitioning based clustering methods are very important and the most popular clustering methods. These methods classify data items of a dataset into different groups based on the similarity between the data points. Partitioning based algorithms include methods like K-Means, PAM, CLARA and FCM.
Because of the continuous increase in threats and attacks on data these days, it is vital to find a secure way to mine the data to produce efficient results. Thus, in this paper, we have compared the performance of partitioning based clustering methods like K-Means, FCM, PAM and CLARA to find which method is more compatible and performs best with Extended NMF. The comparison is done on the basis of different clustering indexes like Dunn Index, Silhouette Index, Xie-Beni Index and Davies-Bouldin Index to find out which of the above mentioned clustering methods gives best clusters from distorted dataset obtained from Extended NMF compared to dataset from NMF.
Section 2 of the paper summarizes the literature survey. In Section 3, we explain Clustering and different clustering methods. Section 4 explains the perturbation method Extended NMF. Various indexes used for evaluation purposes are explained in Section 5. Further, the methodology and results are shown in Section 6. Finally, the conclusion is given in Section 7.
The authors Nagalakshmi et al. in [12] have proposed a hybrid method for privacy preservation using Non-negative Matrix Factorization (NMF) and Principal Component Analysis (PCA) methods. According to the authors, this hybrid method provides privacy and maintains the data utility. K-means clustering has been applied and comparison between NMF and the proposed hybrid method has been done based on degree of privacy and clustering quality measured as misclassification error and Overall F-measure. In [13] the authors have perturbed the original data set using a hybrid method of fuzzy logic and NMF. They have first used S, T and Z membership functions in fuzzy logic to obtain the fuzzy data. Further, based on the accuracy, they have used the S-membership fuzzy data and applied NMF to get final distorted data for analysis. The accuracy of the proposed hybrid method compared to original data is measured by k-Nearest Neighbor (KNN) and C4.5 based on misclassification error. The authors in [14] have proposed four different combinations of Singular Value Decomposition (SVD), NMF and Discrete Wavelet Transformation (DWT) for perturbation. They use Support Vector Machine (SVM) to find the accuracy of mining on the distorted data and hence compare the data utility. Li et al. in [15] use both SVD and NMF matrix decomposition methods for data perturbation and privacy. To check the efficiency, they use five privacy measures including Value Difference (VD) and to check the efficiency of the mining algorithms on the perturbed data they have used classifiers Support Vector Machine (SVM), Nearest Neighbor (NN) and WEKA’s J48 decision tree based on accuracy. The authors in [16] have proposed a hybrid method to distort numeric data. Their proposed method Hybrid Data Transformation method (HDT) combines Double-Reflecting Data Perturbation (DRDP) and Rotation Based Translation (RBT) for perturbation. They have evaluated the performance of their proposed method based on clustering quality by evaluating the misclassification error after applying k-means and the degree of privacy.
The authors Fahad et al. in [17], have compared the performance of various clustering algorithms like FCM (partition-based), BIRCH (Hierarchical), DENCLUE (Density-based), OPTIGRID (Grid-based) and EM (model-based). The comparison was done based on three measurements. First, Validity Evaluation in which various internal and external validation indexes are compared. The internal indexes include compactness, Davies-Bouldin index, Dunn validity index and separation. The external validity indexes include cluster accuracy, adjusted rand index and normalized mutual information. Second measurement used is stability of results and third is the time requirement. Results show that based on external validity indexes EM is the best method followed by FCM. DENCLUE gives compact clusters and EM, DENCLUE and OPTIGRID give most well-separated clusters. Stability is not high for all methods but EM achieves highest stability and FCM achieves the lowest. DENCLUE is the fastest method and EM has least speed.
Reference [18] shows that the authors Ghosh et al. have compared two centroid based partitioning clustering methods: hard clustering method K-Means and soft clustering method FCM. The methods were compared on the basis of elapsed time to find that K-Means takes less time compared to FCM. The comparison was also done on the basis of time complexity by varying the number of clusters. Time complexity was also compared by keeping the number of clusters constant but varying the number of iterations. For both cases, results show that K-Means is better than FCM in terms of computation time.
Maulik et al. [19] have used hard K-means, single linkage clustering and simulated annealing (SA) based clustering methods on real and artificial datasets varying the number of clusters to determine the appropriate number of clusters. They have used four cluster validity indices like Davies-Bouldin index, Dunn’s index, Calinski-Harabasz index and τ index. Since simulated annealing method provided improvement in result over others, clustering was done using SA method once the number of clusters was determined.
The authors Liu et al. in [20] have used 11 internal validation measures to evaluate clustering. These are Root mean square standard deviation (RMSSTD), R-squared (RS), Modified Hubert statistic (Г), Calinski-Harabasz Index (CH), I index (I), Dunn’s Index (D), Silhouette Index (S), Davies-Bouldin Index (DB), Xie-Beni Index (XB), SD validity index (SD) and S_Dbw index (S_Dbw). They have used these to find the impact of five aspects on the validation measures, varying the number of clusters. The five aspects considered were monotonicity, noise, density, subclusters and skewness. The authors have used synthetic data for all five cases. The results show that the internal measure S_Dbw gave the best results and correct number of clusters under the impact of all 5 faces.
Data clustering [10,21] is an important technique in Data Mining which is used to analyze data to obtain statistical results and patterns. It is used to group those data points into same clusters which are similar to each other. The main aim is to get higher intra-cluster similarity and lower inter-cluster similarity. Clustering is used extensively in various applications like market research, pattern recognition, wireless networks, machine learning, image processing and various other research areas. Clustering algorithms can be divided into partitioning methods, hierarchical methods, density-based methods, grid-based methods and model-based methods [10,17,22,23]. The performance of Agglomerative Clustering for Extended NMF has been evaluated in [24] based on the evaluation criteria Agglomerative Coefficient and Cophenetic Correlation Coefficient.
Partitioning-based clustering methods are the most popular type of algorithms used for clustering purposes. These methods use the iterative relocation technique to divide the dataset into k-partitions such that each partition contains atleast one object and each object belongs to one and only one partition. The most common partitioning-based methods are K-Means and K-Medoids. There are various other partitioning based methods other than K-Means and K-Medoids like PAM, FCM, CLARA and CLARANS.
K-Means algorithm [10,18,22,23] is one of the simplest partition-based clustering methods which groups all data items of a given dataset into k disjoint partitions called clusters. The method starts with randomly selecting k data points as cluster mean or center. Then, partitioning is done based upon distance between an object and the centroid (center) of the cluster. Object is assigned to the most similar (close) cluster. It is an iterative process which converges when square-error criterion is minimized. Though the algorithm is very easy but it is very sensitive to outliers.
3.2 PAM (Partitioning Around Medoids)
The Partitioning Around Medoids (PAM) [10,22,23] method is similar to K-Means algorithm but is more robust to noise and outliers than K-Means. It is based upon medoids which are representative objects. Initially, k-medoids are chosen arbitrarily from the dataset. Each object is assigned to a cluster based upon its closeness to the medoid of that cluster. This is also an iterative process where a random representative object is chosen and total cost function is computed to determine a better cluster. This method is costlier to implement compared to K-means and is effective for smaller data sets only.
3.3 CLARA (Clustering Large Applications)
CLARA [10,22,23] is a clustering method which is based upon PAM and can be used on larger data sets as well. It removes the drawbacks of both K-Means and PAM. CLARA does not take the whole data set in one go. Instead, it divides the whole dataset into different samples and uses the PAM algorithm on each sample to get clusters. It then finds the best cluster from these. It might be that if the sample is fair, the medoids chosen would be close to those obtained from whole dataset. One major drawback of CLARA is that it cannot generate best clustering if sample dataset chosen are not fair and medoids obtained are not the best ones.
Fuzzy C-Means (FCM) algorithm [10,17,18] is based on the K-Means clustering method. In this method, clusters are formed based on the distance between data points and cluster centers. Each data point has a degree of belongingness (membership) for every cluster. A data point close to a cluster center will have high degree of belongingness while a faraway point will have a low degree of belongingness to that cluster. This is an iterative method which keeps on updating cluster centers and memberships for data points until the objective function is minimized and convergence is achieved.
Data privacy is a very important aspect which needs to be done to secure data from unauthorized access. Data privacy can be achieved using Privacy Preserving Data Mining (PPDM) techniques. Perturbation based PPDM [6] methods are easy to use data transformation methods which are applied to distort data values before the data mining process. This helps to analyze the data without disclosing the true values of the sensitive dataset. Various perturbation methods exist like noise addition, geometric transformations, SVD, NMF, QR decomposition, Double Reflecting Data Perturbation (DRDP), DWT and many more.
4.1 Non-negative Matrix Factorization (NMF)
NMF [12,25] is a perturbation based data distortion method. Let V be a m x n non-negative data matrix. Non-negative Matrix Factorization method factorizes V into two matrices W and H such that W and H are also non-negative and have size m x k and k x n respectively such that
k is chosen such that k < min (m, n) and (m + n) k < mn. The values of matrices W and H are selected such that the error between V and WH is minimized. The error function is defined as:
4.2 Double Reflecting Data Perturbation (DRDP)
DRDP or Double Reflecting Data Perturbation [16,26] is an easy to implement method which transforms data based on the operation shown below:
where
Extended NMF [8] is a proposed method for perturbation based PPDM which is used to distort the data and make it secure before data mining. In Extended NMF, NMF method is followed by DRDP method to produce the new distorted dataset. Here, a non-negative dataset
1. Input Non-negative numeric dataset
2. Replace missing or NA values with the mean value.
3. Apply NMF on
4. Apply DRDP on
A good cluster partition is one where clusters are compact and well separated. This means that the distance between different clusters is large and the size of each cluster is small. Dunn Index [19,20] is measured as intercluster distance (separation) over intracluster distance (compactness). Separation between two clusters is measured as the minimum distance between two data points, one each from each cluster.
Compactness for each cluster
Dunn Index (D) is defined as:
Higher Dunn Index is required for optimal cluster partitions.
The Silhouette index [20] for a dataset is computed as the average of Silhouette width of all data points in the data set. The silhouette width for each data point is calculated as:
where
The Davies-Bouldin index [19,20] is defined as the ratio of the sum-of within-cluster scatter to between-cluster separation. Here, within-cluster scatter
And distance between cluster
where
where
Best clustering partition is the one which minimizes the DB index.
The Xie-Beni (XB) index [20] is basically a fuzzy clustering index but it can be used to validate other clustering methods as well. This index is defined as ratio of mean quadratic error measured as mean square distance between each data and its cluster center and minimum of the minimal squared distance between points in the clusters measured as minimum square distance between centers of clusters.
Good clustering partition is achieved when XB is minimum.
Best partition is one which has higher values of Dunn index and Silhouette index and lower values of Davies-Bouldin index and Xie-Beni index.
The authors have used R language to perform the experimental work. R is an open source tool which is easily available and is used to perform statistical analysis of data. R can run on different operating systems and hardware. R has various repositories of packages like the CRAN “Comprehensive R Archive Network” which has around 13695 available packages currently. In this paper, various packages used are NMF [27], ppclust [28], cluster [29] and clusterCrit [30] of R. Three datasets from the UC Irvine Machine Learning Repository [31] have been used in the experimental work. The metadata for each dataset is given in Tab. 1 which includes the name of the dataset, its size mentioned as rows x columns and a brief description about the dataset.

The methodology followed is shown in Fig. 1 and is given below:
1. Non-negative dataset was taken and Extended NMF and NMF were applied to get distorted data.
2. The value of k (number of clusters) for clustering was evaluated using the elbow method [32].
3. Various Clustering methods (K-Means, FCM, PAM and CLARA) were applied on distorted dataset obtained by Extended NMF and NMF.
4. Various indices like Xie-Beni, Dunn, Silhouette and Davies-Bouldin were evaluated for the clusters obtained from K-Means, FCM, PAM and CLARA.
5. Results were compared.

Figure 1: Methodology
6.1 Absenteeism_at_work Dataset
The number of clusters is taken as 6 for this dataset using the elbow method. K-Means, FCM, PAM and CLARA methods are used and values of Dunn Index, Silhouette Index, Xie-Beni Index and Davies-Bouldin Index are evaluated. Tab. 2 gives the values of various indexes for this dataset for different algorithms. For this dataset, each column in Tab. 2 represents the index values (Dunn, Silhouette, Davies-Bouldin and Xie-Beni) for both Extended NMF and NMF for all the four clustering methods K-means, FCM, PAM and CLARA represented in each row. It can be seen that values of Dunn Index and Silhouette Index have increased for Extended NMF and the values of Xie-Beni Index and Davies-Bouldin Index have decreased for Extended NMF for K-Means and FCM making them more compatible clustering methods with Extended NMF.
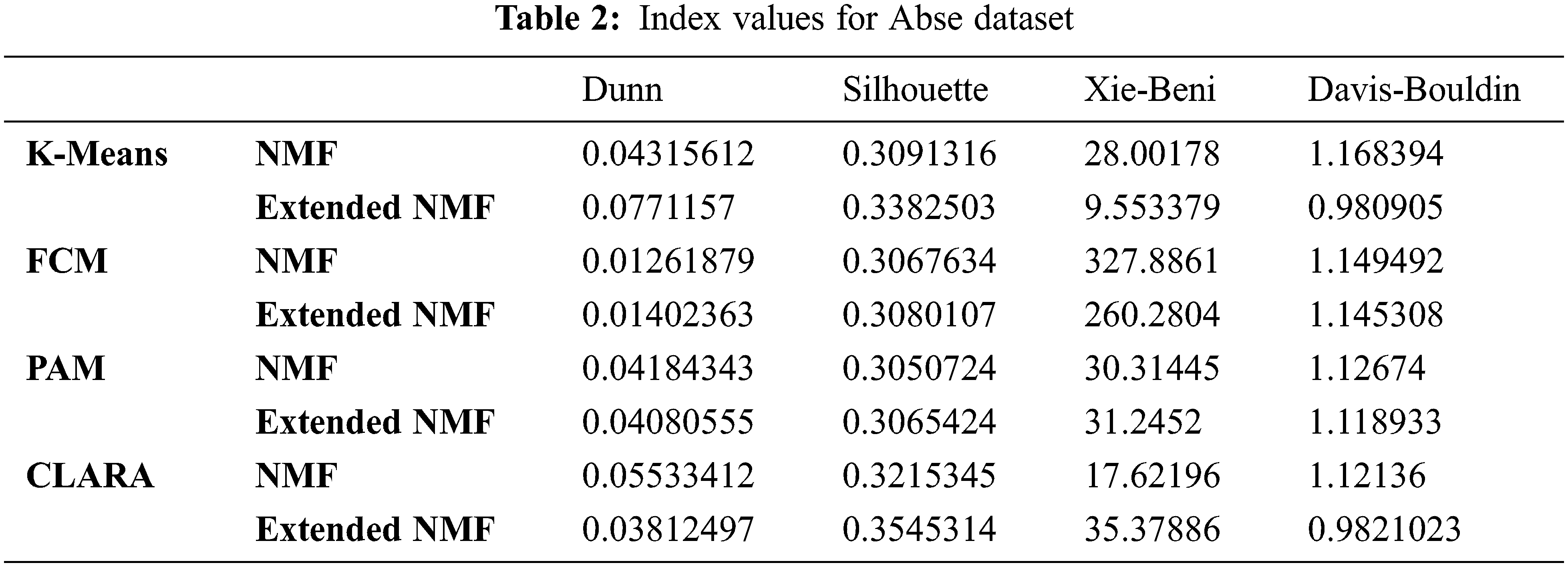
In this dataset, the number of clusters is taken as 6. The values of all indexes for all four algorithms are shown in Tab. 3 below. In Tab. 3, each column represents the index values for Dunn, Silhouette, Davies-Bouldin and Xie-Beni for both Extended NMF and NMF for all the four clustering methods K-Means, FCM, PAM and CLARA represented in each row.
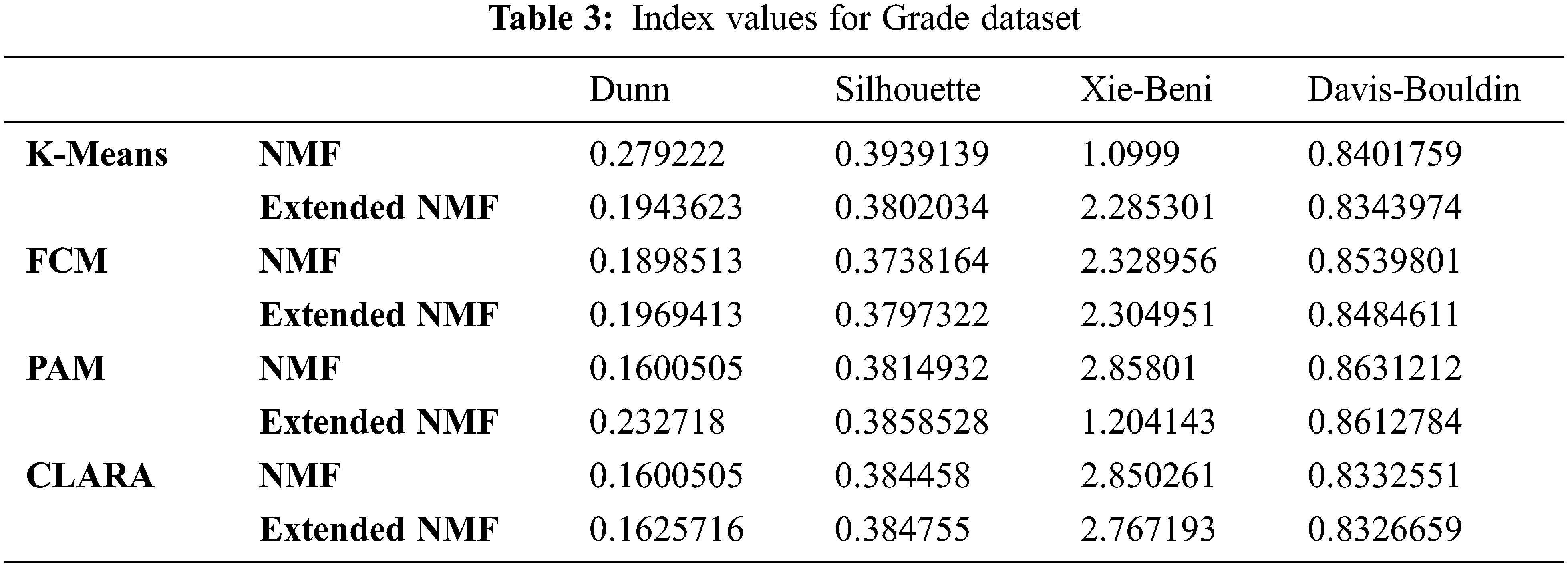
From Tab. 3 it can be seen that FCM, PAM and CLARA have higher values for Dunn Index and Silhouette Index and lower values for Xie-Beni Index and Davies-Bouldin Index for distorted dataset for Extended NMF.
6.3 Wholesale Customers Dataset
Wholesale dataset represents the annual expense for a wholesale distributor on various products. The number of clusters taken in the experiment is 7 based upon the elbow method. The results of all index values for FCM, K-Means, CLARA and PAM are given in Tab. 4 for both NMF and Extended NMF for this dataset. In Tab. 4, for this dataset, each column represents the index values for Dunn, Silhouette, Davies-Bouldin and Xie-Beni for both Extended NMF and NMF for all the four clustering methods in each row.
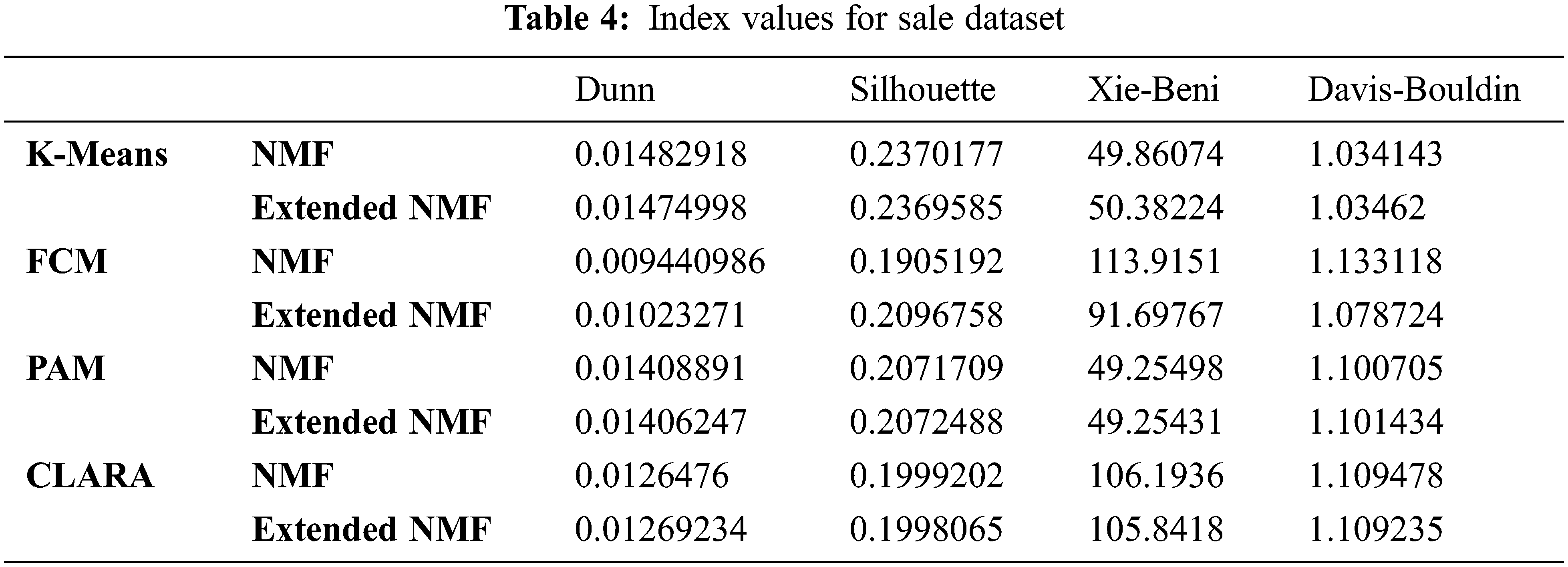
It can be seen from Tab. 4 that Dunn Index and Silhouette Index have increased in FCM for Extended NMF. Also values of Xie-Beni Index and Davies-Bouldin Index have decreased in FCM for the all the datasets for Extended NMF.
The results of Tabs. 2–4 are shown as graphs for Dunn Index, Silhouette Index, Xie-Beni Index and Davies-Bouldin Index in Figs. 2–5 respectively.
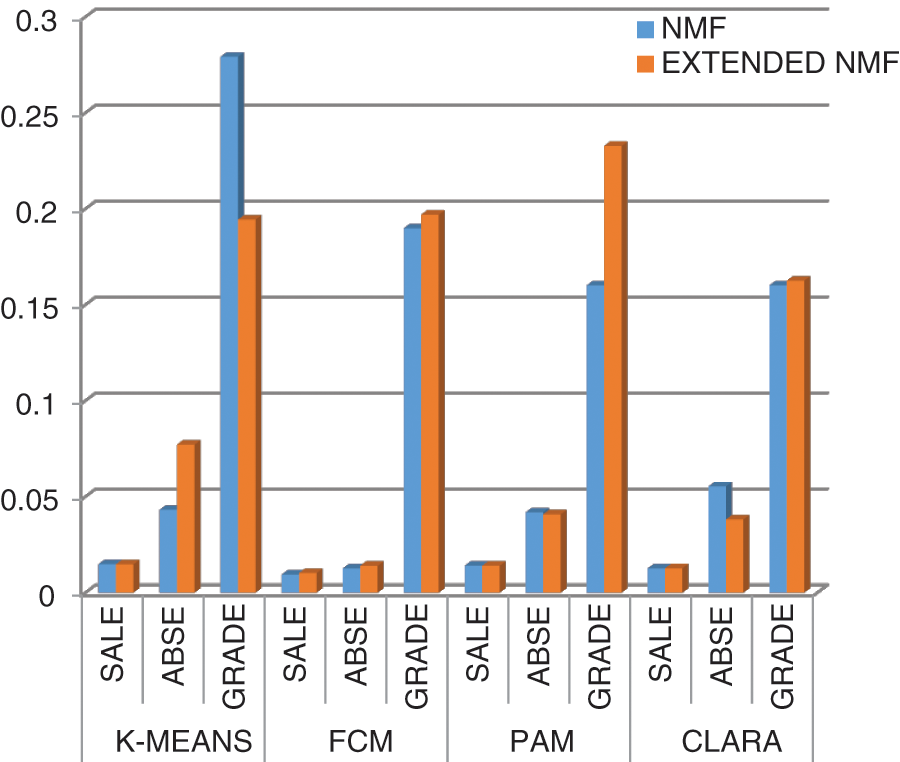
Figure 2: Dunn index for all datasets for NMF and extended NMF
Fig. 2 is the graph representing the values of Dunn index for both Extended NMF and NMF for all the three datasets (Sale, Abse and Grade) for each of the four clustering methods from Tabs. 2–4.
Fig. 3 represents the graph for all values of Silhouette index for Extended NMF and NMF for all datasets and all clustering methods from Tabs. 2–4.
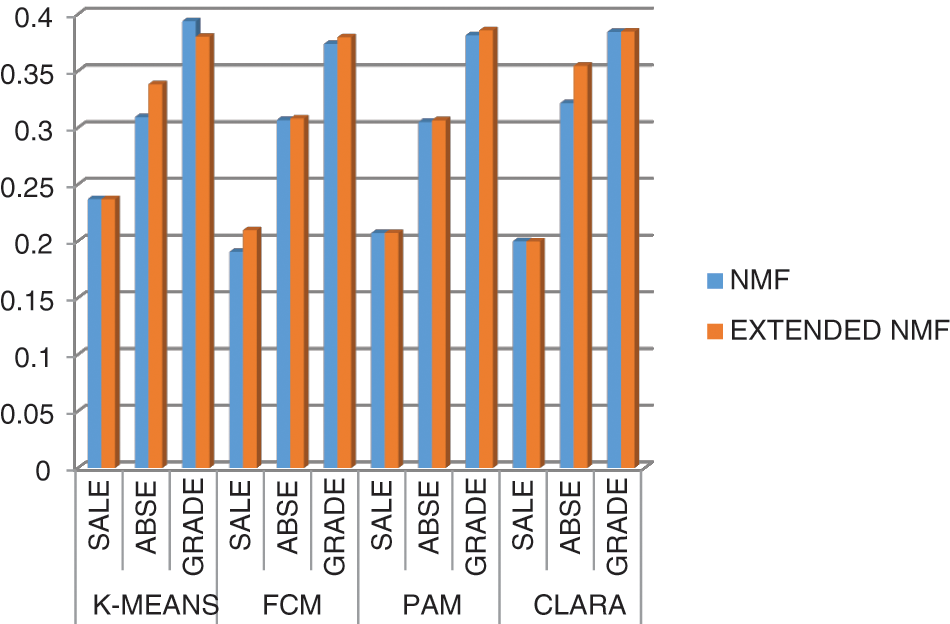
Figure 3: Silhouette index for all datasets for NMF and extended NMF
Fig. 4 gives the graphical display for all values of Xie-Beni index for all datasets and for all four clustering methods (K-means, FCM, PAM, and CLARA) for both Extended NMF and NMF from Tabs. 2–4.
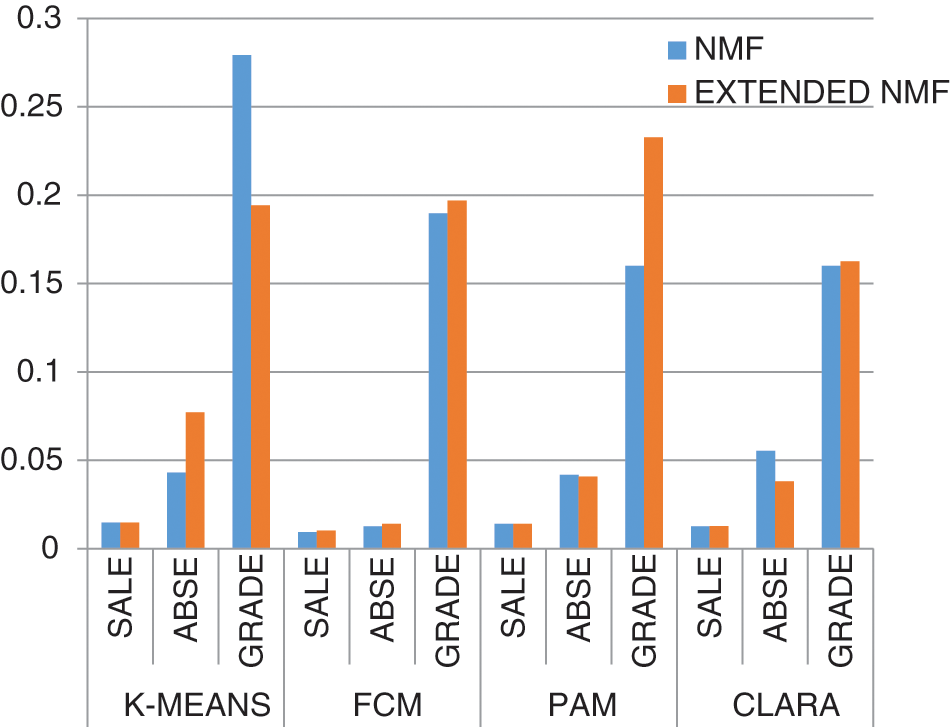
Figure 4: Xie-Beni index for all datasets for NMF and extended NMF
Fig. 5 gives the index values for Davies-Bouldin index values for all datasets and all clustering methods being evaluated for both Extended NMF and NMF.
It can be seen from the above graphs that the values of Dunn Index and Silhouette Index have increased in FCM for all datasets in Extended NMF. Also, the values of Xie-Beni Index and Davies-Bouldin Index have reduced in FCM for Extended NMF making FCM a better clustering method with Extended NMF.
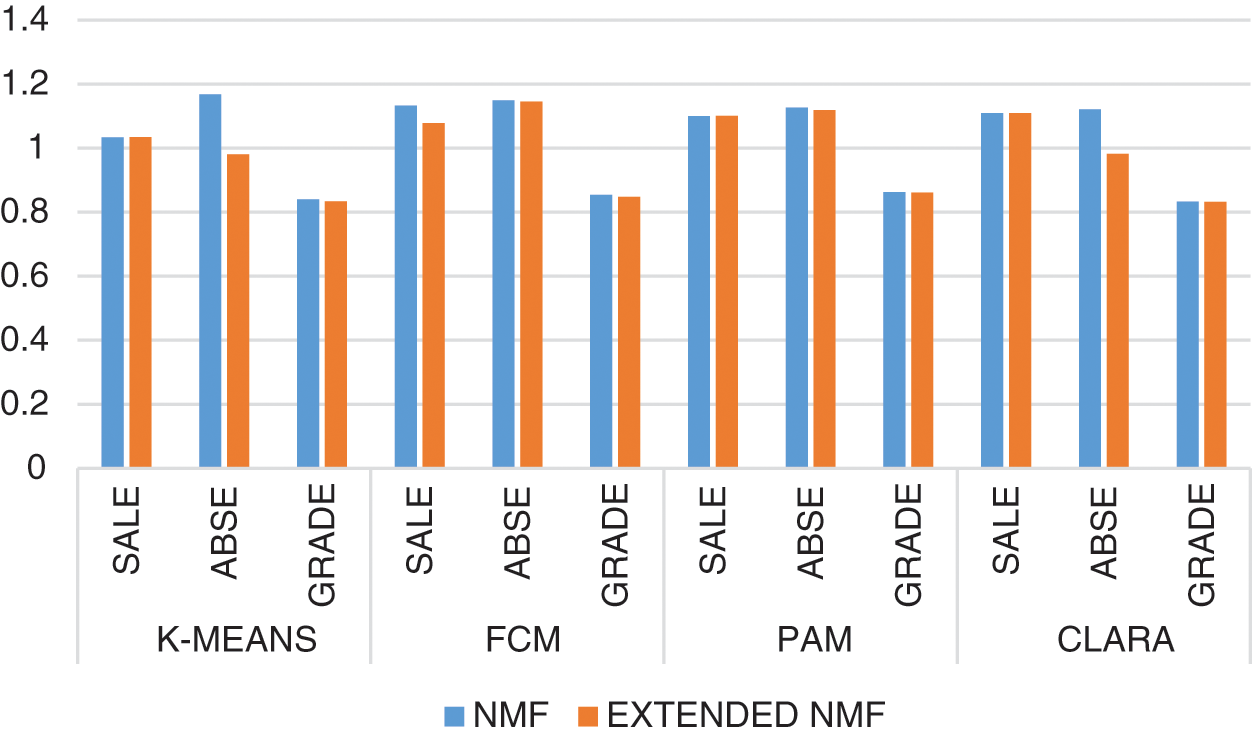
Figure 5: Davies Bouldin index for all datasets for NMF and extended NMF
Data privacy an important aspect which is applied on a dataset before the data mining process as the data used in mining can be collected and shared from various sources. Clustering, a data mining method, is a very important technique used for data analysis. It is important to secure the data before clustering so that the data is harnessed in the correct and secure manner. This is done by applying data perturbation using Extended NMF. In this paper, clustering methods K-Means, FCM, PAM and CLARA are applied on the data which has been distorted using Extended NMF. Various indexes like Dunn Index, Silhouette Index, Xie-Beni Index and Davies-Bouldin Index are computed for comparing the performance of all the clustering methods. The results show that of all the clustering methods used, FCM is the only one in which values of Dunn Index and Silhouette Index increase for Extended NMF compared to NMF and values of Xie-Beni Index and Davies-Bouldin Index reduce in Extended NMF compared to NMF. Thus, it can be inferred that FCM is a better clustering technique compared to K-Means, PAM and CLARA and is more compatible with the Extended NMF data perturbation method.
Therefore, we can conclude that a combination of Extended NMF to secure the data and FCM to mine and analyze the secure perturbed data can be used to enhance the overall performance of the mining process and thus, increase the efficiency. Thus, in the future, it is of interest to evaluate the performance of both Extended NMF and FCM together on some realistic dataset. It is also of interest to evaluate the performance of Extended NMF and FCM on larger datasets. The work can be extended further to perform on datasets having negative values also as realistic datasets can have both negative and non-negative values.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Hi'ovská and P. Koncz, “Application of artificial intelligence and data mining techniques to financial markets,” Economic Studies & Analyses/Acta VSFS, vol. 6, no. 1, pp. 62–76, 2012. [Google Scholar]
2. S. I. T. Joseph and I. Thanakumar, “Survey of data mining algorithm’s for intelligent computing system,” Journal of Trends in Computer Science and Smart Technology (TCSST), vol. 1, no. 01, pp. 14–24, 2019. [Google Scholar]
3. L. Xu, C. Jiang, J. Wang, J. Yuan and Y. Ren, “Information security in big data: Privacy and data mining,” IEEE Access, vol. 2, pp. 1149–1176, 2014. [Google Scholar]
4. M. B. Malik, M. A. Ghazi and R. Ali, “Privacy preserving data mining techniques: Current scenario and future prospects,” in Proc. 2012 Third Int. Conf. on Computer and Communication Technology, Allahabad, pp. 26–32, 2012. [Google Scholar]
5. P. Wang, T. Chen and Z. Wang, “Research on privacy preserving data mining,” Journal of Information Hiding and Privacy Protection, vol. 1, no. 2, pp. 61–68, 2019. [Google Scholar]
6. N. Bhandari and P. Pahwa, “Comparative analysis of privacy-preserving data mining techniques,” in Proc. Int. Conf. on Innovative Computing and Communications, Delhi, pp. 535–541, 2018. [Google Scholar]
7. R. Ratra and P. Gulia, “Privacy preserving data mining: Techniques and algorithms,” SSRG International Journal of Engineering Trends and Technology, vol. 68, no. 11, pp. 56–62, 2020. [Google Scholar]
8. N. Bhandari and P. Pahwa, “Achieving data privacy using extended NMF,” (Accepted and presented in conference2021. [Google Scholar]
9. M. S. Chen, J. Han and P. S. Yu, “Data mining: An overview from a database perspective,” IEEE Transactions on Knowledge and Data Engineering, vol. 8, no. 6, pp. 866–883, 1996. [Google Scholar]
10. J. Han and M. Kamber, Data mining: Concepts and techniques, 2nd ed., New Delhi: Morgan Kaufmann Publishers, 2006. [Google Scholar]
11. F. Jiang, Y. Jiang, H. Zhi, Y. Dong, H. Li et al., “Artificial intelligence in healthcare: Past, present and future,” Stroke and Vascular Neurology, vol. 2, no. 4, pp. 230–243, 2017. [Google Scholar]
12. M. Nagalakshmi and K. S. Rani, “Privacy preserving clustering by hybrid data transformation approach,” International Journal of Emerging Technology and Advanced Engineering, pp. 696–700, vol. 3, no. 8, 2013. [Google Scholar]
13. T. Jahan, G. Narsimha and C. V. G. Rao, “A hybrid data perturbation approach to preserve privacy,” International Journal of Scientific and Engineering Research, vol. 6, no. 6, pp. 1528–1530, 2015. [Google Scholar]
14. B. Peng, X. Geng and J. Zhang, “Combined data distortion strategies for privacy-preserving data mining,” 2010 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE), vol. 1, pp. V1–572, 2010. [Google Scholar]
15. G. Li and R. Xue, “A new privacy-preserving data mining method using non-negative matrix factorization and singular value decomposition,” Wireless Personal Communications, vol. 102, no. 2, pp. 1799–1808, 2018. [Google Scholar]
16. L. Li and Q. Zhang, “A privacy preserving clustering technique using hybrid data transformation method,” in Proc. 2009 IEEE Int. Conf. on Grey Systems and Intelligent Services, Nanjing, pp. 1502–1506, 2009. [Google Scholar]
17. A. Fahad, N. Alshatri, Z. Tari, A. Alamri, I. Khalil et al., “A survey of clustering algorithms for big data: Taxonomy and empirical analysis,” IEEE Transactions on Emerging Topics in Computing, vol. 2, no. 3, pp. 267–279, 2014. [Google Scholar]
18. S. Ghosh and S. K. Dubey, “Comparative analysis of K-Means and Fuzzy C-Means algorithms,” International Journal of Advanced Computer Science and Applications, vol. 4, no. 4, pp. 35–39, 2013. [Google Scholar]
19. U. Maulik and S. Bandyopadhyay, “Performance evaluation of some clustering algorithms and validity indices,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, no. 12, pp. 1650–1654, 2002. [Google Scholar]
20. Y. Liu, Z. Li, H. Xiong, X. Gao and J. Wu, “Understanding of internal clustering validation measures,” in Proc. 2010 IEEE Int. Conf. on Data Mining, Sydney, pp. 911–916, 2010. [Google Scholar]
21. V. Kumar and N. Rathee, “Knowledge discovery from database using an integration of clustering and classification,” International Journal of Advanced Computer Sciences and Applications, vol. 2, no. 3, pp. 29–33, 2011. [Google Scholar]
22. S. K. Popat and M. Emmanuel, “Review and comparative study of clustering techniques,” International Journal of Computer Science and Information Technologies, vol. 5, no. 1, pp. 805–812, 2014. [Google Scholar]
23. S. Saket and S. Pandya, “An overview of partitioning algorithms in clustering techniques,” International Journal of Advanced Research in Computer Engineering & Technology, vol. 5, no. 6, pp. 1943–1946, 2016. [Google Scholar]
24. N. Bhandari and P. Pahwa, “Evaluating performance of agglomerative clustering for extended NMF,” Journal of Statistics and Management Systems, vol. 23, no. 7, pp. 1117–1128, 2020. [Google Scholar]
25. J. Wang, W. Zhong and J. Zhang, “NNMF-based factorization techniques for high-accuracy protection on non-negative valued datasets,” in Proc. Sixth IEEE Int. Conf. on Data Mining – Workshops, Hongkong, pp. 513–517, 2006. [Google Scholar]
26. M. Balajee and C. Narasimham, “Double-reflecting data perturbation method for information decurity,” Oriental Journal of Computer Science & Technology, vol. 5, no. 2, pp. 283–288, 2002. [Google Scholar]
27. R. Gaujoux and C. Seoighe, “A flexible R package for nonnegative matrix factorization,” BMC Bioinformatics, vol. 11, no. 367, pp. 111, 2010. http://www.biomedcentral.com/1471-2105/11/367. [Google Scholar]
28. Z. Cebeci, F. Yildiz, A. T. Kavlak, C. Cebeci, H. Onder et al., “ppclust: Probabilistic and possibilistic cluster analysis,” R Package Version 0.1.3, 2019. https://CRAN.R-project.org/package=ppclust. [Google Scholar]
29. M. Maechler, P. Rousseeuw, A. Struyf, M. Hubert, K. Hornik et al., “Cluster analysis basics and extensions,” R Package Version 2.1.0, 2019. [Google Scholar]
30. B. Desgraupes, “clusterCrit: Clustering indices,” R Package Version 1.2.8., 2018. https://CRAN.R-project.org/package=clusterCrit. [Google Scholar]
31. https://archive.ics.uci.edu/ml/index.php. [Google Scholar]
32. C. Yuan and H. Yang, “Research on K-value selection method of K-Means clustering algorithm,” J, vol. 2, no. 2, pp. 226–235, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |