DOI:10.32604/iasc.2023.027165

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2023.027165 |  |
| Article |
Main Melody Configuration and Chord Algorithm for Relaxing Music Generation
1Department of Health and Marketing, Kainan University, Taoyuan, Taiwan
2Master Program at School of Healthcare Management, Kainan University, Taoyuan, Taiwan
3Ph.D. Program of Mechanical and Aeronautical Engineering, Feng Chia University, Taichung, Taiwan
*Corresponding Author: Chih-Fang Huang. Email: jeffh.me83g@gmail.com
Received: 12 January 2022; Accepted: 06 March 2022
Abstract: This study applies the diatonic chord in music theory, utilization rate, and the close relationship between the main chord system, the dominant chord system, and the subordinate chord system. From the perspective of music theory, the computer can automatically and quickly analyze the music, and establish a set of algorithms for configuring the chord accompaniment for the main melody, called the symmetrical circle of fifths algorithm, SCFA (Symmetrical Circle of Fifths Algorithm). SCFA can immediately confirm the key, perform harmony analysis, configure chord accompaniment for the main melody, and effectively and correctly complete any given melody or interval. It can also quickly analyze and correctly configure the chord accompaniment for any MIDI (Musical Instrument Digital Interface) music, enriching the musicality of the music. It can also allow scorers or computer music creators to quickly deconstruct the harmony configuration of the melody. Through the measurement of bio-feedback sensor HRV (Heart Rate Variability), it can achieve a relaxing music healing effect.
Keywords: Symmetrical circle of fifths algorithm; SCFA; bio-feedback sensor; HRV; heart rate variability; relaxing music healing effect
Music can be quantized, in accordance with the MIDI (Musical Instrument Digital Interface) protocol, it becomes a newly created “medicine”, or so-called “Midicine”, for therapy [1]. With the continuous improvement of computer processing speed, the ability and application of artificial intelligence continue to improve, and the composition of music through computer calculations has become an important research direction of computer music. From Mozart’s dice music [2] to John. Cage’s Opportunity Music [3], and Lejaren Hiller’s ILLIAC (Illinois Automatic Computer) Suite [4,5] are examples of composing music using calculation rules. A complete piece of music can be divided into two parts: the main melody and the chord accompaniment. The chord accompaniment is to increases the integrity and richness of the music. Many composers matched the harmony accompaniment in sequence to create many amazing music pieces. It can be seen that the configuration of the composition harmony is so important. The harmony progression described by the chord sequence is closely related to the tonal structure of the music. There are many ways to construct and explore the characteristics of chords, such as the use of Fourier transform and Mel-Frequency Cepstral Coefficients, MFCCs [6,7], applied chord sequences are recognized by HMM (Hidden Markov Model) trained using audio symbol data [8], chord recognition algorithms [9–11], etc., applied to computer-automated composition. Even though modern music styles such as classical music, pop music, or heavy metal are far apart, the root of music is the same goal by different routes and has a certain musical context to follow. AI (Artificial Intelligence) automated composition has become a specialized subject, which can be divided into two categories. One is the establishment of a specific style of automated composition mode through computer deep learning [12–14]. This type of research requires analysis of a very large number of tracks and takes more time. In addition to knowing what parameters should be analyzed to establish the most effective rules, the programmer needs to analyze the analysis’s accuracy. The other is to automatically analyze music mathematically, and use various parameters in the music to perform statistical analysis to establish a mathematical model to create music. For example, the Spiral Array model proposed by Elaine illustrates the description of the relationship between tonal elements and proposed a new method of reorganizing music information [15,16]. Cope emphasized the importance of using mathematical formulas to deconstruct the music structure model and applying it to computer music creation [17,18]. The Probability Theory and Bayesian Reasoning proposed have been verified by practical research, and prove the advantages of this method in modeling music [19,20]. Many parameters in music can indeed be accurately quantified, but if only these parameters are used, the generated music will still lack organization. For example, music structure, tonality, harmony, etc. need to be included in the direction of analysis and consideration, and through algorithms analyze the results. This article uses the relationship between key and harmony to analyze the music structure and establishes a set of algorithms for configuring chord accompaniment, called the Symmetrical Circle of Fifths Algorithm (SCFA). SCFA can immediately confirm the key, perform harmony analysis, and configure chord accompaniment for the main melody. The music consists of a melody supported by harmony. The basic element of harmony is the chord which is a combination of notes used to support the concept of musical intelligence refers to our awareness of the forces present in the melodic, harmonic, and rhythmic impetus of music [21,22]. In recent years, there are more researches using Heart Rate Variability (HRV) bio-feedback data such as SDNN (Standard Deviation of Normal to Normal R Wave), LF (Low Frequency), and HF (High Frequency) to detect the autonomous nerve system condition as the music therapy effects [23,24].
The design and methodology of the proposed system include pitch class, interval, chord labeling, modal and tonal chord progression, harmony function, and circle of fifths, as the following descriptions.
In the definition of computer music MIDI, an octave has 12 notes [25]. In music theory analysis, although the pitches of the octave are different, from the perspective of acoustics, the frequency difference is double. From the scientific perspective of the theory of harmony music theory, the role of the octave is all it’s the same. In this study, the octave differences are classified into the same category for analysis, using the characteristics of MIDI encoding, the following formula is used to calculate the pitch class [26] to which each tone belongs, as shown in Eq. (1):
where x is the MIDI encoding, and mod represents the modular operation.
Interval is used in music theory to describe the distance of 2 notes. The concept of pitch class can correspond to the concept of interval. Interval is the distance between two notes (x, y), we can use the following formula to calculate the interval between two notes, as shown in Eq. (2):
The chord consists of at least 2 notes. To determine the function of harmony in tonic music, the chord is defined as “stacking at least 2 thirds with the root” and named “Triad” and “7th chord” according to the number of stacks. 7th chord, 9th chord, 11th chord, and 13th chord [27]. For example, the C major chord is C-E-G, and the G major 9th chord is G-B-D-F#-A. The most commonly used types are “Triad” and “7th chord” in practice. Use major thirds and minor thirds to make triads and 7th chords. There are 4 kinds of the former and 8 kinds of the latter. The 7th chord that repeats with the triad is subtracted. The commonly used are Major Triad chord, minor Triad chord, Augmented triad chord, diminished Triad chord, diminished Triad chord, dominant 7th chord, Major 7th chord, minor 7th chord, half-diminished 7th chord, and diminished 7th chord. For example, Tab. 1 is a comparison table of the constituent notes of various common chords.

2.4 Harmony Function and Circle of Fifths
The functions of chords can be divided into three categories [28]: the “Tonic Chord” (code: T, degree: I) based on the tonic; the “Dominant Chord” (code: D, degree: V) on the dominant note; and the “Subdominant Chord” (code: S, degree: IV or iv). T is the harmony on which a key is based. When matching chord, T is the center; D tends to connect to T because the chords tend to connect to T; S is most often used as a transition between T-S. Harmony progressions often used in traditional harmony are D-T, S-D-T, T-D-T. Chords built on other notes will also have one of the functions of S-D-T, which is an alternative option. The harmony progression that occurs at the end of the phrase is “cadence”. Fig. 1 shows the schematic diagram of the association between the tonic chord, the dominant chord, and the subordinate chords. The arrows indicate the mode and direction of the main chord, the dominant chord, and the subdominant chords. In music theory, it is rare for the dominant to progress to the subdominant with the way of chord progression.
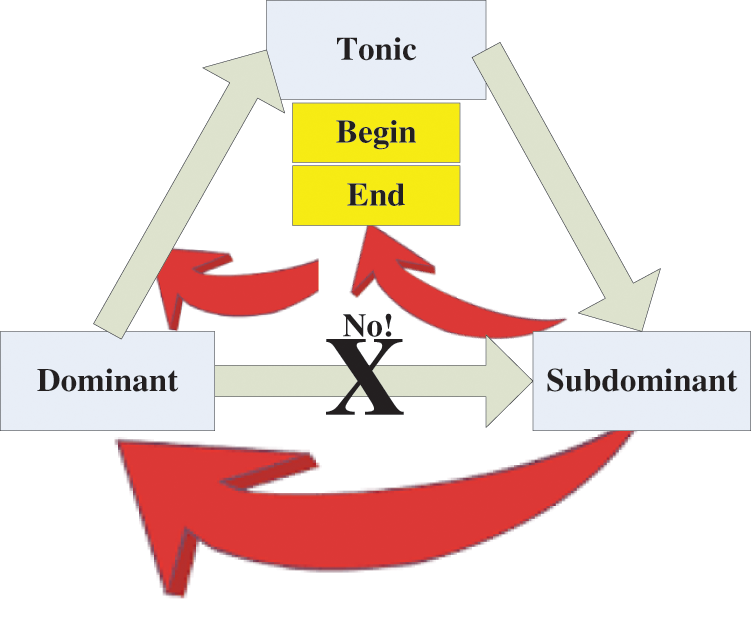
Figure 1: The schematic diagram of the association between the tonic chord, the dominant chord, and the subdominant chords
As shown in Fig. 2, the circle of fifths can be used to explain many principles related to music theory, and many principles can be summarized by the circle of fifths. In tonic music, from a single key point of view, the “dominant” and “subdominant” are separated from the tonic by a complete fifth and a complete fourth is the most important. The natural triads above these two notes are a strong relationship: in traditional harmony, the common connection method of functional harmony is S-D-T (Subdominant-Dominant-Tonic); the three tones of three adjacent tones in the fifth circle and their relationship are collectively called “near key”, on the contrary, is “remote key.” The relationship of the near key is closer than that of the remote key. The SCFA proposed in this research is to use the characteristics of Circle of Fifths to write calculation programs.
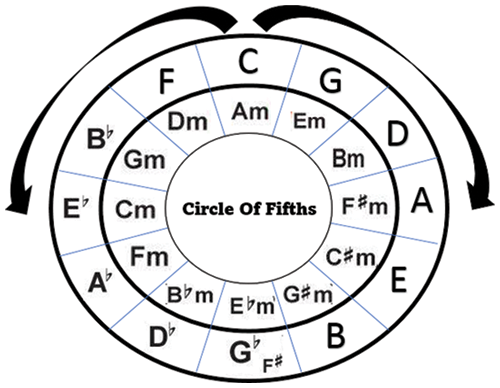
Figure 2: Circle of fifths
From the literature [28], based on the study of common chord progressions on the Chinese pop music charts from 2005 to 2014, we compiled the statistical data of music chord progressions, shown in Tab. 2. From the analysis of the literature statistics, the music completely follows the S-D-T (Subdominant-Dominant-Tonic) function with the connection method.

3 Algorithm and Programming Implementation
The algorithm used in this article is the aforementioned SCFA, and the relevant implementation steps are described in the following sections.
The complete structure of the SCFA programming process in this study is shown in Fig. 3. The first stage of program execution is to obtain the data parameters in the MIDI file to calculate and determine the key of the melody. In the second stage, the melody is divided into fixed lengths into units of bars, and the notes of each bar are compressed into an octave. The algorithm calculates the maximum matching score of the chord pattern of each bar to generate a chord sequence, and finally, another track is incorporated into the original MIDI file to configure harmony accompaniment and output a new file.
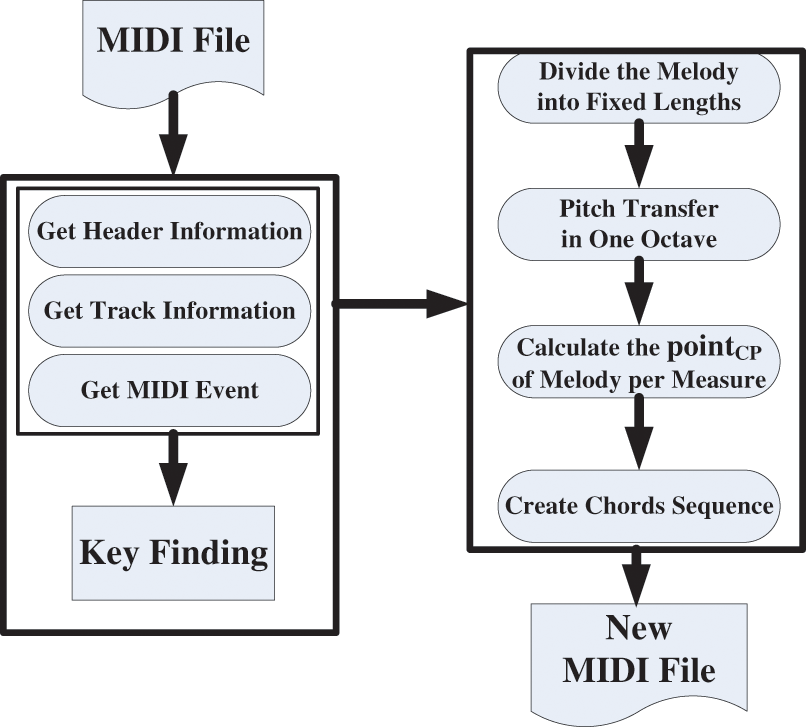
Figure 3: SCFA algorithm process flowchart
The chord pattern is a Boolean array with a length of 12, and its index value is taken as the remainder of the pitch code in the midi file divided by 12, which is compressed into an octave. If the item is True, it means that the chord has this tone, if False, it is a harmonic overtone. For example, the chord pattern of the C major triad is [T, F, F, F, T, F, F, T, F, F, F, F]. The chord pattern will be moved to produce a chord pattern with different root notes and the same shape, as shown in Tab. 3.

3.3 The Melody and Chord’s Coincidence Score Formula
If the melody has n notes, the calculation formula for the coincidence score of the melody is as shown in Eq. (3):
Among them, pitchi is the modulus of notei midi code divided by 12. The lengthi is used to identify how much 1/4 the pitch is. CP is a certain chord pattern, such as C major triad pattern, and pointCP is the coincidence score under CP.
For example, if there is a melody, and the note name and duration are shown in Tab. 4.

Tab. 5 can be obtained by calculating Eq. (3):

After calculation, the coincidence score of the melody is 2. The one with the highest coincidence score is used when deciding the chord. So the above melody CP is C major triad.
3.4 The Transposition Formula of the Chord Pattern
Since there is more than one chord to be judged, use the transposition chord pattern to form other chord patterns with the same structure of different tonics. In the beginning, you can judge directly from the root note of the main key, which makes it easier to quickly find a suitable chord. If there is a harmony pattern CP, if you want to move it up n semitones, the expression is as shown in Eq. (4):
where n mod 12 takes the positive modulus.
Suppose you want to transpose a C major triad to a G major triad, you have to transpose a perfect fifth interval, which is equivalent to transposing 7 semitones. Tab. 6 shows the system transposes CMaj to GMaj.

3.5 The Chord Pattern Transposition
In the method of transposing all the tonic notes in 12 keys, the amount of transposition n must be coprime with 12, that is, the goal can be achieved when n = 1, 5, 7, and 11. The corresponding musical meanings are “transposing up a semitone” and “ “transpose up four degrees” (or 5 degrees down), “5 degrees down”, “transposing down semitones”, in a one-way judgment, as long as the amount of transposition is fixed and repeated 12 times, all the harmony can be transposed. Generally speaking, the result of transposing up and down five degrees is more ideal than the result of transposing up and down semitones.
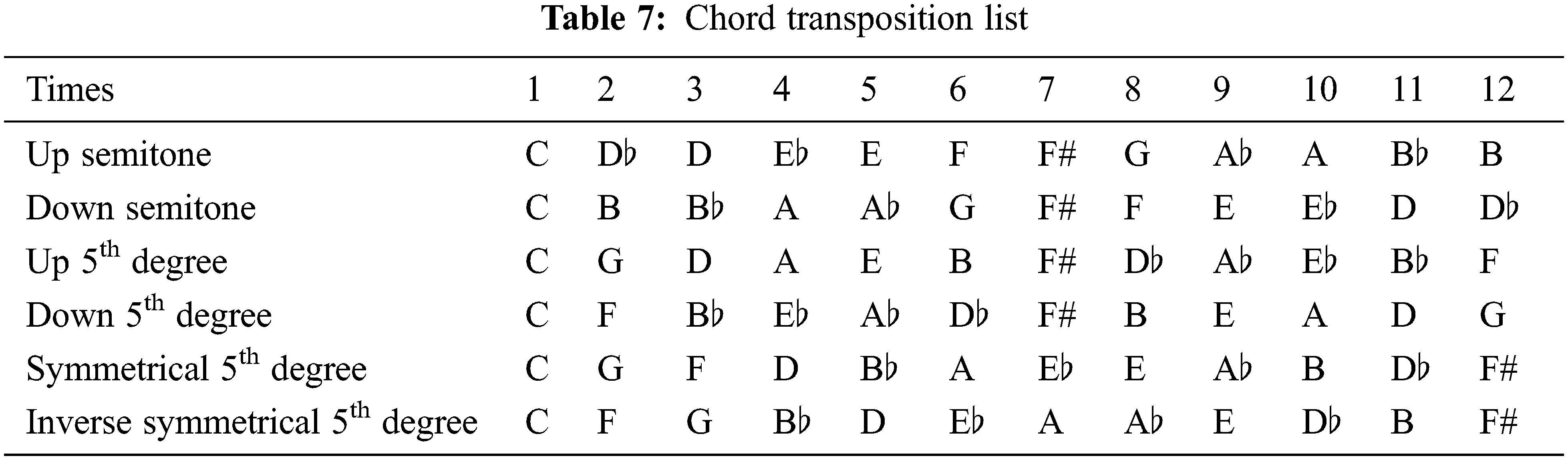
However, if you want to simulate the S-D-T (Subdominant-Dominant-Tonic) process more accurately and fully, the SCFA algorithm bidirectional transposition method will be more accurate. In this method, there will be two sets of transposition methods, which are five degrees downward and five degrees upward, respectively. The beginning is the dominant note and the dominant note. The former transposes down five degrees after each end, and the latter transposes five upwards degrees the loop is executed 6 times. The “anti-symmetrical up and down five-degree cycle method” is the opposite direction. Various chord transposition methods are shown in Tab. 7.
3.6 The Experimental Procedure and Results
In the case study, the more the number of bar notes in the divided block and the more pitch changes (Example 1 and Example 2), the fewer the number of bar notes in the divided block and the less the pitch change (Example 3), to conduct research and verification. After the program reads various MIDI parameters, it first confirms the key, and then converts and compresses the notes in the bar interval into an octave for calculation with modulus 12. Finally, C# minor is calculated using the coincidence score formula of the chord in Section 3.3. The coincidence score: 2.5 is the highest, so the chord configuration in this section is c# minor. Fig. 4 shows the procedure from original melody to chord determination.

Figure 4: From original melody to chord determination
Therefore, in the chord configuration process of the entire music piece, you will find that the chord progression shown in Fig. 5 is the chord difference between the chord progression configured by the original composer Chopin and the other calculated options.

Figure 5: The Chord difference between the chord progression configured by the original composer Chopin and the other calculated options
The 2nd case study experiment is carried out with a piece of music with smaller bars divided into blocks and a smaller pitch change, as shown in Fig. 6. the Chord difference between the chord progression configured by the original composer Mozart’s “little star variation” main them and other calculated options.

Figure 6: The chord difference between the chord progression configured by the original composer Mozart’s “little star variation” main them and other calculated options
Looking at the above study cases, the more the number of bar notes in the divided block and the more pitch changes, the more accurately the matching chord can be calculated. Relative to the divided block, the smaller the number of notes and the smaller the pitch change, the only SCFA can make the correct chord sequence. In addition, C. F. Huang and P. Winsor have jointly developed an AI (Artificial Intelligence) music program for Country West music, based on the west country music MIDI dataset to initialize chord table, generate harmonic system based on Markov Model, generate melody based on Markov model, and generate melody based on Markov model with music theory. The generated Country West music chord progressions are similar to Tab. 2 common chord progressions in popular music charts from 2005 to 2014, which would be lyric and relaxing music with chord progressions and melody. The flow chart for the country west music generation with the AI Markov model is shown in Fig. 7.

Figure 7: Flow chart for the country west music generation with AI Markov model
4 Generated Music Relaxing Effect Result
According to the above-generated Country West music, two subjects are using the Autonomic Nerves System (ANS) bio-feedback sensor Heart Rate Variability (HRV) [22,23], to listen to 5-min. generated music. The gender of the two subjects is both females, and they are both in the range of 40 to 50 years old. The time of not listening to music is a 5-minute pre-test, and the time for listening to music is also a 5-minute post-test. The HRV test instrument for the generated music used in this article is Eureka from Finesse Lifecare Co., Ltd., Taiwan [29]. The operating scene of the experimental HRV instrument for listening to the generated music is shown in Fig. 8. The generated music relaxing effect result is as shown in Tab. 8.

Figure 8: The operating scene of the experimental HRV instrument for listening to the generated music
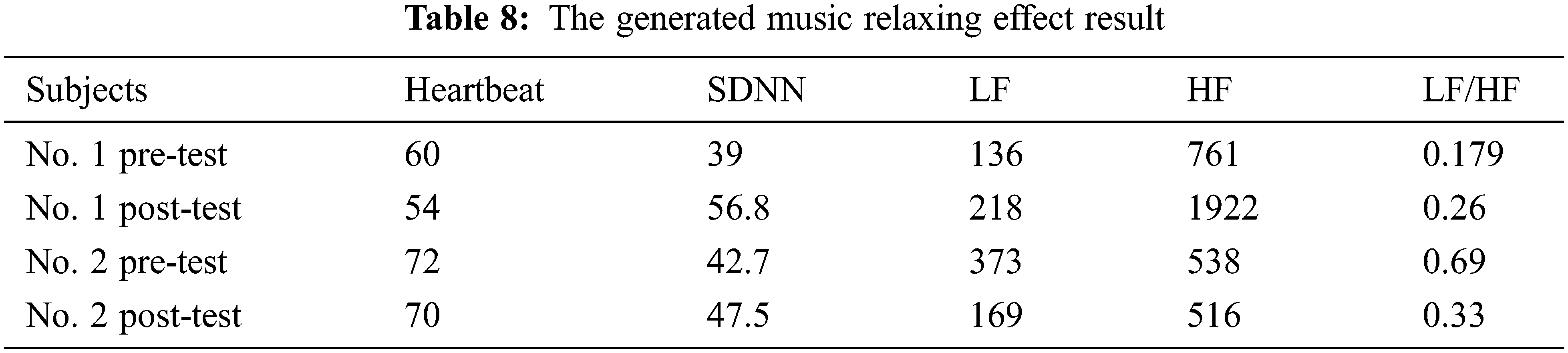
The test results showed that the first subject’s HF after listening to AI relaxing music, that is, the parasympathetic nerve activity was greatly increased, and the overall autonomic nervous system activity also increased; the second subject’s parasympathetic nerve activity decreased slightly, but the heartbeat slowing down, the overall autonomic nervous system activity also increases, and the LF sympathetic nerve activity also drops to a certain degree, so the two subjects both have the effect of relaxing and regulating after listening to the proposed AI relaxing music.
Based on the natural chord usage rate of the tonal scale in music theory, as well as the close relationship between the main chord system, the dominant chord system (V, V7), and the subordinate chord system (IV, iv), the SCFA and Markov model is proposed in this article. Through the verification of the examples in this article, the following conclusions are obtained:
(1) The symmetrical fifth-degree loop algorithm can accurately and quickly filter the note structure of the main chord and immediately generate a more suitable chord accompaniment harmony.
(2) The symmetrical fifth-degree loop algorithm can explore the key of the main melody in advance, immediately analyses the tonal scale, and establish the chord configuration. Therefore, under the same coincidence score, the first chord to be adopted is based on the tonal scale, the higher the probability, the more accurate.
(3) Through the verification of the examples in this article, in terms of the accuracy of chord configuration, the symmetrical fifth-degree loop is the best, the fifth-degree series is the second, and the semitone series is the worst.
(4) The symmetrical up and down five-degree loop algorithm can find the chord with S-D-T function early, so it can produce a chord progression configuration close to S-D-T.
(5) This research of symmetrical five-degree loop algorithm can match any string rhythm with appropriate and correct string rhythm.
(6) Finally, coupled with the West Country music automatically generated by the Markov model, after HRV autonomic nerve measurement, it can indeed achieve a relaxing effect, which can be used for continuous research on music therapy in the future.
The SCFA and Markov model calculation method has been verified through experiments, and it can be added to the composition of AI computer deep learning in the future, as a basis for judging melody and harmony or as a reference for the combination of multi-track harmony soundtrack for the relaxing music generation, eventually. The proposed work can be tested by the code in the link: https://github.com/huangedgar168/Innovative-Design-of-Main-Melody-Configuration-and-Chord-Algorithm-Design.git.
The assumptions studied in this paper can be highlighted to include music theory in tonal or modal music, which can be automatically composed by AI algorithms to generate the required relaxation music. After the test of the HRV heart rate variability measurement from the autonomic nervous system, its bio-feedback data parameters can be carried out in the direction of healthy relaxation, and it has preliminary functions. In the scope limited by this article, the AI automated composition technology is limited to the music theory of harmony so far. In the future, it can be expanded to various music elements such as pitch, rhythm, and timbre for development, making music therapy and health functions more diverse and rich, to achieve a comprehensive and healthy music performance. Therefore, the proposed research will be expanded to both music elements generation to fit the health direction and more detailed research of the relationships between the autonomic nervous system and music elements, and the AI models can be applied to achieve the goal of music therapy in the future. Compared with the previous recent literature, although the protocol using MIDI music elements as proposed in [1] can be regarded as the concept of Midicine, the method proposed in this article includes the use of HRV bio-feedback sensor, which can be measured objectively to prove the relaxing effect. This article takes the effect of relaxing music automatically generated by AI as proof and takes a step for the future field of intelligent music therapy. On the other hand, the algorithm of applying tonal and modal music theory proposed can greatly reduce the large amount of computing time required by traditional AI theories as described in [12,13], which will be more useful for the field of intelligent music therapy in the future, and using the innovative models for efficient integration.
Acknowledgement: The authors are appreciative of the support from the Ministry of Science and Technology project of Taiwan.
Funding Statement: The Ministry of Science and Technology project of Taiwan: MOST 108-2511-H-424-001-MY3.
Conflicts of Interest: Authors declare that there’s no conflicts of interest to report regarding the present study.
1. K. János, “Midicine: Using MIDI (Musical instrument digital interface) in medicine for treating patients who experienced a stroke-review article,” Mentálhigiéné és Pszichoszomatika, vol. 18, no. 4, pp. 365–379, 2017. [Google Scholar]
2. G. Albini, “Combinatorics, probability, and choice in music composition: Towards an aesthetics of composing systems for non-musicians,” in Bridges 2018 Conf. Proc., Mathematics, Art, Music, Architecture, Education, Culture, Tessellations Publishing, pp. 395–398, 2018. [Google Scholar]
3. R. Kruse, “John cage and nonrepresentational spaces of music,” Social & Cultural Geography, vol. 22, no. 6, pp. 767–782, 2021. [Google Scholar]
4. T. Funk, “A musical suite composed by an electronic brain: Reexamining the illiac suite and the legacy of lejaren A. hiller Jr.,” Leonardo Music Journal, vol. 28, pp. 19–24, 2018. [Google Scholar]
5. O. M. Bălan, “Refractions of contemporary music via digital technology,” Tehnologii Informatice şi de Comunicaţii în Domeniul Muzical, vol. 1, no. 1, pp. 60–66, 2010. [Google Scholar]
6. A. M. Warohma, P. Kurniasari, S. Dwijayanti and B. Y. Suprapto, “Identification of regional dialects using Mel frequency cepstral coefficients (MFCCs) and neural network,” in 2018 Int. Seminar on Application for Technology of Information and Communication, Semarang, Indonesia, IEEE, pp. 522–527, 2018. [Google Scholar]
7. A. Benba, A. Jilbab and A. Hammouch, “Detecting patients with Parkinson’s disease using Mel frequency cepstral coefficients and support vector machines,” International Journal on Electrical Engineering and Informatics, vol. 7, no. 2, pp. 297, 2015. [Google Scholar]
8. H. Narimatsu and H. Kasai, “Duration and interval hidden markov model for sequential data analysis,” in 2015 Int. Joint Conf. on Neural Networks (IJCNN), Killarney, Ireland, IEEE, pp. 1–8, 2015. [Google Scholar]
9. S. Sigtia, N. Boulanger-Lewandowski and S. Dixon, “Audio chord recognition with a hybrid recurrent neural network,” ISMIR, Malaga, Spain, pp. 127–133, 2015. [Google Scholar]
10. D. P. Radicioni and R. Esposito, “BREVE: An HMPerceptron-based Chord Recognition System,” in Advances in Music Information Retrieval, Berlin, Heidelberg: Springer, pp. 143–164, 2010. [Google Scholar]
11. D. Jha, L. Ward, A. Paul, W. K. Liao, A. Choudhary et al. “Elemnet: Deep learning the chemistry of materials from only elemental composition,” Scientific Reports, vol. 8, no. 1, pp. 1–13, 2018. [Google Scholar]
12. C. Hernandez-Olivan and J. R. Beltran, “Music composition with deep learning: A review,” arXiv preprint arXiv:2108.12290, 2021. [Google Scholar]
13. B. L. Sturm, O. Ben-Tal, Ú. Monaghan, N. Collins, D. Herremans et al. “Machine learning research that matters for music creation: A case study,” Journal of New Music Research, vol. 48, no. 1, pp. 36–55, 2019. [Google Scholar]
14. D. Herremans and E. Chew, “Towards emotion based music generation: A tonal tension model based on the spiral array,” CogSci, pp. 52–53, 2019. [Google Scholar]
15. E. Chew, “The Spiral Array,” in Mathematical and Computational Modeling of Tonality, Boston, MA: Springer, pp. 41–60, 2014. [Google Scholar]
16. D. Cope, “The well-programmed clavier: Style in computer music composition. XRDS: Crossroads,” The ACM Magazine for Students, vol. 19, no. 4, pp. 16–20, 2013. [Google Scholar]
17. D. Cope, “Music, Artificial Intelligence and Neuroscience,” in Handbook of Artificial Intelligence for Music, Cham: Springer, pp. 163–194, 2021. [Google Scholar]
18. K. C. Lee, S. Phon-Amnuaisuk and C. Y. Ting, “A comparison of HMM, naïve Bayesian, and markov model in exploiting knowledge content in digital Ink: A case study on handwritten music notation recognition,” in 2010 IEEE Int. Conf. on Multimedia and Expo, Singapore, IEEE, pp. 292–297, 2010. [Google Scholar]
19. G. J. Dimitrakopoulos and I. E. Panagiotopoulos, “In-vehicle infotainment systems: Using Bayesian networks to model cognitive selection of music genres,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 11, pp. 6900–6909, 2020. [Google Scholar]
20. A. F. Moore and R. Martin, “Rock: The primary text: Developing a musicology of rock,” Routledge, pp. 1–348, 2018. [Google Scholar]
21. R. E. Radocy and J. D. Boyle, “Psychological foundations of musical behavior,” Charles C Thomas Publisher, vol. 31, no. 1, pp. 85–86, 2012. [Google Scholar]
22. A. L. Roque, V. E. Valenti, H. L. Guida, M. F. Campos, A. Knap et al. “The effects of auditory stimulation with music on heart rate variability in healthy women,” Clinics, vol. 68, pp. 960–967, 2013. [Google Scholar]
23. H. Mojtabavi, A. Saghazadeh, V. E. Valenti and N. Rezaei, “Can music influence cardiac autonomic system? A systematic review and narrative synthesis to evaluate its impact on heart rate variability,” Complementary Therapies in Clinical Practice, vol. 39, no. 101162, 2020. [Google Scholar]
24. R. A. Dobre and C. Negrescu, “Automatic music transcription software based on constant Q transform,” in 2016 8th Int. Conf. on Electronics, Computers and Artificial Intelligence (ECAI), IEEE, pp. 1–4, 2016. [Google Scholar]
25. D. Tymoczko and J. Yust, “Fourier phase and pitch-class Sum,” in Int. Conf. on Mathematics and Computation in Music, Springer, Cham, pp. 46–58, 2016. [Google Scholar]
26. N. L. Lam, “Modal spelled pitch class, La-minor solfège, and schubert’s third relations,” Journal of Music Theory, vol. 64, no. 2, pp. 241–281, 2020. [Google Scholar]
27. G. W. Mark and S. Mark, “A robust parser-interpreter for jazz chord sequences,” Journal of New Music Research, vol. 43, no. 4, pp. 355–374, 2014. [Google Scholar]
28. Y. H. Fan, “Investigating Combination Model of Chords of Chinese Pop Music-Example by Hit FM BillBroad,” Master Thesis of Business Administration Department of Information Management, Tatung University, Taiwan, 2017. [Google Scholar]
29. W. C. Li, “The Therapeutic Effects of AI Music Verified by HRV Measurements,” Master thesis of Master Program at School of Healthcare Management, Kainan University, Taiwan, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |