DOI:10.32604/iasc.2022.026377

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.026377 |  |
| Article |
Deep Learning Based Distributed Intrusion Detection in Secure Cyber Physical Systems
1Department of Electronics and Communication Engineering, University College of Engineering, BIT Campus, Anna University, Tiruchirapalli, 620025, India
2Department of Electronics and Instrumentation Engineering, Kongu Engineering College, Erode, 638060, India
3Department of Electronics and Communication Engineering, Gokaraju Rangaraju Institute of Engineering and Technology, Hyderabad, 500090, India
4Department of Biomedical Engineering, Faculty of Engineering, Karpagam Academy of Higher Education, Coimbatore, 641021, India
*Corresponding Author: P. Ramadevi. Email: ramadevi.mohan@gmail.com
Received: 23 December 2021; Accepted: 16 February 2022
Abstract: Cyber Physical Systems (CPSs) are network systems containing cyber (computation, communication) and physical (sensors, actuators) components that interact with each other through feedback loop with the help of human intervention. The dynamic and disseminated characteristics of CPS environment makes it vulnerable to threats that exist in virtualization process. Due to this, several security issues are presented in CPS. In order to address the challenges, there is a need exists to extend the conventional security solutions such as Intrusion Detection Systems (IDS) to handle high speed network data traffic and adaptive network pattern in cloud. Additionally, the identification of feasible network traffic characteristics is the main issue in precise detection of attacks in the network. With this motivation, the current research paper presents an Optimal Deep Belief Network-based distributed Intrusion Detection System (ODBN-IDS) for secure CPS environment. The proposed model pre-process the cloud network traffic data to improve its quality to next level. Here, a Binary Flower Pollination Algorithm (BFPA) is employed for feature selection process. The attained characteristics are used in optimal Deep Belief Networks (DBN) to detect the presence of intrusion in cloud data and produce alarms, in case of presence of intrusions. Equilibrium Optimizer Algorithm (EOA) is used to fine tune the hyperparameters in DBN model. A detailed set of simulations was conducted on benchmark datasets and the analysis results were compared. A detailed comparison was conducted for various models to satisfy the security requirements of cloud network and the results established the supremacy of the proposed ODBN-IDS model.
Keywords: Security; intrusion detection; cyber physical systems; deep learning; feature selection; parameter tuning
Cyber-Physical Systems (CPSs) integrates the computation process and physical processes. Embedded computers and networks can observe and handle the physical processes with feedback loops, where physical processes influence the computation process and vice versa [1]. It enables the functioning of numerous independent virtual networks through a common framework. Among the cloud components such as internal, external, and virtual networks, the internal network enables the communication among distinct cloud mechanisms like network servers, management systems, storage systems, etc. External network is a main interface between back end (cloud service provider) and front end (cloud user) [2]. Virtual network enables the communication between Virtual Machine (VM) and similar physical server. Virtual network provides an effective cloud service to the user. But, the vulnerabilities in current network technology followed by dynamic and distributed nature of cloud invite a number of privacy problems. Especially, the distribution of network structure increases the vulnerability in Address Resolution Protocol (ARP), Dynamic Host Configuration Protocol (DHCP), Internet Protocol (IP), Domain Name System (DNS) servers, and so on. In addition to these, virtual network has other vulnerabilities too such as poor network isolation between Virtual Machines (VMs), poor design, vSwitch software bugs, bugs in network protocols, open ports, and insecure network channels [3,4]. When these vulnerable areas are exploited in an effective manner, it results in different types of attacks such as port scanning, network probing, Denial of Service (DoS) attack, spoofing, sniffing, etc. Intrusion might be any sort of malicious activity that tries to influence the availability, integrity, and confidentiality of computing services and resources. Intrusion Detection System (IDS) monitors network system activities or traffic to detect malicious activities. Network IDS (NIDS), present in cloud, monitors the network traffic to identify malicious activities that hijack the privacy of cloud resources [5]. There have been various studies conducted till now to find the intrusion in cloud network intrusion. Fig. 1 depicts the infrastructure of IDS technique.

Figure 1: Structure of IDS
Indeed, it is important for all the IDSs to use an appropriate feedback method and take an ultimate decision regarding the suspected intrusions afterward obtaining feedback from the consulted IDSs about the suspected intrusions. This sort of aggregation method is generally expensive in terms of computational time and other factors like IDS expertise and trust levels, number of consulted IDS, etc. [6]. Furthermore, there is no guarantee for simultaneous receipt of the feedbacks due to uneven IDS connection, internet speed and other factors (like compromised IDSs, busy IDSs, etc.) [7]. In the event of missing feedbacks from individual IDS, the decision to, either or not, increase an alarm about the suspected intrusion can be delayed for a long time. Thus, the decision taken by collective IDS is ineffectual in real-time settings, which makes it unsustainable [8–10].
In this background, the current study presents an Optimal Deep Belief Network-based distributed Intrusion Detection System (ODBN-IDS) for secure CPS environment. The proposed model pre-process the cloud network traffic data to enhance the quality of data to next level. Here, Binary Flower Pollination algorithm (BFPA) is used for feature selection process. The characteristics attained are employed in optimal Deep Belief Network (DBN) to detect the presence of intrusion in cloud data and produce alarm in case of presence of intrusions. Equilibrium Optimizer Algorithm (EOA) performs the hyperparameter tuning of DBN model. In order to compare and contrast the results of the proposed methods against existing models, a detailed set of simulations was conducted on benchmark datasets.
Rest of the paper is planned as follows. Section 2 discusses about the works related to this domain, Section 3 details about the proposed model, Section 4 gives the results of the analysis, and Section 5 draws conclusion for the study.
Abusitta et al. [11] presented a Machine Learning (ML)-based collective IDS that effectually leverages historic feedbacks to make proactive decisions. Especially, the presented method depends on Denoising Autoencoder (DA) which is utilized as an element to create Deep Neural Network (DNN). The strength of DA lies in its capability on how to recreate the IDSs’ feedback from partial feedbacks. It enables the users to take proactive decisions about the suspected intrusion, even in the absence of comprehensive feedbacks from IDSs. DNN architecture has two main types such as Recurrent Neural Network (RNN) and Convolutional Neural Network (CNN). Both are commonly used in improving the efficiency of IDS. In the study conducted earlier [12], systematic comparisons were made between RNN and CNN on DL-based IDS with an aim to provide elementary guidance for the selection of DNN. Hajimirzaei et al. [13] presented novel IDS-based Artificial Bee Colony (ABC), Multilayer Perceptron (MLP), and fuzzy clustering methods. Normal and abnormal network traffic packets are recognized by MLP, although MLP is trained using ABC method by enhancing the value of connection biases and weights.
Alghamdi et al. [14] developed an edge-cloud deep IDS method in Lambda framework to resolve the security issues found in IoT. This method reduces the time taken for training phase than conventional ML techniques and increases the precision of true positive-detected attacks. Moreover, Neural Network (NN) layer leads the DL method to attain effective flexibility and performance than traditional ML algorithm. Krishnaveni et al. [15] proposed an effective IDS for cloud using ensemble feature classification and selection methods. The presented technique depends on univariate ensemble Feature Selection (FS) method and is utilized for reduced feature set selection from the provided data sets. The ensemble classifier could effectively combine the individual classifier to yield strong classifiers using the voting method. An ensemble-based technique efficiently categorizes the network traffic behaviour as either normal or an attacked one.
In this study, a new ODBN-IDS technique is developed for detection and classification of intrusions under CPS environment. The proposed model performs the pre-processing of cloud network traffic data to improve its quality to a next level. Secondly, BFPA is applied to choose the optimal feature subsets from cloud data. Thirdly, DBN model is utilized to detect and categorize the intrusions that exist in the network. Finally, EOA is utilized to tune the parameters involved in DBN model. Fig. 2 illustrates the overall processes involved in ODBN-IDS technique.

Figure 2: Overall process of ODBN-IDS technique
At first, the cloud traffic data is preprocessed and the input values are normalized. To accomplish this, min-max normalization technique is followed. Besides, the training process of NN can be enhanced by preprocessing the network input data and target data. This is then used for rescaling the output or features from one range of values into another range. Besides, the features are scaled as either [0, 1] or [−1, 1] and is defined as follows.
where (ymax − ymin) = 0; when (xmax − xmin) = 0.
3.2 Design of BFPA-Based Feature Selection Technique
Once the input data completes pre-processing stage, BFPA technique is utilized to derive an optimal subset of features.
In 2012, Yang presented a natural simulation technique named FPA [16] which is simulated alike the pollination procedure of flowering plants. This technique has an important point to consider i.e., being an optimization technique, it helps in reproduction of the plant through optimum procedures. FPA has four fundamental principles (Yang, 2012) to follow as given herewith.
1) Biotic and cross-pollination are regarded as global pollination procedures with pollen-carrying pollinators implementing Lévy Flight (LF) method.
2) Abiotic and self-pollination are regarded as local pollination procedures.
3) Flower stability is regarded as reproduction probabilities that are proportional to similarity of the two flowers contained.
4) Local as well as global pollinations are led by switching the probabilities, p ∈ [0, 1]. According to physical proximity and other factors like wind, local pollination has an important fraction i.e., p from the entire pollination activity.
During global pollination step (Rules, 1 and 3), the flower pollens are implemented by pollinators like insects. The pollens travel a long distance in line with LF distributions. Global pollination is generally written as follows.
where,
where
Local pollination (Rule 2) is signified as follows
where
Therefore, Eqs. (1) and (3) are exchanged by the subsequent formula.
where
3.3 Design of ODBN Model for Intrusion Detection and Classification
In this final stage, ODBN model is utilized for detection and categorization of intrusions in the network. DBN is a vital model in DL [18]. It is a probabilistic generative method which is a series of Restricted Boltzmann Machine (RBM) units. There is no linkage present amongst the neural units with other layers of RBM method. Further, all neural units from the visible layer are linked with all other neural units from the hidden layer. In addition, the resultant of every RBM layer is utilized as an input for next layer. The bottom layer of DBN method implements a multi-layer RBM framework. The greedy technique is utilized to train the instance data in a layer-by-layer fashion. The parameters, achieved by training the primary layer RBM, are utilized as input for secondary layer RBM. The parameters of all layers are attained by analogy. The trained procedure appears to be unsupervised learning. The combined configuration energy of visible as well as hidden layers from RBM is represented herewith.
where θ = {wij, ai, bj} and it denotes the linking weight value between visible i as well as hidden unit j, ai refers to internal bias of visible layer neurons, and bj represents the hidden layer. Once the parameter θ is set dependent upon energy functions, the combined probability distribution of visible as well as hidden layers are attained in Eq. (8) which are related with Eq. (9) as follows
Once the state of visible layer ν is recognized, the activation probabilities of jth neural units of hidden layer h are attained.
If hidden layer h is recognized, then the activation probabilities of ith neural units of visible layer ν are reached.
where
In unsupervised learning procedure, the solution obtained from the trained RBM is to be used for model parameter that is provided as log-likelihood function given herewith.
During training procedure, sampling techniques are usually utilized for estimation due to difficult computation of normalized factor
EOA technique was initially presented by Faramarzi et al. [19]. It is simulated as a control volume mass balance method that is executed according to the evolution of dynamic as well as equilibrium states. In EOA, all the individuals (solution) with their concentration C (position) are considered as search agents. During EOA, all the individuals in a population are same as the solution whereas an individual concentration is the same as a particle place from Particle Swarm Optimization (PSO) technique. In EOA, the place is upgraded as follows.
where V is determined as the unit, Ce represents the equilibrium candidate and F and G stands for exponential term as well as generation rate correspondingly. λ = (λ1, λ2, …, λn)T implies the arbitrary vector between 0 and 1 and n represents the amount of dimensions of individual attentiveness, C.
The equilibrium condition represents the last convergence state of EOA. The equilibrium pool has five individuals [20].
But, for multi-objective optimization problem, there is generally a group of alternative trade-offs amongst this objective. The external repository solution is considered as an equilibrium candidate. The equilibrium pool from DMOEOA is demonstrated herewith.
where Rep implies the external repository and Rep stands for retaining the historical data of non-dominated solutions initiated together with entire search procedure. All the individuals during complete iterations upgrade their concentration, C (place) with roulette wheel selective amongst equilibrium candidate Ce. Further, there is an equilibrium candidate with similar value from the equilibrium pool which is less possibly chosen for guiding the particle from the population. The above selective technique is capable of maintaining the diversity of attained solutions from search procedure. The concentration upgrading rule is mostly controlled by the exponential term, F.
where t refers to the function of iteration, t reduces with number of iterations and iter and IT imply the existing and maximal iterations correspondingly. a2 stands for constant value that controls the exploitation capability of EOA. To obtain maximum convergence by slowing down the search speed, t0 is determined as follows.
where a1 represents the constant value which affects the exploration capability, sign (r0 − 0.5) is executed to control exploration as well as exploitation phases, r0 stands for arbitrary number between zero and one. In this case, the values of a1 and a2 are fixed as 2 and 1 correspondingly. The selection of two values are consistent with novel EOA technique. So, the exponential term F is expressed as follows
Generation rate roles plays a vital role in equilibrium technique. It can be utilized in enhancing the exploitation capability of EOA.
where G0 defines the primary value. Generation rate Control Probability (GCP) and Generation Probability (GP) are fixed to be 0.5 based on novel EOA technique. r1 and r2 stand for two arbitrary numbers between zero and one. κ refers to the decay vector. This analysis considers κ = λ. Therefore, the generation rate is expressed as follows.
This section discusses the results of performance analysis accomplished by the proposed technique on two benchmark datasets namely, UNSW-NB15 dataset [21] and CICIDS-2017 dataset [22]. Tab. 1 provides the analysis results of ODBN-IDS technique on test UNSW-NB15 partial dataset. The experimental results show that the proposed ODBN-IDS technique obtained a maximum performance during all iterations. For instance, with 200 iterations, ODBN-IDS technique attained a True Positive Rate (TPR) of 0.9944, False Positive Rate (FPR) of 0.0035, True Negative Rate (TNR) of 0.9965, False Negative Rate (FNR) of 0.0056, and an accuracy of 0.9960. Moreover, with 600 iterations, the proposed ODBN-IDS approach reached a TPR of 0.9931, FPR of 0.0036, TNR of 0.9964, FNR of 0.0069, and an accuracy of 0.9948. Furthermore, with 1,000 iterations, ODBN-IDS methodology reached a TPR of 0.9937, FPR of 0.0040, TNR of 0.9960, FNR of 0.0063, and an accuracy of 0.9948.

Fig. 3 plots the accuracy and loss graphs generated by ODBN-IDS technique on test UNSW-NB15 partial dataset. According to the graph, the accuracy value increased and loss value decreased with an increase in epoch count. Further, the training loss is also observed to be low whereas validation accuracy is high on test UNSW-NB15 partial dataset.

Figure 3: Accuracy and Loss graphs of ODBN-IDS technique on UNSW-NB15 partial dataset
Tab. 2 shows the results of analysis achieved by ODBN-IDS method on test UNSW-NB15 full dataset. The experimental outcomes illustrate that the proposed ODBN-IDS technique obtained a maximum performance during all iterations. For instance, with 200 iterations, ODBN-IDS methodology obtained a TPR of 0.9943, FPR of 0.0041, TNR of 0.9959, FNR of 0.0057, and an accuracy of 0.9942. In addition to this, with 600 iterations, the proposed ODBN-IDS technique achieved a TPR of 0.9939, FPR of 0.0033, TNR of 0.9967, FNR of 0.0061, and an accuracy of 0.9948. Besides, with 1,000 iterations, ODBN-IDS algorithm gained a TPR of 0.9945, FPR of 0.0034, TNR of 0.9966, FNR of 0.0055, and an accuracy of 0.9953.

Fig. 4 portrays the accuracy and loss graphs generated from ODBN-IDS technique on test UNSW-NB15 full dataset. The outcomes demonstrate that the accuracy got increased and loss value got decreased with an increase in epoch count. Further, the training loss is also found to be low whereas validation accuracy reached the maximum on test UNSW-NB15 full dataset.

Figure 4: Accuracy and Loss graphs of ODBN-IDS technique on UNSW-NB15 full dataset
Tab. 3 shows the results of analysis accomplished by ODBN-IDS technique on test CICIDS-2017 dataset. The experimental results exhibit that the proposed ODBN-IDS technique obtained a maximal performance during all iterations. For instance, with 200 iterations, ODBN-IDS methodology reached a TPR of 0.9950, FPR of 0.0033, TNR of 0.9967, FNR of 0.0050, and an accuracy of 0.9968. In addition, with 600 iterations, ODBN-IDS algorithm obtained a TPR of 0.9948, FPR of 0.0041, TNR of 0.9959, FNR of 0.0052, and an accuracy of 0.9957. Eventually, with 1,000 iterations, the proposed ODBN-IDS methodology achieved a TPR of 0.9941, FPR of 0.0040, TNR of 0.9960, FNR of 0.0059, and an accuracy of 0.9951.

Fig. 5 showcases the accuracy and loss graphs generated by ODBN-IDS approach on test CICIDS-2017 dataset. The outcomes show that the accuracy value increased and loss value decreased with increase in epoch count. It is also clear that the training loss got reduced whereas validation accuracy increased on test CICIDS-2017 dataset.

Figure 5: Accuracy and Loss graph of ODBN-IDS technique on CICIDS-2017 dataset
Fig. 6 shows the results achieved from average TPR, TNR, and accuracy analyses by ODBN-IDS technique on three datasets. On the applied UNSW-NB15 partial dataset, the proposed ODBN-IDS technique offered an average TPR of 0.9937, TNR of 0.9962, and an accuracy of 0.9949. Besides, on the applied UNSW-NB15 full dataset, ODBN-IDS technique achieved an average TPR of 0.9942, TNR of 0.9963, and an accuracy of 0.9953. Moreover, on the applied CICIDS-2017 dataset, the presented ODBN-IDS technique reached an average TPR of 0.9946, TNR of 0.9961, and an accuracy of 0.9957.

Figure 6: TPR, TNR, and accuracy analyses results of ODBN-IDS technique
Fig. 7 shows the results of average FPR and FNR analyses, accomplished by ODBN-IDS technique on three datasets. On the applied UNSW-NB15 partial dataset, ODBN-IDS technique offered average FPR and FNR values such as of 0.0038 and 0.0063 respectively. Similarly, on the applied UNSW-NB15 partial dataset, the presented ODBN-IDS technique accomplished average FPR and FNR values namely 0.0037 and 0.0058. Furthermore, on the applied CICIDS-2017 dataset, the proposed ODBN-IDS technique reached an average FPR and of 0.0039 and FNR of 0.0054.

Figure 7: FPR and FNR analyses results of ODBN-IDS technique
A comparative analysis was conducted between the presented ODBN-IDS technique and existing methods on test UNSW-NB15 partial dataset and the results are shown in Tab. 4 and Fig. 8. The experimental values demonstrate that Binary Bat Algorithm with Feature Similarity-based Fitness Function (BBAFSFF) and BBA with Classifier Accuracy based Fitness Function (BBACAFF) techniques achieved low accuracy values such as 0.9679 and 0.9694 respectively. Followed by, BBA+ Combined technique accomplished a moderate accuracy of 0.9709. However, the proposed ODBN-IDS technique outperformed all other techniques and achieved a maximum accuracy of 0.9949.
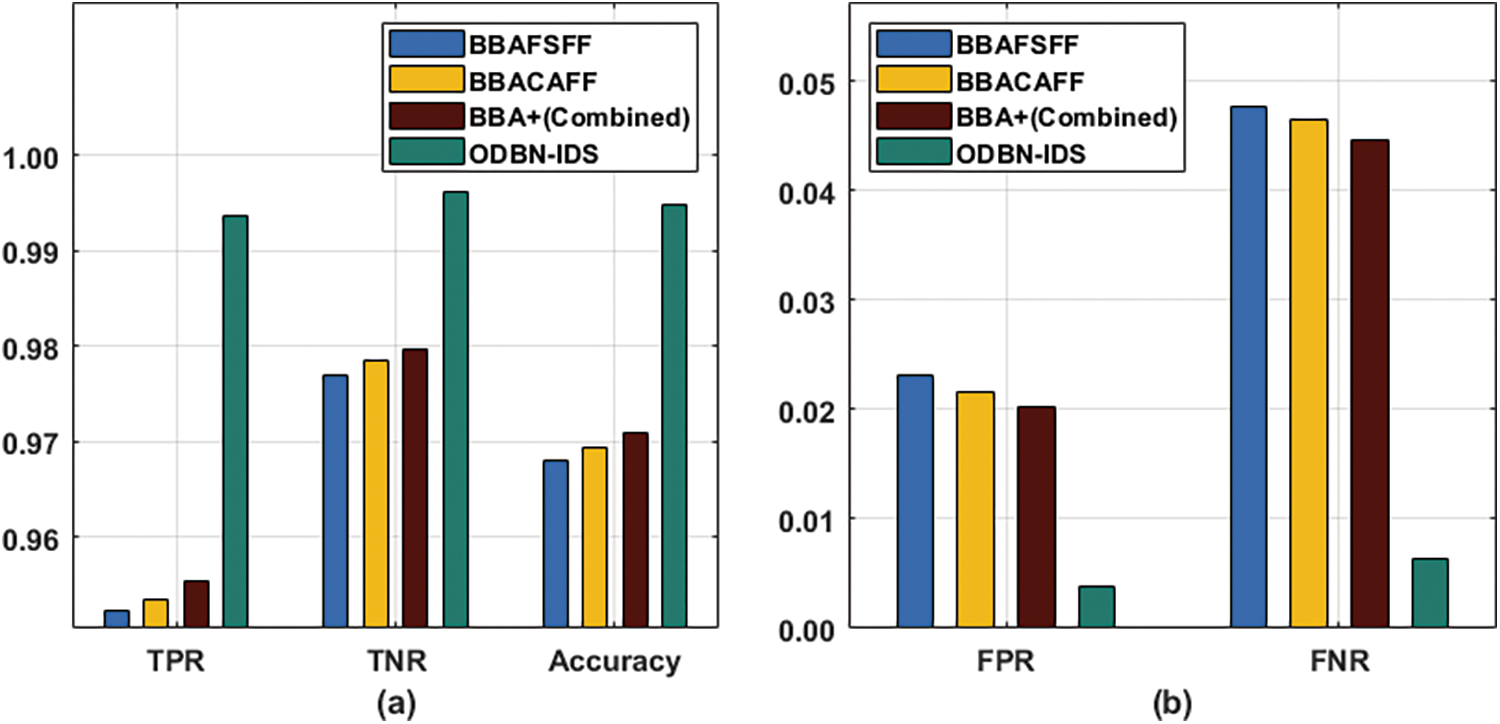
Figure 8: Comparative analysis results of ODBN-IDS technique on UNSW-NB15 partial dataset

A comparative analysis was conducted between ODBN-IDS system against existing algorithms on test UNSW-NB15 full dataset and the results are shown in Tab. 5 and Fig. 9. The experimental values demonstrate that Binary Bat Algorithm (BBA) based Feature Selection with Fitness Function (FSFF) and BBACAFF systems achieved less accuracy values such as 0.9909 and 0.9909 correspondingly. Then, BBA+Combined technique accomplished a moderate accuracy of 0.9943. However, the proposed ODBN-IDS approach outperformed all other techniques and achieved a maximum accuracy of 0.9953.

Figure 9: Comparative analysis results of ODBN-IDS technique on UNSW-NB15 full dataset

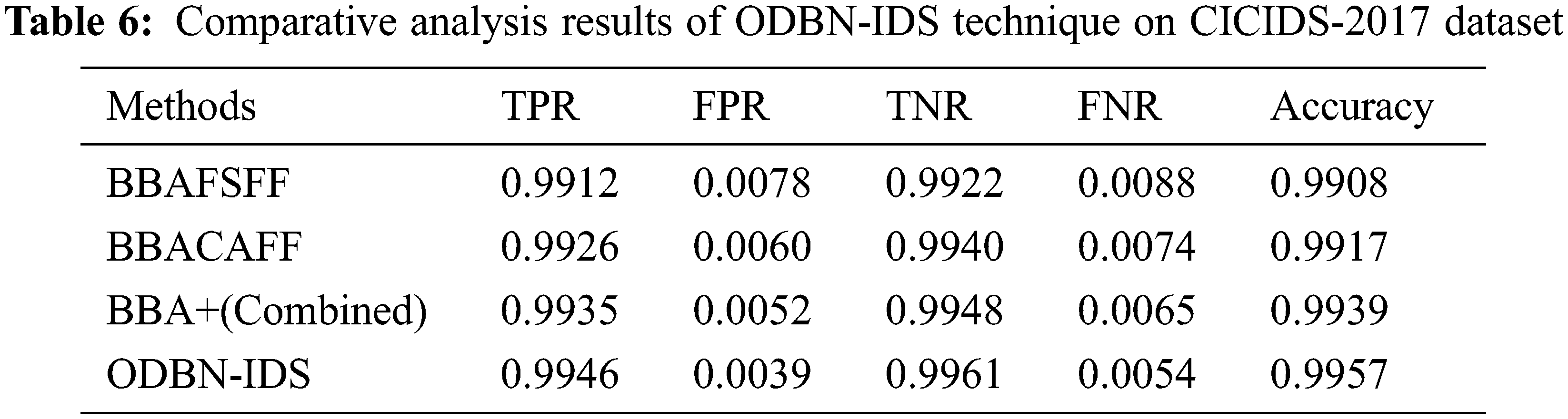
A comparative analysis was conducted between the proposed ODBN-IDS methodology against existing approaches on test CICIDS-2017 dataset and the results are exhibited in Tab. 6 and Fig. 10 [23]. The experimental values showcase that both BBAFSFF and BBACAFF algorithms exhibited minimal accuracy values namely, 0.9908 and 0.9917. Followed by, BBA+Combined technique accomplished a moderate accuracy of 0.9939. At last, the proposed ODBN-IDS technique outperformed all other techniques and achieved a maximum accuracy of 0.9957.

Figure 10: Comparative analysis of ODBN-IDS technique on CICIDS-2017 dataset
In this study, a new ODBN-IDS technique has been developed for detection and classification of intrusions in CPS environment. In first step, the cloud network traffic data is pre-processed to improve its quality to next level. Secondly, BFPA is applied to choose the optimal feature subsets from cloud data. Thirdly, EOA-DBN model is utilized to detect and categorize the intrusions that exist in the network. To validate the performance of the proposed method, a detailed set of simulations was conducted on benchmark datasets. A detailed comparison was conducted between the presented method and existing methods to satisfy the security requirements of cloud network. The results established the supremacy of the proposed ODBN-IDS model. In future, advanced hybrid DL models can be utilized, after testing with several benchmark datasets, to improve intrusion detection efficiency in CPS environment.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. O. Aljehane, “A secure intrusion detection system in cyberphysical systems using a parameter-tuned deep-stacked autoencoder,” Computers, Materials & Continua, vol. 68, no. 3, pp. 3915–3929, 2021. [Google Scholar]
2. M. Alsharif and D. B. Rawat, “Study of machine learning for cloud assisted iot security as a service,” Sensors, vol. 21, no. 4, pp. 1034, 2021. [Google Scholar]
3. A. Alshammari and A. Aldribi, “Apply machine learning techniques to detect malicious network traffic in cloud computing,” Journal of Big Data, vol. 8, no. 1, pp. 90, 2021. [Google Scholar]
4. A. Mondal and R. T. Goswami, “Enhanced honeypot cryptographic scheme and privacy preservation for an effective prediction in cloud security,” Microprocessors and Microsystems, vol. 81, pp. 103719, 2021. [Google Scholar]
5. A. B. Nassif, M. A. Talib, Q. Nasir, H. Albadani and F. M. Dakalbab, “Machine learning for cloud security: A systematic review,” IEEE Access, vol. 9, pp. 20717–20735, 2021. [Google Scholar]
6. S. Thakur, A. Chakraborty, R. De, N. Kumar and R. Sarkar, “Intrusion detection in cyber-physical systems using a generic and domain specific deep autoencoder model,” Computers & Electrical Engineering, vol. 91, pp. 107044, 2021. [Google Scholar]
7. Y. Alghofaili, A. Albattah, N. Alrajeh, M. A. Rassam and B. A. S. Al-rimy, “Secure cloud infrastructure: A survey on issues, current solutions, and open challenges,” Applied Sciences, vol. 11, no. 19, pp. 9005, 2021. [Google Scholar]
8. H. Suhaimi, S. I. Suliman, A. F. Harun, R. Mohamad, Y. W. M. Yusof et al., “Genetic algorithm for intrusion detection system in computer network,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 19, no. 3, pp. 1670, 2020. [Google Scholar]
9. T. Mohanraj and R. Santhosh, “Security and privacy issue in multi-cloud accommodating intrusion detection system,” Distributed and Parallel Databases, vol. 2021, pp. 1–19, 2021, https://doi.org/10.1007/s10619-021-07338-x. [Google Scholar]
10. M. Wang, K. Zheng, Y. Yang and X. Wang, “An explainable machine learning framework for intrusion detection systems,” IEEE Access, vol. 8, pp. 73127–73141, 2020. [Google Scholar]
11. A. Abusitta, M. Bellaiche, M. Dagenais and T. Halabi, “A deep learning approach for proactive multi-cloud cooperative intrusion detection system,” Future Generation Computer Systems, vol. 98, pp. 308–318, 2019. [Google Scholar]
12. Z. Wang, Y. Lai, Z. Liu and J. Liu, “Explaining the attributes of a deep learning based intrusion detection system for industrial control networks,” Sensors, vol. 20, no. 14, pp. 3817, 2020. [Google Scholar]
13. B. Hajimirzaei and N. J. Navimipour, “Intrusion detection for cloud computing using neural networks and artificial bee colony optimization algorithm,” ICT Express, vol. 5, no. 1, pp. 56–59, 2019. [Google Scholar]
14. R. Alghamdi and M. Bellaiche, “A deep intrusion detection system in lamda architecture based on edge cloud computing for IoT,” in 2021 4th Int. Conf. on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, pp. 561–566, 2021. [Google Scholar]
15. S. Krishnaveni, S. Sivamohan, S. S. Sridhar and S. Prabakaran, “Efficient feature selection and classification through ensemble method for network intrusion detection on cloud computing,” Cluster Computing, vol. 24, no. 3, pp. 1761–1779, 2021. [Google Scholar]
16. M. A. Al-Betar, M. A. Awadallah, I. A. Doush, A. I. Hammouri, M. Mafarja et al., “Island flower pollination algorithm for global optimization,” The Journal of Supercomputing, vol. 75, no. 8, pp. 5280–5323, 2019. [Google Scholar]
17. S. A. F. Sayed, E. Nabil and A. Badr, “A binary clonal flower pollination algorithm for feature selection,” Pattern Recognition Letters, vol. 77, pp. 21–27, 2016. [Google Scholar]
18. Y. Hua, J. Guo and H. Zhao, “Deep belief networks and deep learning,” in Proc. of 2015 Int. Conf. on Intelligent Computing and Internet of Things, Harbin, China, pp. 1–4, 2015. [Google Scholar]
19. A. Faramarzi, M. Heidarinejad, B. Stephens and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, vol. 191, pp. 105190, 2020. [Google Scholar]
20. H. Chen, W. Li and W. Cui, “Disruption-based multiobjective equilibrium optimization algorithm,” Computational Intelligence and Neuroscience, vol. 2020, pp. 1–21, 2020. [Google Scholar]
21. N. Moustafa and J. Slay, “UNSW-NB15: A comprehensive data set for network intrusion detection systems (UNSW-NB15 network data set),” in 2015 Military Communications and Information Systems Conf. (MilCIS), Canberra, Australia, pp. 1–6, 2015. [Google Scholar]
22. I. Sharafaldin, A. H. Lashkari and A. A. Ghorbani, “Toward generating a new intrusion detection dataset and intrusion traffic characterization,” in Proc. of the 4th Int. Conf. on Information Systems Security and Privacy, Funchal, Madeira, Portugal, pp. 108–116, 2018. [Google Scholar]
23. R. Patil, H. Dudeja and C. Modi, “Designing an efficient security framework for detecting intrusions in virtual network of cloud computing,” Computers & Security, vol. 85, pp. 402–422, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |