DOI:10.32604/iasc.2022.026355

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.026355 |  |
| Article |
Energy-Efficient Secure Adaptive Neuro Fuzzy Based Clustering Technique for Mobile Adhoc Networks
Department of Instrument Technology, A. U. College of Engineering, Andhra University, Visakhapatnam, Andhra Pradesh, 530003, India
*Corresponding Author: Maganti Srinivas. Email: srinivas.maganti@vrsiddhartha.ac.in
Received: 23 December 2021; Accepted: 10 February 2022
Abstract: In recent times, Mobile Ad Hoc Network (MANET) becomes a familiar research field owing to its applicability in distinct scenarios. MANET comprises a set of autonomous mobile nodes which independently move and send data through wireless channels. Energy efficiency is considered a critical design issue in MANET and can be addressed by the use of the clustering process. Clustering is treated as a proficient approach, which partitions the mobile nodes into groups called clusters and elects a node as cluster head (CH). On the other hand, the nature of wireless links poses security as a major design issue. Therefore, this paper proposes a non-probabilistic and energy-efficient secure adaptive neuro fuzzy-based clustering scheme (NPEE-SANFC) for MANET. The proposed NPEE-SANFC techniques elects CHs in two levels such as tentative CH election and final CH election. Besides, a non-probabilistic way of Tentative CH (TCH) selection takes place by the use of a back-off timer. In addition, ANFC technique is applied for the election of Final CH (FCH)s. The presented model involves a set of input parameters such as residual energy, intra-cluster distance, inter-cluster distance, and trust degree. The incorporation of the trust degree of the node enables to elect secure CHs. Furthermore, the application of two processes for optimal CH selection will result in enhanced network lifetime and energy efficiency. To validate the results regarding the effectiveness of the presented NPEE-SANFC technique, a set of experiments was performed; and the results were determined using distinct measures such as the energy consumption, network lifetime, throughput, and end-to-end delay.
Keywords: Clustering; routing; wireless sensor networks; non-probabilistic; fuzzy logic
Usually, Mobile Ad Hoc Network (MANET) [1] has a set of autonomous and massive nodes that are connected to each other by wireless connections as illustrated in Fig. 1. The network is independent of the stable architecture and comprised of free nodes which are placed in specific domains. Such applications are suitable in case of using costlier applications like disaster control, traffic management, military service, etc. However, it is difficult to overcome the system due to the existence of features in self-developing and the absence of centralized management [2]. Additionally, integrity and stability are considered to be significant issues involved in communication regions. Then, clustering plays an important role in resolving maximum problems involved in MANET and provides power efficiency and stability. It classifies the nodes into a set of clusters and declares a leader called Cluster Head (CH) selected in each cluster. Henceforth, transmitting data from source to destination is carried out by CHs, and gateway nodes belong to the communication region of numerous CHs, thus, the power of alternate nodes could be preserved [3,4].

Figure 1: Structure of WSN
Cluster relied on MANET improves the network management as the route development becomes simple to reduce the size of the routing table. However, CHs experiences maximum overhead because of intra and inter-cluster communication. Simultaneously, the mobile behavior of nodes is one of the major reasons for link damage, hence, in a clustering mechanism the basic strategy while selecting CH is mobile when compared with alternate nodes and split the well-organized cluster and requires a new inter-cluster path setup among 2 ends. Frequent link damage due to the mobility of CHs mitigates the communication process. Additionally, it provides overhead management and limits power efficiency. Hence, the productive clustering approach with a limited burden is considered to be an effectual objective to enhance the duration of MANET.
In MANET, various approaches were deployed for addressing the complexity of mobility and battery-based mobile nodes. In [5] developed taxonomy of clustering approaches in MANET limits the node power consumption. Consequently, improved power consumption and decreased power requirement have been achieved, though a single parameter of the CH election mechanism is simple and demands limited overhead. It depends upon the individual parameter without considering the node qualities to become a CH. An effective Weight Based Clustering Algorithm (WCA) in MANET has been projected in [6]. It is considered that the unified weight of massive variables affects the CH election. In [7] deployed Distributed WCA (DWCA) for MANET that limits the development and redevelopment of clusters and constraints of CHs by means of power demand. But, no parameters show better node reliability in CH election. In [8], improved models of WCA called Enhancement on WCA (EWCA) were projected. Here, the attributes applied for the CH election are transmission energy, communication radius, mobility, and battery energy has been deployed.
In recent times, multiple deterministic, as well as stochastic methodologies, were proposed in [9–16]. The technique based on the gradient mechanism is called a deterministic scheme. Stochastic approaches are multimodal problem search under various perceptions which depends upon biological organisms. Low et al. [9] developed a complete review of metaheuristic approaches for optimizing the issues in MANET. Goldberg [10] introduced a breadth-first search tree (BFS) that relied on the clustering method for selecting the limited overhead of CHs and interlinking the nodes with each other. Gupta et al. [11] presented a Genetic Algorithm (GA) that evolved from the Darwinian theory of endurance significantly. Keerthipriya et al. [12] utilized a GA-based load balancing clustering approach in Wireless Sensor Networks (WSN) in which the high overhead on gateway nodes is reduced and nodes are connected jointly to make load-balanced clusters. Jamali et al. [13] employed a dynamic clustering formation in MANET using Adaptive-Particle Swarm Optimization (A-PSO). Also, different parameters of CH election are involved to make stabilized clusters. However, nodes mobility is impossible to be managed along with the efficacy. On the other hand, PSO is applied for computing the CHs without optimizing the clustering process [14]. In Shahzad et al. [15], energy effective routing approach for MANET was deployed with the help of the PSO framework. Followed by, the challenges involved in routing are assumed as optimization problems and projected new Fitness Function (FF) which depends upon the route length as well as power level. Next, Binary PSO (BPSO) mechanism has been employed to optimize the routing in MANET.
In Khatoon et al. [16], the clustering method in MANET by applying Comprehensive Learning PSO (CLPSO) has been developed. In this study, parameters applied for selecting CHs are similar to WCA without the direction of node's mobility in decision-making process for CH reliability. From the previous models, clustering is considered a resourceful approach to provide power efficiency and stability of the system. The accessibility of the clustering model improves the routing outcome by means of limited overhead and power consumption. Meantime, security is a significant problem in MANET construction. The contribution of the paper is given as follows. This paper proposes a non-probabilistic and energy-efficient secure adaptive neuro fuzzy-based clustering scheme (NPEE-SANFC) for MANET. The proposed NPEE-SANFC technique performs CH selection in two stages such as non-probability-based tentative CH (TCH) selection and adaptive neuro fuzzy-based final CH (FCH) selection. Firstly, a back-off timer with respect to residual energy is employed for the selection of TCHs. Secondly; the TCHs execute the ANFC module to elect the FCHs. The presented model involves a set of input parameters like residual energy (RE), intra-cluster distance, inter-cluster distance, and trust degree. The experimental validation of the NPEE-SANFC technique takes place and the results are investigated against several performance metrics.
2 The Proposed NPEE-SANFC Technique
Fig. 2 depicts the working process involved in the NPEE-SANFC technique. When the nodes are placed in the sensing region, the Base station (BS) telecasts a beacon signal to the complete system. Each node might receive a beacon signal and estimate the actual distance to BS or sink node on the basis of RSSI. Then, sensor nodes start telecasting handshaking messages inside the transmission radius for collecting data regarding the neighbors. The handshaking message encloses details like node ID, link supremacy, RE, and distances to sink. For example, if neighboring node j obtains the handshaking message from node i, then it saves the received data and responds to node i. Then, node i update the Node Degree (ND) and evaluates the distance to adjacent node j by applying node j's distance to sink and records the data of node j. Likewise, node i receives data from nearby nodes, ND, and distance to neighbors might be measured. Under the application of this principle, each node collects data regarding the neighbors to upgrade the details and stimulate a clustering mechanism. In the cluster development approach, TCHs are selected by applying a back-off timer. Next, the TCHs executed the SANFC technique and elected FCHs.

Figure 2: Block diagram of NPEE-SANFC model
2.1 TCH Selection Using Non-Probabilistic Method
In this stage, the TCH election process takes place in a non-probabilistic way where a the back-off timer is introduced. Here, the timer value is conversely proportional to the sensor node's RE; for example, if the power level is maximum, afterward back-off timer would below and it is repeated frequently. Thus, the value of the back-off timer would be finished rapidly when the nodes have maximum power level. Once the back-off timer is 0, then the corresponding node regards itself as tentative CH and telecast the condition to respective neighbors [17]. While a node obtains a tentative CH advertisement message before the expiry of times, then the CH election is not complete and considered as a Cluster Member (CM). Followed by, when no CH message is advertised, then it is considered as tentative CH when the backoff timer is 0. Therefore, the newly developed approach system decides tentative CH in a non-probabilistic fashion. Afterward, tentative CHs implement the SANFC technique for determining proper FCH election.
2.2 FCH Selection Using SANFC Technique
Once the TCHs are elected, the FCHs are chosen by the SANFC technique. The parameters required for cluster development are given in the following: RE level, Distance among CH and BS (inter-cluster distance), Distance among node and CH (intra-cluster distance), and trust degree. Once the CH election is completed, alternate nodes are enabled to join the system by connecting appropriate CH for allocating a CM of clusters and ensured by CH on the basis of fuzzy rules. Hence, the structure of SANFC for the newly developed protocol is illustrated in Fig. 3.

Figure 3: Process involved in SANFC based FCH selection
The network is composed of 4 inputs from the input layer, rules from hidden layers, and result from output layers [18]. Here, 4 linguistic parameters are used with 3 levels with the newly deployed parameter trust degree. The structure of newly presented routing mechanism is depicted in Fig. 3 which contains main models like mobile sensor Nodes, NN model for training and testing, Neuro-Fuzzy inference system (neuro-FIS), Neuro-Fuzzy rule manager, Rule base, BS, Clustering Module, Decision Manager and Cluster Distance Management technologies [19–21].
Initially, a node is allocated to a Trust Factor (TF) value 1. Then, the measure of TF is limited by anomalous prediction mechanism while a node computes anomalous task and node is selected as the apprehensive node and TF nodes are depicted in Eq. (1):
In this work, nodes with
2.2.2 Neuro-Fuzzy Membership Functions
Here, Convolutional Neural Networks (CNN) is employed to perform training of sensor nodes and infrastructure of communication connections in IoT-based WSN. It accelerates the model performance and activates the network to identify the shortest path of nodes to CH and BS using neuro-fuzzy rules. Hence, NFIS employs triangular and trapezoidal membership rates along with CNN to make some decision rules. In addition, the neuro-fuzzy rule system applies the fuzzy Membership Functions (MF). It can be depicted in Eqs. (2) and (3).
In this study, parameters z and x refer to the fuzzy and original distances where the fuzzy distance measure is estimated by MF. Therefore, the energy model applied is the same and provided in (4) and (5). The Eelec implies the electronics power and εfs and εmp is amplifier energy in free space and multipath correspondingly. Also, energy for transmitting the 1-bit message is by estimating the Wireless Sensor Network (WSN) for a distance named dist is measured on the following:
At this time, d0 is the threshold distance to determine the energy levels.
In energy ER(l) is needed to receive a message of size 1-bit is as follows.
Initially, CNN training is carried out with a fuzzy model for the purpose of weight modification and thus Mamdani Fuzzy inference approach is developed because of the hierarchy of CNN. The newly developed NFIS is composed of 4 input parameters and all inputs contain 3 levels. Hence, levels applied for the fuzzy parameters are given in the following:
• CH recent Energy-Less, Medium less, Medium, Highly medium and Highly,
• Dist. from CH and sink-Closer, Medium closer, Medium, Medium Distant and Distant
• Dist. from CH and node-Closer, Medium closer, Medium, Medium Distant, and Distant
• Trust degree-Low, Minimum average, Average, Maximum average, and More.
For example, 4^4 = 256 is a feasible member choice value computed by utilizing fuzzy IF-THEN rules. The triangular and TMF functions are applied for members for representing member choice levels. The Fuzzy logic (FL) relied on IF-THEN rules applied in the newly developed systems.
Consequently, the fuzzy rule-based inference task is the de-fuzzification step. In order to accomplish better results from fuzzy values, de-fuzzification is employed in this work. Over the de-fuzzification models, Center of Area (COA) is one of the commonly applied techniques as depicted in Eq. (6).
Once PB_CH is processed; a single node forwards a CH_CANDITATE_MSG to adjacent nodes in the transmission range. The message is composed of node ID and measure of PB_CH. The nodes with maximum possibility are selected as CH and forward CH_SUCCESS to closer nodes. A node might receive various CH_SUCCESS from the adjacent nodes. At this point, it transmits the CH_JN message and combines it with closer CH. While receiving the CH_JN message, the closer CH ensures the recent cluster size prior to accepting novel members. Since the overall number of CM is minimum than the defined cluster size, it approves the novel CM by responding to CM_ ADMIT message; then, it sends CH_REFUSE message. If a node obtains a the CM_REFUSE message, it resends a CM_JOIN message for upcoming CH with no rejected CH, and it is repeated until joining a novel CH. Sometimes, if a node fails to combine with alternate CH in a coverage region “R,” it considers as CH. Finally, a node falls under the cluster, and no nodes are differentiated in WSN. Subsequently, in various iterations, the earlier death of CHs can be avoided by the CHs rotation model. If the RE of CH attains a threshold value, CH rotation is performed on the basis of PB_CH.
The performance validation of the proposed model was conducted using MATLAB. The proposed model was compared with state-of-the-art methods such as the FUCHAR, COBMA, and EMPSO algorithms using different measures. In addition, the results were examined under varying numbers of CHs, numbers of CMs, and numbers of mobile nodes.
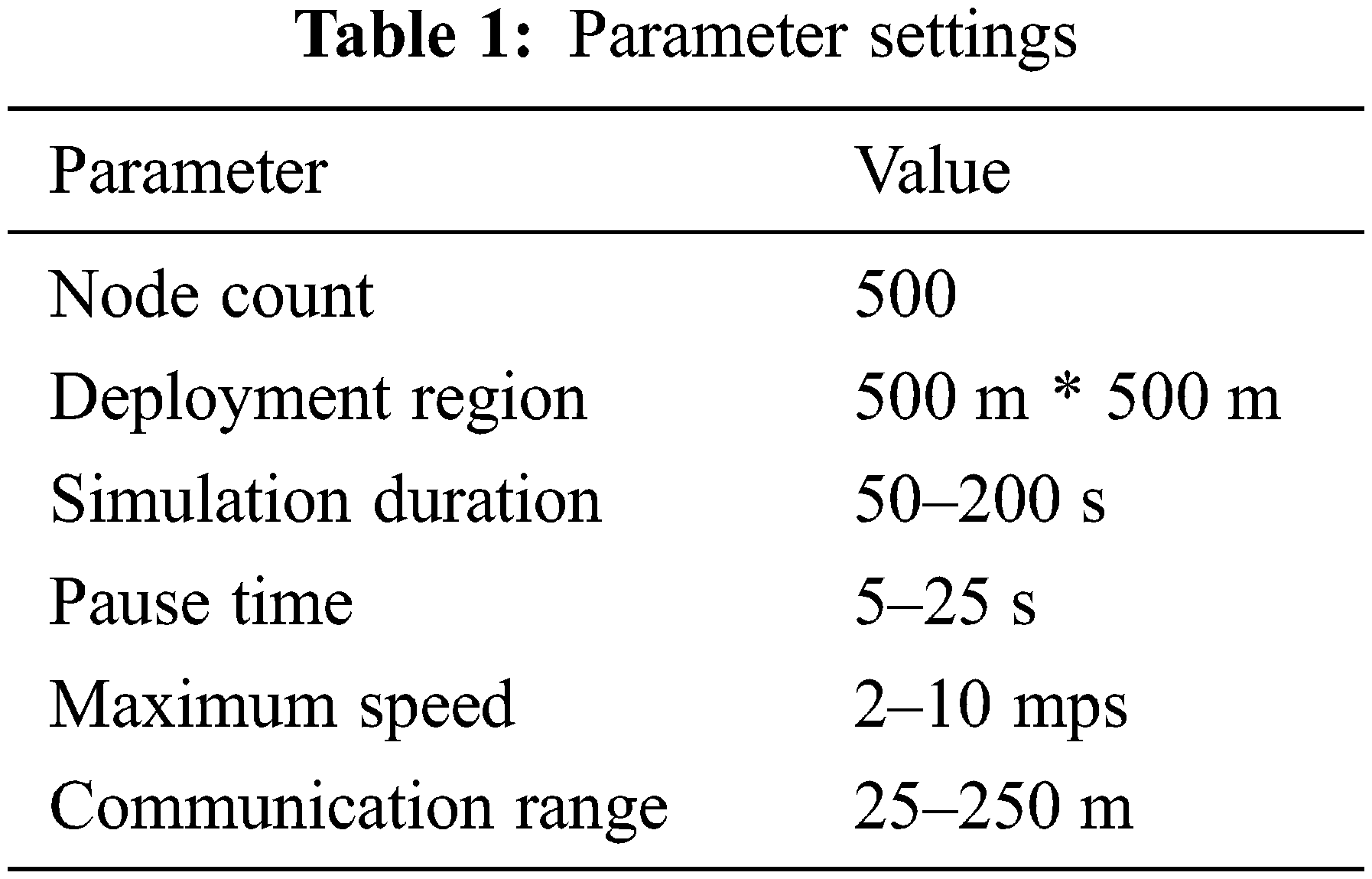
Tab. 1 exhibits the parameter settings of the analysis and The outcomes obtained by the NPEE-SANFC model under the varying speeds of mobile nodes depicted in Tab. 2. Fig. 4 depicts the number of CH changes under varying mobile node speed by the NPEE-SANFC and existing techniques. From the figure, it can be evident that the NPEE-SANFC model has resulted in effective performance over the other methods by accomplishing the minimal number of CH changes irrespective of the mobile node speed. For instance, under the existence of a mobile node speed of 2 m/s, the NPEE-SANFC technique has depicted only 7 CH changes whereas the FUCHAR, COMBA, and EMPSO have resulted in higher CH changes of 9, 10, and 12 respectively.

Figure 4: Result analysis of NPEE-SANFC model in cluster head
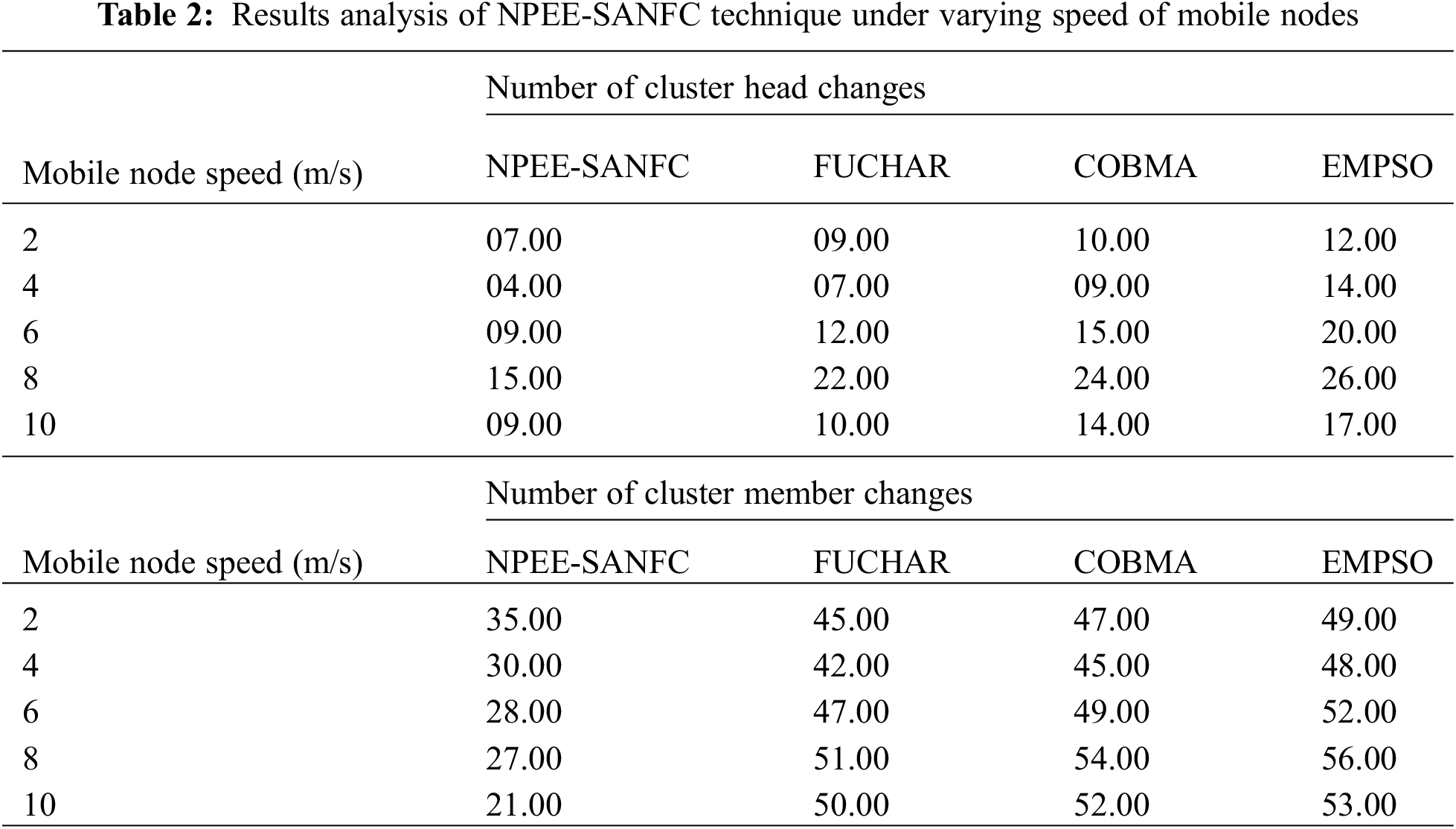
At the same time, under the presence of a mobile node speed of 6 m/s, the NPEE-SANFC technique has demonstrated only 9 CH changes while the FUCHAR, COMBA, and EMPSO have provided maximum CH changes of 12, 15, and 20 respectively. Concurrently, under the application of a mobile node speed of 10 m/s, the NPEE-SANFC scheme has demonstrated only 9 CH changes while the FUCHAR, COMBA, and EMPSO have resulted from maximum CH changes of 10, 14, and 17 respectively.
Fig. 5 illustrates the number of CM changes under varying mobile node speed by the NPEE-SANFC and existing methods. From the figure, it is portrayed that the NPEE-SANFC model has resulted in effective function over the other methods by gaining he reduced number of CM changes irrespective of the mobile node speed. For the sample, under the existence of a mobile node speed of 2 m/s, the NPEE-SANFC method has showcased only 35 CM changes whereas the FUCHAR, COMBA, and EMPSO have resulted in maximum CM changes of 45, 47, and 49 respectively.

Figure 5: Result analysis of NPEE-SANFC model in cluster member
At the same time, under the application of a mobile node speed of 6 m/s, the NPEE-SANFC scheme has shown only 28 CM changes while the FUCHAR, COMBA, and EMPSO have resulted in maximum CM changes of 47, 49, and 52 respectively. Meantime, under the application of a mobile node speed of 10 m/s, the NPEE-SANFC technique has depicted only 21 CM changes whereas the FUCHAR, COMBA, and EMPSO have exhibited maximum CM changes of 50, 52, and 53 respectively.
Tab. 3 provides a comparative results analysis of the NPEE-SANFC model in terms of energy consumption (EC), network lifetime (NC), end to end (ETE) delay, and throughput. Fig. 6 portrays the EC analysis of the presented NPEE-SANFC model with existing methods under the varying number of mobile nodes. The resultant figure demonstrated that the EMPSO algorithm has showcased inferior outcomes by attaining maximum EC. At the same time, the FUCHAR and COMBA models have exhibited somewhat lower EC over EMPSO, but not lower than the NPEE-SANFC model. However, the NPEE-SANFC model has outperformed the compared methods and attained minimum EC over different mobile node counts. For instance, under the existence of 100 mobile nodes, the lowest EC of 34 mJ has been offered by the NPEE-SANFC model whereas a higher EC of 45, 49, and 59 mJ have been attained by the FUCHAR, COMBA, and EMPSO models. Likewise, under the application of 300 mobile nodes, the least EC of 76 mJ has been provided by the NPEE-SANFC model, and the maximum EC of 89, 101, and 116 mJ has been accomplished by the FUCHAR, COMBA, and EMPSO methodologies. At the same time, under the presence of 500 mobile nodes, a low EC of 123 mJ has been showcased by the NPEE-SANFC model while high EC of 141, 156, and 172 mJ have been achieved by the FUCHAR, COMBA, and EMPSO models.

Figure 6: Energy consumption analysis of NPEE-SANFC model
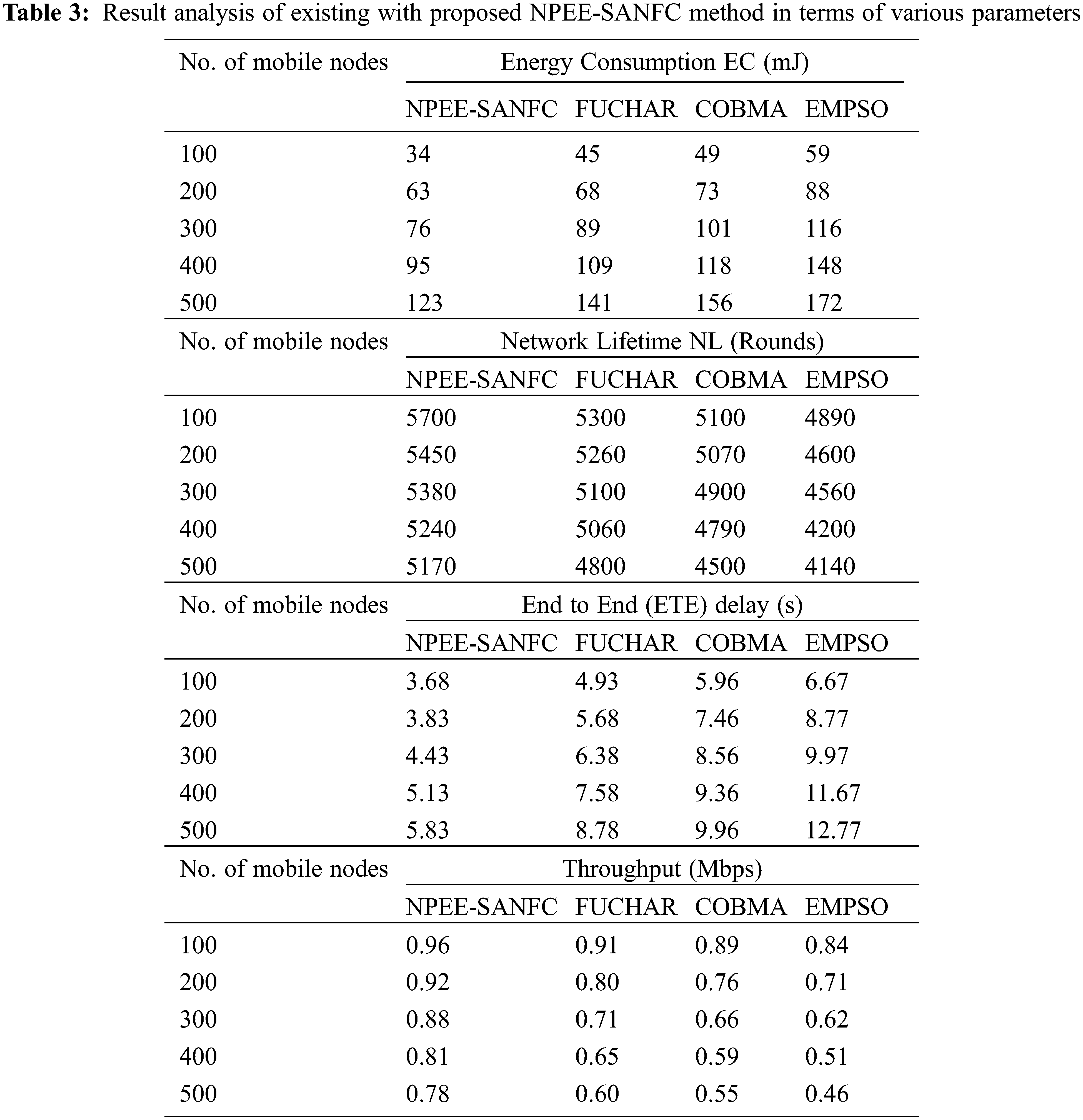
Fig. 7 represents the NL investigation of the presented NPEE-SANFC model with present methods under the varying numbers of mobile nodes. The subsequent figure verified that the EMPSO algorithm has showcased lower outcomes by accomplishing minimum NL. Besides, the FUCHAR and COMBA models have displayed slightly improved NL over EMPSO, but not lower than the NPEE-SANFC model. However, the NPEE-SANFC model has outpaced the compared methods and achieved higher NL over different mobile node counts. For instance, under the presence of 100 mobile nodes, a superior NL of 5700 rounds has been offered by the NPEE-SANFC model whereas a lower NL of 5300, 5100, and 4890 rounds have been attained by the FUCHAR, COMBA, and EMPSO models. In line with, under the existence of 300 mobile nodes, a supreme NL of 5380 iterations has been provided by the NPEE-SANFC model, and a lower NL of 5100, 4900, and 4560 iterations have been accomplished by the FUCHAR, COMBA, and EMPSO models. Simultaneously, under the application of 500 mobile nodes, a superior NL of 5170 rounds has been given by the NPEE-SANFC framework while minimum NL of 4800, 4500, and 4140 iterations have been reached by the FUCHAR, COMBA, and EMPSO models.

Figure 7: Network lifetime analysis of NPEE-SANFC model
Fig. 8 implies the ETE delay analysis of the presented NPEE-SANFC model with existing methods under the varying numbers of mobile nodes. The resultant figure depicted that the EMPSO algorithm has displayed poor results by attaining maximum ETE delay. In line with, the FUCHAR and COMBA techniques have offered moderate ETE delay over EMPSO, but not minimum than NPEE-SANFC model. Therefore, the NPEE-SANFC model has surpassed the existing models and attained lower ETE delay over distinct mobile node count. For example, under the existence of 100 mobile nodes, the lowest ETE delay of 3.68 s has been provided by the NPEE-SANFC model whereas a maximum ETE delay of 4.93, 5.96, and 6.67 s have been achieved by the FUCHAR, COMBA, and EMPSO models. Similarly, under the presence of 300 mobile nodes, the lowest ETE delay of 4.43 s has been showcased by the NPEE-SANFC model while a higher ETE delay of 6.38, 8.56, and 9.97 s have been attained by the FUCHAR, COMBA, and EMPSO models. Meantime, under the application of 500 mobile nodes, a minimum ETE delay of 5.83 s has been provided by the NPEE-SANFC model whereas a higher ETE delay of 8.78, 9.96, and 12.77 s have been achieved by the FUCHAR, COMBA, and EMPSO methodologies.
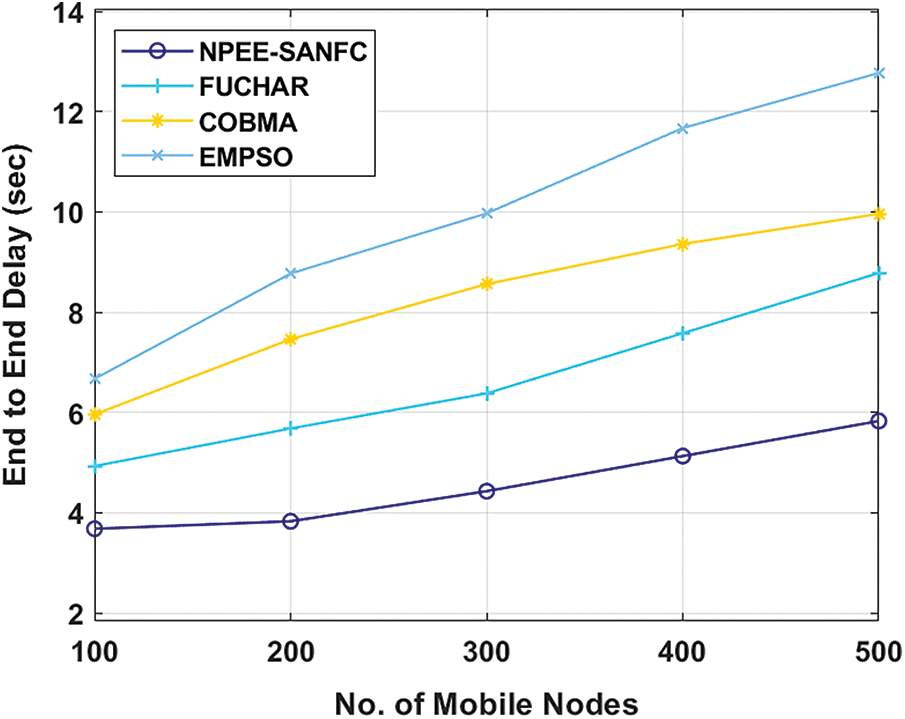
Figure 8: End to end delay analysis of NPEE-SANFC model
Fig. 9 defines the throughput analysis of the newly proposed NPEE-SANFC model with present technologies under the different numbers of mobile nodes. The consecutive figure verified that the EMPSO approach has depicted lower outcomes by accomplishing minimum throughput. Besides, the FUCHAR and COMBA frameworks have displayed slightly improved throughput over EMPSO, but not lower than the NPEE-SANFC model. But, the NPEE-SANFC model has outperformed the compared models and accomplished maximum throughput over different mobile node counts.

Figure 9: Throughput analysis of NPEE-SANFC model
For example, under the existence of 100 mobile nodes, a supreme throughput of 0.96 Mbps has been exhibited by the NPEE-SANFC model whereas a lower throughput of 0.91, 0.89, and 0.84 Mbps has been gained by the FUCHAR, COMBA, and EMPSO models. Similarly, under the application of 300 mobile nodes, a superior throughput of 0.88 Mbps has been offered by the NPEE-SANFC model while a lower throughput of 0.71, 0.66, and 0.62 Mbps have been attained by the FUCHAR, COMBA, and EMPSO models. At the same time, under the existence of 500 mobile nodes, a superior throughput of 0.78 Mbps has been provided by the NPEE-SANFC model and lower throughput of 0.6, 0.55, and 0.46 Mbps rounds have been reached by the FUCHAR, COMBA, and EMPSO models.
From the detailed experimental analysis, it is evident that the presented model achieves energy efficiency and maximizes the network lifetime. The improved performance of the proposed model is due to the inclusion of the NPEE algorithm involving four variables, the energy, distance, ND, and trust factor, for the optimal election of secure CHs.
This paper has presented an effective NPEE-SANFC technique for MANET. The proposed NPEE-SANFC technique performs CH selection in two stages. Firstly, a back-off timer to residual energy is employed for the selection of TCHs. Secondly, the TCHs execute the ANFC module to elect the FCHs. The presented model involves a set of input parameters like RE, intra-cluster distance, inter-cluster distance, and trust degree. The incorporation of the trust degree of the node enables to elect secure CHs. Furthermore, the application of two processes for optimal CH selection will result in enhanced NL and energy efficiency. To examine the superior performance of the NPEE-SANFC technique, a set of experiments were carried out and the results are investigated in terms of diverse evaluation parameters. The experimental outcome ensured that the NPEE-SANFC technique has showcased superior outcomes over the compared methods on the applied evaluation aspects. The experimental outcome justified the superior performance of the presented model over the compared methods. As a part of future work, the proposed model can be deployed in real-time routing applications. In addition, the performance of the proposed model can be improved using data aggregation techniques.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. U. Shuchita and G. Charu, “Node disjoint multipath routing considering link and node stability protocol: A characteristic evaluation,” International Journal of Computer Science, vol. 7, no. 1, pp. 18–25, 2010. [Google Scholar]
2. N. Raza, M. U. Aftab, M. Q. Akbar, O. Ashraf and M. Irfan, “Mobile ad-hoc networks applications and its challenges,” Communications and Network, vol. 8, no. 3, pp. 131–136, 2016. [Google Scholar]
3. S. Arjunan, S. Pothula and D. Ponnurangam, “F5n-based unequal clustering protocol (F5NUCP) for wireless sensor networks,” International Journal of Communication Systems, vol. 31, no. 17, pp. e3811, 2018. [Google Scholar]
4. S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]
5. D. M. Bokhari, H. S. A. Hamatta and S. T. Siddigui, “A review of clustering algorithms as applied in MANETs,” International Journal of Advanced Research in Computer Science and Software Engineering Research, vol. 2, pp. 364–369, 2012. [Google Scholar]
6. M. Chatterjee, S. K. Das and D. Turgut, “On-demand weighted clustering algorithm (WCA) for ad hoc networks,” in Proc. of the IEEE Global Telecommunication Conf. (GLOBECOM ‘00), Sanfransisco, CA, vol. 3, pp. 1697–1701, 2000. [Google Scholar]
7. W. Choi and M. Woo, “A distributed weighted clustering algorithm for mobile ad hoc networks,” in Proc. of the IEEE Advanced International Conference on Telecommunications and International Conference on Internet and Web Applications and Services (AICT/ICIW ‘06), Guadelope, French Caribbean, pp. 1–6, 2006. [Google Scholar]
8. W. Bednarczyk and P. Gajewski, “An enhanced algorithm for MANET clustering based on weighted parameters,” Universal Journal of Communications and Network, vol. 1, no. 3, pp. 88–94, 2013. [Google Scholar]
9. C. P. Low, C. Fang, J. M. Ng and Y. H. Ang, “Efficient loadbalanced clustering algorithms for wireless sensor networks,” Computer Communications, vol. 31, no. 4, pp. 750–759, 2008. [Google Scholar]
10. D. E. Goldberg, Genetic Algorithms: Search Optimization and Machine Learning, 1st edition, Boston, Mass, USA: Addison Wesley, 2007. [Google Scholar]
11. S. K. Gupta, P. Kuila and P. K. Jana, “GAR: An energy efficient GA-based routing for wireless sensor networks,” in Proc. of Int. Conf. on Distributed Computing and Internet Technology, Berlin, Heidelberg, Springer, pp. 267–277, 2013. [Google Scholar]
12. N. Keerthipriya and R. Latha, “Adaptive cluster formation in MANET using particle swarm optimization,” in Proc. of 3rd Int. Conf. on Signal Processing, Communication and Networking (ICSCN), Chennai, India, IEEE, pp. 1–7, 2015. [Google Scholar]
13. S. Jamali, L. Rezaei and S. J. Gudakahriz, “An energy-efficient routing protocol for manets: A particle swarm optimization approach,” Journal of Applied Research and Technology, vol. 11, no. 6, pp. 803–812, 2013. [Google Scholar]
14. P. Kuila and P. K. Jana, “Energy efficient clustering and routing algorithms for wireless sensor networks: Particle swarm optimization approach,” Engineering Applications of Artificial Intelligence, vol. 33, pp. 127–140, 2014. [Google Scholar]
15. W. Shahzad, F. A. Khan and A. B. Siddiqui, “Clustering in mobile ad hoc networks using comprehensive learning particle swarm optimization (CLPSO),” in Proc. Int. Conf. on Future Generation Communication and Networking, Berlin, Heidelberg, Springer, pp. 342–349, 2009. [Google Scholar]
16. N. Khatoon and A. Amirtanjali, “Mobility aware energy efficient clustering for MANET: A bio-inspired approach with particle swarm optimization,” Wireless Communications and Mobile Computing, vol. 2017, no. 1903190, pp. 1–13, 2017. [Google Scholar]
17. S. Arjunan, S. Pothula and D. Ponnurangam, “F5n-based unequal clustering protocol (F5NUCP) for wireless sensor networks,” International Journal of Communication Systems, vol. 31, no. 17, pp. 3811–3827, 2018. [Google Scholar]
18. K. Thangaramya, K. Kulothungan, R. Logambigai, M. Selvi, S. Ganapathy et al., “Energy aware cluster and neuro-fuzzy based routing algorithm for wireless sensor networks in IoT,” Computer Networks, vol. 151, pp. 211–223, 2019. [Google Scholar]
19. N. Wei, J. L. Walteros, M. R. Worden and H. J. O. Pena, “A resiliency analysis of information distribution policies over mobile ad hoc networks,” Optimization Letters, vol. 15, no. 11, pp. 1–23, 2021. [Google Scholar]
20. K. S. Sankaran, N. Vasudevan, K. R. Devabalaji, T. S. Babu, H. H. Alhelou et al., “A recurrent reward based learning technique for secure neighbor selection in mobile AD-HOC networks,” IEEE Access, vol. 9, pp. 21735–21745, 2021. [Google Scholar]
21. J. Swain, B. K. Pattanayak and B. Pati, “A systematic study and analysis of security issues in mobile ad-hoc networks,” International Journal of Information Security and Privacy, vol. 12, no. 2, pp. 144–150, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |