DOI:10.32604/iasc.2022.026263

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.026263 |  |
| Article |
Chaotic Krill Herd with Fuzzy Based Routing Protocol for Wireless Networks
1Department of Computer Science and Information Systems, College of Applied Sciences, Univeristy Name: AlMaarefa University, Ad Diriyah, Riyadh, 13713, Kingdom of Saudi Arabia
2Department of Computer Engineering, College of Computers and Information Technology, Taif University, Taif, 21944, Kingdom of Saudi Arabia
3Computer Information Systems Department, College of Information Technology and Communication, Tafila Technical University, Tafila, 66110, Jordan
4Department of Information Systems, Faculty of Computing and Information Technology, King Abdulaziz Univeristy, Jeddah, 23613, Kingdom of Saudi Arabia
*Corresponding Author: Ashit Kumar Dutta. Email: adotta@mcst.edu.sa
Received: 20 December 2021; Accepted: 24 January 2022
Abstract: Energy is considered a valuable source in wireless sensor networks (WSN) for effectively improving the survivability of the network. The non-uniform dispersion of load in the network causes unbalanced energy dissipation which can result in network interruption. The route selection process can be considered as an optimization problem and is solved by utilize of artificial intelligence (AI) techniques. This study introduces an energy efficient chaotic krill herd algorithm with adaptive neuro fuzzy inference system based routing (EECKHA-ANFIS) protocol for WSN. The goal of the EECKHA-ANFIS method is for deriving a better set of routes to destination in such a way as to improve the survivability in the wireless networks. Primarily, the ANFIS model utilizes the models of fuzzy logic and neural networks (NN) to effectively select the relay nodes for energy efficient communication. Besides, a group of fuzzy rules with membership functions (MF) are designed for selecting the next hop node in wireless networks based on distinct input parameters. Moreover, the optimal selection of MF takes place by the use of chaotic krill herd algorithm (CKHA). In order to showcase the improved performance of the EECKHA-ANFIS approach, a series of simulations are implemented and outcomes are inspected under several aspects. The extensive result analysis demonstrates the betterment of the EECKHA-ANFIS technique over the existing techniques interms of different measures.
Keywords: Energy efficiency; survivability; wireless networks; routing; fuzzy logic; membership function tuning
Wireless transmission is the key constituent of this technological breakthrough, especially while considering the edge of the framework: wireless allows flexibility and mobility that minimizes the weight and cost of equipment and often makes the system deployment simple [1]. For this reason, there has been a growing concern in adopting wireless networks to the strict requirement of different application fields, like intelligent transportation, industrial automation, healthcare, and autonomous robotics [2]. Current development in wireless and mobile networks have provided the basis for them to become an indispensable form of technology viz. utilized by business, technology-savvy, and lay people, anytime and anywhere [3]. Transmission in wireless sensor network (WSNs) consumes considerable amount of energy than sensing and processing implemented by the network node. One of the main problems in WSN is the reduction of power consumption because in almost all instances these nodes are placed in harsh environments, where battery replacement becomes difficult. Also, the significance of power utilization in WSN has been demonstrated in [4]. The general structure of WSN is shown in Fig. 1.
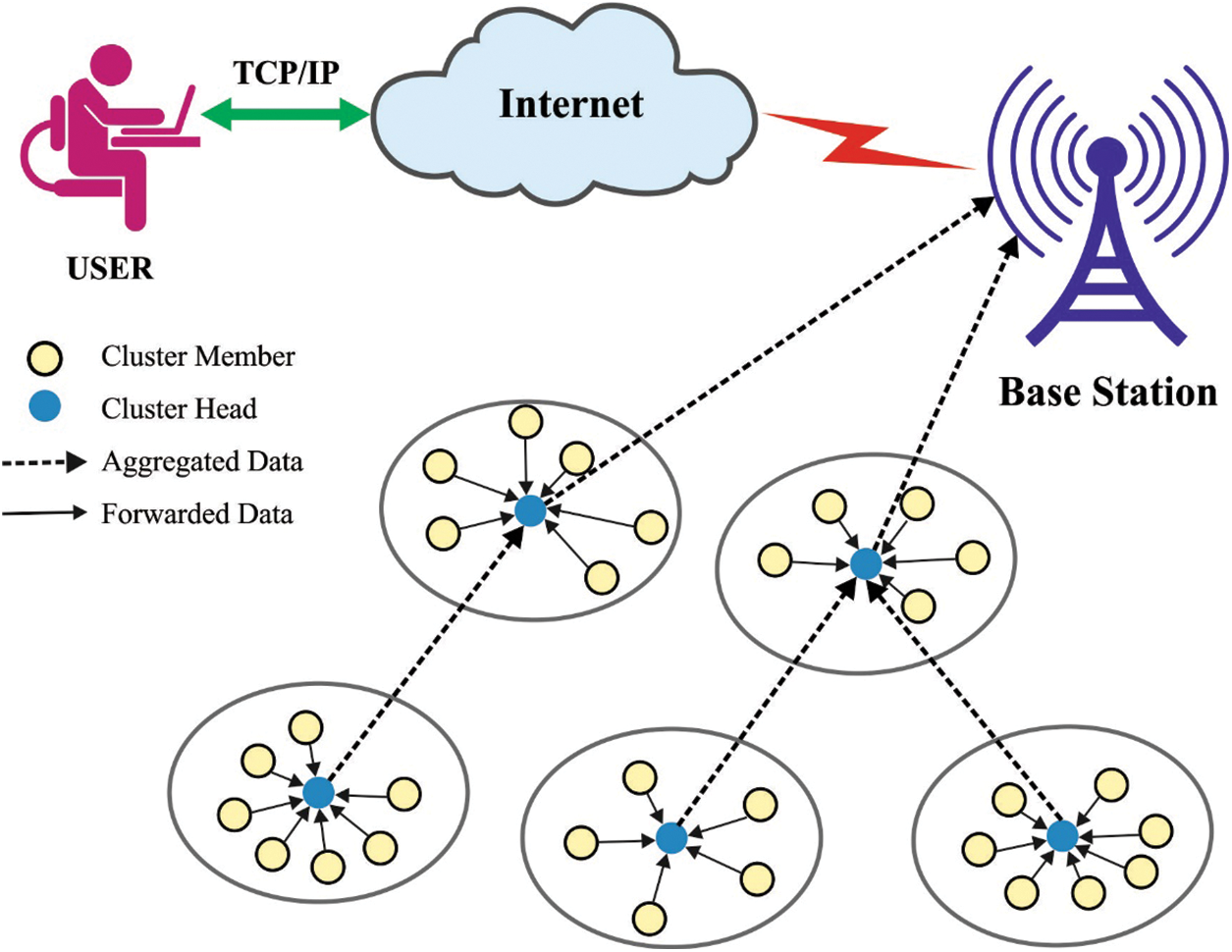
Figure 1: Architecture of WSN
The researchers have proven that communication is the primary reason for power utilization. Such features require the performance of routing policies which allow the sensors to effectively and efficiently communicate with minimal energy utilization [5]. Therefore, the routing protocol for WSNs should possess self-configuration property, which enables us to discover the best possible way to transmit data, considering the energy level and guaranteed delivery amongst the network nodes [6]. When a sensor fails because of insufficient energy, routes must be evaluated in such a way that the collected data could reach the destination node. The transmission among the sensors needs to enhance the power utilization for increasing the network lifetime.
Routing using route-centric parameters is a supportive method used previously to address power utilization balancing problems [7]. In this method, the routing is executed to a smaller network area, and in all the regions, one sensor is carefully chosen as next hop that would transmit the information from other sensors of sink [8]. Further, Parameter-centric routing employs geocast techniques to enhance the packet delivery ratio and reduce delay [9]. Innovative sensor network has slowly become complex; thus, conventional mathematical methods for the selection of next hop aren’t suitable [10]. Fuzzy inference systems provide feasible solution to construct a model for next hop selection since it processes the complete part of human apprehension in absence of mathematical models. There are some benefits with fuzzy modelling such as simple augmentation rule through the extension of new postulates, apprehension of outcome in natural rule portrayal way, usefulness of the system, and ability to convert immanent indecisive of human features into linguistic variable [11].
This study develops an energy efficient chaotic krill herd algorithm with adaptive neuro fuzzy inference system based routing (EECKHA-ANFIS) protocol for WSN in order to improve the survivability in the wireless networks. The ANFIS model utilizes the concepts of fuzzy logic and neural networks (NN) to effectively select the relay nodes for energy efficient communication. In addition, a set of fuzzy rules with membership functions are designed to select the next hop node in wireless networks based on distinct input parameters. Furthermore, the optimal selection of MF takes place by the use of chaotic krill herd algorithm (CKHA). For investigative the enhanced outcomes of the EECKHA-ANFIS technique, a comprehensive experimental analysis takes place and the outcomes are analysed under varying dimensions.
The rest of the paper is organized as follows. Section 2 offers the related works and Section 3 elaborates the proposed model. Then, Section 4 provides the simulation analysis and Section 5 concludes the paper.
Baluz et al. [12] presented a method to assist multipath routing systems in selecting the optimal route based ant colony optimization (ACO) and Fuzzy Inference Systems. The ACO method is employed for adjusting the rule base of fuzzy systems to enhance the classification approach of the routes, and thus increase the survivability and the energy efficacy of networks. The Fuzzy System is utilized for estimating the degree of the route quality, according to low energy levels amongst the nodes that form the path and the number of hops.
Varun et al. [13] introduced an energy-effective routing using a fuzzy neural network (ERFN) to reduce the power utilization when equally balancing power utilization amongst sensor nodes thus as to extend the WSN lifetime. The process uses neural network and fuzzy logic concepts for the smart cluster head (CH) selection will accurately use up equivalent energy of the sensor nodes. In the study, membership function (MFs), fuzzy rules, and sets are proposed for making decisions about the next-hop selection. Zhang et al. [14] developed an energy-effective distributed clustering method based fuzzy system using non-uniform distribution (EEDCF). In CH selection, we considered neighbour node’s residual energy, nodes energy, and degree as the input parameters.
Fu et al. [15] presented an environment fusion multi-path routing protocol (EFMRP) to offer sustainable message transmitting service under harsh environments. The fundamental concept of this model is to instruct messages to choose paths with the optimal trade-offs amongst routing survivability, latency, and energy conservation. Fu et al. [16] proposed a sustainable multi-path routing protocol (SMRP), where the routing decision is made based on a mixed potential field regarding environment, depth, and RE. The fundamental concept of this model is for instructing data packets to choose routes with trade-offs amongst delivery routing survivability, latency, and energy balance. While the environmental field was updated and constructed by the sensing ability of WSN itself, the created multi-path could be protected by evading passing through the hazardous area.
Huang et al. [17] designed a deep learning (DL) based link predictive method, that collectively uses Weisfeiler-Lehman kernel and Dual Convolution Neural Networks (WL-DCNN) for light labelling and weight subgraph extraction. It can be leveraged to improve self-learning capacity of mining topological features with stronger generalization. Selvi et al. [18] proposed two new heuristics methods such as a clustered gravitational routing algorithm and gravitational approach based clustering method to offer an optimum solution to effective routing and effective clustering. Furthermore, a fuzzy logic (FL) based deductive inference model was developed and utilized to select the applicable nodes as CH nodes from the node that exists in all the clusters. Hamzah et al. [19] presented a FL system for CH selective. The presented method employs five descriptors to define the possibility for all the nodes to become a CH. This descriptor includes location suitability, compacting, distance in base station (BS), and density. The study uses FL method in suggesting the Fuzzy Logic-based Energy-Effective Clustering for WSN based minimal separation Distance enforcement among CHs (FL-EEC/D).
In this study, a novel EECKHA-ANFIS technique has been derived for the optimum selection of routes and to accomplish maximum survivability in wireless networks. The selection of routes mainly takes place using the ANFIS model which involves multiple input parameters and produces an optimal route as output. In addition, a collection of fuzzy rules with MFs are designed for the choice of succeeding hop node in wireless networks depending upon varying input parameters and the selection of MF takes place using the CKHA.
Assume that there are N sensor nodes viz. arbitrarily located in network region for monitoring the physical features and its location periodically. All the sensors have neighboring sensors, and they forward information to most neighboring sensors. Consider immobile sensor with equivalent primary energy. The computational abilities of all the sensors were similar. Symmetric radio connections are taken into account among any 2 adjacent sensors. The sink is placed inside the network field. Assume the maximal communication of every sensor is R. Adoptive communication is assumed by utilizing distance among some 2 adjacent sensors. The 1st order radio to examine the energy utilization of presented method has been discussed. Consider 7mm represent the size of packet from bits. The energy was desired to transmit a m bits of packet across d unit distance among a sender sensor and their adjacent sensors is formulated as follows
To obtain a m bits of packet, the energy requirement was expressed as follows
In which ESelect signifies statistics about the energy dissipation to transmit electrons for each bit. Various factors like digital coding, acceptable bit-rate, and modulation affects the ESelect. The ɛfsp and ɛmpf represents the requirement of energy from the free-space path and multi-path environments, correspondingly. If 2 adjacent sensors to which energy utilization is evaluated are divided with distance lesser than or equivalent to
3.2 Design of ANFIS Based Routing Technique
Initially, the ANFIS model receives input parameters as residual energy, distance to BS, and distance to neighbors for determining the optimal route to BS. The network topology is considered to be dynamic when it rapidly changes and that is named an adoptive network. In adoptive network, MFs and fuzzy rule base are generated manually. A mapping of input with output pattern was made using ANFIS by integrating fuzzy inference system (FIS) and neural network architecture. The parameter of the MFs is adjusted by ANFIS using BP method or least square types of algorithms. The ANFIS consists of product, fuzzy, defuzzy, summation, and normalized layers. An underlying structure of ANFIS contains two inputs
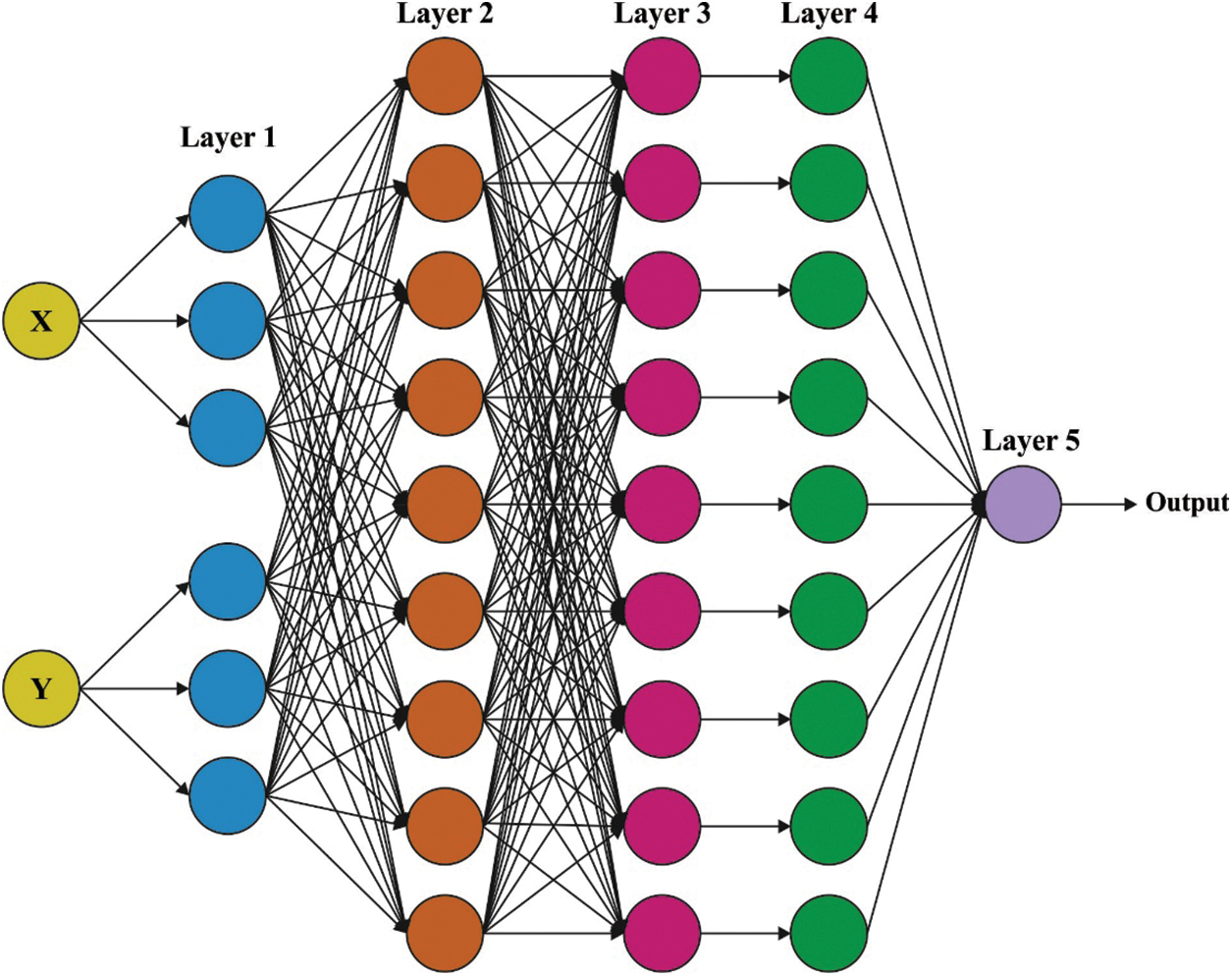
Figure 2: Structure of ANFIS
Let Ai and Bi be the fuzzy set in the antecedent and pi; qi, and ri denotes the linear output parameter that is defined at the time of the training. The explanation of nine rules and five layers of FIS of an ANFIS framework are given in the following:
Layer 1: All the nodes from this layer is named adoptive node [20]. The fuzzy membership grade of input of layer 1 was named outcome of the layer as:
whereas x and y represent input to node i, A and B denotes linguistic label of inputs. O1,i indicates the MF of Ai and Bi.μAi(x) and μBi−3(y) could adapt fuzzy MF.
In the equation, ci and ai denotes the variable group of MF and named as premise parameter.
Layer 2: Layer 2 was termed product layer. It multiplies the incoming signal in outcome of layer 1 and transmits the multiplied product out.
Every node outcome signifies the firing strength of rule.
Layer 3: The nodes in this layer executes the normalized progression of firing strength in the preceding layer as:
Layer 4: The node in these layers are denoted as square node. The function of this layer was same as layer 2. In order to generate the output, it executes multiplication of the normalization firing strength values with first order polynomial as follows:
While wi represent the outcome of layers 3 and pi; qi; ri represent the variable set.
Layer 5: The node in these layers is labelled as
3.3 Design of CKHA Based Tuning Process
KH [21] is a new kind of metaheuristic model for resolving optimized problems. This approach is stimulated by herding of krill swarm while seeking food in nature. For every krill, their location in searching space has impacted by 3 mechanisms as follows:
i) motion induced by other krill;
ii) foraging movement;
iii) random diffusion.
For simplification purposes, the above 3 movements in KH are idealized to the Lagrangian system.
In which Ni, Fi, and Di are equivalent to the abovementioned three movements to the ith krill. The krill number has denoted as i, and t represented as generation. The direction of the first movement, αi, is accurately estimated based on three factors: repulsive, target, and local effecst. For krill i, this motion is modeled in Eq. (11):
While
and N max denotes the maximal speed, ωn indicates the inertia weights in [0, 1],
In which
and Vf indicates the foraging speed, ωf represent the inertia weight within [0, 1] and 1,
In the equation, D max implies the diffusion speed, and δ denotes the random vector from −1 and 1. The second and third movement involves two local and two global systems. Such systems could work concurrently that making KH an efficient and robust system. The location of krill i from r to t + Δt is expressed as follows [23].
Noted that Δt represent a key constantly and must be fine-tuned interms of the certain problems. The reason is that Δt is considered as scale factor of speed vectors. Furthermore, in KH, the inertia weight (ωn, ωf) is fixed to 0.9 at the beginning of KH to emphasize exploration. Later, it can be reduce linearly to 0.1 for stimulating exploitation.
In CKH algorithm, the steps where randomly defined numbers are utilized in the krill herd optimization method are given in the following.
• Establish the initial population
• Computation of Cbest term in the target direction effects of the optimal krill individual
• The directional vector in physical diffusion
• Crossover
Consequently, a new method has been presented in this work where the above first two procedures are also chaotic. The numbers created by chaotic map function are applied in the steps of generating the population initialization and calculating the optimal effect coefficient Cbest.
CKHA is utilized to detect the MFs optimum parameter by the subsequent evaluation and its adjustment of the model. The a, b, f, j, k parameters are equivalent to the MFs of the input variable remain fixed to represent the problems. The system would detect the optimum values of the parameter c, i in a direct way and, by the optimal location of intersection points
Let m1, m2, m3 and m4 be the slopes.
The next step is to determine a proper main purpose for estimating the CKHA efficiency. The main purpose denotes the quality of solutions, and acts as interface among the considered problem and the optimization method. The MSE was utilized for evaluating the fitness of fuzzy model.
Whereas y(k) =Reference value at instant
The performance validation of the EECKHA-ANFIS technique takes place using MATLAB tool. The results are investigated under varying dimensions.
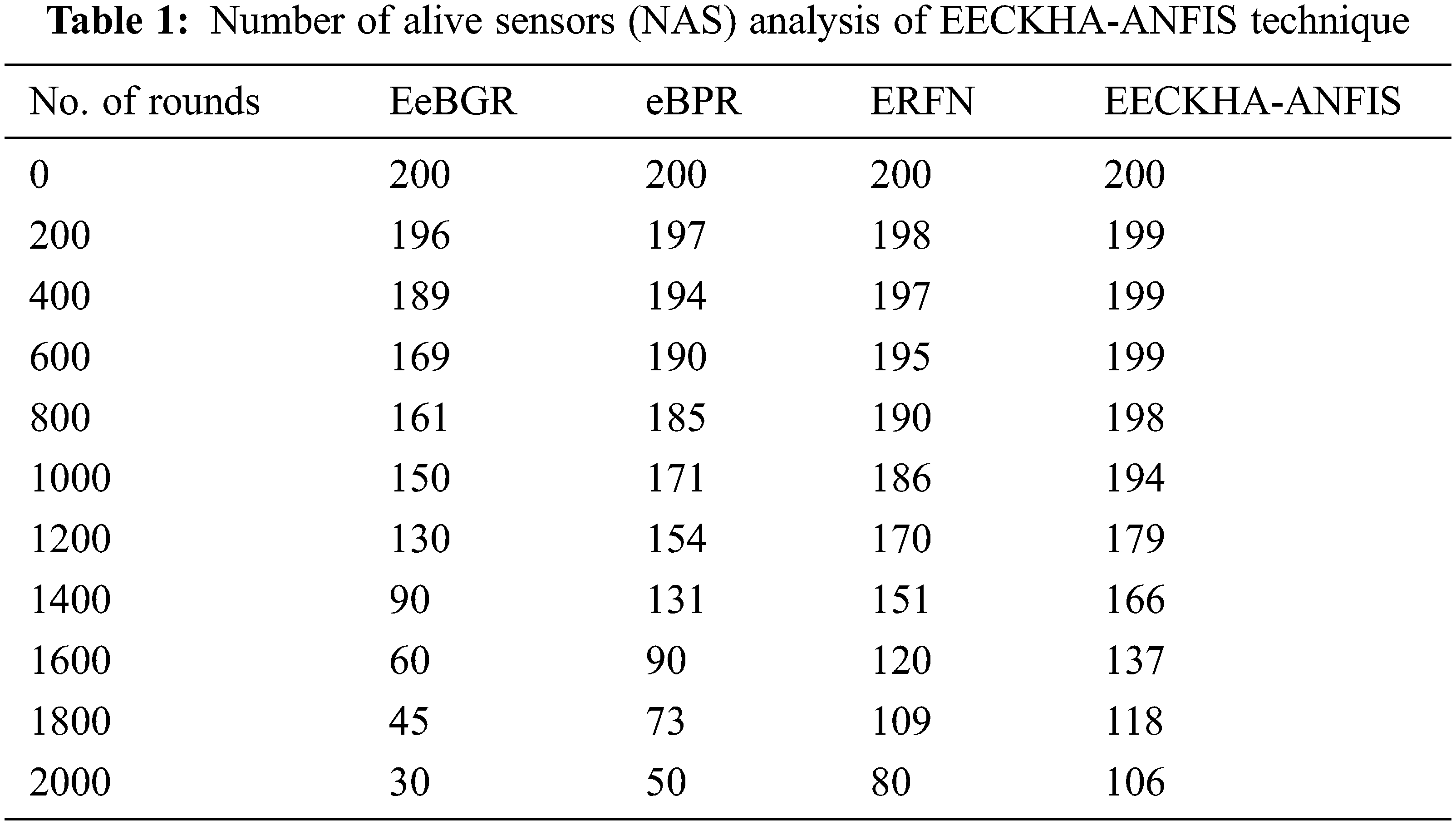
Tab. 1 and Fig. 3 offer the number of alive sensors (NAS) of the EECKHA-ANFIS technique under distinct rounds. The results demonstrated the betterment of the EECKHA-ANFIS technique with the higher NAS. For instance, under 600 rounds, the EECKHA-ANFIS technique has obtained higher NAS of 199 nodes whereas the energy-efficient beaconless geographic routing (EeBGR), energy efficient beaconless position routing (eBPR), and Energy-Efficient Routing Using Fuzzy Neural Network (ERFN) techniques have attained lower NAS of 169, 190, and 195 sensors respectively. Moreover, under 1400 rounds, the EECKHA-ANFIS technique has resulted in increased NAS of 166 nodes whereas the EeBGR, eBPR, and ERFN techniques have attained lower NAS of 90, 131, and 151 sensors respectively. Furthermore, under 2000 rounds, the EECKHA-ANFIS technique has accomplished maximum NAS of 106 nodes whereas the EeBGR, eBPR, and ERFN techniques have reached minimal NAS of 30, 50, and 80 sensors respectively.
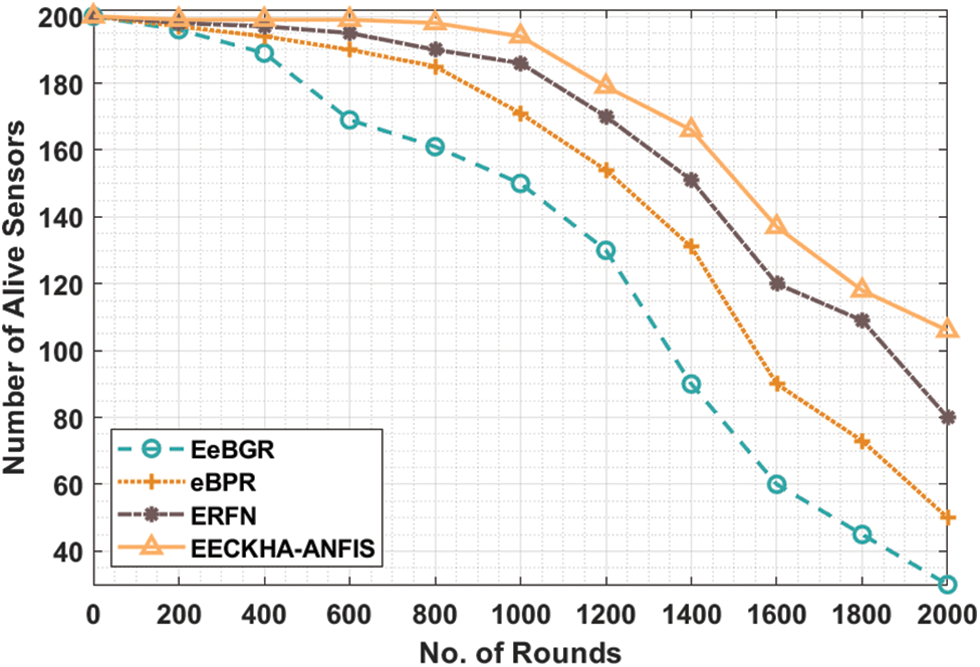
Figure 3: NAS analysis of EECKHA-ANFIS technique with different rounds
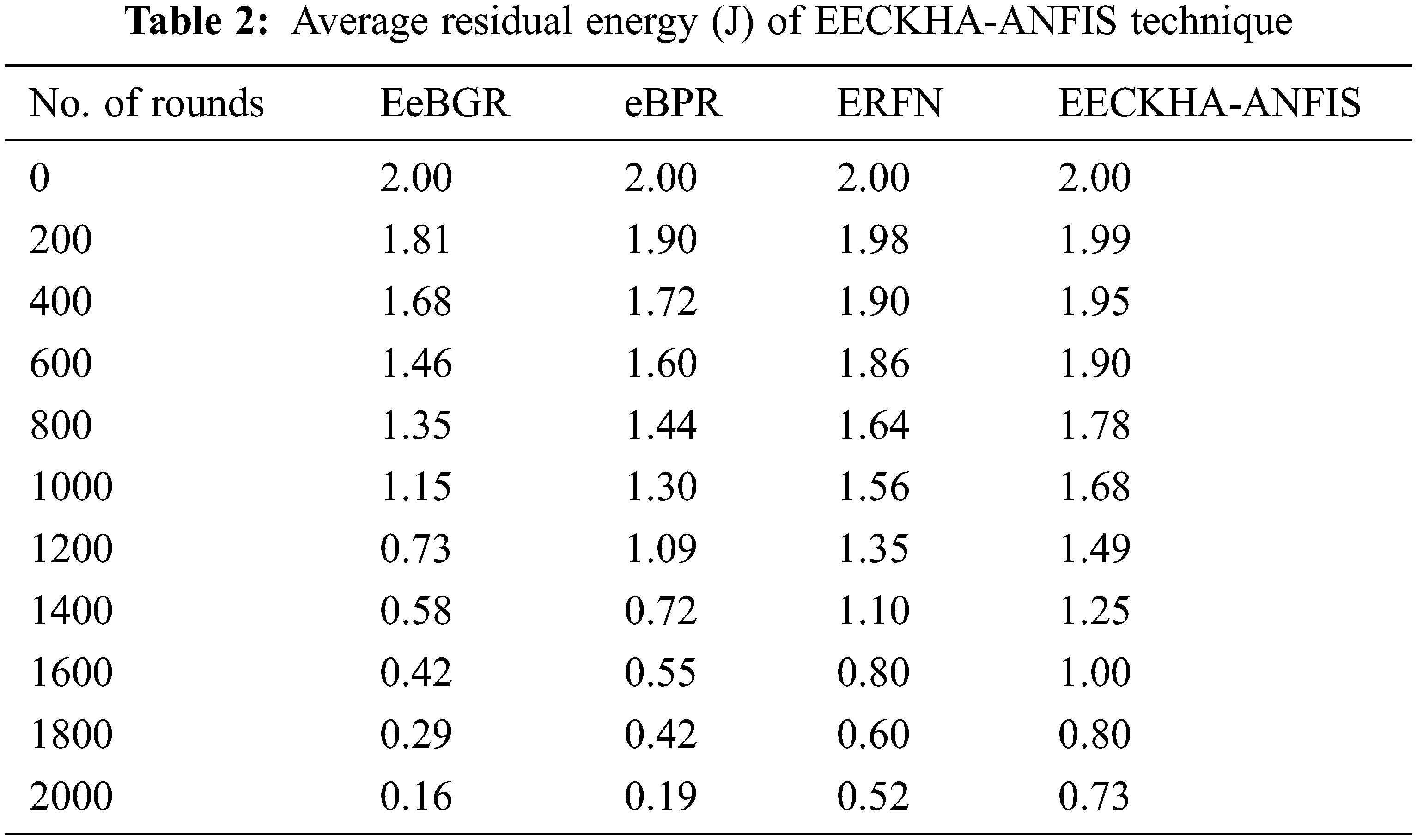
Tab. 2 and Fig. 4 provided the average residual energy (ARE) of the EECKHA-ANFIS approach under distinct rounds. The results demonstrated the betterment of the EECKHA-ANFIS technique with the maximum ARE. For instance, under 600 rounds, the EECKHA-ANFIS approach has obtained higher ARE of 1.90 J whereas the EeBGR, eBPR, and ERFN techniques have gained lower ARE of 1.46, 1.60, and 1.86 J correspondingly. Besides, under 1400 rounds, the EECKHA-ANFIS methodology has resulted in improved ARE of 1.25 J whereas the EeBGR, eBPR, and ERFN systems have gained lesser ARE of 0.58, 0.72, and 1.10 J correspondingly. Besides, under 2000 rounds, the EECKHA-ANFIS technique has accomplished maximal ARE of 0.73 J whereas the EeBGR, eBPR, and ERFN techniques have obtained minimal ARE of 0.16, 0.19, and 0.52 J correspondingly.
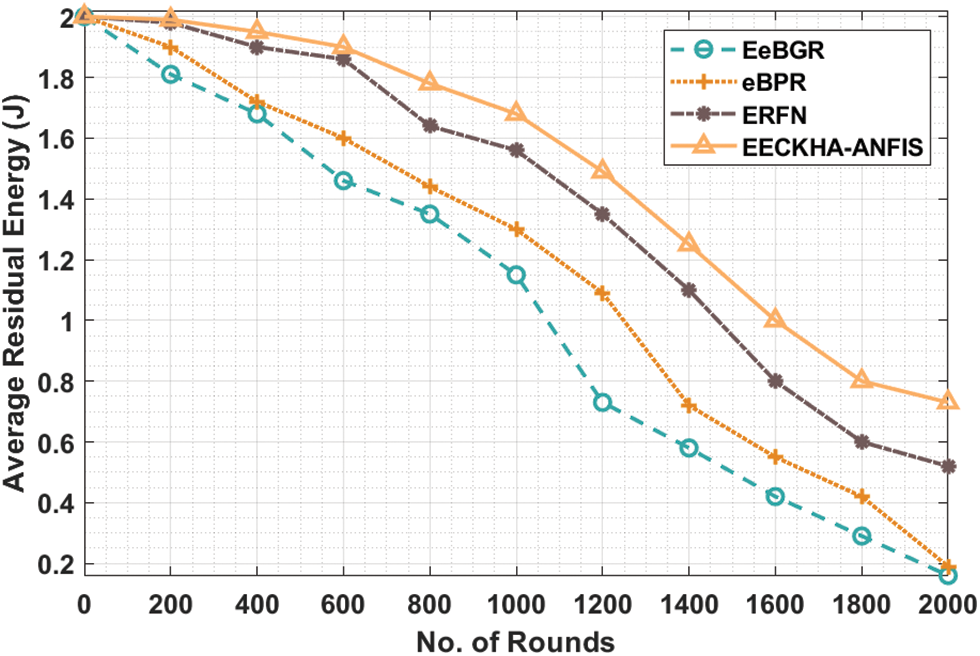
Figure 4: ARE analysis of EECKHA-ANFIS technique with different rounds
Tab. 3 and Fig. 5 inspected the sensor death (SD) analysis of the EECKHA-ANFIS technique with recent methods. The results depicted that the EECKHA-ANFIS technique has attained effective results with the least SDH over the other methods.
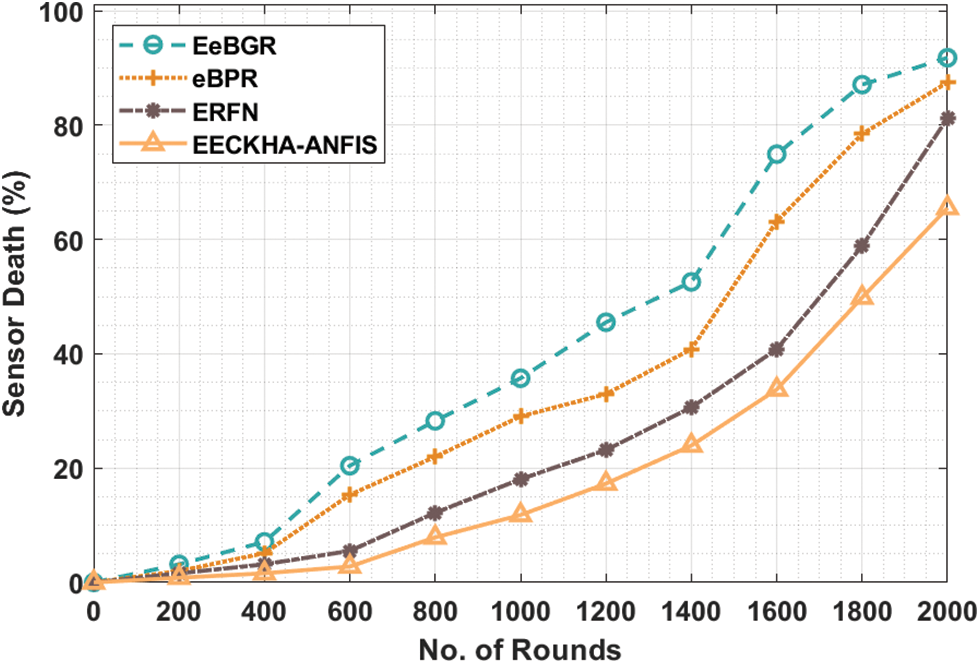
Figure 5: SDH analysis of EECKHA-ANFIS technique with different rounds
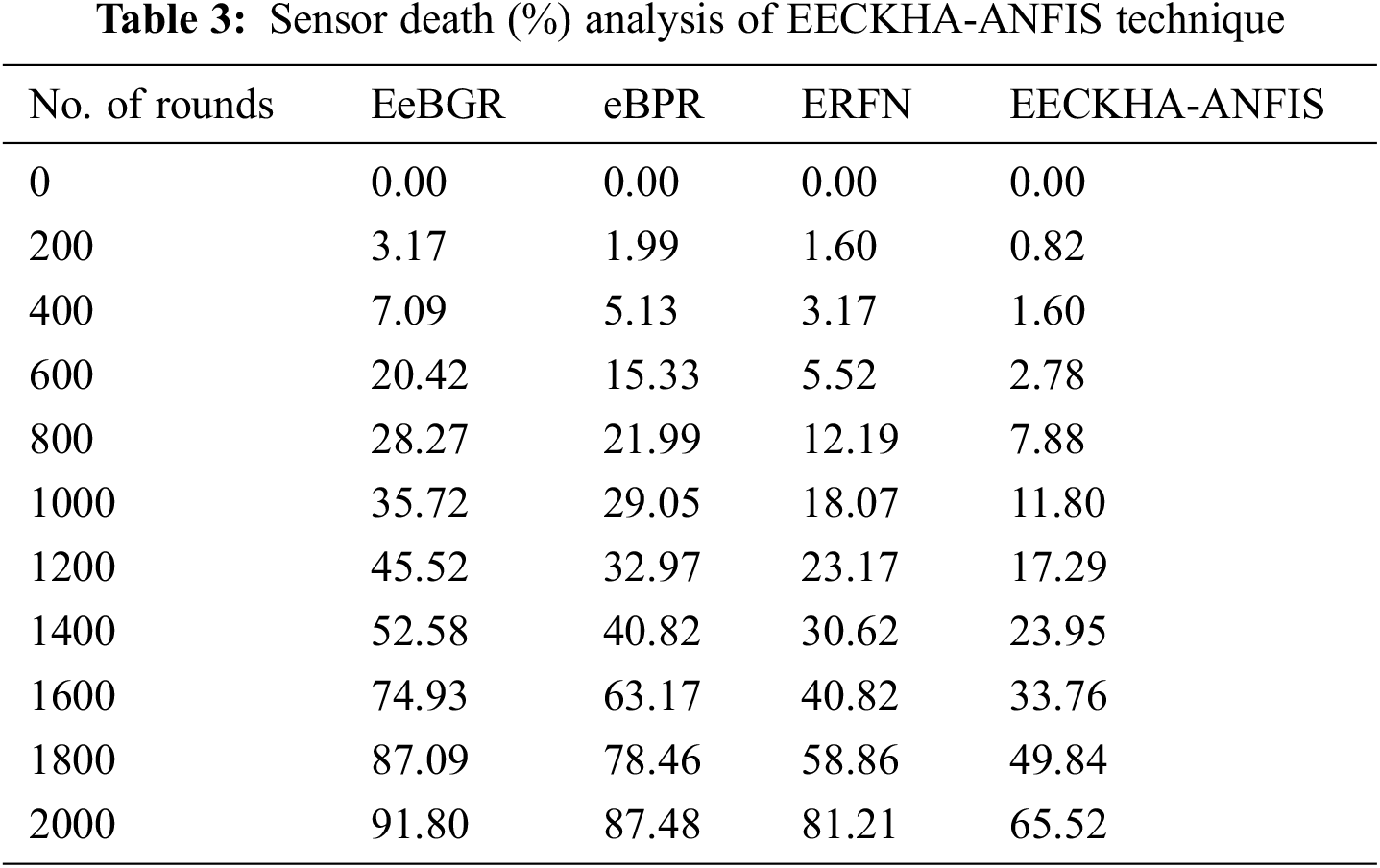
For sample, under 600 rounds, the EECKHA-ANFIS methodology has obtained reduced SDH of 2.78% whereas the EeBGR, eBPR, and ERFN techniques have demonstrated increased SDH of 20.42%, 15.33%, and 5.52% respectively. Simultaneously, under 2000 rounds, the EECKHA-ANFIS system has attained minimal SDH of 65.52% whereas the EeBGR, eBPR, and ERFN techniques have outperformed enhanced SDH of 91.80%, 87.48%, and 81.21% correspondingly.
Tab. 4 and Fig. 6 examined the average energy consumption (AEC) analysis of the EECKHA-ANFIS methodology with recent approaches. The outcomes showcased that the EECKHA-ANFIS approach has reached effectual results with the least AEC over the other methods. For instance, under 600 rounds, the EECKHA-ANFIS method has gained reduced AEC of 0.06 J whereas the EeBGR, eBPR, and ERFN approaches have portrayed increased AEC of 0.59, 0.28, and 0.10 J correspondingly. At the same time, under 2000 rounds, the EECKHA-ANFIS method has attained lower AEC of 1.18 J whereas the EeBGR, eBPR, and ERFN techniques have outperformed higher AEC of 1.89, 1.75, and 1.47 J respectively.
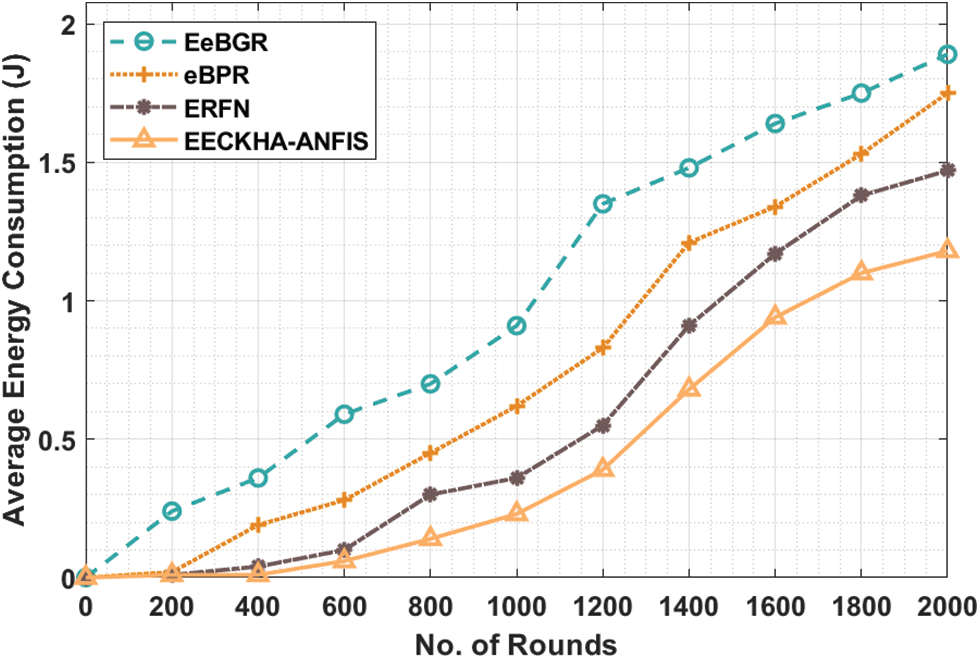
Figure 6: AEC analysis of EECKHA-ANFIS technique with different rounds

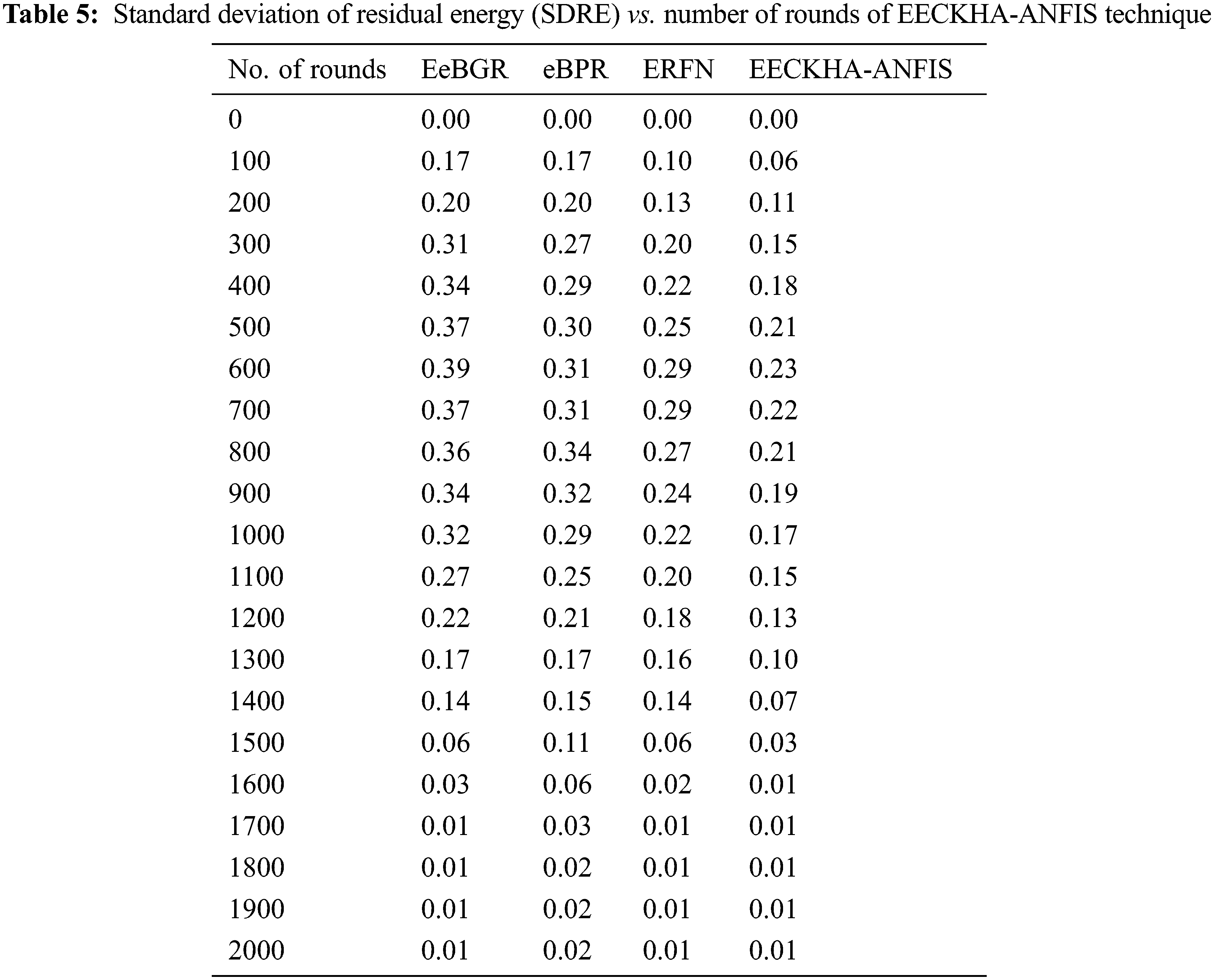
Tab. 5 and Fig. 7 studied the Standard Deviation of Residual Energy (SDRE) analysis of the EECKHA-ANFIS method with recent approaches. The outcomes depicted that the EECKHA-ANFIS technique has attained effective outcomes with the lower SDRE over the other approaches. For instance, under 600 rounds, the EECKHA-ANFIS system has achieved reduced SDRE of 0.23 whereas the EeBGR, eBPR, and ERFN systems have exhibited increased SDRE of 0.39, 0.31, and 0.29 respectively. Followed by, under 2000 rounds, the EECKHA-ANFIS methodology has attained decreased SDRE of 0.01 whereas the EeBGR, eBPR, and ERFN techniques have demonstrated increased SDRE of 0.01, 0.02, and 0.01 correspondingly.
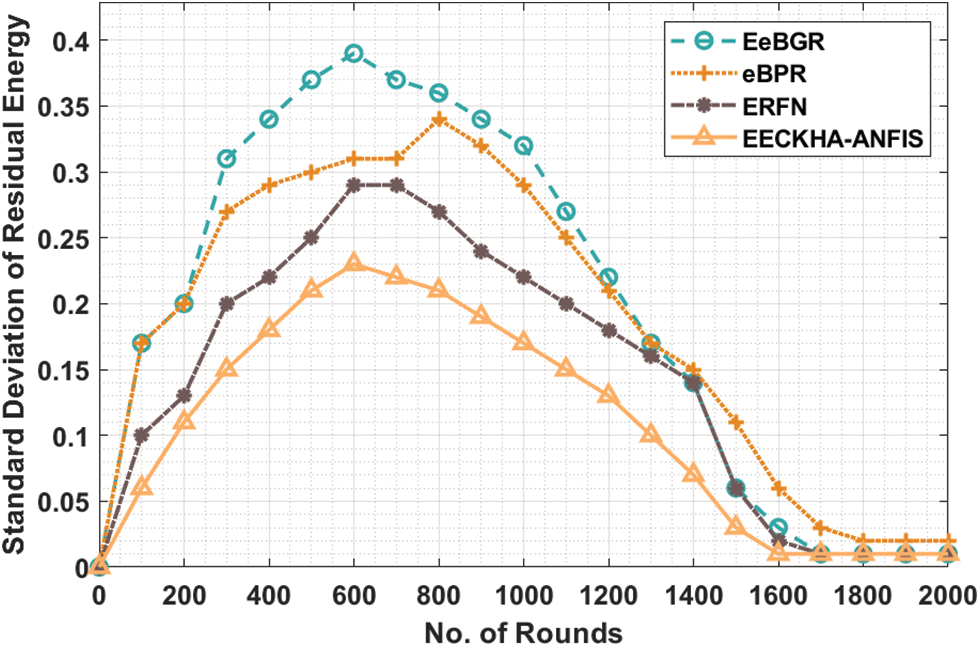
Figure 7: SDRE analysis of EECKHA-ANFIS technique with different rounds
Tab. 6 and Fig. 8 inspected the SDRE analysis with alive sensor nodes of the EECKHA-ANFIS technique with recent methods. The results depicted that the EECKHA-ANFIS method has attained effective results with the least SDRE over the other methods.
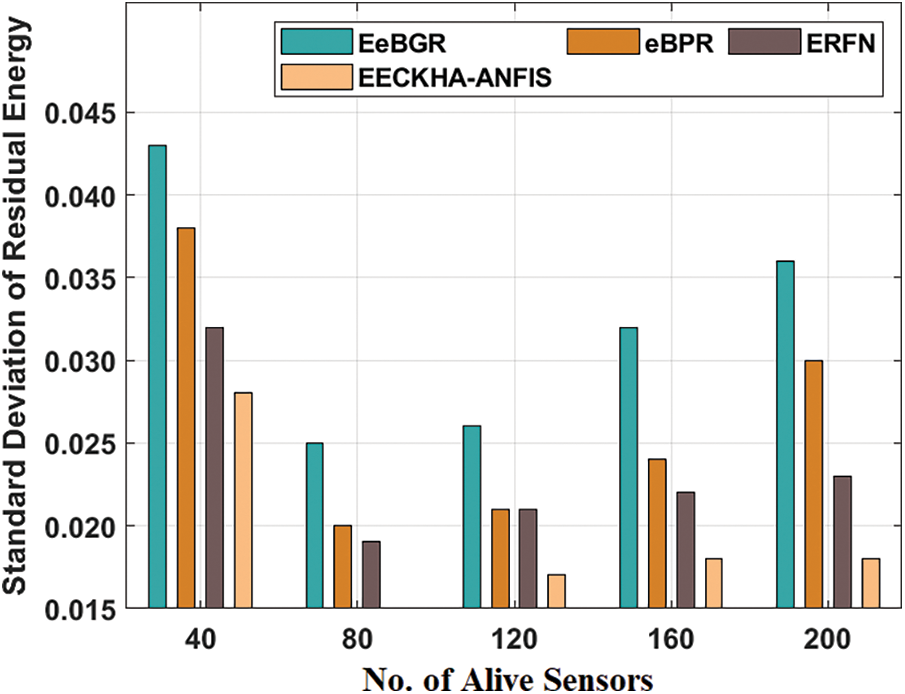
Figure 8: SDRE analysis of EECKHA-ANFIS technique with different alive nodes
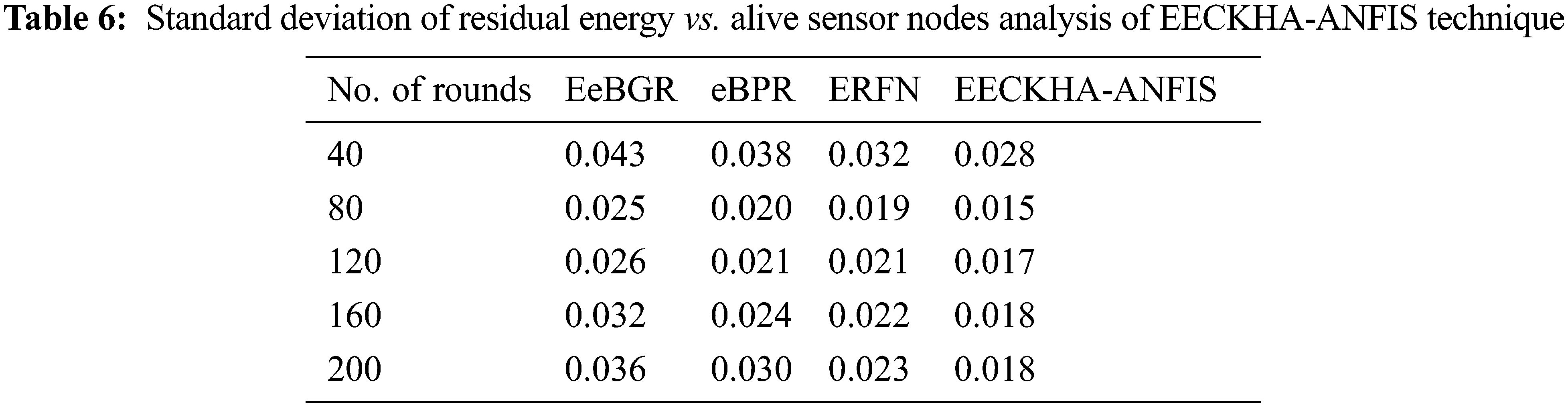
For instance, under 40 nodes, the EECKHA-ANFIS technique has attained minimal SDRE of 0.028 whereas the EeBGR, eBPR, and ERFN techniques have defines enhanced SDRE of 0.043, 0.038, and 0.032 correspondingly. Simultaneously, under 200 nodes, the EECKHA-ANFIS technique has attained lower SDRE of 0.018 whereas the EeBGR, eBPR, and ERFN approaches have demonstrated improved SDRE of 0.036, 0.030, and 0.023 respectively.
In this study, a novel EECKHA-ANFIS technique has been derived for the optimum selection of routes and to accomplish maximum survivability in wireless networks. The selection of routes mainly takes place using the ANFIS model which involves multiple input parameters and produces an optimal route as output. In addition, a collection of fuzzy rules with MFs are designed for the choice of succeeding hop node in wireless networks depending upon varying input parameters and the selection of MF takes place using the CKHA. For investigative the enhanced outcomes of the EECKHA-ANFIS technique, a comprehensive experimental analysis takes place and the outcomes are analyzed under varying dimensions. The detailed comparative study highlighted the superior performance of the EECKHA-ANFIS technique over the existing techniques interms of different measures. In future, the network survivability can be further boosted by the effective design of unequal clustering and data aggregation techniques.
Funding Statement: This research was supported by the Researchers Supporting Program (TUMA-Project-2021-27) Almaarefa University, Riyadh, Saudi Arabia. Taif University Researchers Supporting Project Number (TURSP-2020/161), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. V. Kumar and S. Kumar, “Position-based beaconless routing in wireless sensor networks,” Wireless Personal Communications, vol. 86, no. 2, pp. 1061–1085, 2016. [Google Scholar]
2. Y. Yigit, V. K. Akram and O. Dagdeviren, “Breadth-first search tree integrated vertex cover algorithms for link monitoring and routing in wireless sensor networks,” Computer Networks, vol. 194, pp. 108144, 2021. [Google Scholar]
3. H. Zhang and H. Shen, “Energy-efficient beaconless geographic routing in wireless sensor networks,” IEEE Transactions on Parallel and Distributed Systems, vol. 21, no. 6, pp. 881–896, 2010. [Google Scholar]
4. C. E. Perkins and E. M. Royer, “Ad-hoc on-demand distance vector routing,” in Proc. WMCSA’99. Second IEEE Workshop on Mobile Computing Systems and Applications, New Orleans, Louisiana, pp. 90–100, 1999. [Google Scholar]
5. S. Naeimi, H. Ghafghazi, C. O. Chow and H. Ishii, “A survey on the taxonomy of cluster-based routing protocols for homogeneous wireless sensor networks,” Sensors, vol. 12, no. 6, pp. 7350–7409, 2012. [Google Scholar]
6. S. Arjunan and S. Pothula, “A survey on unequal clustering protocols in Wireless Sensor Networks,” Journal of King Saud University-Computer and Information Sciences, vol. 31, no. 3, pp. 304–317, 2019. [Google Scholar]
7. H. D. S. Araújo, R. H. Filho and W. L. T. d. Castro, “WSN routing: An geocast approach for reducing consumption energy,” in 2010 IEEE Wireless Communication and Networking Conf., Sydney, NSW, Australia, pp. 1–6, 2010. [Google Scholar]
8. J. Wang, Y. Gao, X. Yin, F. Li and H. Kim, “An enhanced PEGASIS algorithm with mobile sink support for wireless sensor networks,” Wireless Communications and Mobile Computing, vol. 2018, pp. 1–9, 2018. [Google Scholar]
9. J. Wang, C. Ju, Y. Gao, A. K. Sangaiah and G. Kim, “A pso based energy efficient coverage control algorithm for wireless sensor networks,” Computers, Materials & Continua, vol. 56, no. 3, pp. 433–446, 2018. [Google Scholar]
10. K. SureshKumar and P. Vimala, “Energy efficient routing protocol using exponentially-ant lion whale optimization algorithm in wireless sensor networks,” Computer Networks, vol. 197, pp. 108250, 2021. [Google Scholar]
11. M. Jeske, V. Rosset and M. C. V. Nascimento, “Determining the trade-offs between data delivery and energy consumption in large-scale WSNs by multi-objective evolutionary optimization,” Computer Networks, vol. 179, pp. 107347, 2020. [Google Scholar]
12. R. A. R. Baluz, R. H. Filho, J. V. V. Sobral, A. S. Sousa, H. S. Araujo et al., “A fuzzy inference system for increasing of survivability and efficiency in wireless sensor networks,” Journal of Communication and Computer, vol. 10, pp. 702–712, 2013. [Google Scholar]
13. R. K. Varun, R. C. Gangwar, O. Kaiwartya and G. Aggarwal, “Energy-efficient routing using fuzzy neural network in wireless sensor networks,” Wireless Communications and Mobile Computing, vol. 2021, pp. 1–13, 2021. [Google Scholar]
14. Y. Zhang, J. Wang, D. Han, H. Wu and R. Zhou, “Fuzzy-logic based distributed energy-efficient clustering algorithm for wireless sensor networks,” Sensors, vol. 17, no. 7, pp. 1554, 2017. [Google Scholar]
15. X. Fu, G. Fortino, P. Pace, G. Aloi and W. Li, “Environment-fusion multipath routing protocol for wireless sensor networks,” Information Fusion, vol. 53, pp. 4–19, 2020. [Google Scholar]
16. X. Fu, Y. Yang and O. Postolache, “Sustainable multipath routing protocol for multi-sink wireless sensor networks in harsh environments,” IEEE Transactions on Sustainable Computing, vol. 6, no. 1, pp. 168–181, 2021. [Google Scholar]
17. R. Huang, L. Ma, G. Zhai, J. He, X. Chu et al., “Resilient routing mechanism for wireless sensor networks with deep learning link reliability prediction,” IEEE Access, vol. 8, pp. 64857–64872, 2020. [Google Scholar]
18. M. Selvi, S. V. N. S. Kumar, S. Ganapathy, A. Ayyanar, H. K. Nehemiah et al., “An energy efficient clustered gravitational and fuzzy based routing algorithm in WSNs,” Wireless Personal Communications, vol. 116, no. 1, pp. 61–90, 2021. [Google Scholar]
19. A. Hamzah, M. Shurman, O. A. Jarrah and E. Taqieddin, “Energy-efficient fuzzy-logic-based clustering technique for hierarchical routing protocols in wireless sensor networks,” Sensors, vol. 19, no. 3, pp. 561, 2019. [Google Scholar]
20. S. Kumar and V. K. Chaurasiya, “A multisensor data fusion strategy for path selection in internet-of-things oriented wireless sensor network (WSNWireless sensor network (WSN),” Concurrency and Computation: Practice and Experience, vol. 30, no. 18, pp. e4477, 2018. [Google Scholar]
21. A. H. Gandomi and A. H. Alavi, “Krill herd: A new bio-inspired optimization algorithm,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 12, pp. 4831–4845, 2012. [Google Scholar]
22. G. Wang, L. Guo, A. H. Gandomi, L. Cao, A. H. Alavi et al., “Lévy-flight krill herd algorithm,” Mathematical Problems in Engineering, vol. 2013, pp. 1–14, 2013. [Google Scholar]
23. H. Bilal and F. Öztürk, “Rubber bushing optimization by using a novel chaotic krill herd optimization algorithm,” Soft Computing, vol. 25, no. 22, pp. 14333–14355, 2021. [Google Scholar]
24. O. Castillo, H. Neyoy, J. Soria, P. Melin and F. Valdez, “A new approach for dynamic fuzzy logic parameter tuning in ant colony optimization and its application in fuzzy control of a mobile robot,” Applied Soft Computing, vol. 28, pp. 150–159, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |