DOI:10.32604/iasc.2022.025387

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.025387 |  |
| Article |
Generating Intelligent Remedial Materials with Genetic Algorithms and Concept Maps
Department of Software Engineering and Management, National Kaohsiung Normal University, Kaohsiung City, 824, Taiwan
*Corresponding Author: Che-Chern Lin. Email: cclin@nknu.edu.tw
Received: 22 November 2021; Accepted: 14 January 2022
Abstract: This study proposes an intelligent remedial learning framework to improve students’ learning effectiveness. Basically, this framework combines a genetic algorithm with a concept map in order to select a set of remedial learning units according to students’ weaknesses of learning concepts. In the proposed algorithm, a concept map serves to represent the knowledge structure of learning concepts, and a genetic algorithm performs an iteratively evolutionary procedure in order to establish remedial learning materials based on students’ understanding of these learning concepts. This study also conducted simulations in order to validate the proposed framework using artificially generated data sets, and problematic issues regarding generalizing the special case of the proposed framework are further discussed. The proposed algorithm can be generally-employed in e-learning, providing a framework for generating remedial learning materials for all kinds of learning fields.
Keywords: Genetic algorithms; concept maps; remedial learning materials; intelligent learning systems
Originally presented by Novak et al. concept maps are utilized to explain the meaningful transitions (relationships) between and among different learning concepts [1]. Basically there are three components in a concept map: vertices, arrowed edges, and linking labels, where a vertex represents a concept, an edge connects two vertices, and a label nearby a particular edge indicates the relationship between the pair of concepts connected by this particular edge. For example, Fig. 1 shows an original concept map consisting of six concepts: horse, animal, run, jump, leg, and motion. The arrowed edges and the labels in this figure indicate the relationships between and among these concepts.
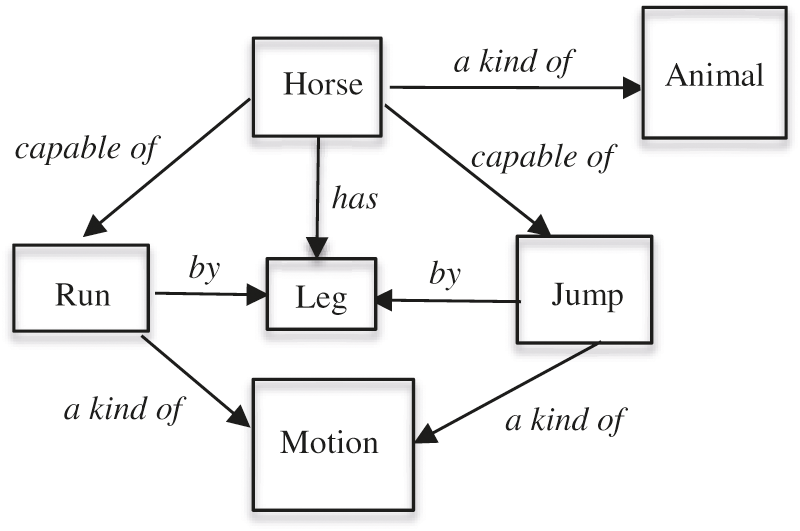
Figure 1: An illustrative example of original concept maps
This study further utilizes a concept map to describe the knowledge structure of learning topics (i.e., the relationships among concepts) in this concept map. Therefore, in this study, a vertex is utilized to represent a particular concept, while an edge connecting two adjacent concepts (vertices) indicates the conceptual relationship between the two connected concepts. An edge can be further marked with an arrow to indicate the relationship’s direction between the pair of vertices linked by this particular edge. In graphic theory, a graphic is called a directed graphic if all of its edges are arrowed. Moreover, an arrowed edge can be marked with a weight to indicate the level of the relationship for this edge. It is important to note that in this study, the value of each weight in a concept map is between 0 and 1.
A graphic is called a weighted directed graphic if all of its edges are arrowed and marked with weights. In graphic theory, a weighted directed graphic is also called a “weighted directed acyclic graphic” if it contains no topological loops. In a weighted directed acyclic graphic, it is impossible to find a consistently and successively directed sequence of edges, starting from a vertex and finally looping back to this particular vertex again. An adjacency matrix is utilized to represent the connectivity relationships between and among the vertices and edges in a weighted directed graphic. In this study, a weighted directed acyclic graphic is utilized as a concept map in order to represent the knowledge structure of a series of learning concepts, and an adjacency matrix is used to indicate the directions and relationship levels of these concepts in the concept map.
In e-learning, the best ways to establish learners’ concepts by providing personalized learning materials would be a worthwhile area of study. More and more e-learning platforms are now adopting intelligent tutoring in order to guide learners to study personalized learning materials according to their individual learning levels or situations. Artificial Intelligence (AI)-based methods might be good ways to generate intelligent learning systems according to learners’ knowledge backgrounds. Popular AI approaches employed to build intelligent learning systems include neural networks, Genetic Algorithms (GAs), fuzzy systems, and data mining techniques.
Based on Darwin’s Theory of Evolution, GAs are among the more widely-used AI methods for finding solutions via a generation-based iterative process. Genes and chromosomes are the fundamental elements in GA manipulations. A gene is a basic unit in GAs; and a chromosome is constituted by a sequence of genes. A chromosome is called a “binary chromosome” if all of its underlying genes have binary values. For instance, a binary chromosome “0110” will be constituted by a sequence of binary genes ‘0’, ‘1’, ‘1’, and ‘0’. Moreover, a fitness function is an evaluation function used to measure the performance of a GA. The goal of GAs is to find optimal or sub-optimal solutions (best or sub-best fitness values) through an iterative process from generation to generation.
There are three basic manipulations of GAs: crossover, selection, and mutation. In a crossover manipulation, each chromosome from parent generations is divided into several parts. These parts are then recombined with the divided parts from other parents, forming new chromosomes for possible child generations. Three most common crossover methods are utilized in GAs: single-point, two-point, and uniform crossovers.
In a selection manipulation, a generation with a better fitness value has a higher probability of being chosen for the next iteration. It is important to note that a generation with the best fitness value is not guaranteed to be chosen for the next iteration. Two well-known selection methods are often utilized in GAs: roulette-wheel and tournament selections. In a roulette-wheel selection, the probability that a child generation will be chosen into the next iteration is in proportion to its fitness value. In a tournament selection, one first randomly picks up m child generations from a candidate pool of all possible child generations, and then selects the n best child generations from the m ones for the next iteration. Moreover, a mutation manipulation randomly chooses a gene and changes the value of the chosen gene. A binary gene’s binary value is changed from 0 to 1 or from 1 to 0 when a mutation manipulation is performed.
Lin et al. have proposed a GA-based method to generate remedial materials according to students’ weakness of ten object-oriented program concepts of Java. However, the work by Lin et al. did not use a concept map to organize the relationships among these learning concepts [2]. Lin et al. have also proposed a concept-transition method to conduct the transitions of the concepts in a concept map according to students’ test results of these concepts [3]. However, there still exists a research gap that how we use a more intelligent method to generate personalized remedial materials for individual students to overcome their learning weakness, from a well-organized concept map which consists of a set of highly related learning concepts. Therefore, in this study, based on a GA and a concept map, we propose a framework to generate intelligent remedial learning materials according to students’ weaknesses of concepts.
The problem statement of this study is conceptually described as follows.
For a learning domain, given (i) a well-organized concept map consisting of a set of relevant learning concepts of this learning domain, and (ii) a set of question-based remedial learning units, conduct an intelligent method to generate personalized remedial learning materials to overcome the weakness of the learning concepts for individual students from these question-based remedial learning units, according to test results of these students. The formal and mathematical problem statement will be discussed in Section 4.3.
To fulfill the problem statement, this study proposes an algorithm called a “Genetic Algorithm With Concept Map” (GAWCM) algorithm. The proposed algorithm uses a GA to generate personalized remedial learning materials according to learners’ weaknesses of the concepts in a concept map. It is basically a framework for generating remedial learning materials for all kinds of learning fields, and can be generally employed in e-learning. The flowchart of the GAWCM is shown in Fig. 2.

Figure 2: The flowchart of the proposed algorithm
Since the remedial learning materials generated by the proposed GAWCM algorithm are quiz-based learning units, this section will first focus on the studies related to test sheet generation. Then, we discuss how to generate concept maps with optimization methods, and how to establish personalized learning paths according to difference learning objects. Finally, research on the use of concept maps to construct knowledge structures will be investigated.
In test sheet generation, several approaches have been proposed in order to optimize the quality of test sheets. For example, Hwang et al. [4] have presented a mixed integer programming-based technique for generating test sheets for multiple learning concepts. Their work has demonstrated two heuristic methods, the feasible time first method and the concept lower-bound first method, in order to produce test sheets with sub-optimal solutions [4]. In addition, a parallel test sheet using the Tabu approach has been proposed for generating parallel test sheets from very large test item banks for national tests, using a multi-criteria assessment [5]. Moreover, Moreno et al. have used a GA and a multiple-agent technique to establish a test sheet generation system in which three factors have been considered: difficulty level, knowledge points, and teaching requirements [6].
Fuzzy cognitive maps, originally proposed by Kosko, are a tool to describe relevant concepts in a graph-like diagram where a vertex represents a single concept, and an edge linking two vertices (concepts) indicates the causal relationships between the two concepts [7]. Furthermore, weights labeled nearby their corresponding edges are used to indicate the influence degree of the causal relationships of these edges. Several studies have utilized different approaches to optimize the weights in a fuzzy cognitive map such as genetic algorithms [8–10] and decomposed parallel ant colony algorithm with gradient descent local search [11]. In addition, Gunel et al. have proposed a concept map mining method combining a neural network and some evolutionary algorithms to detect learning concepts from text-based documents [12]. The work by Gunel et al. automatically extracted learning concepts from educational documents without domain-relevant knowledge, and outperformed traditional concept detection algorithms.
An earlier research project has employed a similarity-based approach to search for suitable online curricula for a trigonometry course using a GA, where eight multiple intelligences were employed as measurements [13]. Huang et al. have utilized a hybrid method combining a GA and case-based reasoning to produce customized learning sequences for Java learners [14]. In this work done by Huang et al. the GA served to generate suitable learning paths according to the difficulties and degrees of relevance between and among the learning materials; the case-based reasoning was utilized to evaluate learners’ learning performance. Based on students’ different knowledge levels, Hovakimyan et al. have implemented a GA-based scenario system to choose teaching resources according to keywords and searching time [15]. This scenario system could be suitable for e-learning and/or web-based learning, selecting appropriate learning resources via a set of keywords within a certain period of time. Moreover, based on learners’ knowledge structures, Chen has employed an enhanced path-finder network to generate remedial learning paths in an introductory Java course [16]. In Chen’s work, personalized diagnosis and a remedial learning system were employed to detect learners’ misconceptions and to recommend learning paths. In addition, a heuristic method has been proposed for finding the optimal paths in a context-aware ubiquitous learning environment for a primary school’s ecology course, according to the relationships among different learning objectors [17]. A GA-based technique to determine learning sequences has been proposed according to the wrong answers on a test, where the difficulty of courses and the continuity of concepts were considered [18]. Based on a set of learning objects in a repository, a navigation system has been established for an ecosystem course, decreasing the learners’ cognitive load [19]. Bina et al. have proposed an immune algorithm to generate adaptive learning paths for learners based on a concept map [20]. In this immune algorithm, learning objects were grouped according to these learning concepts in the concept map, and the optimal learning path for a particular learner was formed by selecting a learning object for each concept.
Many of previous studies have used concept maps to illustrate the knowledge structures of learning topics in different learning fields. For example, Shallcross has presented case studies using a concept map for oil platform safety education [21]. Svanström et al. have applied concept maps and statistical methods to sustainable development education [22]. In computer science education, concept maps have been utilized in teaching computer programming [23], software engineering [24], and floating-point standards [25]. Moreover, concept maps could also be adopted as teaching tools for physical problem solving [26], business processes [27], sports [28], English learning [29], and testing theories [30]. To further reduce learners’ cognitive load, an interface called Airmap has been introduced to automatically manage concept layout [31]. Concept maps could also be employed to correct knowledge ontologies based on two measures, closeness and similarity, making measurements more precise and powerful [32].
Fig. 3 shows an illustrative example of a concept map with four learning concepts. It is a weighted directed acyclic graphic with 4 vertices. Each vertex in the figure represents one of the four learning concepts with a one-to-one correspondence. In this figure, each edge connecting two adjacent vertices is marked with a weight which represents the level of the relationship between the two connected vertices. Each edge in this concept map is an arrowed edge which indicates the direction of two connected vertices linked by it. Consider two vertices, Vertex i and Vertex j, connected by a directed edge marked with an arrow pointing from Vertex i (arrow’s tail) to Vertex j (arrow’s head). Vertex i is called a predecessor of Vertex j. In contrast, Vertex j is called a successor of Vertex i. Thus, for example, in Fig. 3, Vertex 1 and Vertex 2 are connected by an arrow extending from Vertex 1 to Vertex 2. Vertex 1 is the predecessor of Vertex 2, and Vertex 2 is the successor of Vertex 1.
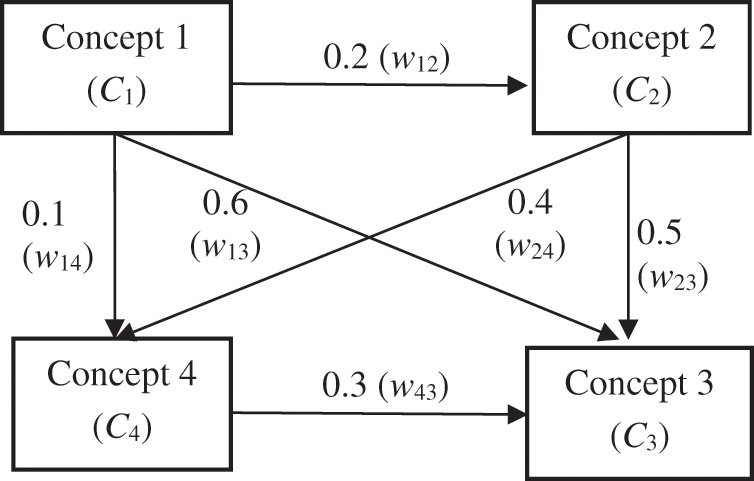
Figure 3: An illustrative example of concept maps used in this study
In a concept map, if Vertex i is a predecessor of Vertex j, it means that Concept i (Ci) is a prerequisite concept of Concept j (Cj), and the weight on the edge indicates the influence level of Concept i on Concept j. For a weight wij connecting Concept i to Concept j, this can be considered as an “influence coefficient” from Concept i to Concept j. A higher value of wij means a higher level of influence that Concept i has on Concept j. For instance, In Fig. 3, Concept 3 has three prerequisite concepts: Concepts 1, 2, and 4, with three “influence coefficients": w13 = 0.6, w23 = 0.5, and w43 = 0.3, respectively. This implies that the influence of Concept 1 on Concept 3 is greater than that of Concept 2 on Concept 3, since w13 > w23. Similarly, the influence of Concept 2 on Concept 3 is greater than that of Concept 4 on Concept 3 since w23 > w43; the influence of Concept 1 on Concept 3 is greater than that of Concept 4 on Concept 3 since w13 > w43.
Definition 1: Adjacency Matrix A
An adjacency matrix A for a concept map is a matrix indicating the levels of relationships between and among the vertices (concepts) in this concept map. Each element in the matrix represents a weight (the level of the relationship) from a source vertex (arrow’s tail) to a destination vertex (arrow’s head). The diagonal elements in an adjacency matrix are all assigned a value of 0. If two vertices are not connected by an edge, the value of this weight is assigned a value of 0. The following matrix is the adjacency matrix associated with the concept map shown in Fig. 3.
Definition 2: Transition Matrix T
A “transition matrix” T for a concept map is defined as follows:
where A is the adjacent matrix of the concept map, and I is an identity matrix whose diagonal elements are 1, and 0 elsewhere. Then by Eq. (1), the transition matrix T for the concept map shown in Fig. 3 is
Definition 3: Concept Vector
In a concept map, a “concept vector”
where n is the number of concepts in the concept map.
Definition 4: Cumulative Concept Vector
For a concept map, a “cumulative concept vector”
where n is the number of concepts in the concept map.
For example, consider the concept map shown in Fig. 3 again. By Eq. (2),
where
As mentioned earlier, wij can be considered as the influence level of Concept i on Concept j. The ith element (qi) in cumulative concept vector
Here, then, q3 is the accumulated value of Concept 3 (p3) itself with a weight (influence coefficient) of 1, Concept 1 (p1) with a weight (influence coefficient) of 0.6, Concept 2 (p2) with a weight (influence coefficient) of 0.5, and Concept 4 (p4) with a weight (influence coefficient) of 0.3. As mentioned above, the structure of a concept map can be considered as the structure of the prerequisite relationships between and among the concepts in this concept map. If a student has a misconception about concept 3, the main reason will be that he or she is not proficient in Concept 3 (p3) itself. Therefore on the right hand side of Eq. (4), p3 is multiplied by 1. Another possible cause of any misconceptions about Concept 3 may be that the student is not proficient in the prerequisite concepts of Concept 3 (i.e., Concepts 1, 2, and 4). Therefore on the right hand side of Eq. (4), p1, p2, and p4 are multiplied by the influence coefficients (weights) of 0.6, 0.5, and 0.3, respectively.
This section discusses the design of the GA which is based on [2]. We first explain the structure of the chromosome and the genes of the GA, and then define a weakness vector and a remedial vector based on a concept map. Finally, we describe the procedure of computing fitness values.
In this study, a single chromosome (binary string) has been utilized to formulate the problem. Each binary character (bit) in the chromosome represents a gene, and is associated with a remedial learning unit in a repository. If the value of a gene is 1, it means that the remedial learning unit associated with this particular gene is chosen. On the other hand, if the value of a gene is ‘0’, it indicates that the remedial learning unit associated with this gene is not chosen. For example, consider a repository consisting of 100 question-based remedial learning units, marked from Q1 to Q100. One can use a single chromosome to represent this repository. The number of binary characters in this chromosome is 100, with a one-to-one correspondence to these 100 remedial learning units. The conceptual structure of this chromosome is shown in Fig. 4, where the binary characters marked with 1 are the questions selected as remedial learning units (e.g., Q2, Q5, and Q98), while those marked with 0 are the ones not selected (e.g., Q1, Q3, Q4, Q99, and Q100).

Figure 4: Conceptual structure of a chromosome
4.2 Weakness Vector and Remedial Vector
Assume that there are n concepts in a concept map. A question is designed to cover multiple concepts (from at least 1 concept to at most n concepts). Consider a question set S, say QS, having m questions. The “concept coverage matrix”
where cij is the concept coverage of Concept i in Question j, and 0 ≤ cij ≤ 1. In Eq. (5), the sum of the concept coverages for each question is normalized to 1, i.e.,
For example, consider a concept map having 4 concepts (C1 to C4), and a question set QS having 7 questions. Suppose that the concept coverage for the 7 questions is shown in Tab. 1.
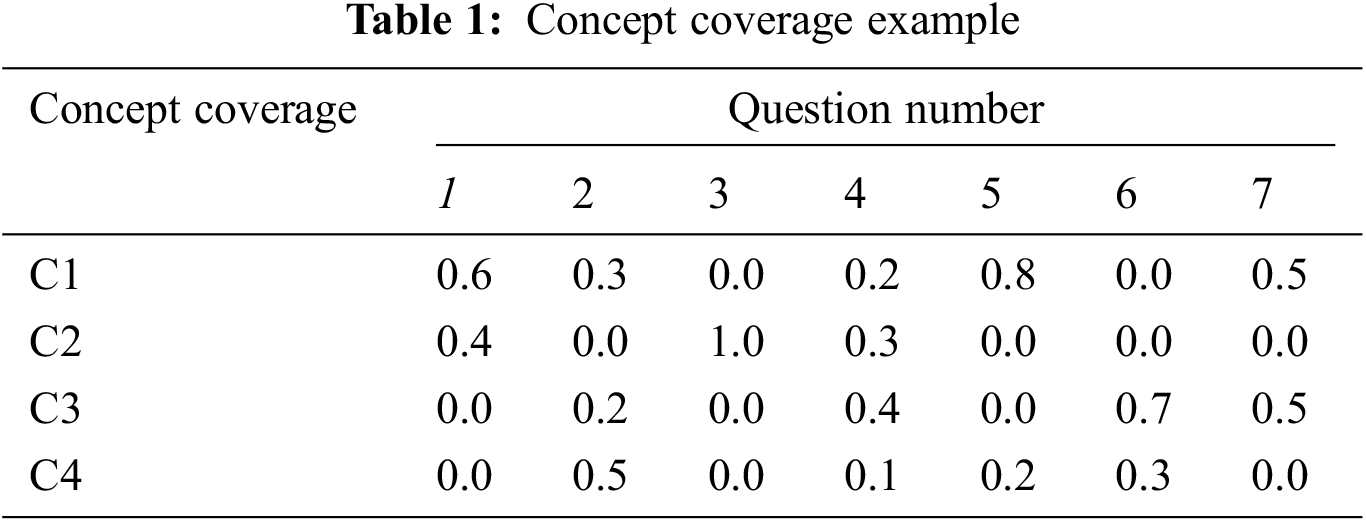
The concept coverage matrix
Now suppose that a particular student takes a test and receives a score. Two sets are defined for calculating the concept weakness for this particular student. They are:
QT: the set of all the questions on the test.
QC: the set of all the questions which have been answered correctly on the test.
In addition, two cumulative concept coverage matrices, U and V, associated with QT and QC, are defined by the following matrix manipulation formulas:
The “un-normalized weakness” for Concept i is defined by the following formula [2].
where
Uij = the element in the ith row and jth column in U
Vij = the element in the ith row and jth column in V
The “normalized weakness” for Concept i is calculated by the following equation [2].
where
ki = the normalized weakness for Concept i
n = the number of concepts in the test
Definition 5: Weakness Vector
Consider a concept map having n concepts. A “weakness vector”
where k1, k2, …, kn are the normalized weaknesses for Concepts 1, 2, …, n, respectively.
Assume that QR is the set of questions in remedial learning materials. The “normalized remedial coverage” for Concept i is obtained by the following formula [2].
where
ri = normalized remedial coverage for Concept i
Definition 6: Remedial Vector
Consider a concept map having n concepts. A “remedial vector”
where r1, r2, …, rn are the normalized remedial coverages for Concepts 1, 2, …, n, respectively.
The main goal of the GAWCM algorithm is to generate optimal remedial learning materials such that the gap between the learning weaknesses of learners and the concepts covered by the remedial materials is minimal.
Definition 7: Gap Vector
A “gap vector”
where
|·| = an absolute value operation
The fitness function is given by the following formula [2].
where
gi: the ith element in
n: the number of concepts.
The goal of the GAWCM algorithm is to minimize the fitness function, and the procedure of computing a fitness value is described as follows.
Step 1: Use a similar way of Eq. (5) to generate concept coverage matrices
Step 2: Compute weakness vector
Step 3: Compute remedial vector
Step 4: Compute gap vector
Step 5: Compute a fitness value by Eq. (15).
To validate the proposed GAWCM algorithm, this study performed simulations with artificially generated data sets. The concept map for the simulations is demonstrated in Fig. 5. The simulations’ parameters are shown as follows:
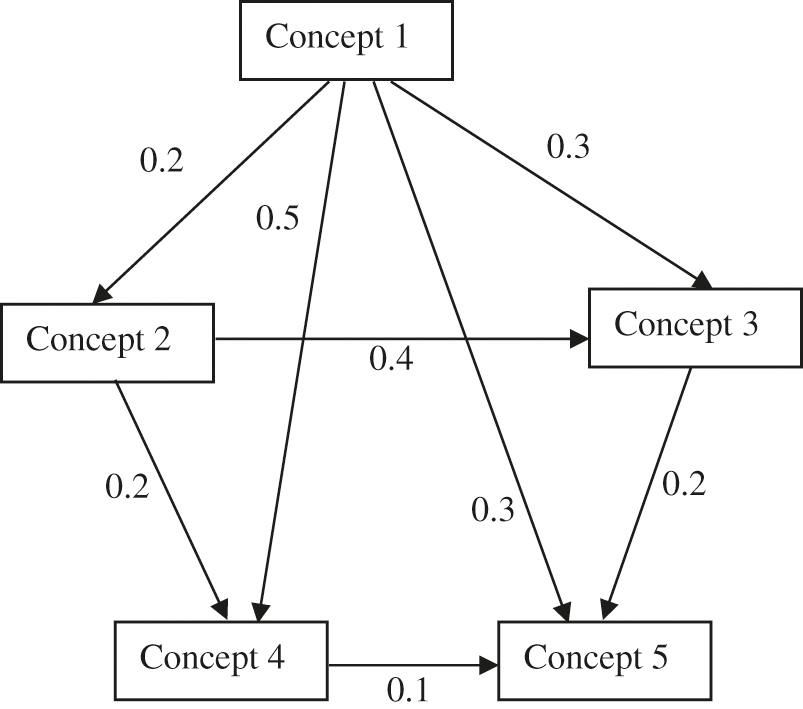
Figure 5: The concept map for the simulations
GA:
Number of generations: 20
Size of selection pool: 100 chromosomes
Selection methods:
(i) Roulette-wheel selection
(ii) Tournament selections: select the best chromosome from among m chromosomes that were randomly chosen from the selection pool, where
Crossover method: uniform crossover
Mutation: no mutation occurred
Number of students: 100
Number of questions in the pre-test: 20
Number of Concepts: 5
Concept coverage for remedial learning units: artificially generated data
Concept coverage for the pre-test: artificially generated data
Sizes of the repository: 50, 100, 150, 200, 250, and 300
Scores of the students: artificially-generated data
To compare results, this study used a random selection method as a counterpart algorithm which selected chromosomes randomly. Tab. 2 shows the results of using the GAWCM algorithm with a roulette-wheel selection method. In Tab. 2, ratios of the fitness values for using the GAWCM algorithm to those for using the random selection method are used to evaluate the performances of the GAWCM algorithms. A lower ratio means a better performance for the GAWCM algorithm. Tabs. 3–6 demonstrate the results of the GAWCM algorithm using tournament selections with m = 2, 4, 6, 8, respectively (m refers to Eq. (16)). Similarly, ratio values are also utilized to indicate the performances of the GAWCM algorithm with these tournament selections. The summarized results are shown in Fig. 6. In this figure, the x-axis denotes the growing sizes of the repository; the y-axis denotes the ratio of a fitness value using the GAWCM algorithm to that using the random selection method.
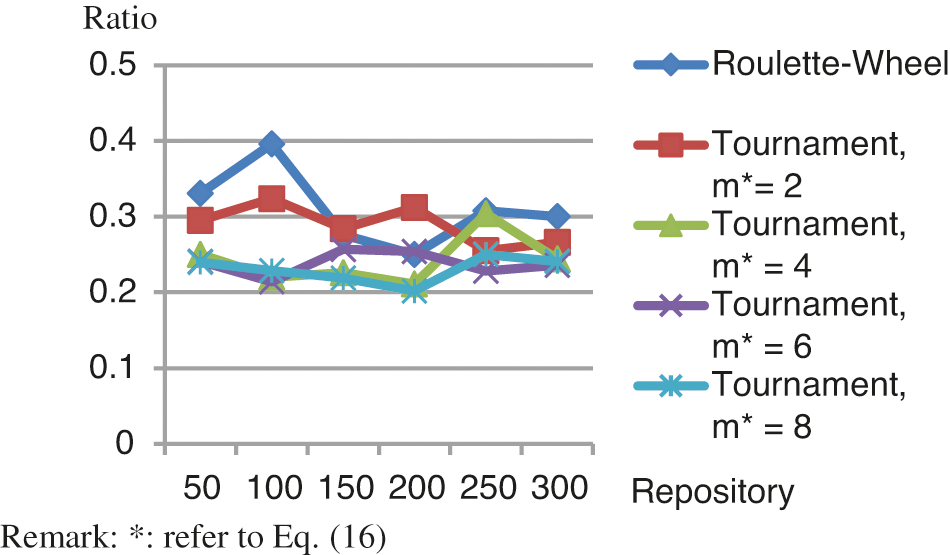
Figure 6: Performances of using the GAWCM algorithm
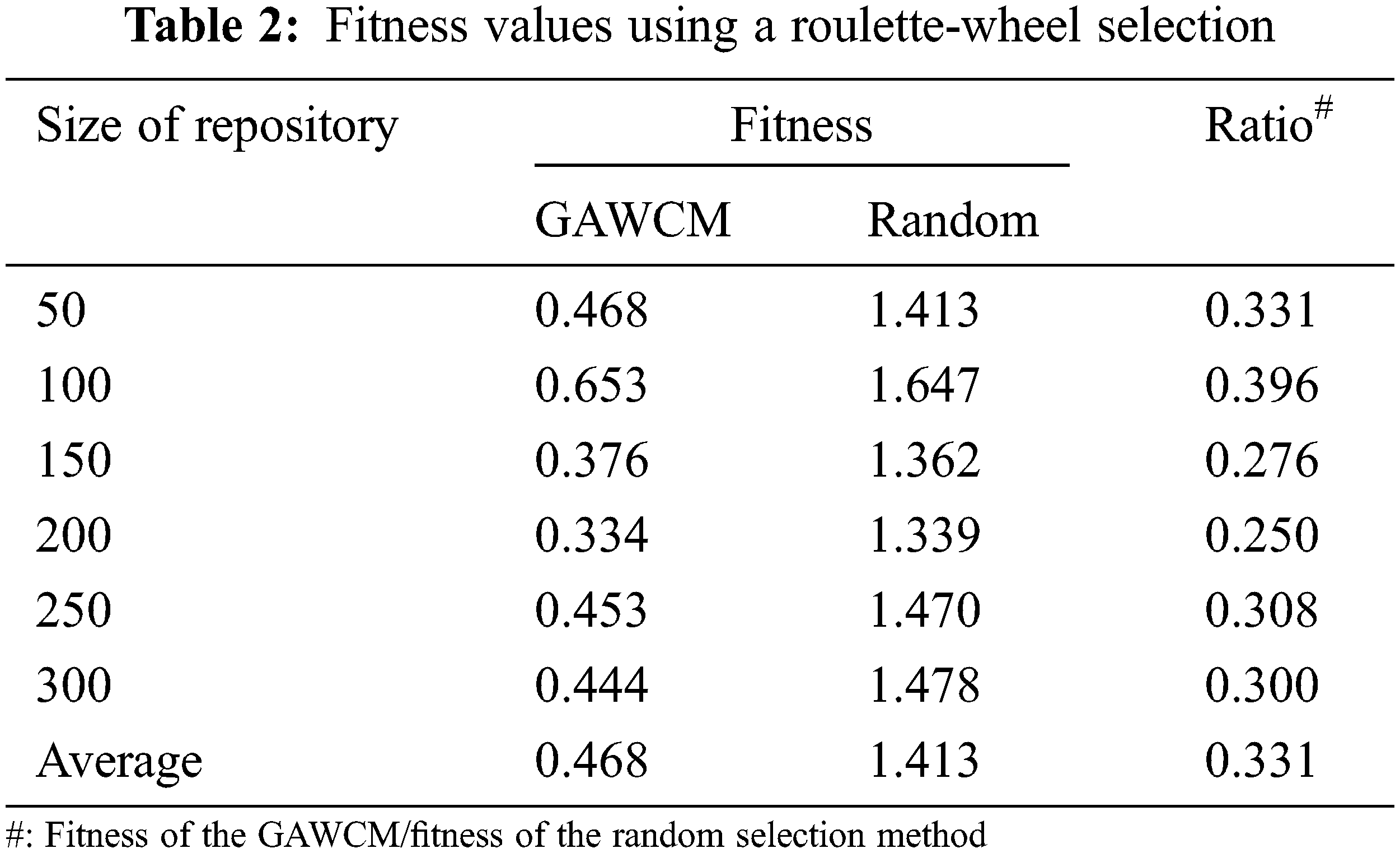
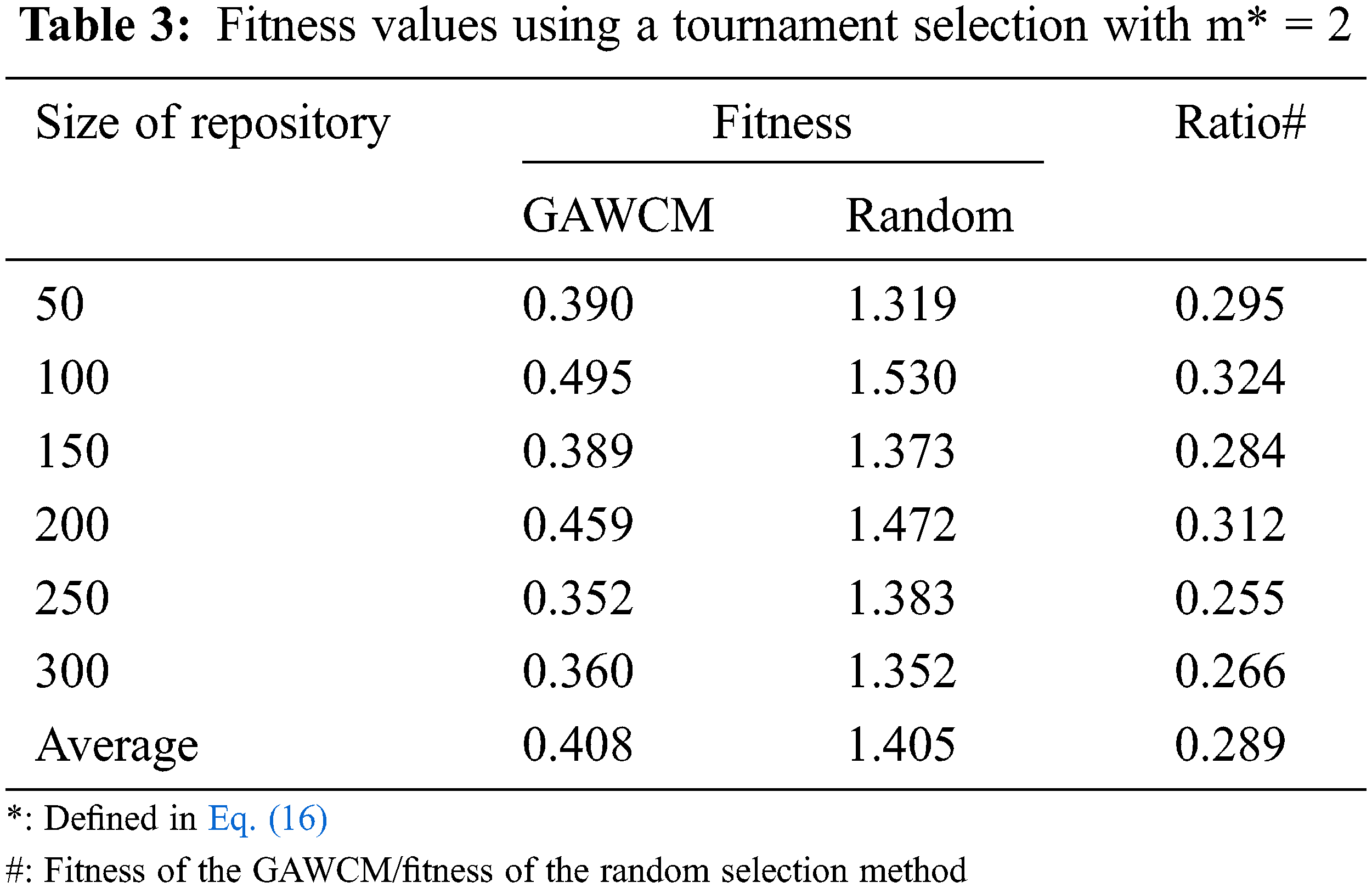
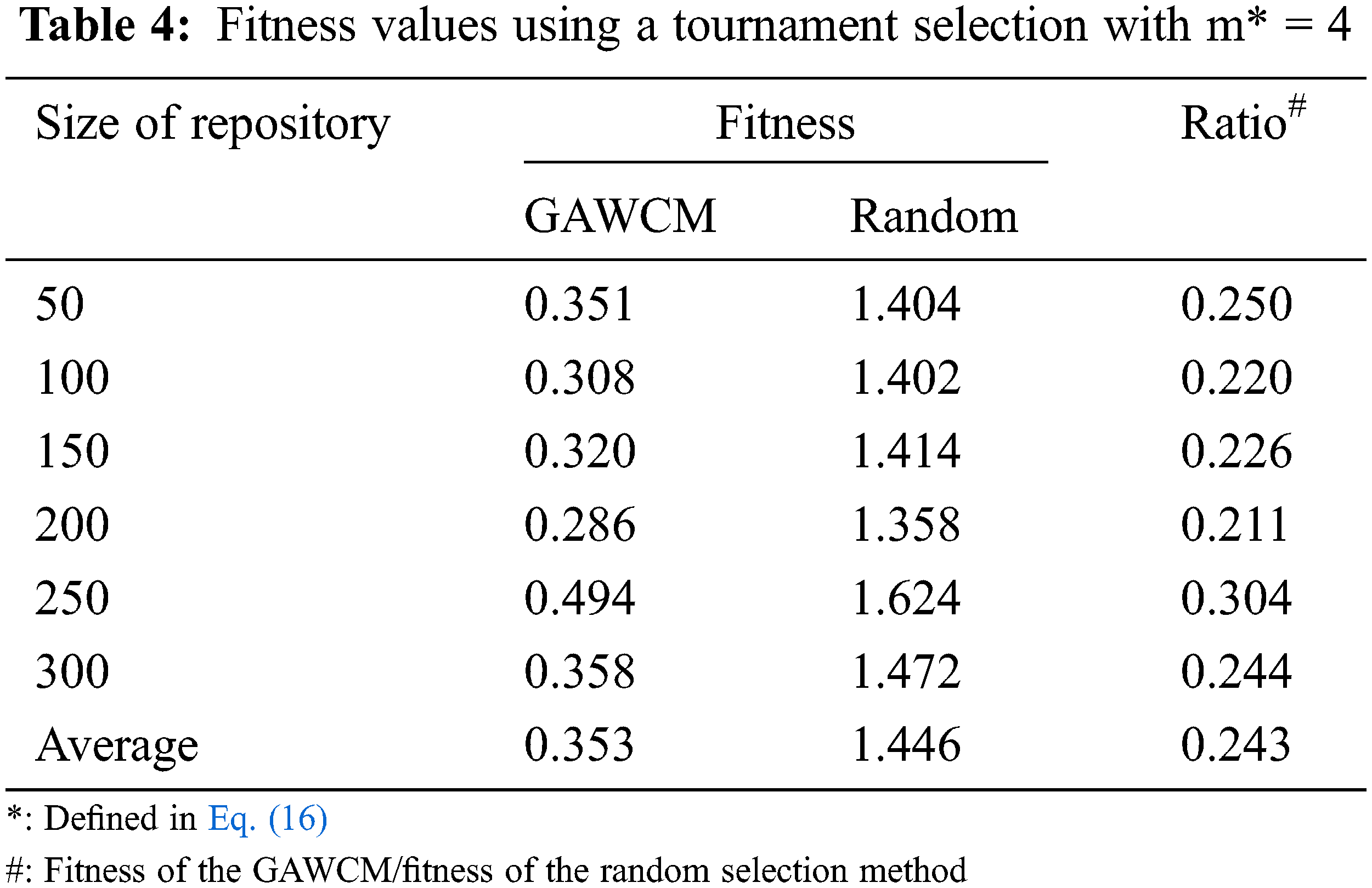
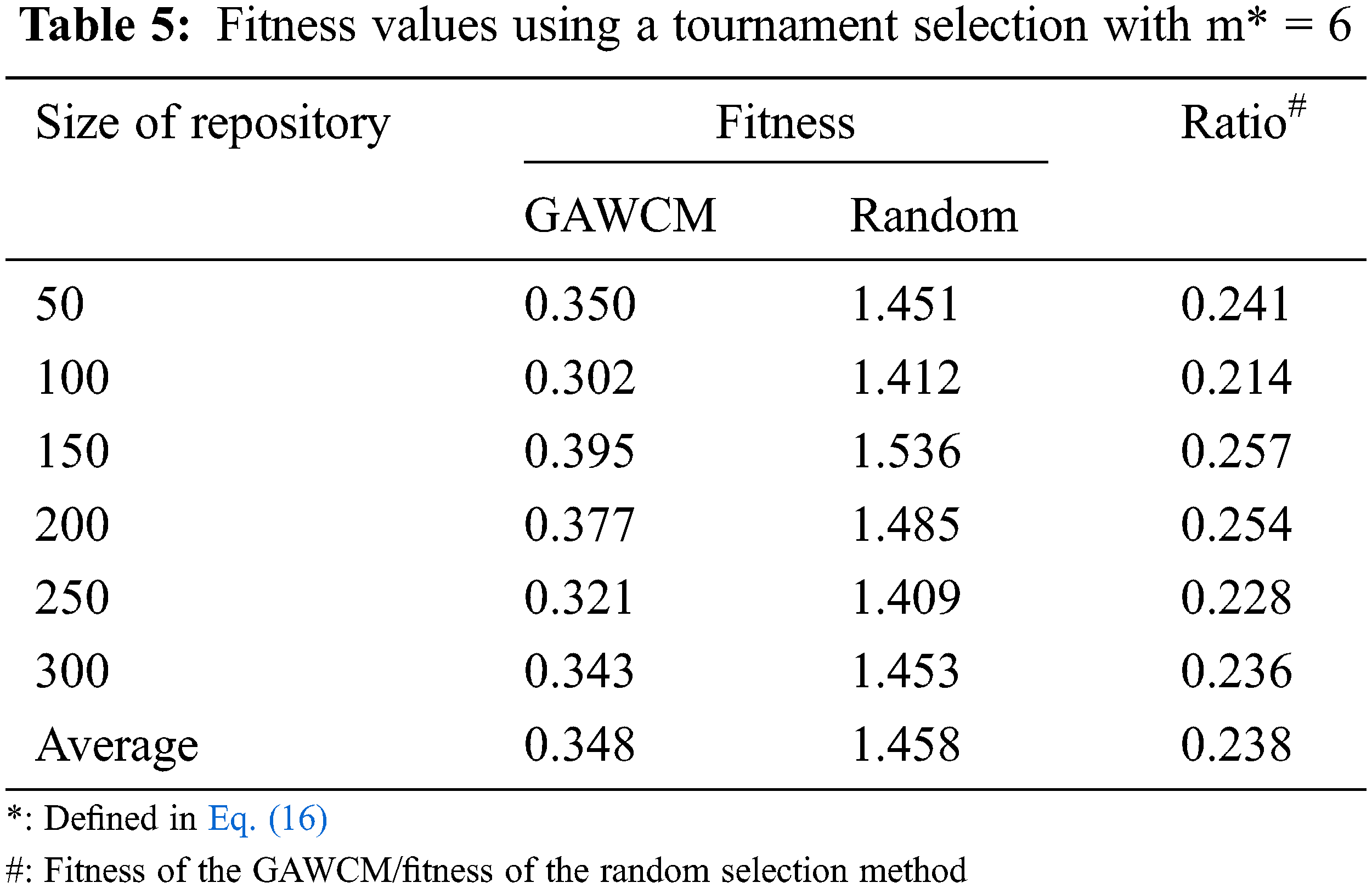
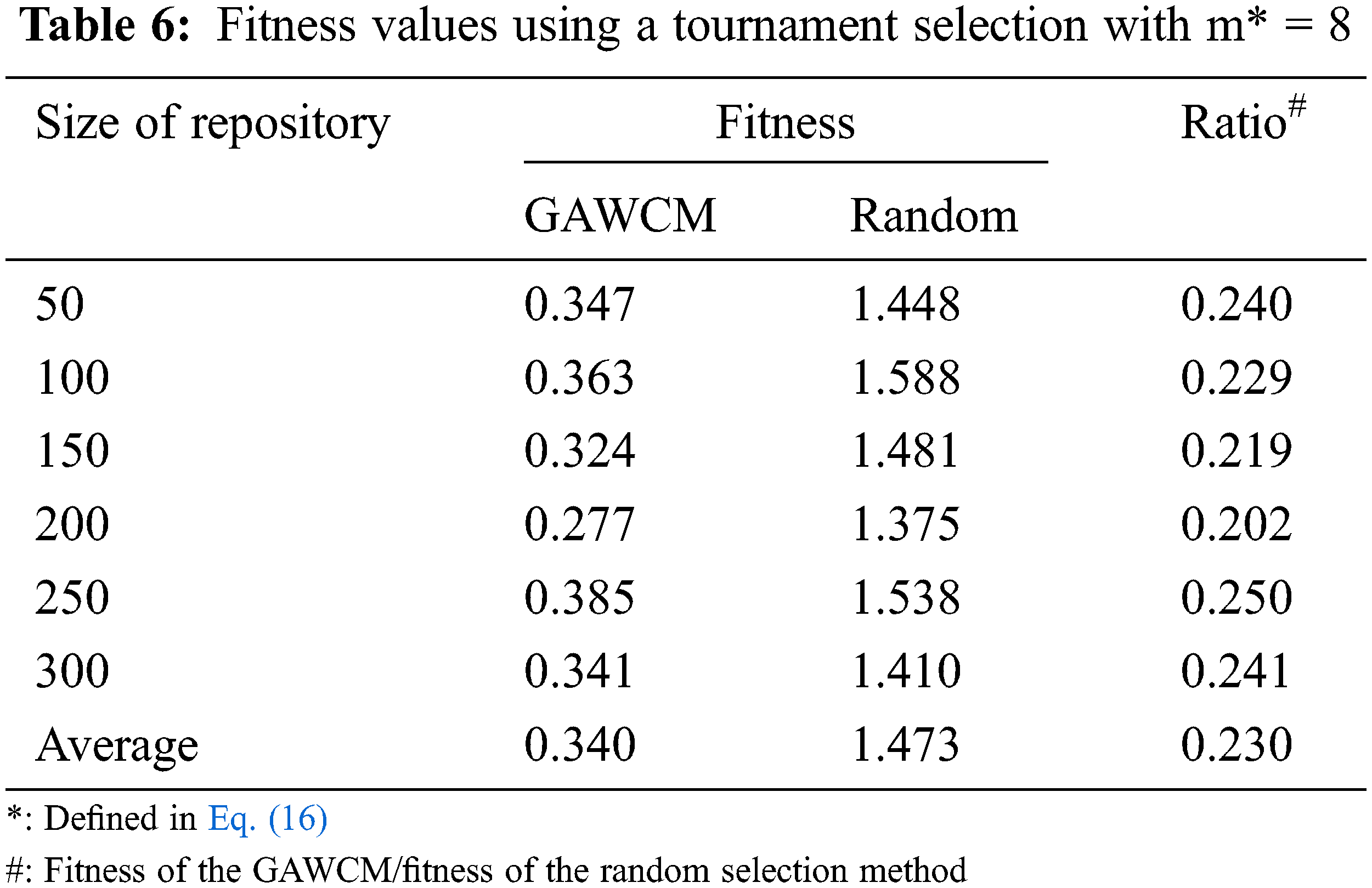
From Tabs. 2–6 and Fig. 6, three findings are stated as follows.
i) The performances of the GAWCM were better than those of the random selection method, significantly reducing the fitness values.
ii) The performances of the tournament selections were slightly better than those of the roulette-wheel selection.
iii) In the tournament selections, a higher m got a better performance.
The GAWCM algorithm uses a weight to indicate an influence-level relationship for two directly-connected concepts. This section first gives some necessary definitions, and then provides examples for further discussion. Next, the generalization of the GAWCM algorithm is discussed, followed by a special case of this algorithm.
Definition 8: Directed Path
In a concept map, a “directed path” from Vertex x to Vertex y (x ≠ y) is a path constructed by a consistently and successively directed sequence of edges starting from Vertex x to Vertex y.
It is important to note that the number of directed paths from Vertex x to Vertex y could be more than 1. (There may be multiple directed paths from Vertex x to Vertex y).
Definition 9: Minimal Directed Path
In a concept map, a “minimal directed path” from Vertex x to Vertex y is a directed path whose total number of elements in all of the directed paths from Vertex x to Vertex y is minimal.
For example, Fig. 7 shows a concept map having 8 concepts. In this figure, there are two directed paths from Vertex 2 to Vertex 6. The first is the sequence {Vertex 2, Vertex 4, Vertex 5, Vertex 8, Vertex 6}; the number of elements in the first directed path is 5. The second directed path from Vertex 2 to Vertex 6 is the sequence {Vertex 2, Vertex 6}; the number of elements in the second directed path is 2. According to Definition 8, the minimal directed path from Vertex 2 to Vertex 6 is the sequence {Vertex 2, Vertex 6}. Similarly, the sequence {Vertex 1, Vertex 2} is a directed path from Vertex 1 to Vertex 2, and is also the minimal directed path from Vertex 1 to Vertex 2 since there is only one directed path from Vertex 1 to Vertex 2.
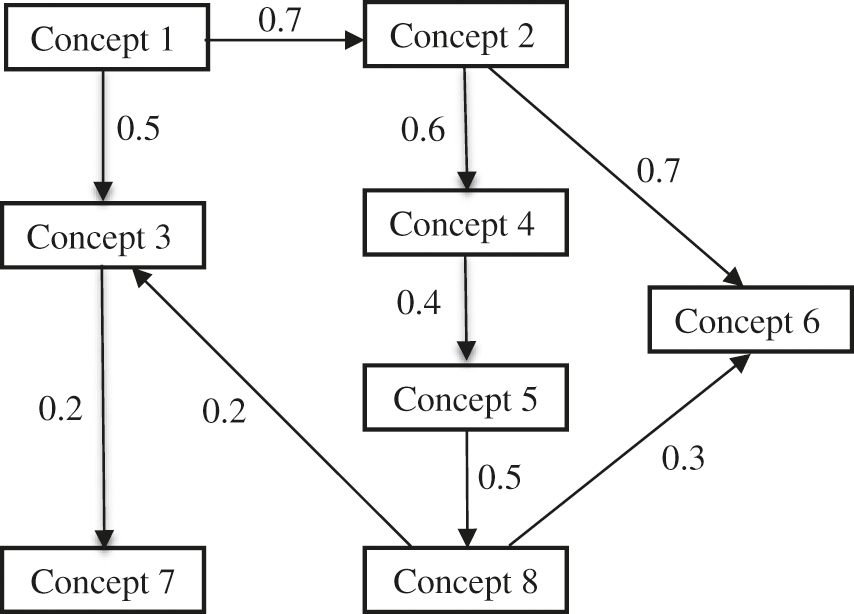
Figure 7: Example of predecessors with P-S degree
Definition 10: The Predecessor-Successor (P-S) Degree of two Vertices
For two vertices in a concept map, Vertex x and Vertex y, if there exists a minimal directed path from Vertex x to Vertex y, the Predecessor-Successor (P-S) degree of the two vertices is the number of preceding vertices in this minimal directed path from Vertex x (inclusive) to Vertex y (exclusive).
For example, in Fig. 7 the P-S degree of Vertex 1 and Vertex 2 is 1, since Vertex 2 has only one preceding vertex (Vertex 1) in the minimal directed path {Vertex 1, Vertex 2}. In this example, Vertex 2 is not considered a preceding vertex since it is exclusive (by Definition 9). Similarly, the P-S degree of Vertex 2 and 4 is 1 via the minimal directed path of {Vertex 2, Vertex 4} since there is only one preceding vertex (Vertex 2) in this minimal directed path. The P-S degree of Vertex 2 and Vertex 8 is 3 since there are three preceding vertices (Vertex 2, Vertex 4, and Vertex 5) via the minimal directed path {Vertex 2, Vertex 4, Vertex 5, Vertex 8}. The P-S degree of Vertex 2 and 6 is 1 via the minimal directed path {Vertex 2, Vertex 6} since there is only one preceding vertex (Vertex 2) in this minimal directed path. It is obvious that for a concept map having n concepts, the maximum P-S degree of any pairs of vertices is less than n.
6.2 Generalization of the GAWCM Algorithm
The GAWCM algorithm uses a P-S degree of 1 for any pairs of connected vertices in a concept map. It can be easily generalized when using a P-S degree of d where 2 ≤ d < n. In this case, Eqs. (7) and (8) should be modified by the following matrix manipulation formulas:
where A is an adjacency matrix in a concept map.
6.3 Special Case of the GAWCM Algorithm
For the GAWCM algorithm, if one uses a P-S degree of 0 for any pairs of vertices in a concept map, the transition matrix (T) of this concept map is an identity matrix whose diagonal elements are all 1, and 0 elsewhere. In this case, the learning concepts in this concept map individually exist without any edges to connect any other concepts. The GAWCM simply performs GA computing without actually using a concept map. Thus, Eqs. (7) and (8) are modified by the following matrix manipulation formulas:
where I is an identity matrix whose diagonal elements are all 1, and 0 elsewhere.
This study proposes the GAWCM algorithm as a framework for generating intelligent remedial learning systems. In this framework, a GA and a concept map are utilized to select a set of remedial learning units from a repository based on learners’ weaknesses in learning concepts. Basically, the GAWCM algorithm employs a concept map to represent the knowledge structure of the learning concepts in this map, and then uses GA computing to generate remedial learning materials according to learners’ understanding of these learning concepts. In the GAWCM algorithm, a weighted directed acyclic graphic is used as a concept map to represent the predecessor-successor relationships between and among the learning concepts in the concept map.
In a predecessor-successor relationship, the predecessors of a particular concept are considered as the prerequisite concepts of this particular concept. A predecessor-successor pair is formed by two connected concepts linked by edges marked with a weight (influence coefficient) to indicate how the predecessor concept affects the successor concept. A transition matrix is utilized to represent the entire structure of the predecessor-successor relationships in a concept map. The transition matrix is then fed into a GA, and the GA employs an iteratively evolutionary procedure to obtain a set of remedial learning units based on the learners’ weaknesses.
To validate the GAWCM algorithm, simulations were conducted using artificially generated data sets. The generalization and the special case of the GAWCM algorithm were also discussed, taking into consideration the different P-S degrees of vertices (concepts) in a concept map. The GAWCM algorithm can be generally-employed in e-learning. It provides a framework for generating remedial learning materials for all kinds of learning fields. This is the main contribution of this study.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the presented study.
1. J. D. Novak and D. B. Gowin, Learning how to Learn, Cambridge, United Kingdom: Cambridge University Press, 1984. [Google Scholar]
2. C.-C. Lin, Z.-C. Liu, C.-L. Chang and Y.-W. Lin, “A genetic algorithm-based personalized remedial learning system for learning object-oriented concepts of Java,” IEEE Transactions on Education, vol. 62, no. 4, pp. 237–245, 2019. [Google Scholar]
3. C.-C. Lin, H.-C. Pu, S.-J. Su and M.-S. Lee, “A concept map-based remedial learning system with applications to the IEEE floating-point standard and MIPS encoding,” IEEE Transactions on Education, vol. 64, no. 2, pp. 147–154, 2021. [Google Scholar]
4. G.-J. Hwang, B. M. T. Lin and T.-L. Lin, “An effective approach for test-sheet composition with large-scale item banks,” Computers & Education, vol. 46, no. 2, pp. 122–139, 2006. [Google Scholar]
5. G.-J. Hwang, H.-C. Chu, P.-Y. Yin and J.-Y. Lin, “An innovative parallel test sheet composition approach to meet multiple assessment criteria for national tests,” Computers & Education, vol. 51, no. 3, pp. 1058–1072, 2008. [Google Scholar]
6. J. Moreno, D. A. Ovalle and R. M. Vicari, “A genetic algorithm approach for group formation in collaborative learning considering multiple student characteristics,” Computers & Education, vol. 58, no. 1, pp. 560–569, 2012. [Google Scholar]
7. B. Kosko, “Fuzzy cognitive maps,” International Journal Man-Machine Studies, vol. 24, no. 1, pp. 65–75, 1986. [Google Scholar]
8. A. Haghanifar, A. Amirkhani and M. R. Mosavi, “Dental caries degree detection based on fuzzy cognitive maps and genetic algorithm, in Proc. 26th Iranian Conf. on Electrical Engineering (ICEE2018), Mashhad, Iran, pp. 976–981, 2018. [Google Scholar]
9. K. Poczeta, A. Yastrebov and E. I. Papageorgiou, “Learning fuzzy cognitive maps using structure optimization genetic algorithm,” in Proc. the Federated Conf. on Computer Science and Information Systems, Lodz, Poland, pp. 547–554, 2015. [Google Scholar]
10. T. G. Altundogan and M. Karakose, “Genetic algorithm based fuzzy cognitive concept relationship determination and sigmoid configuration,” in Proc. 6th IEEE Int. Symp. on Systems Engineering (IEEE ISSE 2020), Vienna, Austria, 2020. [Google Scholar]
11. N. Ye, R. Zhang, K. Yu and D. Wang, “Learning fuzzy cognitive maps using decomposed parallel an colony algorithm and gradient descent,” in Proc. 12th Int. Conf. on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, pp. 78–83, 2015. [Google Scholar]
12. K. Gunel, K. Erdogdu, R. Polat and Y. Ozarslan, “An empirical study on evolutionary feature selection in intelligent tutors for learning concept detection,” Expert Systems, vol. 36, no. 3 (Special Issue Paper), 2019. https://onlinelibrary.wiley.com/doi/10.1111/exsy.12278. [Google Scholar]
13. S.-H. Huang, Y.-C. Liu and W.-K. Wang, “Employing genetic algorithm to explore suitable learning materials,” in Proc. the IEEE Int. Conf. on Advanced Learning Technologies (ICALT), Joensuu, Finland, pp. 878–879, 2004. [Google Scholar]
14. M.-J. Huang, H.-S. Huang and M.-Y. Chen, “Constructing a personalized e-learning system based on genetic algorithm and case-based reasoning approach,” Expert Systems with Applications, vol. 33, no. 3, pp. 551–564, 2007. [Google Scholar]
15. A. Hovakimyan, S. Sargsyan and S. Barkhoudaryan, “Genetic algorithm and the problem of getting knowledge in e-learning systems,” in Proc. the IEEE Int. Conf. on Advanced Learning Technologies (ICALT), Joensuu, Finland, pp. 336–339, 2004. [Google Scholar]
16. L.-H. Chen, “Enhancement of student learning performance using personalized diagnosis and remedial learning system,” Computers & Education, vol. 56, no. 1, pp. 289–299, 2011. [Google Scholar]
17. G.-J. Hwang, F.-R. Kuo, P.-Y. Yin and K.-H. Chuang, “A heuristic algorithm for planning personalized learning paths for context-aware ubiquitous learning,” Computers & Education, vol. 54, no. 2, pp. 404–415, 2010. [Google Scholar]
18. C.-M. Chen, “Intelligent web-based learning system with personalized learning path guidance,” Computers & Education, vol. 51, no. 2, pp. 787–814, 2008. [Google Scholar]
19. K.-K. Chu, C.-I. Lee and R.-S. Tsai, “Ontology technology to assist learners’ navigation in the concept map learning system,” Expert Systems with Applications, vol. 38, no. 9, pp. 11293–11299, 2011. [Google Scholar]
20. C. Bina, S. Dong, C. Li, Z. Shi and W. Lu, “Generation of adaptive learning path based on concept map and immune algorithm,” in Proc. the 12th Int. Conf. on Computer Systems & Education (ICCSE), Houston, USA, pp. 409–414, 2017. [Google Scholar]
21. D. C. Shallcross, “Using concept maps to assess learning of safety case studies–the piper alpha disaster,” Education for Chemical Engineers, vol. 8, no. 1, pp. e1–e11, 2013. [Google Scholar]
22. M. Svanström, J. Sjöblom, J. Segalàs and M. Fröling, “Improving engineering education for sustainable development using concept maps and multivariate data analysis,” Journal of Cleaner Production, vol. 198, pp. 530–540, 2018. [Google Scholar]
23. L. Li, H. Mao and L. Xu, “Application of concept maps-based anchored instruction in programming course,” in Proc. the 10th IEEE Int. Conf. on Computer and Information Technology (CIT), Bradford, West Yorkshire, UK, pp. 2196–2200, 2010. [Google Scholar]
24. C. Yang and Y. Liu, “Research on the application of concept map to software engineering teaching,” in Proc. the 2009 Int. Conf. on Scalable Computing and Communications; Eighth Int. Conf. on Embedded Computing, Dalian, China, pp. 612–615, 2009. [Google Scholar]
25. H.-C. Pu, S.-J. Su, M.-S. Lee and C.-C. Lin, “Generation of personalized learning paths with a concept map: A case study of the IEEE floating-point standard,” in Proc. the 4th IEEE Int. Conf. on Applied System Innovation, Chiba, Japan, 2018. [Google Scholar]
26. C. Tseng, P. Chao and K. R. Lai, “An operational concept map to facilitate physics problem solving,” in Proc. the 13th IEEE Int. Conf. on Advanced Learning Technologies, Beijing, China, pp. 110–111, 2013. [Google Scholar]
27. A. Mejri, S. A. Ghannouchi and R. Martinho, “Representing business process flexibility using concept maps,” Procedia Computer Science, vol. 100, pp. 1260–1268, 2016. [Google Scholar]
28. M. Taşkin, H. Pepe, C. Taşkin, C. Gevat and H. Taşkin, “The effect of concept maps in teaching sportive technique,” Procedia-Social and Behavioral Sciences, vol. 11, pp. 141–144, 2011. [Google Scholar]
29. P.-L. Liu, C.-J. Chen and Y.-J. Chang, “Effects of a computer-assisted concept mapping learning strategy on EFL college students’ English reading comprehension,” Computers & Education, vol. 54, no. 2, pp. 436–445, 2010. [Google Scholar]
30. J. C.-Y. Sun and A. Y.-Z. Chen, “Effects of integrating dynamic concept maps with interactive response system on elementary school students’ motivation and learning outcome: The case of anti-phishing education,” Computers & Education, vol. 102, pp. 117–127, 2016. [Google Scholar]
31. P. G. F. Furtado, T. Hirashima and Y. Hayashi, “Reducing cognitive load during closed concept map construction and consequences on reading comprehension and retention,” IEEE Transactions on Learning Technologies, vol. 12, no. 3, pp. 1–1, 2019. [Google Scholar]
32. R. Iqbal, M. A. Azmi Murad, L. Sliman and C. P. da Silva, “A mathematical evaluation for measuring correctness of domain ontologies using concept maps,” Measurement, vol. 118, pp. 73–82, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |