DOI:10.32604/iasc.2022.025026

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.025026 |  |
| Article |
Energy Efficient Mobile Harvesting Scheme for Clustered SDWSN with Beamforming Technique
Department of Electronics and Communication Engineering, College of Engineering Guindy, Anna University, Chennai, 600025, Tamilnadu, India
*Corresponding Author: Subaselvi Sundarraj. Email: subaselvi05@gmail.com
Received: 08 November 2021; Accepted: 21 January 2022
Abstract: Software Defined Wireless Sensor Networks (SDWSN) provides a centralized scheduling algorithm to decrease energy consumption compared to WSN. The sensor nodes have a finite battery capacity in the SDWSN that reduces the lifetime of the nodes. To harvest energy for energy depleted nodes without interfering with the eventful data transfer in the clustered SDWSN, an energy efficient mobile harvesting scheme with the Multiple Input Single Output (MISO) beamforming technique is proposed. The mobile harvesting scheme transfer the energy to the energy starving node and the beamforming algorithm which transmits the energy in the desired direction increases the lifetime of the nodes. The Secondary Cluster Head (SCH) node in a cluster is selected based on Particle Swarm Optimization (PSO) with the distance between mobile harvester and sensor node, the energy consumption rate of a node and lifetime of a nodes constraints for harvesting energy without interrupting data transfer to sink node in clustered SDWSN. The distributed scheduling algorithm and efficient path planning decrease the energy consumption of mobile harvester in the network. The optimization problem is formulated with Signal to Noise Ratio (SNR) and transmit power constraints to increase the harvested energy for sensor nodes in the network. The simulation results show the enhanced performance of the proposed algorithm compared to the existing algorithm in terms of residual energy, end to end delay, throughput, travel distance, service time and charging delay.
Keywords: Software defined wireless sensor network; secondary cluster head; mobile energy harvesting; multiple input single output; beamforming; particle swarm optimization
In WSN, the sensor nodes are either uniformly or randomly deployed to monitor and send data to the sink node, even in remote areas used for various applications. The various routing protocols and algorithms are proposed to improve the lifetime of the network. The tradeoff between the energy dissipation of a node and total energy consumption has analyzed by different cost function transmission algorithms to increase the lifetime of the first node died in the WSN [1]. Each node frequently sends the broadcast messages to identify the nearby nodes in WSN increases the overhead and energy consumption in the WSN. Hence, the control plane and data plane are separated to conserve energy in the SDWSN.
In SDWSN, the sensor node performs the forwarding task instead of making routing decisions, and broadcasting messages to neighbour nodes decreases the energy consumption of nodes in the network. An adaptive particle swarm optimization algorithm for efficient routing in SDWSN is proposed to increase the lifetime of the nodes [2]. The various proposed energy consumption algorithms are not efficient when the node is battery powered. Nowadays, energy harvesting algorithms have emerged for harvest energy to the sensor nodes when the lifetime of the node is reduced in the network.
The static Radio Frequency transmitters harvest the sensor nodes in SDWSN has proposed to increase the energy-charged and fair distribution of energy in the network [3]. The wireless energy transfer technology by the static source in the network decreases the harvested energy when the distance increases. Therefore, mobile wireless chargers (e.g., SenCar) are deployed to increases the efficiency of the harvesting energy in the network. The uneven cluster-based mobile charging algorithm has been proposed to decrease the number of dead nodes with the multi-hop energy transfer technology in the Wireless Rechargeable Sensor Network (WRSN) [4]. In the mobile energy harvesting network, the scheduling optimization problem is formulated to increase the data collection under the radio link quality and energy harvesting efficiency constraints in the network [5]. However, these harvesting algorithms are implemented with an omnidirectional antenna for harvest energy to sensor nodes decreases the harvesting energy and collection of data by mobile chargers lead to an increase in the end to end delay in the network.
The directional transmission of the signal by the beamforming technique cancels the interference from the other users for a desired user in the network. To maximize the throughput and energy efficiency under a transmit power constraint, the power allocation, and regularization parameters are jointly designed for Regularized Zero forcing Beamforming technique [6]. In MISO–Non Orthogonal Multiple Access (NOMA) system, the energy efficient beamforming technique has formulated to increase the energy efficiency in the network with transmit power constraints and minimum user rate requirements [7]. Hence, the beamforming techniques are implemented between a Base Station (BS) and sensor nodes (users) not in the cluster-based SDWSN and not employed for the mobile chargers in the networks.
The optimization algorithms are implemented to get an optimal solution by maximizing or minimizing the objective function. The Particle Swarm Optimization (PSO) algorithm is one of the swarm intelligence techniques inspired by the behaviour of nature like bird flocking and fish schooling [8]. The PSO algorithm is simple and high speed convergence where multiple iterations of the optimization problem have been performed to increase the quality of the solution. The implementation of a complex optimization algorithm for the election of Cluster Head (CH) in an iteration manner increases the network complexity. If the optimization algorithm is simple, the network efficiency becomes increases hence the PSO algorithm is used to optimize the Cluster Head (CH) [9]. The selection of CH is based on PSO with sink distance, intra-cluster distance and residual energy of sensor nodes metrics in the network [10]. Therefore, the election of CH based on PSO has implemented based on distance and energy without considering the energy consumption rate of a sensor node in the network.
In Literature, various energy harvesting techniques and beamforming algorithms have been proposed to improve the lifetime of the network. However, beamforming algorithms are not utilized for mobile energy harvesting in SDWSN. Therefore a new mobile energy harvesting with MISO beamforming has been presented to improve the lifetime of the SDWSN. The contribution of the proposed algorithm is summarized as follows
1. The mobile chargers with a beamforming technique for energy harvesting in the clustered SDWSN is proposed to increase the lifetime of a node.
2. The election of the Secondary cluster head in each cluster based on the PSO algorithm with distance and energy consumption rate constraints is introduced for harvesting energy in the network.
3. The mobile harvesting scheme with the beamforming algorithm is proposed to transfer the energy to the energy starving node in the desired direction to increases the lifetime of the nodes.
4. The scheduling and efficient path planning of the mobile harvester is estimated to increase the lifetime of the mobile charges.
5. The optimization problem with beamforming design is formulated to increase the harvested power in the network with SNR and transmit power constraints.
6. The performance of the proposed algorithm is evaluated and compared with the existing algorithm.
The paper is organized as follows. Section 2 presents the Network model with the formation of a cluster, the election of cluster head and the energy model. Section 3 discusses the proposed system model and MISO beamforming algorithm in the SDWSN. Section 4 introduces the selection of SCH nodes based on the PSO algorithm. Section 5 presents the mobile charging process in the proposed system. Section 6 compares the performance of the proposed algorithm with the existing algorithm. Finally, the work is concluded in Section 7.
In this section, the network model using cluster formation with the election of the primary cluster head and the energy model for the proposed system are described. The symbols used in the proposed approach described in Tab. 1.
2.1 Cluster Formation and Election of Primary Cluster Head
In the proposed SDWSN, M sensor nodes are randomly deployed in the N x N grid area is shown in Fig. 1. The BS is located in the centre of the network. All Sensor nodes and BS are static in the network. The mobile chargers are initially located at the BS. If the sensor node sends the request to the mobile charger through the SCH node, the charger dispatch from the BS to the energy required sensor node to harvest energy in the network. The sensor nodes send the data to the BS through the Primary CH (PCH) node. In the SDWSN, the election of the PCH node (controller node) is given by
where α = 0.4. The PCHV for all the nodes in the SDWSN is calculated and arranged in descending order. The Sensor node is having the highest PCHV is elected as a PCH. The formation of a cluster in the SDWSN is
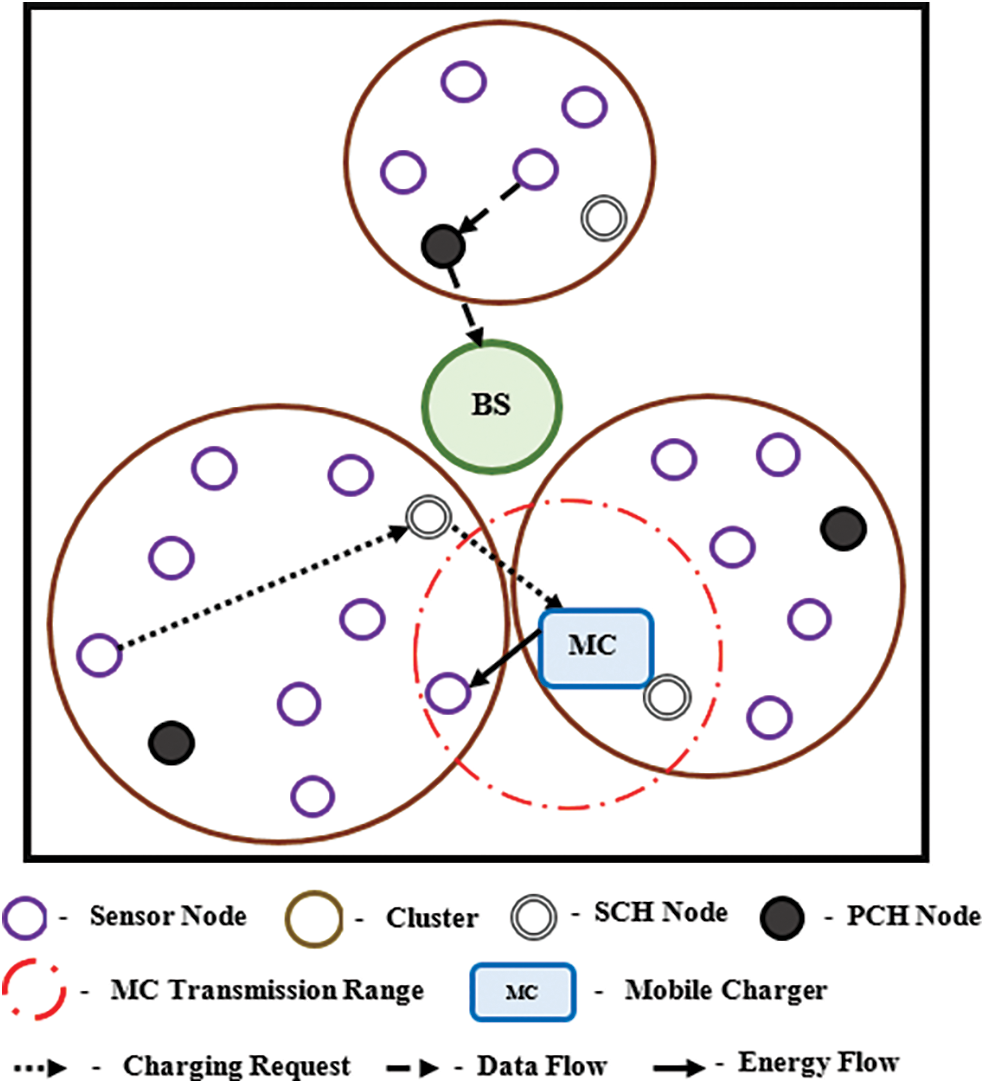
Figure 1: Network model
where β = 0.7 and R = 20 m. The distance between the sensor node and PCH node is less than the CR then the node is added to that cluster otherwise the node added to the cluster having the distance is smaller than the PCH node. The process is repeated until all the M sensor nodes joined the cluster in the SDWSN. Once the sensor nodes are deployed, the clusters are formed and the cluster head is selected based on Eqs. (1) and (2) in the proposed network is shown in Fig. 1. The sensor nodes in each cluster forward data to the PCH node without broadcasting its information to neighbour nodes in the network. It reduces the overheads and the energy consumption of the sensor node in the proposed network. The MC charges the sensor node directly if the node is within the MC transmission range otherwise through the SCH node of a cluster. In the existing system, the sensor nodes send the data directly to the BS. When the energy of the sensor node less than the threshold energy, the sensor nodes in the network send the request to the BS. After the first request has received at the BS, the cluster formation and election of cluster head have started in the existing algorithm. The sensor node sends data individually to the BS and frequently broadcasting the information to neighbour nodes leads to a decrease in the lifetime of the network in the existing algorithm.
The energy consumption model for sensing the data by sensor nodes in the network [11] is
where φ = 60 nJ. The energy consumption model for transmitting the data is
where C = λ1 + λ2dijɑ, λ1 = 45 pJ, λ2 = 1 x 10−3 pJ, the distance between the two nodes is calculated as
where ρ = 135 nJ. The Energy Consumption Rate model while charging and not charging of the sensor node by the mobile charger in the network [12] is given by
where Δ = 10 sec. The charging request includes the ECRi(t) and residual energy of a node at time t while sending to the MC in the SDWSN. Because, the dynamic energy consumption rate made the sensor node become a dead node. Therefore, the MC needs to change the path to charge the node with high energy consumption rate and low residual energy in the network to increase the lifetime of a node.
3 Proposed System with Beamforming Technique
In this section, proposed system model and the MISO beamforming for the proposed system are described.
The proposed system model for clustered SDWSN with mobile chargers is shown in Fig. 2. In the proposed system, the formation of cluster and election of the PCH node is based on Eqs. (1) and (2). The randomly deployed sensor nodes do not broadcast information to the neighbour nodes only it sends data or requests to the PCH and SCH nodes to reduce energy consumption in SDWSN. The sensor nodes in the SDWSN send data to BS through the PCH node if the node energy is greater than the threshold energy. Instead, the sensor node sends the charging request to the SCH node. The SCH node sends a request to BS for dispatching the mobile charger from the BS. The efficient scheduling, routing and path planning are implemented in the proposed network to increase the lifetime of the mobile charger. The beamforming algorithm is implemented between the multi antenna mobile charger and a single antenna sensor node to increase the harvested energy of the sensor node in the network. In the existing algorithm, the cluster formation and cluster head are elected when the first charging request is received at the mobile charger. Hence, the lifetime of the sensor nodes rapidly decreases in the network which made to receive more charging requests and the requirement of a more mobile charger to charge the node to avoid the dead node in the network. Further, the sensor node sends charging requests and data both through the cluster head lead to interruption of sending and receiving data in the network. The mobile charger in the existing network has to collect data from each cluster head results in an increasing end to end delay for sending data to BS. Therefore, the proposed system decreases the energy consumption of the sensor node and increases the lifetime of a mobile charger without interruption of eventful data transfer in the clustered SDWSN.
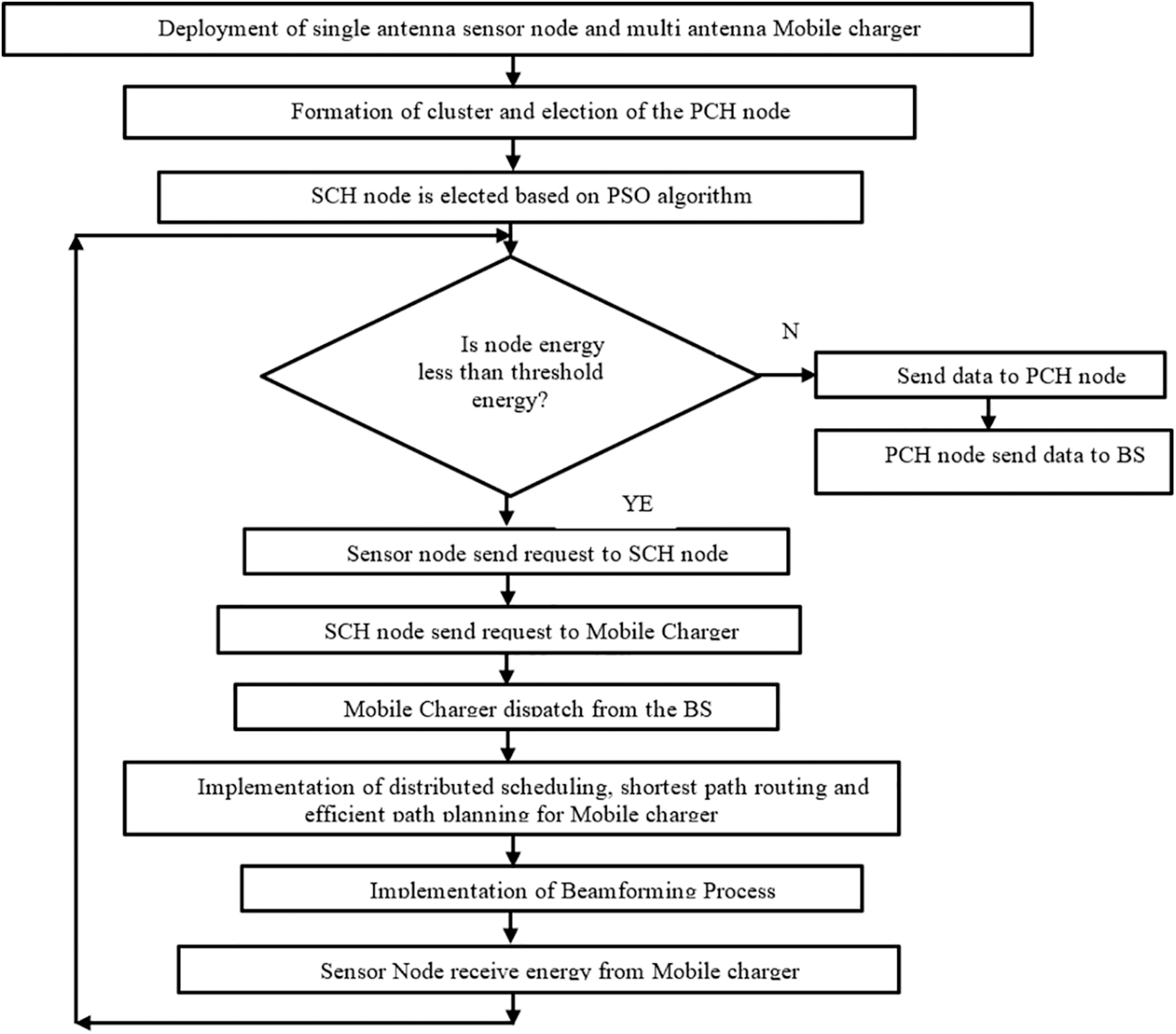
Figure 2: Proposed system model
In the proposed system, the MC is equipped with two antennas and SN has a single antenna. The MC having N > 1 antennas harvest energy to the single antenna SN (k = 1, 2,…, K) using transmit beamforming. The MC sends the signal Sk with the transmit power Pk using the beamforming vector Wk є ℂN x 1. The received signal at the SN can be written as
where Lk is the path loss from MC to requested SN calculated using Eq. (8), 𝕙k=[hk,1, hk,2] is the channel vector between MC and SN. Sk=[ sk,1, sk,2], Wk=[ wk,1, wk,2], and nk is the Additive White Gaussian Noise (AWGN) with zero mean and variance σ2 at the receiver. The harvested power received at the SN is
The total harvested power in the SDWSN is given by
where η is the energy conversion coefficient varies from 0 to 1. The Signal to Noise Ratio (SNR) at the receiver SN is given by
The objective of the MISO beamforming in the proposed system is to maximize the harvested energy of the SN in the network. Thus, the optimization problem is formulated with constraints can be defined as
subject to
where
where Gk= [h1,k, …, hK,k] [13], Gk†=GkH(Gk GkH)−1, ηk =Nσ2/Pk [14] and IN is the N dimensional identity matrix.
The optimization problem in the proposed system is formulated with Wk to get the optimal solution for the beamforming technique. The Wk in the MISO beamforming technique is selected to cancel the interference for the desired user to increase the harvested energy in the network. The problem is formulated with SNR and transmit power constraints for efficiently transmitting the energy in the network. Hence, the mobile harvesting with the MISO beamforming technique using multiple antennas at MC and SN equipped with a single antenna increases the harvested energy and residual energy of the SN in the clustered SDWSN.
4 Selection of SCH Node Based on PSO Algorithm
In the PSO algorithm, the initial particles are distributed randomly in search space. It can handle multiple parameters with a series of iterations for finding all possible solutions. Each particle moves around in space for a better solution and stores the previous solution among which best is chosen to increase the quality of the solution. In each iteration, the best solution achieved by the particle in space is called personal best (pbest) and another best solution achieved by any particle among the neighbourhood of that particle is the global best (gbest). The particle is the potential solution in search space that has two properties velocity and position. The velocity is the speed at which the particle change and position is the location of the particle in the search space. The velocity and position are calculated as follows
where Vk+1 is the current velocity, W is the inertia weight, Vk is the previous velocity, C1= C2 = 2 is the acceleration coefficient [15], r1 and r2 is the random number between 0 and 1, pbestk is the personal best value, xk is the initial position, gbestk is the global best value and Xk+1 is the current position.
The main disadvantage of the PSO algorithm is the fast convergence into a personal best solution. In order to overcome the disadvantage, the inertia weight is given by
where wmax = 0.9 is the maximum inertia weight, wmin = 0.4 is the minimum inertia weight and Iterationmax = 50 is the maximum number of iterations.
The particles are evaluated through fitness function to get the optimal solution in the space. The fitness function for the proposed system is the selection of SCH nodes among the randomly distributed nodes in a cluster other than the PCH node. The optimization problem for the election of the SCH node based on the PSO algorithm in the proposed network is calculated by minimizing the objective function (fitness function) f is given by
where a1, a2, a3 is the weight parameters in the range [0, 1], X1 is the distance between the sensor node and mobile charger, X2 is the energy consumption rate of a node and X3 is the lifetime of a node. The X1, X2 and X3 are calculated as follows
4.1 Distance Between Sensor Node and Mobile Charger
The distance between the sensor node in a cluster and mobile charger in the network is
where X1 is the minimum distance between the sensor node and mobile charger, p is the number of clusters in the network, Mj-PCHj is the number of nodes except PCH node in the jth cluster and d(SNij, MC) is the distance between ith sensor nodes in the jth cluster and mobile charger.
4.2 Energy Consumption Rate of a Node
The energy consumption rate of a sensor node in the network is given by
where ECR is the Energy Consumption Rate. The ECR of sensor node i in a cluster is calculated as follows
where Time is the simulation time at which ECR is calculated.
The lifetime of a sensor node in the network is calculated using Eq. (20). By minimizing X3 the node which has a higher lifetime can be calculated.
Substitute Eqs. (18), (19) and (21) in Eq. (17) to minimize the optimization problem. The problem selects the node with less distance with the mobile charger, higher lifetime and less energy consumption rate than the PCH node as the SCH node in a cluster. The solution to the optimization problem is the PSO algorithm.
The work flow for the election of SCH node in a cluster is shown in Fig. 3. After the formation of the cluster and selection of the PCH node, the election of the SCH node starts. In each cluster, all the sensor nodes are initialized with position and velocity. The fitness value for all sensor nodes are calculated using Eqs. (18), (19) and (21) are updated in Eq. (17). The pbest and gbest are computed from the fitness value. The fitness value calculated by each sensor node in the previous iteration is stored at the local memory of the node. The current fitness value of the node is less than the previous value then the value is updated as pbest. Otherwise, the previous value is updated as pbest in the network. Among all the pbest values of the node in the network, the minimum value is updated as gbest in the network. Since the optimization problem for selecting the SCH node is to minimize the objective function in the network. The pbest and gbest values are updated in Eq. (14). The velocity and position of each sensor node are calculated using Eqs. (14) and (15). The new velocity and position values are taken to calculate pbest and gbest using the fitness function for the next iteration when the maximum iteration is not reached. Instead, the gbest value is selected as an SCH node for a cluster. The number of iterations is increased to get the optimal election of the SCH node in the network.
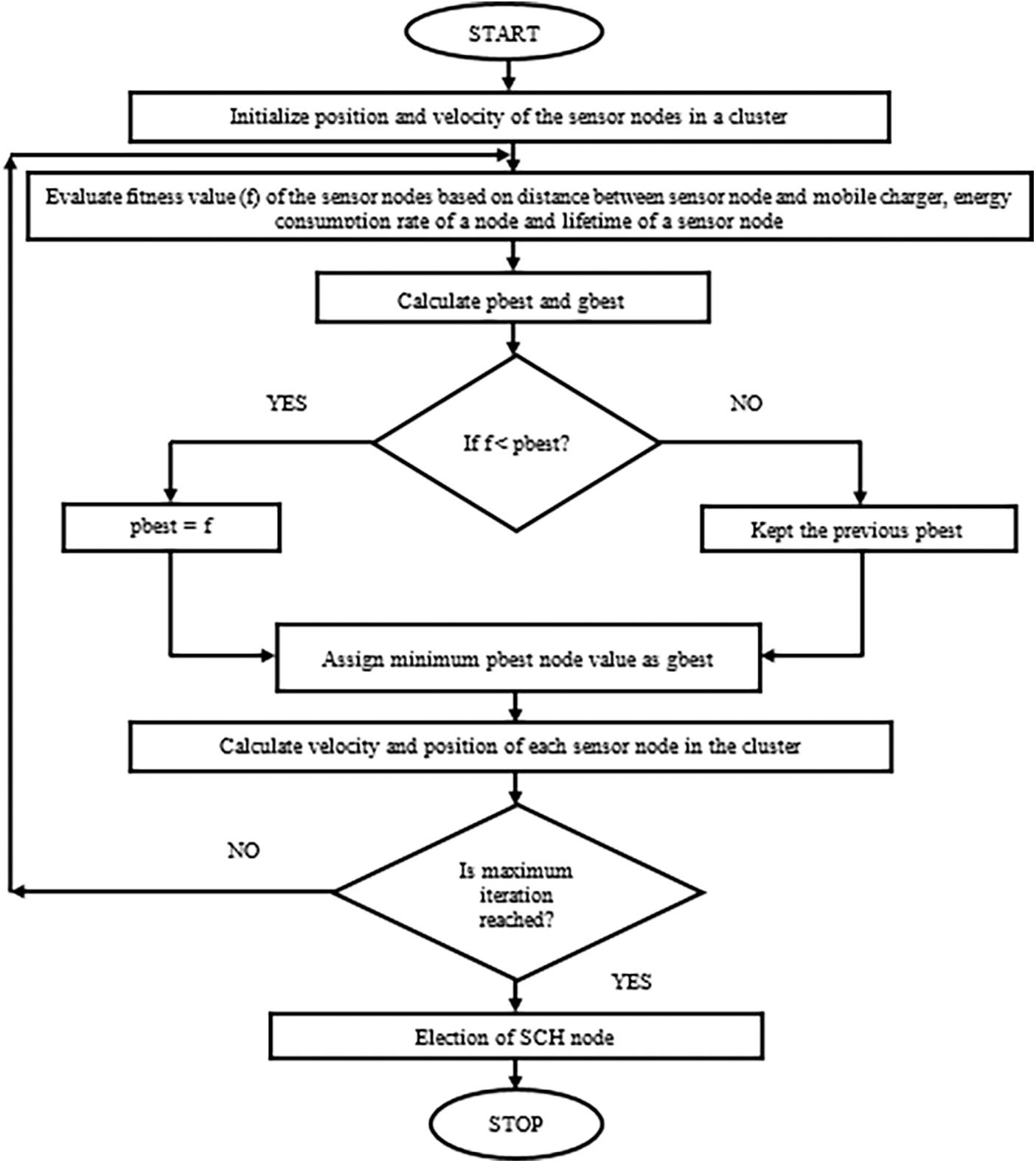
Figure 3: Selection of the SCH node
5 Mobile Charging Process in the Proposed System
The distributed scheduling, shortest path routing and path planning of mobile charger in the clustered SDWSN are illustrated in this section.
5.1 Distributed Scheduling and Routing
In the proposed system, the sensor nodes send the request to the SCH node when the energy is less than the threshold energy. The SCH node sends the charging request to a mobile charger in the network. The process of sending a request to a mobile charger in the proposed network occurs based on the distributed scheduling method. In the distributed scheduling, the requests are sent to the mobile charger without interrupting BS eventful receiving data from the PCH nodes in the network. In the existing system, the sensor node sends a request to the cluster head node. The cluster head sends the request to the mobile charger through BS even the charger is nearby. The charging request sending in the centralized scheduling instead directly to the mobile charger in the network leads to the interruption of receiving data by the BS from the cluster head and cluster head from the sensor node. Further, the delay in receiving a request by the mobile charger in the network increases. Hence, the distributed scheduling method sent requests without interruption of eventful data transfer and reduces the delay for sending a request to the mobile charger in the proposed network.
The mobile charger upon receiving a charging request from the sensor nodes plan the shortest path routing in the clustered SDWSN. The mobile charger to reach the energy required sensor node can go through several intermediate nodes. The shortest path routing objective is to find the minimum distance between the source and destination through intermediate nodes. The mobile charger chose the path which is the total minimum distance to the required sensor node from its current position in the network. The MC routing based on Travelling Salesman Problem (TSP) in the network leads to frequently going to BS when the charging request not received from the sensor node increases the distance travelled and energy consumption of MC in the existing system. Hence, the shortest path routing instead of TSP is implemented to reduce the delay and energy consumption of the mobile charger in the proposed system.
5.2 Path Planning of a Mobile Charger
The Mobile Chargers are located at the BS while the Sensor Nodes (SN) are deployed in the network. When the charging request is started sending by the SN, the Mobile Charger (MC) dispatch from the BS to charge the SN in the network. The path planning for a charger in clustered SDWSN is shown in Fig. 4. The SN sends a request to MC by the SCH node when the energy is less than the threshold energy. Once the requests are received at the charger, the MC check whether SN is in the transmission range. If the SN is in the transmission range of the charger, the MC charges the SN from the current position without going near the requested SN. Otherwise, the MC visits the SCH node to charge the SN when more than one SN is from the same cluster. Instead, MC travelled to request SN in the shortest path for harvest energy to increase the lifetime of the node. Hence, the mobile charger reduces the distance travelled instead of going to every sensor node or cluster head in the network.
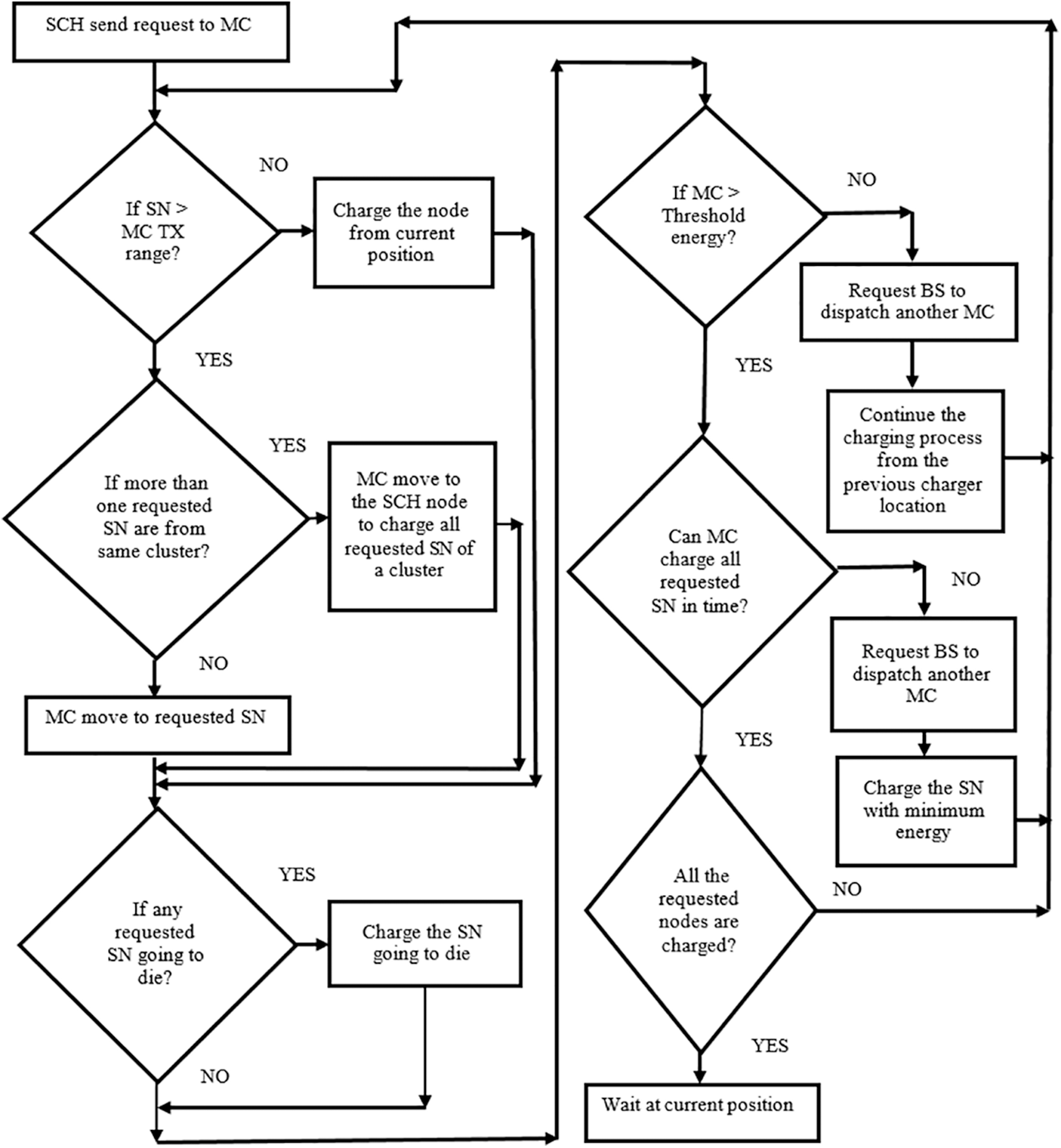
Figure 4: Path planning of a mobile charger
The distance travelled by the MC in the network is
where TD is the total distance travel by MC, d(BS, i) is the distance travelled from BS to SN i, R is the number of SN and SCH visited by MC and d(j, BS) is the distance travelled from SN j to the BS. The time required to charge the SN in the network is
where
where CD is the charging delay,
The MC frequently checks the requested SN lifetime in the network. If any SN residual energy decreases rapidly and the SN depletes energy before the MC reaches to charge, the MC first charges the particular SN later travelled to other requested nodes for charging in the network. The priority given to the nodes with less residual energy in the network increases the number of alive nodes in the network [17]. The requested SN should satisfy before MC leave to the next charging node is
where
If the MC energy is less than the threshold energy, the MC sends a new charger requirement request and return to BS for replacing or charging the battery of the charger. Simultaneously, the BS dispatch the MC with a full battery to replace the energy depleted MC charging process in the network. To charge the SN in the network the MC should satisfy
where ER is the energy required for the SN and EC(i,j) is the energy consumed by MC during traveling from SN i to requested SN j, Et is the threshold energy of the MC. The Service time is the sum of travel time and charging time of MC is given by
where ST is the service time,
The MC ensures that it can charge all the requested SN before the node exhaust energy in the network. If the number of requests received at the MC increases and the MC cannot charge all the nodes before depleting their energy, the MC sends a request to the BS to dispatch another charger in the network. The new charger first charges the SN which is having minimum energy then starts the charging process similar to the first charger in the network. If more than one charger departs from the BS to charge the SN, the coordination process starts among MC in the network. In the coordination process, the chargers provide their location for not to collide with each other and nodes are charged to avoid the SN which are already charged unknowingly visited by MC in the clustered SDWSN. The MC remains at the current position without returning to BS if all the sensor nodes are charged to reduce frequently travelled to the BS in the network. Thus, the path planning process in the proposed system reduces the distance travelled by the MC in the network, increases the lifetime of the SN and decreases the energy consumption of MC in the clustered SDWSN.
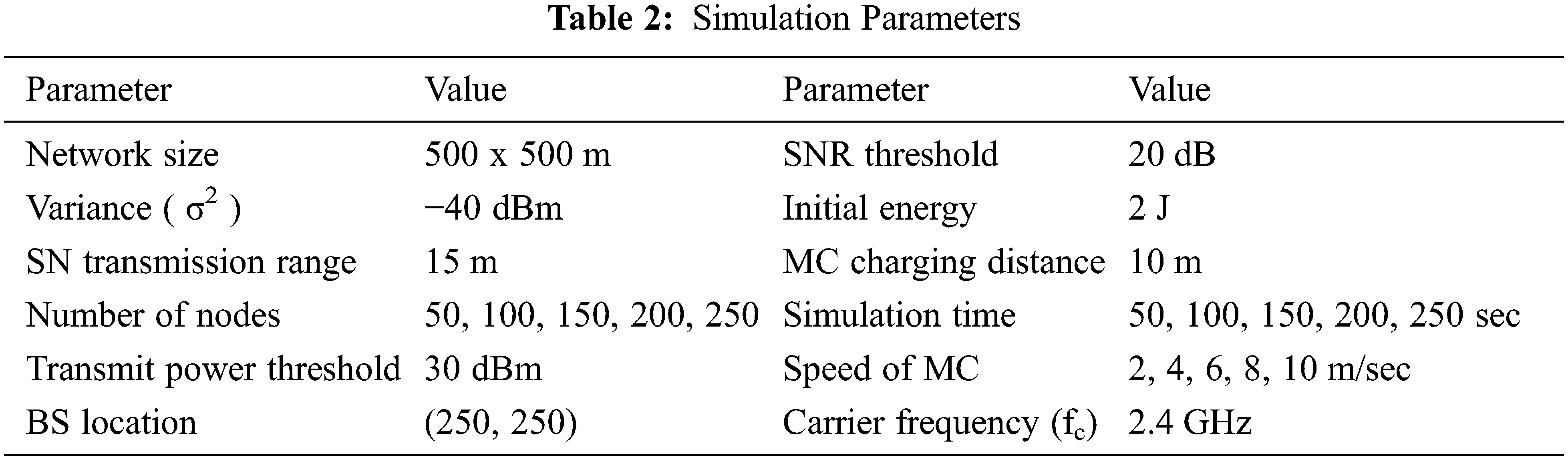
The performance of the proposed algorithm is implemented in Network Simulator. The homogeneous single antenna sensor nodes are randomly deployed in the network with one BS located in the centre of the network. The sensor nodes and BS are immobile. The multiple antenna MC initially located in the BS dispatch to visit the energy depleted node to increase the residual energy of the SN in the network. The performance of the proposed system is compared with the existing system. The simulation parameters in the SDWSN is shown in Tab. 2.
The residual energy of the proposed system is decreased when the number of nodes increases but higher compared to the existing algorithm is shown in Fig. 5. The data collection from the SN increases when the number of nodes in the network increases which decreases the residual energy of the nodes. The SN in each cluster sends the information to the PCH node in the proposed system without frequently broadcasting the information to neighbour nodes reduces the overheads and energy consumption of the SN in the network. The cluster formation and election of CH after the first charging request received at the MC decreases the energy of the SN in the existing system compared to the proposed system. The static RF transmitters in the proposed system increases the distance between the transmitter and nodes in the SDWSN reduces the residual energy compared to the existing and proposed system.
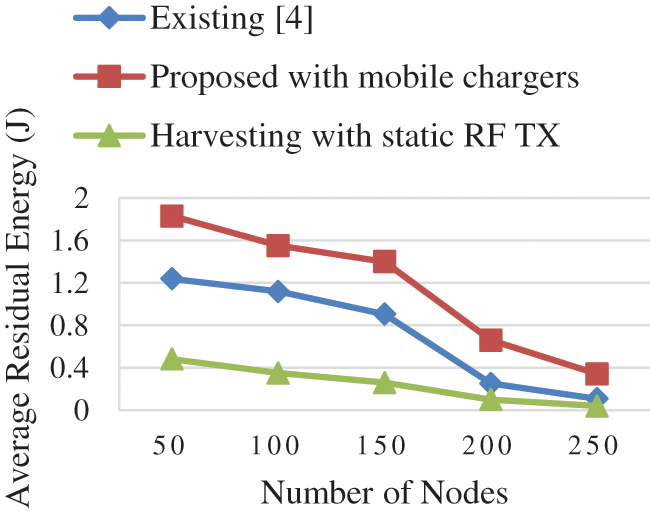
Figure 5: Average residual energy vs. number of nodes
The average end to end delay decreases when the number of nodes increase because the forwarding nodes increases in the network which finds the optimal path for transferring the data in the network. The election of the PCH node for sending data to BS and the SCH node for charging request to MC in the proposed system instead of sending both charging request and data to BS through a single CH node reduces the end to end delay compared to the existing algorithm is shown in Fig. 6. The centralized scheduling algorithm in the existing system sends the charging request from the SN to MC through BS interrupts the reception of data from the other SN and MC has to collect the data from each CH instead of sending it directly to BS increases the end to end delay in the network.
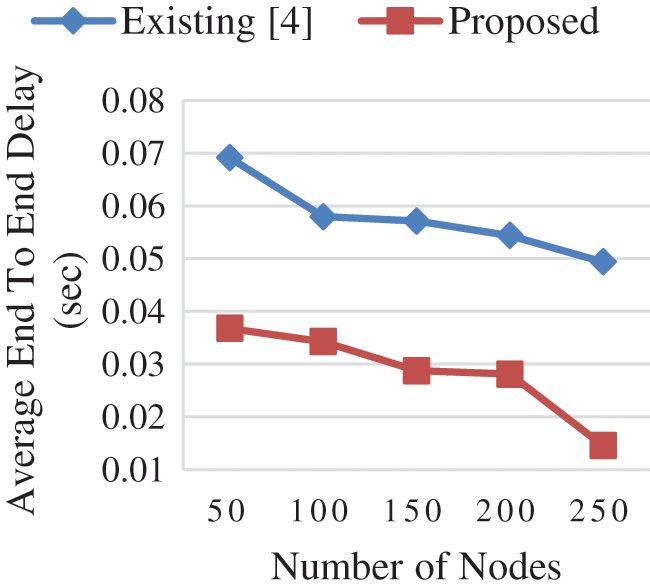
Figure 6: Average end to end delay vs. number of nodes
In Fig. 7, the throughput is decreased because the total data and energy requirement is higher in the network which increases the overheads in the clustered SDWSN when the number of nodes increases. In the proposed system, the PCH node is selected based on the node with high residual energy and the SCH node is determined based on the energy consumption rate of a node, the lifetime of a node and distance between the SN and MC other than the PCH node among the nodes in a cluster. Hence, the eventful data transfer without interruption by the charging request of the SN in the network increases the throughput in the proposed system. The reception of data in the network is unsuccessful by the interruption of the charging request reduces the throughput in the existing system.
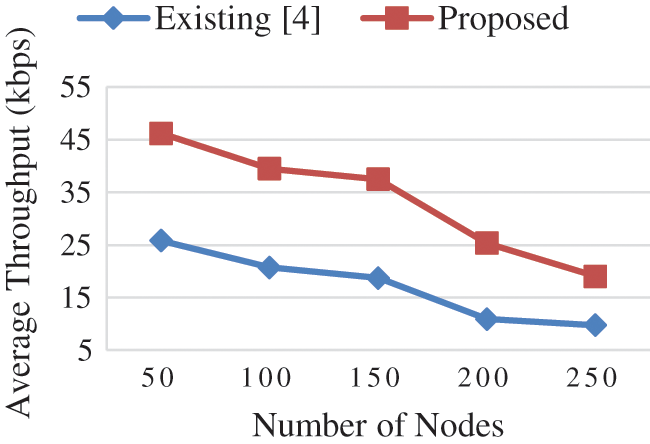
Figure 7: Average throughput vs. number of nodes
The communication between the nodes increases when the number of nodes in the network increases which reduces the residual energy of the nodes. Hence the number of requests by the SN in the network increases which increases the distance travelled by the MC in the proposed network but less than the existing algorithm is shown in Fig. 8. The MC which charge the node without moving to the SN when the node is in the transmission range and MC move to the SCH node which is having more than one requested node in a cluster without going to every SCH node for collecting data and harvest energy to the SN reduces the distance travelled by MC in the proposed system. Further, the shortest path routing to charge the SN decreases the distance travelled by MC in the proposed algorithm compared to the existing algorithm.

Figure 8: Average travel distance vs. number of nodes
The time taken for traveling and charging by the MC to the requested SN in the network is the service time which increases with the number of requests in the network increases. The service time by the MC in the proposed algorithm is reduced compared to the existing algorithm is shown in Fig. 9. The number of requests by the SN increases in the existing algorithm due to the election of CH after the first request in the network. Hence the traveling time to reach and charging time to charge all the SN by MC is increases in the existing system. The MC frequently going to BS if there is no request and to visit all the CH in the network for gathering data increases the service time in the existing system compared to the proposed algorithm. Fig. 10 depicts the average charging delay by varying the speed of the MC in which the performance of the proposed algorithm is better compared to the existing system. The MC travel at high speed can charge more nodes and traveling time to the requested SN is reduced which decreases the charging delay in the network. The charging of the requested SN once the request is received by the MC when the SN is in transmission range without going to the SCH node reduces the delay in the proposed system. The new MC dispatch from the BS when the MC cannot charge all the requested nodes in time which gives priority to the nodes with minimum energy can charge more nodes with higher speed in the proposed network. The implementation of the beamforming algorithm in the proposed system sends the signal in the desired direction reduces the time for charging the particular SN in the network.
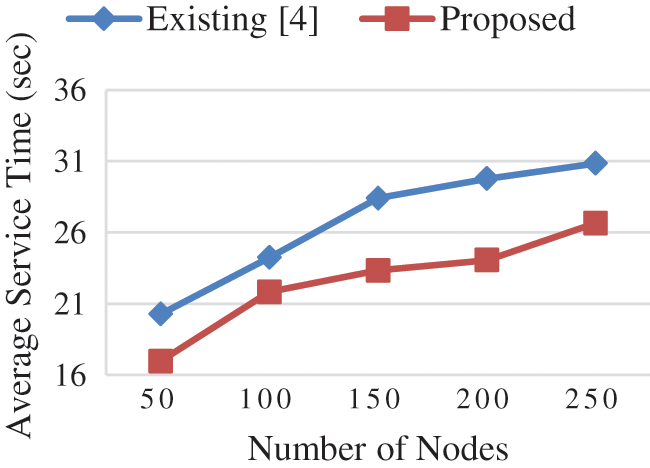
Figure 9: Average service time vs. number of nodes
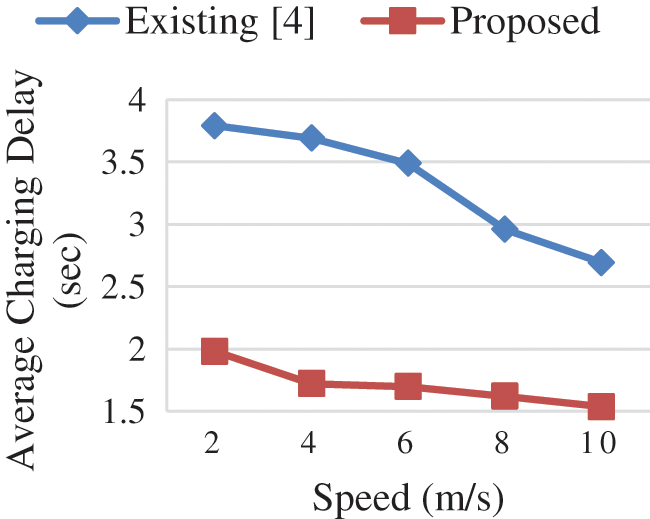
Figure 10: Average charging delay vs. MC SPEED
This paper has proposed a novel mobile harvesting algorithm with the MISO beamforming technique in the clustered SDWSN. The mobile harvesting scheme transfers the energy to the energy starving node and the beamforming algorithm which transmits the energy in the desired direction increases the lifetime of the nodes. The formation of cluster and election of PCH node for sending data to BS initially in the network reduces the energy consumption of nodes. The election of SCH node among the node in a cluster other than the PCH node is based on the PSO algorithm for sending the charging request from SN to MC in the network. The charging requests sent without interruption of the eventful data transfer from the SN to BS increase the throughput and residual energy and reduce the end to end delay in the SDWSN. The distributed scheduling, shortest path routing and efficient path planning of MC in the proposed system to harvest energy decrease the average travel distance, average service time and average charging delay compared to the existing algorithm. The MISO beamforming scheme between the multiple antenna MC and single antenna SN with the SNR and transmit power constraints increases the harvested energy and residual energy of the SN in the clustered SDWSN. The simulation results show that the performance of the proposed algorithm is enhanced compared to the existing algorithm.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Dutta, M. S. Obaidat, K. Dahal, D. Giri and S. Neogy, “Comparative study of different cost functions between neighbors for optimizing energy dissipation in WSN,” IEEE Systems Journal, vol. 13, no. 1, pp. 289–300, 2019. [Google Scholar]
2. N. Kumar and D. P. Vidyarthi, “A green routing algorithm for iot-enabled software defined wireless sensor network,” IEEE Sensors Journal, vol. 18, no. 22, pp. 9449–9460, 2018. [Google Scholar]
3. W. Ejaz, M. Naeem, M. Basharat, A. Anpalagan and S. Kandeepan, “Efficient wireless power transfer in software-defined wireless sensor networks,” IEEE Sensors Journal, vol. 16, no. 20, pp. 7409–7420, 2016. [Google Scholar]
4. G. Han, H. Guan, J. Wu, S. Chan, S. L. Shu et al., “An uneven cluster-based mobile charging algorithm for wireless rechargeable sensor networks,” IEEE Systems Journal, vol. 13, no. 4, pp. 3747–3758, 2019. [Google Scholar]
5. K. Li, C. Yuen, B. Kusy, R. Jurdak, A. Ignjatovic et al., “Fair scheduling for data collection in mobile sensor networks with energy harvesting,” IEEE Transactions on Mobile Computing, vol. 18, no. 6, pp. 1274–1287, 2019. [Google Scholar]
6. L. D. Nguyen, H. Duong, T. Q. Duong and V. H. Poor, “Multi-user regularized zero-forcing beamforming,” IEEE Transactions on Signal Processing, vol. 67, no. 11, pp. 2839–2853, 2019. [Google Scholar]
7. H. Al-Obiedollah, K. Cumanan, J. Thiyagalingam, A. G. Burr, Z. Din et al., “Energy efficient beamforming design for miso non-orthogonal multiple access systems,” IEEE Transactions on Communications, vol. 67, no. 6, pp. 4117–4131, 2019. [Google Scholar]
8. R. V. Kulkarni and G. K. Venayagamoorthy, “Particle swarm optimization in wireless-sensor networks: A brief survey,” IEEE Transactions on Systems, Man, and Cybernetics—Part C: Applications and Reviews, vol. 41, no. 2, pp. 262–267, 2011. [Google Scholar]
9. T. Kaur and D. Kumar, “Particle swarm optimization-based unequal and fault tolerant clustering protocol for wireless sensor networks,” IEEE Sensors Journal, vol. 18, no. 11, pp. 4614–4622, 2018. [Google Scholar]
10. P. C. Srinivasa Rao, P. K. Jana and H. Bankal, “A particle swarm optimization based energy efficient cluster head selection algorithm for wireless sensor networks,” Wireless Networks, vol. 23, no. 7, pp. 2005–2020, 2016. [Google Scholar]
11. W. Xu, W. Liang, X. Lin and G. Mao, “Efficient scheduling of multiple mobile chargers for wireless sensor networks,” IEEE Transactions on Vehicular Technology, vol. 65, no. 9, pp. 7670–7683, 2016. [Google Scholar]
12. Y. Feng, L. Guo, X. Fu and N. Liu, “Efficient mobile energy replenishment scheme based on hybrid mode for wireless rechargeable sensor networks,” IEEE Sensors Journal, vol. 19, no. 21, pp. 10131–10143, 2019. [Google Scholar]
13. S. Timotheou, I. Krikidis, G. Zheng and B. Ottersten, “Beamforming for MISO interference channels with QoS and RF energy transfer,” IEEE Wireless Communication Letter, vol. 13, no. 5, pp. 2646–2658, 2016. [Google Scholar]
14. H. Wan, W. Chen and J. Ji, “Efficient linear transmission strategy for MIMO relaying broadcast channels with direct links,” IEEE Wireless Communication Letter, vol. 1, no. 4, pp. 14–17, 2016. [Google Scholar]
15. Y. Zhou, N. Wang and W. Xiang, “Clustering hierarchy protocol in wireless sensor networks using an improved PSO algorithm,” IEEE Access, vol. 5, no. 4, pp. 2241–2253, 2016. [Google Scholar]
16. O. G. Monakhov, E. A. Monakhova, A. Yu. Romanov, A. M. Sukhov and E. V. Lezhnev, “Adaptive dynamic shortest path search algorithm in networks-on-chip based on circulant topologies,” IEEE Access, vol. 9, pp. 160836–160846, 2021. [Google Scholar]
17. T., Vaiyapuri, V. S. Parvathy, V. Manikandan, N. Krishnaraj, D. Gupta et al., “A novel hybrid optimization for cluster-based routing protocol in information-centric wireless sensor networks for iot based mobile edge computing,” Wireless Personal Communications, vol. 1, pp. 1–24, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |