Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.028264
Article

Secure Multi-Party Quantum Summation Based on Quantum Homomorphic Encryption

Gang Xu1,2, Fan Yun1, Xiu-Bo Chen3,*, Shiyuan Xu1, Jingzhong Wang1, Tao Shang4, Yan Chang5 and Mianxiong Dong6

1School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
2Advanced Cryptography and System Security Key Laboratory of Sichuan Province, Chengdu, 610025, China
3Information Security Center, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
4School of Cyber Science and Technology, Beihang University, Beijing, 100083, China
5School of Cybersecurity, Chengdu University of Information Technology, Chengdu, 610225, China
6Muroran Institution of Technology, Muroran, 050-8585, Japan
*Corresponding Author: Xiu-Bo Chen. Email: flyover100@163.com
Received: 06 February 2022; Accepted: 15 March 2022

Abstract: Secure multi-party computation has been playing a fundamental role in terms of classical cryptography. Quantum homomorphic encryption (QHE) could compute the encrypted data without decryption. At present, most protocols use a semi-honest third party (TP) to protect participants’ secrets. We use a quantum homomorphic encryption scheme instead of TP to protect the privacy of parties. Based on quantum homomorphic encryption, a secure multi-party quantum summation scheme is proposed in which N participants can delegate a server with strong quantum computing power to assist computation. By delegating the computation and key update processes to a server and a semi-honest key center, participants encrypt their private information data using Pauli operators to get the sum. Besides, the server can design and optimize the summation lines itself, and the correct results can be obtained even if the secret information is negative. The correctness analysis showed that the participants could correctly obtain the results of the calculation. The security analysis proves the scheme is resistant to both outside attack and participant’s attack, and is secure against collusive attack by up to N-2 participants. From the theoretical point of view, our protocol can extend to other secure multi-party computing problems.

Keywords: Quantum homomorphic encryption; secure multi-party computation; TP; correctness analysis; security analysis

1  Introduction

Secure multi-party computation (SMC) means that two or more users who do not trust each other want to cooperate to complete a certain computing task without disclosing their input information in a distributed network environment. The initial SMC protocol was proposed in Yao’s millionaire problem [1], which compares the property of two millionaires without knowing others’ any private information. The secure multi-party summation is an elementary aspect of SMC that enables multiple parties to calculate their private inputs without revealing any private inputs information. It is extensively applied to solve some privacy preservation problems in the classical background [2] and is developed to the quantum related region [3–8]. In 2010, Chen et al. [9] proposed a quantum summation protocol by using Greenberger–Horne–Zeilinger (GHZ) states. In 2015, Zhang et al. [10] designed a quantum three-party summation protocol based on the genuinely maximally entangled six-qubit states. Then Liu et al. [11] presented a quantum summation protocol using Pauli matrices operations to encode information for extracting information, and a quantum summation protocol based on the commutative encryption [12] was proposed. In 2017, Zhang et al. [13] put forward a multi-party quantum summation protocol based on single particles without a trusted third party.

Most secure multi-party computation needs to consider semi-honest parties to the protocol, but homomorphic encryption does not. Some researchers use homomorphic encryption [14,15] (HE) algorithm to solve SMC’s problem. HE is utilized for users to process and calculate encrypted information without decryption. As an essential branch of quantum cryptography, QHE allows the client to delegate quantum data to the server for computation. Boykin et al. [16] proposed a quantum encryption algorithm and quantum one-time pad (QOTP). They also proved that it is perfect security. Based on QOTP, Liang [17] proposed three symmetric quantum homomorphic encryption schemes and a symmetric quantum fully homomorphic encryption (QFHE), but this novel scheme requires the private key, and the untrusted server can steal client information. In their subsequent studies, a QFHE scheme with the universal quantum circuit (UQC) was proposed [18], and the decryption key depends on the structure of the UQC. When a T-gate occurs for the UQC, the client and server need interact once. In 2014, Fisher et al. [19] proposed a QHE scheme for performing universal set of quantum gates on untrusted servers. However, when the server performs T-gate evaluation, an S-error will occur, requiring the client to prepare auxiliary quantum states to communicate with the server to eliminate the S-error. Broadbent et al. [20] prepared two QHE schemes to handle S-error, namely entanglement-based scheme and auxiliary-qubit scheme. These two schemes are based on a classical quantum homomorphic encryption scheme suitable for low complexity quantum circuit, and the efficiency will be low when the circuit has enormous complexity. Recently, Liang [21] proposed two QHE schemes that are based on gate teleportation and its modified version. Both are non-interactive schemes. Then, Zhou et al. [22] propose a homomorphic search protocol based on QHE, in which a client with limited quantum ability can implement a search job on the encrypted superposition state with the help of a powerful but untrusted quantum server.

However, some of the existing protocols need to perform the exclusive-OR (XOR) operation, which is too difficult to apply on applications. Motivated by the works of References [19,22], we propose a secure multi-party quantum summation protocol based on QHE. Our protocol implements the addition of the integers to the participants, even if there are negative integers. A third party is required to assist the calculation in the protocol. In order to separate computing and key management in third party, it is divided into servers with strong computing power and semi-honest key centers. In addition, Yu et al. [23] prove the no-go result: A perfectly secure QFHE scheme requires exponential overhead. QFHE with no-interaction consumes more resources than one with interaction. Hence, we use Fisher et al.’s key update scheme in our protocol.

The rest of our paper is organized as follows. In Section 2, we summarize the preliminary knowledge of quantum computation, QHE and quantum full adder circuit. In Section 3, we propose a novel multi-party quantum summation protocol based on QHE. In Section 4, we give the security analysis of our protocol. In Section 5, we conclude this paper with a brief conclusion.

2  Preliminaries

2.1 Quantum Computation

QHE is a way of delegating computation. The client sends the encrypted data to a powerful server to perform general quantum computation. As for quantum computation, the single qubit gates are Pauli operation X, Y, Z; the Hadamard gate H; the phase gates T and S, where,

X = (0110),  Y=(0−ii0),  Z=(100−1),  H=12(111−1),  T=(100eiπ/4),  S=(100i) (1)

Also, the double-qubits gate is CNOT gate; the triple-qubits gate is Toffoli gate, where,

CNOT=(1000010000010010),Toffoli=(1000000001000000001000000001000000001000000001000000000100000010) (2)

The CNOT gate implements the following quantum transformation CNOT(|c⟩⊗|t⟩)=|c⟩⊗|c⊕t⟩ , where |c〉 is control qubit, |t〉 is target qubit.

The Toffoli gate implements the following quantum transformation Toffoli(|a⟩⊗|b⟩⊗|t⟩)=|a⟩⊗|b⟩⊗|t⊕a⋅b⟩ , where |a〉 and |b〉 is control qubit, |t〉 is target qubit.

To realize universal quantum computation, one element of non-Clifford gate must be composed. Therefore, two different quantum gate sets to make up universal quantum computation can be obtained. The first set is {H, S, CNOT, T}, and the second set is {H, S, CNOT, Toffoli}. And in the second set, the T-gate and T† -gate in non-Clifford gate should be evaluated. Because of T†= T7 , the T† -gate can be implemented by seven T-gates.

T=(100eiπ/4),T†=(100e−iπ/4) (3)

2.2 Quantum Homorphic Encryption Basedon Quantum One-Time Pad

A quantum homomorphic encryption scheme includes four algorithms [18], and the process of each algorithm is described below.

(1)   Key generation algorithm. The client uses the unary representation of security parameters as the algorithm’s input to obtain a set of keys, i.e., a classical public encryption key pk, a classical secret decryption key sk and a quantum evaluation key ρevk.

(2)   Encryption algorithm. According to the value of the encryption key pk, the client encrypts the plaintext information M and sends the encrypted information C to the server.

(3)   Homomorphic evaluation algorithm. The server performs unitary operator U on the received encrypted information C, and sends the evaluation information E to the client. This process will consume the quantum evaluation key.

(4)   Decryption algorithm. Due to the unitary operator U executed by the server, the client updates the decryption key sk to decrypt the received evaluation information E. The client’s decryption information is essentially the unitary operator U acting on the plaintext information M.

Like many QHE schemes [17–19,22,24], this paper combines X and Z to encrypt the plaintext qubit |φ〉.

|φ⟩↦XaZb|φ⟩,∀a,b∈{0,1} (4)

According to the perfect secure QOTP and proved by Boykin et al. [16], there is Eq. (5)

122n∑a,b∈{0,1}nXaZbσ(XaZb)†=I2n2n (5)

where σ is an arbitrary quantum state, and I2n2n is the complete maximum mixed state of n qubits. Because a and b are randomly selected from {0, 1}, this encryption method is perfectly secure.

In the homomorphic evaluation algorithm, Clifford gate set {X, Z, H, S, CNOT} evaluates the encrypted qubit, and the evaluation results are as follows.

XXaZb|φ⟩=XaZbX|φ⟩ (6)

ZXaZb|φ⟩=XaZbZ|φ⟩ (7)

HXaZb|φ⟩=XbZaH|φ⟩ (8)

SXaZb|φ⟩=XaZa⊕bS|φ⟩ (9)

CNOT1→2(X1aZ1b⊗X2cZ2d)|φ⟩1|ϕ⟩2=(X1aZ1b⊕d⊗X2a⊕cZ2d)CNOT1→2|φ⟩1|ϕ⟩2 (10)

It can be found that only by executing the new combination of X and Z on the evaluation results, the decryption results can be obtained that Clifford gate set {X, Z, H, S, CNOT} acts on the plaintext qubit respectively.

When the server performs the evaluation of a T or T† gate, it will occur an unexpected S-error.

TXaZb|φ⟩=XaZa⊕bSaT|φ⟩ (11)

If only X and Z are executed on the evaluation result, they cannot be completely obtained T|φ〉, and there may be a S-error. In order to eliminate S-error, based on the idea of U-rotated Bell measurement, Gong et al. [24] designed the quantum circuit shown in Fig. 1 to complete the homomorphic evaluation process of T-gate.

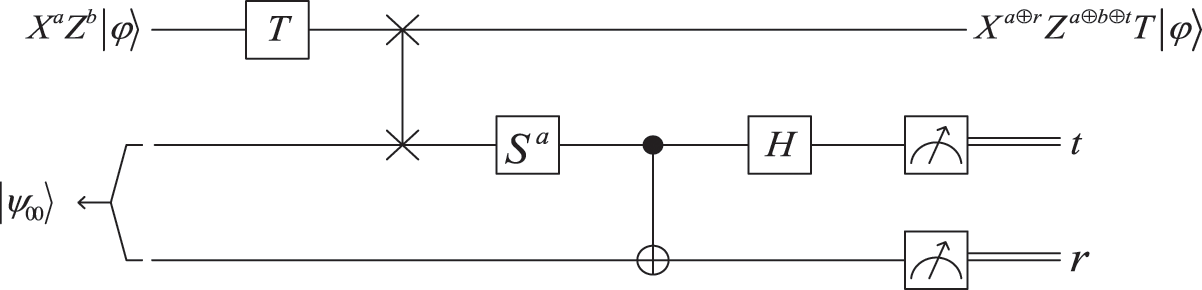
Figure 1: Quantum circuit for the homomorphic evaluation process of T-gate

In Fig. 1, according to the value of the encryption key a, the client performs Sa-rotated Bell measurement to obtain the values of r and t. Based on the key-updating algorithm, the client updates the decryption key to a⊕r and a⊕b⊕t , which will be used in the decryption algorithm to accomplish the evaluation of T-gate.

TXaZb|φ⟩→Xa⊕rZa⊕b⊕tT|φ⟩ (12)

2.3 The Quantum Full Adder Circuit

In this section, we describe how to construct a quantum full adder circuit based on classical binary addition. Suppose there are two unsigned binary digits, A = (a0,a1,…,an−1) and B = (b0,b1,…,bn−1) . The sum of these two numbers is C = (c0, c1, …, cn), where q is the carry qubit.

ci=ai⊕bi⊕qi+1,cn=an⊕bn,qi=(ai⋅bi)⊕(qi+1⋅(ai⊕bi)),qn=an⋅bn,i∈(0,1,…,n−1) (13)

Binary addition involves exclusive-OR and AND operations. CNOT and Toffoli gates in the quantum circuits that do these two operations. A full adder circuit of the two participants consisting of CNOT gate and Toffoli gate, a two-bit quantum full adder circuit is shown in Fig. 2.

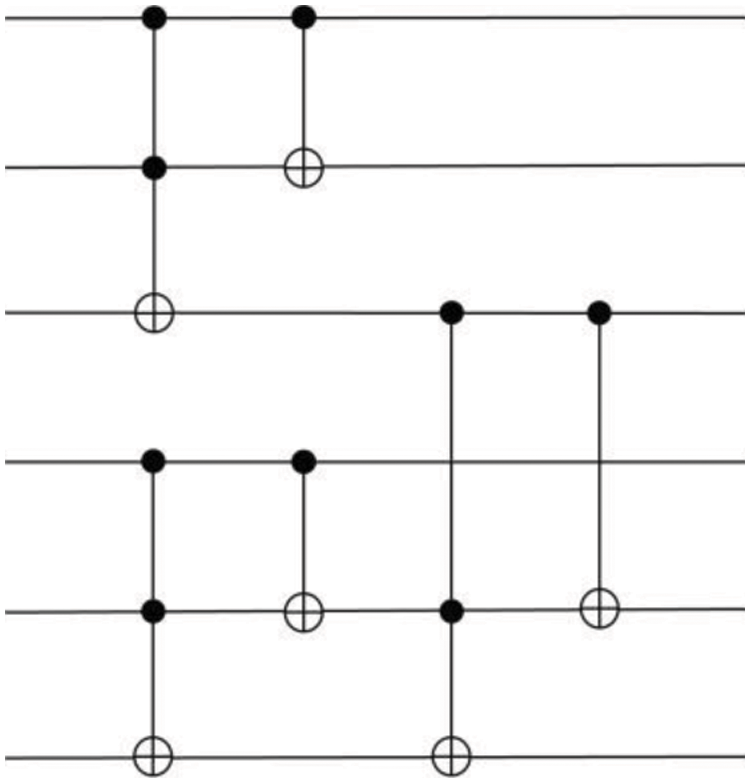
Figure 2: The two-bit quantum full adder circuit

The Toffoli gate can be decomposed into two H gates, one S gate, six CNOT gates, three T-gates and four T† -gates, and the detailed circuit is shown in Fig. 3.

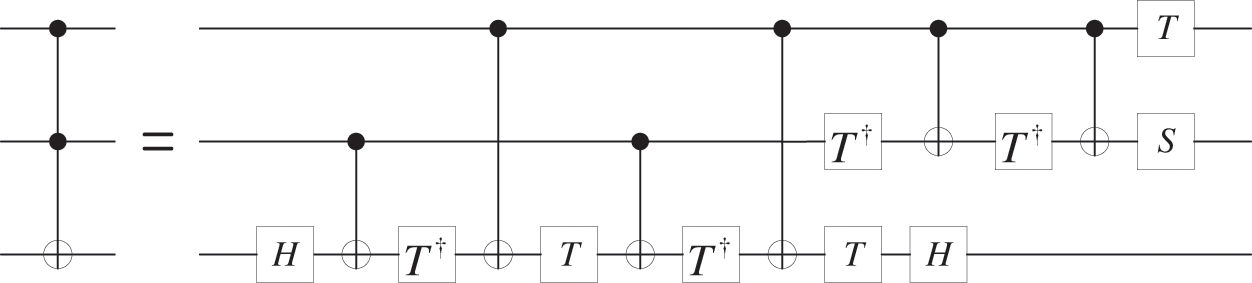
Figure 3: Quantum circuit of Toffoli gate

The detailed decomposition circuit of the Toffoli gate is the basic element to realize a two-bit quantum full adder. It transforms the realization of a three-qubit gate into a combination of single-qubit and two-qubit gates, which is to some extent easy to implement experimentally and technically.

3  A Protocol of Multi-Party Quantum Summation Based on QHE

In our protocol, the participant’s message to be encrypted is classical binary data that can be represented by utilizing horizontal and vertical polarization. The vertically polarized photon |1〉 represents one and the horizontally polarized photon |0〉 represents zero. Before transmitting those photons, all the photons are encrypted by using QOTP. Note that if the encrypted message is classic, it is possible to use QOTP to generate the perfectly secure ciphertext.

Suppose that there are N participants (P1, P2, …, Pn), each holding a M-length secret information Ii(i = 1, 2, …, n) known only to themselves. They can calculate the summation of Ii with the help of the server and a trusted key center, and the communication model between them and TP is shown in Fig. 4. A security parameter K is required to prevent computation overflow, where K = [log2(N)] + 2. In Fig. 5 we show the flow chart of this scheme.

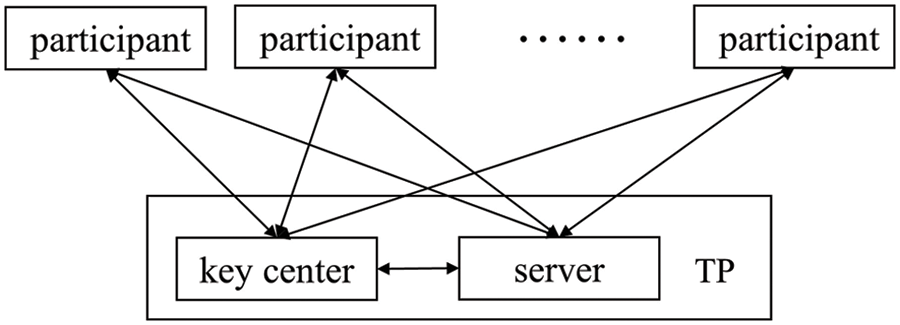
Figure 4: The communication model between participants and TP

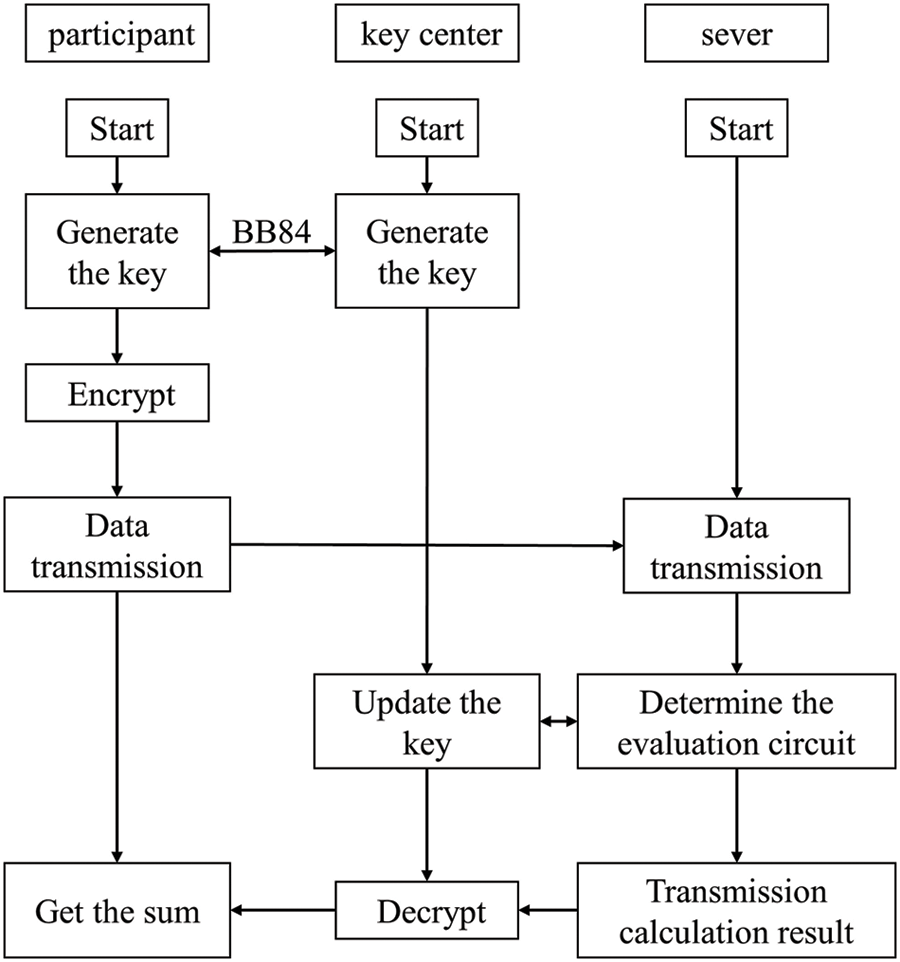
Figure 5: The flow chart of this scheme

Step 1: The key center randomly generates N secret keys of 2M-length, and sends Keyi0 to the participant Pi through a secure key distribution protocol, such as the BB84 protocol.

Step 2: If the number of the participant’s secret information Ii is positive or zero, the participants don’t have to do anything on their 0–1 code. Otherwise, they convert their 0–1 code into a two’s complement. And then they prepare the photon sequence |φ1i⟩|φ2i⟩…|φMi⟩ based on their 0–1 code, if Binji=1 , then |φji⟩=|1⟩ ; if Binji=0 , then |φji⟩=|0⟩ . And then they use the Keyi0 to encrypt the photon sequence and obtain |ψ1i⟩|ψ2i⟩…|ψMi⟩=Xa1(0)Zb1(0)|φ1i⟩⊗Xa2(0)Zb2(0)|φ2i⟩…⊗XaM+L(0)ZbM+L(0)|φMi⟩ based on QOTP. Finally, the key center adds 2K zero key according to the security parameter K. The participants whose information is positive add K-length |0〉 photons in front of the photon sequence, the new photon sequence is |01⟩|02⟩…|0K⟩|ψ1i⟩|ψ2i⟩…|ψMi⟩ . The participants whose information is negative add K-length |1〉 photons in front of the photon sequence, the new photon sequence is |11⟩|12⟩…|1K⟩|ψ1i⟩|ψ2i⟩…|ψMi⟩ .

Step 3: To prevent the eavesdropping, the participants prepare Di decoy photons and randomly insert them in their photon sequence, each photon is selected from {|0〉, |1〉, | +〉, | −〉}, and send the new photon sequence to the sever.

Step 4: Once the server gets their photon sequences, the participants announce the position Poi and basis Bai of the inserted decoy photons. If the insert decoy is |0〉 or |1〉, the measurement basis is {|0〉, |1〉}; If the insert decoy is |+⟩ or | −〉, the measurement basis is {|+⟩,|−⟩} . The server calculates the accuracy rate based on the measurement results, and if the accuracy is less than the threshold they preset, that indicates the presence of eavesdroppers, then terminate the protocol. Otherwise, the server discards these decoy photons and continues to the next step.

Step 5: The server constructs a quantum full adder circuit, with each participant’s photon sequence as input to the circuit. In the evaluation operation, the key center updates the key based on the quantum gates performed by the server and the key update algorithm of quantum gates. After the server has performed all the quantum gates in the quantum circuit, the key center obtains the final updated Keyifinal , which is the decryption key. The server sends the calculated results to the key center.

Step 6: The key center uses the decryption key to decrypt and measure all the photons in the photon sequence, and then releases the measurements to all participants. Then participants calculate the bits sequence to get the summation of their secret information.

In Step 5, in the homomorphic evaluation algorithm, when the server performs Clifford gates operation on ciphertext, according to the commutation rules between Clifford gate and Pauli matrices, the new intermediate keys can be obtained without any additional classical or quantum resources. Suppose the i-th Clifford gate operation performed by the server is defined as Gi, which acts on the k-th in the photon sequence GiXak(j)Zbk(j)|φ⟩ , (if Gi = CNOT and the input qubit are k-th and l-th then Gi(Xak(j)Zbk(j)|φ⟩⊗Xal(j)Zbl(j)|φ⟩) , where Gi ∈ {X, Y, Z, H, T, S, CNOT}, ak(j), bk(j) are (j+1)-th intermediate keys. As for the operation Gi and key update algorithm, the calculation procedure of the (j+1)-th intermediate key is as follows:

(1)   If Gi = X, Y, Z, then (ak(j + 1), bk(j + 1)) = (ak(j), bk(j));

(2)   If Gi = H, then (ak(j + 1), bk(j + 1)) = (bk(j), ak(j));

(3)   If Gi = S, then (ak(j+1),bk(j+1))=(ak(j),ak(j)⊕bk(j)) ;

(4)   If Gi = CNOT, then (ak(j+1),bk(j+1))=(ak(j),bk(j)⊕bl(j)) and

(al(j+1),bl(j+1))=(ak(j)⊕al(j),bl(j))

Any arbitrary unitary operator can be composed of H, S, CNOT and T gates, and a T-gate key update is required for the client to perform any unitary operation on the server. But when a T-gate apply on the encrypted qubit, an S-error occurs: if a = 1, TXak(j)Zbk(j)|φ⟩=Xak(j)Zbk(j)⊕ak(j)Sak(j)T|φ⟩ . Fisher et al. used an auxiliary qubit to solve the error caused by T-gate in the evaluation algorithm, which is a basis of the protocol in this paper. Before the server starts doing its calculations, the key center needs to prepare and send the same number of auxiliary photons as the T-gate in the quantum circuit. These photons are encrypted as YyZd| + 〉, with y, d ∈ {0, 1}. When the server performs a T-gate on the k-th qubit. The server first performs a CNOT gate on the k-th qubit and t-th auxiliary photons (Suppose this is the k-th T-gate that the server performs), where the control qubit is the auxiliary qubit. Then, according to the intermediate key (ak(j), bk(j)) of the k-th qubit and the encryption key for t-th auxiliary qubit, the key center sends a classic message ak(j)⊕y(t) to the server. The server performs a Sak(j)⊕y(t) gate on the auxiliary, measures the k-th qubit and sends the measurement result c(t) to the key center. The key center performs the key update algorithm to obtain a new intermediate key Keyij+1 .

In order to prevent the eavesdropping in the evaluation algorithm, the server and key center convert the classical information bits ak(j)⊕y(t) and c(t) into qubit transmission and insert some decoy photons in them. The key center (the sever) prepares D′ photons which are randomly selected from four photon states, and randomly insert the photon |ak(j)⊕y(t)⟩ (|c(t)〉) into the decoy photon sequence to send the new photon sequence to the sever (the key center). When the server (the key center) receives the photon sequence, it first checks the sequence for eavesdroppers. If there is no eavesdropper, proceed to the next step, otherwise abort the protocol.

Two examples are given to verify that the calculation of the protocol is correct. Without loss of generality, after ignoring the eavesdropper checking and evaluating algorithm process, suppose there are three participants named P1, P2, P3 who have a secret integer information I1, I2, I3, respectively. We convert their secret information into binary and give some examples to illustrate the correctness of our protocol.

Suppose that participants P1, P2, P3 have positive integer information I1 = 145, I2 = 201, I2 = 78, respectively. The security parameter is K = [log2(3)] + 2 = 2. The 0–1 code of length M = 8 (i.e., M = MAX.Length(log2(Ii)), i ∈ (1, 2, 3)) are I1 = (1, 0, 0, 1, 0, 0, 0, 1), I2 = (1, 1, 0, 0, 1, 0, 0, 1), I3 = (0, 1, 0, 0, 1, 1, 1, 0). According to the security parameter K, the new 0–1 code I1′=(0,0,1,0,0,1,0,0,0,1) ; I2′=(0,0,1,1,0,0,1,0,0,1) ; I3′=(0,0,0,1,0,0,1,1,1,0) . Calculated by binary addition, the summation of I1′,I2′,I3′ is (0, 1, 1, 0, 1, 0, 1, 0, 0, 0). We can know the summation is ∑i=13Ii=DEC(∑i=13I′i)=424 , where DEC is a binary to the decimal algorithm.

Suppose that participants P1, P2 have positive integer information I1 = 138, I2 = 49, and P3 have I3 = −223. The security parameters are K = [log2(3)] + 2 = 2. The 0–1 code of length M = 8 (i.e., M = MAX.Length(log2(Ii)), i ∈ (1, 2, 3)) are |I1| = (1, 0, 0, 0, 1, 0, 1, 0), |I2| = (0, 0, 1, 1, 0, 0, 0, 1), |I3| = (1, 1, 0, 1, 1, 1, 1, 1). According to the two’s complement rule and the security parameter K, the new 0–1 code I1′=(0,0,1,0,0,0,1,0,1,0) ; I2′=(0,0,0,0,1,1,0,0,0,1) ; I3′=(1,1,0,0,1,0,0,0,0,1) , where the highest qubit is the sign bit. Calculated by binary addition, and the summation of I1′,I2′,I3′ is (1, 1, 1, 1, 0, 1, 1, 1, 0, 0). We can know the summation is ∑i=13Ii=DEC(∑i=13I′i)=−36 , where DEC is a binary to decimal algorithm.

4  Security Analysis

4.1 Outside Attack

In our protocol, outside attackers can attack during key distribution, ciphertext transmission and evaluation algorithm execution.

Firstly, in step 1 of our protocol, the key center and the participants use the BB84 protocol to distribute the key, which is a secure protocol from which the attacker cannot obtain the key information.

Secondly, the participants encrypt their secret information using QOTP, which is a perfectly secure encryption scheme where outside attackers cannot recover secret information from the ciphertext without knowing the encrypt key. During ciphertext transmission, the outside attacker might attack the quantum channel when the participants send their encrypted photon sequence to the sever in Step 3. Because of the participants insert some decoys into the photon sequence, the attacker cannot distinguish decoy photons from signal photons without knowing the position and bases of decoy photons insertion.

Thirdly, in the evaluation algorithm, the key center needs to communicate with the server once quantum and twice classical when the server performs a T or T† gate evaluation. We use qubit instead of bit and insert it into decoy photon sequence in the evaluation communication, the outside attacker cannot get effective information.

4.2 Participant’s Attack

In this type of attack, the dishonest participants, server and semi-honest key center involved in the protocol try to steal secret information from other participants. In our protocol, a collusive attack by N-2 dishonest participants is secure. If there are N-1 dishonest participants, they can calculate the secret information of the last participant according to the summation and their secret information. We initially analyze the case that Pi desires to know the secret information of other N-1 participants. Secondly, we analyze the case that the key center and the sever want to learn the secret information of N participants.

Case 1: Pi wants to steal the secret information of other N-1 participants.

There is no communication between dishonest participant Pi and other honest participants in our scheme, and he cannot get any information from other participants. Suppose a dishonest server cooperates with Pi to attack other participants, Pi cannot decrypt and measure these encrypted photon sequences without the decrypt key. Hence, arbitrary dishonest Pi cannot infer secret information about other N-1 participants. If a dishonest participant in the protocol with virtual secret information, only he can get the final summation, but he still cannot infer the secret information of other participants.

Case 2: The semi-honest key center and the server desire to steal the secret information of N participants.

The participant N interact with the key center who is semi-honest in our protocol. This means that key center must faithfully implement the protocol and cannot cooperate with anyone participants or the sever, but it can use the key data it obtains to try to get the participant’s secret information.

In Step 1, the key center generates the initial key with the participants by the BB84 protocol, and it does not obtain any secret information of participants in this process.

In Step 4, the server receives the ciphertext data of the participants. Without the decryption key, it cannot decrypt and measure the secret information of the participants.

In Step 5, the key center communicates with the server to generate the intermediate key in this process, there is only the interaction of the key information and no interaction of the secret information. The server only obtains ak(j)⊕y(t) , the intermediate key cannot be inferred without knowing the specific values of ak(j) and y(t).

5  Conclusion

In summary, we propose a secure multi-party quantum summation protocol based on quantum homomorphic encryption. In our scheme, N participants utilize the QOTP to encrypt their photon sequences which are qubit forms of their secret information. The server and the semi-honest key center work together to complete the calculation, and then the key center publishes the decryption and measurement results ∑i=1NIi . Our protocol allows participants to have not only a positive integer secret information but also a negative integer. Meanwhile, the proposed protocol can also prevent outside attacks and protect the secret information of participants. Theoretically, our works can be applied to many other secure multi-party quantum computing problems.

Funding Statement: This work was supported by the Open Fund of Advanced Cryptography and System Security Key Laboratory of Sichuan Province (Grant No. SKLACSS-202101), NSFC (Grant Nos. 62176273, 61962009, U1936216, 62076042), the Foundation of Guizhou Provincial Key Laboratory of Public Big Data (No. 2019BDKFJJ010, 2019BDKFJJ014), the Fundamental Research Funds for Beijing Municipal Commission of Education, Beijing Urban Governance Research Base of North China University of Technology, the Natural Science Foundation of Inner Mongolia (2021MS06006), Baotou Kundulun District Science and technology plan project (YF2020013), and Inner Mongolia discipline inspection and supervision big data laboratory open project fund (IMDBD2020020).

Conflicts of Interest: We declare that we have no conflicts of interest to report regarding the present study.

References

 1.  A. C. Yao, “Protocols for secure computations,” in 23rd Annual Symp. on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, pp. 160–164, 1982. [Google Scholar]

 2.  D. H. Vu, T. D. Luong and T. B. Ho, “An efficient approach for secure multi-party computation without authenticated channel,” Information Sciences, vol. 527, pp. 356–368, 2020. [Google Scholar]

 3.  G. Xu, K. Xiao, Z. P. Li, X. X. Niu and M. Ryan, “Controlled secure direct communication protocol via the three-qubit partially entangled set of states,” Computers, Materials & Continua, vol. 58, no. 3, pp. 809–827, 2019. [Google Scholar]

 4.  G. Xu, Y. B. Cao, S. Y. Xu, K. Xiao, X. Liu et al., “A novel post-quantum blind signature for log system in blockchain,” Computer Systems Science and Engineering, vol. 41, no. 3, pp. 945–958, 2022. [Google Scholar]

 5.  Z. G. Qu, S. Y. Chen and X. J. Wang, “A secure controlled quantum image steganography algorithm,” Quantum Information Processing, vol. 19, no. 380, 2020. [Google Scholar]

 6.  Z. G. Qu, S. Y. Wu, W. J. Liu and X. J. Wang, “Analysis and improvement of steganography protocol based on bell states in noise environment,” Computers, Materials & Continua, vol. 59, no. 2, pp. 607–624, 2019. [Google Scholar]

 7.  V. S. Naresh and S. Reddi, “Multiparty quantum key agreement with strong fairness property,” Computer Systems Science and Engineering, vol. 35, no. 6, pp. 457–465, 2020. [Google Scholar]

 8.  X. B. Chen, Y. R. Sun, G. Xu and Y. X. Yang, “Quantum homomorphic encryption scheme with flexible number of evaluator based on (k, n)-threshold quantum state sharing,” Information Sciences, vol. 501, pp. 172–181, 2019. [Google Scholar]

 9.  X. B. Chen, G. Xu, Y. X. Yang and Q. Y. Wen, “An efficient protocol for the secure multi-party quantum summation,” International Journal of Theoretical Physics, vol. 49, pp. 2793–2804, 2010. [Google Scholar]

10. C. Zhang, Z. W. Sun, X. Huang and D. Y. Long, “Three-party quantum summation without a trusted third party,” International Journal of Quantum Information, vol. 13, no. 2, 2015. [Google Scholar]

11. W. Liu, Y. B. Wang and W. Q. Fan, “An novel protocol for the quantum secure multi-party summation based on Two-particle bell states,” International Journal of Theoretical Physics, vol. 56, pp. 2783–2791, 2017. [Google Scholar]

12. W. Liu, Y. B. Wang, A. N. Sui and M. Y. Ma, “Quantum protocol for millionaire problem,” International Journal of Theoretical Physics, vol. 58, pp. 2106–2114, 2019. [Google Scholar]

13. C. Zhang, M. Razavi, Z. W. Sun, Q. Huang and H. Z. Situ, “Multi-party quantum summation based on quantum teleportation,” Entropy, vol. 21, no. 7, 2019. [Google Scholar]

14. L. W. Kuang, L. T. Yang, J. Feng and M. X. Dong, “Secure tensor decomposition using fully homomorphic encryption scheme,” IEEE Transactions on Cloud Computing, vol. 6, no. 3, pp. 868–878, 2018. [Google Scholar]

15. L. C. Wang, Z. H. Zhang, M. X. Dong, L. H. Wang, Z. F. Cao et al., “Securing named data networking: Attribute-based encryption and beyond,” IEEE Communications Magazine, vol. 56, no. 11, pp. 76–81, 2018. [Google Scholar]

16. P. O. Boykin and V. Roychowdhury, “Optimal encryption of quantum bits,” Physical Review A, vol. 67, 2003. [Google Scholar]

17. M. Liang, “Symmetric quantum fully homomorphic encryption with perfect security,” Quantum Information Processing, vol. 12, pp. 3675–3687, 2013. [Google Scholar]

18. M. Liang, “Quantum fully homomorphic encryption scheme based on universal quantum circuit,” Quantum Information Processing, vol. 14, pp. 2749–2759, 2015. [Google Scholar]

19. K. A. G. Fisher, A. Broadbent, L. K. Shalm, Z. Yan, J. Lavoie et al., “Quantum computing on encrypted data,” Nature Communications, vol. 5, 2014. [Google Scholar]

20. A. Broadbent and S. Jeffery, “Quantum homomorphic encryption for circuits of low T-gate complexity,” in Advances in Cryptology–CRYPTO 2015, Santa Barbara, CA, USA, pp. 609–629, 2015. [Google Scholar]

21. M. Liang, “Teleportation-based quantum homomorphic encryption scheme with quasi-compactness and perfect security,” Quantum Information Processing, vol. 19, 2020. [Google Scholar]

22. Q. Zhou, S. F. Lu, Y. G. Cui, L. Li and J. Sun, “Quantum search on encrypted data based on quantum homomorphic encryption,” Scientific Reports, vol. 10, 2020. [Google Scholar]

23. L. Yu, C. A. Pérez-Delgado and J. F. Fitzsimons, “Limitations on information-theoretically-secure quantum homomorphic encryption,” Physical Review A, vol. 90, 2014. [Google Scholar]

24. C. Q. Gong, J. Du, Z. Y. Dong, Z. Z. Guo, A. Gani et al., “Grover algorithm-based quantum homomorphic encryption ciphertext retrieval scheme in quantum cloud computing,” Quantum Information Processing, vol. 19, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.