DOI:10.32604/iasc.2022.027067

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.027067 |  |
| Article |
Movie Recommendation Algorithm Based on Ensemble Learning
1School of Computer and Software, Engineering Research Center of Digital Forensics, Ministry of Education, Nanjing University of Information Science and Technology, Nanjing, 210044, China
2State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing, 100081, China
3Department of Computer, Texas Tech University, Lubbock, TX 79409, USA
*Corresponding Author: Wei Fang. Email: Fangwei@nuist.edu.cn
Received: 10 January 2022; Accepted: 15 March 2022
Abstract: With the rapid development of personalized services, major websites have launched a recommendation module in recent years. This module will recommend information you are interested in based on your viewing history and other information, thereby improving the economic benefits of the website and increasing the number of users. This paper has introduced content-based recommendation algorithm, K-Nearest Neighbor (KNN)-based collaborative filtering (CF) algorithm and singular value decomposition-based (SVD) collaborative filtering algorithm. However, the mentioned recommendation algorithms all recommend for a certain aspect, and do not realize the recommendation of specific movies input by specific users which will cause the recommended content of the website to deviate from the need of users, and affect the experience of using. Aiming at this problem, this paper combines the above algorithms and proposes three ensemble recommendation algorithms, which are the ensemble recommendation of KNN + text, the recommendation of user KNN + movie KNN, and the recommendation of user KNN + singular value decomposition. Compared with the traditional collaborative filtering algorithm based on matrix factorization, the method we proposed can realize the recommendation of specific movies input by specific users and make more personalized recommendations and can deal with the problem of cold start and sparse matrix processing issues to a certain extent.
Keywords: KNN; CF; SVD; ensemble recommendation; personalized recommendation
With the rapid development of the Internet, the Internet has gradually become an important way for people to obtain information resources. It is easy to obtain abundant movie resources on major search engines. However, it is impossible that users can accurately find the movies they are more interested in a short time because of the dazzling array of movies. In order to help user find movies of interest efficiently, the recommendation system has attracted the attention of many researchers. As the core part of recommendation system, the quality of recommendation algorithm directly determines the quality of recommendation system.
The oldest type of recommendation algorithm is the content-based recommendation algorithm [1]. The content-based recommendation process is: extracting the item features that represent the item firstly, and then using the past interest and disinterest item feature data to learn the preference feature of the user. Finally, by comparing the preference feature and the candidate item feature can recommends a group of items with the most relevance for the user [2]. This algorithm generally only relies on the own behavior to provide recommendations for user, and does not involve the behaviors of other users. It can well identify the taste of user, which is very intuitive and easy to understand, has strong interpretability, and it is easier to solve the cold start problem [3]. However, the content-based recommendation algorithm has some shortcomings, such as range is narrow, the novelty is not strong, and the recommendation accuracy is not high.
Collaborative filtering algorithm [4–6] is one of the most widely used and most successful technologies in recommendation systems [7]. This algorithm assumes that users with similar interests may like similar items or users may show similar degrees of preference for similar items. The core idea is a recommendation algorithm based on neighbors, which uses the similarity between users or items [8] and historical behavior data to effectively recommend target users [9]. It filters through the user’s feedback on the movies that have been watched, so as to find the movies that users may be interested in the massive movie data. This paper introduces two KNN-based collaborative filtering algorithms [10], one of which is based on movie similarity recommendation algorithm, but for different users, the results of the recommendation are not any different, and no personalized recommendation for different users is realized. Therefore, the second recommendation algorithm for user similarity is proposed, but the collaborative filtering algorithm has cold start and sparseness data [11] processing issues.
Aiming at this problem, this paper introduces the third type of collaborative filtering algorithm based on SVD [12]. By performing SVD decomposition on the user-movie rating matrix, users or movies that have little significance in predicting the final result are deleted. Predictive ratings for movies not rated. Since the user-movie rating matrix is a coefficient matrix with very high dimensions, this paper uses different algorithms to decompose, including stochastic gradient descent algorithm (SGD) [13], Langevin dynamic system stochastic gradient method (SGLD) and Stochastic Gradient Hamiltonian Monte Carlo method (SGHMC). Through experimental results, it is found that the Root Mean Squared Error (RMSE) loss of the SGHMC algorithm is the lowest, reaching 0.84117, which is a better optimization method, and the obtained model also has a better recommendation effect.
The above recommendation algorithms all recommend for a certain aspect, and do not realize the recommendation of specific movies input by specific users. In response to this problem, this paper combines the above algorithms and proposes three ensemble recommendation algorithms, namely KNN + text. The ensemble recommendation of user KNN + movie KNN, the ensemble recommendation of user KNN + singular value decomposition to achieve a better personalized recommendation [14,15] effect.
This paper first introduces the principles, advantages and disadvantages of three traditional recommendation algorithms, followed by content-based recommendation algorithm, KNN-based collaborative filtering algorithm and singular value decomposition-based collaborative filtering algorithm.
2.1 Principles of Content-based Recommendation Algorithm
The content-based recommendation algorithm builds a recommendation algorithm model based on the subject-related information, user-related information, and the user’s operating behavior on the subject to provide users with recommendation services. The subject-related information here may be information such as the category of the movie purchased by the user, tags, and user comments. User-related information refers to information such as the age, gender, preference, and region of the ticket purchaser. The user’s operation behavior on the subject matter can be comments, favorites, likes, watching, browsing, clicking, buying tickets, etc. The basic principle of the content-based recommendation algorithm is to obtain the user’s interest preferences based on the user’s historical behavior, and recommend objects that are similar to his interest preferences, which is very intuitive and easy to understand, and has strong interpretability. The algorithm mainly extracts the characteristics of movies first, then calculates the similarity between movie contents, and finally judges whether users like a movie with similar characteristics. Since the algorithm only needs to calculate the similarity based on the characteristics of the movie and does not involve other user information, there is no cold start problem. The formula for calculating cosine similarity is shown below.
2.2 The Principle of Collaborative Filtering Recommendation Algorithm Based on KNN
2.2.1 Principles of Movie-based Collaborative Filtering Algorithm
The movie-based collaborative filtering algorithm obtains the relationship between movies by calculating the ratings of different users on different movies, and recommends similar movies to users based on the relationship between movies. For example, if A has watched movie A and movie B, it means that movie A and movie B are highly correlated. When B also watches movie A, it can be inferred that he also needs to watch movie B. The formula for calculating the similarity between movies is:
Among them, u(i) represents the set of users who have watched movie i, and u(j) represents the set of users who have watched movie j. The prediction formula for the target user u unrated movie i in the movie-based collaborative filtering algorithm is:
where I(u) represents the set of overrated movies used by target user u, Si,j represents the similarity between movie i and movie j, and rj,u represents the rating of movie j of target user u.
2.2.2 User-based Collaborative Filtering Algorithm Principle
The user-based collaborative filtering algorithm discovers the interest of user through the historical behavior data, such as buying tickets, clicking, commenting, and watching, and measures and scores. The relationship between users is calculated according to the attitudes and preferences of different users towards the same movie, and movie recommendations are made among users with the same preferences. The formula for calculating the similarity between users is:
Among them, N(u) represents the collection of movies watched by user u, and N(V) represents the collection of movies watched by user v. The prediction formula for the unrated movie i of the target user u in the user-based coordination filtering algorithm is:
where N(i) represents the set of users who have rated movie i, wu,v represents the similarity between user u and user v, and rv,i represents the rating of movie I of user v.
2.2.3 Principle of Collaborative Filtering Recommendation Algorithm Based on SVD
SVD has obvious physical meaning [16]. In the field of machine learning, many applications are related to singular value decomposition, such as principal component analysis (PCA) [17], data compression [18], image compression [19], and LSI (latent semantic indexing) [20] algorithms used in feature reduction [21]. Since the collaborative filtering algorithm needs to process the complete user product matrix Data, this matrix is generally sparse, which results in the collaborative filtering algorithm processing a large amount of useless data and inefficient. To solve this problem, we can use SVD to perform dimensionality reduction processing [22] on the original user product data, and delete those users or movies that have little significance in predicting the final result. Assuming that the diagonal matrix of the intercepted singular value decomposition is Δ, the user product matrix New Data after dimensionality reduction is:
where U is the left singular matrix in singular value decomposition.
The above-mentioned recommendation algorithms all recommend for a certain aspect, and do not realize the recommendation of specific movies input by specific users. This paper combines the above algorithms and proposes three ensemble recommendation algorithms.
3.1 KNN + Text Ensemble Recommendation Algorithm
This paper first uses the KNN algorithm to find the 10 users closest to the input current user ID and selects the movies that similar users have seen and the current user has not seen as candidate movie. After that, the text input by the user is converted into a vector, and the text information (introduction, name, director, etc.) of the candidate movie is encoded into a vector. Finally, according to the cosine distance between the extracted candidate movie vector and the input text vector, the most recent top 10 movies are recommended for the user. Given a movie vector A and a text vector B, the cosine similarity θ is given by the dot product and the vector length. The pseudo code of the algorithm is shown in Tab. 1.

The cosine similarity formula is as follows:
Among them, the cosine value between two vectors can be obtained by using the Euclidean dot product formula: a ⋅ b = ‖a‖‖b‖cosθ, it can be seen that the value range of cosine similarity is: [−1, 1], but the distance cannot be negative, so the cosine distance is defined as:
The value range of the cosine distance is: [0, 2], non-negative.
3.2 The Ensemble Recommendation Algorithm of User KNN + Movie KNN
This paper first uses the KNN algorithm to find the 10 users closest to the input current user ID, and then uses the movies that similar users have seen and the current user has not seen as candidate movies. Afterwards, KNN processing is performed on the movie data, and the 10 movies closest to the user input movie are selected for recommendation. The principle of the KNN algorithm is to find K pieces of data that are most similar to the sample, and the sample belong to the category that most of the K data belong to. The KNN algorithm process is divided into three steps. First, calculate and sort the distance between the test data and all the training data, then select the K points with the smallest distance, and finally use the category of the K points with the smallest distance as the prediction classification. Euclidean distance is commonly used to measure the distance of neighbors, the Euclidean distance formula between two n-dimensional vectors a (x11, x12, …x1n) and b (x21, x22, …x2n) is:
It can also be expressed as a vector operation:
The pseudo code of the algorithm is shown in Tab. 2.

3.3 User KNN + SVD Ensemble Recommendation Algorithm
This paper first uses the KNN algorithm to find the 10 users closest to the input current user ID, and then uses the movies that these similar users have watched and the current user has not watched as candidate movies. After that, matrix decomposition is used to simulate the current rating of candidate movies, and the ten highest-rated movies are selected for recommendation. The pseudo code of the algorithm is shown in Tab. 3.

Singular value decomposition shows the internal structure of a matrix to a certain extent. A more complex matrix can be expressed as the product of several smaller and simpler sub-matrices. These sub-matrices describe important characteristics of the matrix. Singular value decomposition is a decomposition method that can be applied to any matrix. For any matrix A, there is always a singular value decomposition:
Assuming that A is an m*n matrix, then the obtained U is an m*m square matrix, and the orthogonal vector in U is called the left singular vector.
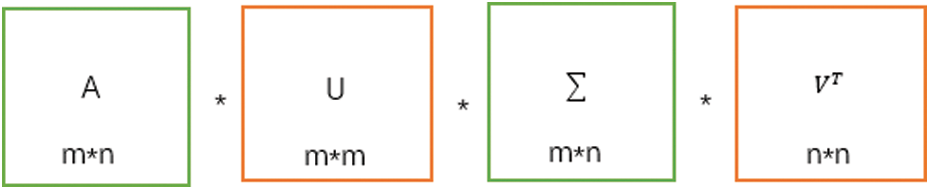
Figure 1: Changes in the dimensions of each matrix in singular value decomposition
For movie recommendation, we use the TMDB5000 dataset collected from The Movie Database (TMDB) dataset and some data collected from the movie dataset MovieLens [23], including id, budget, content introduction, keywords and other characteristics, which also contains the rating matrix for the movie.
We use RMSE and Coverage as the criteria for the evaluation of the recommendation system. The root mean square error refers to the average value of the square root of the difference between the recommended scores of all items in the test set and the scores of the actual users. The smaller the error, the better the optimization method and the better the model recommendation effect obtained. The corresponding formula is shown below.
How to evaluate the pros and cons of the recommendation system can be measured by the recommended content coverage. Coverage refers to the proportion of items recommended by the recommendation system to the total items, and describes the ability of a recommendation system to mine long-tail products. The formula for coverage is shown below.
Among them, Ku = {v∈U|distance (u, v) < δ} represents the set of neighbors of user u, and δ is the threshold;
In this experiment, firstly, some features of movie data are visualized and analyzed [24] to provide help for the subsequent movie recommendation, and then experiments and analysis are done on the traditional recommendation algorithm and the proposed ensemble recommendation algorithm.
4.3.1 Visual Analysis of Movie Characteristics
The experiment in this paper first draws a diagram of the relationship between box office and budget, welcome, and drama, as shown in Figs. 2–4.
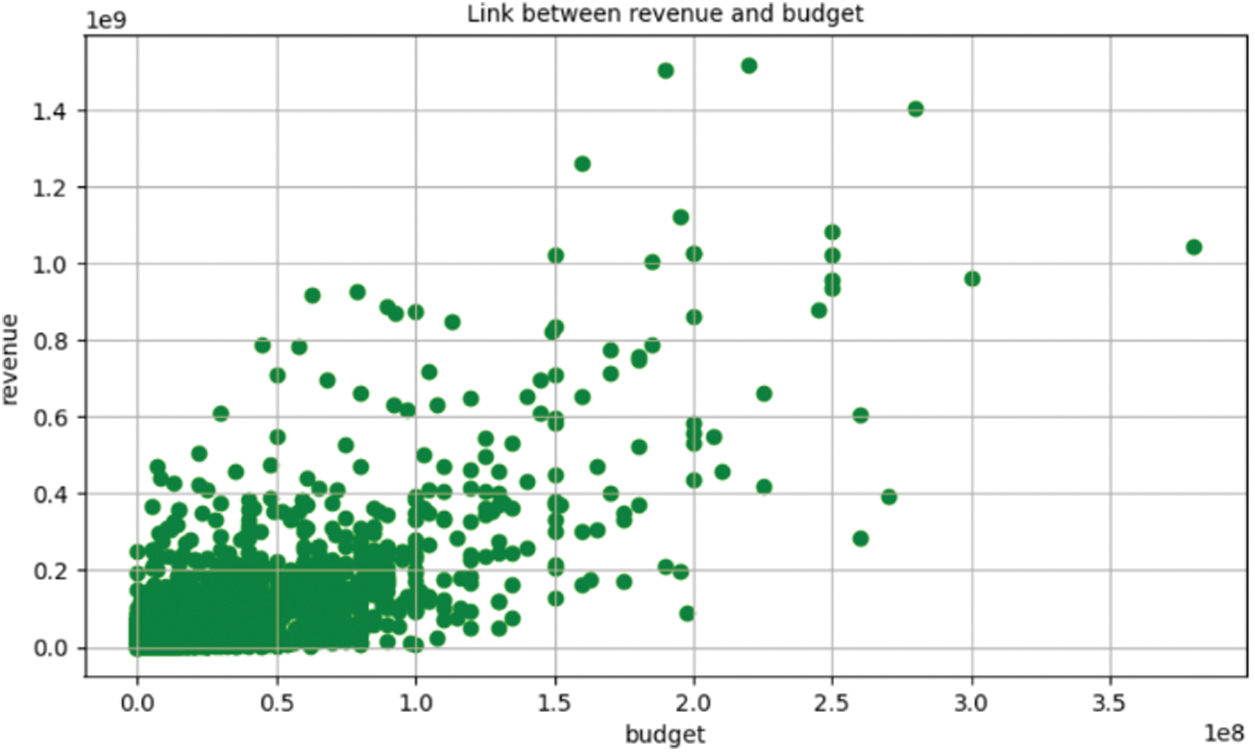
Figure 2: The relationship between box office and budget
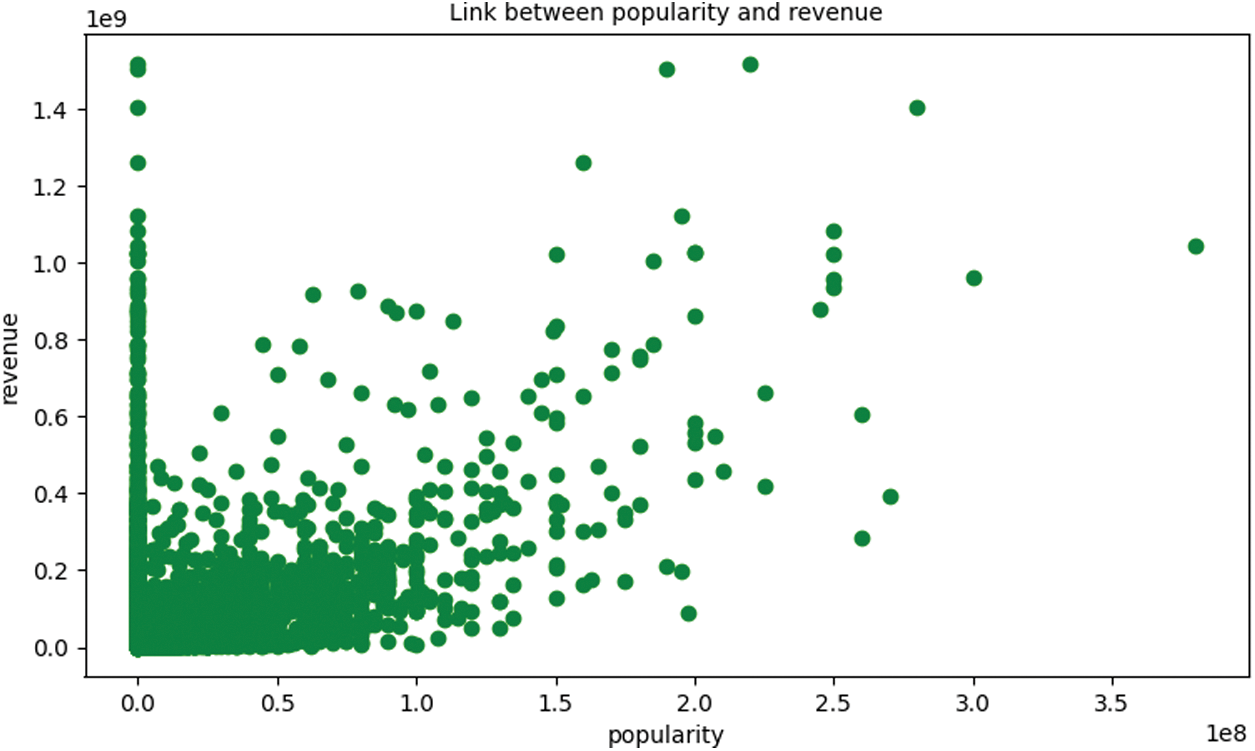
Figure 3: The relationship between box office and popularity

Figure 4: The relationship between box office and drama
It can be seen from the above diagram that there is a strong relationship between box office and budget, welcome, and drama. Therefore, this paper selects 7 characteristics of box office, budget, welcome, drama, screening time, ID, and release year, and draws the correlation diagram between them, as shown in Fig. 5.

Figure 5: Correlation diagram of multiple features
Among them, the darker the color indicates the stronger the correlation. It can be seen that the box office has a strong correlation with the budget, the degree of popularity, and the degree of drama. It has almost no correlation with the release time, ID, etc., which is in line with expectations. In addition, this paper also studies the relationship between box office and film language, as shown in Fig. 6.

Figure 6: The relationship between box office and film language
Finally, this paper studies the relationship between the movie budget and the movie release year, and mainly selects the movie budgets of 1983, 1984, 1985, 1991, and 2017 to estimate the density. The results are shown in Fig. 7.

Figure 7: The relationship between movie budget and movie release year
It can be seen from the figure that the release year has a greater impact on the budget distribution. Earlier years, the budget is concentrated in the lower part. The closer to the present, the more even the budget distribution of the film, corresponding to more and more large productions movie.
4.3.2 Content-based Recommendation Algorithm
This article first uses the keywords, genres, directors, actors and other information in the movie, and uses the CountVectorizer in sklearn to convert the text into a word frequency matrix, and then uses the cosine distance to measure the similarity between the movies. The experimental results show that the recommended movie content is very similar to the input movie, which is in line with the original intention of the algorithm design.
4.3.3 Recommendation Algorithm Based on Movie Similarity
In this paper, the ratings of all users for a certain movie are used as the feature vector of the movie, and the KNN algorithm is used to select the ten most similar movies for the movie input by the user for recommendation. The experimental results show that the input movie is Avengers III, nine of the ten recommended movies are superhero movies produced by Marvel, and the other one is also a sci-fi blockbuster, which shows that the method of measuring the similarity between movies is very effective.
4.3.4 Recommendation Algorithm Based on User Similarity
In this paper, a rating of all movies is used as the feature vector of the user, using the KNN algorithm, for the input user ID, first select 10 users that are most similar to the current user, and then select these 10 most similar users Movies that have been watched and not watched by the current user, and finally the ten movies with the highest average rating among these movies are selected and recommended to the user. The experimental results show that for different users, the recommended results are different, and personalized recommendations for users are achieved.
This experiment uses 85% of the user rating matrix for training and 15% for testing. The specific division method is: generate a random number for each user’s rating for each movie. If it is greater than 0.85, it is a test; less than or equal to 0.85 is training. Then 10 movies are recommended for each user, a total of 6040 movies are recommended, and the coverage ratios of the above three algorithms are calculated respectively. The values are shown in Tab. 4 below.

The experimental results show that among the above three algorithms, the recommendation algorithm based on user similarity has a higher coverage rate and a better model recommendation effect.
4.3.5 Recommendation Algorithm Based on SVD
In this paper, we perform SVD decomposition of the user-movie rating matrix to predict ratings for movies that are not rated by users. This paper uses this algorithm as a secondary screening method. Using the input user id and a series of movie ids to predict the current rating for this series of movies, and select the 10 highest rated movies for recommendation. Since the user-movie rating matrix is a coefficient matrix with very high dimensions, different algorithms are used for decomposition, including the SGD, the SGLD, and the SGHMC. Among them, SGD is an optimization-based method, and SGLD and SGHMC are sampling-based Bayesian [25] probability matrix decomposition algorithms. The final results are shown in Tab. 5.

Experiments show that the RMSE loss of the SGHMC algorithm is the lowest, reaching 0.84117, which is a better optimization method, and the obtained model also has a better recommendation effect.
4.3.6 Ensemble Recommendation Algorithm
In this experiment, 10 movies are recommended for each user, and a total of 6040 movies are recommended. Among them, the number of movies in the test set is 602, accounting for 9.97%, which realizes the recommendation of specific movies input by specific users.
This paper introduces traditional recommendation algorithms firstly, including a content-based recommendation algorithm, two KNN-based collaborative filtering algorithms, and a singular value decomposition-based recommendation algorithm. The advantages and disadvantages of these recommendation algorithms are summarized. On this basis, this paper proposes three ensemble recommendation algorithms that can recommend specific movies entered by specific users. Through experiments on multiple algorithms, it is found that the ensemble algorithm can achieve more personalized recommendations, but the effect is slightly inferior to the algorithm that only uses user KNN. Because the user and movie score matrix contains the score for each movie, the score is high or low. Even if the user has watched the movie, there will be a very low score. In this method, such movies will be excluded. The user recommends movies with high scores after simulated scoring. This problem was not involved in the test, so the difference in results was brought about. The method proposed in this paper can also be rewritten as a similar ensemble recommendation algorithm for other datasets in the future. For example, we can propose an integrated recommendation algorithm of user KNN + product KNN for product recommendation to recommend specific products input by specific users and find products that meet user needs more quickly.
Acknowledgement: The author would like to thank the researchers in the field of recommendation algorithm and other related fields. This paper cites the research literature of several scholars. It would be difficult for me to complete this paper without being inspired by their research results. Thank you for all the help we have received in writing this article.
Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant No. 42075007), the Open Project of Provincial Key Laboratory for Computer Information Processing Technology under Grant KJS1935, Soochow University.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. I. A. Shoukat, A. Al-Dhelaan and M. Iftikhar, “A virtualized information indexing and filtering method for web contents reside on remotely communicated networks,” World Applied Sciences Journal, vol. 23, no. 8, pp. 1053, 2013. [Google Scholar]
2. A. M. Nair, O. Benny and J. George, “Content based scientific article recommendation system using deep learning technique,” in Inventive Systems and Control, Singapore: Springer, pp. 965–977, 2021. [Google Scholar]
3. J. Lin, K. Sugiyama and M. Y. Kan, “Addressing cold-start in app recommendation: Latent user models constructed from twitter followers,” in The 36th Int. ACM SIGIR Conf. on Research and Development in Information Retrieval, Dublin Ireland, pp. 283–292, 2013. [Google Scholar]
4. N. Chekkai, I. Chorfi and S. Meshoul, “SCOL: Similarity and credibility-based approach for opinion leaders detection in collaborative filtering-based recommender systems,” International Journal of Reasoning-Based Intelligent Systems, vol. 12, no. 1, pp. 34, 2020. [Google Scholar]
5. G. Parthasarathy and S. S. Devi, “Ensemble learning based collaborative filtering with instance selection and enhanced clustering,” Computers, Materials & Continua, vol. 71, no. 2, pp. 2419–2434, 2022. [Google Scholar]
6. T. Vaiyapuri, “Deep learning enabled autoencoder architecture for collaborative filtering recommendation in iot environment,” Computers, Materials & Continua, vol. 68, no. 1, pp. 487–503, 2021. [Google Scholar]
7. X. Zhao and P. Keikhosrokiani, “Sales prediction and product recommendation model through user behavior analytics,” Computers, Materials & Continua, vol. 70, no. 2, pp. 3855–3874, 2022. [Google Scholar]
8. T. Mahara, “A new similarity measure based on mean measure of divergence for collaborative filtering in sparse environment,” Procedia Computerence, vol. 89, pp. 450–456, 2016. [Google Scholar]
9. C. Li, “Research on the bottleneck problems of collaborative filtering in E-commerce recommender systems,” Ph.D. dissertation, Hefei University of Technology, Hefei, 2009. [Google Scholar]
10. J. H. Su, H. H. Yeh and P. S. Yu, “Music recommendation using content and context information mining,” IEEE Intelligent Systems, vol. 25, no. 1, pp. 16–26, 2010. [Google Scholar]
11. W. H. Cho, S. K. Kim, M. H. Na and I. S. Na, “Fruit ripeness prediction based on dnn feature induction from sparse dataset,” Computers, Materials & Continua, vol. 69, no. 3, pp. 4003–4024, 2021. [Google Scholar]
12. B. M. Sarwar, G. Karypis and J. A. Konstan, “Application of dimensionality reduction in recommender system–A case study,” in Proc. of the ACM WebKDD Web Mining for E-Commerce Workshop, Boston, United States, pp. 82–90, 2000. [Google Scholar]
13. L. Bottou, “Large-scale machine learning with stochastic gradient descent,” in The 19th Int. Conf. on Computational Statistics, Paris, France, Physica-Verlag HD, pp. 177–186, 2010. [Google Scholar]
14. Y. Tian, B. Zheng and Y. Wang, “College library personalized recommendation system based on hybrid recommendation algorithm,” Procedia CIRP, vol. 83, pp. 490–494, 2019. [Google Scholar]
15. Z. Cui, X. Xu, F. Xue, X. Cai, Y. Cao et al., “Personalized recommendation system based on collaborative filtering for IoT scenarios,” IEEE Transactions on Services Computing, vol. 13, no. 4, pp. 685–695, 2020. [Google Scholar]
16. Y. Koren, R. Bell and C. Volinsky, “Matrix factorization techniques for recommender systems,” Computer, vol. 42, no. 8, pp. 30–37, 2009. [Google Scholar]
17. S. Wold, K. Esbensen and P. Geladi, “Principal component analysis,” Chemometrics and Intelligent Laboratory Systems, vol. 2, no. 1–3, pp. 37–52, 1987. [Google Scholar]
18. D. A. Lelewer and D. S. Hirschberg, “Data compression,” ACM Computing Surveys (CSUR), vol. 19, no. 3, pp. 261–296, 1987. [Google Scholar]
19. B. Sujitha, V. S. Parvathy, E. L. Lydia, P. Rani and K. Shankar, “Optimal deep learning based image compression technique for data transmission on industrial internet of things applications,” Transactions on Emerging Telecommunications Technologies, vol. 32, no. 7, pp. e3976, 2021. [Google Scholar]
20. A. M. Aquino and E. P. Chavez, “Analysis on the use of Latent Semantic Indexing (LSI) for document classification and retrieval system of PNP files,” EDP Sciences, vol. 189, no. 4, pp. 03009, 2018. [Google Scholar]
21. K. Samina and A. Tehmina, “A survey of feature selection and feature extraction techniques in machine learning,” in Proc. of Science and Information Conf., Piscataway, NJ, IEEE Press, pp. 372–378, 2014. [Google Scholar]
22. S. Ayesha, M. K. Hanif and R. Talib, “Overview and comparative study of dimensionality reduction techniques for high dimensional data,” Information Fusion, vol. 59, pp. 44–58, 2020. [Google Scholar]
23. J. L. Herlocker, J. A. Konstan, A. Borchers and J. Riedl, “An algorithmic framework for performing collaborative filtering,” in Proc. of the 22nd Annual Int. ACM SIGIR Conf. on Research and Development in Information Retrieval, Berkeley California USA, pp. 230–237, 1999. [Google Scholar]
24. X. Fan, C. Li, X. Yuan, X. Dong and J. Liang, “An interactive visual analytics approach for network anomaly detection through smart labeling,” Journal of Visualization, vol. 22, no. 5, pp. 955–971, 2019. [Google Scholar]
25. R. S. Subramanian and D. Prabha, “Ensemble variable selection for naive Bayes to improve customer behavior analysis,” Computer Systems Science and Engineering, vol. 41, no. 1, pp. 339–355, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |