DOI:10.32604/iasc.2022.025290

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.025290 |  |
| Article |
Discrete Firefly Algorithm for Optimizing Topology Generation and Core Mapping of Network-on-Chip
Department of Information Technology, Anna University, MIT Campus, Chennai, 600044, India
*Corresponding Author: S. Parvathi. Email: parvathi.sivakumar@gmail.com
Received: 18 November 2021; Accepted: 31 December 2021
Abstract: Network-on-chip (NoC) proves to be the best alternative to replace the traditional bus-based interconnection in Multi-Processor System on a Chip (MPSoCs). Irregular NoC topologies are highly recommended and utilised in various applications as they are application specific. Optimized mapping of the cores in a NoC plays a major role in its performance. Firefly algorithm is a bio-inspired meta-heuristic approach. Discretized firefly algorithm is used in our proposed work. In this work, two optimization algorithms are proposed: Topology Generation using Discrete Firefly Algorithm (TGDFA) and Core Mapping using Discrete Firefly Algorithm (CMDFA) for multimedia benchmark applications, Video Object Plane Decoder (VOPD), Multimedia Window Display (MWD) and MP3 Encoder. The irregular topology generated using TGDFA is mapped using CMDFA onto a reconfigurable mesh with switches in between the routers to make it a fault tolerant one. The proposed TGDFA provides better optimization of communication cost. The speed-up on the average run time of the tasks and the time taken to attain the best solution by the proposed TGDFA is significant. The dynamic energy consumption of core mapping obtained by the proposed CMDFA is lesser when compared to the existing work. Finally, the optimized core mapping is implemented in a cycle accurate NoC simulator: Noxim. It is substantiated experimentally that the proposed CMDFA outperforms the previous work.
Keywords: Network-on-chip (NoC); firefly algorithm; irregular topology; core mapping
Network-on-Chip (NoC) communication systems have evolved over the years because of the various drawbacks and limitations encountered in traditional bus-based communication [1,2]. It has taken a paradigm shift due to the requirements of high-speed processing capabilities in many applications [3]. Multi core processor technology is used in many applications across various domains. On-chip interconnection is employed for connecting the cores in the multi core architectures [4]. In a NoC framework, the information in the form of packets is transferred between the cores or the Processing Elements (PE) through the routers [5]. The cores, routers, links, and the Network Interface (NI), which helps in the connectivity are the basic elements of the framework. And its performance depends on the topology, the number of cores involved, routing schemes applied, mapping of the cores for the applications, scheduling of the various tasks of the application etc [6].
NoC topologies are broadly categorized as regular and irregular. As the name infers the structure of a regular topology is mostly fixed and the size of the cores would be homogenous. Regular topologies possess defined connections among network components. Mesh, ring, torus, and butterfly topologies are few of the examples for regular topology structures [7]. The major benefit of a regular topology is its reusability and fault tolerance capability. Reusability feature enables different applications to be mapped using the same topology and mapping algorithm. Fault tolerant feature is the availability of two different routing paths between the communicating nodes.
Irregular topologies are mostly application specific, and the cores would be heterogenous. They are designed for a particular application. Hence, it is not reusable as a regular one. The mapping of the application nodes onto the irregular topology is a very important step. A proper mapping function helps in the reduction of latency and improvement in dynamic energy consumption. Generally, highly communicating nodes are placed nearer to each other. But this placement of nodes is not always possible practically every time. To shorten the hop distances between nodes of the mesh topology, the concept of reconfigurable switches is applied [8]. These switches offer alternative fast routes between remote routers.
The rest of the paper is organized as follows. In Section 2 a summary about the related works is given. Section 3 gives a brief introduction on Firefly Algorithm (FA). The proposed works, algorithms and the steps involved in topology generation and core mapping are explained in Section 4. The results are summarized and discussed in Section 5. Section 6 concludes this paper.
In this section, related works on topology generation algorithms, core mapping and optimization algorithms are studied. Few of the previous works are summarized here.
In this work [9], the focus is on how to map the IP cores onto mesh NoC while minimizing the communication cost. A Neural Network IP core Mapping Model (NNMM) and a neural mapping algorithm (NMA) have been proposed. The authors used communication cost, runtime, and average latency as performance parameters for comparison. In the paper [3], an energy aware mapping algorithm has been proposed. The proposed algorithm searches for the mapping solution with best communication locality. In [7], authors have presented a discussion on the trends in system-on-chip designs and the evolution of Network on Chip (NoC). An irregular topology generation using genetic algorithm has been proposed in [8] as a two-step method combining the benefits of both regular and irregular topologies. This generated topology is area and energy optimized. A Power-Aware Topology Construction (PATC) method to construct application-specific low power irregular NoC topologies have been proposed in [10]. The power savings attained by the customized irregular topologies constructed using PATC are very much higher than the regular structures. A reconfigurable architecture for networks-on-chip (NoC) has been presented in [11]. The NoC changes the inter-router connections to some predefined configuration.
In [12], two algorithms namely TopGen and GATGA are proposed. A two-phase application-specific topology generation algorithm, TopGen is a heuristic method that works based on the clustering of cores depending on the traffic pattern involved. These clusters are mapped onto the routers. A novel genetic-based hyper-heuristic algorithm (GHA) has been proposed as the core algorithm in [13]. This algorithm is a flexible energy and delay aware approach for core mapping. The basic Kernighan-Lin graph bi-partitioning algorithm has been extended in [14]. The algorithm is done for the partitioning of the core graphs. A fault tolerant irregular topology-generation method for application specific NoC designs has been proposed in [15]. A quadratic assignment problem (QAP) has been proposed in [16]. QAP is a linearized model applied for mapping of cores to minimize the power consumption. In this work [17], a hierarchical and dependency aware (HDA) task mapping has been proposed. The proposed algorithm focuses on the concepts of spatial mapping and inter-task dependency. In this work [18], a hybrid, branch & bound (BB)-based exact mapping (BEMAP) algorithm, for mapping real-time embedded applications on the NoC architecture has been proposed. An innovative preference-based multi-objective evolutionary methodology has been proposed in [19]. A bandwidth-constrained multi-objective segmented brute-force mapping (SBMAP) algorithm has been proposed in [20]. The applications are divided into multiple segments. Firefly algorithm (FA) and genetic algorithm (GA) are proposed and compared for the multi-objective Flexible job-shop scheduling problem (FJSP) in [21]. A new enhanced form of Firefly Algorithm (FA): Hybrid Adaptive Firefly Algorithm (HAdFA) has been presented in this work [22]. Two adaptive strategies, i.e., an adaptive Randomization parameter (α) and an effective heterogeneous update rule for fireflies are the two strategies being adopted to solve FJSP, a NP-hard problem.
In our proposed work, Firefly Algorithm (FA) has been discretized i.e., Discrete Firefly Algorithm (DFA), and applied to the proposed optimization approaches, Topology Generation using Discrete Firefly Algorithm (TGDFA) and Core Mapping using Discrete Firefly Algorithm (CMDFA).
3 A Brief Introduction on Firefly Algorithm
The Firefly Algorithm (FA) [23] is a meta heuristic and nature inspired algorithm derived from the behaviour of fireflies. FA is based on swarm intelligence. FA works based on social behaviour of fireflies. The search algorithm involved in the FA depends on the brightness of the fireflies [24–26]. FA is highly employed in solving various optimization problems. Optimization is the process which involves in the maximization or minimization of the parameters involved in an operation or problem. Optimization is performed to identify a best solution for a problem and to make it more effective. The basic Rules of Firefly Algorithm are:
• One firefly will be attracted to other fireflies since they are unisex in nature.
• For any two fireflies, the less bright one will move towards the brighter one and the attractiveness is proportional to the brightness.
• The brightness of a firefly is determined by the scope of the objective function.
For minimization problems, the brightness is the reciprocal of the objective function. For maximization problems, the brightness is proportional to the objective function.
3.2 Light Intensity and Attractiveness
Light intensity variation and the formulation of the attractiveness are the two important parameters taken into consideration while applying firefly algorithm. The attractiveness of a firefly is determined by its brightness. Based on the light intensity and attractiveness of the fireflies the objective function is derived. For maximization optimization problems, the brightness ‘I’ of a firefly at a particular location ‘x’ can be chosen as I(x) ∝ f(x). However, attractiveness ‘β’ is relative, that is the attractiveness depends on the other fireflies moving around. It will vary in accordance with the distance between two fireflies ‘i’ and ‘j’. The light intensity ‘I(r)’ varies according to the Inverse Square Law as given in Eq. (1)
Is denotes the intensity at the source. For a given medium with a fixed light absorption coefficient ‘ϒ’, the light intensity ‘I’ varies with the distance ‘r’ as given in Eq. (2)
‘I0’ is the original light intensity. To avoid the singularity at r = 0 in the expression Is/r2, the combined effect of both the Inverse Square Law and absorption can be approximated the Gaussian form given in Eq. (3) and the attractiveness function β(r) is given by Eq. (4)
where ‘β0’ is the attractiveness at r = 0, and r is the distance between the fireflies. As it is often faster to calculate 1/(1 + r2) than an exponential function, the attractiveness is represented as in Eq. (5)
The distance between any two fireflies ‘i’ and ‘j’, at positions xi and xj, can be given as in Eq. (6)
where ‘xik’ is the kth component of the spatial coordinate xi of the ith firefly. The random movement of a firefly ‘i’ towards another more brighter firefly ‘j’ is determined by Eq. (7)
where the second term considers a firefly's attractiveness, the third term is randomization with ‘α’ being the randomization parameter, and ‘ɛi’ is a vector of random numbers drawn from a Gaussian distribution or uniform distribution. ‘ɛi’ can be replaced by rand −1/2, where rand is a random number generator uniformly distributed in [0,1]. For most applications β0 = 1, α ∈ [0, 1]. In this implementation of the algorithm β0 = 1.0, α ∈ [0, 1] and γ ∈ [0.01, 0.15]. In our approach, the general firefly algorithm is discretized and used for irregular topology generation and core mapping for multimedia benchmark applications.
In our proposed work, irregular topology is generated, and core mapping is done for three multimedia applications: VOPD [14], MP3 Encoder [15] and MWD [10]. The Core Flow Graph (CFG) of these applications are given in Figs. 1–3, respectively. The CFG is represented as G (V, E), where ‘V’ represents the set of nodes/tasks and ‘E’ represents the set of edges of the graph. Every edge, ei,j is assigned with a weight (Wij), volume of communication from task ‘i’ to task ‘j’.
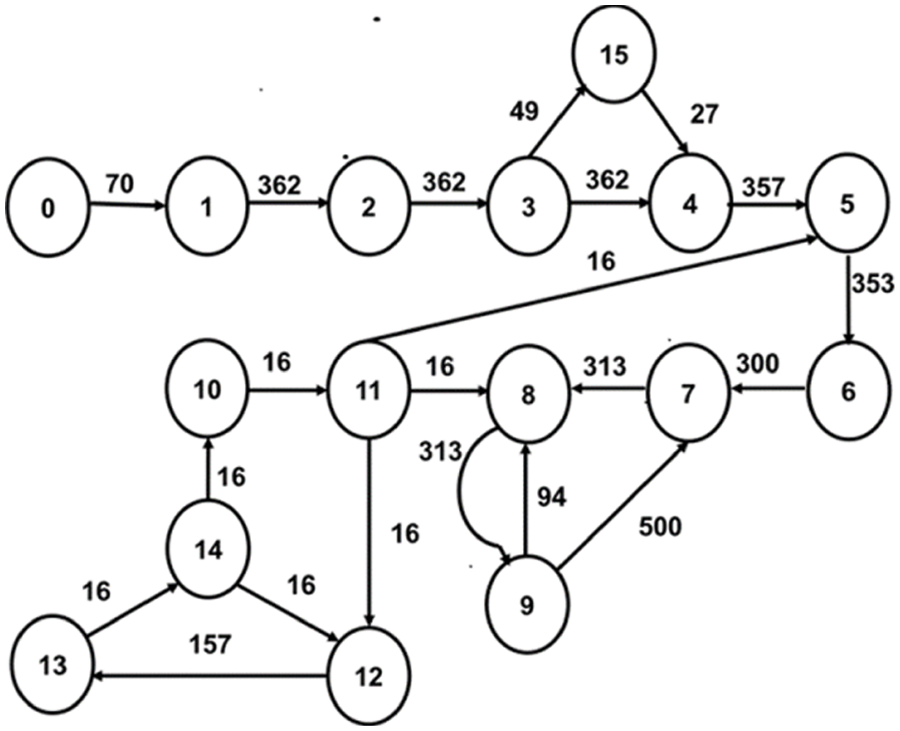
Figure 1: CFG of VOPD
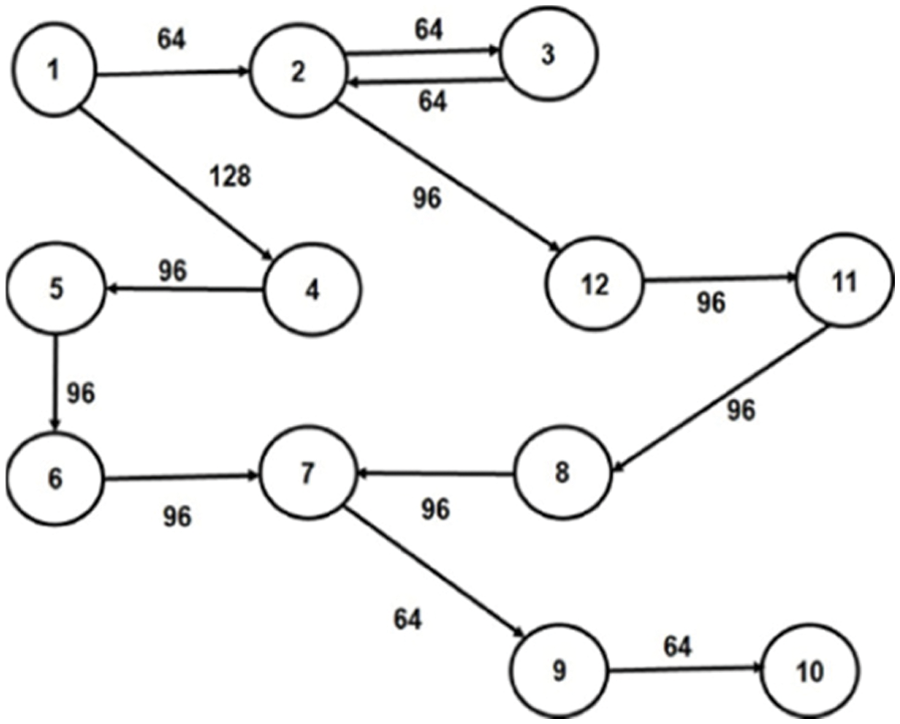
Figure 2: CFG of MWD
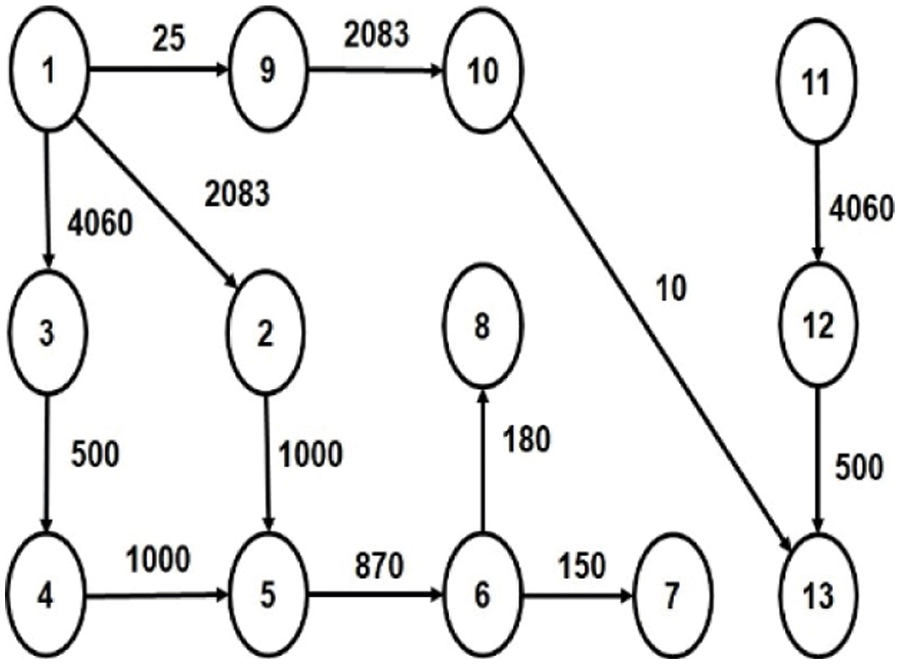
Figure 3: CFG of MP3 Encoder
4.1 Irregular Topology Generation Using Discrete Firefly Algorithm (TGDFA)
The Firefly Algorithm (FA) is an algorithm used in continuous optimization problems. In this proposed work, FA has been discretized to solve a permutation problem. The Discrete Firefly Algorithm (DFA) has been successfully implemented to solve irregular topology generation and core mapping of NoC applications [21]. The computation of the hamming distance between the two fireflies is a major challenge in the irregular topology generation. Some discretization is added to the FA for irregular topology generation and to the mapping function [27].
4.1.1 Problem Formulation-Objective Function
The objective function is to minimize the total communication cost of the generated irregular topology. The communication cost of a single bit from the source node ‘ni’ to the destination node ‘nj’ is given by Eq. (8).
where ‘ηi,j’ is the hop count between the source node ‘ni’ and destination node ‘nj’.
The total communication cost of the application is given by Eq. (9)
where ‘Wij’ is the communication volume between the tasks i and j connected by ei,j in the CFG and task i and j are scheduled on nodes ‘ni’ and ‘nj’ respectively in the generated topology.
The irregular topology is generated for the three multimedia applications and the CFGs are shown in Figs. 1–3 for VOPD, MWD, MP3 Encoder respectively. The first step in topology representation is determining the minimum number of routers required, and it is found using Eq. (10)
where r is the number of routers, n is the number of nodes and p represents the number of ports in a router. The irregular topology generated from the CFG of the application is represented in the form of string. Each string is constructed by the nodes. The nodes of the string are representing the ports of the router. Each router has 4 ports in 4 directions. A topology having ‘m’ routers and ‘n’ port per router would be having ‘nm’ positions in the string. Now, each ‘nm’ position is indicated by a variable having 2 indices gk,l. In this, ‘k’ and ‘l’ represent the router index and port number respectively [8]. The position of a particular node in the string can be represented as gPk,l, and can be calculated as in Eq. (11)
Now illustrating the calculation of the position of a node with an example string, 4th port i.e., l = 4, of the 2nd router i.e., k = 2 would be assigned to the position ‘8’ by the equation above, by calculation: gP4,2 = (2−1)4 + 4 = 8. A sample topology is shown in Fig. 4. The port labels of the router are given in Fig. 5 and the topology representation as a string is shown in Tab. 1.
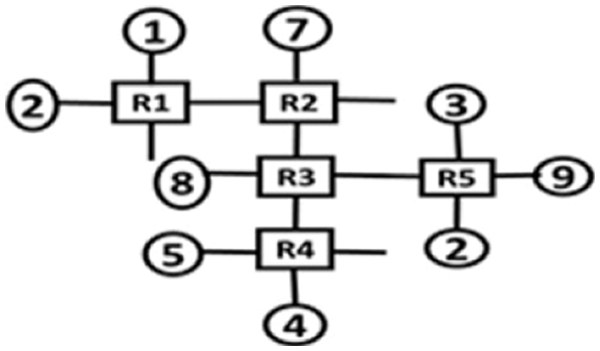
Figure 4: Sample topology
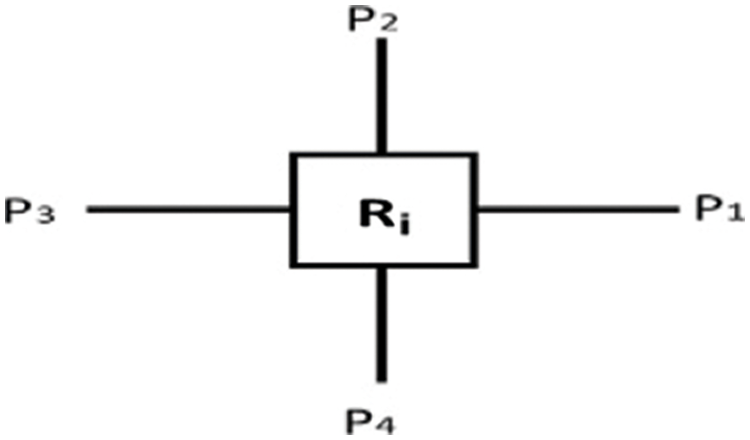
Figure 5: Port labels

Always a negative number indicates the possibility of router-to-router connection. An individual string contains a negative number twice indicating that these two ports are connected. The number 0 is placed to a port if there is no node assigned to it. Also, an individual string will contain a positive number exactly once as it can take single position only once in the topology.
4.1.3 Irregular Topology Generation
The steps involved in the irregular Topology Generation using Discrete Firefly Algorithm (TGDFA) is given in Tab. 2. In the first step of topology generation, individual strings are created to form an initial population by randomly assigning nodes and communication links to the positions. The initial population size is taken as three, Psize = 3. After this, connection test is performed by which it is ensured that there is a path from each router to all the other routers. The router pairs are merged to obtain one complete list which shows that the string is valid. Once the validity check is over, the strings are added to a population list. For calculating the cost of each solution, a distance matrix is created. This is based on the hop distance between two routers.

Hamming distance is calculated based on the difference between two topologies. Here, the initial population consists of three topology strings out of which each time only two strings are considered for calculating the difference. For example, the two topology strings of MP3 Encoder application are considered.
Topology P −1 7 3 4 −2 5 −1 9 −3 0 −2 −4 2 −4 1 11 10 6 −3 8 (2592)
Topology Pbest −1 0 5 7 −2 3 −1 11 −3 8 −2 −4 2 −4 1 9 10 6 −3 4 (2368)
Difference {(2,0), (3,5), (4,7), (6,3), (8,11), (10,8), (16,9), (20,4)}
The difference is calculated based on dissimilarity in the positions of the topology strings. The difference vector {(i, j)} where i indicates the position and j indicates the value in the Pbest. So, the hamming distance, r = 8 in this case which is the total number of elements in the difference vector. The attractiveness β(r), depends on the attraction between the more and less bright fireflies. Always a less bright firefly is attracted towards the brighter firefly. As per the algorithm, the higher communication cost topology will undergo the changes made by the algorithm. So, by this, the communication cost of the topology will be reduced when compared with the previous cost. β(r) is given in Eq. (5)
After substituting the values, β(r) = 0.6097 for the example chosen. In this step, the total of r random numbers is generated. The random numbers are generated between 0 and 1, rand ∈ [0,1]. In this case, 8 random numbers are generated. {0.935, 0.244, 0.362, 0.054, 0.481, 0.939, 0.532, 0.610}.
A pair-wise exchange mechanism is used to advance the firefly towards the global best firefly position in the β step. In the list of random numbers generated the positions whose values are lower than β(r) are exchanged with the Pbest. Now the position after exchange is: {(3,5), (4,7), (6,3), (8,11), (16,9)}. So, after the exchange mechanism process, the topology is changed as {−1 7 5 7 −2 3 −1 11 −3 0 −2 -4 2 −4 1 9 10 6 −3 8}. After pair wise exchange of positions, a swapping operation is performed. Swapping is done by selecting an element position and a non-equal position at random, which generates two random numbers 8 and 9. So the values in the positions 8 and 9 are swapped and the topology becomes {−1 7 5 7 −2 3 −1 −3 11 0 −2 −4 2 −4 1 9 10 6 −3 8}.
A validity check is performed at this stage to check whether the generated topology string is valid or invalid. The validity check criteria for this step are given below:
• A string should contain a node exactly only once
• No node of CFG is missing in the string
• In a string, each link is assigned twice
• gk, l and gm, n can be same satisfying the condition k ≠ m. That is a single router should not be assigned with same negative values twice
• A connection check is performed, which ensures a node has a path to all other nodes.
Finally, the communication cost for the generated topology is calculated. In this case the cost reduces from 2592 to 1888. Only if the cost of the topology generated is lesser than the previous one, it is updated. The procedure and the steps are repeated for all the combinations. The maximum number of iterations in our proposed work is fixed as 50.
4.2 Core Mapping Using Discrete Firefly Algorithm (CMDFA)
Mapping of the cores to the application plays a vital role in NoC systems. Fig. 6 shows an example mapping of tasks of a CFG to the cores or processing elements. Mapping involves efficient and appropriate placement of tasks in a NoC. In general, highly connected, or highly communicating cores are placed nearer to each other. This ensures faster transfer of information in the form of data packets and minimizes dynamic energy consumption.
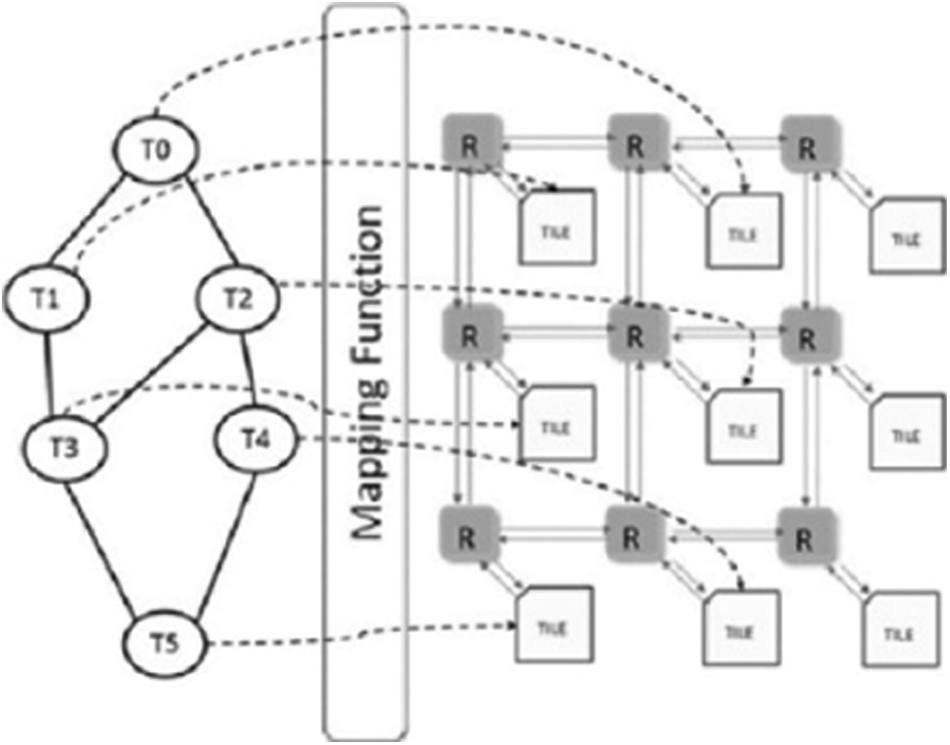
Figure 6: Core mapping
In [10], Modarressi et al. proposed a reconfigurable mesh NoC architecture. In this architecture, routers are connected through configurable switches as shown in Fig. 7a. The switches can be configured in different ways. Three such configurations are shown in Fig. 7b. With the dynamic reconfiguration of switches, some of the routers are bypassed in establishing connection from a source node to destination node. Hence, energy consumption is reduced as switches consume five time less energy compared to routers. This architecture also supports mapping of applications on NoC. This reconfigurable mesh NoC [10] is used to map the irregular topology generated using the proposed TGDFA. Each node in the application must be exactly mapped to one router on the reconfigurable mesh topology. Thus, R ≥ n must hold, where R is the number of routers in the topology and n is the total number of nodes in the irregular topology.
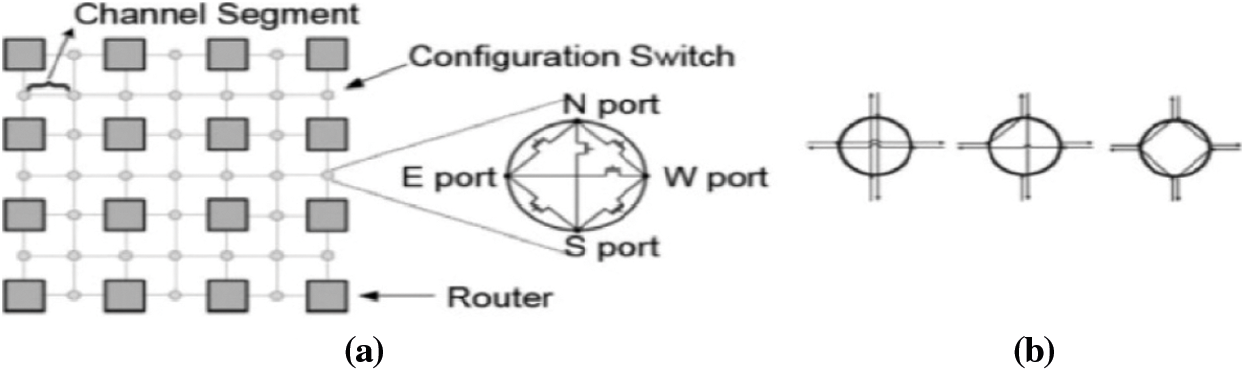
Figure 7: (a) Reconfigurable NoC architecture [11] (b) Three possible switch configurations [11]
4.2.1 Problem Formulation-Objective Function
The objective function used in the core mapping is to minimize the overall energy consumption. The dynamic energy is consumed during the packet traversal between nodes or the cores. Hence, the highly communicating nodes are placed closer to each other to attain the optimization of energy. The dynamic energy for core mapping is given by Eq. (12)
where, comm (vs., vd) is the amount of data in bits from source node vs. to the destination node vd. ES and ER are the energy consumed per bit by a switch and a router respectively. NS and NR are the number of switches and the number of routers respectively for the bit to travel from source node to destination node.
4.2.2 Core Mapping Representation
For core mapping, the topology is represented as a two-dimensional matrix of size n x m. The matrix can also be a square matrix based on the number of nodes in the CFG of an application. VOPD consists of 16 nodes, so a 4 x 4 mesh is chosen. MP3 Encoder has 13 nodes in that case also a 4 x 4 mesh is chosen, and the unused routers are made as dummy router. In the case of MWD, it has only 12 nodes, so a 3 x 4 mesh is sufficient.
The steps for the core mapping process are mentioned in Tab. 3. The nodes are randomly positioned in the mesh for a CFG. In the experiments, the initial population is 3. To perform the connection test, the node numbers in the matrix should not be repeated and it should contain all the nodes of the CFG. Following that, the difference between two topologies is used for computing the hamming distance. The same is explained with the two topologies of MP3 Encoder application.

Difference: {[(0,0), 14], [(1, 1), 12], [(1,2), 15]}
The difference is calculated based on the dissimilarity in the positions of the topologies. The difference vector {(i, j), k} where (i, j) indicates the position and k indicates the value in the Pbest. The indices are zero-based. The hamming distance which is the total number of elements in the difference vector in this case is 3. The difference vector is represented as {[(0,0), 14], [(1,1), 12], [(1,2), 15]}. The value of the attractiveness β(r) as in Eq. (5) depends on the movement between the less bright firefly which is attracted towards the brighter firefly. The topology which has a higher value of communication energy must undergo the changes made by the applied algorithm. By this, the overall communication energy is reduced when compared with the previous cost. β(r) is given in Eq. (5).
After substituting the values, β(r) = 0.917431 for the example chosen. After this, random numbers are generated between 0 and 1, rand ∈ [0,1]. In this case, 3 random numbers are generated: {0.164, 0.568, 0.037}.

A pair-wise exchange mechanism is used to advance the firefly towards the global best firefly position in the β step. The positions of the random numbers whose values are lower than the β(r) are chosen and exchanged with the Pbest. Now the positions are: {[(0,0),14], [(1,1), 12], [(1,2), 15]}. A swapping operation is carried out between two non-equal positions chosen at random. The positions chosen are {(0,1), (1,0)}. After swapping the values in the position (0,1) and (1,0), the topology P becomes:
A validity check is performed to check whether the mesh topology is valid or not. Repetition of nodes in the mesh and missing of node in the mesh are the two constraints to check for its validity. That is the generated mesh topology may contain multiple nodes and may miss a node in a mesh which makes it invalid. In the β-step, when two mesh topologies are compared the advancement towards the best may cause the mesh topology to contain multiple nodes in it which in turn yields to the missing of node in the mesh topology. To make the mesh topology valid, one of the repeating values is chosen and is replaced with the missing value. After this check, the communication energy of the new topology P is reduced from 7125 to 7091. A topology is updated only if the energy of the generated one is lesser than the previous one. The procedure is repeated for all the combinations and the number of iterations is 50.
The optimization algorithms for irregular topology generation and core mapping are implemented using C++ for the three multimedia applications: VOPD, MWD and MP3 Encoder. The results are presented and discussed in this section.
5.1 Results of Irregular Topology Generation
The optimized irregular topologies are generated for the three multimedia applications: VOPD, MWD, and MP3 Encoder using the proposed TGDFA. The generated optimized irregular topologies are shown in Figs. 8–10 for VOPD, MWD and MP3 Encoder respectively.
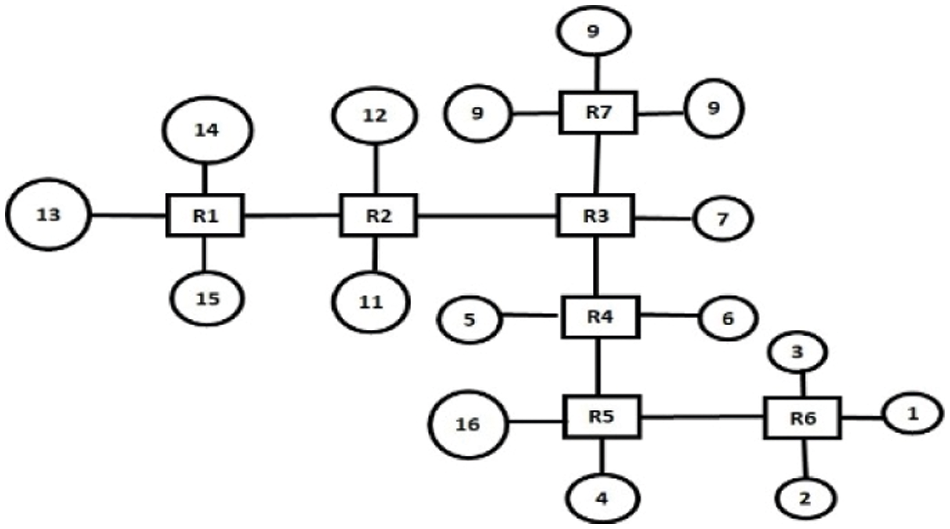
Figure 8: Topology for VOPD
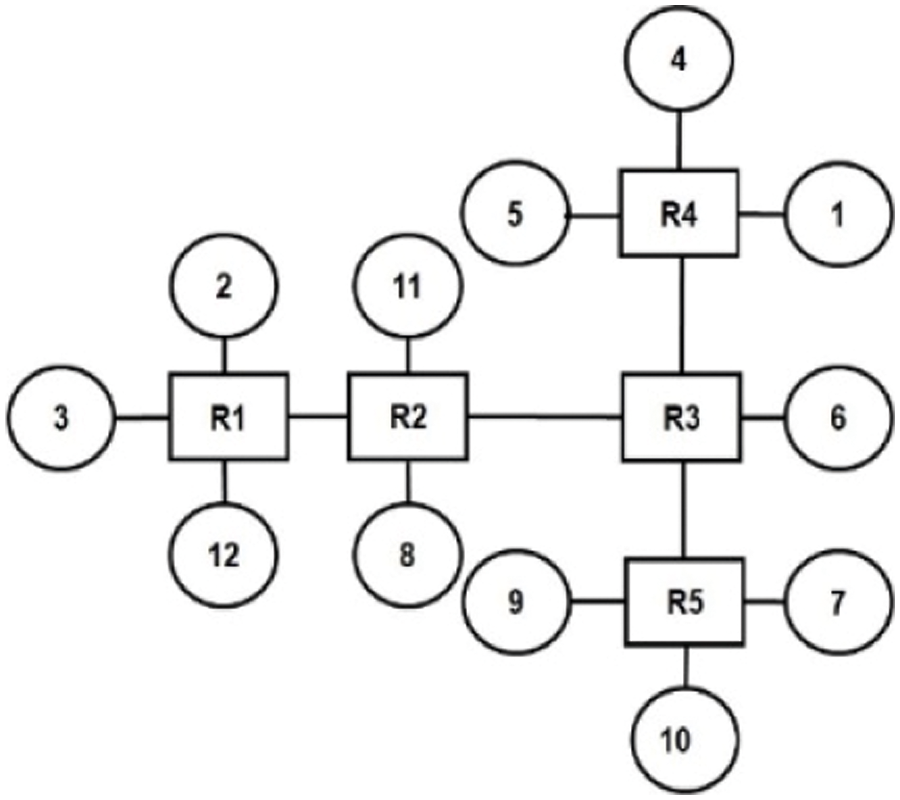
Figure 9: Topology for MWD
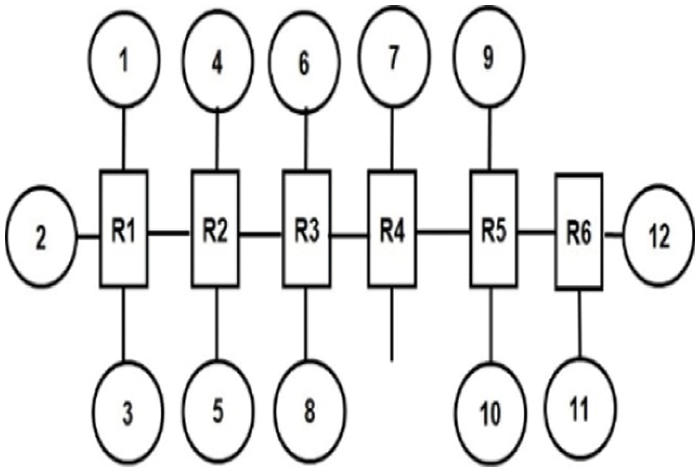
Figure 10: Topology for MP3 Encoder
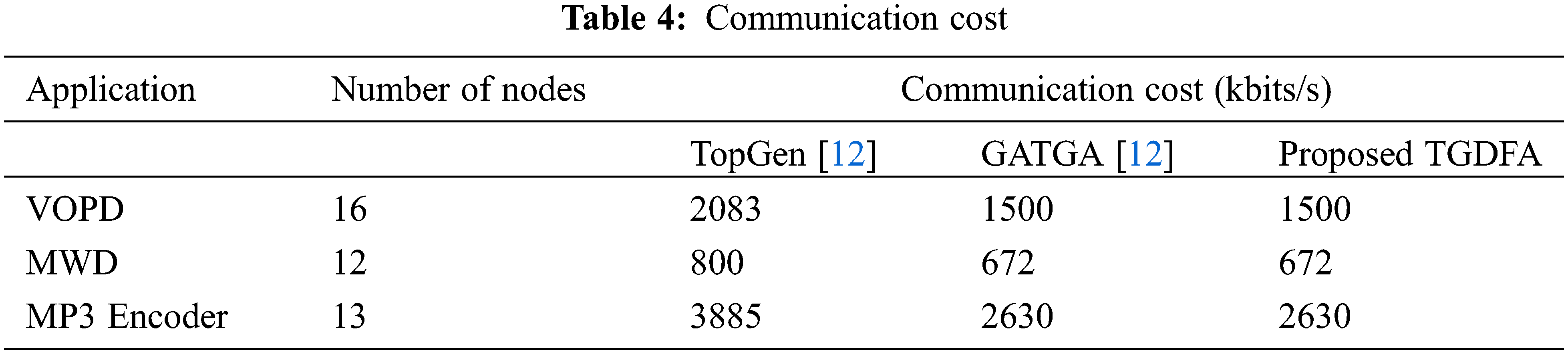
The TopGen [12], GATGA [12] algorithms are applied for the same multimedia applications. The communication cost is given in Tab. 4. The communication cost of the three algorithms: TopGen [12], GATGA [12] and the proposed TGDFA for the three benchmark multimedia applications are expressed in units of kilobits per second (kbits/s). It is evident that the communication cost of the GATGA [12] and the proposed TGDFA are same, and it is lesser when compared to the TopGen [12] algorithm. The reduction in the communication cost has been achieved with the decrease in the number of hops. The communication cost reduction obtained using the proposed TGDFA in percentage against the TopGen [12] are 27.9, 12.5 and 32.3 for VOPD, MWD, and MP3 Encoder respectively. Hence the proposed TGDFA is better in terms of communication cost (kbits/s) in comparison with the TopGen [12] algorithm.
Since the communication cost in topology generated by both GATGA [12] and the proposed TGDFA are equal, the average run time taken to complete the 50 iterations of execution and average time when the best solution achieved in seconds are observed for both the cases and presented in Figs. 11 and 12 respectively. On comparing the average run time, proposed TGDFA takes lesser time to execute and complete the 50 iterations. Also, the average time taken to achieve at the best irregular topology is lesser for the proposed TGDFA. From Figs. 11 and 12, it is observed that the time taken by both GATGA [12] and the proposed TGDFA for MWD application is almost same. On the other hand, the speed-up in average runtime of 50 iterations achieved by the proposed TGDFA in percentage when compared to GATGA [12] are 75.01, 65.69 for VOPD and MP3 Encoder respectively. The speed-up in getting the best solution in percentage by the proposed work are 77.52, 78.15 for the same applications respectively.
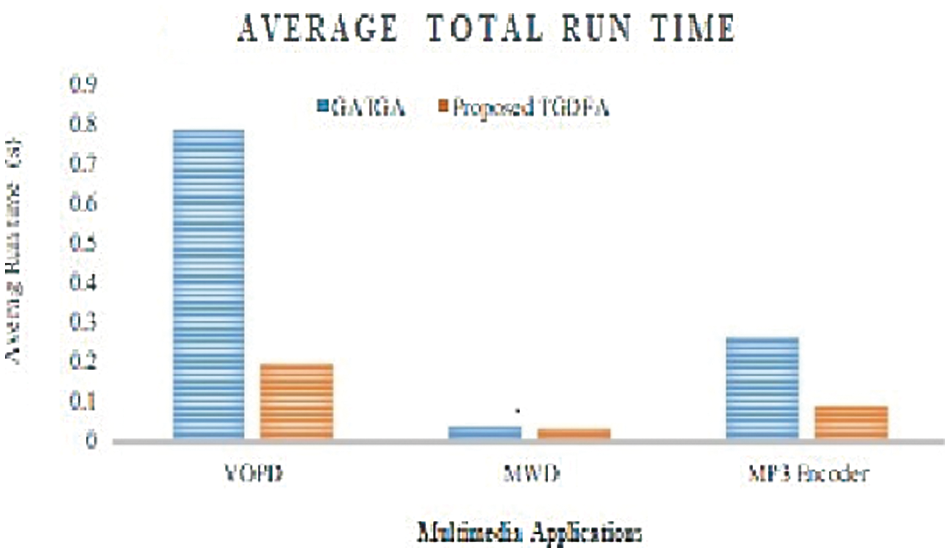
Figure 11: Average runtime
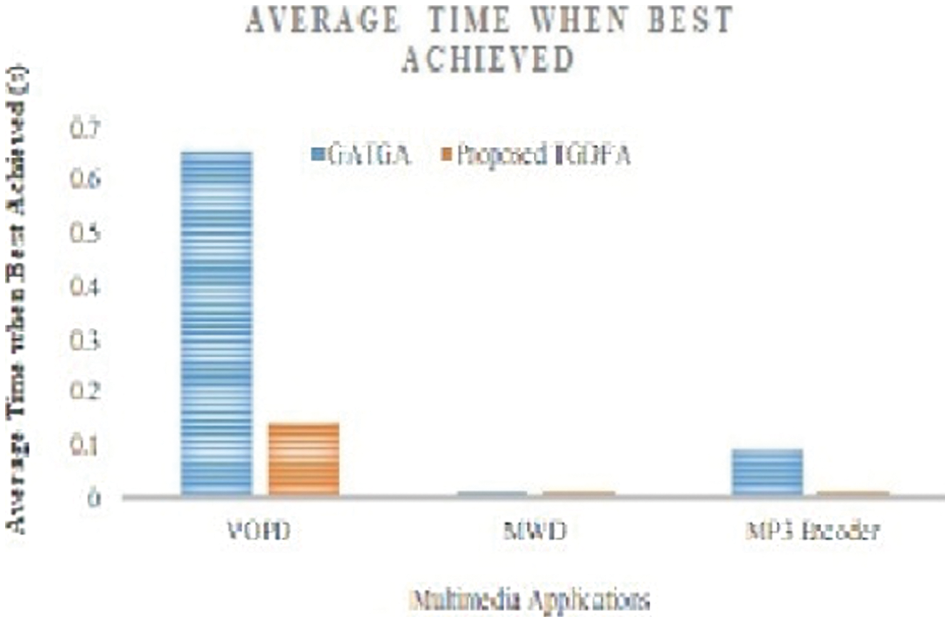
Figure 12: Average time when best achieved
5.2 Results for Core Mapping on Reconfigurable Mesh Topology
The optimized Core Mapping using Maximum Spanning Tree (MST) [8] and the proposed Discrete Firefly Algorithm (CMDFA), on the reconfigurable mesh topology [12] for the three multimedia applications are shown in Fig. 13.
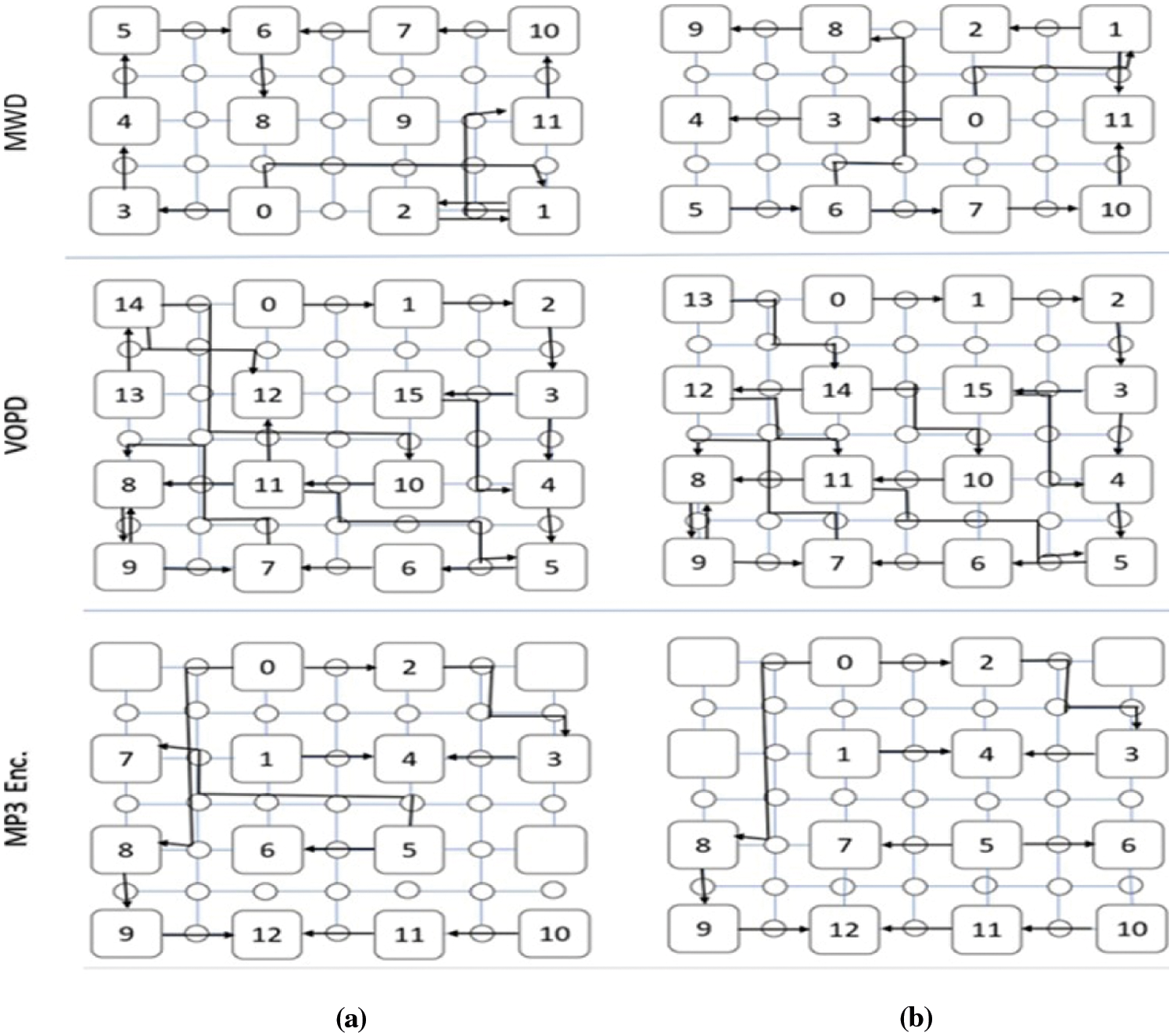
Figure 13: Optimized core mapping on reconfigurable mesh topology using: (a) MST (b) Proposed CMDFA
The dynamic energy consumption of core mapped reconfigurable mesh topologies are obtained. The values are given in Tab. 5. The energy consumption for the core mapping of the irregular topology is given in unit of nano Joules (nJ). It is assumed that the switch consumes 1 nJ/bit [8].
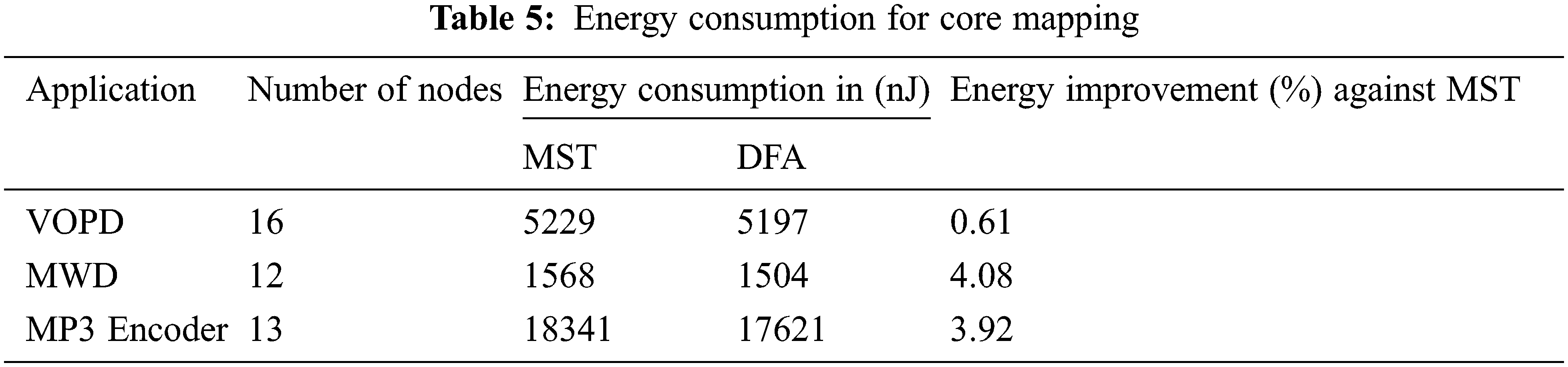
From the Tab. 5, it can be inferred that the proposed CMDFA achieved an improvement in the energy consumption than the MST [8]. This has been achieved by the mapping of the generated irregular topology onto a reconfigurable mesh topology. The percentage reduction on energy consumption of the proposed CMDFA against MST [8] are calculated and listed in Tab. 5.
5.3 Comparison of Theoretical Dynamic Energy Consumption with Experimental Results
The optimal core mapping on regular mesh topology without reconfigurable switches are obtained by MST [5] and the proposed CMDFA. The energy consumption of these mappings is obtained using Eq. (13) theoretically and tabulated in Tab. 6.
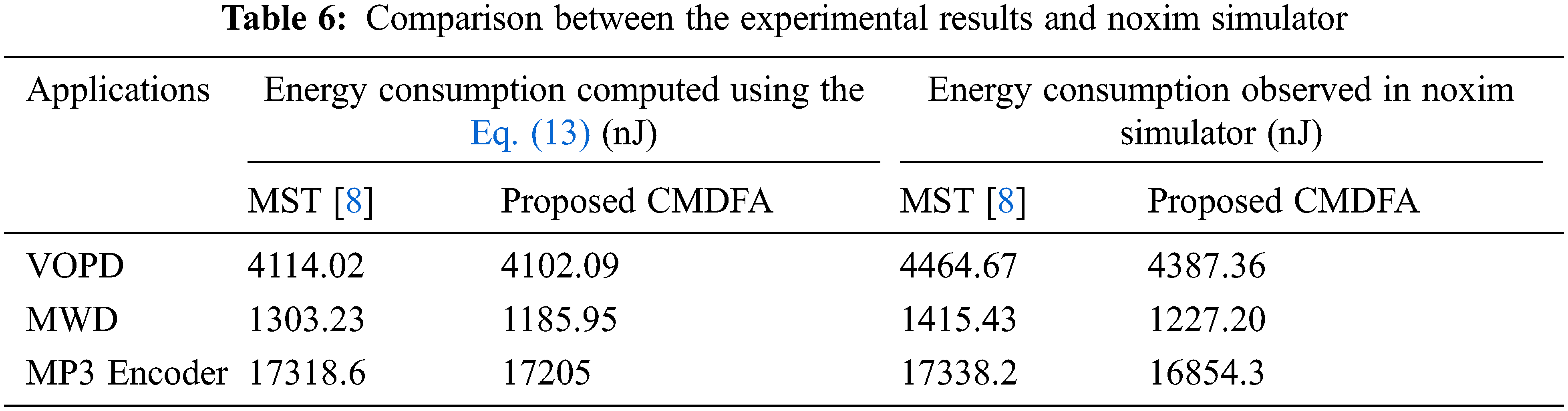
where comm (vs, vd) is the amount of data from source node vs. to destination node vd. ER, the energy consumed by router per bit is taken as 0.284 nJ [28], and NR is the number of routers between the source and destination nodes. Also, the optimal core mappings obtained are implemented using the Noxim simulator [29], a cycle accurate NoC simulator and dynamic energy consumption is measured.
The computed results using Eq. (13) and the observed results using Noxim simulator are almost the same for the three multimedia applications. The dynamic energy consumption in case of MST [8] is higher than that of the proposed CMDFA obtained using Eq. (13). It is also verified that the proposed CMDFA is better than the MST [8] experimentally.
In simulations using noxim simulator, the average latency is observed for the three multimedia applications: VOPD, MWD, and MP3 Encoder. It is presented in Tab. 7 for both optimal core mappings obtained by the MST [8] and the proposed CMDFA. From the table, it is evident that there is a reduction in latency by the proposed CMDFA. The simulation is run for 100000 cycles.
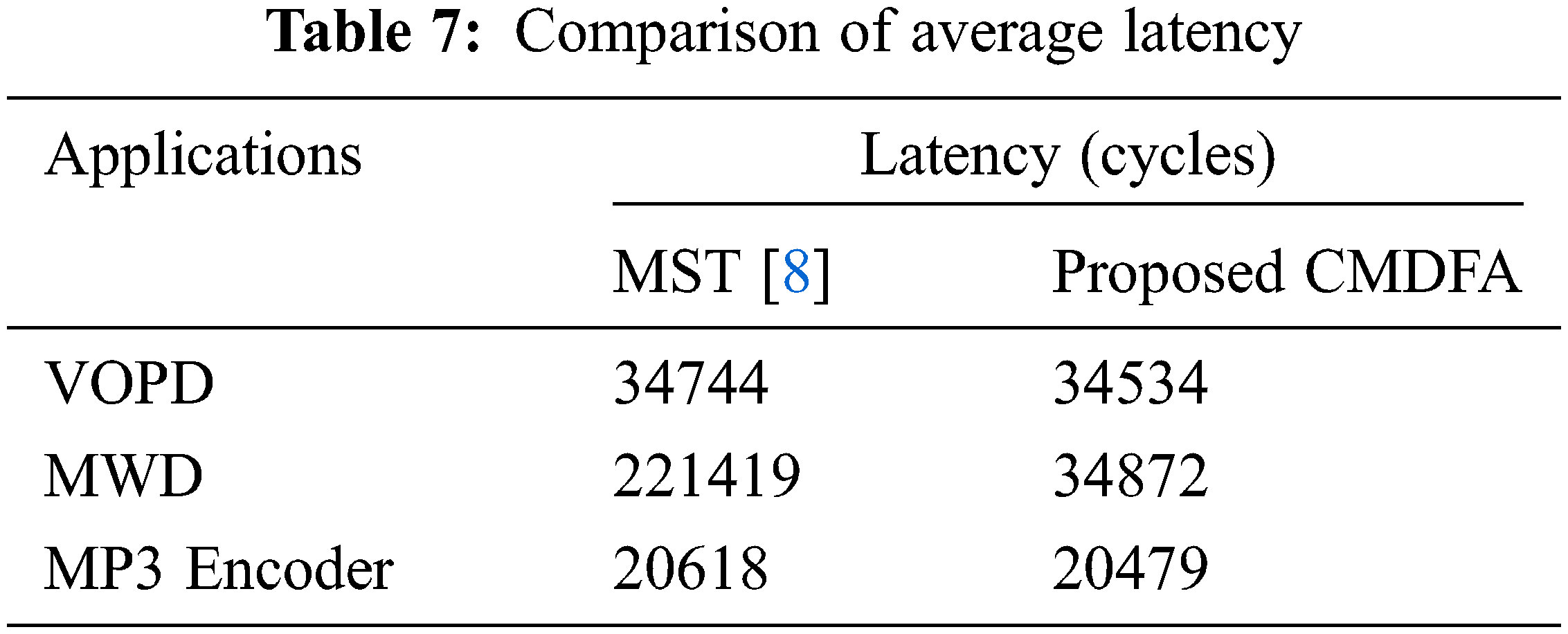
In this work, we have proposed a novel approach for irregular topology generation and core mapping: Topology Generation using Discrete Firefly Algorithm (TGDFA) and Core Mapping using Discrete Firefly Algorithm (CMDFA). The generated irregular NoC topology by the proposed TGDFA is better in terms of average run time and the average time taken to achieve best solution for the three multimedia applications. The speed up attained in the average run time by the proposed TGDFA in percentage compared with the existing algorithm GATGA [12] is 75.01 for VOPD application and 65.69 for MP3 Encoder application. The speed up in average time to best solution in percentage is 77.52 and 78.15 for the same applications respectively. The communication cost of topology obtained by the proposed TGDFA is lesser when compared to that of the TopGen [12]. The proposed CMDFA proves to be energy effective than the existing works. The percentage of energy reduction in the core mapping obtained by the proposed CMDFA against MST [8] is 0.61, 4.08 and 3.92 for VOPD, MWD, and MP3 Encoder respectively. The energy improvement attained using the proposed CMDFA has been verified experimentally using a cycle accurate NoC simulator: Noxim. The optimal core mapping by the proposed CMDFA has also reduced the average latency.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. W. C. Tsai, Y. C. Lan, Y. H. Hu and S. J. Chen, “Networks on chips: Structure and design methodologies,” Journal of Electrical and Computer Engineering, vol. 2012, no. 2, pp. 2, 2012. [Google Scholar]
2. H. G. Lee, N. Chang, U. Y. Ogras and R. Marculescu, “On-chip communication architecture exploration: A quantitative evaluation of point-to-point, Bus, and network-on-chip approaches,” ACM Transactions on Design Automation of Electronic Systems, vol. 12, no. 3, pp. 1–20, 2008. [Google Scholar]
3. J. Henkely, W. Wolfz and S. Chakradhary, “On-chip networks: A scalable, communication-centric embedded system design paradigm,” in Proc. 17th Int. Conf. on VLSI Design (VLSID), Mumbai, India, pp. 845–851, 2004. [Google Scholar]
4. J. L. Hennessey and D. A. Patterson, “Thread-Level Parallelism,” in Computer Architecture-A Quantitative Approach, Waltham, MA 02451, USA, Morgan Kaufmann/Elsevier, 5th ed., ch.5, pp. 363, 2012. [Google Scholar]
5. J. Sun and Y. Zhang, “An energy-aware mapping algorithm for mesh-based network-on-chip architectures,” in 2017 Int. Conf. on Progress in Informatics and Computing (PIC), Nanjing, China, pp. 357–361, 2017. [Google Scholar]
6. L. Benini and G. De Micheli, “Network Architecture: Principles and Examples,” in Networks on Chips: Technology and Tools, San Francisco, USA, Morgan Kaufmann/Elsevier, ch. 2, pp. 23, 2006. [Google Scholar]
7. W. J. Dally and B. Towles, “Torus Networks,” in “ Principles and Practices of Interconnection Networks,” San Francisco, CA 94111, USA, Morgan Kaufmann/Elsevier, ch. 5, pp. 89, 2004. [Google Scholar]
8. P. Kullu, A. R. Yilmaz, S. Tosun and S. Ozdemir, “Mapping application-specific topology to mesh topology with reconfigurable switches,” IET Computers & Digital Techniques, vol. 14, no. 1, pp. 9–16, 2019. [Google Scholar]
9. Q. Chen, W. Huang, Y. Zhang and Y. Huang, “An IP core mapping algorithm based on neural networks,” IEEE Transactions on Very Large-Scale Integration (VLSI) Systems, vol. 29, no. 1, pp. 189–202, 2021. [Google Scholar]
10. K. C. Chang and T. F. Chen, “Low-power algorithm for automatic topology generation for application-specific networks on chips,” IET Computers & Digital Techniques, vol. 2, no. 3, pp. 239–249, 2008. [Google Scholar]
11. M. Modarressi, A. Tavakkol and H. S. Azad, “Application-aware topology reconfiguration for on-chip networks,” IEEE Transactions on Very Large-Scale Integration Systems, vol. 19, no. 11, pp. 2010–2022, 2011. [Google Scholar]
12. S. Tosun, Y. Ar and S. Ozdemir, “Application-specific topology generation algorithms for network-on-chip design,” IET Computers & Digital Techniques, vol. 6, no. 5, pp. 318–333, 2012. [Google Scholar]
13. C. Xu, Y. Liu, P. Li and Y. T. Yang, “Unified multi-objective mapping for network on-chip using genetic-based hyper-heuristic algorithms,” IET Computers & Digital Techniques, vol. 12, no. 4, pp. 158–166, 2018. [Google Scholar]
14. P. K. Sahu, K. Manna, N. Shah and S. Chattopadhyay, “Extending kernighan–Lin partitioning heuristic for application mapping onto network-on-chip,” Journal of Systems Architecture, vol. 60, no. 7, pp. 562–578, 2014. [Google Scholar]
15. S. Tosun, V. B. Ajabshir, O. Mercanoglu and O. Ozturk, “Fault-tolerant topology generation method for application-specific network-on-chips,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 34, no. 9, pp. 1495–1508, 2015. [Google Scholar]
16. M. Taassori, S. Niroomand, S. Uysal, B. Vizvari and A. H. Vencheh, “Optimization approaches for core mapping on networks on chip,” IETE Journal of Research, vol. 64, no. 3, pp. 394–405, 2017. [Google Scholar]
17. C. H. Huang, “HDA: Hierarchical and dependency-aware task mapping for network-on-chip based embedded systems,” Journal of Systems Architecture, vol. 108, pp. 101740, 2020. [Google Scholar]
18. S. Khan, S. Anjum, U. A. Gulzari, M. K. Afzal, T. Umer et al., “Efficient algorithm for mapping real time embedded applications on NoC architecture,” IEEE Access, vol. 71, pp. 676–691, 2018. [Google Scholar]
19. N. Nedjah, M. V. C. da Silva and L. de, M. Mourelle, “Preference-based multi-objective evolutionary algorithms for power-aware application mapping on NoC platforms,” Expert Systems with Applications, vol. 39, no. 3, pp. 2771–2782, 2012. [Google Scholar]
20. S. Khan, S. Anjum, U. A. Gulzari, T. Umer and B. S. Kim, “Bandwidth-constrained multi-objective segmented brute-force algorithm for efficient mapping of embedded applications on NoC architecture,” IEEE Access, vol. 6, pp. 2169–3536, 2017. [Google Scholar]
21. W. T. Lunardi and H. Voos “Comparative study of genetic and discrete firefly algorithm for combinatorial optimization,” in Proc. of the 33rd Annual ACM Symposium on Applied Computing, Pau, France, pp. 300–308, 2018. [Google Scholar]
22. K. G. Devi, R. S. Mishra and A. K. Madan, “A dynamic adaptive firefly algorithm for flexible Job shop scheduling,” Intelligent Automation & Soft Computing, vol. 21, no. 1, pp. 429–448, 2021. [Google Scholar]
23. X. S. Yang, “Firefly algorithms for multimodal optimization,” in Int. Symp. on Stochastic Algorithms, Lecture Notes in Computer Science, Berlin, Heidelberg, vol. 5792, pp. 169–178, 2009. [Google Scholar]
24. N. F. Johari, A. M. Zain, N. H. Mustaffa and A. Udin, “Firefly algorithm for optimization problem,” Applied Mechanics and Materials,” Trans Tech Publications, vol. 421, pp. 512–517, 2013. [Google Scholar]
25. T. T. Nguyen, N. V. Quynh and L. V. Dai, “Improved firefly algorithm: A novel method for optimal operation of thermal generating units,” Hindawi, Complexity, vol. 2018, pp. 1–23, 2018. [Google Scholar]
26. W. Pei. G. Huayu, Z. Zheqi and L. Meibo, “A novel hybrid firefly algorithm for global optimization,” in 2019 IEEE 4th Int. Conf. on Computer and Communication Systems (ICCCS), Singapore, pp. 164–168, 2019. [Google Scholar]
27. Y. Yun, E. J. Hwang and Y. H. Kim, “Adaptive genetic algorithm for energy-efficient task scheduling on asymmetric multiprocessor system-on-chip,” Microprocessors and Microsystems, vol. 66, pp. 19–30, 2019. [Google Scholar]
28. M. Tassori and S. Uyshal, “Effective routing algorithm and topology on power consumption in networks on chip,” Journal of Computers, vol. 13, no. 2, pp. 204–211, 2018. [Google Scholar]
29. V. Catania, A. Mineo, S. Monteleone, M. Palesi and D. Patti, “Noxim: An open, extensible and cycle-accurate network on chip simulator,” in IEEE 26th Int. Conf. on Application-Specific Systems, Architectures and Processors (ASAP), Toronto, ON, Canada, pp. 162–163, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |