DOI:10.32604/iasc.2022.027034

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.027034 |  |
| Article |
Energy-saving-oriented Berth Scheduling Model at Bulk Terminal
1Huzhou Vocational &Technical College, Huzhou, 313000, China
2Shanghai Maritime University, Shanghai, 201306, China
3International Business Machines Corporation (IBM), NY, USA
4Wuxi University, Wuxi, 214105, China
5College of Management Science and Engineering, Anhui University of Technology, Ma’anshan, 243002, China
*Corresponding Author: Baiqing Zhou. Email: zhoubaiqinghuzhou@163.com
Received: 09 January 2022; Accepted: 23 February 2022
Abstract: With the global warming to the survival and development of mankind, more and more attention is paid to low-carbon, green and energy-saving production. As one of the main modes of international transportation, the wharf has been facing a serious problem of its high carbon-emission. In order to balance the relationship between port energy consumption and efficiency, it is necessary to study the berth allocation, loading and unloading of bulk terminal from the perspective of energy saving with the proposal of energy saving and emission reduction in China. Both energy saving and efficiency can be achieved at the bulk terminal in the study. First, the latest layout and basic operation process of the bulk terminal are obtained by analyzing its process system. Secondly, a new model of energy consumption is constructed through regression analysis, based on which a mathematical model of berth scheduling is then constructed toward the aim with the minimum cost of distance deviation, of delayed departure and of energy consumption. Finally, by taking Tianjin Port for example, the model is verified to be feasible and efficient in reducing the loading and unloading cost, the total cost of ship in port time, in improving its service quality and achieving a low-carbon production. Moreover, the model can serve as a reference for other ports to reduce mechanical energy consumption.
Keywords: Energy-saving; bulk terminals; berth scheduling
There has been an increasing recognition that more attention should be paid to energy saving and consumption reduction under the pressure of resource consumption on environment in China. Transportation is one of the most essential industries that consumes a large amount of energy. There are four forms of transportation: vehicle, ship, road and port. Port plays so important a role in transportation that it is of great significance to reduce its energy consumption for the whole energy consumption in transportation industry [1–3].
Both the bulk and the container terminals are important sections of the port system and play irreplaceable strategic roles in logistic industry. The Ministry of Transport of China has been drawing more and more attention to energy saving in port due to the fact there are a great deal of large-scaled equipment, which is complicated to handle and with high energy-consumption. With the improvement of informationization and the development of digitization and intellectualization, the port equipment is becoming much more large-scaled, integrated and automatic [4–6]. Though most ports can take account into both energy-saving and effectiveness during operation, there are still much more room for them to improve berth scheduling, dispatch of the loading and unloading machinery, distribution and management etc [7–9].
2 Current Situation of Berth Scheduling
2.1 Basic Layout and Operation Process at Bulk Terminal
With the enlargement of the loading capacity and the improvement of infomationization, challenges have been raised in the scale of bulk terminal, automation and specialization of the equipment. Keys that affect the whole terminal’s system lie in how to coordinate all the parts and to distribute all the equipment evenly [10–12]. With the continuous development of new technology, there are continuous improvement of layouts and designs of the bulk terminal [13]. Take coal terminal as an example and you will find the differences in layout between the traditional and the new type [14]. The traditional layout is shown in Fig. 1 and the new type that is closed is shown in Fig. 2. We can draw a conclusion from Fig. 1 that the stacking yard is open and there is only one operation path. Coal particles float in the air, which causes serious pollution around there. With the development of technology, silo is used to load coal. The yard is then closed to reduce air pollution. In the new-type yard, two operation paths are used, one is for entering and the other for exiting and hence the work efficiency is greatly improved [15].

Figure 1: Layout of traditional coal terminal

Figure 2: Layout of new-type coal terminal
2.2 Description of Berth Scheduling Problem at Bulk Terminal
It has been several decades since the research on port began in the 1980s. Queuing theory, queuing network theory and computer simulation were commonly used in the research which involved predicting the throughput of the port, optimizing and configuring the equipment, optimizing the construction of the port, configuring the handling operation line for one-ship operation, port system simulation, analyzing and optimizing bottleneck, coordinating and configuring the container truck and operation line, berth scheduling and distributing and optimizing ship etc. Most of the research focused on the container terminal.
As one kind of multi-resource scheduling, the berth scheduling of bulk terminal has the same characteristic with scheduling. It differs greatly in equipment and process from the berth scheduling of the container terminal [16,17], so the method of berth resources and machine scheduling of the container terminal is not suitable for the bulk terminal, while the method of energy saving is. The study of the bulk terminal on energy saving is based on the berth and mechanical allocation of the container terminal [18].
The core resources of bulk terminal are berthing position, loading and unloading machinery and stacking yard. Their allocation will directly influence the economic benefits [19–21]. The uncertainly of the key factors of the port will lead to two kinds of situations. One is that ships have to be waited for too long a time and cargos cannot be unloaded in time when there are too many ships arrive at the port and what’s more, the unreasonable allocation of berthing positions will cause greater loss in economic; The other is that ships can directly berth without waiting at the port with large scale and big investment in the port, which will result in a low utilization and an unnecessary waste when there are few ships arrived [22,23]. In general, before the ship arrives, the dispatcher will assign appropriate berthing positions and handling machinery to it based on the relevant information such as its arrival plan, length, berthing positions, the handling machinery and its length [24–26]. Four parts are involved in the working process of the bulk terminal: arrival, berthing, handling and departure. The vessel will not dock and start loading and unloading until it meets the requirement such as whether the length of shoreline is suitable [27,28].
At present, a large number researches of port focus on the optimization of cost, time and benefit in the allocation of core resources, especially on the modeling of port efficiency, but few on energy saving. In order to balance the relationship between energy consumption and efficiency [29,30], Here in the paper, a new model of energy consumption is first constructed through regression analysis based on the functional nodes that the core resources act as. Then, a mathematical model of berth scheduling is constructed by linear and nonlinear method. Finally, a reasonable plan of berth scheduling is proposed on the basis of assessment and optimization with algorithm and simulation
3 Mathematical Model of Berth Scheduling
This model is built on basis of the following assumptions: (1) the ship’s arrival time is known and it will arrive on time within the planned port time. (2) the berthing length is 1.2 times that of the ship. (3) regardless of shifting and only one chance is given to every ship to berth. (4) the depth of continuous shoreline is the same and greater than the drainage. (5) every ship has been assigned the minimum and maximum loading machinery respectively. (6) the loading machinery will move in orbit and won’t stride over. (7) the ratio of every loading machinery is a constant and regardless of the mutual interference between machinery. (8) the ship’s loading time is inversely proportional to the loading machinery numbers and there are a certain proportion.
S-Set of ships to port, S = {1, 2,…, s}; C-Set of cranes, C ={1, 2,…, c}; L-Total length of shoreline; B-Sequential set of ship service; b-Sequence in which ships are served, b ={1, 2,…, s} ∈ B; i, j-Arriving ships, i, j = 1, 2,.., s. li-Length of Ship i. zi-Deadweight of Ship i (unit: ton). Ati-Arrival time of Ship i; Eti-Exiting time of Ship i. Ei-Berthing position of Ship i. Xi*-Best berthing position of Ship i. Dti-Expected departure time of Ship i. if Eti ≤ Dti, then Ri = 0, else Ri = 1. SCmaxi-Maximum crane number assigned to Ship i; SCmini-Minimum crane number assigned to Ship i; Ti-Loading and unloading operation time of Ship i; Vo-Operation efficiency of the crane (unit: ton/move); Ho-Energy consumption of one crane in one unit time for one operation, usually a constant; M1-Cost per unit energy consumption when the crane is working (unit: yuan/move); M2-Cost per unit waiting time of ship (unit: yuan/h); M3-Cost per unit energy consumption when the crane is waiting (unit: yuan/move); M4-Cost per distance caused by berthing deviation (unit: yuan/h); ηk-Ratio of effective energy consumption when Crane k is assigned to one ship; ω1-Weight of distance cost influenced by berthing deviation; ω2-Weight of delayed cost caused by departure; ω3-Weight of energy cost produced by cranes; g-Interference coefficient between cranes, which is less than 1, usually equals to 0.9; qic-Operation quantity distributed to Crane c by Ship i. If qic = 0, then the crane doesn’t serve for Ship i; Si-Berthing start position of Ship i; Sti-Berthing time of Ship i; SCi-Number of cranes assigned to Ship i.
Here, we aim to get the lowest berth scheduling costs that are made up of three parts, the lowest cost influenced by distance between the actual and the optimum berthing positions, the lowest delayed departure cost and the lowest energy consumption cost of cranes that serve for ship.
Since a simple mathematical formula can be used to describe the cost of berthing deviation distance and departure delay cost, a regressive analysis is employed to discuss the energy consumption of the portal crane, that is, different distribution numbers of crane, different operation time and non-operation time. Based on the relationship of energy consumption between the working time and the idle status, the crane’s energy consumption is thus computed by being converted into the cost of energy consumption.
There are two forms of energy consumption of machinery: the effective and the in-effective. The former is the energy consumed when the machinery is working properly, while the latter the energy consumed when the machinery is not working properly. Corresponding formulas are shown as follows:
Effective Energy Consumption for Per Unit:
eyx=ηkH0 (1)
In-effective Energy Consumption for Per Unit:
ewx=(1−ηk)H0 (2)
Just as the energy consumption of machinery, there are two forms of energy consumption of cranes: the effective and the in-effective. When the different crane operates on the same ship, there is interference between each other. So, the effective energy consumption of crane can’t be computed directly on the basis of the ratio of the single crane.
The more the crane numbers distributed to ship, the lower the efficiency of the single crane. According to some statics, when different crane numbers are assigned to the same ship, the ratio of nonworking to working time is as shown in Tab. 1.
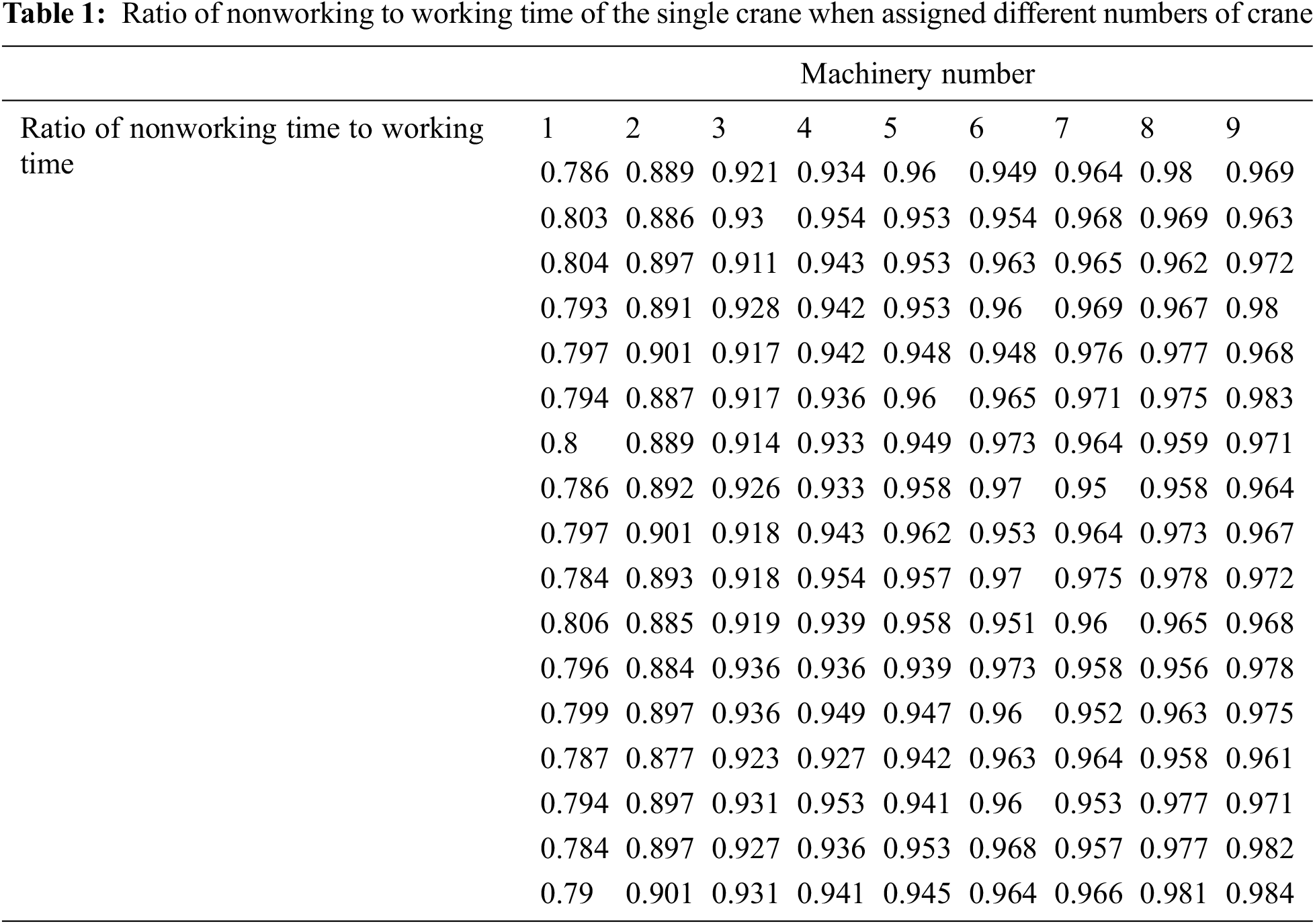
By regressive analysis, Tab. 2 shows the average value of the ratios of nonworking to working time for different machinery numbers.

A regression curve is obtained by use of the regression analysis module with a simulation software named eM-Plant, as shown in Fig. 3.

Figure 3: Regression curve influenced by the assigned numbers of crane
It can be seen from the figure that the ratio of nonworking to working time follows the formula when assigned different numbers of crane to the single ship.
f(x)=0.01x∧3−0.1x∧2+0.31x+0.57 (3)
It shows that the correlation of the crane number assigned to one ship to the ratio of nonworking to working time reveals the third power function. According to the functional relation, we can build a ratio table of effective energy consumption of the crane when assigning different numbers of crane to one ship. It is shown in Tab. 3

Therefore, we can get the utilization ratio for per unit.
ηk=H011+f(xik) (4)
where, xik represents Crane k that is assigned to Ship i. f(xik) is the ratio function of nonworking to working time.
The objective function of this paper is as follows:
The minimum cost influenced by distance between the actual and the optimum berthing positions is:
f1=minM4s∑i=1|Ei−Si2−xi∗| (5)
The minimum delayed departure cost is:
f2=minM2s∑i=1Ri(Eti−Dti) (6)
The minimum energy consumption cost is:
f3=mins∑i=1c∑k=1SCixikH0(V0/(SCi)g)[M1ηk+M3(1−ηk)](Eti−Sti) (7)
Because there are differences in magnitude in the decision objective, it is necessary to normalize the destination function. By converting the destination function into a number with the same order of Magni-tude, the lowest cost can be computed directly according to weights of these three destination functions. f1min is the minimum distance deviation cost. Generally speaking, when all ships berth at the optimum position, we get the lowest distance deviation cost of 0. f1max is the maximum deviation cost and the maximum deviation distance equals to the length of one shoreline at most. The destination function of the berthing deviation distance is normalized as follows:
f′1=f1−f1minf1max−f1min (8)
f2min is the minimum delayed departure cost. When all ships leaves port on time, we get the lowest delayed departure cost of 0. f2max is the maximum delayed cost. Here is a general assumption that the maximum delayed time is 24 h. The cost of penalty for delayed departure is then normalized as:
f′2=f2−f2minf2max−f2min (9)
f3min is the minimum energy consumption cost of the crane. When all ships are assigned the optimum numbers of cranes, the energy consumption cost reach a minimum. f3maxis the maximum energy consumption cost that is given a larger number.
f′3=f3−f3minf3max−f3min (10)
So, the total destination function integrates the berthing deviation cost, the delayed time cost for departure and the energy consumption cost for loading and unloading into the following formula:
f=min{ω1f′1+ω2f′2+ω3f′3} (11)
In practice, the importance is different among the distance deviation cost for berthing, the delayed time cost for departure and the energy consumption cost for loading and unloading. Different weights will be given to these three costs by experts according to the actual requirement. Finally, the result is computed.
In order to solve problems of linear programming, constraint conditions must be taken into account. The constraint conditions of the destination function mentioned in Section 3.3 is as follows.
Si≥0 (12)
Ei≤L (13)
(Ei−Sj)(Si−Ej)Sij≥0 (14)
(Eti−Stj)(Sti−Etj)Pij≥0 (15)
(Ei−Si)≥1.2L (16)
Sti−Ati≥0 (17)
s∑i=1xi=s (18)
C∑c=1qic=Zi (19)
(Eti−Dti)≤Ti (20)
SCmini≤SCi≤SCmaxi (21)
Eti−Sti=Zi/(V0×SCi) (22)
xi=0or 1, ∀i={1,2,…,s} (23)
xik=0or 1, ∀i={1,2,…,s},k={1,2,…,c} (24)
Sij=0or 1, ∀i={1,2,…,s},j={1,2,…,s} (25)
Pij=0or 1, ∀i={1,2,…,s},j={1,2,…,s} (26)
Formula (12) ensures that all the starting position of the berthing ship is within the shoreline, Formula (13) that all the ending position of the berthing ship is within the shoreline, Formula (14) the berthing ship position won’t be crossed if the time doesn’t intersect, namely, there are not overlapping parts between two berthing ships in the same time, Formula (15) the berthing time won’t be intersected if the potion doesn’t cross, Formula (16) that the vacant position is 2.2 times longer than that of the ship, Formula (17) that the ship can only be served after arriving at port, Formula (18) that all the ship arriving at port have berth, Formula (19) that all the cargos in Ship i can be unloaded completely, Formula (20) that all the delayed departure time is no longer than the loading time. Formula (21) means that the numbers of cranes assigned to ship cannot be less than that of the minimum cranes accepted, Formula (22) that the operation time equals to the quotient of the total handling quantity divided by the handling efficiency of cranes. Formulas from (23) to (26) is the binary constraints, where, if xi = 1 then Ship i berths, else if xi = 0 then Ship i does not; if xik = 1, then the number of cranes assigned to Ship i isn’t equals to k; if Sij= 1 then there is a time intersection between Ship i and Ship j, or Sij= 0; if Pij= 1 then there is a berthing intersection between Ship i and Ship j, or Pij= 0.
4 Coal Terminal at Tianjin Port
The shoreline is 1100 meters long in Tianjin Coal Terminal Port. Let assume that the coal terminal not only has a continuous berth, but also the same draught depth and berthing capacity. What’s more, the draught depth is less than the berthing capacity for all the ships. Let’s take 24-hour-data of ships that are waiting at port and expected to arrive ranging from 10th to 11th, October 2017. In order to satisfy the regulated time format and to calculate easily, the berthing time starts from 0:00 PM and the maximum waiting time is less than the loading and unloading time. Basic data is shown as in Tab. 4.
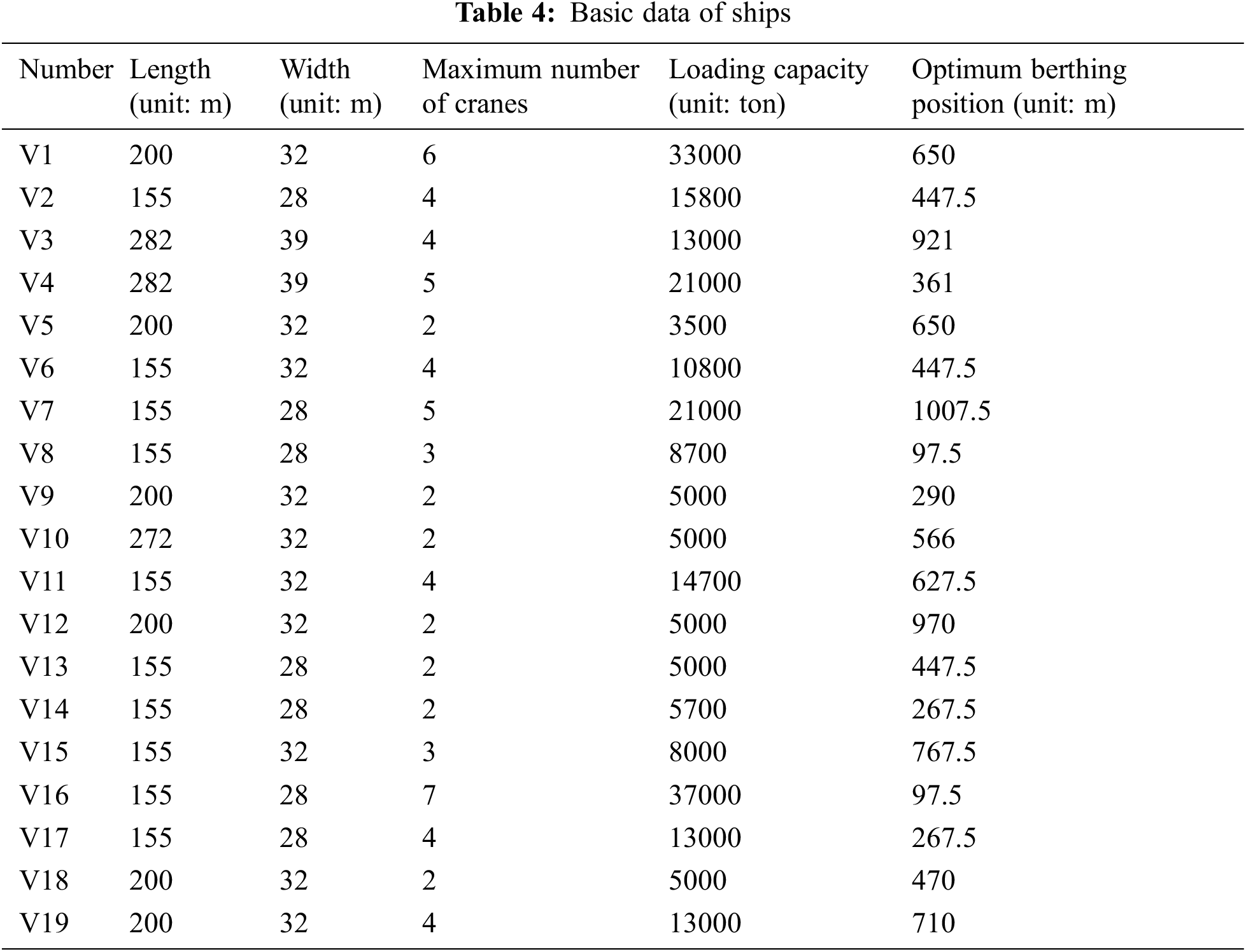
From the table above, it can be concluded that: number of ships, length and width of each ship, maximum number of machineries to be allocated, loading capacity and optimal berthing position. There are 4 loading machines and 4 cranes at Tianjin Port. Tab. 5 shows their efficiency.
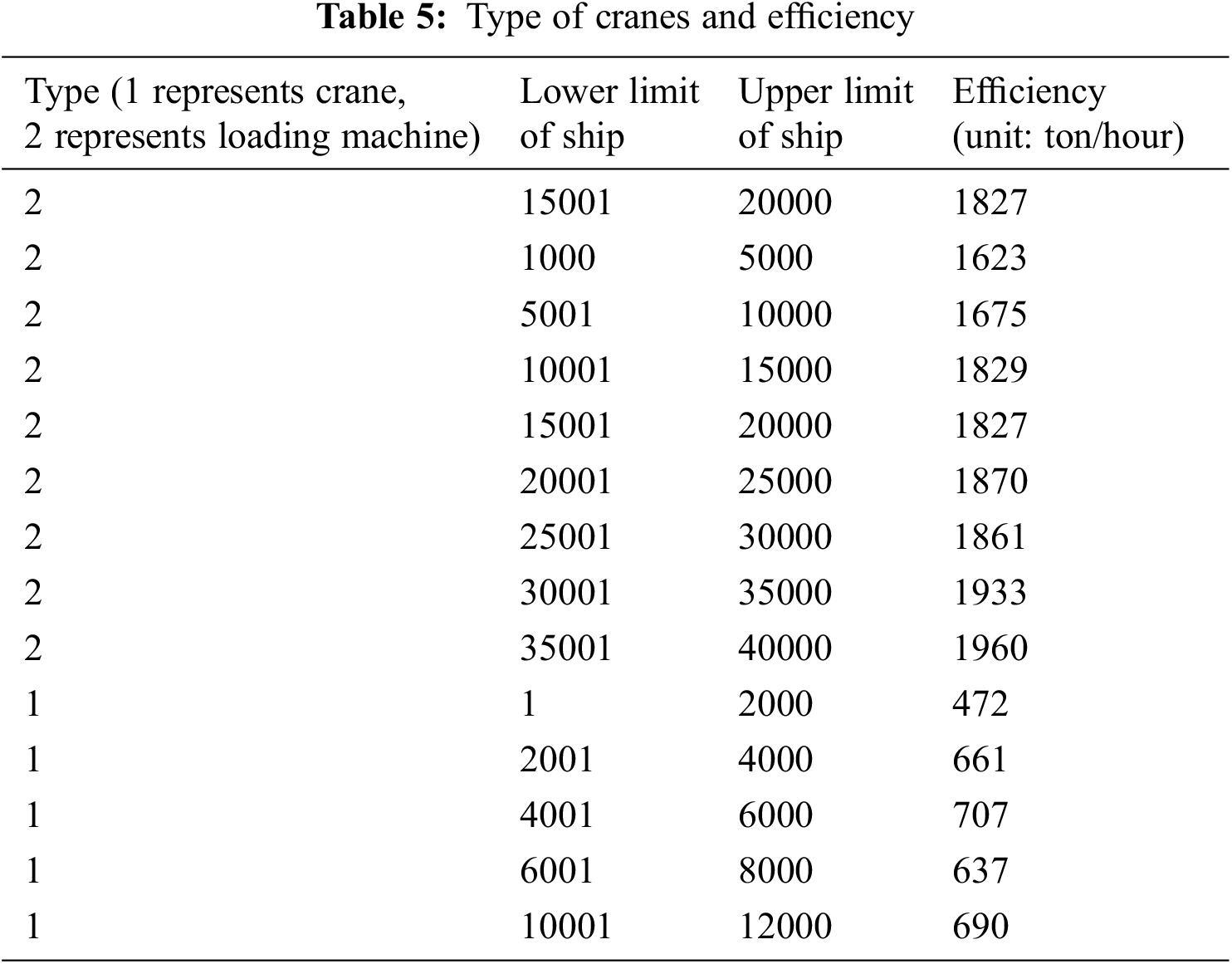
The upper and lower bounds of tonnage range in the above table mainly distinguish the efficiency of different types of machinery. It is known that the penalty cost for the delay departure is 4944 yuan/h, the electricity charges for industrial use is 0.8 yuan/kwh, the operation efficiency of cranes is 40t/move, the unit energy consumption for cranes is 149.7 kwh. Preset the relevant experimental parameters as following: the coefficients of the penalty cost for the delay departure is ω1 = 0.4, ω2 = 0.4, ω3 = 0.2 respectively; Population and subpopulation in genetic algorithms is 100 and 50 respectively; the cross rate is 0.7; the uniform variation probability is 0.04; the maximum generative algebra is 40; the migration frequency and number is 3 and 5 respectively.
Simulation and optimization algorithm are used to solve the model. There are variations in berthing position, berthing time, departure time and cranes’ number before and after simulation optimization. The comparisons between initial data and optimized data are shown in Tab. 6.
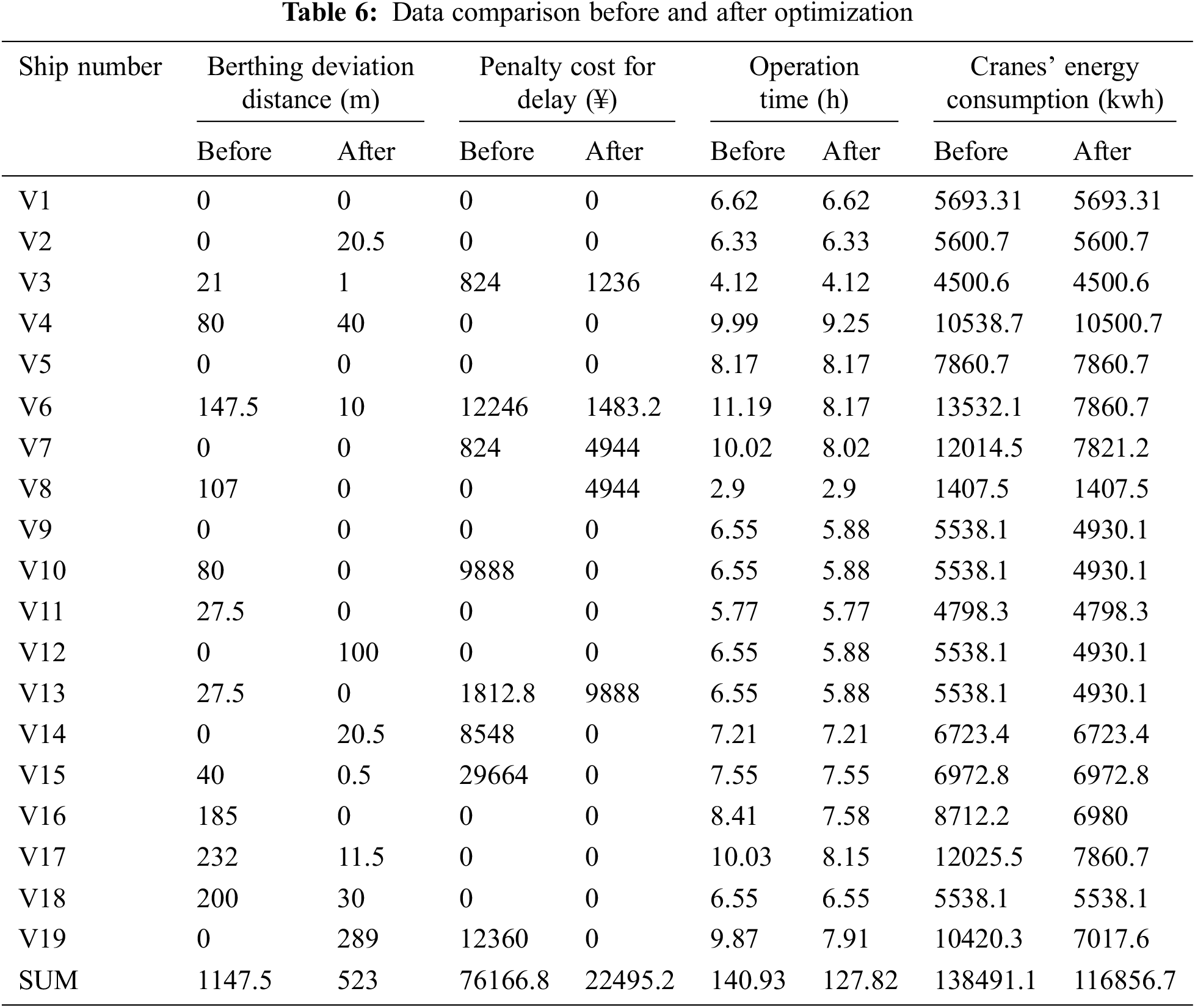
Referring to the above comparison, the established model can reduce the berthing deviation distance, reduce the penalty cost of departure delay, reduce the operation practice and reduce the mechanical energy consumption. It has suggested that the mathematical model is appropriate and reflects an actual bulk terminal. It’s an effective and feasible way to solve berth scheduling by combining simulation model and genetic algorithm.
This paper conducts a deep analysis on the characteristic and operation of the bulk terminal. And it constructs a new model of energy consumption through regression analysis. When different crane numbers are assigned to the ship, the working and nonworking time varies. A regression curve is then obtained for the effective and ineffective energy consumption.
With the combination of both linear and non-linear method in Operational Research, a mathematical model for berth scheduling is constructed. By simulation and taking data of one day from Tianjin Port for example, the model is verified according to the actual conditions, which includes the berthing deviation distances, the penalty cost for delay, the operation time and the cranes’ energy consumption before and after optimization.
Funding Statement: This work is supported by the project of Research Topic of Zhejiang Social Science Federation in 2022 (NO: 2022B36), Xiaona Hu received the grant and URL to the sponsor’s website is https://www.zjskw.gov.cn/. This work is also supported by the Natural Science Foundation of Anhui Province, China (No: 2108085MG236), Gang Hu received the grant and URL to the sponsor’s website is http://kjt.ah.gov.cn/. This work is supported by the Natural Science Foundation from the Education Bureau of Anhui Province, China (No. KJ2021A0385), Gang Hu received the grant and URL to the sponsor’s website is http://jyt.ah.gov.cn/.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Y. J. Ren, F. J. Zhu, S. P. Kumar, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]
2. L. M. Fang, M. H. Li, Z. Liu, C. T. Lin, S. L. Ji et al., “A secure and authenticated mobile payment protocol against off–site attack strategy,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 3, pp. 1–12, 2021. [Google Scholar]
3. J. Dai, W. Lin, R. Moorthy and C. P. Toe, Berth Allocation Planning Optimization in Container Terminals. Springer, vol. 119, no. 6, pp. 69–104, 2008. [Google Scholar]
4. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “Revocable attribute–based encryption with data integrity in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 11, pp. 1–12, 2021. [Google Scholar]
5. J. Wang, H. Han, H. Li, S. M. He, P. K. Sharma et al., “Multiple strategies differential privacy on sparse tensor factorization for network traffic analysis in 5G,” IEEE Transactions on Industrial Informatics, vol. 18, no. 3, pp. 1939–1948, 2022. [Google Scholar]
6. Y. J. Ren, K. Zhu, Y. Q. Gao, J. Y. Xia, S. Zhou et al., “Long–term preservation of electronic record based on digital continuity in smart cities,” Computers, Materials & Continua, vol. 66, no. 3, pp. 3271–3287, 2021. [Google Scholar]
7. C. P. Ge, W. Susilo, Z. Liu, J. Y. Xia, L. M. Fang et al., “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 6, pp. 2787–2800, 2021. [Google Scholar]
8. C. B. Liu, K. L. Li, K. Q. Li and R. Buyya, “A new service mechanism for profit optimizations of a cloud provider and its users,” IEEE Transactions on Cloud Computing, vol. 17, no. 2, pp. 1–12, 2017. [Google Scholar]
9. A. Imai, E. Nishimura and S. Papadimitriou, “Berth allocation with service priority,” Transportation Research Part B, vol. 15, pp. 312–329, 2002. [Google Scholar]
10. Y. J. Ren, Y. Leng, J. Qi, K. S. Pradip, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, pp. 304–313, 2021. [Google Scholar]
11. T. Li, N. P. Li, Q. Qian, W. Xu, Y. Ren et al., “Inversion of temperature and humidity profile of microwave radiometer based on bp network,” Intelligent Automation & Soft Computing, vol. 29, no. 3, pp. 741–755, 2021. [Google Scholar]
12. J. Wang, C. Y. Jin, Q. Tang, N. X. Xiong and G. Srivastava, “Intelligent ubiquitous network accessibility for wireless–powered MEC in UAV–assisted B5G,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 4, pp. 2801–2813, 2021. [Google Scholar]
13. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “A verifiable and fair attribute–based proxy re–encryption scheme for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 7, pp. 1–12, 2021. [Google Scholar]
14. Y. J. Ren, J. Qi, Y. P. Liu, J. Wang and G. Kim, “Integrity verification mechanism of sensor data based on bilinear map accumulator,” ACM Transactions on Internet Technology, vol. 21, no. 1, pp. 1–20, 2021. [Google Scholar]
15. C. Bierwirth and F. Meisel, “A survey of berth allocation and quay crane scheduling problems in container terminals,” European Journal of Operational Research, vol. 202, no. 3, pp. 615–627, 2010. [Google Scholar]
16. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
17. Y. J. Ren, J. Qi, Y. P. Cheng, J. Wang and O. Alfarraj, “Digital continuity guarantee approach of electronic record based on data quality theory,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1471–1483, 2020. [Google Scholar]
18. C. P. Ge, Z. Liu, J. Y. Xia and L. M. Fang, “Revocable identity–based broadcast proxy re–encryption for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1214–1226, 2021. [Google Scholar]
19. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
20. J. Y. Hu, K. L. Li, C. B. Liu and K. Q. Li, “A game–based price bidding algorithm for multi–attribute cloud resource provision,” IEEE Transactions on Services Computing, vol. 14, no. 4, pp. 1111–1122, 2021. [Google Scholar]
21. A. Lim, “The berth planning problem,” Operations Research Letters, vol. 22, no. 2–3, pp. 105–110, 1998. [Google Scholar]
22. X. Zhou, K. L. Li, Y. T. Zhou and K. Q. Li, “Adaptive processing for distributed skyline queries over uncertain data,” IEEE Transactions on Knowledge & Data Engineering, vol. 28, no. 2, pp. 371–384, 2016. [Google Scholar]
23. Y. J. Ren, Y. Leng, Y. P. Cheng and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]
24. Y. P. Guan and R. K. Cheung, “The berth allocation problem: Models and solution methods,” Or Spectrum, vol. 26, no. 1, pp. 75–92, 2004. [Google Scholar]
25. C. L. Li, X. Cai and C. Y. Lee, “Scheduling with multiple–job–on–one–processor pattern,” IIE Transactions, vol. 30, no. 5, pp. 433–445, 1998. [Google Scholar]
26. H. B. Zhang, J. H. Zhang and J. Z. Xuan, “A heuristic algorithm for berth scheduling problem in container ports,” Journal of Qingdao University (Engineering & Technology Edition), vol. 25, no. 4, pp. 57–60, 2010. [Google Scholar]
27. Y. J. Ren, F. Zhu, J. Wang, P. Sharma and U. Ghosh, “Novel vote scheme for decision–making feedback based on blockchain in internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 1639–1648, 2022. [Google Scholar]
28. J. Qin, L. X. Miu, C. B. Chen and J. H. Tao, “Model and algorithm for the berth allocation problem with time windows,” Ship & Ocean Engineering, vol. 39, no. 2, pp. 142–145, 2010. [Google Scholar]
29. A. Agra and M. Oliveira, “MIP approaches for the integrated berth allocation and quay crane assignment and scheduling problem,” European Journal of Operational Research, vol. 264, no. 1, pp. 138–148, 2018. [Google Scholar]
30. R. Filipe and A. Agostinho, “An exact robust approach for the integrated berth allocation and quay crane scheduling problem under uncertain arrival times,” European Journal of Operational Research, vol. 295, no. 2, pp. 499–516, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |