DOI:10.32604/iasc.2022.025181

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.025181 |  |
| Article |
Research on Cross-domain Representation Learning Based on Multi-network Space Fusion
1School of Artificial Intelligence, Wuxi Vocational College of Science and Technology, Wuxi, 214028, China
2School of Computer Science and Technology, Harbin Institute of Technology, Weihai, 264209, China
3Department of Mathematics, Harbin Institute of Technology, Weihai, 264209, China
4School of Astronautics, Harbin Institute of Technology, Harbin, 150001, China
5School of Mathematics and Statistics, University College Dublin, Dublin, Ireland
*Corresponding Author: Dongjie Zhu. Email: zhudongjie@hit.edu.cn
Received: 15 November 2021; Accepted: 05 January 2022
Abstract: In recent years, graph representation learning has played a huge role in the fields and research of node clustering, node classification, link prediction, etc., among which many excellent models and methods have emerged. These methods can achieve better results for model training and verification of data in a single space domain. However, in real scenarios, the solution of cross-domain problems of multiple information networks is very practical and important, and the existing methods cannot be applied to cross-domain scenarios, so we research on cross-domain representation is based on multi-network space integration. This paper conducts representation learning research for cross-domain scenarios. First, we use different network representation learning methods to perform representation learning in a single network space. Second, we use the attention mechanism to fuse representations in different spaces to obtain a fusion representation of multiple network spaces; Finally, the model is verified through cross-domain experiments. The experimental results show that the fusion model proposed in this paper can improve the performance of cross-domain scenarios.
Keywords: Network embedding; cross-domain representation; graph neural network
Today, information networks are widely used in academia, such as social and communication networks, media relations networks, and publication networks. The scale of these networks ranges from hundreds of nodes to millions or even billions of nodes. The data analysis and information aggregation of these information networks and their applications in scenarios such as node classification, node clustering, link prediction, intelligent transportation [1], big data [2], and intelligent recommendation have attracted more and more attention from the academic community.
Under normal circumstances, the models we build are limited to a single space, so the model built will have unity. Generally, the relevant models built in this space and the conclusions and indicators drawn from their predictions are very reliable. However, this situation only applies to itself. At present, when many network representation learning methods are proposed, they are only optimized for the features they are concerned about. For example, GCN focuses on how to gather neighbor information, and metapath2vec focuses on how to gather information of different relationships. However, when the content of its concern is missing or its characteristics are not obvious enough, its performance is not as expected.
To solve the problem of cross-domain representation, we applied the method of multi-network space fusion for testing. The results obtained by testing the various models and methods used on different representative data sets use neural networks.
We applied several models and methods that are representative in these scenarios to conduct experiments and perform fusion operations on them. We fused GCN [3], metapath2vec [4], Deepwalk [5]. GCN is an effective variant of convolutional neural network based on the direct operation of the graph. Deepwalk leveraged the random walk method to sample the co-occurrence relationship between nodes and then to learn the network embedding method of the vector representation of nodes. metapath2vec [4] is a formalized random walk based on metapaths to construct heterogeneous neighbors of nodes. It is a scalable representation learning model that performs node embedding [6,7]. Test experiments and comparisons were conducted based on the three distinctive data sets of ACM, DBLP, and IMDB [8,9].
For the representation of cross-domain problems, we construct different domain graphs by removing a certain proportion of edges from the original graph and then used the model trained by the complete original graph to perform network embedding on the newly constructed domain graphs. The K-Nearest Neighbor (KNN) classifier method [10] is used to verify the network embedding results of the newly constructed domain, and the data of the newly constructed domain is used to iterate and expand the model to achieve the purpose of establishing a cross-domain applicable model.
In general, the model and cyberspace we tested basically exist as an information network embedding problem, so the overall definition starts from the information network embedding [11]. There may be many different types of nodes in the information network [12–17], such as movie nodes, director nodes, actor nodes in the data set IDMB. There are also different types of edges between different nodes, and their weights represent different meanings. To simplify the problem, we only use isomorphic graphs for experiments and tests. We first define the concept of a homogeneous information network as Definition 1.
Definition 1: A homogeneous information network is defined as
Because we use isomorphic graphs for experimentation and testing, this involves a conversion process. When the dataset we used is constructed into a graph, it will eventually be constructed into a heterogeneous graph containing all types of nodes and all types of edges. We need use metapath [4] to filter edges, and finally construct an isomorphic graph that meets our expectations from the original heterogeneous graph. The definition of metapath needs to be based on the definition of heterogeneous information networks. So here we define the concept of heterogeneous information network as Definition 2:
Definition 2: Based on the description in Definition 1, the heterogeneous information network refers to the type of object
At the same time, to better define metapath, we introduce a concept of Network Schema, which is defined as Definition 3:
Definition 3: Network schema is defined as
Based on Definitions 2 and 3, we give the definition of metapath as Definition 4.
Definition 4: metapath P is defined on the network schema
The schematic diagram of metapath is shown by Fig. 1.
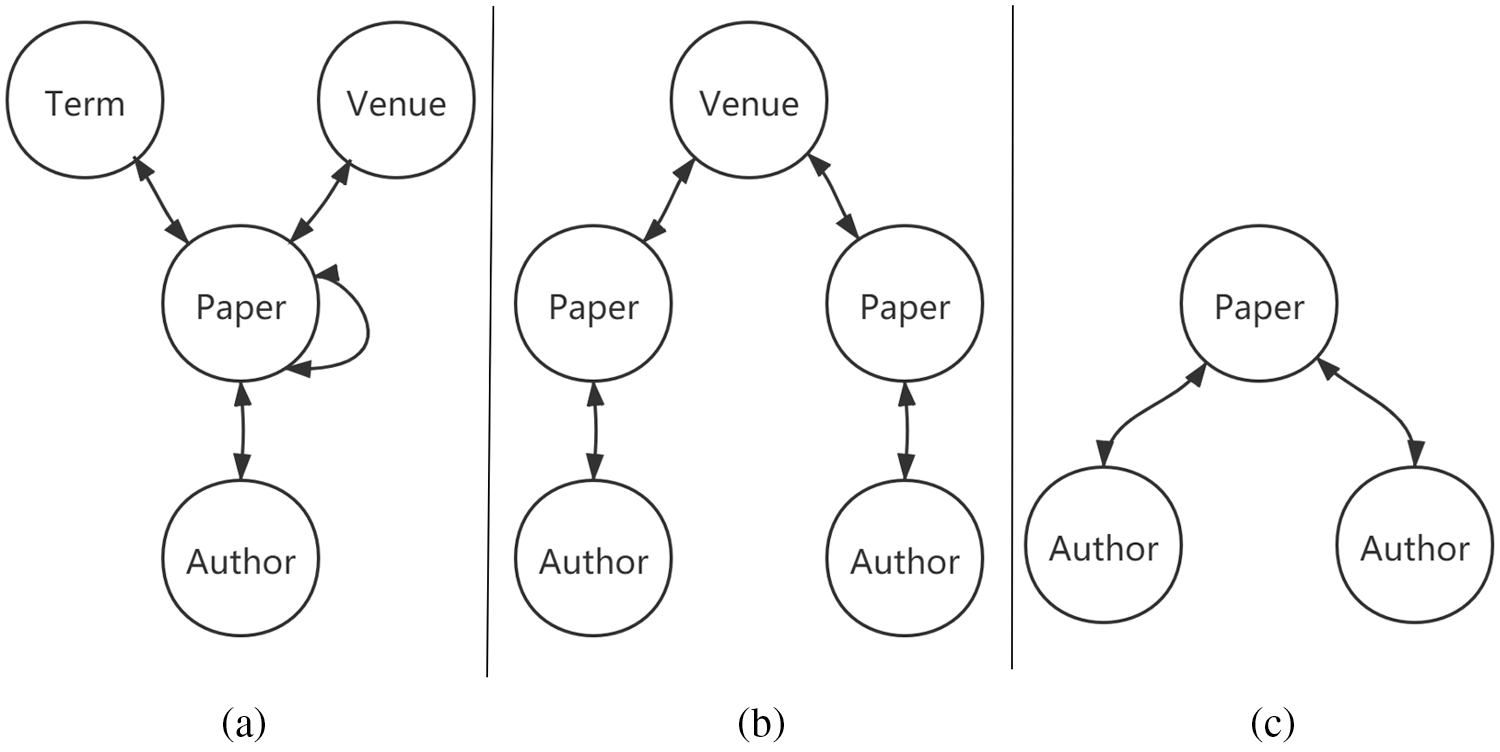
Figure 1: Diagram of network schema and metapath. (a) Network schema, (b) Metapath (APVPA), (c) Metapath (APA)
3 Cross-domain Representation Learning Based on Multi-network Space Fusion
Fig. 2 shows the overall process diagram. There are different network embedded model methods in the information network, and they perform relatively well in their respective areas of expertise. In the cross-domain problem of multi-space networks, they perform relatively well in different scenarios, but they are not universal and comprehensive. To establish a network embedding model method that performs well on cross-domain problems in multi-network space and can consider the advantages of each existing model, we first train different network embedding model methods in a single network space to obtain the corresponding the result vector, and then use the neural network with attention mechanism to fuse the result vector. The model obtained by the fusion is our MCR model. The result vector is evaluated using the KNN classifier for index evaluation, and it is compared with other previous models. To compare with the indicators, to show the superiority of the model we built.
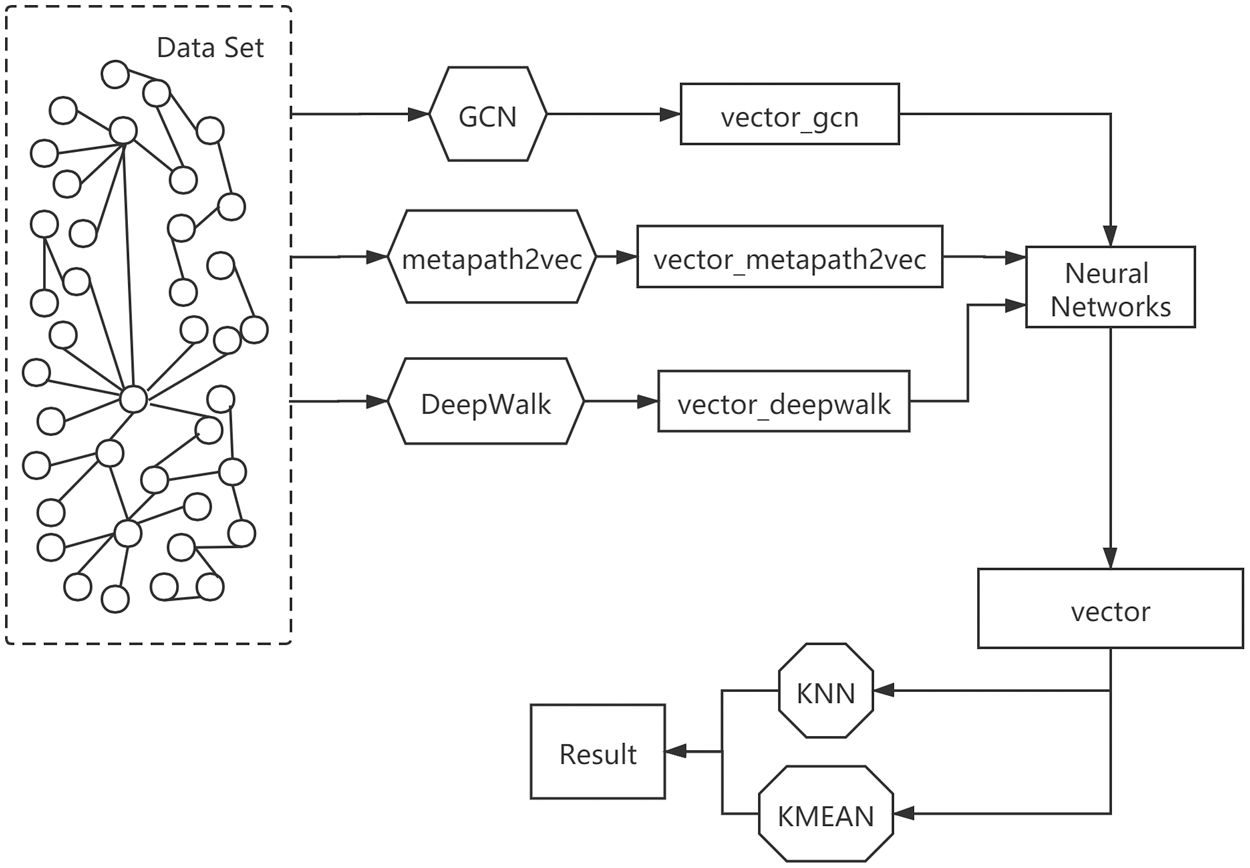
Figure 2: Schematic diagram of the overall process of multi-network space integration
3.1 Single-space Network Representation
As we all know, using different network embedding model methods in the same network space will have different effects. Each network embedding model has its own characteristics in different fields and will get good results in its own good aspects. Different network embedding models have their own different characteristics and are suitable for different scenarios, but in real life, as the perception environment and application scenarios change, the performance of the trained model will be greatly reduced, and the generalization ability of the model is insufficient, the retraining cycle is long and the cost is high, so there is a cross-domain problem. To solve the cross-domain problem, we introduce a neural network model with an attention mechanism. The result vectors obtained by different network embedding models are first superimposed horizontally, and then merged.
First, we explain GCN [3], which is a multi-layer graph convolutional network, which has the following layer-by-layer propagation rules:
At this,
The GCN is built by stacking multiple convolutional layers in the form of equations. This model can alleviate the overfitting problem of the local neighborhood structure of the graph with very wide node degree distribution, such as social networks, citation networks and many other real-world graph datasets. However, its shortcomings are also very prominent. For example, memory requirements increase linearly with the size of the data set, because the K-th order neighborhood of a GCN with K layers must be stored in memory for precise procedures. Large and densely connected graph data sets may require further approximation; implicitly assumes locality (depending on the order neighborhood of GCN with K layers) and the equal importance of self-connections relative to the edges of adjacent nodes; only can deal with undirected graphs.
Then we elaborate on metapath2vec [4], as a scalable representation learning model, the metapath2vec [4] model formalizes random walks based on metapath, constructs heterogeneous neighborhoods of nodes, and then uses heterogeneous tabbed models to perform node embedding. It formalizes the heterogeneous network representation learning problem. The goal is to learn the low-dimensional and potential embeddings of multiple types of nodes at the same time. At the same time, it first proposes a metapath-based random walk in a heterogeneous network to generate network semantics for various types of nodes. Heterogeneous neighborhood. In metapath2vec [4], we enable skip-gram to learn the effective node representation of heterogeneous network
Among them,
Finally, we elaborate on DeepWalk. Deepwalk [5] uses the co-occurrence relationship between nodes in the graph to learn the vector representation of nodes. The method it gives is to use Random Walk to sample nodes in the graph. Random Walk is a depth-first traversal algorithm that can repeatedly visit visited nodes. Given the current visit start node, randomly sample nodes from its neighbors as the next visit node and repeat this process until the visit sequence length meets the preset condition. After obtaining a sufficient number of node access sequences, use the skip-gram model for vector learning.
The DeepWalk [5] algorithm mainly includes two steps. The first step is to sample a sequence of nodes in a random walk to construct a homogeneous network. Random Walk samples are performed from each node in the network to obtain locally associated training data; the second step is using skip-gram modelword2vec to learn expression vectors, performing Skip-Gram training on sampled data, and representing discrete network nodes as vectorized to maximize node co-occurrence.
To establish a network embedding model method that performs well on cross-domain problems in multi-network space and can consider the advantages of each existing model, we introduce a neural network with an attention mechanism. The attention mechanism is used in the encoder-decoder structure. The encoder embeds the input as a vector, and the decoder gets the output according to this vector. For the training of the encoder-decoder structure, since this structure is differentiable everywhere, the parameters θ of the model can be obtained through the training data and maximum likelihood estimation to obtain the optimal solution, and the log likelihood function is maximized to obtain the optimal model’s Parameters, namely:
This is an end-to-end training method. The MCR model we proposed here is based on this training method. It can handle various types of nodes and relationships and integrate rich semantics in heterogeneous networks. Information can be transmitted from one node to another through different relationships, and the efficiency and quality of contributed data can be maintained through user and task analysis. The MCR model we proposed has potentially good explanatory properties. By understanding the importance of nodes and meta-paths, the model can pay more attention to certain meaningful nodes or meta-paths to complete specific tasks and provide a more comprehensive description of heterogeneous graphs. It is helpful to analyze and interpret our results. In the following, we will prove the superiority of our model through experiments.
In this module, we first perform network embedding processing on the network model we have selected and the model we have built on different data sets and perform the KNN classification of the result vector and obtain related indicators. Then by removing a certain proportion of edges on the data set to establish a cross-domain problem scenario and re-evaluate and compare each model to prove the superiority of our model.
The heterogeneous information network dataset we use is shown in Tab. 1:
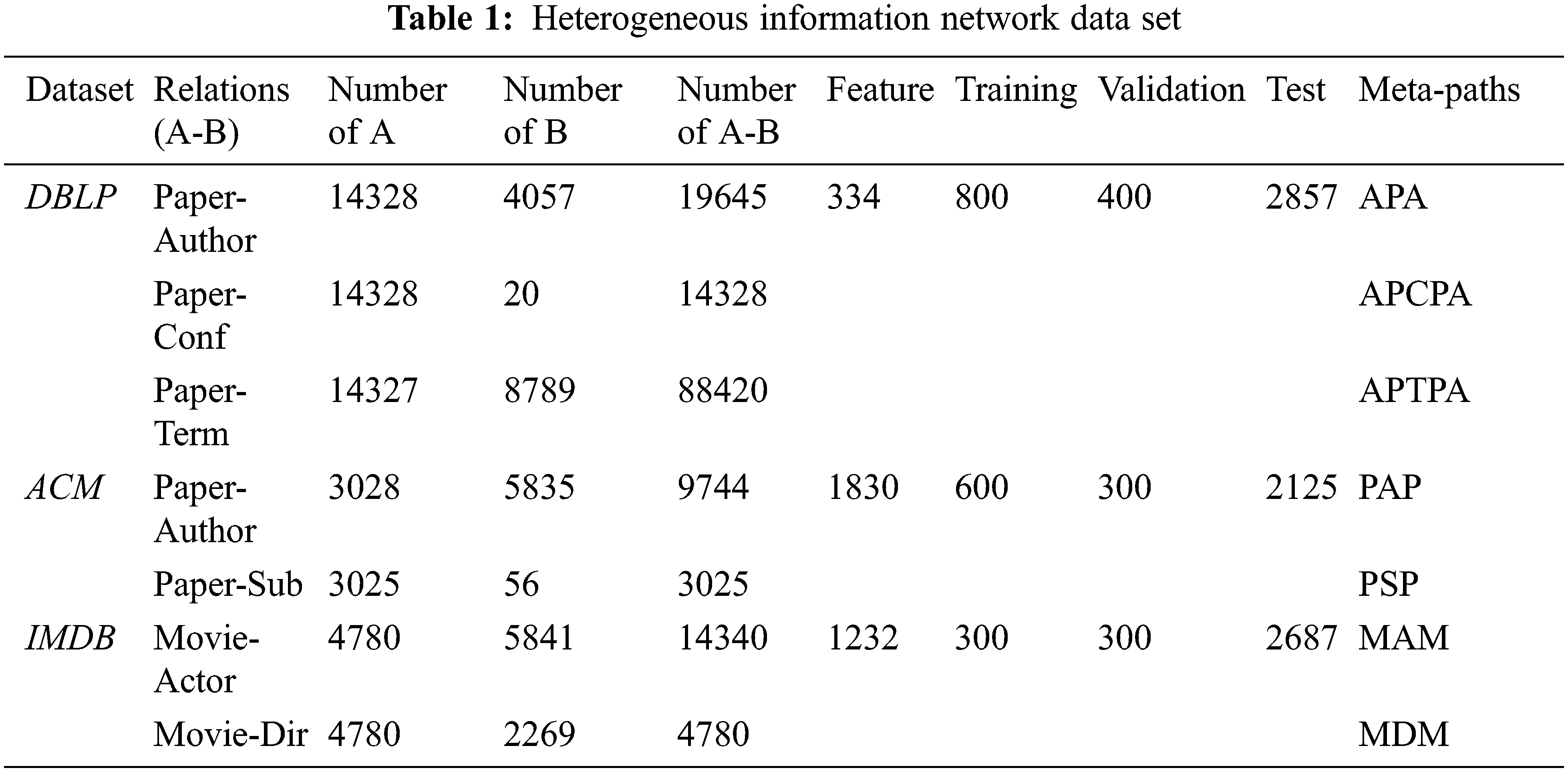
DBLP, we extracted a subset from the DBLP data set to be used as the data set for our experiment, which contains 14,328 papers in four fields (database, data mining, machine learning, information retrieval), 4057 authors, 8789 Terms, 20 meetings. To mark their research fields, we obtained information from the conferences submitted by each author in the data and marked them. The characteristics of the author are the elements of a word bag composed of keywords. In our experiment, we use metapath as {APA, APCPA, APTPA} to carry out the experiment.
ACM, we extract related published papers in KDD, SIGMOD, SIGCOMM, MobiCOMM and VLDB according to three categories (database, wireless communication, data mining), thus constructing an information network which includes 3025 papers, 5835 authors and 56 subjects. The paper features correspond to the elements of the word bag represented by keywords, and at the same time, we label them according to the conference where the paper was published. In our experiment, we use metapath as {PAP, PSP} to carry out the experiment.
IMDB, we extracted a subset from the IMDB data set to be used as the data set for our experiment, which contains 4780 movies (M) of three types ((action movies, comedies, dramas), 5841 actors (A) and 2269 directors (D). The features of the movie correspond to the elements of a word package composed of plots. We use metapath as {MAM, MDM} to conduct experiments.
We compare the previously selected network model methods on the listed data sets, including network embedding methods and graph neural network-based methods:
GCN [3]: A semi-supervised graph convolutional network designed for homogeneous information networks.
Deepwalk [5]: A random walk-based network embedding method designed for homogeneous information networks.
Metapath2vec [4]: a heterogeneous information network embedding method that performs random traversal based on metapath.
Here, we tested all meta-paths and reported the best performance. To verify the effectiveness of our proposed artificial neural network model MCR.
Node Classification Experiment and Analysis. In the node classification task experiment using the low-dimensional vector representation of the nodes obtained by using the selected models for network embedding, first uniformly use different ratios of verification set nodes to train KNN and use the remaining as KNN classification test data to obtain the node The results of the classification experiment are shown in Tab. 2.
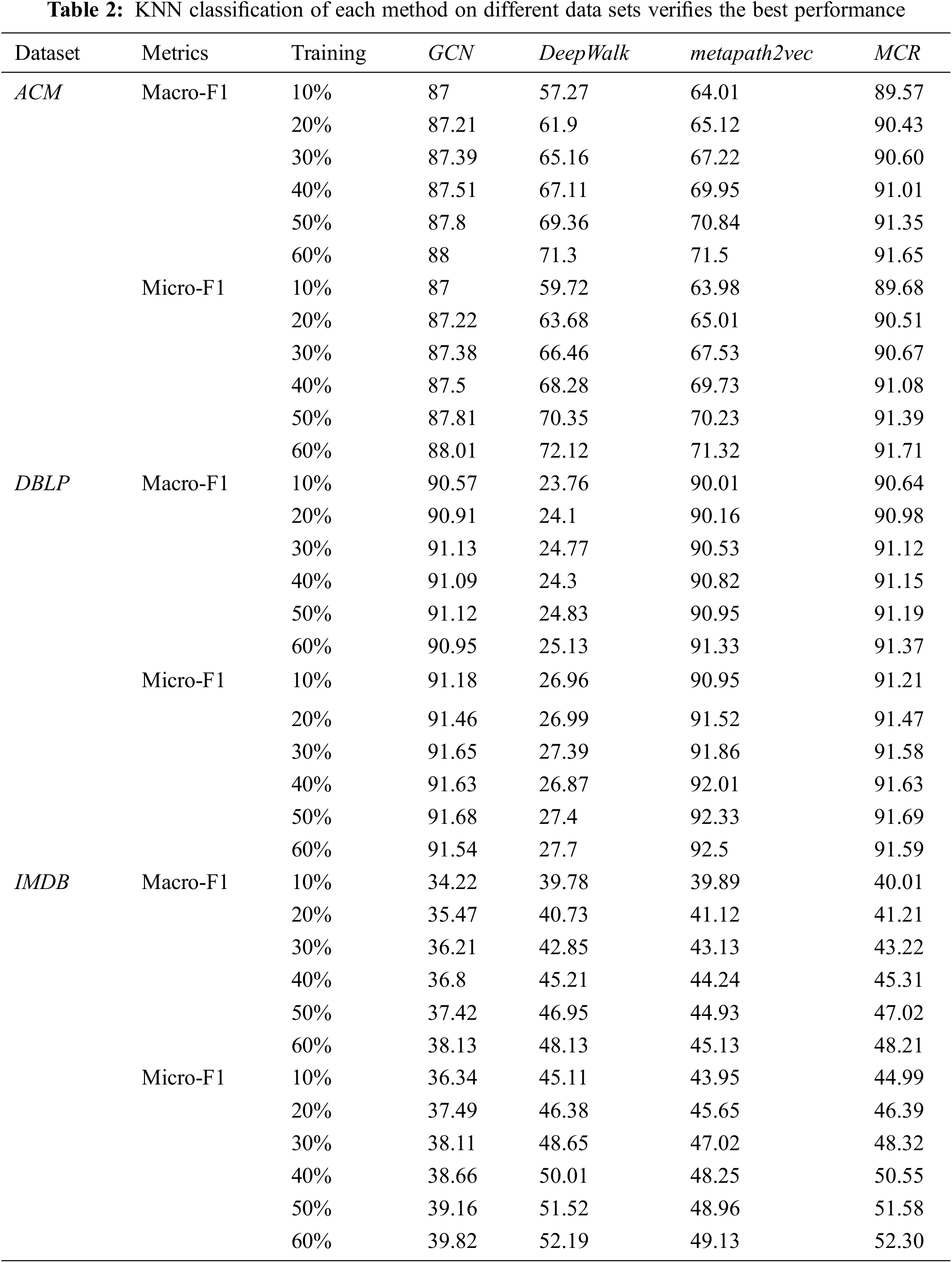
It can be seen that the model proposed in this paper improves the node classification task by 1%~5% compared with the existing methods. In addition, all models perform better on the ACM and DBLP datasets than on the IMDB dataset. After analysis, the reason may be that the distribution of the attributes of the IMDB dataset in the field of film and television is more scattered and inferior to the distribution of the attributes of the IMDB dataset. The correlation of the labels is lower, and the structure of the IMDB data set graph is more random, not as stable as the network of other data sets.
Node Clustering Experiment and Analysis. The results of node clustering experiments are shown in Tab. 3. It can be seen that, except for the MCR model proposed in this paper, the best results have been achieved in node clustering tasks. The comparison between different data sets can also draw the same conclusion as in the node classification experiment, that is, all models perform better on the ACM and DBLP data sets than on the IMDB data for the same reason as the analysis in the node classification experiment.
Visual Experiment and Analysis of Node Distribution. In order to more intuitively show the distribution of the low-dimensional vector representation of nodes obtained by the network representation model and the ability to support node classification tasks. This part visually analyzes the node vectors obtained by the proposed multi-source interactive fusion network method. First, according to the commonly used method of network representation to study the neighborhood, the node vector obtained by the model is reduced to a two-dimensional space using t-sne, and then visually displayed. The Figs. 3 and 4 show the node distribution of each model on the ACM and DBLP data sets. The different colors in the figure represent the types of nodes.
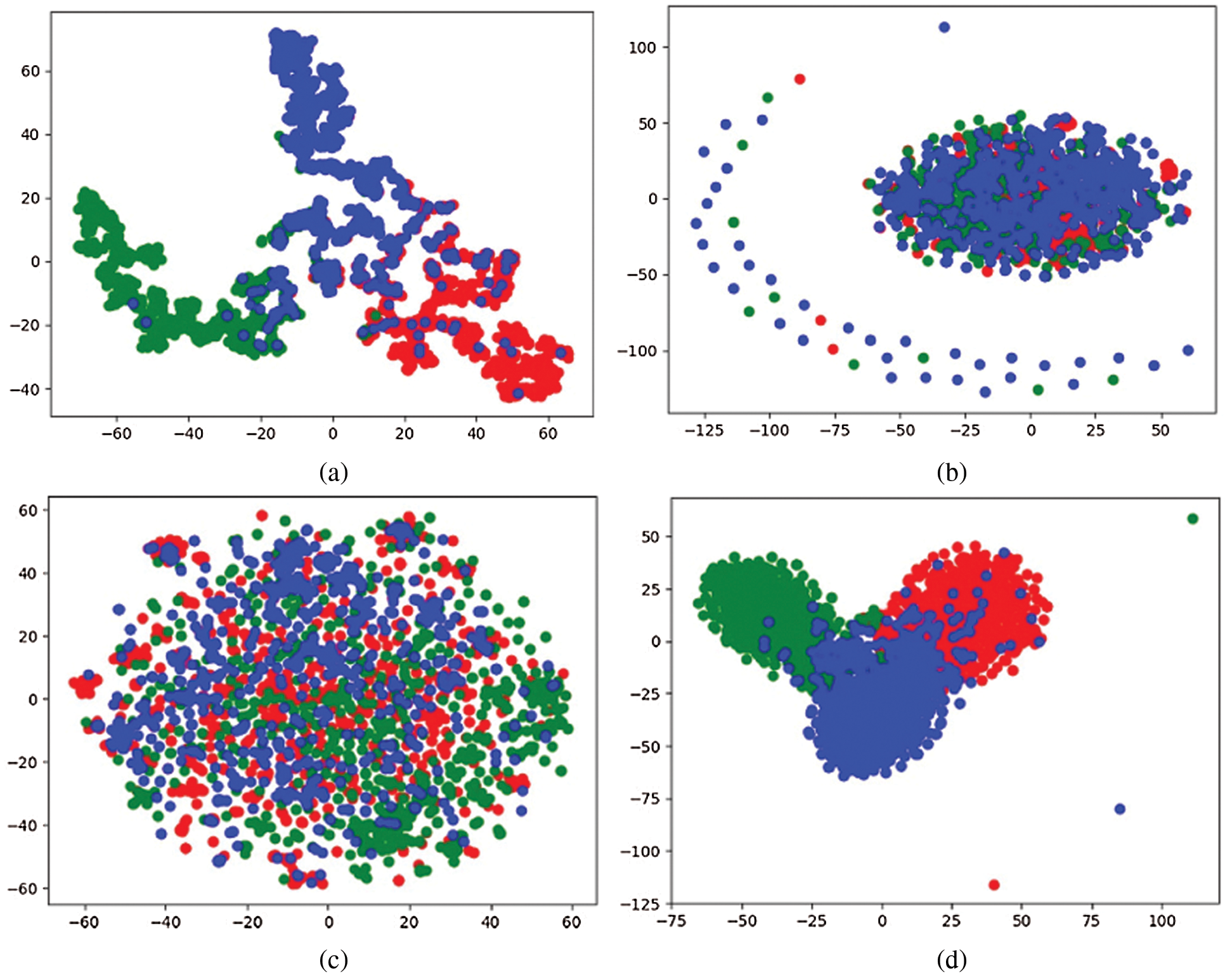
Figure 3: Visual embedding on ACM (a) GCN, (b) DeepWalk, (c) Metapath2Vec, (d) MCR
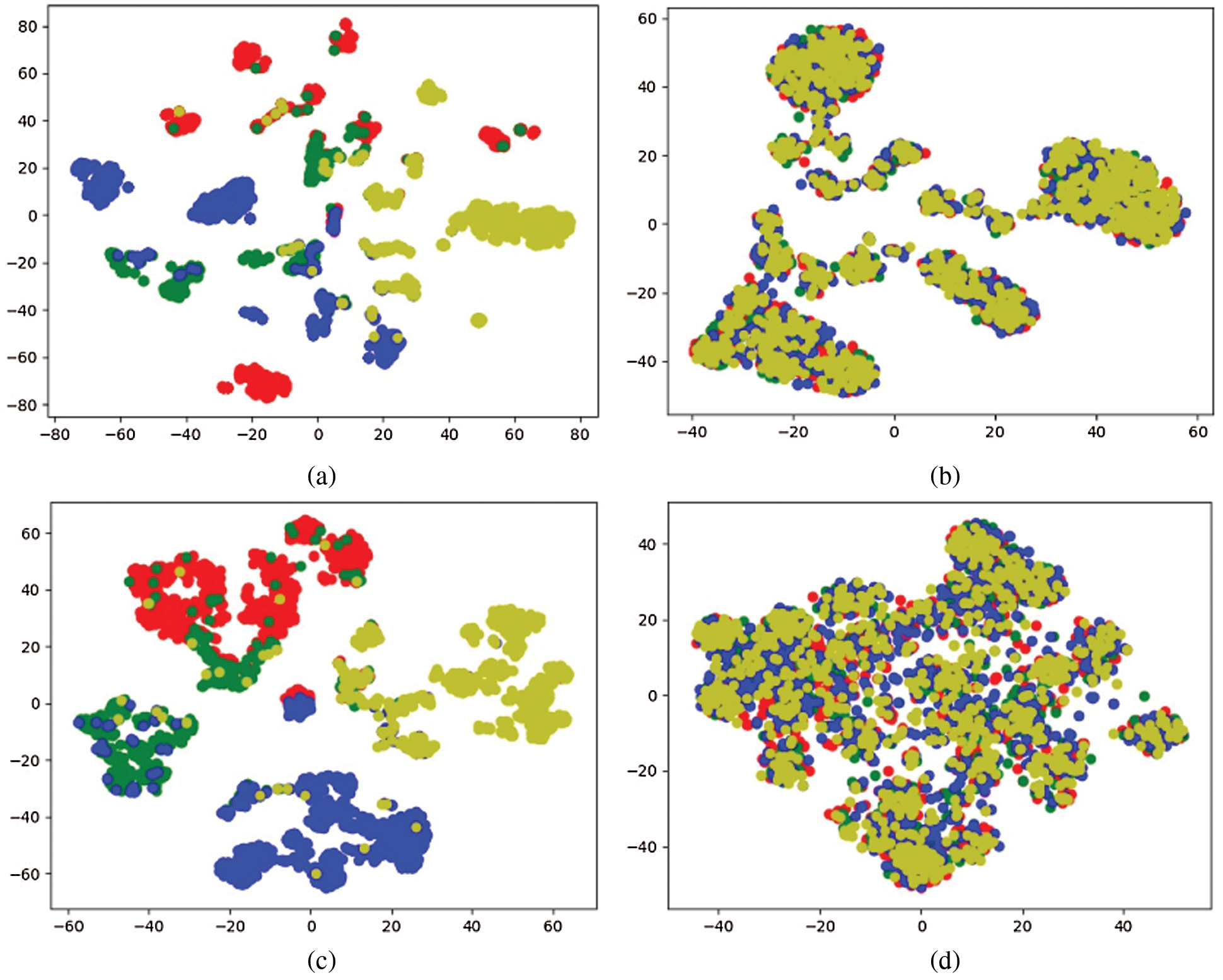
Figure 4: Visual embedding on DBLP (a) GCN, (b) DeepWalk, (c) Metapath2Vec, (d) MCR
It can be seen intuitively from the figure that in different data sets, the distribution of embedded nodes of different models is very confusing, and the effect of our proposed MCR model is significantly better than that of other models, which is enough to use the method proposed in this article The obtained low-dimensional vector of nodes indicates that it has strong support ability for node classification tasks.
For the selected method, we initialize the parameters randomly and use the Adam optimization model. We set the learning rate to 0.005, the regularization parameter to 0.001, and the dimension of the generated vector q to 128. For GCN, to optimize its parameters, we use a validation set. We separate the training set, validation set, and test set to ensure the fairness of the experimental results. For the meta path-based random walk methods Deepwalk [5] and metapath2vec [4], we set the window size to 5, the walk length to 100, the number of walks for each node to 40, and the number of negative samples to 5. We set the embedding dimension of all the above algorithms to 128.
After getting the vector results, we use the KNN classifier with k = 3 to classify the nodes. Since the variance of the classified data may be very high, we repeat the process 10 times and average the Macro-F1 and Micro-F1 The value is filled in the table. From the comparison of information in Tab. 2, it can be seen that in general, the method based on graph neural network combines structure and feature information, such as GCN, and usually performs better. For the traditional heterogeneous graph embedding method, compared with Deepwalk [5], metapath2vec [4] successfully captures rich semantics and shows its superiority. On different data sets, the result values obtained by different models are usually quite different. For example, on the DBLP data set, the importance of the metapath of APCPA is much greater than that of other metapaths, which leads to the random walk of the Deepwalk model [5]. The index of walking is greatly reduced. On the IMDB data set, the relationship between directors, movies and actors is very general, so it is difficult to learn from the graph convolutional neural network, which causes the GCN index on IMDB to be compared with the other two A model based on metapath random walk is much worse.
4.5 Cross-domain Learning Research
To create a cross-domain scenario, we used the method of removing different proportions of edges in the data set to create different domains for testing. Use the model that has been trained on the complete data set above to embed the network of the new domain on different domains, and then classify the results obtained according to the above processing method. Taking the index with a training ratio of 0.5 to represent the effect data of each domain, the comparison result can be converted into a line graph as Fig. 5.
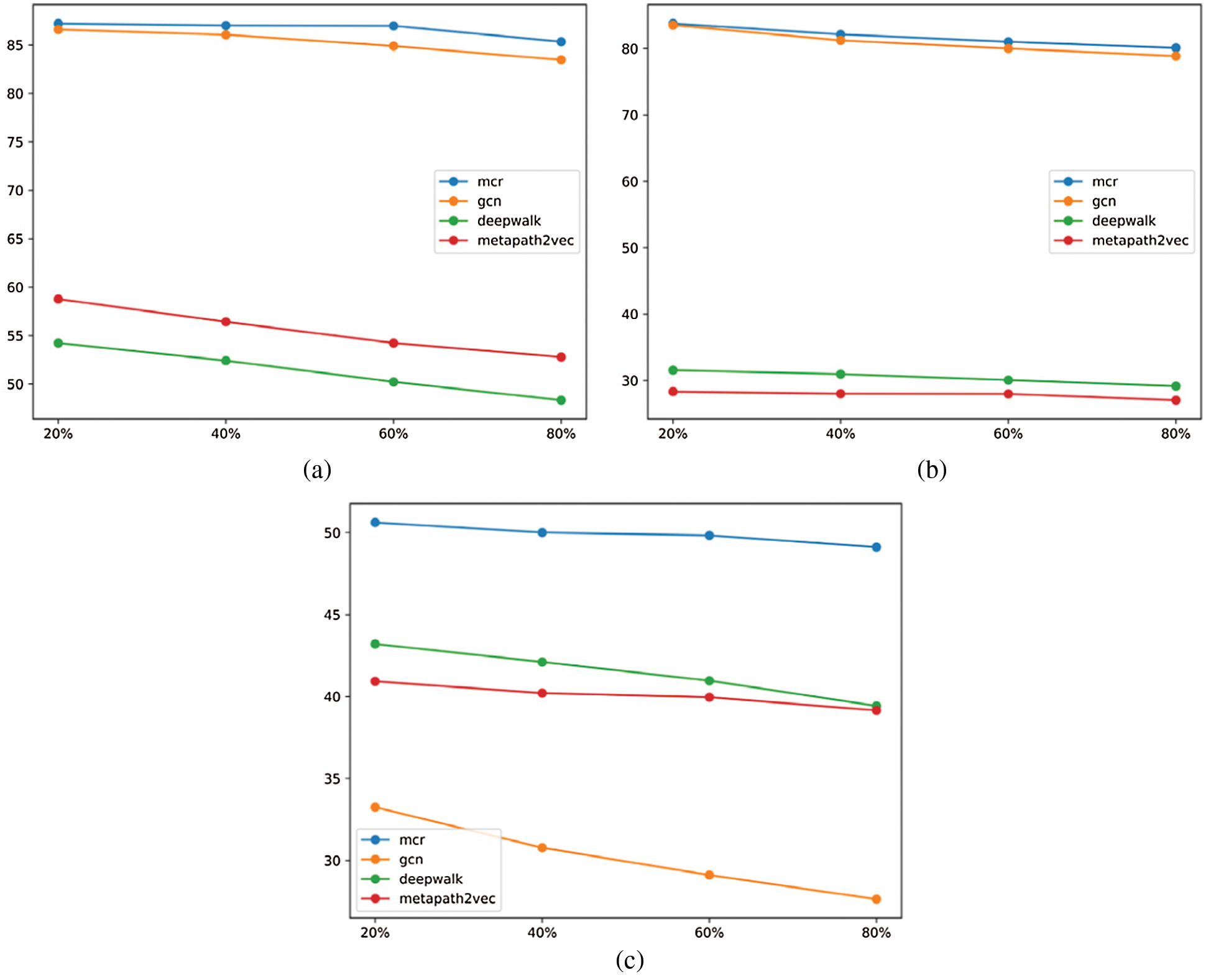
Figure 5: Comparison of cross-domain indicators of each model (a) ACM, (b) DBLP, (c) IMDB
Through the analysis of Figs. 4 and 5, we can easily see that the index of classification decreases as the proportion of edges removed in the graph increases, and the proportion of edges removed is proportional to the difference between domains. Therefore, the greater the difference between domains, the worse the index. Compared with Deepwalk [5] and metapath2vec [4], GCN performs relatively well in cross-domain problems on the ACM dataset, but the performance of cross-domain problems on the two datasets of DBLP and IMDB is very bad, and metapath2vec [4] and Deepwalk [5] performed well on the cross-domain issues of the IMDB and DBLP data sets, respectively.
As for the MCR model after our fusion, the indicators on each data set are not the best one. For example, the indicators for cross-domain issues on the ACM data set are not as good as GCN and the cross-domain on the DBLP data set. The index of the problem is not as good as Deepwalk [5], and the index of cross-domain problems on the IMDB data set is not as good as metapath2vec [4], but overall, the index of MCR is the one with the smallest difference from the original domain. This proves that our proposed MCR model, which is the result of multi-network space fusion, can be used to solve cross-domain problems.
At present, when many network representation learning methods are proposed, they are only optimized for the features they are concerned about. For example, GCN focuses on how to gather neighbor information, and metapath2vec focuses on how to gather information of different relationships. However, when the content of its concern is missing or its characteristics are not obvious enough, its performance is not as expected. This paper studies several network embedding methods in the information network and uses a neural network with attention mechanism to fuse them and proposes a new semi-supervised neural network model MCR based on the attention mechanism. First, the model imitates metapath2vec [4] and uses node-level and semantic-level attention to learn the importance of nodes and meta-paths respectively. Then, the model combines GCN and uniformly uses structural information and feature information to prove the effectiveness of artificial neural networks. Sex. Finally, MCR is a network embedding model method that integrates a variety of different types and different fields, and it has proved its good cross-domain representation performance.
Acknowledgement: The authors are grateful to the anonymous referees for having carefully read earlier versions of the manuscript. Their valuable suggestions substantially improved the quality of exposition, shape, and content of the article.
Funding Statement: This work is supported by State Grid Shandong Electric Power Company Science and Technology Project Funding under Grant no. 520613200001, 520613180002, 62061318C002, Weihai Scientific Research and Innovation Fund (2020).
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. Li, G. Sun, H. He, Y. Jiang, R. Sui et al., “Gender forecast based on the information about people who violated traffic principle,” Journal of Internet of Things, vol. 2, no. 2, pp. 65–73, 2020. [Google Scholar]
2. C. Li, P. Liu, H. Yu, M. Ge, X. Yu et al., “Research on real-time high reliable network file distribution technology,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1739–1752, 2020. [Google Scholar]
3. T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” in Int. Conf. of Legal Regulators (ICLR) (Poster), San Juan, Puerto Rico, 2016. [Google Scholar]
4. Y. Dong, N. V. Chawla and A. Swami, “metapath2vec: Scalable representation learning for heterogeneous networks,” in 23rd ACM SIGKDD Int. Conf., Halifax, Canada, pp. 135–144, 2017. [Google Scholar]
5. B. Perozzi, R. Al-Rfou and S. Skiena, “Deepwalk: Online learning of social representations,” in 20th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, New York, USA, pp. 701–710, 2014. [Google Scholar]
6. D. Zhu, Y. Sun, H. Du, N. Cao, T. Baker et al., “HUNA: A method of hierarchical unsupervised network alignment for IoT,” IEEE Internet of Things Journal, vol. 8, no. 5, pp. 3201–3210, 2020. [Google Scholar]
7. J. Tang, M. Qu and M. Wang, “Line: Large-scale information network embedding,” in The World Wide Web Conf., Florence, Italy, pp. 1067–1077, 2015. [Google Scholar]
8. P. Cui, X. Wang, J. Pei and W. Zhu, “A survey on network embedding,” IEEE Transactions on Knowledge and Data Engineering, vol. 31, no. 5, pp. 833–852, 2019. [Google Scholar]
9. X. Wang, H. Ji and C. Shi, “Heterogeneous graph attention network,” in The World Wide Web Conf., San Francisco, CA, USA, pp. 2022–2032, 2019. [Google Scholar]
10. A. Bachir, I. M. Almanjahie and M. K. Attouch, “The k nearest neighbors estimator of the m-regression in functional statistics,” Computers Materials & Continua, vol. 65, no. 3, pp. 2049–2064, 2020. [Google Scholar]
11. D. Zhu, Y. Sun, X. Li, H. Du, R. Qu et al., “MINE: A method of multi-interaction heterogeneous information network embedding,” Computers Materials & Continua, vol. 63, no. 3, pp. 1343–1356, 2020. [Google Scholar]
12. T. Fu, W. Lee and Z. Lei, “HIN2Vec: Explore Metapaths in heterogeneous information networks for representation learning,” in ACM Int. Conf. on Information and Knowledge Management, Singapore, pp. 1797–1806, 2017. [Google Scholar]
13. C. Shi, B. B. Hu, X. Zhao and P. Yu, “Heterogeneous information network embedding for recommendation,” IEEE Transactions on Knowledge and Data Engineering, vol. 31, no. 2, pp. 357–370, 2018. [Google Scholar]
14. L. C. Sun, L. F. He, Z. P. Huang, B. K. Cao, C. Y. Xia et al., “Joint embedding of meta-path and meta-graph for heterogeneous information networks,” in IEEE Int. Conf. on Big Knowledge (ICBK), Singapore, pp. 131–138, 2018. [Google Scholar]
15. X. Fu, J. Zhang and Z. Meng, “Magnn: Metapath aggregated graph neural network for heterogeneous graph embedding,” in Proc. of the Web Conf., Taipei, Taiwan, pp. 2331–2341, 2020. [Google Scholar]
16. H. Ji, J. Zhu, X. Wang, C. Shi, B. Wang et al., “Who you would like to share with? A study of share recommendation in social e-commerce,” Proc. of the AAAI Conf. on Artificial Intelligence, Virtual Conference, vol. 35, 2021. [Google Scholar]
17. X. Wang, M. Zhu, D. Bo, P. Cui, C. Shi et al., “AM-GCN: Adaptive multi-channel graph convolutional networks,” in Proc. of the 26th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Virtual Event CA, USA, pp. 1243–1253, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |