DOI:10.32604/iasc.2022.024687

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.024687 |  |
| Article |
Improved Homomorphic Encryption with Optimal Key Generation Technique for VANETs
1Department of Computer Applications, Alagappa University, Karaikudi, 630004, Tamilnadu, India
2Department of Computer Science, Alagappa University Model Constituent College, Paramakkudi, 623707, Tamilnadu, India
*Corresponding Author: G. Tamilarasi. Email: prithvi6781@gmail.com
Received: 27 October 2021; Accepted: 09 December 2021
Abstract: In recent years, vehicle ad hoc networks (VANETs) have garnered considerable interest in the field of intelligent transportation systems (ITS) due to the added safety and preventive measures for drivers and passengers. Regardless of the benefits provided by VANET, it confronts various challenges, most notably in terms of user/message security and privacy. Due to the decentralised nature of VANET and its changeable topologies, it is difficult to detect rogue or malfunctioning nodes or users. Using an improved grasshopper optimization algorithm (IGOA-PHE) technique in VANETs, this research develops a new privacy-preserving partly homomorphic encryption with optimal key generation. The suggested IGOA-PHE approach is intended to provide privacy and security in VANETs. The proposed IGOA-PHE technique consists of two stages: an ElGamal public key cryptosystem (EGPKC) for PHE and an optimised key generation procedure based on IGOA. To enhance the security of the EGPKC approach, the keys are selected ideally utilising the IGOA. Additionally, the IGOA is derived by using Gaussian mutation (GM) and Levy flights ideas. The experimental investigation of the proposed IGOA-PHE approach is extensive. The resulting results demonstrated that the provided IGOA-PHE technique outperformed recent state-of-the-art methods.
Keywords: VANETs; security; privacy; homomorphic encryption; optimal key generation; levy flight; GOA
VANETs are being developed as a subset of Mobile Adhoc Network (MANET) applications [1,2]. VANET is being considered as a viable technology for intelligent transportation systems (ITS) [3]. Recently, several scientists working in the field of wireless mobile transmission have placed a premium on VANET. The purpose of VANET is to provide an inter-vehicle transmission and road side unit (RSU) to vehicles in order to improve road safety, local traffic flow, and road traffic performance by providing timely and reliable data to road customers [4]. In a VANET, vehicles serve as network nodes, as seen in Fig. 1. In a VANET, the OBU and RSU establish a link between themselves via dedicated short range communication (DSRC) via single/multi hop transmission [5]. VANET provides a variety of applications and services to the user, all of which are centred on infotainment, navigation assistance, and driver security [6].
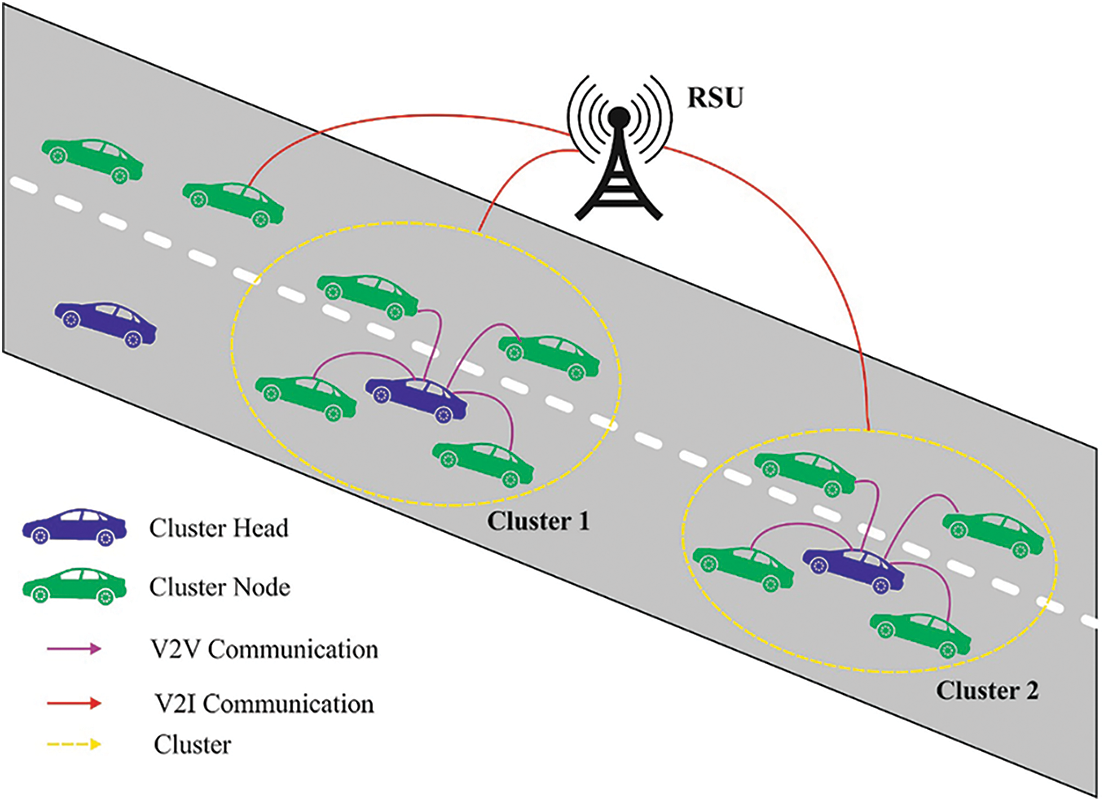
Figure 1: Structure of VANET
While interest in the major benefits of VANETs is growing, the dynamic nature of VANETs (vehicles may quit and rejoin willingly) combined with a plethora of scheme and application-related requirements makes establishing an efficient way to maintain vehicle privacy extremely challenging [7]. Privacy refers to the driver's (vehicle) privacy and the vehicle's position. If a vehicle transmits a message, nobody (save the proper authority) can deduce the vehicle's position/identity from the transmission. Simultaneously, the entire set of messages transmitted by the vehicle must be validated prior to processing. Until this issue is fixed to the user's satisfaction, significant VANET placement cannot be accomplished. Verification should occur on two levels: first at the node level, which corresponds to node verification, and then at the message level, which corresponds to message verification [8]. The fundamental standard of message authentication can be shortened by having the sender sign a message and then verifying the message's integrity and authenticity at the receiver end. Specific verification requirements such as scalable and robust authentication, effective and scalable certificate revocation, and reduced computation overhead should be addressed and handled in order to provide safe transmission in the VANET. Assuring the vehicle's (driver's) privacy is a significant issue that requires an appropriate solution; otherwise, an adversary can trace a vehicle's travelling route by analysing and collecting its message [9] and identify the vehicle (driver), which could have a detrimental impact on the drivers.
To address this issue, numerous scientists have proposed techniques in which vehicles can transmit under a pseudonym rather than their true identity, allowing authorities to retrieve the true identity from pseudonyms in order to penalise and trace mischievous vehicles [10]. This protocol is referred to as a privacy-preserving conditional protocol. Allocating pseudonyms to cars and changing them on a regular basis is another method of ensuring the vehicle's anonymity. To maximise privacy, cars should modify pseudonyms more frequently, however the frequency of these modifications is unknown. Features such as storage capacity and availability significantly influence the rate at which the pseudonym must be adjusted [11]. The majority of studies in the survey that address privacy, security, and authentication make use of TA to get and load OBU & RSU using security variables such as pseudonyms, keys, and certificates. Fig. 2 depicts the safe transfer of data in a VANET. Conventional methods for authenticating and securing message dissemination, which rely heavily on key management and message encryption, are capable of ensuring secure message exchange between destination pairs and known sources. This strategy cannot be directly used to VANETs due to their dynamic nature. The propagation of messages in a VANET may be vulnerable to insider attacks (i.e., attacks by valid VANET members), which may corrupt the substance of the message or transmit malicious messages. As a result, ensuring the validity and integrity of messages transmitted across VANET is a serious issue. In VANETs, this article proposes a new privacy-preserving partly homomorphic encryption strategy with optimal key generation based on an improved grasshopper optimization algorithm (IGOA-PHE). The suggested IGOA-PHE approach is intended to provide privacy and security in VANETs. The proposed IGOA-PHE technique consists of two stages: an ElGamal public key cryptosystem (EGPKC) for PHE and an optimised key generation procedure based on IGOA. To enhance the security of the EGPKC approach, keys are chosen ideally utilising the IGOA. Additionally, the IGOA is derived by adding Gaussian mutation and Levy flights ideas. To evaluate the proposed IGOA-PHE technique's security outcomes, a large number of simulations were run and the results examined using a variety of metrics.
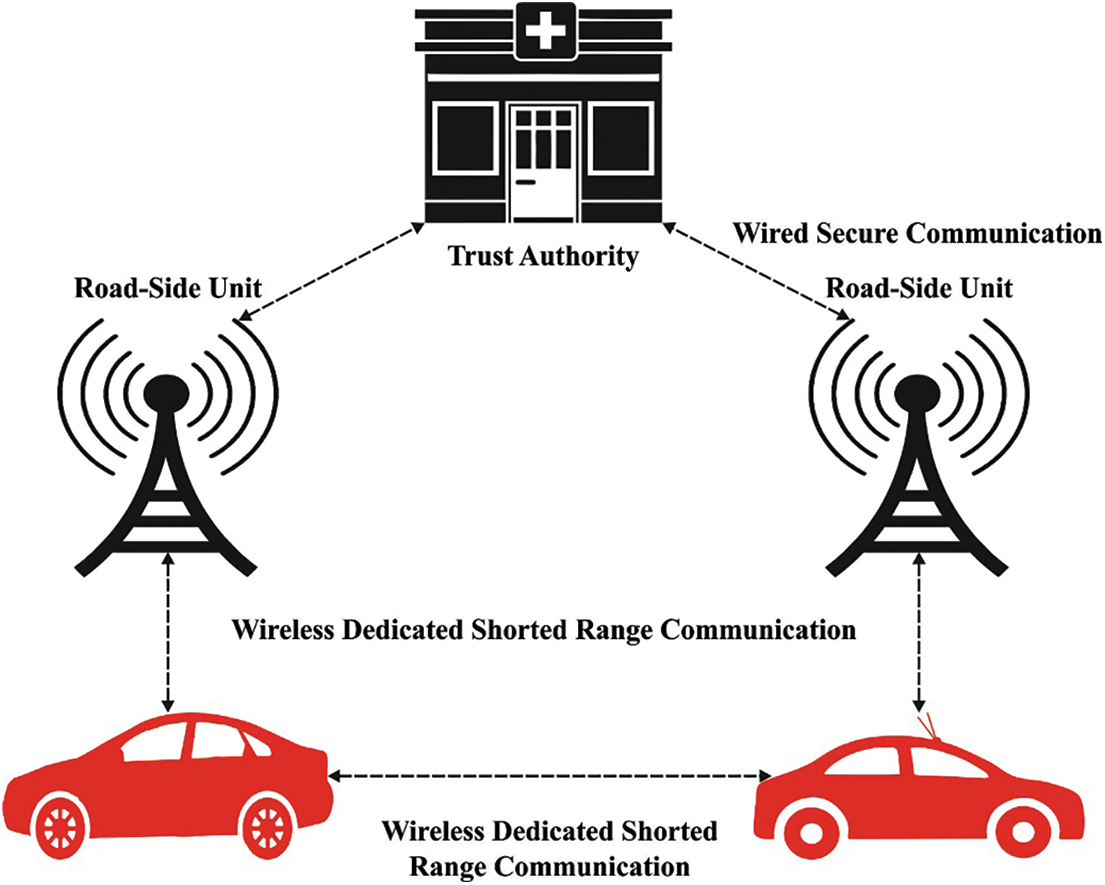
Figure 2: Secure data transmission in VANET
Al-Shareeda et al. [12] described a privacy-preserving communication scheme (VPPCS) based on the VANET that satisfies the criteria for contextual and content privacy. It makes use of elliptic curve cryptography (ECC) and a system of identity-based encryption. They conducted extensive security assessments on the proposed system (random oracle module, BAN logic, security attribute, and security of proof). The analyses demonstrated that this method is secure and also efficient when performing calculations. Cui et al. [13] suggested a data downloading method for VANET that is both effective and private, based on the edge computing architecture. In the proposed method, an RSU may detect shared data simply by inspecting the encrypted requests transmitted by neighbouring cars, without compromising the privacy of their downloaded request. Additionally, the RSU stores shared data in a near-qualified vehicle called an ECV. When a vehicle requires current data upload, it can do it immediately from the next ECV. This strategy improves the scheme's upload performance.
Alfadhli et al. [14] proposed a low-weighted multifactor authentication and privacy-preserving security solution for VANETs. Additionally, it eliminates the heavyweight reliance on the scheme key by decentralising the CA's broad region to local areas and achieving strong domain key management. Ali et al. [15] suggested an efficient ID-CPPA signature system for V2I transmission based on a bilinear map. This increases the efficacy of the RSU's operation by signing and authenticating messages. Additionally, this ID CPPA signature system provides batch signature authentication, which reduces the computational burden on the RSU and enables it to authenticate a large volume of traffic-related messages in a high-traffic area.
Wang et al. [16] suggested a novel anonymous authentication mechanism based on identification. The system's master key will not be configured directly in TPD in this system. Additional secrecy is required to generate the vehicle's private key, which is provided via RSU. Thus, revoking a malicious vehicle in the VANET is effective, and the RSU should discontinue the car's present privacy. Additionally, the signature authentication approach does not require bilinear pairing, resulting in a highly effective authentication procedure. Wang et al. [17] suggested a hybrid CPPA protocol that relies on both public key infrastructure certificates and identity-based signatures. The TA assigns an exclusive long-term certificate to each of the mentioned nodes in this system approach. Vehicles with valid certificates could use the present RSU's anonymous short term identity to sign security-related messages. Identity-based signatures obviate the need for CRL verification and complex bilinear parsing processes. Moni et al. [18] suggested a privacy-preserving authentication system for VANET that is scalable, distributed, and has a minimal overhead. This approach authenticates RSUs using MHT and verifies cars using MMPT. Benarous et al. [19] provide a novel privacy-preserving approach for pseudonym on-road on-demand replenishment, in which the vehicle authenticates itself anonymously to the local authority subsidiaries of the central trusted authority in order to seek a novel pseudonyms pool. This technique entails a challenge-based authentication process and the creation of an anonymous ticket. Al-shareeda et al. [20] introduced an identity-based CPPA system that enables concurrent authentication of several messages with each node via a batch authentication technique. Section 2 describes the literature survey in the field privacy preserving homomorphic encryption, Section 3 deals with the proposed technique called IGOA-PHE, Section 4 elaborates the results and discussion and final section 5 describes the conclusion and future work.
3 The Proposed IGOA-PHE Technique
The overall working principle involved in the proposed IGOA-PHE technique is here. It is stated that the IGOA-PHE technique follows a 2-stage process namely EGPKC for PHE and IGOA based optimal key generation process. These processes are neatly elaborated in the following subsections.
Generally, it is stated in 1985 using discrete method cause problems to constrained areas (partial HE technique). It has key decryption, generation, and encryption operations. Usually, this technique has private key (an arbitrary amount)
Most of this technique takes an equivalent ciphertext by selecting a plaintexts attack for every probabilistic polynomial time adversaries Ai. Also, the message encrypting arbitrarily in two different messages assured by Ai, to identify the elected message is increased to random resolving. For considering, the ElGamal cryptosystem is determined by the game module with the challenger Ci and opponent Ai.
• Initially, Ai elects two separate messages as mi0, mi1 ∈ Gi1 and forward it to Ci′.
• After, this technique calculates Ci′ elects ai ∈ {0, 1} and ri1,
• The calculated challenge Ci′ analyses Ai on ai.
• For calculating a guess as Ai provides ai′ and forward it return to Ci′.
Now, Ai becomes a success when ai′ = ai otherwise fails.
In Above mentioned game, consider Ai recognizes
In Eq. (2), Pi denotes success possibility and negl represent trivial improvement. Eventually, the ciphertext along with an optimum private key is revealed in MAC.
Generally, the MAC frames are modelled to maintain minimal sophisticated form by a sufficient strength for declaring stable transmission on the noisy channel. Also, each successive protocol layer is added to the frame from layer specific footers & headers. The MAC structure has four frames.
• Initially, the beacon frame, employed with the coordinator to transfer beacons.
• In 2nd, the data frame, utilized to broadcast the whole data.
• In 3rd, the acknowledgment is used for assuring the efficient frame is delivered.
• Laslty, the MAC command frame is utilized for managing the whole MAC peer entity control transmissions.
Now, the data frames transmit the MAC payload and aforementioned procedure is finished in the data frame. MAC payload executes the ciphertext with corresponding transmissions and private keys. On the recipient side, an equal decoder process takes place and eventually, attains the original data.
3.2 Design of IGOA for Optimal Key Generation
The private key in ElGamal cryptosystem is enhanced to accomplish the accurate ciphertext. A novel technique is developed; where it is implemented to create the ciphertext using numerical values. In general, the proposed ciphertext has numbers (1, 2, 3. . .), alphabets (a, A, b, D, …) and special characters
Grasshopper is deliberated as pest depending upon the loss they impose on vegetation and crops. In place of performing separately, grasshopper creates few biggest swarms amongst all living beings. The impact of an individual in a wind, swarm, food source, and gravity affects swarm motion. The GOA is a new SI based metaheuristic method that is stimulated using longer range and sudden movement of adult grasshoppers in a group. Metaheuristic algorithm reasonably separates the search procedure as to exploitation & exploration phases. The longer range and sudden motions of the grasshopper denote exploration stage, and local motions for searching for an optimal food source represent exploitation stage. A numerical module for this behavior is given in Mirjalili [21] can be denoted as:
Whereas xi denotes location of i grasshopper, Si indicates social interaction in a group, G represents force of gravity performing on i grasshopper, and A signifies wind direction. By extending Si, G & A in (1), the formula is given by:
Whereas s(r) = fe−r/l − e−r denotes function stimulate the influence of social interaction and N represents amount of grasshopper.
Since grasshoppers rapidly detect comfortable zone and show poor convergence, the impacts of wind and gravity are far weaker compared to the relationship among grasshoppers, means numerical module must be altered by:
Whereas ub & lb represents upper & lower boundaries of the search space, Td indicates value comparative to the target (optimal solution establish until now), and c denotes reducing coefficient which balance the process of explorations & exploitations can be denoted by:
Whereas cmax denotes maximal value (equivalent to one), cmin represents minimal value (equivalent to 0.00001), iter indicates present iteration, and Maxiter signifies maximal amount of iterations.

Fig. 3 demonstrates the flowchart of GOA. In IGOA, to confront the drawback of fundamental GOA, GM and Levy flight are presented to GOA for keeping an appropriate balance among the exploitation & exploration. The GM function was derived from Gaussian normal distribution and thier applications to evolution search [23]. This concept was represented by classical evolutionary programming (CEP). It is highly possible for creating a novel offspring nearby the original parent due to its narrow tail. Because of this, the search formula would take small steps permitting all the corners of the search space to be examined well [24–26]. Henceforth it is predictable for providing comparatively fast convergence. The Gaussian density operation can be denoted as:
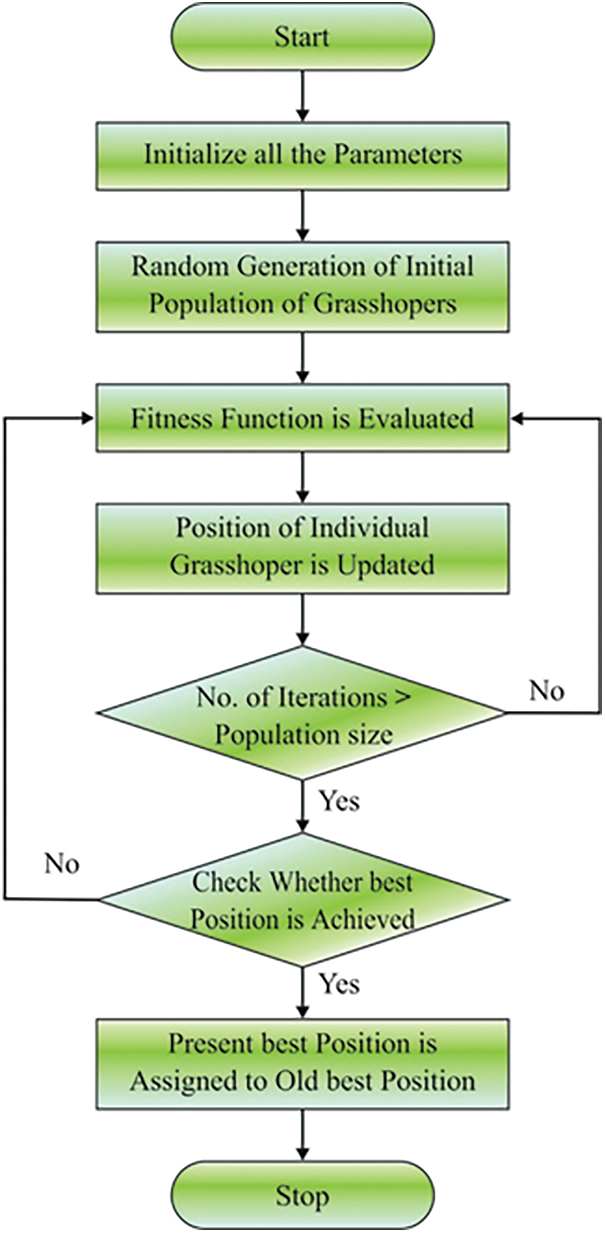
Figure 3: Flowchart of GOA
Whereas σ2 denotes difference for every member of the population. This operation is additionally decreased for generating a single n-dimension arbitrary parameter by locating the mean value to 0 and SD to one. The arbitrary parameter created is employed for the common formula of metaheuristic method can be denoted by
where G(α) denotes Gaussian step vector made by Gaussian density function using α as Gaussian arbitrary amount among zero and one.
LF was initially presented by the French mathematician in 1937 called Paul Levy. A varied kind of natural and artificial phenomena are defined based on Levy statistics. The LF is a well-regarded class of stochastic non Gaussian walks that step length value must be distributed regarding Levy stable distribution. It is obtained as:
β denotes significant Levy index for adjusting the stability. The Levy arbitrary amount is estimated using:
Whereas μ & v denotes regular distribution, Γ represents normal Gamma function, β = 1.5, & φ is given by:
For obtaining a tradeoff among the exploitation and exploration abilities of metaheuristic method, LF method is utilized for updating search agent location that can be given by:
where
As mentioned, the range of search agents is critical for metaheuristic method, since diversity provides the population a robust search ability to global optimal. In IGOA, GM method has been applied for increasing the range of GOA population. The altered numerical module is introduced by:
Afterward the location of ith grasshopper Xi is upgraded, Levy flight method would be adapted for generating a novel candidate solution that can be given by:
whereas
Authors are required to adhere to this Microsoft Word template in preparing their manuscripts for submission. It will speed up the review and typesetting process. This section validates the performance of the proposed IGOA-PHE technique with other techniques in terms of different measures.
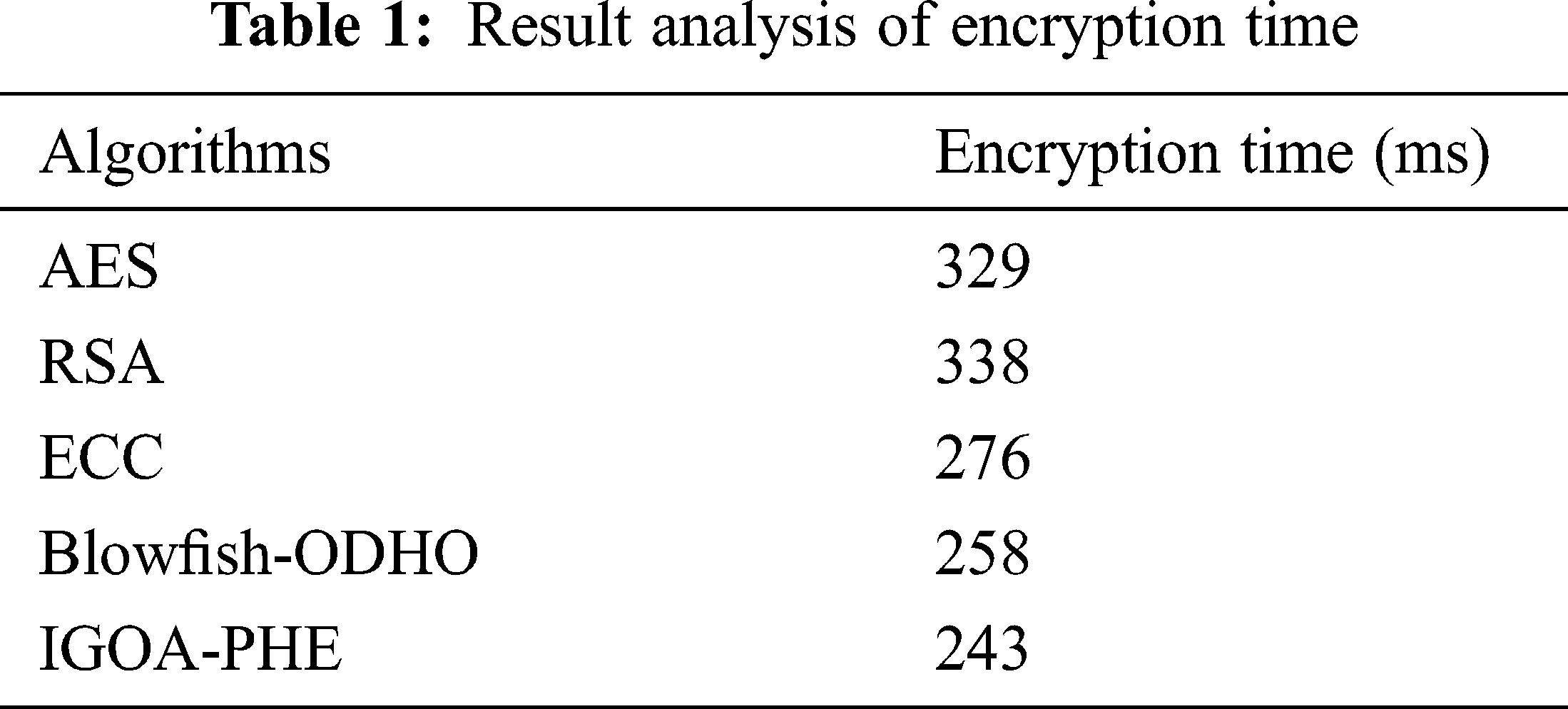
Tab. 1 and Fig. 4 investigates the encryption time analysis of the IGOA-PHE technique with other encryption algorithms. The experimental outcomes demonstrated that the AES and RSA techniques have accomplished poor outcomes with the higher encryption time of 329 and 338 ms. At the same time, the ECC and Blowfish-ODHO techniques have gained slightly reduced encryption time of 276 and 258 ms respectively. But the IGOA-PHE technique has required a minimum encryption time of 243 ms. Key similarity analysis of the proposed IGOA-PHE technique with other encryption algorithms under different attacks is provided in Tab. 2 and Fig. 5. The resultant values demonstrated that the IGOA-PHE technique has showcased effective outcomes under all different types of attacks. Under the presence of DoS attack, the IGOA-PHE technique has accomplished a lower key similarity of 11.06% whereas the AES, RSA, ECC, and Blowfish-ODHO techniques have obtained a higher key similarity of 25.58%, 22.54%, 19.35%, and 12.21% respectively.
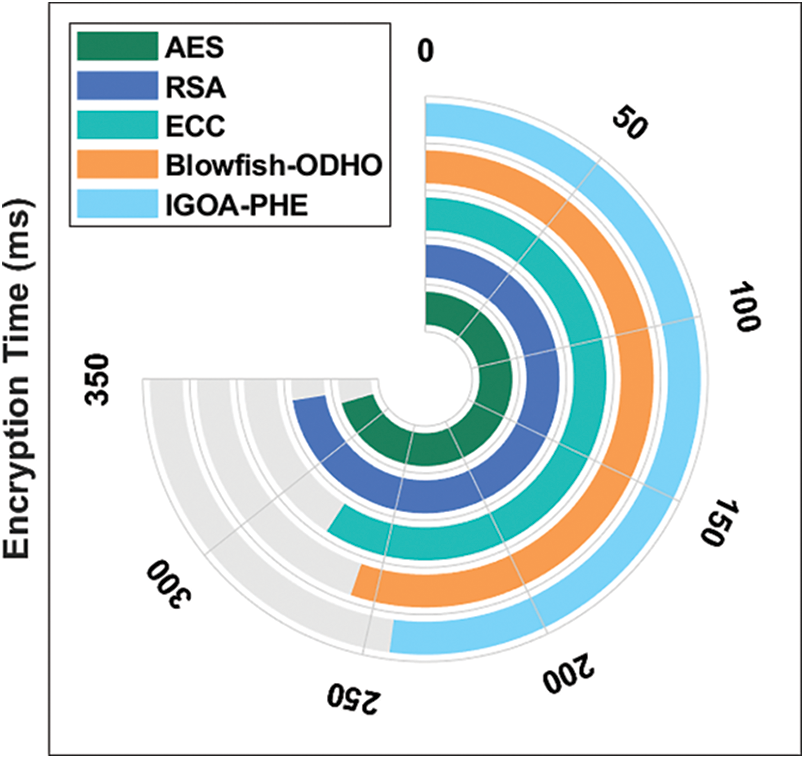
Figure 4: Encryption time analysis of IGOA-PHE model
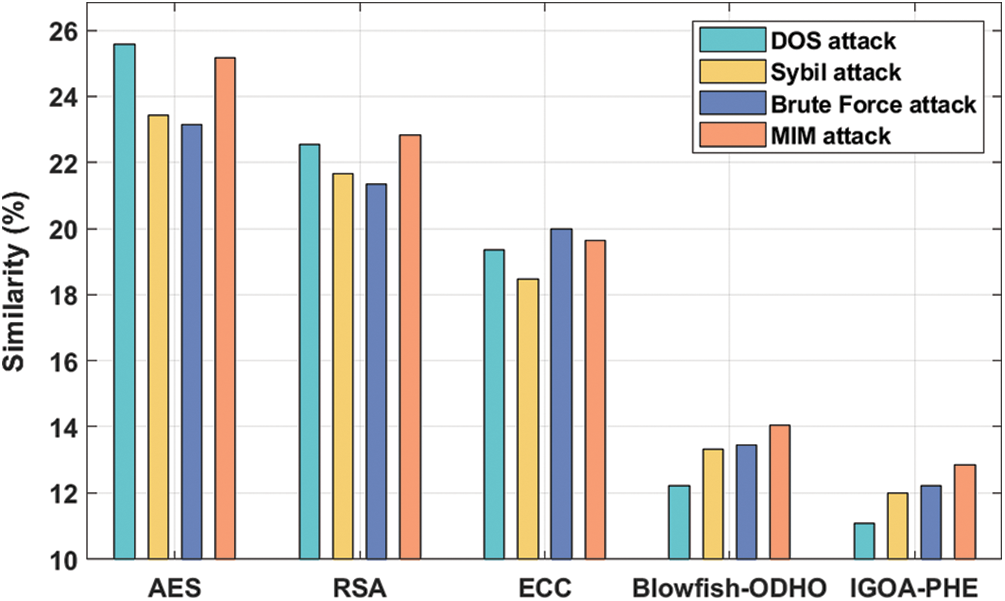
Figure 5: Similarity analysis of IGOA-PHE model
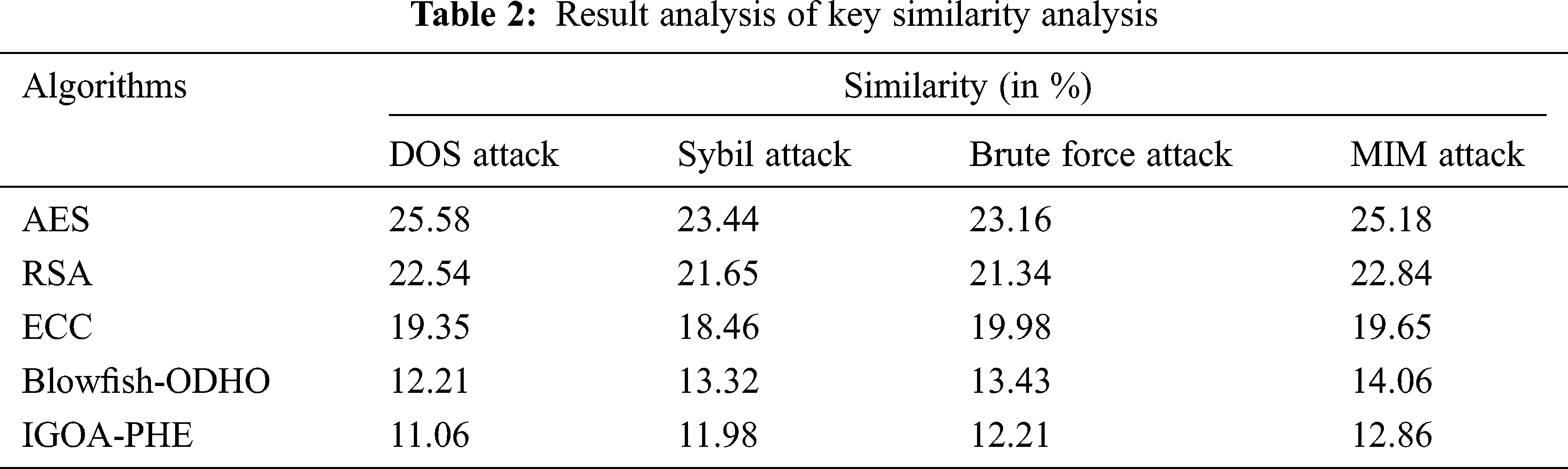
In addition, under the presence of Sybil attack, the IGOA-PHE approach has accomplished a lesser key similarity of 11.98% whereas the AES, RSA, ECC, and Blowfish-ODHO methods have gained a maximum key similarity of 23.44%, 21.65%, 18.46%, and 13.32% correspondingly. Eventually, under the presence of Brute force attack, the IGOA-PHE manner has accomplished a minimum key similarity of 12.21% whereas the AES, RSA, ECC, and Blowfish-ODHO algorithms have obtained a higher key similarity of 23.16%, 22.34%, 19.98%, and 13.43% correspondingly. Meanwhile, under the presence of MIM attack, the IGOA-PHE technique has accomplished a minimal key similarity of 12.86% whereas the AES, RSA, ECC, and Blowfish-ODHO methodologies have attained a superior key similarity of 25.18%, 22.84%, 19.65%, and 14.06% correspondingly.
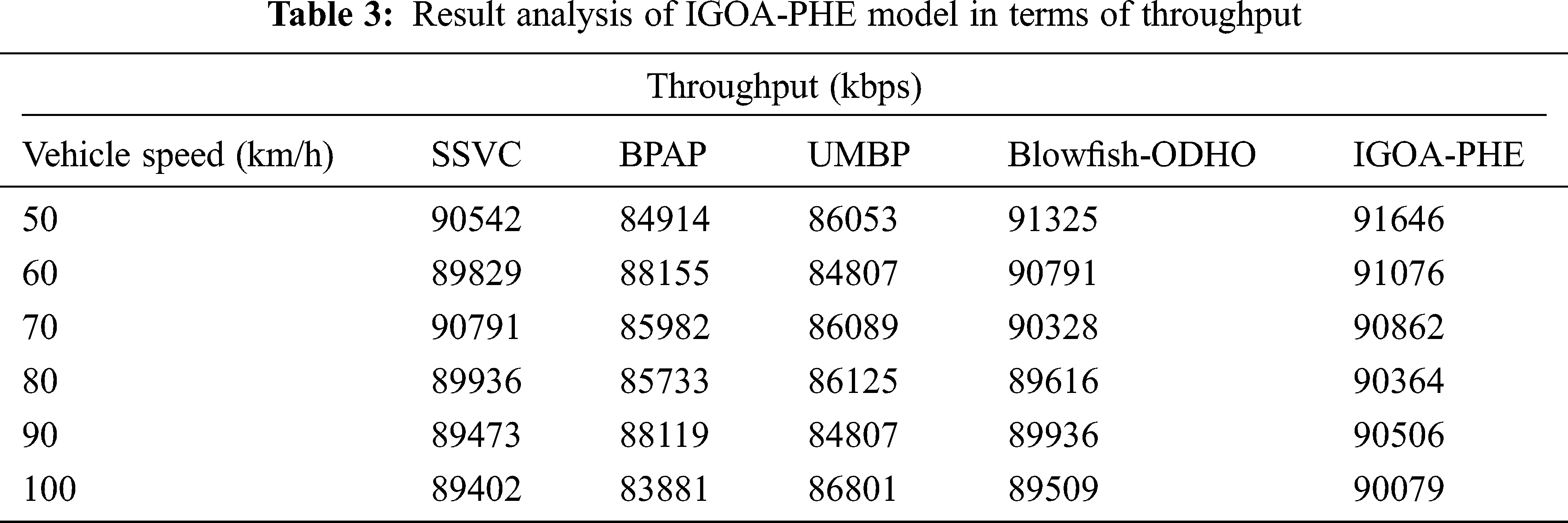
Tab. 3 and Fig. 6 portrays the throughput analysis of the proposed IGOA-PHE technique under varying vehicle speed. The experimental results showcased that the IGOA-PHE technique has gained effective outcome over the other techniques with the maximum throughput values. For instance, under the vehicle speed of 50 km/h, the IGOA-PHE technique has achieved a higher throughput of 91646 kbps whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have attained a reduced throughput of 90542, 84914, 86053, and 91325 kbps respectively. Besides, under the vehicle speed of 70 km/h, the IGOA-PHE approach has attained a superior throughput of 90862 kbps whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO manners have gained a lower throughput of 90791, 85982, 86089, and 90328 kbps correspondingly. Moreover, under the vehicle speed of 100 km/h, the IGOA-PHE method has achieved a superior throughput of 90079 kbps whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO approaches have obtained a minimum throughput of 89402, 83881, 86801, and 89509 kbps correspondingly.
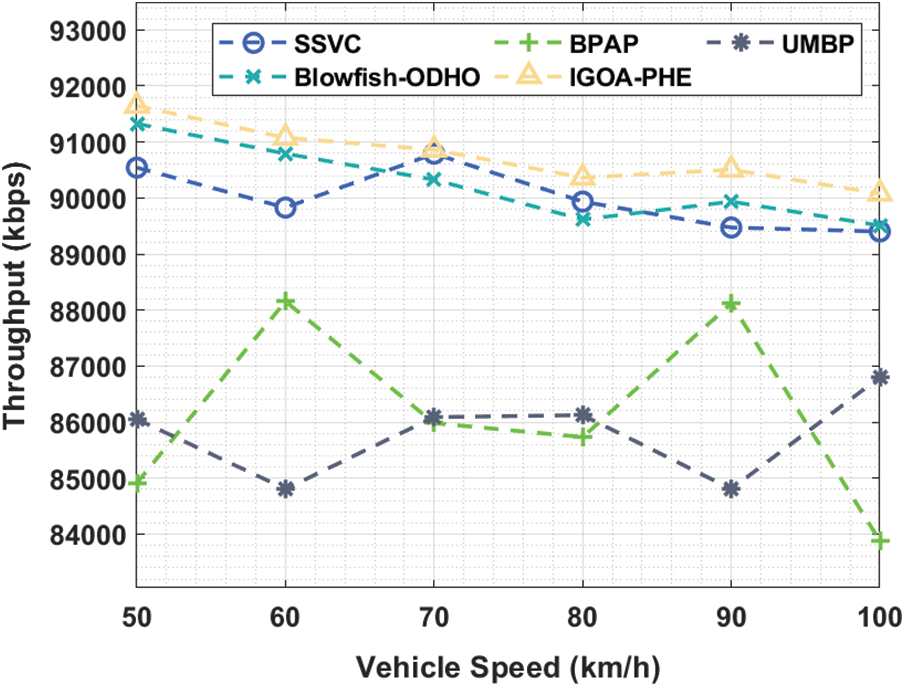
Figure 6: Throughput analysis of IGOA-PHE model
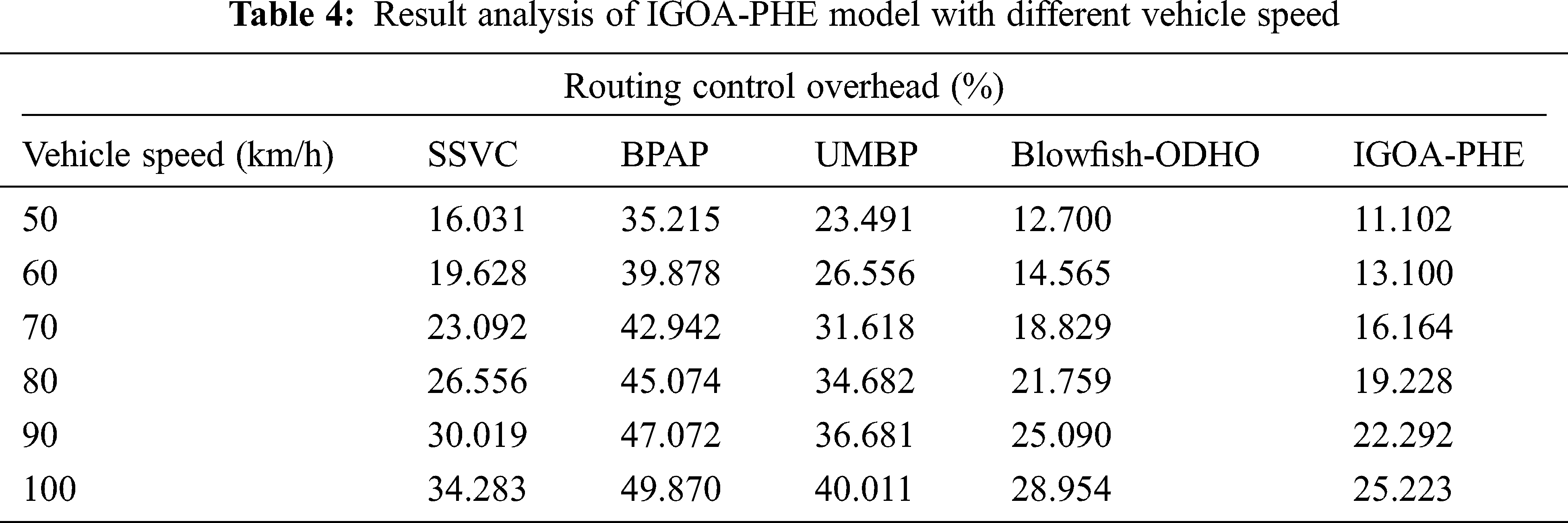
Tab. 4 and Fig. 7 demonstrates the RCO analysis of the IGOA-PHE technique over the other methods under different vehicle speed. The experimental results highlighted that the IGOA-PHE technique has accomplished superior results with the lower RCO under distinct vehicle speed. For instance, with the vehicle speed of 50 km/hr, the IGOA-PHE technique has showcased a lower RCO of 11.102% whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have obtained a higher RCO of 16.031%, 35.215%, 23.491%, and 12.700% respectively. Additionally, with the vehicle speed of 70 km/hr, the IGOA-PHE method has outperformed a minimal RCO of 16.164% whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO manners have achieved a maximal RCO of 23.092%, 42.942%, 31.618%, and 18.829% correspondingly. Concurrently, with the vehicle speed of 100 km/hr, the IGOA-PHE technique has demonstrated a lesser RCO of 25.223% whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO methodologies have attained a superior RCO of 34.283%, 49.870%, 40.011%, and 28.954% correspondingly.
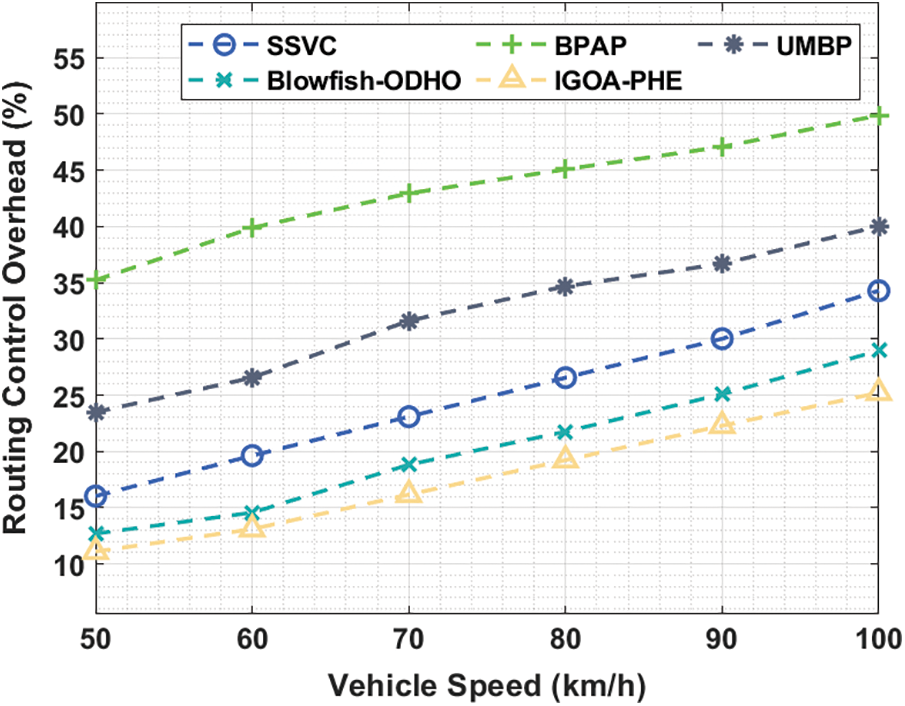
Figure 7: Routing control overhead analysis of IGOA-PHE model
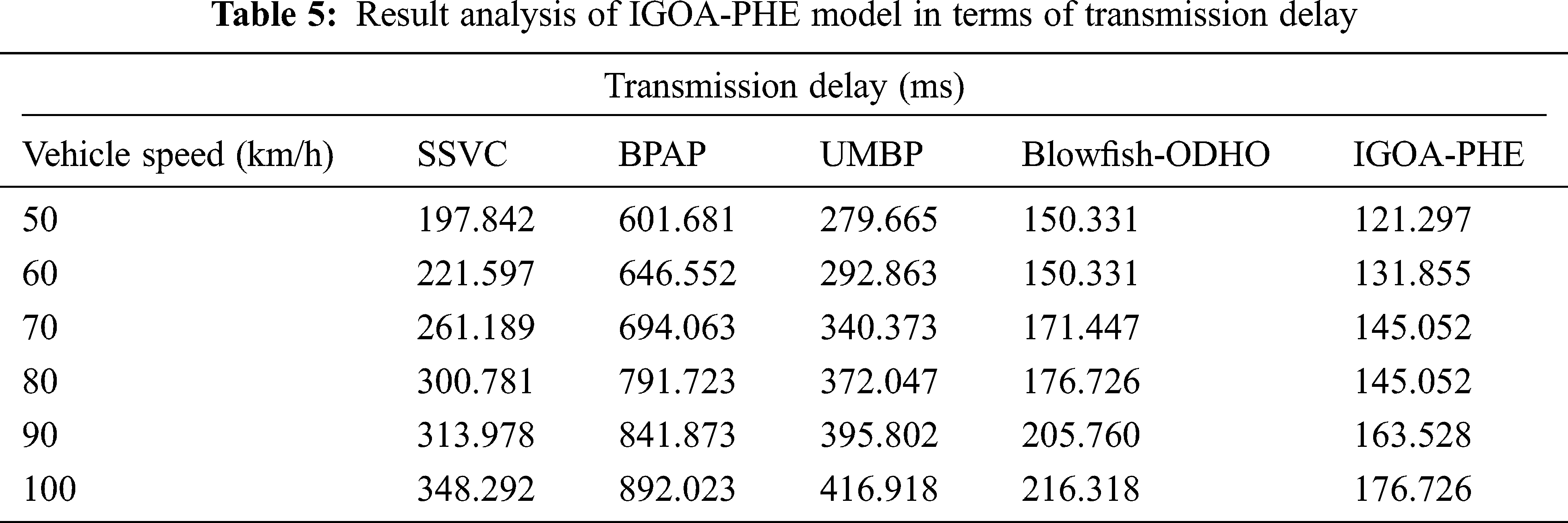
Tab. 5 and Fig. 8 showcase the transmission delay analysis of the IGOA-PHE approach over the other techniques under various vehicle speeds. The experimental outcomes exhibited that the IGOA-PHE method has accomplished maximal results with the lesser transmission delay under various vehicle speeds. For sample, with the vehicle speed of 50 km/hr, the IGOA-PHE algorithm has depicted a lower transmission delay of 121.297 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO methodologies have attained a superior transmission delay of 197.842, 601.681, 279.665, and 150.331 ms correspondingly. Also, with the vehicle speed of 70 km/hr, the IGOA-PHE manner has demonstrated a lower transmission delay of 145.052 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have obtained a maximum transmission delay of 261.189, 694.063, 340.373, and 171.447 ms respectively. Simultaneously, with the vehicle speed of 100 km/hr, the IGOA-PHE methodology has showcased a lower transmission delay of 176.726 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have obtained a superior transmission delay of 348.292, 892.023, 416.918, and 216.318 ms correspondingly.
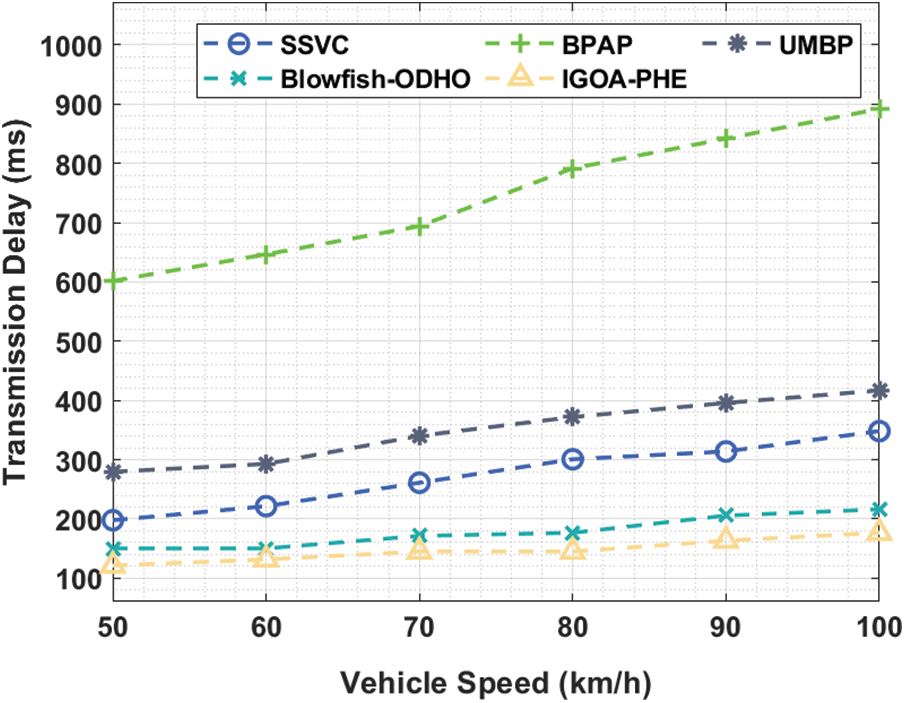
Figure 8: Transmission delay analysis of IGOA-PHE model
Tab. 6 and Fig. 9 exhibits the KCT analysis of the IGOA-PHE approach over the other algorithms under distinct key sizes. The experimental results highlighted that the IGOA-PHE technique has accomplished superior results with the lower KCT under distinct key size. For instance, with the key size of 64bits, the IGOA-PHE technique has showcased a lower KCT of 1111.06 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have attained a higher KCT of 1975.19, 2787.27, 2995.50, and 1267.23 ms correspondingly. Moreover, with the key size of 256 bits, the IGOA-PHE scheme has showcased a minimum KCT of 1506.69 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have gained a higher KCT of 2662.34, 3495.24, 3870.04, and 1694.09 ms correspondingly. At the same time, with the key size of 512 bits, the IGOA-PHE manner has outperformed a lower KCT of 1714.91 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO methodologies have obtained a maximum KCT of 2974.68, 3849.22, 4182.38, and 1975.19 ms respectively.
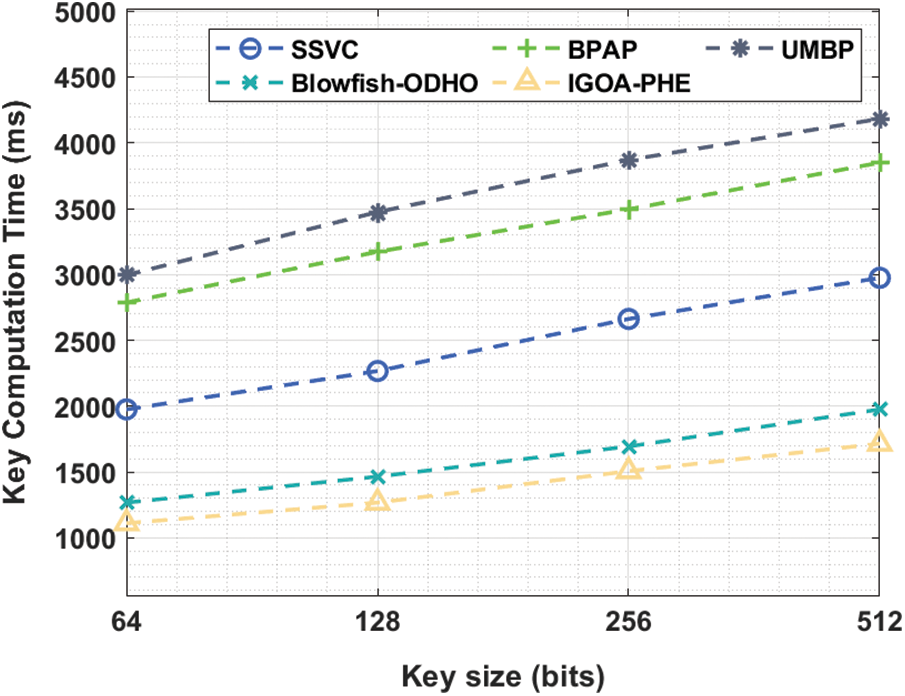
Figure 9: Key computation time analysis of IGOA-PHE model
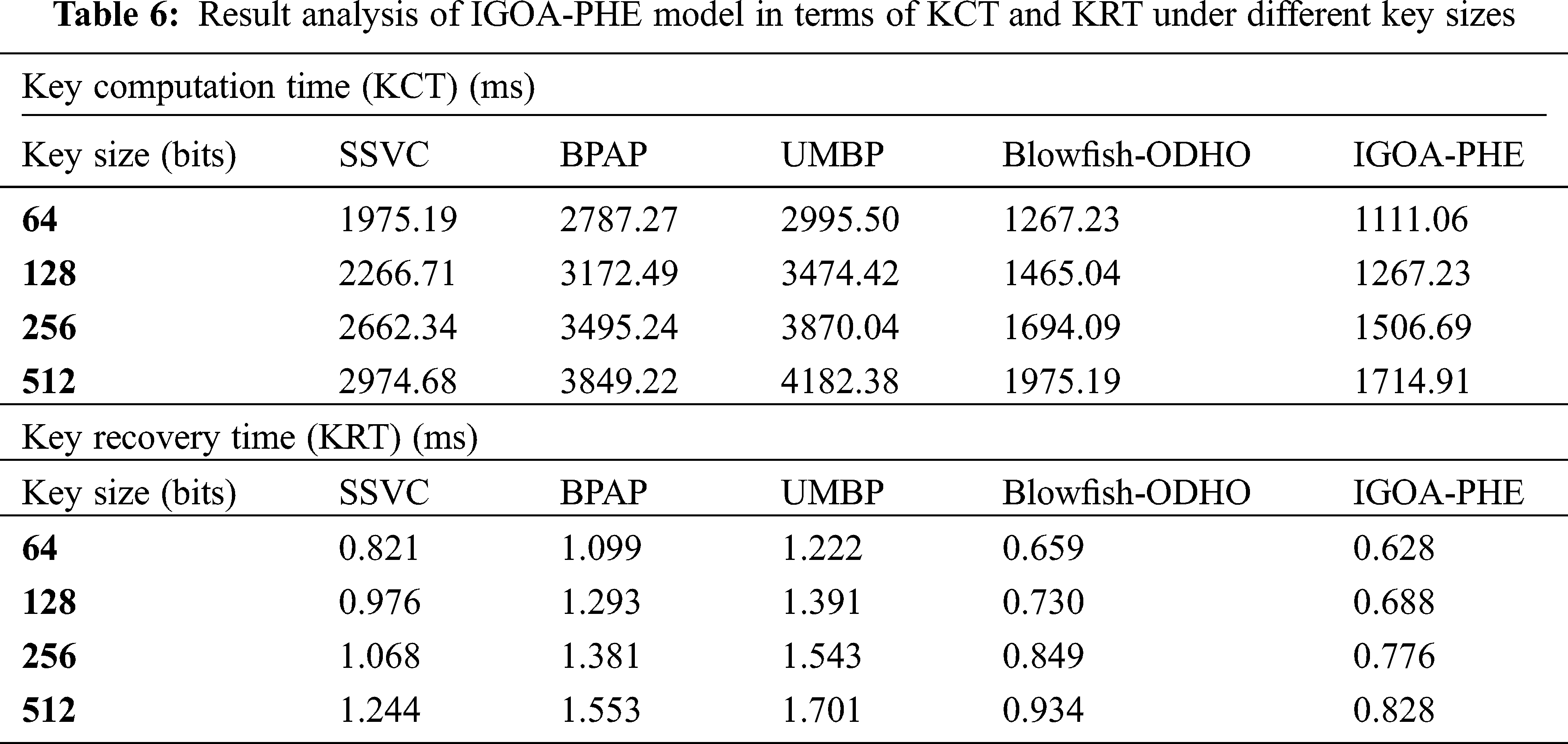
Fig. 10 defines the KRT analysis of the IGOA-PHE approach over the other techniques under distinct key size. The experimental outcomes outperformed that the IGOA-PHE technique has accomplished maximum results with the lower KRT under distinct key size.
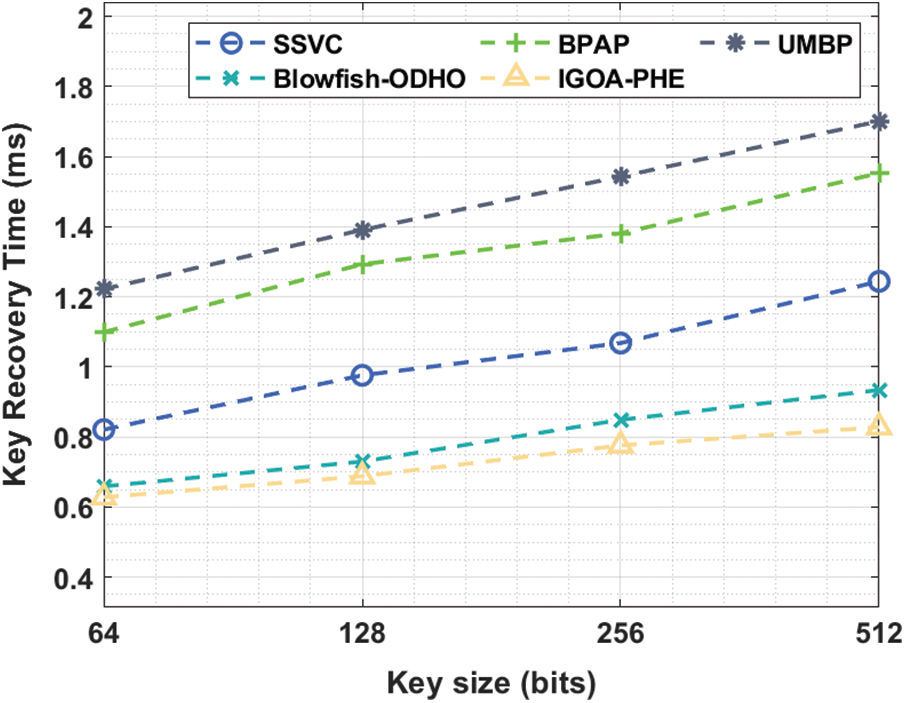
Figure 10: Key recovery time analysis of IGOA-PHE model
For instance, with the key size of 640 bits, the IGOA-PHE technique has showcased a lower KRT of 0.628 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have gained a superior KRT of 0.821, 1.099, 1.222, and 0.659 ms respectively. Additionally, with the key size of 256 bits, the IGOA-PHE method has exhibited a lower KRT of 0.776 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO techniques have obtained a higher KRT of 1.068, 1.381, 1.543, and 0.849 ms correspondingly. Concurrently, with the key size of 512bits, the IGOA-PHE algorithm has demonstrated a lower KRT of 0.828 ms whereas the SSVC, BPAP, UMBP, and Blowfish-ODHO approaches have gained a superior KRT of 1.244, 1.553, 1.701, and 0.934 ms correspondingly.
The purpose of this study is to present a novel IGOA-PHE technique for achieving privacy and security in VANETs. The suggested model begins by encrypting data using the EGPKC technique. Additionally, the IGOA is used to optimise the key selection for the EGPKC approach with the goal of enhancing security performance. The inclusion of Gaussian mutation and Levy flights into the design of IGOA significantly improves the outcomes of the standard IGOA. To evaluate the proposed IGOA-PHE technique's security outcomes, a large number of simulations were run and the results examined using a variety of metrics. The experimental results demonstrated that the IGOA-PHE technique outperformed recent state-of-the-art procedures in a variety of ways. In the future, data aggregation techniques based on steganography can be used to improve network performance and overall security.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. S. Khan, K. Balan, Y. Javed, S. Tarmizi and J. Abdullah, “Secure trust-based blockchain architecture to prevent attacks in VANET,” Sensors, vol. 19, no. 22, pp. 1–27, 2019. [Google Scholar]
2. M. R. Ghori, K. Z. Zamli, N. Quosthoni, M. Hisyam and M. Montaser, “Vehicular ad-hoc network (VANETReview,” in Proc. of the 2018 IEEE Int. Conf. on Innovative Research and Development (ICIRD), Bangkok, Thailand, pp. 1–6, 2018. [Google Scholar]
3. S. Gillani, F. Shahzad, A. Qayyum and R. Mehmood, “A survey on security in vehicular ad hoc networks,” in Communication Technologies for Vehicles, Nets4Cars/Nets4Trains 2013, Heidelberg/Berlin, Germany: Springer, pp. 59–74, 2013. [Google Scholar]
4. I. A. Abbasi and A. S. Khan, “A review of vehicle-to-vehicle communication protocols for VANETs in the urban environment,” Future Internet, vol. 10, no. 14, pp. 1–18, 2018. [Google Scholar]
5. N. Malik, P. Nanda, A. Arora, X. He and D. Puthal, “Blockchain based secured identity authentication and expeditious revocation framework for vehicular networks,” in Proc. of the 2018 17th IEEE Int. Conf. on Trust, Security and Privacy in Computing and Communications/12th IEEE Int. Conf. on Big Data Science and Engineering, New York, NY, USA, pp. 674–679, 2018. [Google Scholar]
6. S. Zeadally, R. Hunt, Y. S. Chen, A. Irwin and A. Hassan, “Vehicular ad hoc networks (VANETSStatus, results, and challenges,” Telecommunication Systems, vol. 50, pp. 217–241, 2012. [Google Scholar]
7. B. Alaya and L. Sellami, “Clustering method and symmetric/asymmetric cryptography scheme adapted to securing urban VANET networks,” Journal of Information Security and Applications, vol. 58, pp. 1–8, 2021. [Google Scholar]
8. S. K. Bhoi, P. M. Khillar, M. Singh, M. M. Sahoo and R. R. Swain, “A routing protocol for urban vehicular ad hoc networks to support non-safety applications,” Digital Communications Networks, vol. 4, pp. 189–199, 2018. [Google Scholar]
9. S. Zeadally, R. Hunt, Y. S. Chen, A. Irwin and A. Hassan, “Vehicular ad hoc networks (VANETSStatus, results, and challenges,” Telecommunication System, vol. 50, pp. 217–241, 2012. [Google Scholar]
10. R. Begum, S. Raziuddin and V. K. Prasad, “A survey on VANETs applications and its challenges,” in Proc. of the Int. Conf. on Advanced Computer Science & Software Engineering, Hyderabad, India, pp. 1–12, 2016. [Google Scholar]
11. R. G. Engoulou, M. Bellaïche, S. Pierre and A. Quintero, “VANET security surveys,” Computer Communications, vol. 44, pp. 1–13, 2014. [Google Scholar]
12. M. A. Al-Shareeda, M. Anbar, S. Manickam and A. A. Yassin, “Vppcs: Vanet-based privacy-preserving communication scheme,” IEEE Access, vol. 8, pp. 150914–150928, 2020. [Google Scholar]
13. J. Cui, L. Wei, H. Zhong, J. Zhang, Y. Xu et al., “Edge computing in VANETs-an efficient and privacy-preserving cooperative downloading scheme,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 6, pp. 1191–1204, 2020. [Google Scholar]
14. S. A. Alfadhli, S. Lu, K. Chen and M. Sebai, “Mfspv: A multi-factor secured and lightweight privacy-preserving authentication scheme for vanets,” IEEE Access, vol. 8, pp. 142858–142874, 2020. [Google Scholar]
15. I. Ali and F. Li, “An efficient conditional privacy-preserving authentication scheme for vehicle-to-infrastructure communication in VANETs,” Vehicular Communications, vol. 22, pp. 1–18, 2020. [Google Scholar]
16. Y. Wang, H. Zhong, Y. Xu, J. Cui and G. Wu, “Enhanced security identity-based privacy-preserving authentication scheme supporting revocation for vanets,” IEEE Systems Journal, vol. 14, no. 4, pp. 5373–5383, 2020. [Google Scholar]
17. S. Wang, K. Mao, F. Zhan and D. Liu, “Hybrid conditional privacy-preserving authentication scheme for VANETs,” Peer-to-Peer Networking and Applications, vol. 13, pp. 1600–1615, 2020. [Google Scholar]
18. S. S. Moni and D. Manivannan, “A scalable and distributed architecture for secure and privacy-preserving authentication and message dissemination in VANETs,” Internet of Things, vol. 13, pp. 1–12, 2021. [Google Scholar]
19. L. Benarous, B. Kadri, S. Bitam and A. Mellouk, “Privacy-preserving authentication scheme for on-road on-demand refilling of pseudonym in VANET,” International Journal of Communication Systems, vol. 33, no. 10, pp. 1–18, 2020. [Google Scholar]
20. M. A. Al-shareeda, M. Anbar, S. Manickam and I. H. Hasbullah, “An efficient identity-based conditional privacy-preserving authentication scheme for secure communication in a vehicular ad hoc network,” Symmetry, vol. 12, no. 10, pp. 1–25, 2020. [Google Scholar]
21. S. Saremi, S. Mirjalili and A. Lewis, “Grasshopper optimisation algorithm: Theory and application,” Advances in Engineering Software, vol. 105, pp. 30–47, 2017. [Google Scholar]
22. H. Feng, H. Ni, R. Zhao and X. Zhu, “An enhanced grasshopper optimization algorithm to the Bin packing problem,” Journal of Control Science and Engineering, vol. 2020, no. 3894987, pp. 1–19, 2020. [Google Scholar]
23. J. Luo, H. Chen, Y. Xu, H. Huang and X. Zhao, “An improved grasshopper optimization algorithm with application to financial stress prediction,” Applied Mathematical Modelling, vol. 64, pp. 654–668, 2018. [Google Scholar]
24. A. Bechir, “Efficient privacy-preservation scheme for securing urban P2P VANET networks,” Egyptian Informatics Journal, vol. 22, no. 3, pp. 317–328, 2021. [Google Scholar]
25. F. Farouk, Y. Alkady and R. Rizk, “Efficient privacy-preserving scheme for location based services in VANET system,” IEEE Access, vol. 8, pp. 60101–60116, 2020. [Google Scholar]
26. M. M. Salim, I. Kim, U. Doniyor, C. Lee and J. H. Park, “Homomorphic encryption based privacy-preservation for IoMT,” Applied Sciences, vol. 11, no. 18, pp. 8757–8772, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |