DOI:10.32604/iasc.2022.023270

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023270 |  |
| Article |
Differential Evolution Algorithm with Hierarchical Fair Competition Model
1Delhi Skill and Entrepreneurship University, Okhla Campus 1, New Delhi, 110020, India
2Department of Computer Engineering, College of Computers and Information Technology, Taif University, Taif, Saudi Arabia
3Department of Mechanical Engineering, Chandigarh Engineering College, Jhanjeri, Mohali, India
4Department of Computer Science, College of Computer and Information Systems, Umm Al-Qura University, Makkah, Saudi Arabia
5Al-Nahrain University, Al-Nahrain Nano-Renewable Energy Research Center, Baghdad, Iraq
6School of Computer Science and Engineering, Galgotias University, Greater Noida
7Department of Information Technology, College of Computers and Information Technology, Taif University, Taif, Saudi Arabia
*Corresponding Author: Amit Ramesh Khaparde. Email: amitkhaparde@gbpec.edu.in
Received: 01 September 2021; Accepted: 30 November 2021
Abstract: This paper presents the study of differential evolution algorithm with hierarchical fair competition model (HFC-DE). HFC model is based on the fair competition of societal system found in natural world. In this model, the population is split into hierarchy and the competition is allowed between the hierarchical members. During evolution, the population members are allowed to move within the hierarchy levels. The standard differential evolution algorithm is used for population evolution. Experimentation has carried out to define the parameter for proposed model on test suit having unimodal problems and multi-model problems. After analyzing the results, the two variants of HFC-DE are proposed, named hierarchical fair competition model in differential evolution algorithm with replacement, I,e, HFCDE-R and hierarchical fair competition model in differential evolution algorithm without replacement, I,e, HFCDE-wR. The problem-solving capabilities of both algorithms are checked and the results are compared with differential evolution algorithm (DE) and other variants of DE. The early results are encouraging and motivating.
Keywords: Optimization; artificial intelligence; evolutionary algorithms; uni-model problems; multi-model problems
The optimization problems are resolved by stochastic algorithms. The meta-heuristics like evolutionary algorithms (EA) belong to set of stochastic algorithms. The evolutionary computational model, is a metaphor of any evolutionary algorithms. Various fitness oriented, variation driven, population based evolutionary algorithms are proposed in last century. They all evolved in their own way using selection, mutation and reproduction. These processes are depending upon the individual structures which are defined by an environment.
Differential evolution algorithm [1] has capability to solve the non-linear, non-differential, continuous space optimization problem. DE is very simple and robust. It has few control parameters. It imparts itself to parallel computation with high convergence speed. DE has successfully solved engineering optimization problems in majority of engineering domains [2].
There are some lacunas within the architecture of standard DE (SDE) which makes SDE inefficient, incompatible to solve large-scaled, complex optimization problems (discrete space, combinatorial optimization etc.). These lacunas are follows:
• As, there are only three control parameters in DE, but still, the parameter adjustment is a difficult task [3]. Inappropriate value of the control parameters results premature convergence or may leads to stagnation. Theses parameters controls the population diversity in the evolution. DE literature provides the rules for parameter setting [4,5]. Self-adaptive parameter techniques [6,7] have relatively unraveled parameter setting issue for some extent. To improve the performance of DE, problem independent or self-adaptive (according to problem landscape) parameter setting technique is required.
• The mutation strategies differentiate DE from another evolutionary algorithms. Both explorative and exploitative strategies are supported by DE. The convergence speed and parameter setting [8] are decided by mutation strategies. The imbalanced selection strategies may result premature convergence/stagnation [9] because they exert low selection pressure in evolution. Moreover, the efficiency of mutation operator/strategy is depending upon the problem's type–Example-“DE/rand/1/exp highly” efficiently preserve the population diversity whereas DE/current-to-random/1 inefficient to preserve diversity [10]. The problem independent, balanced (explorative at stating and exploitative at end) mutation strategy is required to tackle this problem.
• DE support panmictic population structure and greedy selection mechanism. It increases its convergence speed but at a cost of losing genetic information. This lost genetic information can be useful while solving complex multi-optima problems. The performance of DE can be enhanced by developing a mechanism which can preserve the genetic information without disturbing the convergence speed.
The hierarchical competition model divides the population into the hierarchical structure (level). Each individual is allocated to specific level, based on its fitness value. Each level parallelly evolved using differential evolution algorithm. HFC allows the fair competition as our societal system, i,e, the strong individuals do not dominate the whole population and all individuals get the equal chance to produce the offspring. As the offspring generated in HFCDE, the offspring are allocated to respective fitness level. HFC ensure the preservation of genetic material.
Preserving the weak individuals throughout the evolution cannot give the desired results. Hence, HFC support replacement method. Like in natural world, a birth of new member and demise of weak member. In HFC model, the weak individuals in lowest level are replaced by new population individuals by method name–replacement method.
The HFCDE is the Differential Evolution algorithm with hierarchical competition model. The HFCDE is rigorously tested on multi-model problems and uni-model problems. It has been observed that replacement method is not required in uni-model problems, whereas, replacement is required in muli-model problems, Hence two new variants of HFCDE are proposed called hierarchical fair competition model in differential evolution algorithm with replacement, I,e, HFCDE-R and hierarchical fair competition model in differential evolution algorithm without replacement, I,e, HFCDE-wR are proposed for uni and multi model problems, respectively.
The manuscript is divided in six sections, in second section the introduction of DE is provided. Third section is related work. In fourth, the proposed method is discussed. In section five results are presented and discussed. Finally, the manuscript is concluded in last section.
2 Differential Evolution Algorithm
Differential evolution algorithm (DE) is a paralleled direct search technique. Population size (NP), crossover rate (Cr), scaling factor (F) are its parameter. It has four stages-generation, mutation, crossover and selection. It starts with generation of population (NP) vectors in a search space, the process of population generation can be described by Eq. (1).
In Eq. (1),
Next step is mutation. As mentioned in previous section, mutation differentiate DE from other evolutionary algorithms. It creates a new vector. Which is called mutant vector. The mutant vectors are generated for every member of population using Eq. (2).
In Eq. (2), r1, r2, r3 belongs to 1. . . NP and they are mutually different integers, F > 0 belongs to [0,2] called as scaling factor. There are two different methods to choose r1, i,e, r1 can be any random vector in a present generation or it can be the fittest vector of a present generation.
Recombination (crossover) is the third stage. It adds diversity in population. The result of crossover is the trial vector. It is generated by crossing the mutant vector with target vector. In crossover, each member gets a chance for reproduction. Crossover is represented by Eq. (3).
In Eq. (3), the rand(i) is random number generator, which generated number between (0, 1]. ‘Cr’ is probability of crossover, which lie between (0, 1]. randi(j) is random index between (1,D], it ensure that Vi,j will take at least one parameter from Mi,j. The DE literature, support two varieties of crossover-binomial crossover and exponential crossover. Eq. (3) represents the binomial crossover.
Fourth stage is selection, DE has a greedy selection policy. In selection, the trail vector and target vector, both are compared with each other and the fittest is retain for the next generation. Selection is represented by Eq. (4).
The exploration and exploitation in balanced manner is an idea used to enhance the DE performance. The hemostatic mutation operator [11], enhance the diversity by using the good vectors in early stages. It avoids stagnation in latter stages and gives much promising results. It accelerates the convergence speed and overcomes form the problem of stagnation. The performance of DE is improved by the balancing the trade-off between exploration and exploitation, and it has been achieved by MADE [12]. The variant of DE/current-to-best called DE/current-to-gr-best [13] has increases the efficiency of DE.
Differential evolution algorithm does not support any PDF (probability density function) [14]. But, in order to improve the DE capability of exploration and exploitation in search space, the Gaussian PBX alpha, also knowns as GBPX-alpha, advance CRDE [15] used the probability density functions. The multi-scaled DE [16], uses the subpopulation structure and covariance learning enabled coordinate system for the crossover. It has efficiently and successfully solved the global optimization problems.
As mentioned in previous section, the selection is the last stage in DE. But logically, the selection occurred during mutation also. By applying the selection criteria, the selection pressure can be exerted in the mutation operator and this can improve the DE performance. By using same idea, the proximate mutation operator [17] uses the Euclidian distance and ranked based mutation operator [18] uses fitness value to select the mutation vectors and improve DE performance.
DE support a large number of mutation operators. But DE has static mutation strategy, i.e., the mutation strategy remains same throughout the process of evolution. Runtime mutation strategy selection (dynamic mutation strategy selection) based on historical knowledge or problem landscape has given the desired results [19]. The run time selection of trial vector in CoDE [20] increases the DE performance. ISAMODE-CMA [21], uses covariance matrix in sub-population structure to improve DE performance.
EPSDE [22] creates the group of distinct mutation strategies, control parameters and then conduct the competition between them to produce the offspring for the next generation. It successfully solved the optimization problems.
DESBS [23] divides the population into many clusters (Sub-population), each subpopulation evolved in parallel using Differential Evolution algorithm. The performance of all the clusters evaluated periodically and non-performing cluster is merged into the nearby performing cluster. The DESBS has efficiently solved complex problems.
The clustering techniques play the vital role in natural language processing, the artificial neural network with clustering techniques efficiently and effectively update the knowledge system [24]. A proposed novel structure modelling methods uses the structure deviation relations. The results of the proposed method are effective than other methods.
The Machine learning techniques (ML) are used for the optimization of objective problems. The ML techniques are used for the prediction and forecasting of Business-to-Business (B2B) sales. The forecasting and predication of B2B sales are evaluated on parameters like accuracy and reliability. Based on the experimentation [25], the Gradient Boost algorithm provides better results than other compared methods.
Convolutional neural network (CNN) has successfully solved the multi-variable, multi criteria problems. The application of CNN is in healthcare monitoring system. CNN is used for the pitch highlight identification [26] with low-level acoustic descriptors and without express data span. The CNN has successfully resolved the issues.
IoT is the interconnection of computing devices and other machines that have capability to communicate with each other. The electronic commerce has to deal with effective deployment of IoT and management model [27]. It is multi-objective optimization problem. The feasible solution gives the better relationship between internal and external structure on the internet.
The Machine Learning (ML) is used for optimization, classification and forecasting. The knowledge demand visualization system [28] increases the performance of extended-machine learning algorithm (X-ML). The results are greater and coherent in the majority of test cases.
The scientific workflow application (SWA) require cost estimation and it is an optimization problem. As the number of criteria increases, it becomes multi-objective in nature. The novel method is proposed to SWA cost estimation problem [29]. The results shows that the proposed method has successfully solved the large and small case problems, whereas, the hybrid method has successfully solved the medium scale problem.
A novel fuzzy based approach has proposed to resolve energy efficiency (EE) and spectrum efficiency (SE) problems in the 5G System [30]. The proposed method has enhanced the system performance by successfully achieving the trade-of between the SE and EE.
There is a huge information is on the social media. Extraction of useful information is big challenge. Efficient, optimize techniques/tools are required to extract the useful information from this colossal intelligence. The information's characteristics can be analyzed to classify the information. A suggestion mining extraction method [31], classifies the information using XGboost classifier. The proposed method has efficiently outperformed the other methods.
The optimization of objective metrics and subjective quality in image processing is difficult task. Here, the user has to choose the objective base on real-time constraints. The Magnetic Resonance (MR) image Super Resolution (SR) method [32] has been used in Very Deep Residual network (VDR-net). It has been trained by Low Resolution and High-Resolution sub-bands. Here, the Gaussian Edge Preservation method has been used to maintain the image structure. The proposed method outperforms in four objective different metrics and subjective quality than compared methods.
Economically expensive transaction problems are multi-objective in nature. Cost optimization is one constraint in them. In developing country, like India, the insurance system is a complex problem, hence, a large group of farmers do not utilize the crop insurance in regular practices. The blockchain based [33] affordable, efficient and low-cost crop insurance techniques have proposed for crop insurance problem. The proposed technique has tested on the google cloud and the possible solutions are achieved in minimal transaction within low processing time.
The intrusion detection (IDS) is the one of the constraints in Database design system. The novel design technique for unmapped role organization [34] has used a tube search for record creation in clustering algorithm. Each entry has been checked with these records. The proposed method gives the effective and desired results on performance-deciding parameters.
The new distributed differential evolution [35] support hierarchical island model, it is time efficient. It has master-worker scheme for bi-level parallel computation. The cooperative hierarchical scheme provides the complete search in solution space.
Modified multi-objective and self-adaptive DE, (MMOSADE) [36], has improves the precision of multi-objective optimization design problem of nuclear power system and it has been used to design the model of nuclear plant.
The new Memetic framework with Alopex Local Search [37] has proposed for DE (MFDEALS), it provides the control global exploration of solution space. The new framework has enhanced the performance of DE and outperform the compared memetic algorithms. The new framework has been used with both standard DE and Adaptive DE.
The DPADE (Dichotomy-based parameter adaptation DE) [38] is new parameter adaptation scheme. It compresses the parameter spaces using pre-experience to decides the parameter setting. DPADE has effectively enhanced the performance of DE.
A Multi-Population Inflationary Differential Evolution algorithm with Adaptive Local Restart [39] is a new self-adaptive evolutionary algorithm. It has multi-population structure. It has the combination of adaptive Differential Evolution and local search. It uses the local restart procedure as well as global restart procedures. It has avoided the staking in local minima.
SaDSE [40], is a novel self-adaptive dual-strategy in Differential Evolution Algorithm. It has improved the DE performance in large dimension problems. SaDSE uses the “DE/best/2” for exploitation and “DE/rand/2” for exploration, and achieves the balanced exploration/exploitation. It has self-adaptive scaling factor scheme which depends on population fitness.
MRDE (Multi Role Differential Evolution) Algorithm has new method for trial vector generation. MRDE has divides the population into small groups. All individuals have different role (task) in the group. The role of the individuals is decided by the respective fitness value. MRDE has the pool of the generation strategies and control parameters. Each individuals utilizes pool based upon the role (task) assigned. MRDE is more comparative, effective and reliable than another state-of-art algorithm and SDE.
The differential evolution algorithm follows the Darwin's principal, i,e, survival of fittest for evolution and unlike others, the average fitness of the population increases with evolution . The premature convergence in differential evolution is handled by maintaining the population diversity during evolution. Many optimization problems have highly enormous multi-model search space, DE stuck to local minima or stagnation. This can solve by either recoupment of new individuals or by protecting the fitness level of the individuals.
The hierarchical fair competition model is based on Fair Competition Principle of Biological and Social Systems. The unfair competition is not allowed in biological and societal system. There is a competition but fair competition, i,e, mature or developed individuals never compete with the immature or undeveloped individuals in biological and societal system. The nature and society achieve this fair competition by arranging the individuals in different level and allow the competition only between the levels. This fair competition is the metaphor of the hierarchical fair competition model (HFC). The HFC model is proposed for the evolutionary algorithm [41]. It has three main components
1. Hierarchical arrangement of individuals to underlay the fitness gradient
2. Randomly generating the individuals at entry level
3. Migrating the individual from lower to upper level
The sequential flow of proposed algorithm is explained in block diagram shown in Fig. 1. Unlike other EAs, it starts with the initial population generation. Then all individuals are arranged at different levels according to fitness value. Each level is defined by using two threshold–Admission threshold and export threshold. The export threshold of lower level is admission threshold of next level and so on. Hence, each level has individuals of specific range and fitter individuals are migrate to the upper level. Individuals having fitness value above admission threshold and below the export threshold are allowed to enter in the respective level; otherwise it has to move corresponding level. It protects the potential degradation of individuals in higher level which may be caused due to presence of unqualified individuals. Each level is independently evolved by standard differential evolution algorithm. The replacement method replaces the non-performing individuals with new individuals. This method makes the proposed algorithm independent of size of population. In-between the evolution of individuals, the fitness value of individuals is evaluated and they are allowed to migrate between the levels. This process is continuing till stopping criteria does not satisfy.

Figure 1: Block diagram of proposed algorithm
The pseudocode of the algorithm for better understanding are as follows:
1: Create initial population using Eq. (1).
2: Apply Population Division Method to determine the admission threshold of each level L and Divide each individual of population between the L levels
4: Repeat
{
4.1 For each level population do
{
4.1.1 differential evolution algorithm
}
4.2 Apply Individual Migration Method to migrate individual of population between the L levels
4.3 Replacement method, Replace ‘n’ of individuals with random individuals in bottom level.
4.4 Population Division Method, rearrange the population between the levels.
}
} Until (termination condition)
a) Population Division Method
Population division method (PDM) divides the initial population in different level of hierarchy. PDM first compute the threshold for the admission for each level, i,e,
In this method, fitness value of every individual is compared with threshold value of each level. If individual having fitness value is less than or equal to threshold value of given level and more than the threshold value of next higher level than the individual is assign to respective level. The Algorithm is shown as follows.
popleve (i) = j
End for
End for
b) Individual Migration Method
The standard differential evolution (SDE) algorithm is used to generate the new solution. SDE has greedy selection mechanism, i.e., the child is only allowed to enter in population, when it is fitter than his respective parent. Hence, the average fitness of population at any level is always lower than the admission threshold.
After certain cycles of evolution, the fitness value of individuals is checked with the admission value of each levels. And, based on the fitness value, individuals are allocated to respective levels.
m = 1;
popleve(i) = m m = m + 1
End while
End for
End for
c) Replacement Method
This method provides the continuous flow of genetic material at bottom level. This method make the given algorithm independent of the population size. In this method, a random number is generated, if this number is less than replacement probability, then the ‘n’ number of individuals are replaced by new individuals.
As, the population is structure into various hierarchy levels. It ensures the competition between the same type (in term of fitness) individuals. The competition between the same level individuals retain the genetic material of all performing individuals and provide the equal opportunity to prove themselves. The outperforming individuals are move up to hierarchical levels and the non-performing individuals are replaced by new individuals over period of time. This algorithm ensures the elitism of healthy individuals and the convergence to solution in respective of the type of solution space.
Like any other evolutionary algorithm, hierarchical fair competition differential evolution algorithm (HFC-DE), start with random number of feasible set of solutions called initial population. After that, HFC-DE uses the population division method (PDM) to allocate individuals to different ‘L’ levels. Then, standard differential evolution algorithm (SDE) is used for evolution of new individuals in the population. The newly generated individuals are allocated to ‘L’ levels using individual migration method. At last, the Replacement Method (RM) is to provide continuous supply of genetic material. RM makes HFC-DE independent of large population size, but the RM depend upon the parameter called replacement probability (Rp). The scale-up study of Rp is carried by using first eight problems of CEC 2005 test suite.
a) Scale-Up Study of Parameters
HFC-DE uses standard differential Evolutionary algorithm (SDE) for evolution. The parameter setting is shown in Tab. 1. The CEC 2005 [42] test suite is used for experimentation.

For all the problems HFC-DE euns for 25 times. The performance is evaluated on following criteria;
1. Success rate (SR) = Ratio of number of successful runs and total number of runs
2. Success Performance (SP) = Ratio of average of Max function evaluation of Successful runs to success rate
3. Minimal value of function (MV)
4. Maximum function evaluated for min value. (MFE)
The results of the scale-up study are shown in Fig. 2. The replacement probability (Rp) is zero, i,e, no new genetic material is generated and added to bottom level population and Rp = 0.5%, 50% of total population's the genetic material is generated and added replace 50% of bottom level population.

Figure 2: Performance of HFC-DE at Rp = 0 Vs. Rp = 0.5
When Rp = 0.5, it has found that the maximum function evaluation and success performance is high as compare to maximum function evaluation and success performance, when Rp = 0. This trend shows that the adding generic material at the end of population incurred extra computational cost.
At Rp = 0.5, minimal value is better as compare to minimal value of Rp = 0. But every time both are able to find desired values, except for function number 3, 5, and 8. The success rate of problem number 4, is 100% when Rp = 0, whereas, 92% when Rp = 0.50, adding of genetic material at bottom level incurred extra computation, it slow down the convergence speed and
Algorithm terminates before finding solution. However, in problem number. 7, Rp = 0.5 is always solve the problem and the Rp = 0 is 92% of time able to solve the problem. i,e, in multi-model function, adding genetic material avoid the stuck to local minima. When function is uni-model it is not useful to add genetic material at bottom level whereas when function is multi-model it is better to add genetic material. i,e the diversity incurred by Rp is not advisable in uni-modal function whereas diversity by Rp is advisable in multimodal function.
b) Comparison with SDE and Other State-of-Art Algorithms
Based on the above findings, two different new differential evolution algorithms for uni-model and multi-model functions are proposed. Theses algorithms are as follows:
• Hierarchical fair completion in differential evolution algorithm without replacement (DE-HFC-/w R). It is same as above algorithm with Rp = 0.
• Hierarchical fair completion in differential evolution algorithm with replacement. (DE-HFC/R). It is same as above algorithm with Rp = 0.5.
These above mention algorithms are compared with other state-of-art algorithm like CoDE, EPSDE and standard differential algorithm (SDE). The parameter setting for both CoDE, EPSDE are same as the parameter setting that their corresponding authors have proposed. In experimentation, Non parametric two-trail Wilcoxon ranksum test with significance level 0.05 is used to check the null hypothesis. The null hypothesis is “there is no difference exists between the original SDE/variant of SDE and proposed algorithm (HFC-DE/wR and HFC-DE/R)”. The cases are marked as positive “+” when the null hypothesis is rejected and the proposed algorithms are outperforms the other one in a statistically significant way and marked with “–” when the null hypothesis is rejected and the original SDE/variant of SDE is significantly better than the proposed algorithms and with “=” when the null hypothesis is accepted and no performance difference is significant.
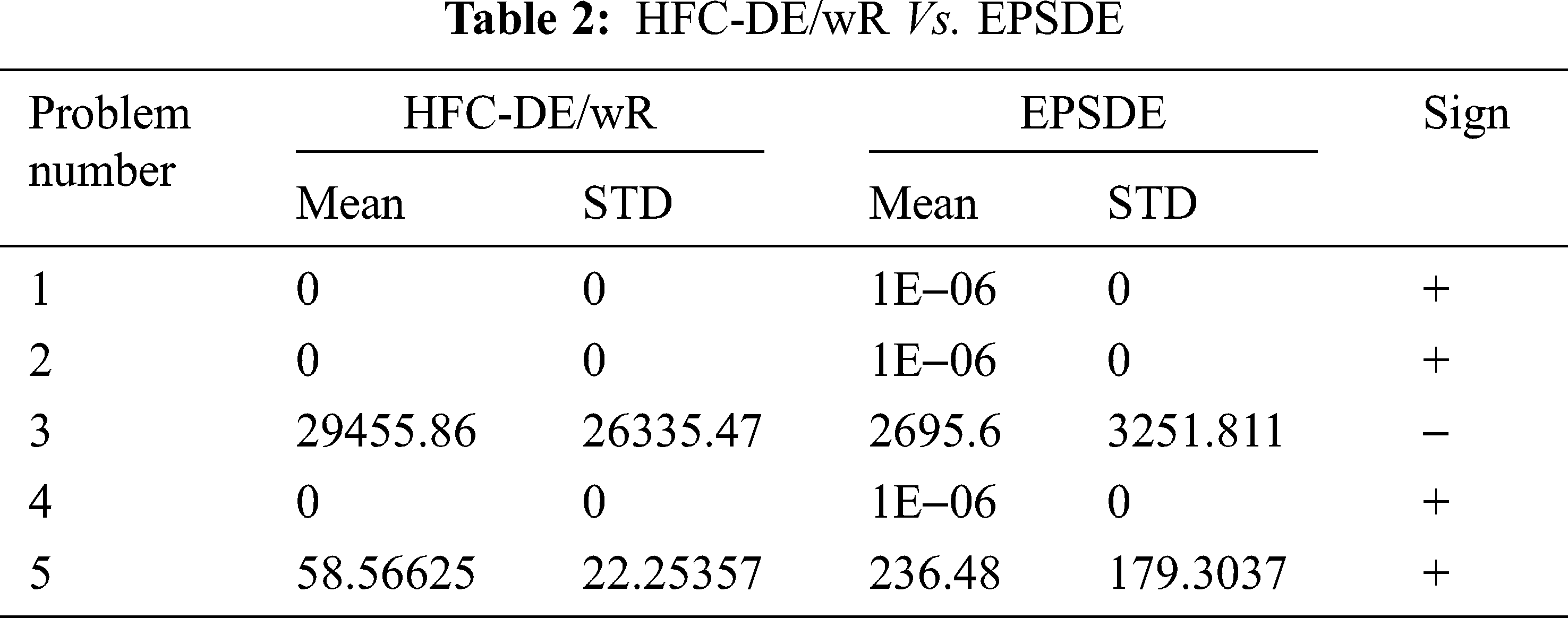
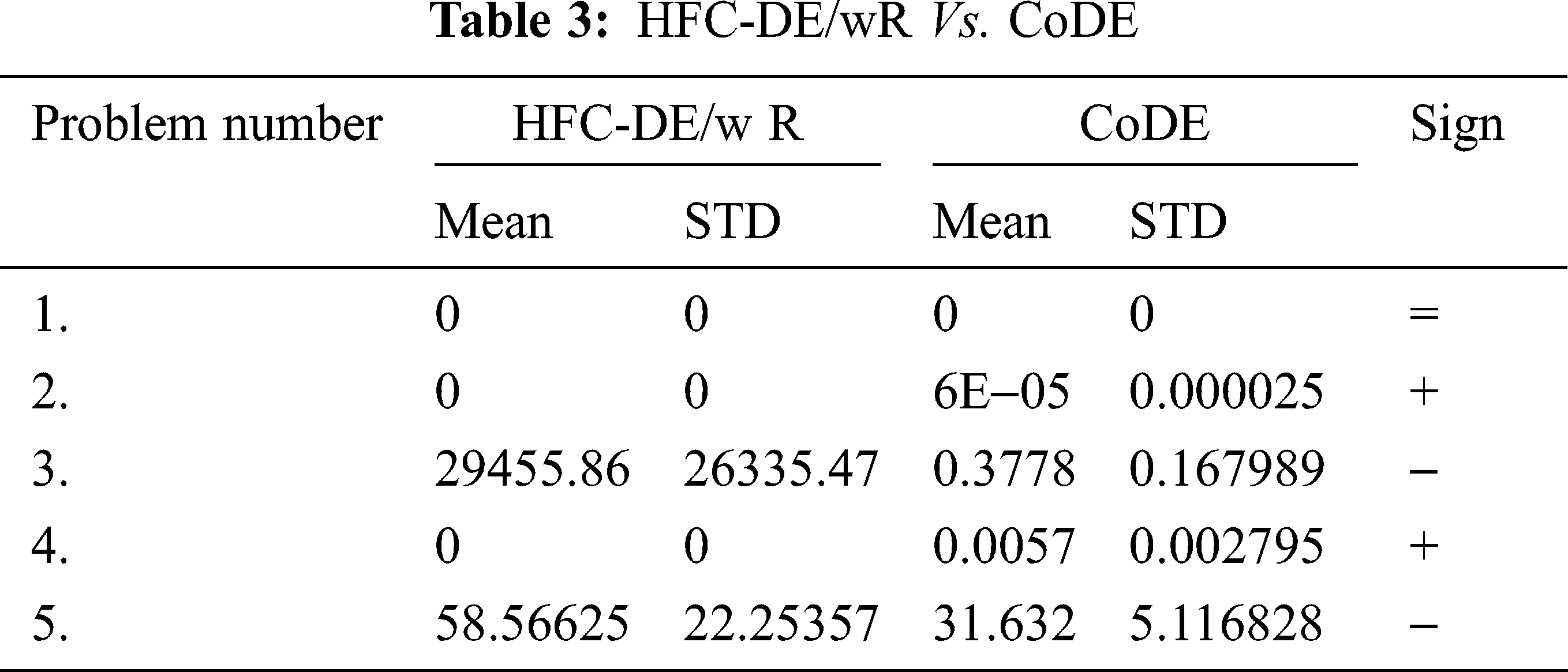
1) HFC-DE/wR Vs. SDE, CoDE, EPSDE
HFC-DE/wR is compared with SDE and other state of art variants of SDE algorithms–CoDE, EPSDE. As shown in Tab. 4, HFC-DE/wR is non-comparable in problem 1, 2, 4. Its performance is same with standard differential evolutionary algorithm in uni-model function. As per Tab. 2, HFC-DE/wR outperform the EPSDE in uni-model problems. Except problem 3. The results of HFC-De/wR Vs. CoDE are shown in Tab. 3. It outperform perform CoDE in problem number 2 & 4, whereas, CoDE has performed well in problem number 3, 5 than HFC-DE/wR. Performance of HFC-DE/wR and CoDE is statically same in problem number 1.
2) HFC-DE/R Vs. SDE, CoDE, EPSDE

In multi-model functions the performance of HFCDE/R is compared with EPSDE. The results are shown in Tab. 5. In problem number 17, the null hypothesis is true, I,e, no statically significant difference between HFCDE/R and EPSDE. In Problem no 3–12, the null hypothesis is not true and the performance of EPSDE is better than HFCDE/R, whereas, in problem number 1, 2 and problem number 13–20 (except 17) the performance of HFCDE/R is better than EPSDE.

While in comparison of HFCDE/R with SDE, results available in Tab. 6. In problem number. 14, 15, 17, the null hypothesis is true, I,e, no statically significant difference between HFCDE/R and SDE. In Problem number 3, 4, 7, 810, 19, 20, the null hypothesis is not true and the performance of SDE is better than HFCDE/R, whereas, in problem number 1, 2 , 5, 6, 9, 11, 12, 13, 16, 18 the performance of HFCDE/R is better than SDE . The results of comparison between HFCDE/R and CoDE are shown in Tab. 7. In problem number. 3–12 and problem number 16, 18, 19 the CoDE is better than HFCDE/R and in problem number 1, 2, 13, 1415, 17 and 20 HFCDE/R is performed better than CoDE. The overall performance of HFC/R Vs. other algorithms is shown in Fig. 3.

Figure 3: Performance of HFC-DE/Rin multi-model problem


c) Discussion
The two novel differential evolution algorithms having hierarchical fair competition model have been proposed. The HFC models uses the method called ‘replacement method’ for the replacing the non-performing individuals with new individuals. During experimentation, it was found that the unimodal problems does not requires the replacement method, whereas, the multi-model problems require the replacement method. Hence, two new algorithms name hierarchical fair competition model in differential evolution algorithm with replacement, I,e, HFCDE-R for multi-model functions and hierarchical fair competition model in differential evolution algorithm without replacement, I,e, HFCDE-wR for the unimodal function are proposed.
The HFCDE-wR is compared with SDE, CoDE and EPSDE on five unimodal functions. The HFCDE-wR statistically incomparable with SDE in three functions. Whereas, it has outperformed in one function and SDE has performed better in other function. In problem no. 3 and 5, the HFCDE-wR achieved the minimal value but because the termination criteria were exhausted it could not reach to target minimal value, whereas, the SDE had high speed of convergence but SDE has stuck to local minima. The HFCDE-wR has outperformed all four problems except in problems no. 3, while it compared with EPSDE. EPSDE was stuck to local minima all five problems. CoDE was not able to solve the problem no. 2 and 4, whereas, HFCDE-wR has successfully solved the same. EPSDE has outperform in problem no. 5 with high convergence speed. In the comparison it has been found that the HFCDE-wR has low speed of convergence, because it retains the unfit individuals for long time and HFCDE-wR does not allows new individuals in mid of evolution process.
The HFCDE-R is used to solve the multi model problem. The results of the HFCDE-R are compared with CODE, EPSDE and HFCDE-R has underperformed in problem 3 and HFCDE-R has not converged to local minima in problem 4. SDE has the low convergence speed in problems no. 8 & 10. HFCDE-R and SDE are statistically incomparable in three problems (14, 15 & 17). EPSDE has outperform HFCDE-R in ten problem (3–12) with fast convergence rate, whereas, HFCDE-R perform better in nine problems and in one the performance is statically incomparable. CoDE has performed better in twelve problems but it never achieved the target minimal value. all time it stuck to local minima, whereas, the HFCDE-R never stuck to local minima.
The proposed methods are depending upon the fact that there is various type of problems. All problems have different in nature. They have different landscapes. There cannot be the same method to solve all of them. The method applicable to solve uni-model problem cannot be applied on the multi-model problem. But, there should be provision in method itself to modify either by itself or by user to solve all type of the problem. HFC-DE provide this facility in term of parameter to implement same. The replacement method is fruitful if the problem is multi-model otherwise not.
As discuss earlier, the HFC model automatically maintain the fair competition between the individuals and able to maintain the elitism of healthy individuals during the evolution. The performing individuals move toward upper level as the evolution progress whereas the non-performing individuals or if the search is stuck to local minima then the replacement method handle the search. The proposed algorithm ensures the convergence of solution.
As the two new variants of standard differential evolutionary algorithms are proposed. These algorithms used the fair competition principal of societal system of natural world. The proposed algorithms are independent of the population size. The replacement probability is used to handle the replacement pressure in the algorithm. HFC-DE/wR which represent HFC-DE without has outperformed the EPSDE, and its performance is moderate while it compares with CoDE.
The HFC-DE/R represent the HFC-DE with replacement has performed well compare to EPSDE in multi-model problems. Whereas, The CoDE and SDE perform better to than HFC-DE/R, more fine tuning of the parameters is requiring to get better results.
Acknowledgement: We deeply acknowledge Taif University for supporting this study through Taif University Researchers Supporting Project Number (TURSP-2020/150), Taif University, Taif, Saudi Arabia.
Funding Statement: This research is funded by Taif University, TURSP-2020/150.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Das and P. N. Suganthan, “Differential evolution: A survey of the state-of-the-art,” IEEE Transactions on Evolutionary Computation, vol. 15, no. 1, pp. 4–31, 2011. [Google Scholar]
2. M. Georgioudakis and V. Plevris, “A comparative study of differential evolution variants in constrained structural optimization,” Frontiers in Built Environment (Computational Methods in Structural Engineering), vol. 6, no. 102, pp. 1–14, 2020. [Google Scholar]
3. S. Das, S. S. Mullick and P. N. Suganthan, “Recent advances in differential evolution–an updated survey,” Swarm and Evolutionary Computation, vol. 27, no. 1, pp. 1–30, 2016. [Google Scholar]
4. D. Zaharie, “Differential evolution from theoretical analysis to practical insights,” in Proc. of the 19th Int. Conf. on Soft Computing, Brno, Czech Republic, pp. 26–28, 2013. [Google Scholar]
5. F. Penunuri, C. Cab, O. Carvente, M. A. Zambrano-Arona and J. A. Tapia, “A study of the classical differential evolution control parameters,” Swarm and Evolutionary Computation, vol. 26, pp. 86–96, 2016. [Google Scholar]
6. R. C. Silva, R. Lopes, A. Freitas and F. Guimaraes, “Performance comparison of parameter variation operators in self-adaptive differential evolution algorithms,” in Proc. of Brazilian Symp. on Neural Networks, Curitiba, Brazil, pp. 148–153, 2012. [Google Scholar]
7. A. Zamuda and J. Brest, “Self-adaptive control parameters׳ randomization frequency and propagations in differential evolution,” Swarm and Evolutionary Computation, vol. 25, pp. 72–29, 2015. [Google Scholar]
8. G. Jeyakumar and C. Shanmugavelayutham, “Convergence analysis of differential evolution variants on unconstrained global optimization functions,” International Journal of Artificial Intelligence & Applications, vol. 2, no. 2, pp. 116–127, 2011. [Google Scholar]
9. M. Leon and N. Xiong, “Investigation of mutation strategies in differential evolution for solving global optimization problems,” in Proc. of Int. Conf. on Artificial Intelligence and Soft Computing, Zakopane, Poland pp. 372–383, 2014. [Google Scholar]
10. A. Yaman, G. Iacca and F. Carafinni, “A comparison of three differential evolution strategies in terms of early convergence with different population sizes,” in Proc. LeGO–14th Int. Global Optimization Workshop, AIP Conf. Proc. 2070, Melville, NY, USA, pp. 020002-1–020002-4, 2019. [Google Scholar]
11. S. Prabha and R. Yadav, “Differential evolution algorithm with biological-based mutation operator,” Engineering Science and Technology, An International Journal, vol. 23, no. 2, pp. 253–263, 2020. [Google Scholar]
12. S. M. Islam, S. Das, S. Ghosh, S. Roy and P. N. Suganthan, “An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization,” IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, vol. 42, no. 2, pp. 482–500, 2012. [Google Scholar]
13. E. Shi, F. Leung and J. Lai, “An adaptive differential evolution with unsymmetrical mutation,” in Proc. of IEEE Congress of Evolutionary Computation (CECNew Orleans, LA, USA, pp. 1879–1886, 2011. [Google Scholar]
14. R. Zhou, J. Hao, H. Cao and H. Fan, “An empirical study on differential evolution algorithm and its several variants,” in Proc. of Int. Conf. on Electronic & Mechanical Engineering and Information Technology, Harbin, Heilongjiang, China, pp. 3266–3271, 2011. [Google Scholar]
15. L. Chen and L. Ding, “An improved crowding-based differential evolution for multimodal optimization,” in Int. Conf. on Electrical and Control Engineering, Yichang, China, pp. 1973–1977, 2011. [Google Scholar]
16. Y. Du, Y. Fan, X. Liu, J. Tang and P. Liu, “Multiscale cooperative differential evolution algorithm,” In Computational Intelligence and Neuroscience, vol. 2019, no. 5259129, pp. 1–17, 2019. [Google Scholar]
17. M. G. Epitropakis, D. K. Tasoulis, N. G. Pavlidis, V. P. Plagianakos and M. N. Vrahatis, “Enhancing differential evolution utilizing proximity-based mutation operators,” IEEE Transactions on Evolutionary Computation, vol. 15, no. 1, pp. 99–119, 2011. [Google Scholar]
18. W. Gong and Z. Cai, “Differential evolution with ranking-based mutation operators,” IEEE Transactions on Cybernetics, vol. 43, no. 6, pp. 2066–2081, 2013. [Google Scholar]
19. S. M. Islam, S. Das, S. Ghosh, S. Roy and P. N. Suganthan, “An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization,” IEEE Transactions on Systems, Man, and Cybernetics—Part B: Cybernetics, vol. 42, no. 2, pp. 482–500, 2012. [Google Scholar]
20. Y. Wang, Z. Cai and Q. Zhang, “Differential evolution with composite trial vector generation strategies and control parameters,” IEEE Transactions on Evolutionary Computation, vol. 15, no. 1, pp. 55–66, 2011. [Google Scholar]
21. S. M. Elsayed, R. Sarker and D. L. Essam, “An improved self-adaptive differential evolution algorithm for optimization problems,” IEEE Transactions on Industrial Informatics, vol. 9, no. 1, pp. 89–99, 2013. [Google Scholar]
22. R. Mallipeddi, G. Iacca, P. N. Suganthan, F. Neri and E. Mininno, “Ensemble strategies in compact differential evolution,” IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, pp. 1972–1977, 2011. [Google Scholar]
23. A. R. Khaparde, “Analysis of new distributed differential evolution algorithm with best determination method and species evolution,” in Proc. of Int. Conf. on Computational Intelligence and Data Science (ICCIDS 2019Procedia Computer Science, Gurugram, India, vol. 167, pp. 263–272, 2020. [Google Scholar]
24. G. Li, F. Liu, A. Sharma, O. I. Khalaf, Y. Alotaibi et al., “Research on the natural language recognition method based on cluster analysis using neural network,” Mathematical Problems in Engineering, vol. 2021, no. 9982305, pp. 1–13, 2021. [Google Scholar]
25. R. Rout, P. Parida, Y. Alotaibi, S. Alghamdi and O. I. Khalaf, “Skin lesion extraction using multiscale morphological local variance reconstruction based watershed transform and fast fuzzy c-means clustering,” Symmetry, vol. 13, no. 11, pp. 2085, 2021. [Google Scholar]
26. S. Dalal and O. I. Khalaf, “Prediction of occupation stress by implementing convolutional neural network techniques,” Journal of Cases of Information Technology, vol. 23, no. 3, pp. 27–42, 2021. [Google Scholar]
27. H. Zhao, P. L. Chen, S. Khan and O. I. Khalafe, “Research on the optimization of the management process on internet of things (IoT) for electronic market,” The Electronic Library, vol. 39, no. 4, pp. 526–538, 2021. [Google Scholar]
28. A. Alsufyani, Y. Alotaibi, A. O. Almagrabi, S. A. Alghamdi and N. Alsufyani, “Optimized intelligent data management framework for a cyber-physical system for computational applications,” Complex & Intelligent Systems, vol. 7, pp. 1–13, 2021. [Google Scholar]
29. E. N. A. Khanak, S. P. Lee, S. U. R. Khan, N. Behboodian, O. I. Khalaf et al., “A heuristics-based cost model for scientific workflow scheduling in cloud,” Computers, Materials and Continua, vol. 67, no. 3, pp. 3265–3282, 2021. [Google Scholar]
30. O. I. Khalaf, K. A. Ogud and M. Singh, “A Fuzzy-based optimization technique for the energy and spectrum efficiencies trade-off,” Cognitive Radio-Enabled 5G Network. Symmetry, vol. 13, no. 1, pp. 47, 2021. [Google Scholar]
31. Y. Alotaibi, M. N. Malik, H. H. Khan, A. B. S. ul Islam, A. Alsufyani et al., “Suggestion mining from opinionated text of big social media data,” Computer, Material & Continua, vol. 68, no. 3, pp. 3323–3338, 2021. [Google Scholar]
32. G. Suryanarayana, K. Chandran, O. I. Khalaf, Y. Alotaibi, A. Alsufyani et al., “Magnetic resonance image super-resolution using deep networks and Gaussian filtering in the stationary wavelet domain,” IEEE Access, vol. 9, pp. 71406–71417, 2021. [Google Scholar]
33. N. Jha, D. Prashar, O. I. Khalaf, Y. Alotaibi, A. Alsufyani et al., “Blockchain based crop insurance: A decentralized insurance system for modernization of Indian farmers,” Sustainability, vol. 13, no. 16, pp. 8921-1–8921-17, 2021. [Google Scholar]
34. Y. Alotaibi, “A new database intrusion detection approach based on hybrid meta-heuristics,” Computers,Materials and Continua, vol. 66, no. 2, pp. 1879–1895, 2021. [Google Scholar]
35. M. L. Tardivo, P. C. Scutrai, G. Bianchini and M. M. Garabetti, “Hierarchical parallel model for improving performance on differential evolution,” in Concurrency Computation: Practice and Experimentation, Wiley, New Jersy, USA, vol. 29, no. 10, 2017. [Google Scholar]
36. Y. Yang, S. Peng, L. Zhu, D. Zhang, Z. Qiu et al., “A modified multi objective self-adaptive differential evolution algorithm and Its application on optimization design of the nuclear power system,” Hindawi, Science and Technology of Nuclear Installations, vol. 2019, no. 1041486, pp. 1–9, 2019. [Google Scholar]
37. M. Leon, N. Xiong, D. Molina and F. Herrera, “A novel memetic framework for enhancing differential evolution algorithms via combination with Alopex local search,” in International Journal of Computational Intelligence Systems, vol. 12, no. 2, pp. 795–808, 2019. [Google Scholar]
38. L. Cui, G. Li, Z. Zhu, Z. Ming, Z. Wen et al., “Differential evolution algorithm with dichotomy-based parameter space compression,” Soft Computing, SpringerLink, vol. 23, pp. 3643–3660, 2019. [Google Scholar]
39. M. Di. Carlo, M. Vasile and E. Minisci, “Multi-population inflationary differential evolution algorithm with adaptive local restart,” Mathematics and Computer Science, IEEE Congress on Evolutionary Computing (CEC), Sandai, Japan, pp. 632–639, 2015. [Google Scholar]
40. M. Duan, H. Yang, S. Wang and Y. Liu, “Self-adaptive dual-strategy differential evolution algorithm,” PLOS ONE, vol. 14, no. 10, pp. 1–25, 2019. [Google Scholar]
41. J. Hu, Sustainable evolutionary algorithms and scalable evolutionary synthesis of dynamic systems, Dissertation, Michigan State University, 2004. [Google Scholar]
42. P. N. Suganthan, N. Hansen, J. J. Liang, K. Deb, Y. P. Chen et al., “Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization,” Technical Report, 2005. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |