DOI:10.32604/iasc.2022.023344
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.023344 | |
| Article |
Robust Node Localization with Intrusion Detection for Wireless Sensor Networks
1Department of Information Technology, M.Kumarasamy College of Engineering, Karur, 639 113, India
2Department of Computer Science and Engineering, Vel Tech Rangarajan Dr. Sagunthala R&D Institute of Science and Technology, Chennai, 600062, India
3Department of ECE, HKBK College of Engineering, Nagawara, Bengaluru, 560045, India
4School of Computer Science and Applications, REVA University, Bengaluru, 560064, India
5Department of Computer Applications, Chandigarh Business School of Administration, CGC Laundran, 140307, Mohali, India
6Electrical Engineering Department, King Khalid University, Abha, 62529, Saudi Arabia
*Corresponding Author: G. Kadiravan. Email: kathirkadir@gmail.com
Received: 04 September 2021; Accepted: 18 October 2021
Abstract: Wireless sensor networks comprise a set of autonomous sensor nodes, commonly used for data gathering and tracking applications. Node localization and intrusion detection are considered as the major design issue in WSN. Therefore, this paper presents a new multi-objective manta ray foraging optimization (MRFO) based node localization with intrusion detection (MOMRFO-NLID) technique for WSN. The goal of the MOMRFO-NLID technique is to optimally localize the unknown nodes and determine the existence of intrusions in the network. The MOMRFO-NLID technique encompasses two major stages namely MRFO based localization of nodes and optimal Siamese Neural Network (OSNN) based intrusion detection. The OSNN technique involves the hyperparameter tuning of the traditional SNN using the MRFO algorithm and consequently increases the detection rate. In order to assess the enhanced performance of the MOMRFO-NLID technique, a series of simulations take place and the results reported superior performance compared to existing techniques interms of distinct evaluation parameters.
Keywords: WSN; intrusion detection; node localization; manta ray foraging optimization; parameter tuning
The wireless sensor network (WSN) is a distributed smart network system [1]. It is made up of huge amount of microsensors placed in a sensing region that have the capability of wireless computing and communication. It could achieve the allocated task individually based on the environment changes [2]. With the rapid growth of embedded computing technology, wireless sensor technology, wireless communication technology, and distributed information processing technology, WSN has an extensive applications prospect, like ecological observation, national defense, volcano observation, space exploration, medical security, city management, architecture, environmental monitoring, and so on. The WSNs could realize realtime sensing, monitoring, and gathering data of different monitoring objects/environments via the support of several incorporated micro sensor nodes [3]. Later, process the data through embedded systems. Fig. 1 shows the framework of WSN model.
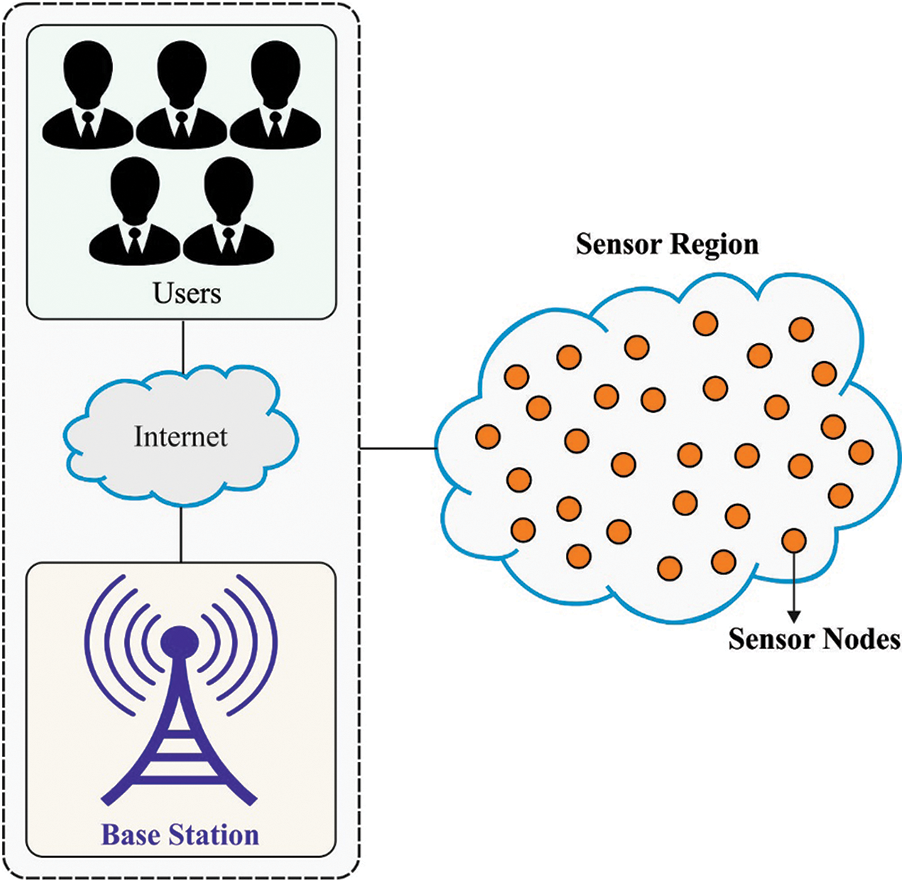
Figure 1: Overview of WSN
WSN node localization technique could be categorized as to the range free and range based localization methods based on the distance measure is required in the localization procedure [4]. The previous need is to measure the distance among the anchor and unknown nodes while measuring the positions of unknown nodes. Later, estimate the positions of unknown nodes through the entire network’s connectivity. Thus, the precision of range based localization methods is effective when compared to range-free localization methods. Ranging approaches used commonly in the range based localization methods are received signal strength indicator (RSSI), angle of arrival (AOA), and time of arrival (TOA) [5,6]. In realtime applications, combination of multiple measurement approaches is an efficient way to enhance the localization effects. Based on the anchor nodes move or not, it is separated into dynamic and static anchor node localization methods [7]. The usage of dynamic anchor node localization could highly decrease the numbers of anchor nodes as well enhance the localization effects. To decrease the number of static anchor nodes, decrease the cost of operations of entire networks, also enhance the localization effects, the localization method depends on dynamic anchor node has clear benefits [8,9]. An energy effective, range free, localization method on the basis of mobile anchor node for largescale machine-machine environments. An RSSI dependent localization method employed the RSSI value attained through sensors from mobile anchor nodes for estimating the location of the sensors [10]. The concept of localizing target nodes by shifting individual anchor nodes through computation intelligence based applications of H-best particle swarm optimization and particle swarm optimization.
At present, the security of WSNs has become primary concern. How to find different network attacks is one of the basic technologies which should be resolved [11]. The security study of WSN focus largely on the succeeding factors: (1) network intrusion detection systems and response models; (2) different network defense and attack models; (3) key management, authentication technology, and encryption algorithm; and (4) the security of data fusion and network routing [12,13]. Currently, various intrusion detection systems (IDSs) for WSN is rule based system in which the performances are based highly on the rule determined by means of security expert. Because of the large number of network traffics, the procedure of encoding rule is slow and expensive. For overcoming the limitations of rules based scheme, data mining technique is employed in IDSs for WSNs [14]. Data mining is an effective result to detect active network attacks on the basis of features hidden in the data of network behaviors.
This paper presents a new multi-objective manta ray foraging optimization (MRFO) based node localization with intrusion detection (MOMRFO-NLID) technique for WSN. The MOMRFO-NLID technique encompasses two major stages namely MRFO based localization of nodes and optimal Siamese Neural Network (OSNN) based intrusion detection. The OSNN technique involves the hyperparameter tuning of the traditional SNN using the MRFO algorithm and consequently increases the detection rate. The MOMRFO-NLID technique has the ability to optimally localize the unknown nodes and determine the existence of intrusions in the network. For examining the enhanced performance of the MOMRFO-NLID technique, a comprehensive experimental analysis is carried out and the results are inspected interms of distinct measures. In short, the key contributions are listed as follows.
• A novel MOMRFO-NLID technique consists of MRFO based localization of nodes and OSNN based intrusion detection is presented. To the best of our knowledge, the MOMRFO-NLID technique has been never presented in the literature.
• An intelligent MRFO based localization technique is designed to optimally localize the sensor nodes in WSN.
• The parameter tuning of the SNN model using MRFO technique using cross-validation (CV) helps to improve the predictive performance of the MOMRFO-NLID technique for unseen data.
The rest of the paper is arranged as follows. Section 2 provides the literature review and section 3 discusses the proposed model. Section 4 offers the performance validation and section 5 draws the conclusion.
Li et al. [15] presented a novel heuristic approach called PCCSO through 3 individual transmission approaches. The advantages of PCCSO reflect in improving the capability of local search, as well as in storing the computer memory. The experiment result shows that the PCCSO is increasingly high to CSO, PSO, as well as enhanced CSO in getting convergent. Next, the PCCSOs are used for DVHop to efficiently enhance the localization performance of unknown nodes when storing WSNs memory. In order to decrease the errors in the distance estimate phase, a node localization method for WSN based VP-DC is developed [16]. In distance estimate phase, first, the distance of all hops on the shortest transmission paths among the beacon and unknown nodes are estimated through the deployment of virtual partition method; Next, the length of shortest transmission paths is attained by adding the distance of all the hops; lastly, the unknown distance between nodes is attained on the basis of distance correction formula and optimum path search method.
In Annepu et al. [17], non-linear ANN methods like MLP and RBF are employed efficiently to non-linear node localization problems. Also, ANN based localization techniques can able to localize the mobile UN. Furthermore, the RBF using Gaussian activations has a small edge on the MLP using sigmoid activation since the wireless network is modelled usually by Gaussian random variables. Hao et al. [18] proposed node location models on the basis of SVM and Voronoi diagram. The main concept is to split the regions into various segments via anchor node and Voronoi diagram. The range of primary location of the targeted nodes is attained by localizing the targeted nodes in all the regions and the SVM is employed for optimizing the location of the targeted nodes precisely. The localization accuracy is examined through realtime experiments and simulations. The experiment result shows that the localization method is effective when compared to the optimum region election strategies based Voronoi diagram based on localization system as well as Weighted Voronoi diagram based on localization system localization algorithm with respect to localization precision.
Song et al. [19] presented a Monte Carlo node localizing method based on enhanced QUATRE optimization. Firstly, the model selects the higher quality node in the range of single hop of unknown node as temporary anchor node, and take the temporary anchor node and anchor node as the reference node to localization, for constructing a precise sampling region; Later, the enhance QUATRE optimization is employed for obtaining the calculated position of unknown node in the sampling region. Safaldin et al. [20] proposed an improved IDS through the adapted binary GWOSVM. This model employed three wolves, five wolfs and seven wolves for finding an optimal amount of wolves. The presented model’s aim is to improve the detection rate and IDS accuracy as well as decrease the runtime in the WSN environments by minimizing false alarm rate, and the amount of feature results from the IDS in the WSN environments.
Alruhaily et al. [21] proposed a multilayer IDS for WSN; where they adapt a defense indepth security approach, in which 2 layers of detections were placed. The initial layers are placed on the network edge sensor is distributed; it uses NB classifiers to make realtime decisions of the investigated packet. Next, it is placed on the cloud and utilizes RF multiclass classifiers for an indepth analysis of the investigated packet. Gavel et al. [22] proposed a method which employs the integration of multivarying kernel density estimate using distributed computing. This integration analyses the single possibility of the survival of data and calculates the global value of the PDF. PE model is used for effective in-network estimation and detection of intrusions at lower FPR.
Zhang et al. [23] proposed an IDS based TVP-IPSO method using PCA and SVM models. The PCA is intended at the data reduction dimension through compressing the data to decrease the power utilization, and IDS based SVM is deliberated for ensuring higher detection precision. In order to improve the SVM method and find its optimum parameter, the TVP-IPSO is employed for improving the convergence speed and IDS accuracy.
3 The Proposed MOMRFO-NLID Technique
In this study, a new MOMRFO-NLID technique is derived to achieve optimal node localization and intrusion detection in WSN. The MOMRFO-NLID technique encompasses a two-stage process namely MRFO based localization of nodes and OSNN based intrusion detection. The detailed working of these modules is given in the following sections.
3.1 Overview of MRFO Algorithm
The stimulus of MRFO is dependent on the smart foraging performances of MR. It contains 3 exclusive foraging rules of manta ray (MR) to recognizing optimum food sources. A few of the objectives were explained in the following:
• Chain foraging: At this point, a huge amount of MRs begins foraging, and it stands individually as a straight line development. The small male MR is supported by female MR and swims on top of abdomen and strikes the pectoral fin of female MR. Eventually, the plankton which is left by previous MR will be scooped up next MR. By cooperating with one another, it funnels maximal plankton as to its gills and improves the food resource.
• Cyclone foraging: During this component, when the concentration of plankton was superior, set of MRs are collected. The end of all plankton tails are related to head and it reproduces the spiral development to create the spiraling vertex from cyclone and the attained water has been pushed to top surface. It pulls plankton to its opened mouths.
• Somersault foraging: This metric has much splendid scenery obviously. When the MR classifies better food sources, afterward, it will conduct sequential backward somersault, surrounding the plankton to grab them near MRs. The somersault is a random, sequential, local and cyclical performance which guides MR to utilize optimum food. However, these foraging performances are extremely unseen at maximal times.
At this point, the MR is said that exist the ornamental species in sea world. However, its form is dreadful. It has a flat body and a couple of pectoral fins that are helpful to swimming freely. Besides, the couple of cephalic lobes was presented in front of its big, incurable mouths. Without sharp teeth, the MR feed planktons with small animal existing in the water. Whereas foraging, funnel the water as well as prey to mouth with horn-shaped cephalic lobe. The MR utilizes massive amount of planktons regularly. The well grown up MR is eating 5 kg of plankton daily. Besides, the MR is travel either solely or together with over 50, and the foraging rule was observed collected.
The MRFO has been operated by 3 foraging performances as Chain foraging, Cyclone foraging, and Somersault foraging. A few numerical techniques are provided below.
In MRFO, the MR monitors the place of plankton and move concerning it. When plankton concentration is superior, next the place is optimum in that, all places are upgraded with remarkable solutions recognized. This numerical technique of chain foraging was demonstrated as:
where represents the location of xth individuals at time n in dim is a dimensionality, rand implies an arbitrary vector from [0, 1], φ stands for weight coefficients, signifies the plankton with maximal focus.
During this approach, the MR was moved spirally to the location of food sources; the MR swim from the plankton [24]. It follows the one in front of it and swims near food spirally. The numerical notion of spiral-shaped event of MR was explained in the subsequent;
This performance upgrades to d space. The arithmetical method of cyclone foraging has been demonstrated as:
where α implies the weight coefficients, T illustrates the superior amount of iterations, and rand1 demonstrates the rand value from [0,1]. All the individuals explore the new place away from current optimum one by assigning a novel arbitrary place from the search space place. This procedure was extremely concentrated on MRFO for accomplishing wider global search; the mathematical operation was presented as:
where refers the arbitrary place, LB and UB refers the lower and upper restricts of dimensional correspondingly.
All MRs propose to move and somersault to novel place. Therefore, it maximizing the places and creates better places. The numerical illustration of this performance is showcased as:
where som depicts the somersault factor that elects a somersault threshold of MRs and Som= rand2 and rand3 determines 2 arbitrary values from [0, 1].
Therefore, the whole time complexity of MRFO was represented as:
where T implies the superior amount of iterations.
3.2 Design of MRFO Based Node Localization Process
The MRFO based localization method is applied to estimate the coordinate of sensors. The major goal of node localization in WSNs is to compute the coordinate of preferred node by reducing the objective function. The localization problems of WSNs are assumed as optimization issues that have been evolved by different meta-heuristic approaches. The given strategy has been employed to localize the sensors in WSN:
1. Upload M targeted node as well as N anchor nodes in a random manner in the sensor fields. All anchor nodes are composed of position awareness for identifying the position. Every anchor node as well as target node contains a broadcast range R.
2. Distance between the anchor and target nodes are estimated as well modify by additive Gaussian noises. The targeted nodes determine the distance with
3. The preferred nodes are named localized nodes when they contain three anchor nodes inside the transmission radius of the targeting nodes. A cause afterward this demand is that, depending upon tri-lateral localization method, coordinate of three anchor nodes (x1, y1), B(x2, y2), and C(x3, y3), as well as the distance among the targeting nodes di as well three anchor nodes are recognized. Afterward, the applications of trigonometric law of cosine/sine, the coordinate of targeting nodes is determined. In a similar manner, in multi-lateral targeting node estimated method, distance metrics of massive anchor nodes are applied to reduce the error from an original distance as well as evaluated distance.
4. In the event of localizable nodes, the MRFO based approach is executed separately for identifying the position of the targeting nodes. The MRs are invoked using the centroid of anchor node inside a communication radius using the given functions:
5. The HSSO-DE approach is applicable to identify the coordinate (x, y) of the targeting nodes which reduces the localization errors. The primitive applied in localization problems is a mean square distance among targeting nodes as well as an anchor node that has been reduced with the application of given notion:
6. The optimal measure (x, y) has been determined using HSSO-DE model once the number of rounds is limited.
7. The overall localization error can be determined after estimating the localizable target nodes NL. This is evaluated as a mean square of distance from determined node coordinate (Xi, Yi) whereas the actual node coordinates (xi, yi) can be represented as:
8. The procedure of 2 to 6 is continued still the targeting node is positioned. The localized model depends upon the maximum localization error E1 and count of unlocalized nodes
The localized node count gets enhanced as the iteration develops. Also, it maximizes the anchor nodes count inside the communication radius of the localizing targeted nodes as the evaluated location of the targeting nodes acts as anchor nodes in the successive iteration. It is used for limiting the issue of flip ambiguity that generates maximum localization error. Thus, processing duration for localization data of the targeting nodes enhances when the iterations are improved.
3.3 Design of OSNN Based Intrusion Detection Process
At this stage, the OSNN technique is utilized for determining the presence of intrusions in the network. The networks comprise of 2 indistinguishable FFNN joined at their yield. Amid training, all networks peruse a profile composed of genuine value and form its value at all the layers. The network enacts some neurons according to this value and upgrades its weight via error backpropagation, and finally, it creates an output profile i.e., related to the output of another network. The last output could be related to ith its respective ground truth values.
The presented Siamese neural network architecture includes twin NN (top & bottom network), whereas all of them include 3 dense layers (excluding the input layer). The input layer includes sixty four neurons, and other layers include 128 neurons. The activation function employed for the 1st three layers is “tanh”. In order to evade overfitting, dropouts are employed among layers 1 and 2, as well as layers 2 and 3 using 10%fraction. The 2 twin NN outputs are combined to make the output layer using single neuron, whereas the Euclidean distance is employed among the outputs of top and bottom network for measuring the comparison among the 2 outputs [25]. The datasets are divided into 2 partitions, thus two-third of the datasets are dedicated to training and remaining dedicated to testing. Random pair of record of the datasets are made; the pairs are positive when the 2 record belongs to the similar classes; or else the pairs are negative. This can be made by the contrastive loss functions:
whereas L represents the loss function, (X, Yp) denotes a positive pair, (X, Yn) indicates a negative pair, D signifies the distance among 2 records of the similar pair, and m represents the margin value that shows 2 records of negative pairs are distant enough. In order to attain the value of networks weight where the loss is optimal, the RMSprop optimization algorithms are employed.
In order to update the weight parameters of the SNN model, the MRFO algorithm can be employed.
Step 1: Initialize the parameters of the MRFO algorithm.
Step 2: Train the SNN model and compute the fitness function (FF) using MRFO algorithm.
The 10-fold CV approach has been employ to evaluate the FF. In 10-fold CV, the trained dataset has been arbitrarily separated as to group of 10 mutually exclusive subsets of almost matching sizes where 9 subsets are employed to trained drives and the last subset has been employed for testing purposes. This procedure develops iterated ten times to all subsets are employed to testing method. The FF is demonstrated as 1 − CAvalidation of the 10-fold CV manner during the trained dataset as provided in Eq. (16). Besides, the solutions with superior CAvalidation outcomes in lesser fitness value.
where, yc and yf represents the true and false classifier count correspondingly.
Step 3: Updating the location of MRs. At this stage, the local and global best positions of the MRs are updated based on the value of the FF.
Step 4: Termination Condition
The above steps 2–3 get iterated till the termination condition gets satisfied.
This section investigates the performance of the proposed MOMRFO-NLID technique in MATLAB tool. In addition, the results are inspected under varying anchor node density (AND), communication range, and measuring distance. Besides, the intrusion detection results are examined on benchmark KDD Cup’99 dataset. Tab. 1 and Fig. 2 offer a brief ALE analysis of the MOMRFO-NLID technique under distinct AND. The experimental results demonstrated that the MOMRFO-NLID technique has accomplished effective outcomes with minimal ALE. For instance, with the AND of 5%, the MOMRFO-NLID technique has received a lower ALE of 3.16 m whereas the RSSI, TOA, and RSSI-TOA techniques have obtained a higher ALE of 10.41, 9.92, and 4.99 m respectively. Likewise, with the AND of 15%, the MOMRFO-NLID approach has received a lesser ALE of 2.17 m whereas the RSSI, TOA, and RSSI-TOA methodologies have reached a superior ALE of 8.44, 7.95, and 3.46 m correspondingly. Similarly, with the AND of 25%, the MOMRFO-NLID manner has received a minimal ALE of 1.93 m whereas the RSSI, TOA, and RSSI-TOA methods have obtained an increased ALE of 8.05, 7.01, and 3.16 m correspondingly.
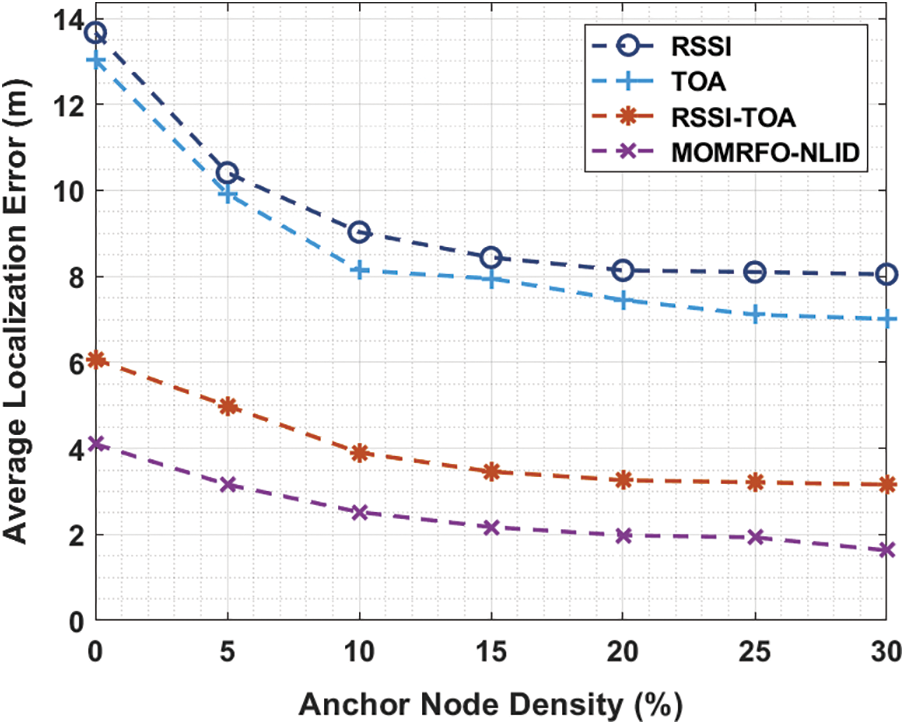
Figure 2: ALE analysis of MOMRFO-NLID model under varying AND
Tab. 2 and Fig. 3 gives a brief ALE analysis of the MOMRFO-NLID method under varying communication ratio. The experimental outcomes exhibited that the MOMRFO-NLID algorithm has accomplished effectual results with lesser ALE.
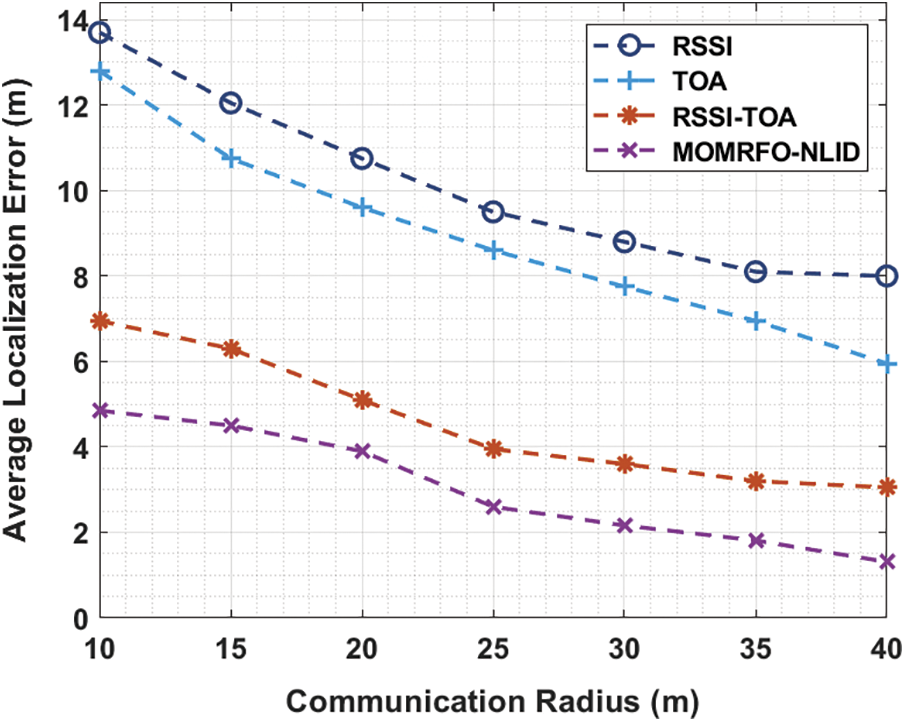
Figure 3: ALE analysis of MOMRFO-NLID model under varying communication radius
For instance, with the AND of 5%, the MOMRFO-NLID manner has received a lower ALE of 4.29 m whereas the RSSI, TOA, and RSSI-TOA techniques have gained a higher ALE of 12.54, 11.99, and 7.11 m correspondingly. In addition, with the AND of 15%, the MOMRFO-NLID system has received a lower ALE of 3.36 m whereas the RSSI, TOA, and RSSI-TOA manners have obtained a higher ALE of 11.06, 10.46, and 5.38 m respectively. Also, with the AND of 25%, the MOMRFO-NLID approach has received a reduced ALE of 2.02 m whereas the RSSI, TOA, and RSSI-TOA methods have reached a maximum ALE of 8.34, 7.06, and 3.06 m respectively.
Tab. 3 and Fig. 4 provides a detailed ALE analysis of the MOMRFO-NLID manner under distinct measuring position (MP).
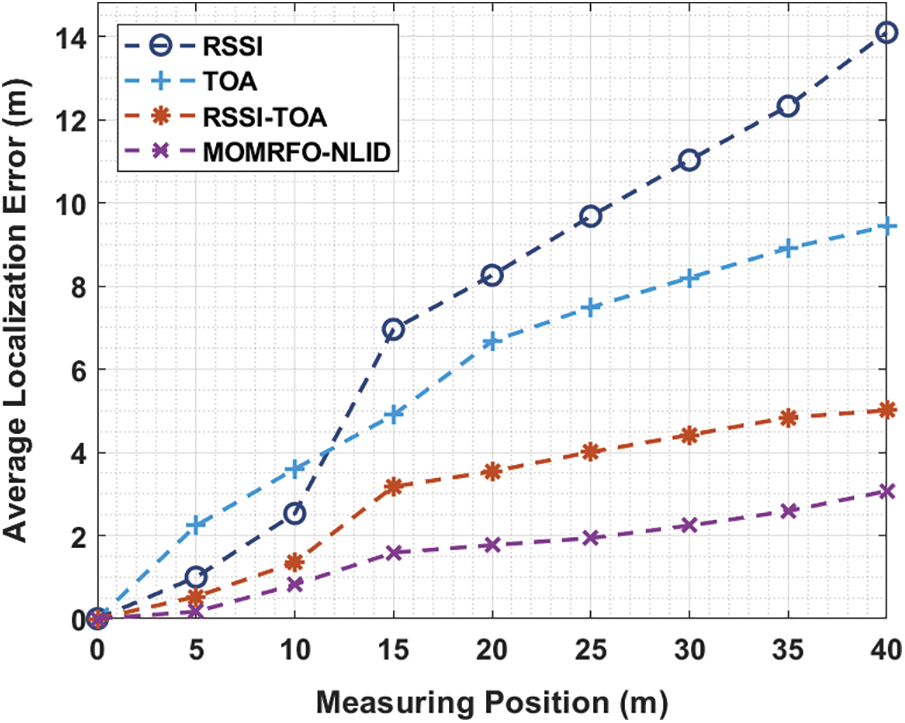
Figure 4: ALE analysis of MOMRFO-NLID model under varying measuring position
The experimental results demonstrated that the MOMRFO-NLID technique has accomplished effective outcomes with minimal ALE. For instance, with the MP of 5 m, the MOMRFO-NLID technique has received a lower ALE of 0.17 m whereas the RSSI, TOA, and RSSI-TOA techniques have obtained a higher ALE of 1.00, 2.24, and 0.53 m respectively. At the same time, with the MP of 15 m, the MOMRFO-NLID manner has received a lower ALE of 1.59 m whereas the RSSI, TOA, and RSSI-TOA techniques have obtained a superior ALE of 6.96, 4.90, and 3.18 m correspondingly. Eventually, with the MP of 35 m, the MOMRFO-NLID method has received a lower ALE of 2.59 m whereas the RSSI, TOA, and RSSI-TOA approaches have reached a maximum ALE of 12.33, 8.91, and 4.84 m respectively.
The intrusion detection performance of the MOMRFO-NLID technique on the applied KDDCup’99 dataset is given in Tab. 4. The results have shown that the MOMRFO-NLID technique has effectually classified all different types of attacks. For instance, the MOMRFO-NLID technique has classified the DoS attack with an accuracy of 0.9961, detection rate of 0.9925, training time of 0.0021 s, and testing time of 0.0003 s. Moreover, the MOMRFO-NLID manner has classified the Probe attack with an accuracy of 0.9650, detection rate of 0.9640, training time of 0.0009 s, and testing time of 0.0006 s. Furthermore, the MOMRFO-NLID approach has classified the R2L attack with an accuracy of 0.7845, detection rate of 0.6273, training time of 0.0041 s, and testing time of 0.0005 s. Lastly, the MOMRFO-NLID method has classified the U2R attack with an accuracy of 0.9384, detection rate of 0.7525, training time of 0.0021 s, and testing time of 0.0003 s.
A detailed comparison study of the MOMRFO-NLID technique with existing techniques interms of accuracy is made in Tab. 5 and Fig. 5. The results showcased that the MOMRFO-NLID technique has attained maximum DoS classification results with the accuracy of 0.996 whereas the NB, SVM, DT, AdaBoost-DT, RF, and CVM techniques have resulted in an ineffective outcome with the accuracy of 0.995, 0.990, 0.020, 0.010, 0.010, and 0.980 respectively. Eventually, the results outperformed that the MOMRFO-NLID method has reached maximal Probe classification outcomes with the accuracy of 0.965 whereas the NB, SVM, DT, AdaBoost-DT, RF, and CVM methods have resulted in an ineffective outcome with the accuracy of 0.920, 0.100, 0.100, 0.310, 0.090, and 0.950 respectively.
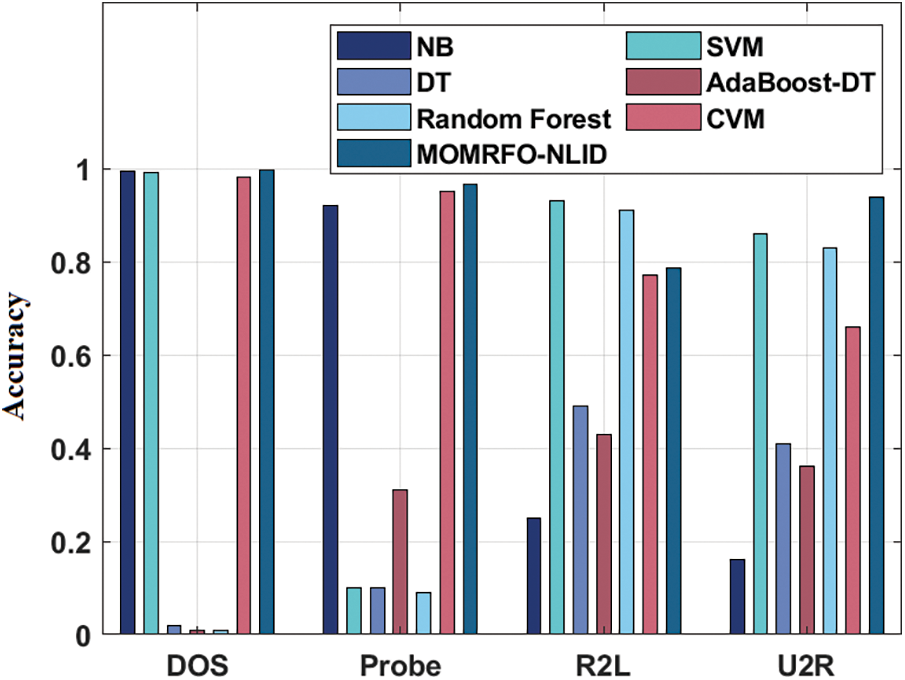
Figure 5: Accuracy of MOMRFO-NLID model with existing techniques
Concurrently, the results portrayed that the MOMRFO-NLID methodology has attained maximum R2L classification outcomes with the accuracy of 0.785 whereas the NB, SVM, DT, AdaBoost-DT, RF, and CVM techniques have resulted in an ineffective outcome with the accuracy of 0.250, 0.930, 0.490, 0.430, 0.910, and 0.770 correspondingly.
Lastly, the results depicted that the MOMRFO-NLID technique has reached maximal U2R classification results with an accuracy of 0.938 whereas the NB, SVM, DT, AdaBoost-DT, RF, and CVM methods have resulted in an ineffective outcome with the accuracy of 0.160, 0.860, 0.410, 0.360, 0.830, and 0.660 correspondingly. From the above mentioned result analysis, it is proved that the MOMRFO-NLID technique is found to be an appropriate tool for effective node localization and intrusion detection in WSN environment.
This paper has presented an effective MOMRFO-NLID technique for WSN to optimally localize the unknown nodes and determine the existence of intrusions in the network. The MOMRFO-NLID technique encompasses two major stages namely MRFO based localization of nodes and OSNN based intrusion detection. The OSNN technique involves the hyperparameter tuning of the traditional SNN using the MRFO algorithm and consequently increases the detection rate. For examining the enhanced performance of the MOMRFO-NLID technique, a comprehensive experimental analysis is carried out and the results are inspected interms of distinct measures and accomplished a maximum accuracy of 0.921. The experimental values highlighted the better performance of the MOMRFO-NLID technique over the existing techniques interms of different evaluation parameters. In future, the performance of the MOMRFO-NLID technique can be boosted by the use of load balancing and scheduling approaches.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. L. Zhang, Z. Yang, S. Zhang and H. Yang, “Three-dimensional localization algorithm of WSN nodes based on RSSI-TOA and single mobile anchor node,” Journal of Electrical and Computer Engineering, vol. 2019, pp. 1–8, 2019. [Google Scholar]
2. M. Shafiq, H. Ashraf, A. Ullah, M. Masud, M. Azeem et al., “Robust cluster-based routing protocol for iot-assisted smart devices in wsn,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3505–3521, 2021. [Google Scholar]
3. A. Ullah, M. Azeem, H. Ashraf, N. Jhanjhi, L. Nkenyereye et al., “Secure critical data reclamation scheme for isolated clusters in IoT enabled WSN,” IEEE Internet of Things Journal, 2021. https://doi.org/10.1109/JIOT.2021.3098635. [Google Scholar]
4. G. Kadiravan, A. Sariga and P. Sujatha, “A novel energy efficient clustering technique for mobile wireless sensor networks,” in 2019 IEEE Int. Conf. on System, Computation, Automation and Networking (ICSCAN), pp. 1–6, Pondicherry, India, 2019. [Google Scholar]
5. G. Han, J. Jiang, C. Zhang, T. Q. Duong, M. Guizani et al., “A survey on mobile anchor node assisted localization in wireless sensor networks,” IEEE Communication Surveys & Tutorials, vol. 18, no. 3, pp. 2220–2243, 2016. [Google Scholar]
6. J. Uthayakumar, M. Elhoseny, and K. Shankar, “Highly reliable and low-complexity image compression scheme using neighborhood correlation sequence algorithm in WSN,” IEEE Transactions on Reliability, vol. 69, no. 4, pp. 1398–1423, 2020. [Google Scholar]
7. R. Zhang and X. Xiao, “Intrusion detection in wireless sensor networks with an improved nsa based on space division,” Journal of Sensors, vol. 2019, pp. 1–20, 2019. [Google Scholar]
8. J. Zheng and B. X. Zhang, “Wireless Sensor Network Technology,” Tianjin, China, China Machine Press, 2012. [Google Scholar]
9. S. Arjunan, S. Pothula, and D. Ponnurangam, “F5n-based unequal clustering protocol (F5NUCP) for wireless sensor networks,” International Journal of Communication Systems, vol. 31, no. 17, pp. e3811, 2018. [Google Scholar]
10. I. Butun, S. D. Morgera, and R. Sankar, “A survey of intrusion detection systems in wireless sensor networks,” IEEE Communication Surveys & Tutorials, vol. 16, no. 1, pp. 266–282, 2014. [Google Scholar]
11. J. Uthayakumar, T. Vengattaraman, and P. Dhavachelvan, “A new lossless neighborhood indexing sequence (NIS) algorithm for data compression in wireless sensor networks,” Ad Hoc Networks, vol. 83, pp. 149–157, 2019. [Google Scholar]
12. A. Ghosal and S. Halder, “A survey on energy efficient intrusion detection in wireless sensor networks,” Journal of Ambient Intelligence and Smart Environments, vol. 9, no. 2, pp. 239–261, 2017. [Google Scholar]
13. S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]
14. V. Bhuse, A. Gupta and A. Al-Fuqaha, “Detection of masquerade attacks on wireless sensor networks,” in 2007 IEEE Int. Conf. on Communications, pp. 1142–1147, Glasgow, Scotland, UK, 2007. [Google Scholar]
15. J. Li, M. Gao, J. -S. Pan and S. -C. Chu, “A parallel compact cat swarm optimization and its application in DV-Hop node localization for wireless sensor network,” Wireless Networks, vol. 27, no. 3, pp. 2081–2101, 2021. [Google Scholar]
16. Y. Meng, Q. Zhi, M. Dong and W. Zhang, “A node localization algorithm for wireless sensor networks based on virtual partition and distance correction,” Information, vol. 12, no. 8, pp. 330, 2021. [Google Scholar]
17. V. Annepu, A. Rajesh and K. Bagadi, “Radial basis function-based node localization for unmanned aerial vehicle-assisted 5G wireless sensor networks,” Neural Computing and Applications, vol. 33, pp. 12333–12346, 2021. [Google Scholar]
18. Z. Hao, J. Dang, Y. Yan and X. Wang, “A node localization algorithm based on voronoi diagram and support vector machine for wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 17, no. 2, pp. 155014772199341, 2021. [Google Scholar]
19. L. Song, X. Jiang, L. Wang and X. Hu, “Monte carlo node localization based on improved QUARTE optimization,” Journal of Sensors, vol. 2021, pp. 1–12, 2021. [Google Scholar]
20. M. Safaldin, M. Otair and L. Abualigah, “Improved binary gray wolf optimizer and SVM for intrusion detection system in wireless sensor networks,” Journal of Ambient Intelligence and Human Computing, vol. 12, no. 2, pp. 1559–1576, 2021. [Google Scholar]
21. N. M. Alruhaily and D. M. Ibrahim, “A multi-layer machine learning-based intrusion detection system for wireless sensor networks,” International Journal of Advanced Computer Science and Applications, vol. 12, no. 4, pp. 281–288, 2021. [Google Scholar]
22. S. Gavel, A. S. Raghuvanshi and S. Tiwari, “A novel density estimation based intrusion detection technique with Pearson’s divergence for wireless sensor networks,” ISA Transactions, vol. 111, pp. 180–191, 2021. [Google Scholar]
23. T. Zhang, D. Han, M. D. Marino, L. Wang and K. C. Li, “An evolutionary-based approach for low-complexity intrusion detection in wireless sensor networks,” Wireless Personal Communications, pp. 1–24, 2021. https://doi.org/10.1007/s11277-021-08757-w. [Google Scholar]
24. M. Zounemat-Kermani, A. Mahdavi-Meymand, M. Fadaee, O. Batelaan and R. Hinkelmann, “Groundwater quality modeling: On the analogy between integrative PSO and MRFO mathematical and machine learning models,” Environmental Quality Management, p. tqem.21775, pp. 1–11, 2021. [Google Scholar]
25. M. Shalaby, N. A. Belal and Y. Omar, “Data clustering improves siamese neural networks classification of Parkinson’s disease,” Complexity, vol. 2021, pp. 1–9, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |