DOI:10.32604/iasc.2022.022586
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.022586 | |
| Article |
Error Rate Analysis of Intelligent Reflecting Surfaces Aided Non-Orthogonal Multiple Access System
1Department of ECE, SRM Institute of Science and Technology, Vadapalani, Chennai, 600026, India
2Department of ECE, SRM Institute of Science and Technology, SRM Nagar, Kattankulathur, Chengalpattu, 603203, India
*Corresponding Author: Vijayakumar Ponnusamy. Email: vijayakp@srmist.edu.in
Received: 12 August 2021; Accepted: 27 October 2021
Abstract: A good wireless device in a system needs high spectral efficiency. Non-Orthogonal Multiple Access (NOMA) is a technique used to enhance spectral efficiency, thereby allowing users to share information at the same time and same frequency. The information of the user is super-positioned either in the power or code domain. However, interference cancellation in NOMA aided system is challenging as it determines the reliability of the system in terms of Bit Error Rate (BER). BER is an essential performance parameter for any wireless network. Intelligent Reflecting Surfaces (IRS) enhances the BER of the users by controlling the electromagnetic wave propagation of a given channel. IRS is able to boost the Signal to Noise Ratio (SNR) at the receiver by introducing a phase shift in the incoming signal utilizing cost-effective reflecting materials. This paper evaluates users’ error rate performance by utilizing IRS in NOMA. The error probability expression of users is derived under Rayleigh and Rician fading channel. The accuracy of derived analytical expressions is then validated via simulations. Impact of power allocation factor, coherent and random phase shifting of IRS is evaluated for the proposed IRS-NOMA system.
Keywords: NOMA; interference cancellation; bit error rate; signal to noise ratio
The role of wireless communication systems has become inevitable across domains. The utility has increased with devices and various applications. Then, there is a need for massive connectivity with ultra-reliable and low latency among devices [1,2]. Appropriate techniques are developed and similar techniques are integrated into the Fifth generation (5G) wireless communication system to meet these requirements. This combined effect of technologies fulfills essential requirements, including high achievable rate, user fairness, energy efficiency, high spectral efficiency, low latency and achieving extremely low error rate within a wireless communication system [3,4]. To fulfill these demands of achieving enhanced spectral efficiency and low-latent transmission, Non-Orthogonal Multiple Access (NOMA) is utilized as a channel accessing mechanism in 5G and beyond cellular systems [5,6]. NOMA enables simultaneous transmission from multiple users to share their information by super-positioning either on the power or code domain. In the power domain, different power levels are assigned for users based on the channel fading conditions. In case of two-user NOMA system, users are categorized as near user and far user. It is assumed that near user has better channel condition than far user. Therefore, near user is allocated with less power and far user with high power. NOMA differs from conventional OMA techniques wherein a single user alone is allowed to access resources in a given time or frequency. It’s feasible with NOMA as it employs Successive Interference Cancellation (SIC) mechanism at the receiver to decode the user’s information based on their power allocation order. SIC decodes the highest power signal and then detects the concerned user’s signal, thereby canceling the user with the highest power allocation. Multiple users in the NOMA system can complicate the SIC mechanism. Accuracy in SIC decides the user’s error rate at the receiving end.
With the evolution of integrated electronics [7], Intelligent Reflecting Surfaces (IRS) is a fabricated structure to make the complete wireless system intelligent [8]. IRS has been integrated with other technologies, which require a highly reliable and energy-efficient system. It interacts with the environment and enables constructive energy focusing on the users. The incident signal at IRS is reflected by an angle to achieve the energy focusing in the broadcast environment. The reflected signal is strengthened to extend the coverage area of the system. In recent times, many research works utilize the benefits of IRS and NOMA to accomplish the demands of the next-generation wireless communication system [9].
1.1.1 Error Rate Analysis for NOMA Systems
In the research work [10], error rate performance of cooperative-NOMA network is analyzed. The expression of error probability is derived and the effect of power allocation on BER performance is analyzed. In [11], BER performance is investigated for two-user NOMA system with square Quadrature Amplitude Modulation (QAM) scheme. The authors of [12] consider the analysis of BER in downlink-NOMA system under Rayleigh fading channel for Binary Phase Shift Keying (BPSK) modulation scheme. The BER analysis of relay assisted NOMA system is considered in [13]. Pair-wise error probability expression is derived by considering Simultaneous Wireless Information Power Transfer (SWIPT). The exact expression of average BER for a two-user NOMA system is obtained for generalized frequency in the flat-fading channel [14]. In [15], BER performance for two-user NOMA system is analyzed by considering SIC for both uplink and downlink transmission. Similarly, the authors of [16] also address BER performance in downlink NOMA system with consideration of SIC errors. The average bit error probability is derived for Space-Shift-Keying (SSK)-NOMA system with three users in [17]. The error rate performance of cooperative Orthogonal Frequency Division Multiplexing (OFDM)-NOMA system with index modulation is investigated in [18]. The Maximum-Likelihood detector (ML) and greedy detector are considered for deriving the analytical expression of BER at the destination. The error probability of the OFDM-NOMA system is analyzed in [19] by considering Quadrature Phase Shift Keying (QPSK) modulation. The BER performance is analyzed over Rayleigh, Rician and Nakagami-m fading channels in [20] by using Minimum-Mean-Square-Error (MMSE) detector for downlink NOMA system.
1.1.2 Error Rate Analysis for IRS Aided Systems
IRS is utilized for improving error rate performance in the wireless communication system. The research works of [21–23] analyze the error rate of IRS aided transmission. IRS acts as an access point as well as the reflector in [21]. Blind transmission (without knowing the environment) is assumed between the transmitter and users. Enhanced symbol error probability is achieved in IRS aided system. SNR performance of IRS aided wireless system is compared with massive MIMO in [22]. It also provides the relationship between a number of array elements and SNR. It is stated that SNR in the IRS system varies nonlinearly with the number of reflective elements, wherein massive MIMO has linear variation. The closed-form bit error rate expression of IRS-NOMA is derived in [23], the number of reflecting elements in IRS is equally divided to enhance the signal propagation for the near and far user.
Motivated by the above-mentioned recent works on NOMA and IRS, the proposed work considers NOMA-based wireless communication supported by IRS. The closed form expression of bit error probability in two-user downlink NOMA system is derived in [15]. Based on [15,21], the error probability of the two-user downlink IRS-NOMA system is derived in this paper. In the article [15], the near user signal is modulated using QPSK and BPSK modulation is used for far user. In this article, BPSK modulation is considered for both users. The main contributions of this article are
• Closed-form expressions of average error probability of received signal at IRS-NOMA are derived by considering SIC mechanism under Rayleigh and Rician fading channel.
• We consider Coherent and Random phase shifting at IRS and evaluate the BER performance of users.
• Optimum power allocation on BER performance is investigated in the proposed IRS-NOMA system.
This article is organized as follows. IRS-NOMA system model is described in Section 2. In Section 3, the analytical expression of NOMA users is derived. The BER performance of the proposed IRS-NOMA system is discussed in Sections 4 and 5. The article is concluded in Section 6.
The detailed symbols and corresponding descriptions are listed in Tab. 1.
2 System Model for Proposed IRS Supported NOMA Communication
A downlink IRS-supported NOMA system is considered, as shown in Fig. 1. The proposed system consists of two users, IRS with N passive reflective elements and a Base Station (BS). In NOMA system, users are ordered and allocated with different power levels according to their average channel power. In the proposed two-user IRS-NOMA system, near user is termed as U1 and the far user is termed as U2. The power allocation (α) should satisfy the condition
where Pt and si (i = 1, 2) denote the total transmit power and modulated symbols of users. The product terms Ptα and Pt(1 − α) are substituted as a1 and a2 for near and far users respectively.
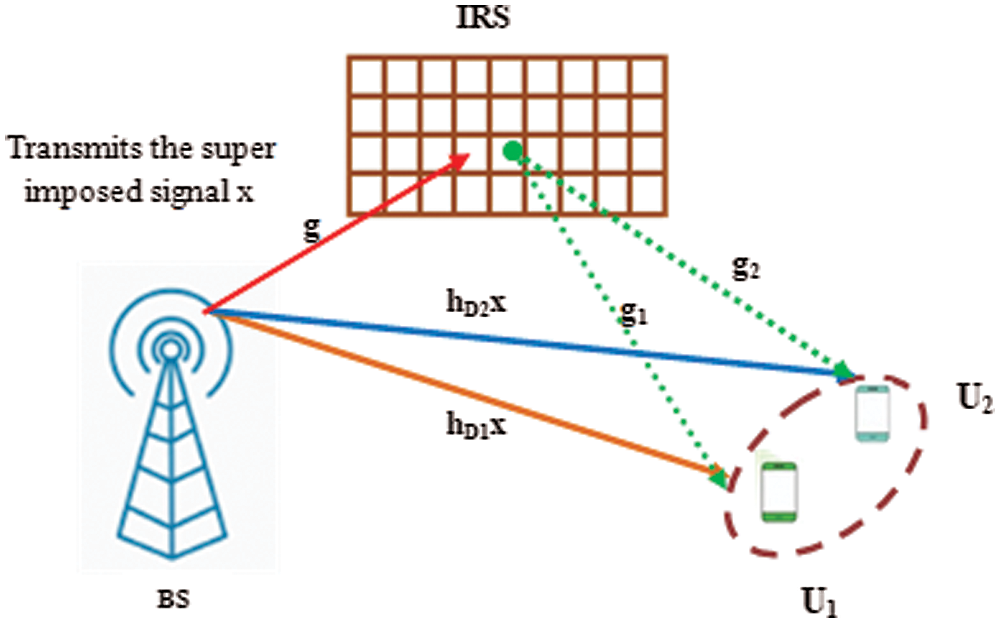
Figure 1: An illustration of IRS-NOMA aided transmission
2.1 Impact of IRS on Signal Transmission
In the system proposed, IRS is kept in between the BS and users to aid NOMA transmission. The users are assumed to receive a signal from BS and IRS. IRS is a reflecting array made up of periodic metasurfaces. Metasurfaces are artificially composite materials, which have been utilized in wireless communication for introducing considerable phase shift on the incident signal [24]. The array elements are termed as cell fabricated with PIN or varactor diode to introduce phase shift on the RF signal. The unusual characteristics of metamaterials in IRS make it to interrelate with both electric and magnetic fields of the input signal. The collective effect of array elements is utilized to focus the energy in the directions of users. As illustrated in Fig. 1, the IRS receives the incoming superimposed signal (x) and introduces the phase shift of θ on the reflected signal. The users in the focusing area can receive the reflected signal from IRS. The phase shift θ can be tuned or adjusted to focus and de-focus the energy in the relevant and irrelevant directions.
This paper assumes that the users receive direct signal as well as reflected signal. We analyze the IRS aided NOMA transmission in both Rayleigh as well as Rician fading. The direct channel fading coefficients between BS-U1 and BS-U2 are denoted as hD1 and hD2. Let g denotes channel fading between BS and IRS, g1 and g2 be the channel coefficients between IRS and users (U1,U2). Therefore, the received signals at the end-users (U1,U2) are written as
where hD1x and hD2x represent the direct signal received at the users from BS.
In (4), K1 is the Rician factor of hDk,
2.3 Types of Phase-Shifting at IRS
Introduction of phase shift θ at IRS can be coherent phase shifting and random phase shifting as mentioned in [21]. In the case of intelligent transmission, it is assumed that IRS has known the channel characteristics perfectly; the reflection angle θ between IRS and users could be adjusted to maximize the received signal strength at the user. The IRS introduces phase shift randomly in the random phase-shifting method. In this paper, both phase-shifting methods are considered at IRS to evaluate the BER performance.
In this section, the average bit error probability of users (U1 and U2) in IRS-NOMA system is derived by assuming BPSK modulation for both the users under Rayleigh and Rician fading channel.
3.1 Average Error Probability of Far User Under Rayleigh Fading
For the BPSK modulation signal, the constellations of the received signal at U1 and U2 are as illustrated in Fig. 2. (b1, b2) represents the binary symbols of U1 and U2. The ML detector [26] is employed to decode the user symbols. The decision boundary depends on the amount of AWGN noise (ni) present in the received signal. For BPSK signal, decision boundary could be
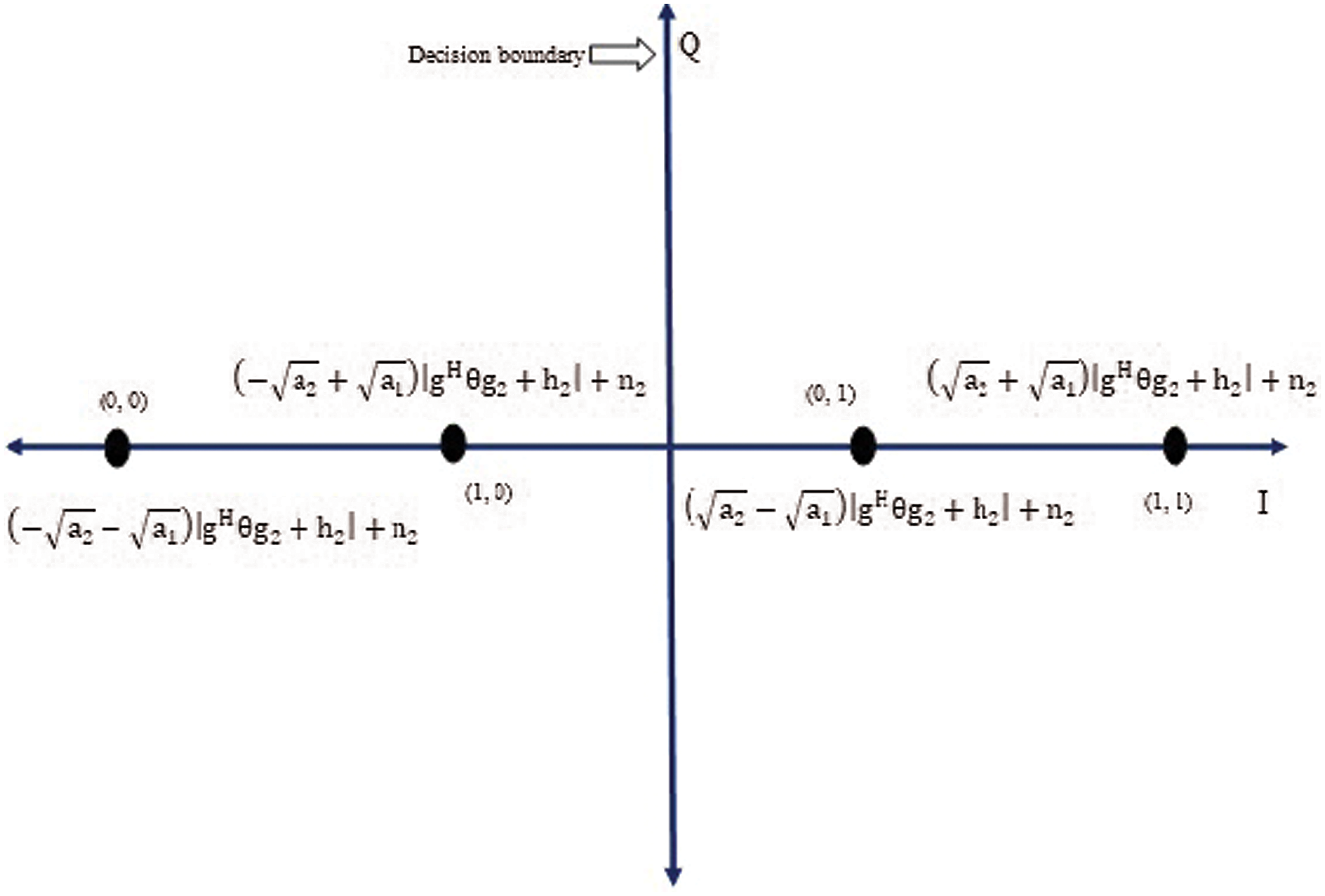
Figure 2: Signal constellation map for two-user IRS-NOMA system
Using the ML detection principle, the conditional error probability is written as
The error probability expressed in (8) can be written using complex Q-function [[28], Eq. (7.108)] with noise variance of
Eq. (9) can be represented using instantaneous SNR as
In (10) and (11) γ1 and γ2 represent SNRs,
Average error probability in AWGN over fading channel at far user is calculated by integrating the product of Gaussian Q-function and channel fading Probability Density Function (PDF)
By substituting the Gaussian Q-function (10) can be rewritten using [[29], Eq. (5.2)]
where PDF of the SNRs for the Rayleigh distribution is given by [[29], Eq. (5.4)]
Using [[29], Eq. (5.3)], the term
Using [[29], Eq. (5.5)],
where
3.2 Average Error Probability of Near User Under Rayleigh Fading
In NOMA system, the near user signal is decoded after canceling the far user information using SIC process. Far user information can be decoded correctly or erroneously during SIC process. Therefore, the error probability of near user is calculated as the sum of error probability under far user information decoded successfully and erroneously. The constellation map is shown in Fig. 3.
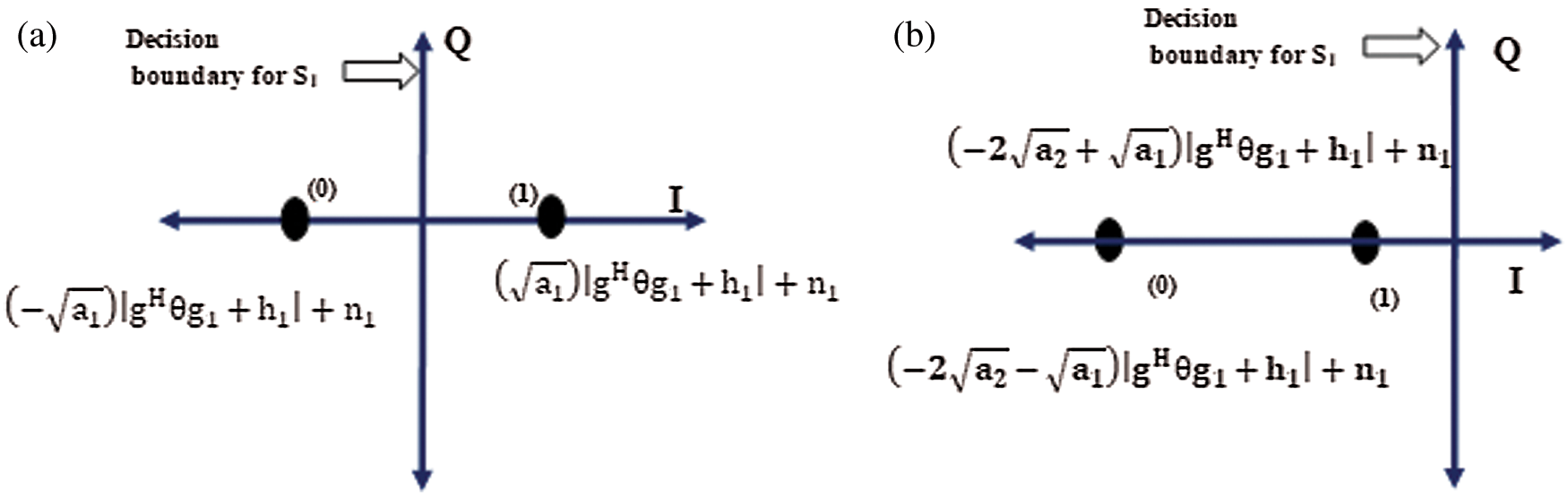
Figure 3: Signal constellation map for U1 signal detection (a) Decision boundary for U1 when U2 is detected successfully, (b) Decision boundary for U1 when U2 is detected unsuccessfully
In (20), P1(e) represents the probability of error at U1, p1(e|U2successful) indicates error probability of U1, while U2 the signal is detected successfully. p1(e|U2unsuccessful) represents error probability of U1, when U2. signal is detected incorrectly. The constellation map of correct decoding and incorrect decoding of U2 is illustrated in Fig. 3. U1 signal is affected by channel fading and AWGN noise after SIC mechanism. During the detection of U1 symbol, the error probability of successful detection of U2 the symbol is considered as prior probability of different superimposed signals. Therefore, p1(e|U2successful) is expressed as
Using conditional probability of two events A and B,
The first term
where,
Therefore error probability of U1 when s2 detected correctly is calculated by substituting (23) and (24) in (22) as
In case of incorrect detection of s2, this is shown in Fig. 3b. When the symbol b2 = 1 is transmitted for U2 and is decoded as b2 = −1. Thus, the error probability of symbol s1 at U1 is calculated by taking the product of the error probability of every symbol in the constellation map shown in Fig. 3b. with respective prior error probability of U2 symbol. From the constellation map, p1(e|U2unsuccessful) is expressed as
P1(e|U2unsuccessful) in (26) is rewritten using ML principle as
The first
where
By substituting (28) and (29) in (27), P1(e|U2unsuccessful) is written as
By combining (25) and (30) and using (13), (14), (17) and (18) the probability of error for near user U1 signal is written using as,
3.3 Average Error Probability of Far User Under Rician Fading
The average error probability of far users under the Rician fading channel is derived by substituting the PDF and MGF of Rician distribution in (14). Where PDF of Rician fading is expressed using [[29], Eq. (5.10)]
where Io [] represents the modified Bessel function. Similarly, the MGF of Rician fading using [[29], Eq. (5.11)] is represented by
By substituting alternate representation of MGF for Rician fading in (17), the average error probability of far user is expressed as
Therefore by substituting (34), the average error probability for the far user under Rician fading can be expressed as
3.4 Average Error Probability of Near User Under Rician Fading
Similarly, the error probability of successful detection of U2 signal at near user under Rician fading can be expressed by introducing (32) and (33) in (25)
The error probability of unsuccessful detection of U2 signal at near user for Rician fading is expressed by rewriting (30)
Thus the total average error probability at U1 under Rician fading is calculated by summing (36) and (37)
In this section, we analyze the error probability expressions of near and far user numerically and verify the results via simulations. The simulation parameters are listed in Tab. 2.
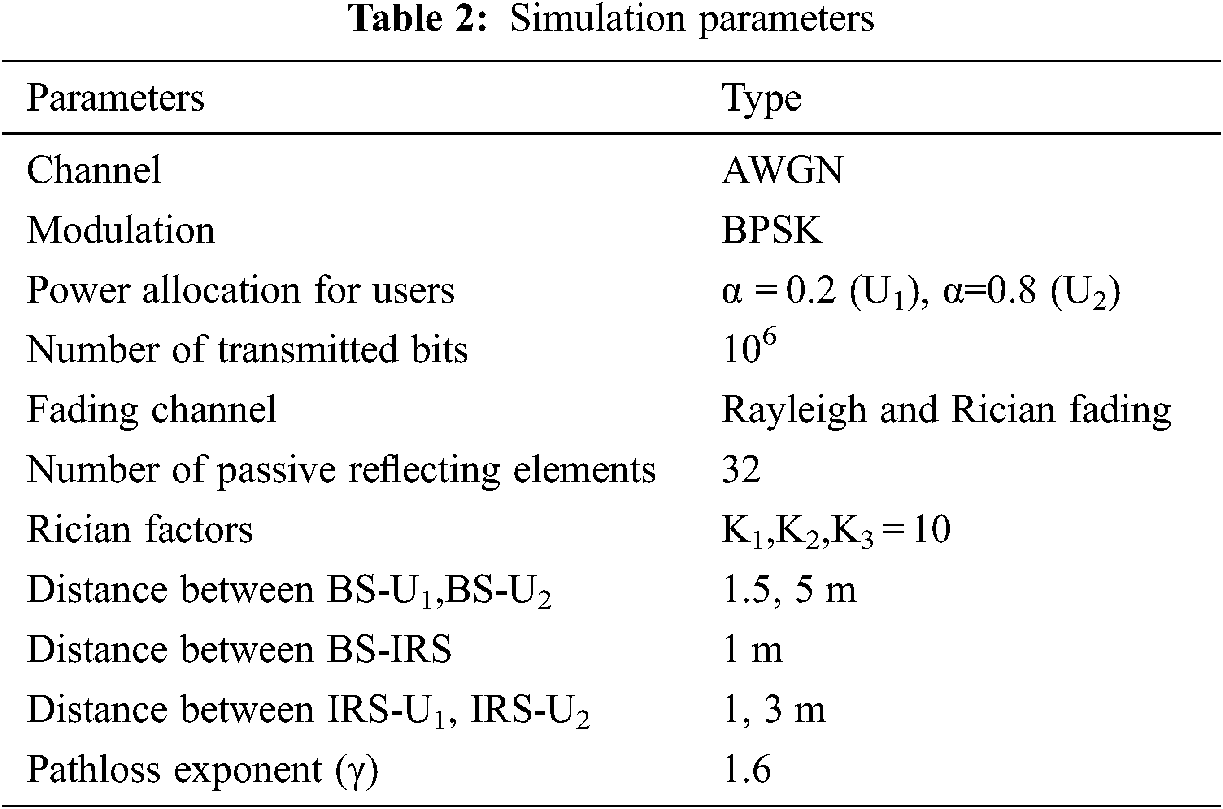
4.1 Theoretical BER Evaluation of Proposed Method with Coherent Phase Shifting
In the simulation results, near and far users are denoted as U1 and U2. The IRS-NOMA transmission is investigated at an indoor environment model [30] with a path loss exponent of 1.6. Far user is allocated with the factor of α =0.8, wherein near user with α =0.2. The derived analytical expressions for Rayleigh [(19) and (31)] and Rician fading [(35) and (38)] channel are verified via simulations as shown in Figs. 4a and 4b. The simulation results show the accuracy of the derived expression. We also compare the performance of the derived BER expressions of the proposed two-user IRS-NOMA system with simulation results.
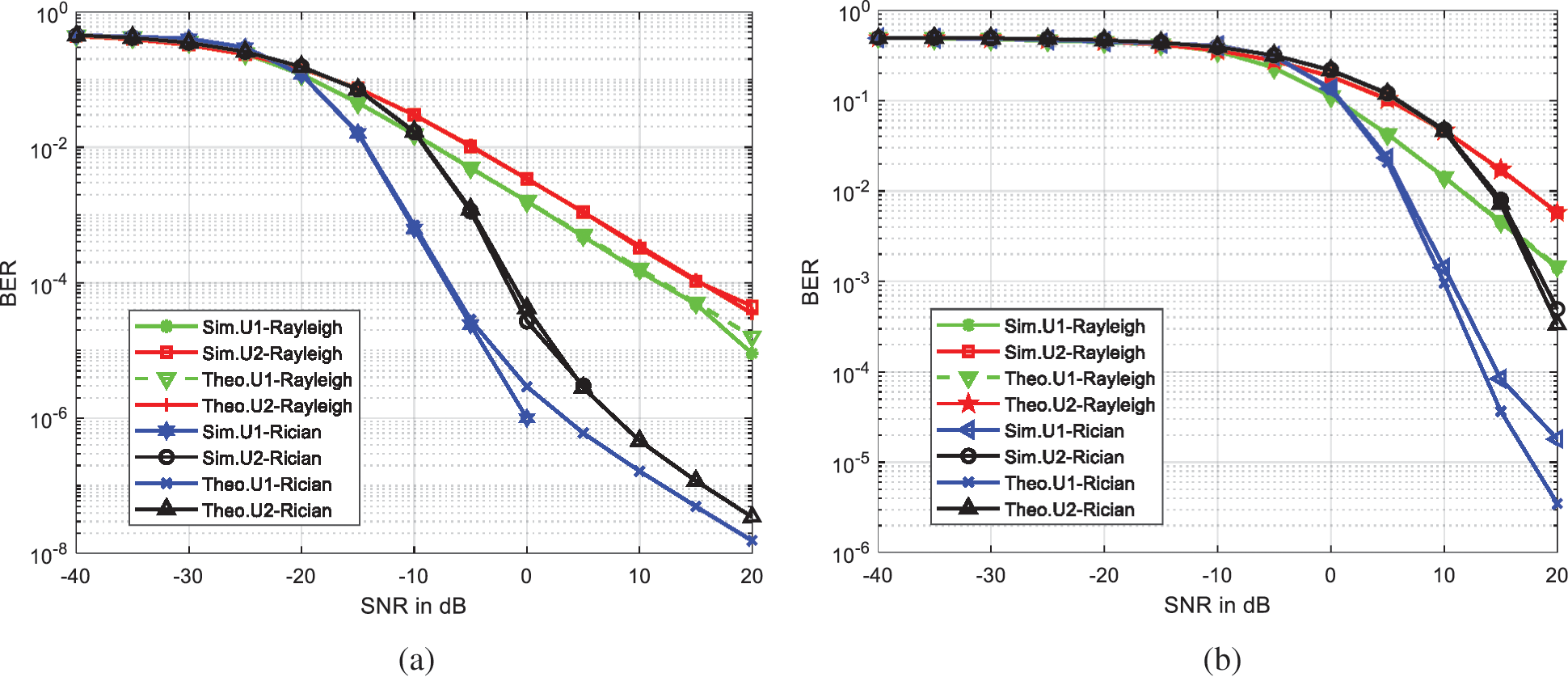
Figure 4: Performance verification of derived expressions under Rayleigh and Rician channel (a) coherent phase shifting, (b) random phase shifting
4.2 Theoretical BER Evaluation of Proposed Method with Random Phase Shifting
Fig. 4b illustrates the analytical BER performance of the IRS-NOMA system with random phase shifting at IRS under Rayleigh and Rician fading. It has been shown that the BER of users at coherent phase-shifting outperforms the random phase-shifting method in low SNR regions.
4.3 Performance Comparison Between NOMA and IRS Aided NOMA System
The impact of IRS in the NOMA system is evaluated as shown in Fig. 5, it has been demonstrated that BER performance of IRS aided NOMA system outperforms the conventional NOMA system under both fading channels. The proposed IRS-NOMA system achieves an approximate 30 dB SNR gain to obtain 10−3 BER than NOMA system for both users from the simulation results. From the simulation analysis, the proposed IRS-NOMA outperforms NOMA, especially in the low SNR region. While comparing the BER-performance of the proposed IRS-NOMA system with the conventional NOMA system in [15], the former has a gain of 30 dB SNR at BER of 10−3 under Rayleigh fading channel. Wherein [15] considers QPSK modulation for near users and BPSK for far users. The performance comparison between the proposed IRS-NOMA system with reference to NOMA system [[15], Fig. 4a] is listed in Tab. 3. It has been shown that introducing IRS in NOMA system enhances the BER performance considerably than NOMA system. The proposed simulation work as shown in Fig. 5 is obtained by considering BPSK modulation for both users with the pathloss exponent of 1.6 and 32 number of reflective elements in IRS under Rayleigh fading channel.
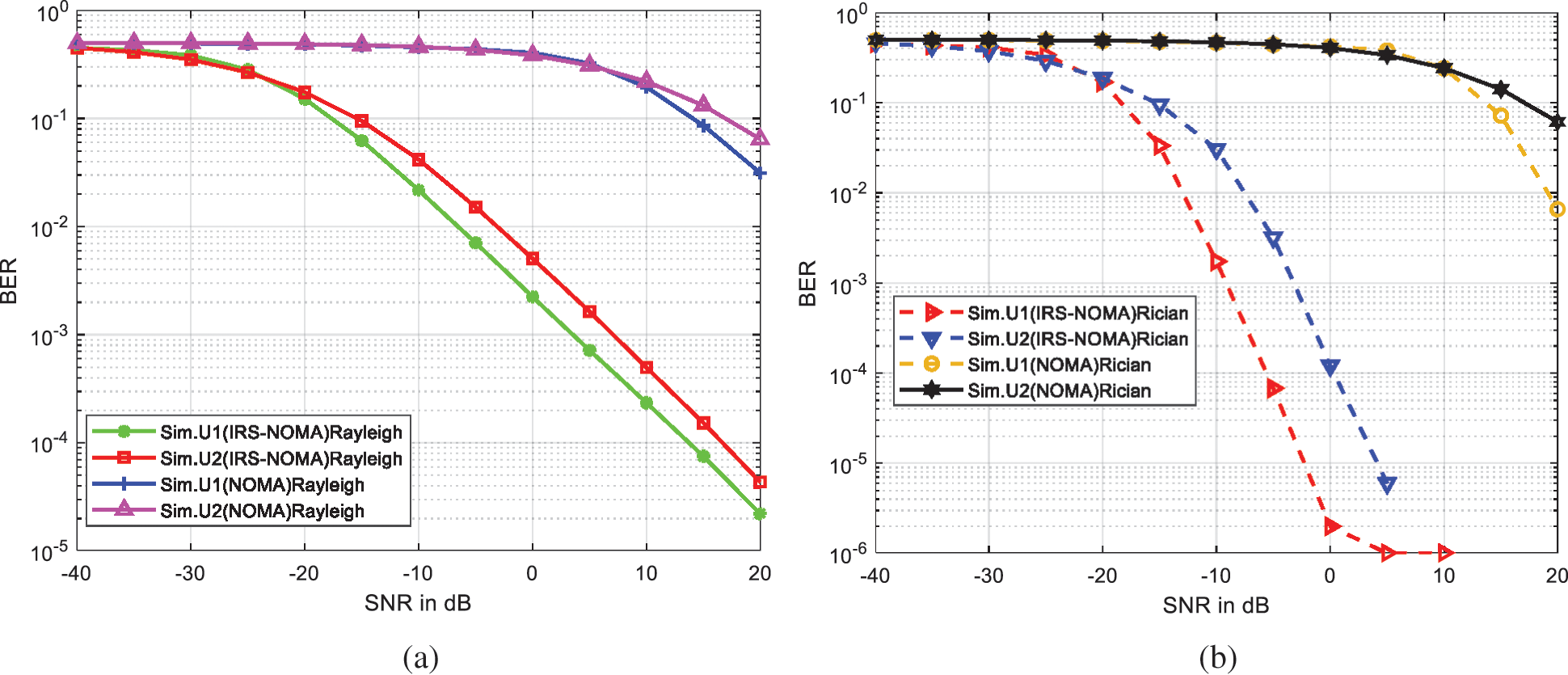
Figure 5: BER comparison between IRS-NOMA and conventional NOMA system (a) Rayleigh fading, (b) Rician fading
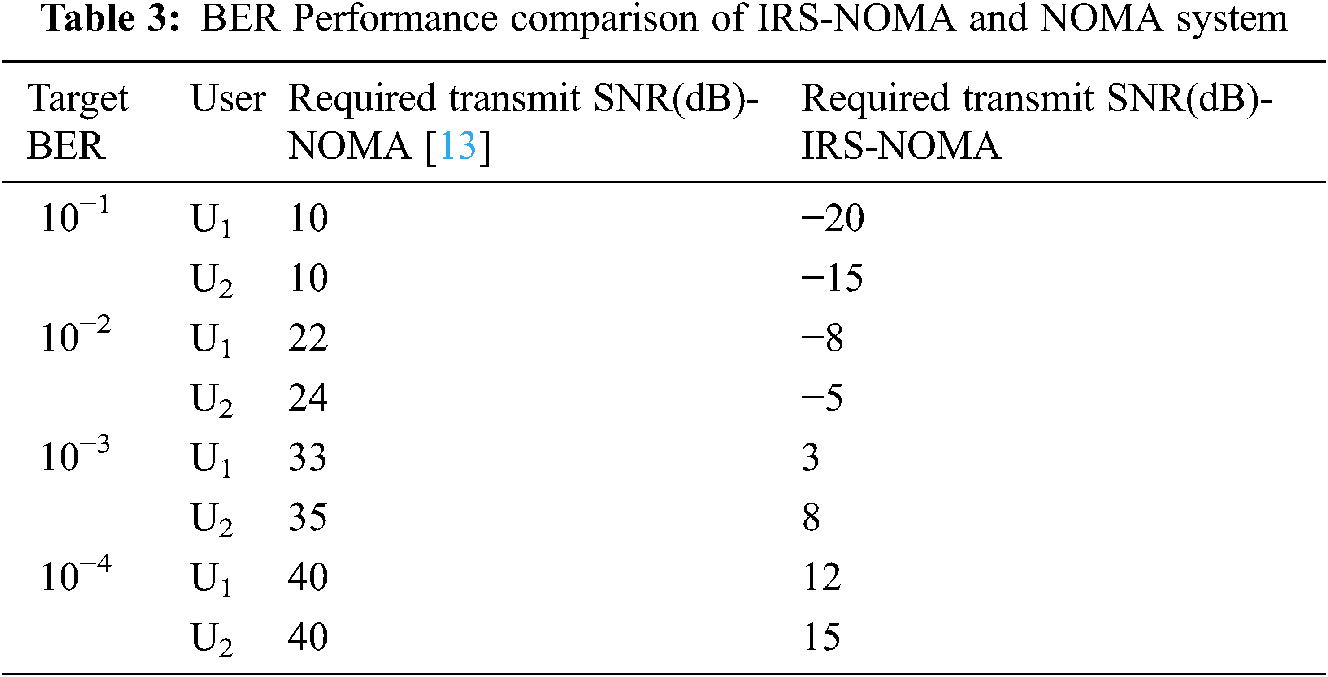
4.4 Effect of Power Allocation Factor on IRS-NOMA System Under Rayleigh and Rician Fading
The effect of power allocation on BER performance of IRS-NOMA system is investigated and illustrated as shown in Fig. 6. The variations of BER performance with power allocation for various transmit SNR are analyzed and illustrated as shown in Fig. 7. In case of U1, though the power allocation is increased, the BER performance is limited because of SIC process. The better BER performance is achieved at α = 0.25with the transmit SNR of −10 dB under both fading channels.
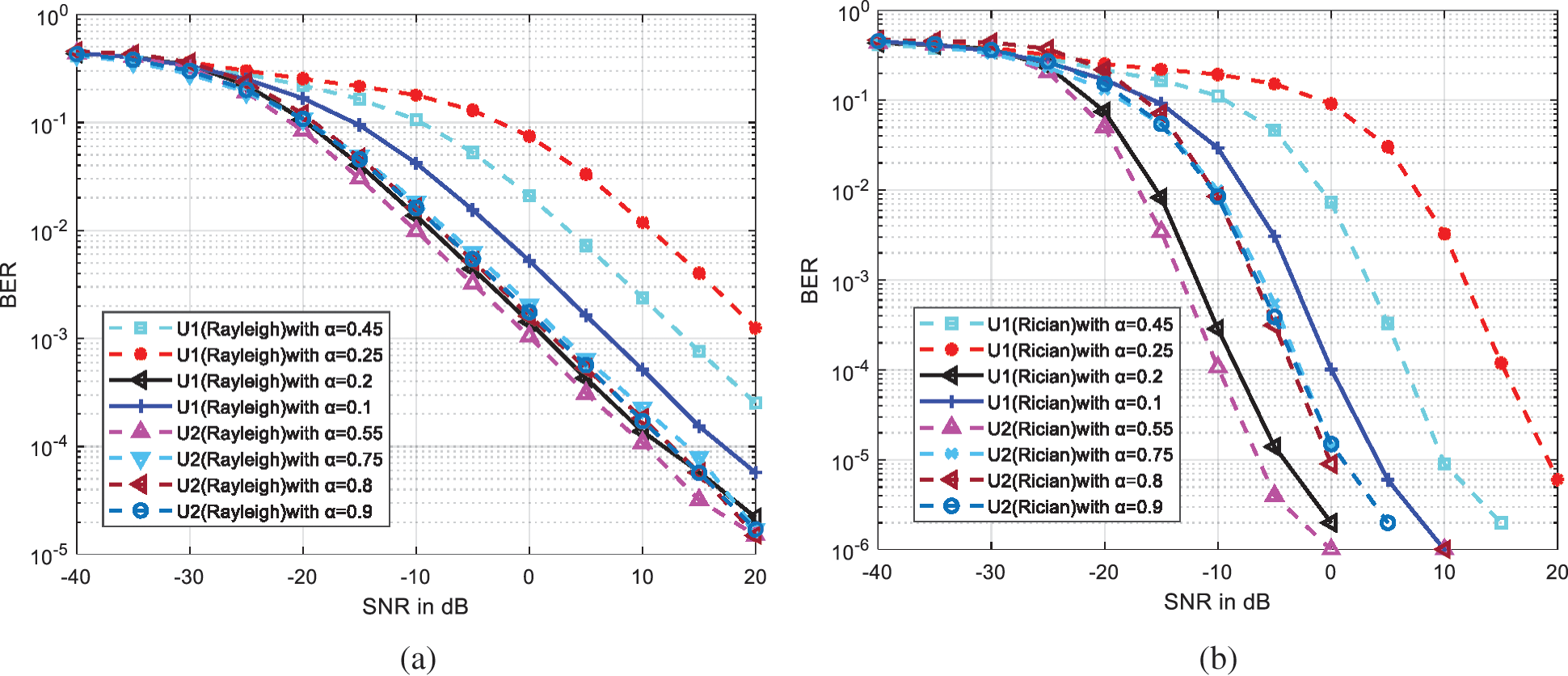
Figure 6: BER performance evaluation for different power allocation factors (a) Rayleigh fading, (b) Rician fading
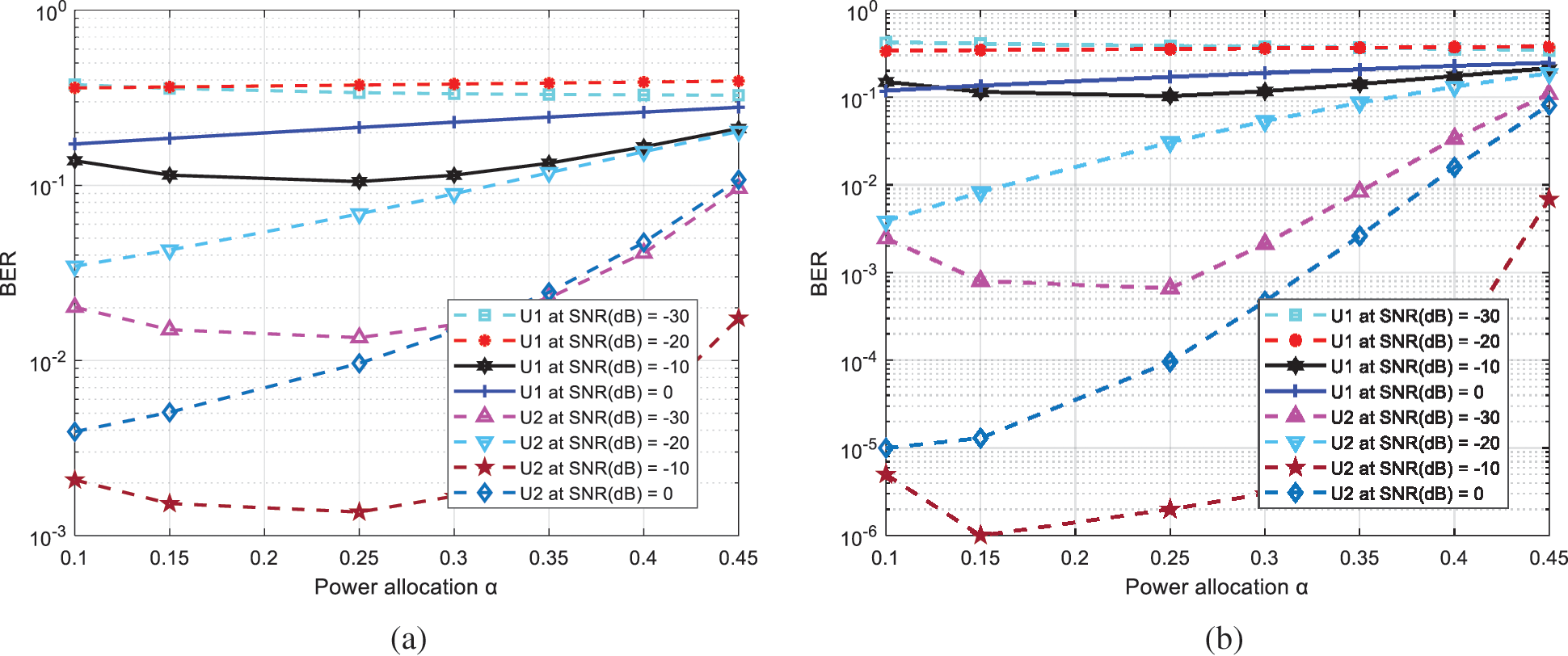
Figure 7: Impact of power allocation on BER performance for different SNR (a) Rayleigh fading, (b) Rician fading
In the simulation results, both Rayleigh and Rician channel fading are considered. Rician distribution has dominant LoS component, therefore the performance of Rician channel is better than Rayleigh channel. In Rician fading BER of 10−3 is obtained with 10 dB lesser SNR compared to Rayleigh fading channel as illustrated in Fig. 4a. Similarly, the random phase-shifting method requires 20 dB more SNR than coherent phase shifting to achieve the particular BER as shown in Fig. 4b.
As shown in Fig. 6, effect of power allocation also influences the performance of IRS-NOMA system. Under Rayleigh fading, the BER performance of U2 is better at power allocation α = 0.55, it achieves 2 dB SNR gain to reach the BER of 10−3 than power allocation of α = 0.8. In the case of U1, the better performance is obtained at α = 0.2. In case of Rician fading, a 5 dB SNR gain is obtained for far users at α = 0.55 than α = 0.8. The proposed work is analyzed for an indoor environment; the optimum number of reflective elements with appropriate power allocation factor decides the performance of the proposed system.
In this paper, we derive the closed-form error probability expressions for two-user downlink NOMA system by considering SIC over Rayleigh and Rician fading channel. We consider random and coherent phase shifting at IRS. Based on the simulation results, we analyze performance comparison between IRS aided NOMA and NOMA systems. Our objective is to improve the error rate performance of the proposed system considering the practical SIC method. From the evaluation results, the proposed IRS-NOMA outperforms NOMA in the low SNR region. We evaluate the effect of the number of reflective elements on BER performance. The proposed system is analyzed by considering the simulation set up of indoor pathloss model with minimum pathloss. We have considered the fixed distance among the devices. The proper placement of IRS could be explored. The simulation results are obtained with 32 number of reflecting elements at IRS. The power consumption of the passive reflecting elements will be considered for evaluation in the future. In the future, we optimize the IRS parameters to further enhance the performance of the proposed IRS-NOMA system.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. G. Wunder, P. Jung, M. Kasparick, T. Wild, F. Schaich et al., “5GNOW: Non-orthogonal, asynchronous waveforms for future mobile applications,” IEEE Communications Magazine, vol. 52, no. 2, pp. 97–105, 2014. [Google Scholar]
2. P. Vijayakumar, J. George, S. Malarvizhi and A. Sriram, “Analysis and implementation of reliable spectrum sensing in OFDM based cognitive radio,” in Smart Computing and Informatics, Smart Innovation, Systems and Technologies, Singapore: Springer, pp. 565–572, 2017. [Google Scholar]
3. J. G. Andrews, S. Buzzi and W. Choi, “What will 5G be?,” IEEE Journal on Selected Areas in Communications, vol. 32, no. 6, pp. 1065–1082, 2014. [Google Scholar]
4. P. Vijayakumar and S. Malarvizhi, “Hardware impairment detection and prewhitening on MIMO precoder for spectrum sharing,” Wireless Personal Communications, vol. 96, no. 1, pp. 1557–1576, 2017. [Google Scholar]
5. Y. Saito, Y. Kishiyama, A. Benjebbour, T. Nakamura, A. Li et al., “Non-orthogonal multiple access (NOMA) for cellular future radio access,” in 2013 IEEE 77th Vehicular Technology Conf. (VTC Spring), Dresden, Germany, pp. 1–5, 2013. [Google Scholar]
6. Z. Ding, Z. Yang, P. Fan and H. V. Poor, “On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users,” IEEE Signal Proc. Letters, vol. 21, no. 12, pp. 1501–1505, 2014. [Google Scholar]
7. P. Vijayakumar and S. Malarvizhi, “Wide band full-duplex spectrum sensing with self-interference cancellation–an efficient sdr implementation,” Mobile Networks and Applications, vol. 22, no. 4, pp. 702–711, 2017. [Google Scholar]
8. S. Hu, F. Rusek and O. Edfors, “Beyond massive MIMO: The potential of data transmission with large intelligent surfaces,” IEEE Transactions on Signal Processing, vol. 66, no. 10, pp. 2746–2748, 2018. [Google Scholar]
9. X. Yu, D. Xu and R. Schober, “MISO wireless communication systems via intelligent reflecting surfaces,” in IEEE/CIC Int. Conf. on Communications in China (ICCC), Changchun, China, pp. 735–740, 2019. [Google Scholar]
10. F. Kara and H. Kaya, “On the error performance of cooperative-NOMA with statistical CSIT,” IEEE Communications Letters, vol. 23, no. 1, pp. 128–131, 2019. [Google Scholar]
11. T. Assaf, A. J. Al-Dweik, M. S. E. Moursi, H. Zeineldin and M. Al-Jarrah, “Exact Bit error-rate analysis of Two-user NOMA using QAM with arbitrary modulation orders,” IEEE Communications Letters, vol. 24, no. 12, pp. 2705–2709, 2020. [Google Scholar]
12. M. Aldababsa, C. Goztepe, G. K. Kurt and O. Kucur, “Bit error rate for NOMA network,” IEEE Communications Letters, vol. 24, no. 6, pp. 1188–1191, 2020. [Google Scholar]
13. L. Bariah, S. Muhaidat and A. Al-Dweik, “Error probability analysis of NOMA-based relay networks with SWIPT, “ IEEE Communications Letters, vol. 23, no. 7, pp. 1223–1226, 2019. [Google Scholar]
14. A. S. Alqahtani and E. Alsusa, “Performance analysis of downlink NOMA system over α-η-μ generalized fading channel,” in 2020 IEEE 91st Vehicular Technology Conf. (VTC2020-Spring), Antwerp, Belgium, pp. 1–5, 2020. [Google Scholar]
15. F. Kara and H. Kaya, “BER performances of downlink and uplink NOMA in the presence of SIC errors over fading channels,” IET Communications, vol. 12, no. 15, pp. 1834–1844, 2018. [Google Scholar]
16. J. Monika, S. Sandhya, S. Nikhil and R. Divyang, “Performance analysis at far and near user in NOMA based system in presence of SIC error,” International Journal of Electronics and Communications, vol. 114, no. 19, pp. 1–16, 2019. [Google Scholar]
17. F. Kara and H. Kaya, “Performance analysis of SSK-NOMA,” IEEE Transactions on Vehicular Technology, vol. 68, no. 7, pp. 6231–6242, 2019. [Google Scholar]
18. X. Chen, M. Wen and S. Dang, “On the performance of cooperative OFDM-NOMA system with index modulation,” IEEE Wireless Communications Letters, vol. 9, no. 9, pp. 1346–1350, 2020. [Google Scholar]
19. H. S. Ghazi and K. W. Wesołowski, “Improved detection in successive interference cancellation NOMA OFDM receiver,” IEEE Access, vol. 7, no. 9, pp. 103325–103335, 2019. [Google Scholar]
20. A. Vasuki and P. Vijayakumar, “Analysis of error rate for NOMA system different fading channel,” in 1st Int. Conf. on Mathematical Techniques and Applications, AIP Conf. Proc., Chennai, India, pp. 1–6, 2020. [Google Scholar]
21. E. Basar, “Transmission through large intelligent surfaces: A New frontier in wireless communications,” in European Conf. on Networks and Communications, Valencia, Spain, pp. 112–117, 2019. [Google Scholar]
22. J. Ye, S. Guo and M. S. Alouini, “Joint reflecting and precoding designs for SER minimization in reconfigurable intelligent surfaces assisted MIMO systems,” IEEE Transactions on Wireless Communications, vol. 19, no. 8, pp. 5561–5574, 2020. [Google Scholar]
23. V. C. Thirumavalavan and T. S. Jayaraman, “BER analysis of reconfigurable intelligent surface assisted downlink power domain NOMA system,” in 2020 Int. Conf. on COMmunication Systems & NETworkS (COMSNETS), Bengaluru, India, pp. 519–522, 2020. [Google Scholar]
24. H. Yang, X. Cao, F. Yang, J. Gao, S. Xu et al., “A programmable metasurface with dynamic polarization, scattering and focusing control,” Scientific Reports, vol. 6, no. 1, pp. 1–11, 2016. [Google Scholar]
25. R. Liu, A. K. Sadek, W. Su and A. Kwasinski, “Introduction,” in Cooperative Communications and Networking, 1st ed., New York, Cambridge University Press, pp. 3–42, 2009. [Google Scholar]
26. E. Caliskan, A. Maatouk, M. Koca, M. Assaad, G. Gui et al., “A simple NOMA scheme with optimum detection,” in 2018 IEEE Global Communications Conf. (GLOBECOM), Abu Dhabi, United Arab Emirates, pp. 1–6, 2018. [Google Scholar]
27. J. W. Craig, “A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations,” in MILCOM 91-Conf. Record, McLean, VA, USA, pp. 571–575, 1991. [Google Scholar]
28. S. Haykin, “Signaling over AWGN Channels,” in Digital Communication Systems, 1st ed., vol. 1, New York: John Wiley & Sons, Inc., pp. 323–444, 2004. [Google Scholar]
29. M. K. Simon and M. S. Alouini, “Useful expressions for evaluating average error probability performance,” in Digital Communication Over Fading Channels, 1st ed., vol. 1, New York: John Wiley & Sons, Inc., pp. 99–139, 2000. [Google Scholar]
30. A. Goldsmith, “Pathloss and Shadowing,” in Wireless Communications, 1st ed., vol. 1, New York: Cambridge University Press, pp. 27–60, 2005. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |