DOI:10.32604/iasc.2022.022239

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.022239 |  |
| Article |
Deep Embedded Fuzzy Clustering Model for Collaborative Filtering Recommender System
College of Computer Engineering and Sciences, Prince Sattam bin Abdulaziz University, AL Kharj, Saudi Arabia
*Corresponding Author: Adel Binbusayyis. Email: a.binbusayyis@psau.edu.sa
Received: 01 August 2021; Accepted: 11 October 2021
Abstract: The increasing user of Internet has witnessed a continued exploration in applications and services that can bring more convenience in people's life than ever before. At the same time, with the exploration of online services, the people face unprecedented difficulty in selecting the most relevant service on the fly. In this context, the need for recommendation system is of paramount importance especially in helping the users to improve their experience with best value-added service. But, most of the traditional techniques including collaborative filtering (CF) which is one of the most successful recommendation technique suffer from two inherent issues namely, rating sparsity and cold-start. Inspired by the breakthrough results and great strides of deep learning in a wide variety of applications, this work for the first time proposes a deep clustering model leveraging the strength of deep learning and fuzzy clustering for user-based collaborative filtering (UCF). At first, the proposed model applies deep autoencoder (AE) to learn users’ latent feature representation from the original rating matrix and then conducts fuzzy clustering assignments on learnt users’ latent representation to form user clusters. More importantly, the proposed model defines a unified objective function combining the reconstruction loss and clustering loss to yield end-to-end UCF process that can jointly optimize the process of data representation learning and clustering assignment. The effectiveness of the proposed model is evaluated with two real-world datasets, MoiveLens100K and MovieLens1M using two standard performance metrics. Experimental results of the proposed model demonstrated the prospects for gain in top-K recommendation accuracy against recent related works with resistant to rating sparsity and cold start problems.
Keywords: Collaborative filtering; deep learning; autoencoder; fuzzy clustering; Top-K recommendations; cold-start problem; data sparsity
With accelerated use of internet, last decade has witnessed rapid introduction of large number of online services such as e-news, e-commerce etc., to bring great convenience and transformative development in people's lives [1,2]. At the same time, the integration of these online services into our daily life has not only provided us social platform to share our views and thoughts about a product but also with massive amount of online contents. In recent years, most of the ecommerce companies such as Amazon, eBay and Netflix are continuously endeavoring to utilize the online contents to predict their customer preferences accurately and recommend relevant items to the user [3]. In view of this, recommendation system (RS) has become the key service for many customer-oriented online services to help customer find their most desired products wisely and save their search time. Consequently, RS has become decisive in the commercial success of many ecommerce companies [4,5]. To this end, increasing interest has been devoted over the past decades to the design and development of efficient RS.
In recent years, many approaches are brought forth for designing RS [6]. Based on the input data type, there are mainly two different types of approaches for RS namely, Content-Based Filtering (CBF) and Collaborative Filtering (CF) [7]. The CBF approaches recommend items comparing the descriptive attributes of the items with the user profile. But, at times, modeling the user profile is a challenging task for some items [8]. Alternatively, the CF approaches recommend items based on the user ratings rather than demanding information about descriptive attributes of the items or users. Thereby, they are simple and most successfully used across various domains in the development of RSs. Although CF approaches are very effective, their performance and usefulness are limited by series problems when applied in real practice. The two major problems of concern are [9–11]: The cold start user problem occurs when it is difficult to infer the preferences of new users based on their insufficient rating history. The data Sparsity: occurs when a few users show interest in rating the visited items. In essence, with the explosive growth in Internet technologies, the number of users and items are ever increasing. Consequently, this increase causes the rating matrix to become increasingly larger with higher data sparsity. As such, achieving accurate recommendations under data sparsity problem has become a hotspot of research.
In the past decade, a wide range of literature are proposed taking the benefits of clustering to combat the effects of data sparsity in CF process. For example, the authors in [12] applied graph clustering algorithm to improve CF and recommend new items for target user. Where after, Nilashi et al. in [13] proposed an integrated approach combining clustering algorithms with CF. Besides, the approach utilizes dimensionality reduction and ontology techniques to achieve better accuracy in recommendation results. Similarly, authors in [14] investigates how the application of Bayesian non-negative matrix factorization (BNMF) method can enhance the clustering performance during CF process. Recently, a novel recommendation algorithm based on K-medoids clustering is proposed in [15] to enhance the recommendation performance against rating matrix data sparsity problem.
Despite clustering-based CF approaches are being studied extensively, their success depends completely on the representation of original data points and may become inept while the original data points live in high-dimensional space. Much endeavor has been devoted in the literatures to learn better data representation that can evade curse of dimensionality for clustering. For example, in [16], the authors apply principal component analysis to reduce the features of product and customers. Later, they apply K-means clustering to develop product recommendation systems for e-commerce business applications. Similarly, kernel principal component analysis is utilized in [17] to diminish the dimension of rating matrix and then fuzzy c-means clustering is applied to cluster user profiles for improving the recommendation accuracy. Also, in [18], K-means and SVD algorithms are applied to reduce dimensionality and cluster similar users to generate more accurate recommendations.
Deep neural networks (DNN) have recently shown promise in learning high-quality data representations on account its capability to perform successive non-linear data transformations for feature extraction. Recently, the application of DNN to clustering process has gained additional interest due to their promising results. Several interesting works have been brought forward combining DNN and clustering in two different ways. For example, some works in [19–21] have applied DNN to discover the promising data representation and then performs clustering assignments on learned representation in sequential manner. In these works, the data representation learning and the clustering are conducted independently which might undermine the clustering performance. Lately, researchers have paid attention to address this problem devising a joint framework that can seek to learn data representation and cluster centers simultaneously to achieve promising results in multitude of fields [22–24].
Encouraged by the prospective application of DNN in the above literature for clustering process, this paper presents deep embedded fuzzy clustering model for UCF process. The proposed model integrates stacked sparse autoencoder (SSAE) network and fuzzy clustering technique within a joint framework for UCF process. Further, this work defines a unified objective function combining data reconstruction loss and clustering loss to guide the SSAE in learning deep high-quality users’ latent representation and which can be very effective in forming user clusters. In short, the main contributions of this work are as follows:
a) This is the first work to propose a deep cluster model taking the advantage of DNN and clustering technique within a joint framework to discover users’ latent representation which can be effective in forming user clusters and achieve accurate recommendations.
b) A unified objective function is defined combining the reconstruction loss and clustering loss to yield end-to-end UCF process that can simultaneously guide DNN in user latent representation learning and optimize the fuzzy clustering assignments.
c) The proposed model intends to utilize only implicit rating data because they can be collected relatively easily by the service providers.
d) Experiment results on benchmark datasets strongly demonstrate the prospects of the proposed model in gaining better recommendation accuracy compared to recent related works.
This section presents the deep embedded fuzzy clustering model for UCF. As discussed earlier, traditional fuzzy clustering technique face challenging task to cluster high-dimensional rating matrix with increasing number users and items. to combat this challenge, the proposed model leverages the benefits of AE and fuzzy clustering as shown in Fig. 1 to discover the low-dimensional latent representation for users and then performs clustering assignments on learnt users’ latent representation. Specifically, it defines a unified objection function combining the reconstruction loss and clustering loss to optimize representation learning and clustering simultaneously. The subsections that follows details the key components of the proposed model.
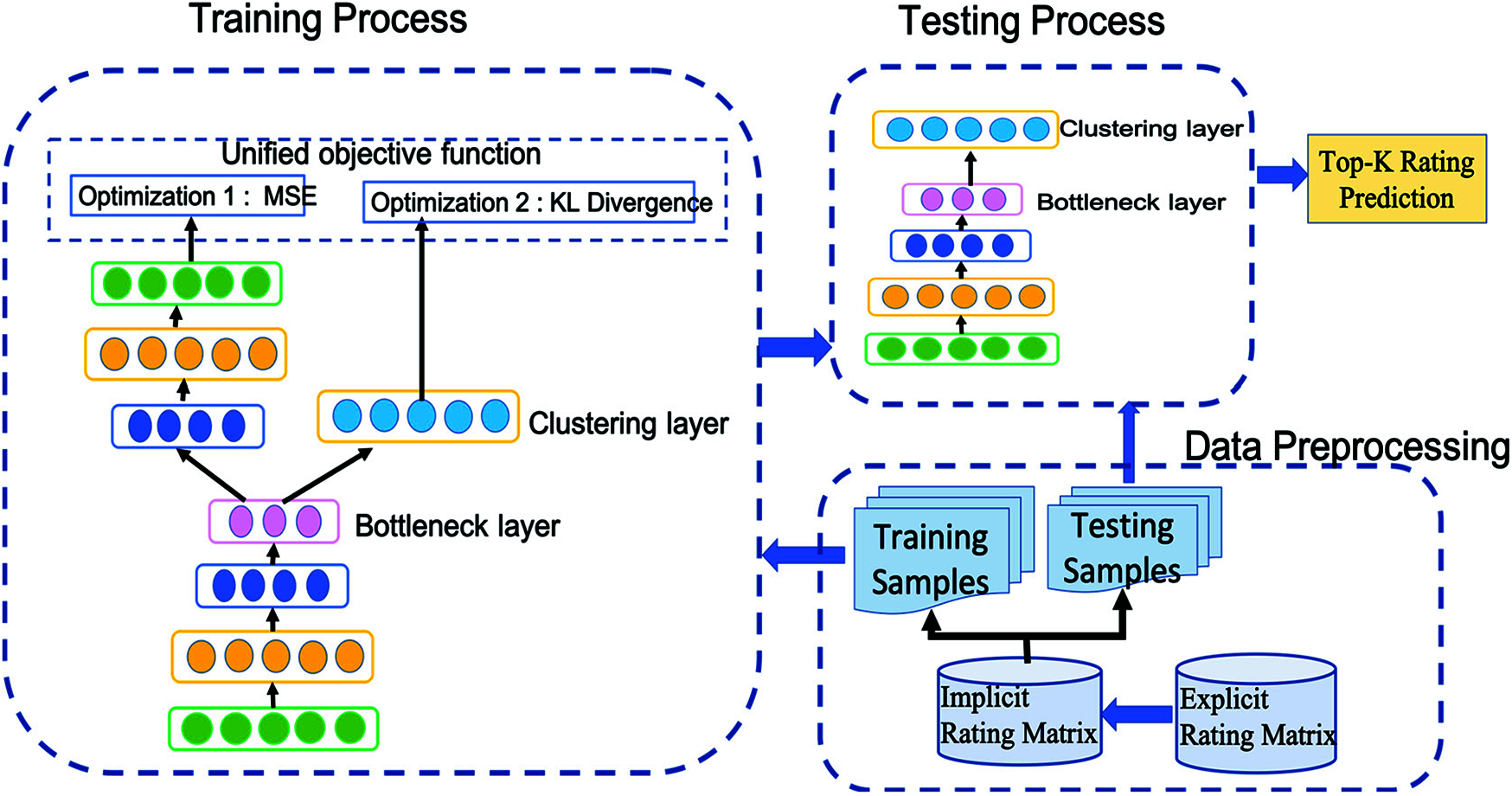
Figure 1: Proposed deep embedded fuzzy clustering model for CF recommendation framework
2.1 User Rating Matrix Representation
A rating matrix for a recommendation problem expresses the historical user rating preferences for involved items. More formally the rating matrix with M users and N items of dimension |M × N | with each element Rui defining the rating preference of user u for the item i. Also, here, the user can express their rating either explicitly or implicitly. In explicit rating, the user can rate an item on sliding scale like 3 stars, 5 stars etc. On contrary, the implicit ratings are binary in the form of user clicks or purchase records. In this work, only implicit rating is considered for two-fold reasons: first, it's easy for service providers to acquire and second, users are not enforced to rate all involved items. Thus, rating matrix with implicit user preferences is represented as below:
These rating scores given by each user on all items are used for representation learning. Therefore, the feature vector of user u is defined using the user u rating on all involved items as follows,
Thus, the dimension of user feature vector equals to the dimension of N. As in [16,25], the work here also attempts aims to use just user ratings and no other additional information to gain good rating prediction performance.
2.2 Stacked Sparse Autoencoder (SSAE) for Dimensionality Reduction
The autoencoder (AE) is a feed-forward neural network with a pair of connected symmetrical networks, encoder and decoder. The encoder part of AE performs feature representation learning to extract the high-level latent features from the given input data X. Thus, the encoding function based on the idea of dimensionality reduction is formulated as follows [26]:
On other hand, the decoder part of AE performs reconstruction-oriented learning to decode the learnt latent features and recover the input data as follows,
As shown in Eqs. (3) and (4), f(.) and g(.) empowers the network to learn more complex non-linear information. They are called activation function of hidden units and are chosen from sigmoid, tanh and rectified linear unit (ReLU) function. Further, the parameters (W, b) and (W’, b’) denote the weight matrix and bias vector of encoder and decoder respectively. Thus, the learning process of AE aims to find the optimal network parameters θ = {W, W’, b, b’} minimizing the reconstruction error between the input data and reconstructed input which is represented as follows,
Despite AE demonstrates perfect reconstruction, it is probable that the network can just copy their input to the output layer without learning effective features for subsequent process utilization. To address this problem, Poultney et al. [27] introduced a variant of AE imposing sparsity constraint on hidden units called sparse AE (SAE) to achieve sparse feature learning and enable the AE learn discriminative robust features. Consequently, the cost function given in Eq. (5) is revised and expressed as below with sparsity penalty term,
As given in the above equation, Kullback–Leibler (KL) divergence is employed to constraint the average activation of each hidden neuron
It is reported in literature that the shallow architecture affects the expressive power of SAE for many complex tasks; therein in this work three SAEs are stacked together to construct deep neural network called stacked SAE (SSAE) such that the hidden layer of first SAE acts as the input of the second SAE and so on. Each SAE in SSAE is pretrained in an unsupervised manner sequentially in succession adopting hierarchical greedy layer-wise training strategy to acquire optimal network parameters for the entire SSAE. Further to extract more robust discriminative features of user and items from the given raw rating matrix, a supervised fine-tuning process is applied to train the whole SSAE network through backpropagation method until the cost function in Eq. (6) is minimized. After the two-step training process, the user latent representation generated from SSAE as follows are used in the subsequent clustering-based CF process.
2.3 Fuzzy Clustering for Neighborhood Formation
As shown in Fig. 1 the proposed model has a fuzzy clustering layer connected to the bottleneck layer of SSAE network. The fuzzy clustering layer as in [28] takes the users latent representation Zu as input and performs clustering to provide the fuzzy membership quj as output. Inspired by the superior performance of fuzzy compactness and separation (FCS) algorithm in previous literature [28–30], the clustering layer in this work aims to employ FCS as vehicle to embed both within and between cluster distances for clustering process which is defined as below,
In the above objective function, the jth cluster center is denoted by μj, the average ratings of all users is denoted by
where η is given by
Finally, the clustering loss function Lc of the clustering layer is defined employing KL divergence to minimize the distributions between quj and desired target distribution puj as follows
2.4 Unified Objective Function
Unlike the existing clustering-based UCF approaches, the proposed architecture aims to optimize the user latent representation learning and clustering assignments simultaneously by combining the reconstruction loss in Eq. (6) with clustering loss in Eq. (11) as given below,
The above defined objective function ensures that the clustering loss guides the SSAE to learn user latent representation that are very effective in forming user clusters
In the proposed architecture, first the SSAE network is pretrained by setting = 0 to learn its network parameter and obtain the target distribution. After pretraining, parameters of SSAE are fine-tuned by training it along with the clustering layer by setting γ = 0.1. Here, the cluster center gradient
In this work, stochastic gradient descent (SGD) optimization is used to tune the network parameters of SSAE and clustering layer.
After clustering process, the proposed architecture applies defuzzification as in [28] to decide the neighbor users, to be considered in prediction process. Specifically, each user is assigned to all clusters with different degree of membership. Taking into account the degree of membership, the prediction is evaluated considering neighbor users from all clusters in a proportional way. For example, if there are 3 user clusters and target user membership is (0.1, 0.3, 0.6) when 10 neighbor users are to be considered then we select one user from cluster 1, three users from cluster 2 and six users from cluster 3. After finding the neighbor users, the proposed architecture employs Pearson correlation measure for rating prediction process [30]. This measure predicts the rating of a user x for an item i as weighted average of neighbor users’ rating on item i which is expressed as follows,
As given in the above equation, Pearson similarity measure sim(x, y) that considers the ratings of most relevant users in a cluster is employed rather than considering all nearest users NU. Further, in the above equation,
2.7 Computational Complexity Analysis
This section characterizes the computational complexity for training the proposed model. To appropriately analyze the computational complexity with asymptotic notations, the complexity associated with two main components of the proposed model are considered namely, representational learning and neighborhood formation. As representational learning utilizes SSAE with three hidden layers, the computational complexity approximates to O((u∗D2) [26] where u denotes maximum number of users and D denotes maximum number of neurons in hidden layers. Similarly, the computational complexity of fuzzy clustering is given by O(udC) [28] where d and C denotes the dimension of latent representation and number of clusters respectively. Thus, the overall computational complexity of the proposed model equals to O(uD2+udC). Further, taking into account that the constraint C ≤ d ≤ D holds in reality, the computational complexity approximates to O(uD2).
This section begins by briefly describing the benchmark datasets used for experimental evaluation and then it defines the metrics used for experimental evaluation.
We employed the well-known CF benchmark dataset, MovieLens to assess the quality of the proposed CF method in recommendation system. The dataset is released in several versions by GroupLens research team. The most prevalent variants, Movielens100k and Movielens1M with different levels of data density are used as benchmark for experimental evaluation. Here, the MovieLens100K dataset includes 100k ratings applied on 1682 movies by 943 users. While MovieLens1M dataset consists of 1,000,209 ratings from 6,040 users for 3,952 movies. Also, each user of these datasets has applied 5 stars rating to rate at least 20 movies. This means there are several unrated movies. Therein, both these datasets are preprocessed first to remove the unrated movies. As a result, the number of movies leftover in MovieLens100K and MovieLens1M are 1682 and 3706 with sparsity level of 93.70% and 95.75% respectively. Now, the serial numbers of the movie which are discontinuous are processed in a such way that all rated movies hold serial number in sequence. Furthermore, since these two datasets contain explicit user feedbacks, the strategy as in [25,30] is followed to get implicit user feedback ignoring the user rating stars and retaining just the user rating signal. Also, following the same experimental setup as in [29], we divide the observed ratings using 80/20 split to create training and testing set respectively. As well validation set was created with 10% of the training set.
To sufficiently assess the effectiveness of the proposed model for recommendation performance, we choose two most commonly used evaluation metrics including Hit Ratio (HR) and Normalized Discounted Cumulative Gain (NDCG) [31] which are formulated as follows
The work uses HR and NDCG metrics to evaluate the performance of proposed model in determining top-N ranked recommendation lists. As HR indicates the ranking accuracy by measuring whether the preferred items are listed in the top-N recommendation list of a user. Similarly, NDCG evaluates hit positions by assigning higher scores to the hits at top ranks.
4 Experimental Results and Discussion
In this section, two sets of experiments are conducted to evaluate the accuracy and efficiency of the proposed model against existing state-of-the-art CF models. In this direction, since only very few works that utilize the clustering process for UCF as we do in this work are published in literature, we consider a baseline neighborhood CF model (eALS) [32,33], two baseline MF models (SVD++ [34], NMF [35]) and two baseline clustering based UCF models (Kmeans, Fuzzy) [30] for comparison. Further, to achieve a fair comparison, we have used the results published by the authors in the respective articles. If the particular type of experiment is not conducted by the respective authors then efforts are taken to implement the respective CF models to obtain the results for fair comparison. More importantly, the experimental evaluation is conducted from two different perspectives on two benchmark datasets, MovieLens100K and MovieLens1M as follows,
In practical applications, RS aims to create list of top-K ranking items that are personalized to the target user based on rating prediction. In this direction, first set of experiments was conducted to show how the proposed model is efficient in generating the top-K recommendations. Here, setting the ranking position K to (5, 10, 15), the performance of the proposed model is analyzed against all the chosen models using HR@K and NDCG@K as evaluation criteria. The top-K performance results of all models are recorded in Tabs. 1 and 2 for two benchmark datasets, MovieLens100K and MovieLens1M respectively. To enhance further the interpretation of top-K recommendation results in Tabs. 1 and 2, the values are plotted for visual comparison in Figs. 2 and 3 respectively.

Figure 2: Visual comparison of top-K recommendation results with other related models on MovieLens100 K (a) HR@K analysis (b) NDCG@K analysis

Figure 3: Visual comparison of top-K recommendation results with other related models on MovieLens1 M (a) HR@K analysis (b) NDCG@K analysis
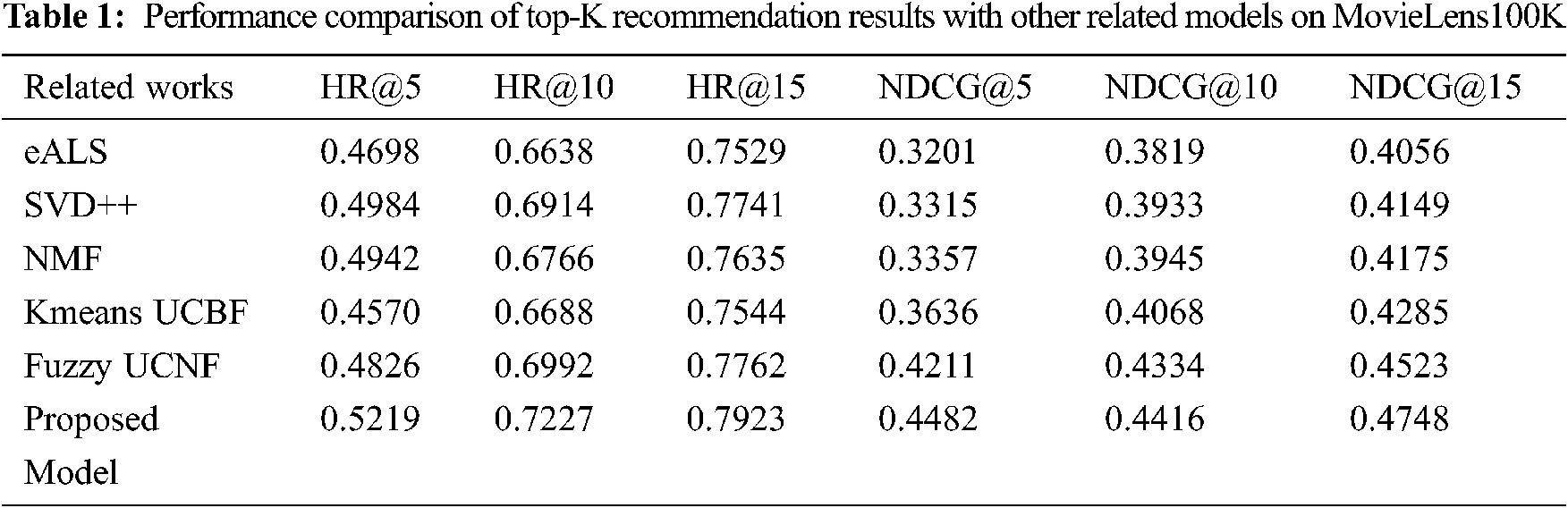
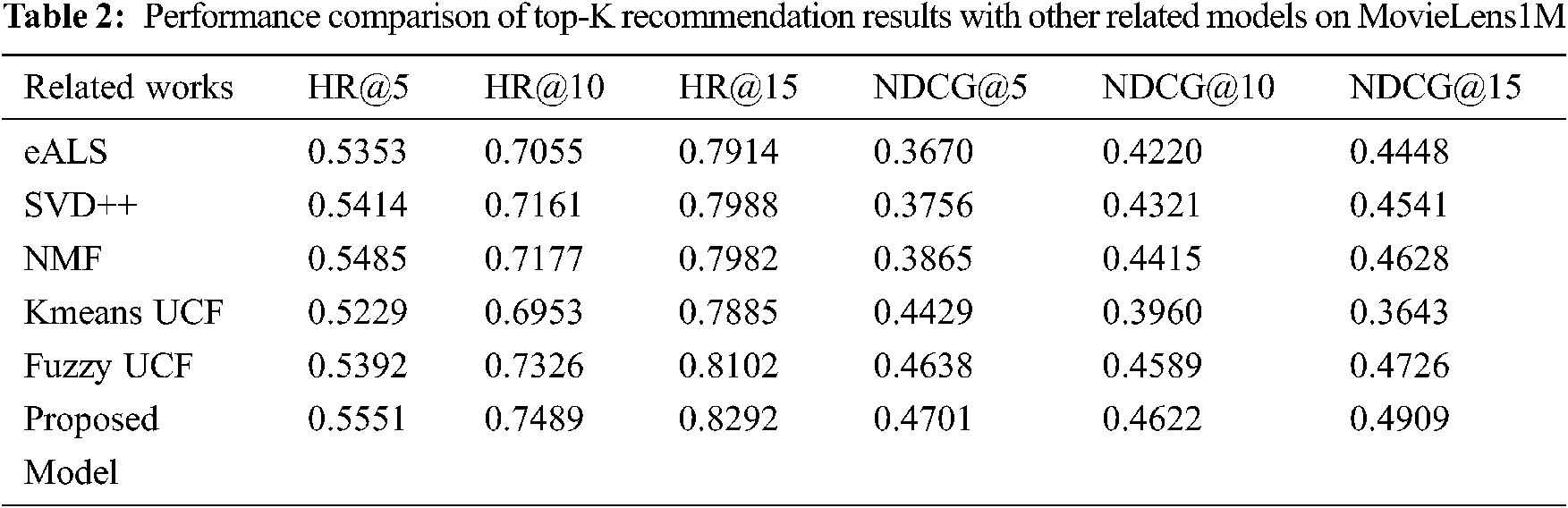
Observing the results in both Tabs. 1 and 2, it is evident that in-crease in the value of ranking position K improves the performance of all models consistently with regard to both HR and NDCG. This might be because the likelihood for a recommended item to be selected by a target user increases as the size of the recommendation list increase. Also, we can find from the comparison results that the neural models such as NMF and pro-posed model achieve better performance over other CF models on both the datasets with regard to both HR and NDCG. This finding demonstrates that the deep neural network structure enables to learn more robust user feature representations and model user-item interactions more effectively. As we can see among clustering based CF models, the proposed model yields significant improvements, which demonstrates that the integration of SSAE helps to boost the performance of clustering process and gain improvement in CF process.
Specifically, on MovieLens100 K, the proposed model achieves on average a relative improvement of 2.7% and 4.6% on HR and NDCG respectively com-pared to fuzzy UCF model. Similarly, on MovieLens1M, the proposed model achieves on 2.6% and 2.3%. All the above observations validate and confirm the effectiveness of the proposed model in creating top-k recommendation lists with improved performance in terms of HR and NDCG.
4.2 Data Sparsity and Cold Start Problem
In the real-world practice, the collected user ratings for involved items are extremely sparse and leads to data sparsity problem that has significant impact on RS performance. In this direction, the second set of experiments was conducted to investigate and analyze the efficiency of the proposed model in mitigating the impact of data sparsity problem.
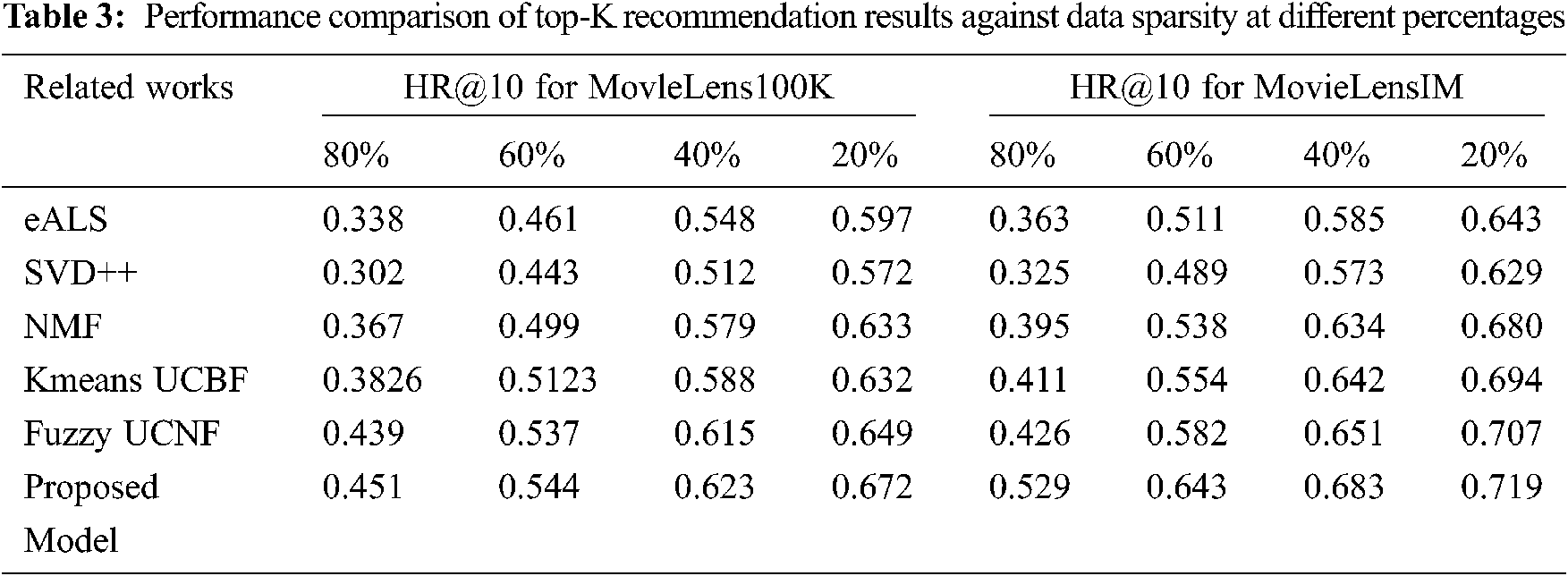
For this purpose, sparse matrix with four different densities were created by randomly removing some entries from training set. For example, to create a sparse user-item matrix with data density of 80%, we randomly choose 80% of user-item entry as training set and used the remaining 20% as testing set. Following the same procedure, we created sparse user-item matrices of different densities n the set (20%, 40%, 60%). As stated in literature, if the training set is less sparse then its data density is high and vice versa.
The performance accuracy of all chosen models is recorded in Tab. 3 for different data sparsity levels in terms of HR@10 on two benchmark datasets, MovieLens100 K and MovieLens1M. To enhance further the interpretation of top-K recommendation results in Tab. 3, the values are plotted for visual comparison in Fig. 4. Observing these results on both datasets across different data sparsity levels, it is clear that the increase in data sparsity degrades the recommendation accuracy of all chosen models. This finding demonstrates that the data sparsity negatively impacts recommendation accuracy regard-less of recommendation model. Further, observing the results on both datasets across all chosen recommendation models, we can note that the neural models such as NMF and proposed model achieve better performance over other CF models on both the datasets. This finding demonstrates that the deep neural network structure is effective in learning robust user feature representations even when the provided data are sparse. On the whole, experimental results on different data sparsity level confirms that the performance of recommendation model can be improved with resistance to data sparsity if autoencoder is integrated within CF process to learn more robust user feature representation.

Figure 4: Visual comparison of top-k recommendation results against data sparsity at different percentages (a) MovieLens100 K (b) MovieLens1 M
This paper proposed a deep clustering model for UCF. Unlike the previous works, the potency of the deep learning and clustering technique is integrated into CF framework for the first time in this paper. The advantage gained through this integration is that designed SSAE enables to overcome rating sparsity and cold-start problem by extracting the primary user latent representation from user rating matrix. Further, the learnt user latent features are applied to improve the learning ability of clustering assignment. Finally, the strengths of SSAE and fuzzy clustering are combined defining a unified objective function to guide SSAE in learning the robust latent representation for effective clustering and improve recommendation accuracy of the model. Besides, the proposed model is based only on implicit rating to achieve improved accuracy. The top-K recommendation analysis and conducted on two established datasets, MovieLens100 K and MoiveLens1 M proved that the proposed model is effective in improving the accuracy of top-N recommendations with resistance to rating sparsity and cold-start problems when compared to the state-of-the-art CF-based recommendation models.
Acknowledgement: I want to dedicate this work to my wife, father, mother, and Prince Sattam bin Abdulaziz University. Further, I am very much thankful to the reviewers and Journal Authorities.
Funding Statement: The author receives funding from Prince Sattam bin Abdulaziz University, Grant Number (2018/01/9397), https://www.psau.edu.sa.
Conflicts of Interest: The author declares that there is no conflicts of interest to report regarding the present study.
1. S. Fu, H. Li, Y. Liu, H. Pirkkalainen and M. Salo, “Social media overload, exhaustion, and use discontinuance: Examining the effects of information overload, system feature overload, and social overload,” Information Processing & Management, vol. 57, no. 6, pp. 102307, 2020. [Google Scholar]
2. L. Quijano-Sánchez, I. Cantador, M. E. Cortés-Cediel and O. Gil, “Recommender systems for smart cities,” Information Systems, vol. 92, pp. 101545, 2020. [Google Scholar]
3. R. Dhir, “Internet marketing and its impact on society,” International Journal of Recent Advances in Multidisciplinary Topics, vol. 1, no. 1, pp. 33–36, 2020. [Google Scholar]
4. P. M. Alamdari, N. J. Navimipour, M. Hosseinzadeh, A. A. Safaei and A. Darwesh, “A systematic study on the recommender systems in the E-commerce,” IEEE Access, vol. 8, pp. 115694–115716, 2020. [Google Scholar]
5. J. Shokeen and C. Rana, “A study on features of social recommender systems,” Artificial Intelligence Review, vol. 53, no. 2, pp. 965–988, 2020. [Google Scholar]
6. M. Srifi, A. Oussous, A. A. Lahcen and S. Mouline, “Recommender systems based on collaborative filtering using review texts-a survey,” Information (Switzerland), vol. 11, no. 6, pp. 317, 2020. [Google Scholar]
7. J. Bobadilla, F. Ortega, A. Gutiérrez and S. Alonso, “Classification-based deep neural network architecture for collaborative filtering recommender systems,” International Journal of Interactive Multimedia & Artificial Intelligence, vol. 6, no. 1, pp. 68–77, 2020. [Google Scholar]
8. S. N. Mohanty, J. M. Chatterjee, S. Jain, A. A. Elngar and P. Gupta, “Recommender system with machine learning and artificial intelligence: Practical tools and applications in medical, agricultural and other industries,” John Wiley & Sons, 111 River Street, Hoboken, NJ 07030, USA, pp. 167, 2020. [Online]. Available: https://books.google.gr/books?id = 36TqDwAAQBAJ. [Google Scholar]
9. Z. Tan and L. He, “An efficient similarity measure for user-based collaborative filtering recommender systems inspired by the physical resonance principle,” IEEE Access, vol. 5, pp. 27211–27228, 2017. [Google Scholar]
10. R. Abdelkhalek, I. Boukhris and Z. Elouedi, “A new user-based collaborative filtering under the belief function theory,” in Proc. of the Industrial, Engineering and other Applications of Applied Intelligent Systems Conf., Springer, vol. 10350, pp. 315–324, 2017. [Google Scholar]
11. J. Li, K. Zhang, X. Yang, P. Wei, J. Wang et al., “Category preferred canopy–k-means based collaborative filtering algorithm,” Future Generation Computer Systems, vol. 93, pp. 1046–1054, 2019. [Google Scholar]
12. P. Moradi, S. Ahmadian and F. Akhlaghian, “An effective trust-based recommendation method using a novel graph clustering algorithm,” Physica A: Statistical Mechanics and its Applications, vol. 436, pp. 462–481, 2015. [Google Scholar]
13. M. Nilashi, O. Ibrahim and K. Bagherifard, “A recommender system based on collaborative filtering using ontology and dimensionality reduction techniques,” Expert Systems with Applications, vol. 92, pp. 507–520, 2018. [Google Scholar]
14. J. Bobadilla, R. Bojorque, A. H. Esteban and R. Hurtado, “Recommender systems clustering using Bayesian non-negative matrix factorization,” IEEE Access, vol. 6, pp. 3549–3564, 2017. [Google Scholar]
15. J. Deng, J. Guo and Y. Wang, “A novel k-medoids clustering recommendation algorithm based on probability distribution for collaborative filtering,” Knowledge-Based Systems, vol. 175, pp. 96–106, 2019. [Google Scholar]
16. S. Bandyopadhyay, S. S. Thakur and J. K. Mandal, “Product recommendation for e-commerce business by applying principal component analysis (PCA) and k-means clustering: Benefit for the society,” Innovations in Systems and Software Engineering, vol. 17, pp. 45–52, 2021. [Google Scholar]
17. H. Yi, Z. Niu, F. Zhang, X. Li and Y. Wang, “Robust recommendation algorithm based on kernel principal component analysis and fuzzy C-means clustering,” Wuhan University Journal of Natural Sciences, vol. 23, no. 2, pp. 111–119, 2018. [Google Scholar]
18. H. Zarzour, Z. Al-Sharif, M. Al-Ayyoub and Y. Jararweh, “A new collaborative filtering recommendation algorithm based on dimensionality reduction and clustering techniques,” in Proc. of the Ninth IEEE Information and Communication Systems (ICICS) Conf., Irbid, Jordan, pp. 102–106, 2018. [Google Scholar]
19. S. Affeldt, L. Labiod and M. Nadif, “Spectral clustering via ensemble deep autoencoder learning (SC-EDAE),” Pattern Recognition, vol. 108, article 107522, 2020. [Google Scholar]
20. C. Song, Y. Huang, F. Liu, Z. Wang and L. Wang, “Deep auto-encoder based clustering,” Intelligent Data Analysis, vol. 18, no. 6, pp. S65–S76, 2014. [Google Scholar]
21. J. Chang, L. Wang, G. Meng, S. Xiang and C. Pan, “Deep adaptive image clustering,” in Proc. Int. IEEE Conf. on Computer Vision, Venice, Italy, pp. 5879–5887, 2017. [Google Scholar]
22. X. Guo, L. Gao, X. Liu and J. Yin, “Improved deep embedded clustering with local structure preservation,” in Proc. of the Artificial Intelligence Joint Conf., Melbourne, Australia, pp. 1753–1759, 2017. [Google Scholar]
23. J. Xie, R. Girshick and A. Farhadi, “Unsupervised deep embedding for clustering analysis,” in Proc. of the Machine Learning Conf., New York, USA, pp. 478–487, 2016. [Google Scholar]
24. X. Guo, X. Liu, E. Zhu and J. Yin, “Deep clustering with convolutional autoencoders,” in Proc. of the Neural Information Processing Conf., Springer, Guangzhou, China, pp. 373–382, 2017. [Google Scholar]
25. D. Ji, Z. Xiang and Y. Li, “Dual relations network for collaborative filtering,” IEEE Access, vol. 8, pp. 109747–109757, 2020. [Google Scholar]
26. Y. Wang, H. Yao and S. Zhao, “Auto-encoder based dimensionality reduction,” Neurocomputing, vol. 184, pp. 232–242, 2016. [Google Scholar]
27. C. Poultney, M. Ranzato, S. Chopra and Y. LeCun, “Efficient learning of sparse representations with an energy-based model,” Advances in Neural Information Processing Systems, vol. 19, pp. 1137, 2007. [Google Scholar]
28. Q. Feng, L. Chen, C. L. P. Chen and L. Guo, “Deep fuzzy clustering-a representation learning approach,” IEEE Transactions on Fuzzy Systems, vol. 28, no. 7, pp. 1420–1433, 2020. [Google Scholar]
29. X. L. Xie and G. Beni, “A validity measure for fuzzy clustering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 13, no. 8, pp. 841–847, 1991. [Google Scholar]
30. H. Koohi and K. Kiani, “User based collaborative filtering using fuzzy C-means,” Measurement, vol. 91, pp. 134–139, 2016. [Google Scholar]
31. K. G. Saranya, G. S. Sadasivam and M. Chandralekha, “Performance comparison of different similarity measures for collaborative filtering technique,” Indian Journal of Science and Technology, vol. 9, no. 29, pp. 1–8, 2016. [Google Scholar]
32. X. Wan, B. Zhang, G. Zou and F. Chang, “Sparse data recommendation by fusing continuous imputation denoising autoencoder and neural matrix factorization,” Applied Sciences, vol. 9, no. 1, pp. 54, 2019. [Google Scholar]
33. Y. Yang, Y. Xu, E. Wang, J. Han and Z. Yu, “Improving existing collaborative filtering recommendations via serendipity-based algorithm,” IEEE Transactions on Multimedia, vol. 20, no. 7, pp. 1888–1900, 2017. [Google Scholar]
34. Y. Jia, C. Zhang, Q. Lu and P. Wang, “Users’ brands preference based on SVD++ in recommender systems,” in Proc. of the IEEE Workshop on Advanced Research and Technology in Industry Applications, Ottawa, ON, Canada, pp. 1175–1178. 2014. [Google Scholar]
35. X. He, L. Liao, H. Zhang, L. Nie, X. Hu et al., “Neural collaborative filtering,” in Proc. of the Twenty Sixth World Wide Web Conf., Perth, Australia, pp. 173–182, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |