DOI:10.32604/iasc.2022.022187

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.022187 |  |
| Article |
Enhanced Mesh Network Using Novel Forgotten Polynomial Algorithm for Pharmaceutical Design
Noorul Islam Centre for Higher Education, Kumaracoil-629180, Tamilnadu, India
*Corresponding Author: D. Ahila Jeyanthi. Email: ahilajeyanth@gmail.com
Received: 30 July 2021; Accepted: 31 August 2021
Abstract: The molecular structures are modelled as graphs which are called the molecular graphs. In these graphs, each vertex represents an atom and each edge denotes covalent bond between atoms. It is shown that the topological indices defined on the molecular graphs can reflect the chemical characteristics of chemical compounds and drugs. A large number of previous drug experiments revealed that there are strong inherent connections between the drug’s molecular structures and the bio-medical and pharmacology characteristics. The forgotten topological index is introduced to be applied into chemical compound and drug molecular structures, which is quite helpful for medical and pharmaceutical workers to test the biological features of new drugs. Such approaches are widely applied in developing areas which are not rich enough to afford the relevant equipment and chemical reagents. In this paper, deals with an interconnection network motivated by molecular structures. The different forms of silicate available in nature lead to the introduction of the dominating silicate network. The first section deals. In this paper, the distinct degrees of enhanced Mesh network, triangular Mesh network, star of silicate network, and rhenium trioxide lattice are listed with drug structure analysis and edge dividing technique, we determine the forgotten polynomial of some molecular structure. The second section contains an algorithm of forgotten polynomial. The third section deals with an application of forgotten polynomial of some drugs.
Keywords: Forgotten polynomial; chemical structure; edge partition; enhanced mesh; triangular mesh
Each year, a large number of new drugs are introduced due to the rapid growth of pharmacology. Testing these new medications’ physical, chemical, and biological qualities requires a lot of time and work, and it is becoming increasingly challenging. However, there are insufficient funds to purchase the necessary equipment and reagents to measure biochemical properties in poor, backward, and low-income countries. Fortunately, earlier research has shown that drug chemical properties and molecular architectures [1] are tightly linked. If we study the topological indices’ indicators for these drugs, medical and pharmaceutical scientists will be able to better grasp their medicinal qualities, which influence experimental flaws. In this regard, the topological index computation methodology [2] is ideal for underdeveloped nations, as it allows them to receive medical and biological information on new pharmaceuticals without having to do chemical experiments. A drug’s structure is represented as a graph in the medical computation model [3,4]. Let G stand for a drug structure, and V(G) and E, respectively, for atoms and chemical bonds (G). (f: G R+) is a real-valued map that converts the chemical structure of each drug into a set of real numbers in the topological index.
The molecular graph is a graph theoretic representation of a chemical compound’s structural formula, with vertices representing atoms and edges representing chemical relationships between atoms. Network structures are critical in today’s society in fields including chemistry, information technology, communication [5], and physical structures. When specific characteristics are met, each network can be recognized by a numerical quantity connected with it. Topological indices are the names given to these rules. A numerical value also known as the topological index is assigned to a graph to classify the structure of the graph. The popular types of topological indices are degree based topological indices, distance based topological indices, counting related polynomials and graph indices. Degree based topological indices, are fundamental in chemical graph theory and chemistry, which are highly valued by many organizations. The biological activity of diverse chemical compounds are assessed using these topological indicators. When analyzing the activity of quantitative structure and structure property models, atom bond connectivity, the Wiener Index, the Szeged Index, the Randic Index, the Zagreb Indices, and the geometric arithmetic index are all significant topological indices and physicochemical features to be considered. The Wiener index was the first topological index to be thoroughly studied. In chemistry, it was the first molecular topological index to be employed. According to Wiener, the boiling temperatures of alkane molecules are closely related to the Wiener Index number [6]. For wiener polynomial we refer [7]. Later study into quantitative structure activity links reveals that it is also connected to critical point parameters, liquid phase density, surface tension, and viscosity. The two by two of past rots, the utilization of graph hypothetical strategies to clarify the compound design has acquired furthermore, more significance. Significant progress has been made to predict simple features on fundamental particles, such as alkane edges of boiling over, for example, in the discovery of innovative lead anticancer treatments. Randic introduced a topological index based on first degrees in 1975, which is described as
Later on, Amic and Bollobas introduced General Randic Index separately, and they substituted any real number α in the place of exponent
Furthermore, we define the Forgotten polynomial of some networks graphs and application of some graphs. For Wiener polynomial and Domination polynomial we refer.
Forgotten Index is a variant of the well-known Randic Index. Recently the chemical applications of the forgotten index has been explored by, Hosmani et al. explored. They discovered that forgotten index is also a useful tool in predicting the heats of vaporization and critical temperatures of alkanes. In [8] another topological index has been introduced which is called as the forgotten index or the F-index
The relation between forgotten index and forgotten polynomial is established as
A mesh is a closed path during a circuit with no other paths inside it. A typical type of lattice network in a plane has integer co-ordinates [9] x and y where x ranges from 1, 2…n and y ranges from 1, 2…m and there is an edge connecting the two vertices. It has a unit distance for the given set of points in the graph.
A variety of graph with a specific structure n-mesh [10] is the term that has been applied. The path of the Cartesian product is of the order a1,a2,…, an, which is a mesh M(a1,a2,…, an) and defined as
Form, n ≥ 5, the forgotten polynomial of enhanced mesh
Suppose that G is a graph of enhanced mesh [13–15]. These to fall distinct degrees du for u ∈ V(EM(m, n)) is {3, 4, 5, 8}. From Fig. 1, we see that the number of edges of type (3, 4) and (3, 5) are 4 and 8 respectively. Every vertex that is lying on the boundary of the graph EM (m, n) except the corner vertices are of degree 5 and the oblique edges which are adjacent to the vertex of degree 4 are edges of type (4, 5). Total of 2(m − 2) + 2(n − 2) = 2m + 2n − 8 = 2(m + n − 4) vertices on the boundary of degree 5, and each vertex induces two edges of type (4, 5). Thus, the number of edges of type (4, 5) is 4(m + n − 4). The central vertex of each wheel graph W4 is of degree 4. This implies that there are total (m − 1)(n − 1) vertices of degree4.The corner vertices of degree4 induces one edge of type (4, 8), and the remaining 2(m − 3) + 2(n − 3) = 2(m + n − 6) vertices lying adjacent to the boundary vertices induces 2 edges of type (4, 8). Each of the remaining (m − 3)(n − 3) vertices of degree 4 induces 4 edges of type (4, 8). Thus, the number of edges of type (4, 8) is 4 + 4(m + n − 6) + 4(m − 3)(n − 3) = 4(mn − 2m − 2n + 4). There are total 2(m + n − 4) vertices on the boundary of the graph G which are of degree 5. Each vertex induces one edge of type (5, 8) and two edges of type (4, 5). Thus the number of edges of type (5, 8) are 4(m + n − 4). Furthermore, there are total 4(m + n − 6) edges of type (5, 5). This edge partition of enhanced mesh based on the degrees of end vertices is shown in Tab. 1.
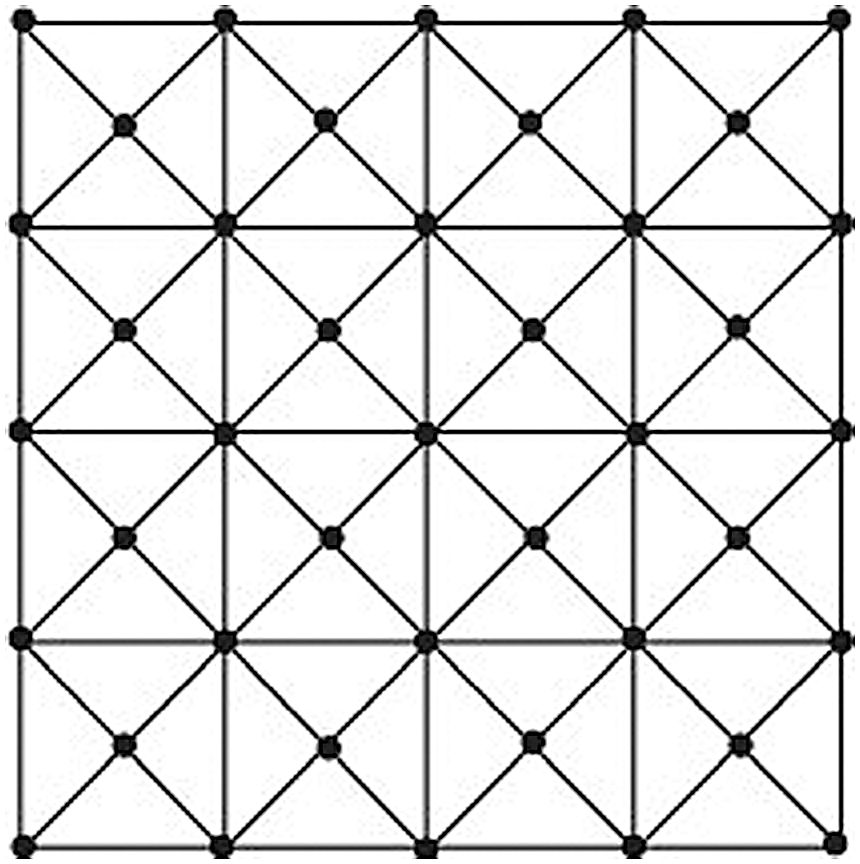
Figure 1: Graph of the enhanced mesh

A triangle mesh is a type of polygon mesh in computer graphics. It comprises a set of triangles that are connected by their common edges or corners. Tn denotes the radix-n of the triangular mesh network [16] whose vertex set V(Tn) = (x, y), 0 ≤ x, y and 0 ≤ x + y ≤ n, and there exists a mesh arc between nodes (x1, y1) and (x2, y2) if |x1 − x2| + |y1 − y2| ≤ n − 1 and x1 + y1 ≤ x2 + y2. The number of vertices in a Tn is
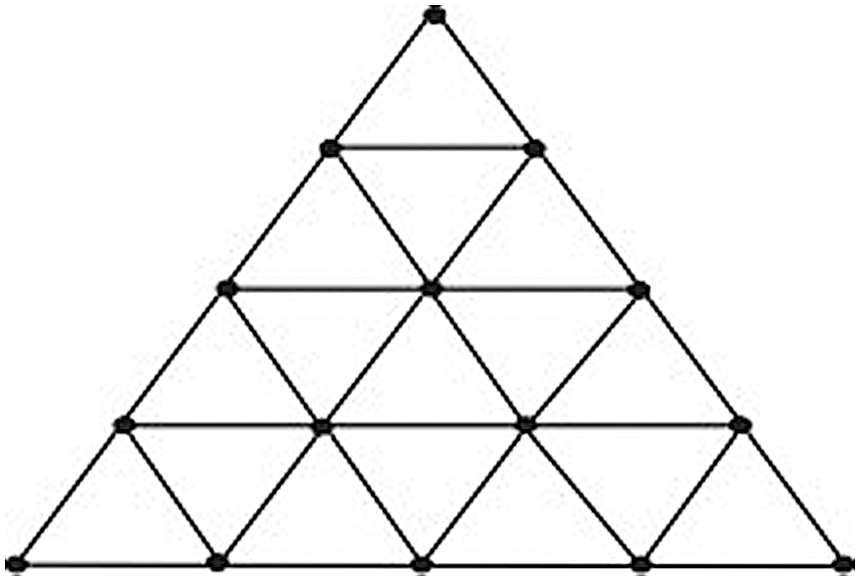
Figure 2: Graph of the triangular mesh T5
For n ≥ 4, the forgotten polynomial of Tn is
The distinct degrees du for u ∈ V(G) is

2.3 Star of the Silicate Network
Step 1: Create an H-dimensional Star of David graph in Fig. 3.
Step 2: partition each of the edge of H into 2n−1 edges by putting 2n−2 vertices at the edge.
Step 3: Except for the pairs at a distance of 1, 3, 5, 7,…,(6n−1) connects the two vertices u and v from one corner of the vertex by an edge, if one is the mirror image of the other and they are at an odd distance 1, 3, 5, 7,…,(6n−1) from one corner vertices (2n−1).
Step 4: At each new edge crossing, add a new vertex.
Step 5: For each K3 sub graph, substitute a tetrahedron. SSL stands for the n-dimensional star silicate star, also known as the star of the silicate network star (n). In this section, the graph G depicts the star silicate network SSL (n) in Fig. 4. The vertices inserted in the second step of the construction have a degree of four. A degree of six has been assigned to all of the remaining vertices. For u ∈ V(SSL(n)), the set of all different degrees du is thus 3, 4, 6. The graph G’s edge division is shown in the Tab. 3.
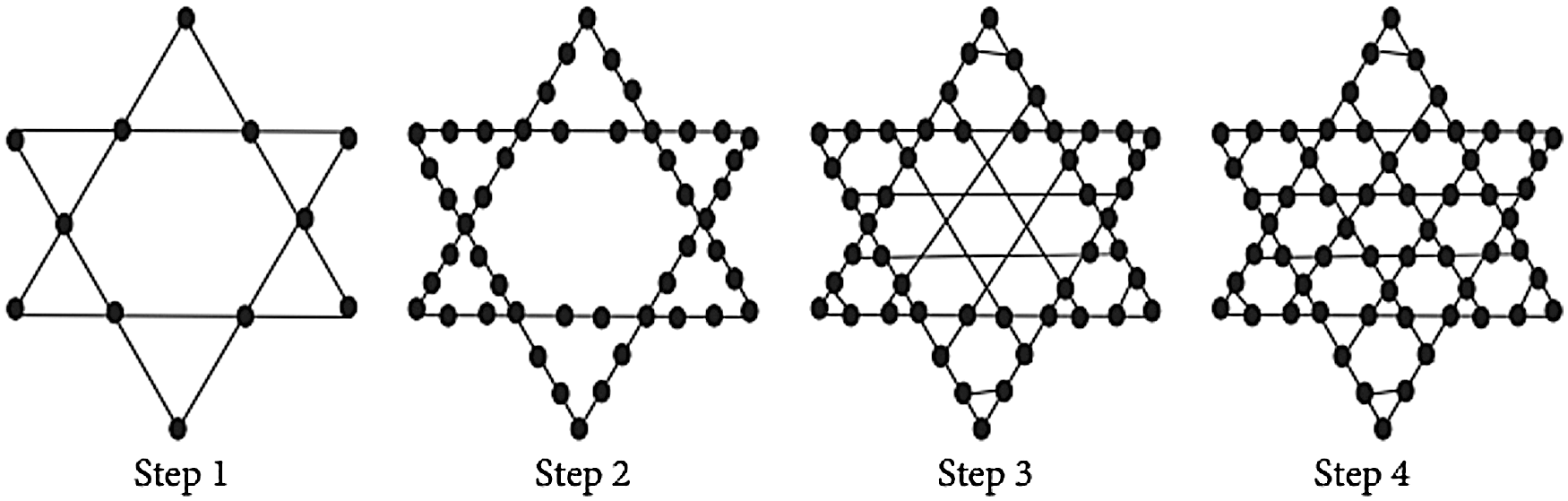
Figure 3: Create an H-dimensional star of DAVID graph
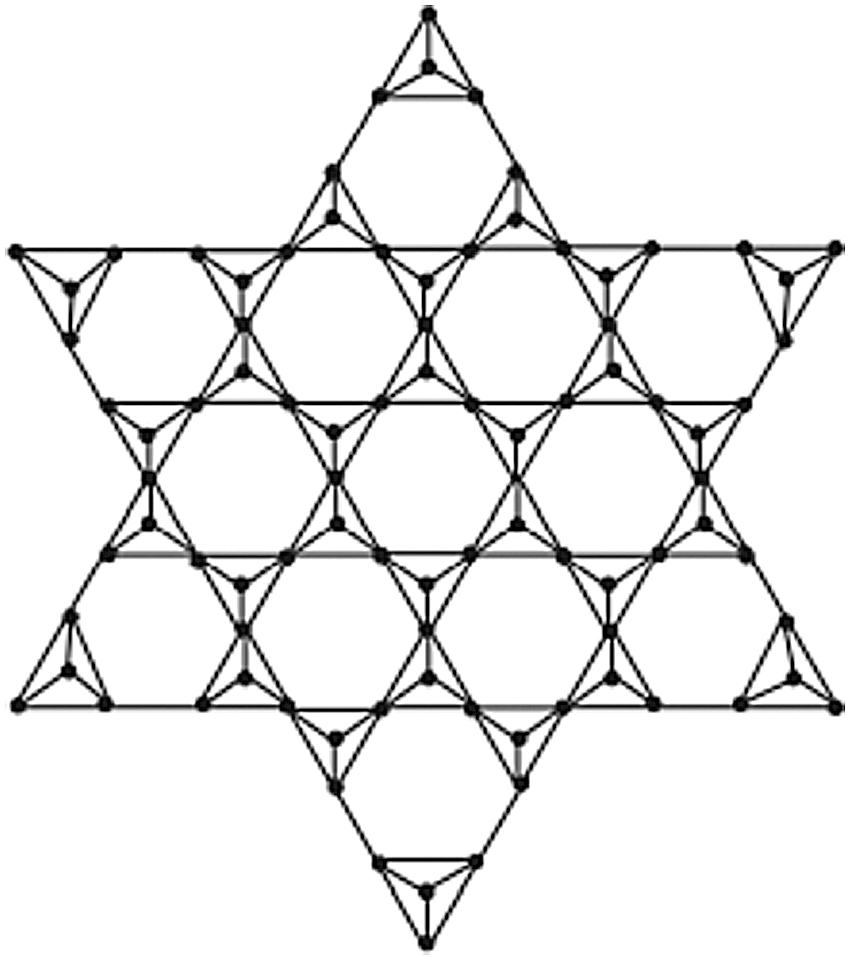
Figure 4: Star silicate network SSL (N)

For n ≥ 3, the forgotten polynomial of SSL(n) is 6x18 + 12(2n − 1) x25 + (36n2 − 60n + 36) x45 + (24n − 30) x32 + 24(n − 1) x52 + (36n2 − 72n + 48) x72.
The information given in Tab. 3 can be used to compute the forgotten polynomial in the star of silicate network as follows:
The vertices of a hollow circle indicate rhenium atoms, while the vertices of solid circles indicate oxygen atoms. Twelve oxygen atoms and 8 rhenium atoms make up the unit cell ReO3 in Fig. 5. The pqrReO3 lattice is represented by the symbol ReO3. There are p unit cell rows, q unit cell columns, and r unit cell pages on the X-axis; q unit cell columns are on the Y-axis; and r unit cell pages are on the Z-axis. The graph of RO(p, q, r) rhenium trioxide is composed of the following elements:
Step 1: A three-dimensional grid M(p, q, r), which is defined by the Cartesian product of the pathways Pp Pq Pr is created. Rhenium atoms are represented by such vertices.
Step 2: At this point, each of the M(p, q, r) edges will be partitioned. The new vertices are used to represent the oxygen atoms. The vertices of RO will now be determined (p, q, r). The identical 3d-grid mark will be applied to the vertices and rhenium atoms. The oxygen atom will be labelled in the space between two rhenium atoms (a′, b′, c′) and
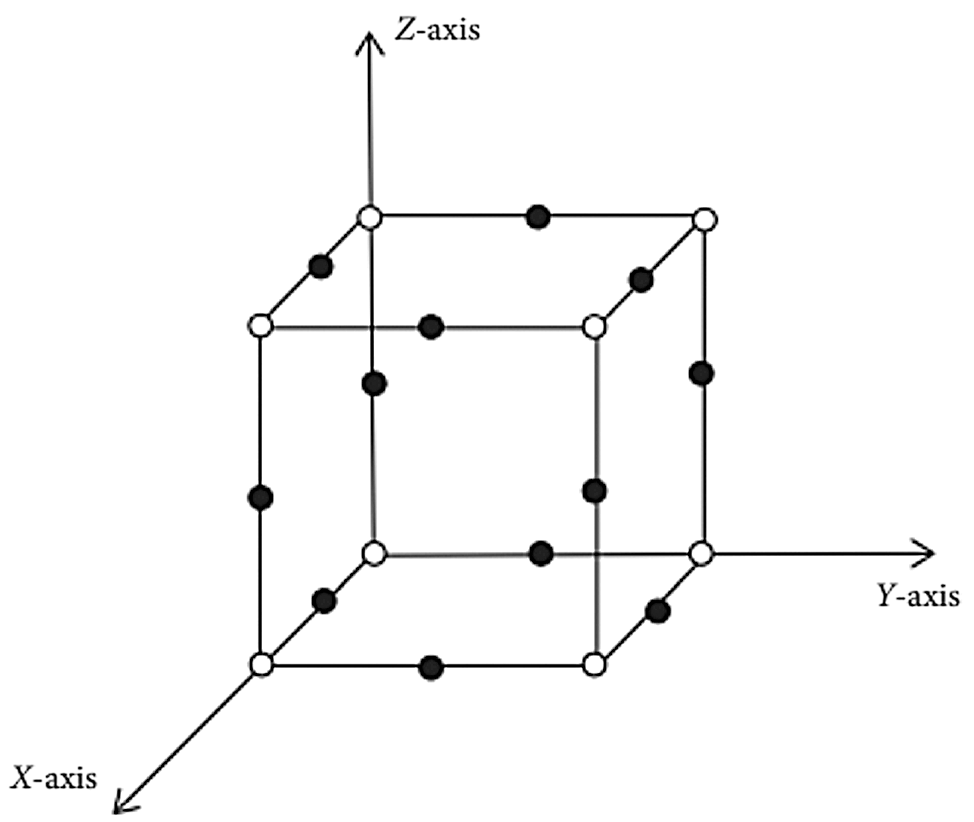
Figure 5: ReO3 unit cell
For p, q, r ≥ 4, the forgotten polynomial of RO(p, q, r) = 24x13 + 16(p + q + r − 6) x20 + 10(pq + qr + pr − 4p − 4q − 4r + 12) x29 + 6(pqr − 2pq − 2qr − 2pr + 4p + 4q + 4r − 8) x40.
The calculation of the forgotten polynomial of rhenium trioxide lattice is done by using the information from Tab. 4

where uv ∈ E(G).

To examine the physical, chemical, and natural features of these new treatments, a huge amount of study is required, and this job has become increasingly complicated. Satisfactory hardware, reagents are, HR are expected to test the performance and the results of medications. Nonetheless, in poor, in reverse and lower pay nations (like a few nations in Southeast Asia, South America also, Africa), there are inadequate assets to manage gear and reagents which can be utilized to test the biochemical properties. The past research has uncovered that synthetic attribute of medications and their sub-atomic constructions are intently related. Benzenoid and Graphene are used to formation of drugs. In this section we use the structure of benzenoid and graphene. Furthermore we obtain the Forgotten polynomial of benzenoid and graphene.
Let T(n) be a triangular benzenoid in Fig. 6. Then
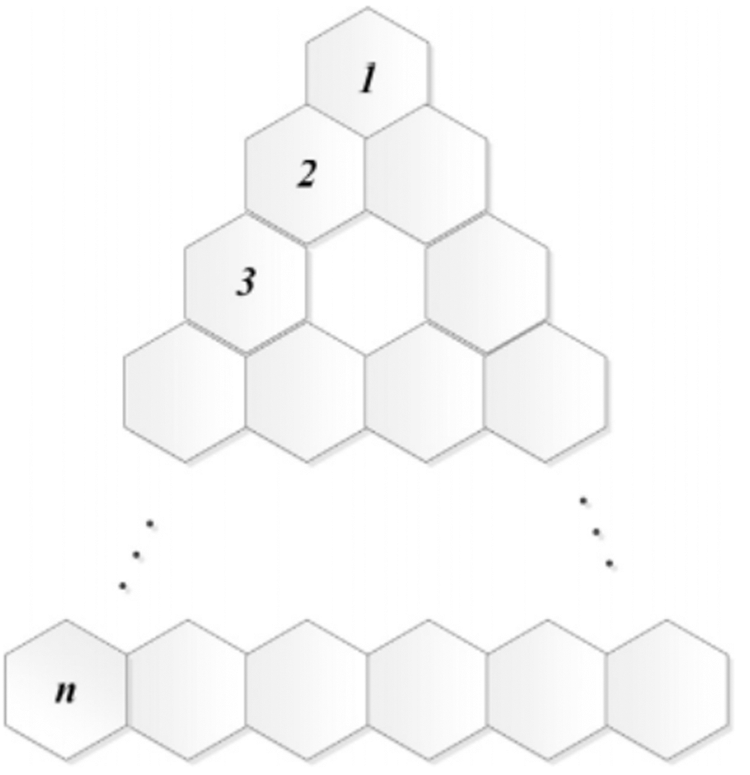
Figure 6: Triangular benzenoid structure
Tab. 5 is used to compute the forgotten polynomial of the triangular Benzenoid.

3.3 Graphene G (M, N) Structure
The densely packed planar sheet of carbon atoms present in a honeycomb precious stone grid is known as graphene. Some carbon allotropes have it as the major component. Fig. 7 shows the graphene G (m, n) structure, which has n rows and m columns. It is made up of mn hexagons. Graphene is one of the most critical application in cancer treatments.

Figure 7: Graphene G (m, n) structure
Let the graphene sheet be G(m, n) with rows and columns. Then F(G(m, n), x) = (n + 4) x8 + (4m + 2n − 4) x13 + (3mn − 2m − n − 1) x18.
If n = 1and m ≥ 1, then the result is obtained by direct observation. The information given in Tab. 6 is used to compute the forgotten polynomial of grapheme.

where uv ∈ E(G).
Every year, an enormous number of new sicknesses are found because of the combatively developing infections. This necessitates more new medications to treat new infections. Topological records are acquainted with test the therapeutic properties of new medications. The failed to remember topological record of a few medication structures has been introduced in this paper by drug structure assessment and edge isolating innovation. The result obtained in the paper demonstrates the application’s great potential for pharmaceutical design.
Acknowledgement: The author with a deep sense of gratitude would thank the supervisor for his guidance and constant support rendered during this research.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. C. Das, A. Yurttas, M. Togan, A. Cevik and I. Cangul, “The multiplicative Zagreb indices of graph operations,” Journal of Inequalities and Applications, vol. 2013, no. 1, pp. 1–14, 2013. [Google Scholar]
2. H. Wiener, “Structural determination of paraffin boiling points,” Journal of the American Chemical Society, vol. 69, no. 1, pp. 17–20, 1947. [Google Scholar]
3. N. R. Jafari, A. Jahanbani and I. Gutman, “Zagreb energy and Zagreb estrada index of graphs,” MATCH Communications in Mathematical and in Computer Chemistry, vol. 79, no. 2018, pp. 371–386, 2018. [Google Scholar]
4. K. Das and K. Xu, “On relation between kirchhoff index laplacian-energy-like invariant and laplacian energy of graphs,” Bulletin of the Malaysian Mathematical Sciences Society, vol. 39, no. 1, pp. 59–75, 2016. [Google Scholar]
5. F. Simanraj and A. George, “On the metric dimension of silicate stars,” ARPN Journal of Engineering and Applied Sciences, vol. 10, no. 5, pp. 2187–2192, 2015. [Google Scholar]
6. S. Stephena, B. Rajana, J. Ryan, C. Grigoriousc and A. Williama, “Power domination in certain chemical structures,” Journal of Discrete Algorithms, vol. 33, pp. 10–18, 2015. [Google Scholar]
7. W. Gao, M. R. Farahani and L. Shi, “Forgotten topological index of some drug structures,” ACTA Medica Mediterranea, vol. 32, no. 1, pp. 579–585, 2016. [Google Scholar]
8. W. Gao, W. F. Wang and M. R. Farahani, “Topological indices study of molecular structure in anti-cancer drugs,” Journal of Chemistry, vol. 2016, pp. 1–8, 2016. [Google Scholar]
9. W. Gao, M. K. Siddiqui, M. Imran, M. K. Jamil and M. R. Farahani, “Forgotten topological index of chemical structure in drugs,” Saudi Pharmaceutical Journal, vol. 24, no. 3, pp. 258–264, 2016. [Google Scholar]
10. W. Gao and W. F. Wang, “The vertex version of weighted wiener number for bicyclic molecular structures,” Computational and Mathematical Methods in Medicine, vol. 2015, pp. 1–10, 2015. [Google Scholar]
11. T. M. Selvarajan and D. A. Jeyanthi, “Dominating sets and domination polynomial of fan related graphs,” Journal of Advanced Research in Dynamical and Control Systems, vol. 12, no. 3, pp. 233–243, 2020. [Google Scholar]
12. D. A. Jeyanthi and T. M. Selvarajan, “Forgotten polynomial of sub division graphs,” Journal of Advanced Research in Dynamical and Control Systems, vol. 12, no. 3, pp. 365–369, 2020. [Google Scholar]
13. D. A. Jeyanthi and T. Selvarajan, “Wiener polynomial and degree distance polynomial of some graphs,” Advances in Mathematics: Scientific Journal, vol. 9, no. 9, pp. 6863–6869, 2020. [Google Scholar]
14. C. Fan, M. M. Munir, Z. Hussain, M. Athar and J. B. Liu, “Polynomials and general degree-based topological indices of generalized sierpinski networks,” Complexity, vol. 2021, no. 7, pp. 1–10, 2021. [Google Scholar]
15. J. H. Tang, U. Ali, M. Javaid and K. Shabbir, “Zagreb connection indices of subdivision and semi-total point operations on graphs,” Journal of Chemistry, vol. 2019, no. 13, pp. 1–11, 2019. [Google Scholar]
16. A. Appathurai and P. Deepa, “Design for reliablity: A novel counter matrix code for FPGA based quality applications,” quality electronic design,” IEEE, vol. 3, pp. 56–61, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |