Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.020674
Article

Volumetric Object Modeling Using Internal Shape Preserving Constraint in Unity 3D

Do-kyeong Lee1, Tae-won Kim2, Yoo-joo Choi2 and Min Hong3,*

1Department of Software Convergence, Soonchunhyang University, Asan, 31538, Korea
2Department of AI S/W Engineering, Seoul Media Institute of Technology, Seoul, 07590, Korea
3Department of Computer Software Engineering, Soonchunhyang University, Asan, 31538, Korea
*Corresponding Author: Min Hong. Email: mhong@sch.ac.kr
Received: 02 June 2021; Accepted: 16 July 2021

Abstract: In real-time contents, such as games and interactive simulators, it is very important to reduce the amount of simulation computation of 3D deformable objects. Although position-based dynamics has been proposed to reduce the amount of computation, the number of nodes for the tetrahedral model to represent a volumetric deformable object has to be increased, which makes the real-time simulation difficult. Therefore, this paper proposes an Internal shape preserving constraint(ISPC) generation algorithm integrated into the position-based dynamics to represent the physical properties of the 3D volumetric deformable object, while reducing the number of nodes filling the interior of the object. The proposed algorithm not only provides motion behavior similar to the tetrahedral model by using a surface model, but also enables real-time simulation by reducing the number of nodes constituting the 3D virtual object. It showed high FPS with reduced computation time compared to the tetrahedral model, and the volume maintenance and physical properties of model were expressed similarly to the tetrahedral model.

Keywords: Position-based dynamics; physically-based simulation; unity3D; simulation; volumetric deformable modeling

1  Introduction

Objects in the real world have various physical properties, thus various physically-based simulation methods have been researched to generate by computer realistic virtual objects with the properties of these objects. Since the motion expression of a virtual object plays an important role in visually improving the sense of reality, a real-time physically-based simulation technique is required in various fields, such as entertainment, education, and medical applications.

In recent years, research on applying the simulation of a model with deformable physical properties to medical simulation and education have been actively applied [1,2]. In general, a deformable object used to present as the inertial properties interconnected between vertices through a mass–spring connection. In the deformable object, each vertex is subject to the laws of mechanics, and can be transformed through collision and interaction with other objects. The inter-connection between two vertices can be generalized as a constraint formed by a three-dimensional spring consisting of tension, torsion, and flexion. The simulation method of a deformable object can be classified by a method of directly calculating a force, a velocity-based method, and a position-based method. The position of each vertex of the virtual object is updated at all stages of the dynamics simulation based on Euler's method [3,4].

The virtual object model used in this paper was modeled with the surface model composed of only properties of the surface of the object, and the tetrahedral model composed of some tetrahedra for the whole object. The tetrahedral model basically proceeds using the Delaunay triangulation to generate the tetrahedra for a virtual object [5]. Using a tool such as TetGen [6], which generates a tetrahedron with the Delaunay triangulation algorithm implemented, a tetrahedron can be created in the surface model. Tools such as TetGen [6], which generate virtual objects composed of tetrahedra, use the Delaunay triangulation algorithm to create virtual objects composed of tetrahedra from the surface model. Various physical properties can be expressed by applying specific constraints of the simulation that can be transformed through the generated tetrahedral model. However, not all surface models can be generated as tetrahedral models through the TetGen tool, and there is a possibility that errors will occur, depending on the shape of the mesh, or input parameters. In conclusion, it is possible to generate a tetrahedral model through the TetGen tool after the surface model is fully implemented. In general, it is difficult for those who are not familiar with modeling tools, such as the 3D software Max and Maya, to readily generate the tetrahedral models. In addition, although users successfully generate the tetrahedral model, the real-time simulation becomes more difficult using these complex models, due to an increase in the amount of computational cost.

This paper proposes a limited solution to two problems (difficulty of creating the tetrahedral model and heavy computational cost) mentioned above that may occur in modeling and real-time simulation. With this method, we discovered two possibilities.

1.    Enables volumetric model simulation through surface models (Unclosed mesh or many holes) that are likely to cause problems with tetrahedral model creation.

2.    When the model generated using our algorithm is compared to tetrahedral model, faster real-time simulation is passible.

We developed a deformable object simulation using a Position-based dynamic (PBD) method among various methods using Unity3D. The PBD method is fast and stable, and allows easy control of the dynamic simulation. Therefore, PBD is widely used in real-time interactive applications. The algorithm used in this paper applies Newton's law of inertia used in the PBD. Before executing the PBD solver, the pre-processing step is performed to maintain the original shape as much as possible, and then the stored data is transferred to the GPU-based PBD solver to execute the calculation through parallel processing. When the computational process is completed, the updated positions and velocity data are transferred to the CPU. During the execution time of simulation, the PBD solver operation and the process of transferring data to the CPU were performed in the update function for every frame, excluding the preprocessing process in the Unity3D start function. While the Jacobian method is easy to implement in GPU, it can cause serious stability problems [7], so the nonlinear Gauss-Seidel equation was used to solve the dynamic equation of the PBD system. The proposed method utilizes parallel processing through computation using the GPU shader provided by Unity3D, to provide better computation speed while maintaining simulation accuracy [8,9]. In addition, the vertex information of the surface model can be utilized without additional costs, and a similar physical property model is implemented, while reducing the amount of computation compared to the tetrahedral model.

2  Related Works

2.1 Physically-Based Simulation Methods

Physically-based simulation methods are currently widely used in various applications for dynamic simulation. The Mass–Spring System (MSS) was used for face modeling and human body simulation [10,11]. However, when deformation occurs, it is difficult to present the volume of the object, and it is very difficult to adjust the stiffness parameter according to the characteristics of the virtual object model. For this reason, the deformation accuracy of the MSS is low, and this system can readily be unstable [12]. Although the Finite Element Method (FEM) provides relatively higher precision than other methods, it generally requires heavy computational cost. FEM has been applied to simulation of the liver, and to an ophthalmic surgery simulator [13–15]. In the case of a simulation with complex object deformation, low computational performance becomes a disadvantage that cannot be ignored. Therefore, the fast, stable, and controllable PBD has been widely used in real-time interactive applications.

The PBD has been proposed as a new paradigm for simulating dynamic systems, such as deformable objects [3], and is still the most widely used method for physically-based simulation with MSS. Unlike previous dynamic simulation approaches that are based on force or some successful impulse/velocity-based approaches, PBD manipulates the position of the virtual object directly. This provides various advantages, such as preventing the overshooting problem in the explicit integration system, and being able to handle collision constraints more easily [2]. The PBD has been applied to simulate models with various properties, such as cloth, deformable objects, rigid bodies, and fluids [16,17].

In order to perform volumetric model simulation for the existing PBD, simulations were performed by setting conditions such as strain constraint and volume constraint in the Tetrahedral model. However, in this study, a preprocessing operation that creates an internal link was added to the existing PBD framework in order to proceed with the simulation using a model with only a triangle surface, not a tetrahedron.

2.2 VR/AR Simulation

AR/VR-related researches are also on the rise, due to the remarkable improvement of hardware and software technologies in recent years. Research and the commercialization of AR/VR contents have been conducted in various fields, such as medical, defense, education, and the game industry, and various research efforts are being conducted to improve the sense of immersion [18,19]. In the case of PBD, deformable objects are constantly being researched for the application of VR and AR, and various solutions have been derived to enable real-time simulation through GPU parallel processing. In particular, in recent years, PBD has been grafted into the medical and educational fields; it has become possible to provide immersive simulation contents, and it is being used in various fields [12,20].

3  The Proposed Internal Shape Preserving Constraint for Deformable Object Simulation

3.1 Full Algorithm Overview

Algorithm 1 shows the pseudo code of the proposed simulation algorithm in this paper, which is based on the algorithm of PBD [3]. The proposed method represents a deformable object with N vertices and M constraints. Vertex i = (1, ⋅ ⋅ ⋅ , N) has velocity V = (V1, ⋅ ⋅ ⋅ , Vn), position X = (X1, ⋅ ⋅ ⋅ , Xn), and mass m = (m1, ⋅ ⋅ ⋅ , mn). Input data includes position Xi of vertex i = (1, ⋅ ⋅ ⋅ , N), velocity Vi, mass mi, external force vector f, time step Δt, and all constraint set of the model, etc. The output data that are finally output after performing calculation through compute shader that supports writing GPU parallel code on the computer are the updated position Xi  and velocity Vi. In steps (1)–(3), the velocity V = (V1, ⋅ ⋅ ⋅ , Vn) and position X = (X1, ⋅ ⋅ ⋅ , Xn) are initialized, and  wi is set up with 1/mi. Afterwards, the proposed algorithm stores the data of the vertex to be connected to create the Internal Shape Preserving Constraint (ISPC) to preserve the shape of the virtual object. In addition, after setting constraints in the offline phase (C# code), computation is performed through GPU parallel processing of the computer shader. GPU computation is shown in lines (7)–(20). In line (8), the new velocity is calculated using the external force and the current velocity. The velocity is controlled through a damping method in line (9). The velocity and current position of the vertex are utilized to calculate the next position of vertex Pi  on line (10) by the Euler step. In line (11), collision constraints created in the current time step to solve the collision between virtual objects are created. Iterative solver lines (12)–(14) estimate the position of vertex to satisfy the applied constraints. The calculation in this step is performed as many times as the iteration times each constraint is specified through the Gauss–Seidel equation. In lines (16) and (17), the position of the vertex is moved to an optimized position, and the velocity is updated accordingly. Since this algorithm estimates the position firstly using current state information, and then calculates the velocity and position by applying Pi  in the integration steps, which are shown in lines (16) and (17), this system can provide a stable simulation.

In this paper, we applied the constraints set that includes distance constraint, bending constraint, and internal shape-preserving constraint on the 3D model in the PBD simulation. The proposed method applies distance constraints to the surface of the virtual 3D object and the inside of the object to perform with fast computation, compared to the existing tetrahedral model, while preserving the shape of the 3D object during simulation. Fig. 1 shows the distance, bending, and internal shape-preserving constraints applied in the simple model by the proposed method.

Figure 1: The simple model with the distance, bending, and internal shape-preserving constraint

Eqs. (1)–(3) show the proposed distance constraint and internal shape-preserving constraint for PBD simulation. The distance constraint formula of Eqs. (1)–(3) is used to set the length constraint of each edge of the triangle mesh constituting the surface of the surface model. Also, in the case of the internal shape- preserving constraint, the original shape of the model can be maintained by setting the limit of the length of the internal link.

ΔP1=w1w1+w2(P1−P2−d)P1−P2|P1−P2| (1)

ΔP2=w2w1+w2(P1−P2−d)P1−P2|P1−P2| (2)

Cdistance(|P1−P2|)−d (3)

where, P1 and P2 are two nodes constituting the constraint, and d  is the original distance between the two nodes, which should be maintained during the simulation. Fig. 1 shows an example of distance constraint between nodes P1, P2, and P3. To maintain the constraint, ΔPi is weighted according to wi = 1/mi.

Eq. (4) sets the degree of bending of two adjacent triangles to find the original angle between the mesh triangles interacting with the surface to maintain the original shape. Eq. (4) shows the bending constraint that sets the angle of the adjacent triangle.

Cbend(P1,P2,P3,P4)=arccos(P2−P1)×(P3−P1)|(P2−P1)×(P3−P1)|⋅(P2−P1)×(P4−P1)|(P2−P1)×(P4−P1)|−φ0 (4)

where, φ0 is the angle of the initial triangle with respect to the adjacent triangles (P1, P3, P2) and (P1, P2, P4). The stiffness parameter kbend refers to the bending stiffness to maintain the angle between two triangles. Bending constraint can be applied regardless of the edge length of the mesh, because it uses the formula to find the initial angle and the deformation angle, even if the edge length of the deformable object is changed. Through these properties, the elastic stiffness and bending resistance can be set, and users can express models with different physical properties.

The virtual 3D object modeled with the proposed algorithm is compared with the same 3D object modeled with the existing strain constraint method [21]. The strain constraint method uses the same PBD, but a single constraint is identified for each mesh element by applying a distance constraint to each edge of the triangle mesh element. Therefore, the strain constraint method is appropriate for the tetrahedral model. Eqs. (5) and (6) show the strain constraints that are applied for the tetrahedron:

P=[P1−P0P2−P0P3−P0] (5)

Q=[q1−q0q2−q0q3−q0] (6)

When the projected position (P0, P1, P2, P3) and the initial position (q0, q1, q2, q3) before the simulation of tetrahedron are given, the current position and the initial position are given a new coordinate system with P0 and  q0 as the origin. The deformation gradient F is defined by the continuum mechanics formulation with 3 × 3 matrices P and Q. Using this deformation gradient F, the Green's strain tenor G can be calculated by Eq. (9):

F=PQ−1 (7)

S=FTF (8)

G=S−I (9)

Finally, Eqs. (10) and (11) are the stretch constraints and shear constraints applied to the tetrahedron as strain constraints. Here, si is a parameter for controlling the initial deformation of the current tetrahedral element.

Cstrech(P0,P1,P2,P3)=Sij−si,i,j∈{0,1,2}andi=j (10)

Cshear(P0,P1,P2,P3)=Sij,i,j∈{0,1,2}andi≠j (11)

3.2 Overview of Proposed ISPC Generation Algorithm

Algorithm 2 is an algorithm that generates the proposed ISPC in this paper. In Algorithm 1, the ISPC generation algorithm is simply indicated in lines (4)–(6). The ISPC generation algorithm proceeds in the preprocessing stage of PBD simulation, and is implemented through some functions that are provided by the Unity3D engine. Figs. 2–4 show the implementation process of the proposed ISPC generation algorithm.

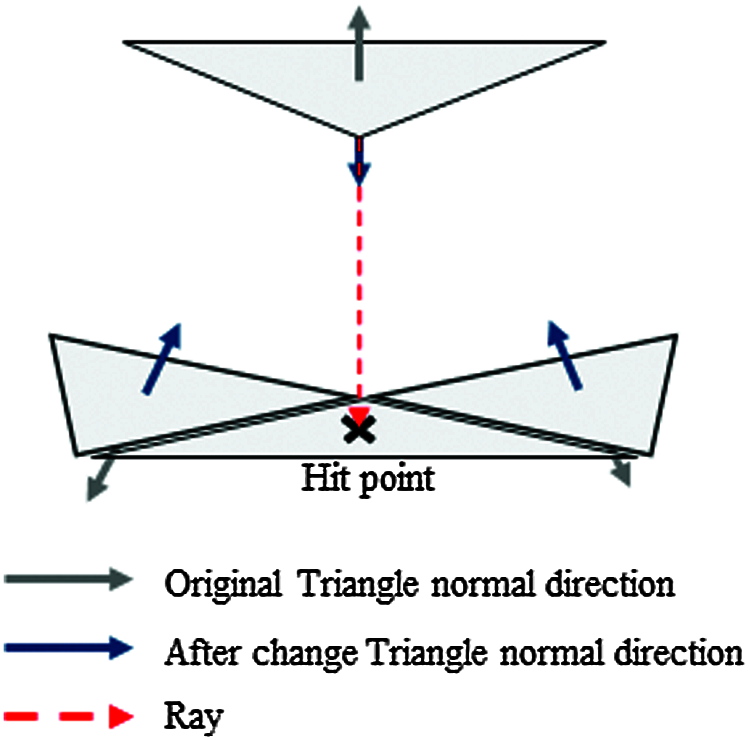
Figure 2: Finding a triangle opposite the vertex

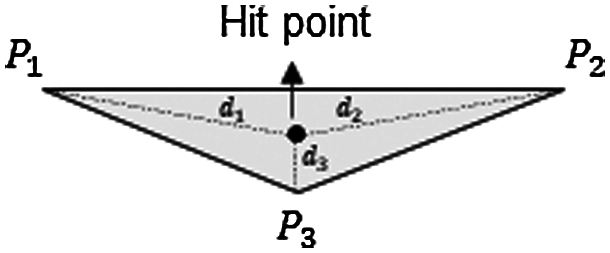
Figure 3: Selecting the closest vertex between the hit point and the 3 vertices (P1, P2, P3)

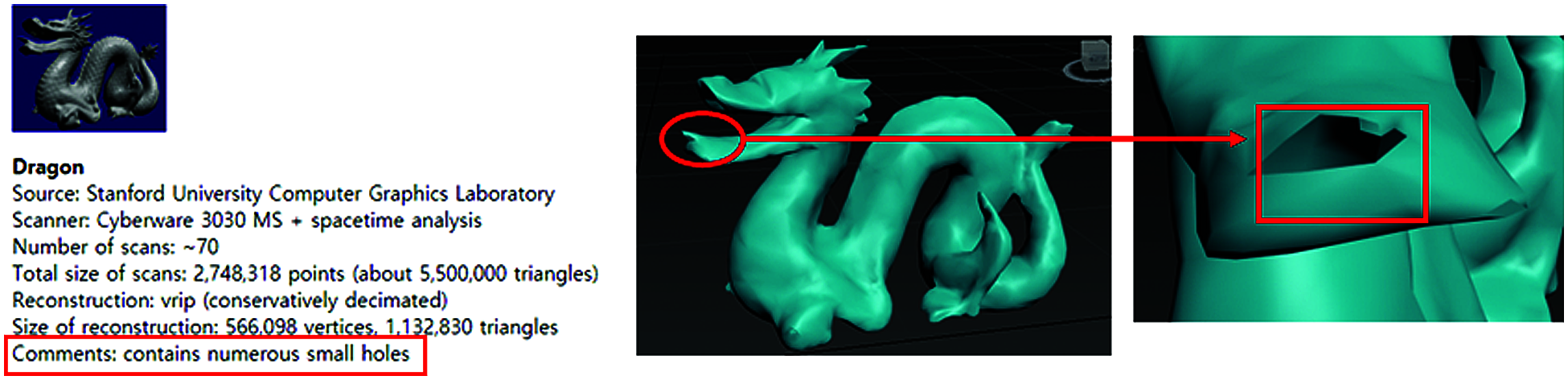
Figure 4: The surface model of the stanford dragon that contains some holes

Lines (1)–(9) of Algorithm 2 are the process of finding a triangle facing the reference vertex located in the opposite direction of the triangle using Unity3D's Raycast function. This Raycast function can check whether the ray has collided with the mesh surface or not. In order to find the opposite mesh through Raycast, we reversed the direction of the surface normal of mesh, and then a ray is emitted from one node constituting the virtual 3D object in the opposite direction to find the mesh colliding with the ray. Lines (1)–(3) in Algorithm 2 are the process of changing the normal direction of triangles. Fig. 2 shows the process of lines (4)–(9) of the algorithm. After creating a reverse mesh by reversing all of the normal directions, Raycast is conducted to find the triangle mesh on the opposite side. At all vertices ⅈ = (1,⋅⋅⋅,N), the proposed algorithm finds the collided triangle mesh with the hit position coordinates.

Fig. 3 shows the process of setting up start vertexi  and end vertexi by finding the closest vertex from start vertexi  for ISPC. Lines (10)-(13) of Algorithm 2 find the hit point through which the ray emitted from start vertexi passed to the triangle, which are formed by the three vertices P1, P2, P3, and then selects the nearest vertex between the hit point and P1, P2, P3. In line (11), the distance between the three vertices is calculated based on the hit point of the ray, in order to connect start vertexi  and end vertexi as a ISPC after finding a triangle located in the opposite direction of normal, and in line (12), the index of the nearest vertex and the index of the vertex that is the starting point of the ray are stored in an array for ISPC information. Lines (14)–(18) of Algorithm 2 are the process of removing duplicated ISPC information. The newly created ISPC information stored in an array, are more likely to be duplicated, because the position of the triangle in the opposite direction of the normal and the nearest vertex are similar in a symmetrical 3D model. Therefore, to eliminate the overlap of ISPC information, the start vertexi  index and end vertexi  index of all ISPC can only be stored once.

4  Experiment

4.1 Experimental Settings and Implementation Details

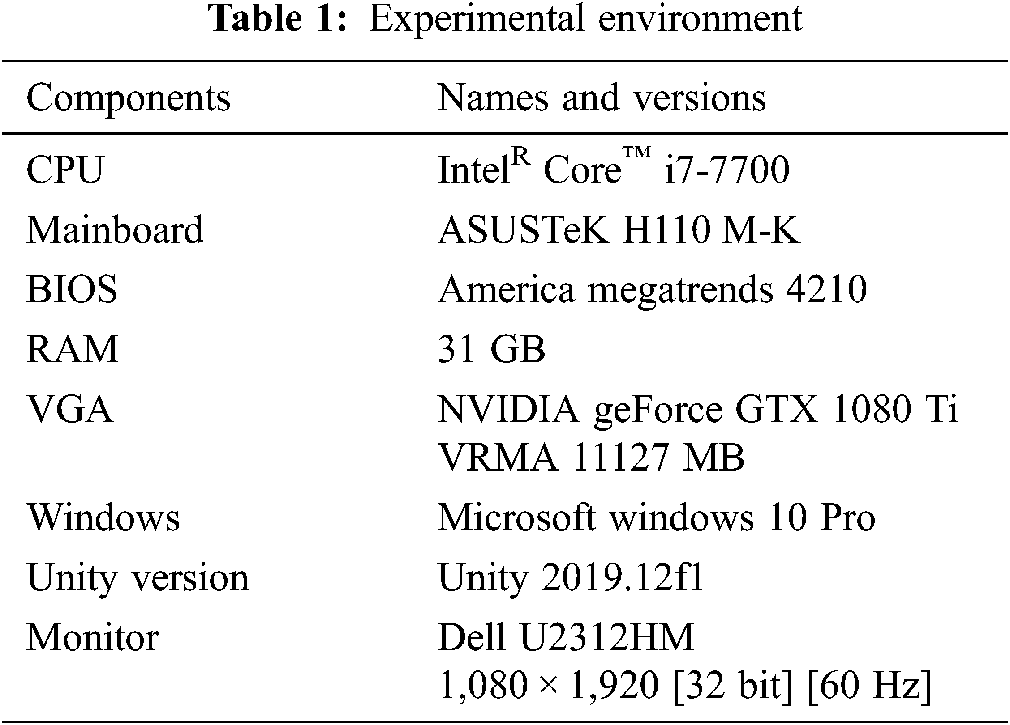
Tab. 1 shows the computer specifications used in the proposed method for the experimental test. This experimental test was conducted by classifying the frame per second (FPS) and behavior comparison between the tetrahedral and ISPC models, and whether it is possible to create the ISPC model from the surface model. To verify the performance of the ISPC model, the experimental test was conducted using two models, which are the proposed ISPC model, and the tetrahedral model. When it was not possible to create the 3D tetrahedral model from the 3D surface model, we performed the experimental test to compare the surface model with the ISPC model. The tetrahedral model was generated through the open source TetGen program, and all experimental tests were conducted in Unity3D. For the constraint applied 3D tetrahedral model, the strain constraint, distance constraint, and bending constraint were applied to represent the properties of 3D deformable virtual objects. Tab. 2 shows the detailed information of the 3D object models that were used in this experimental test.

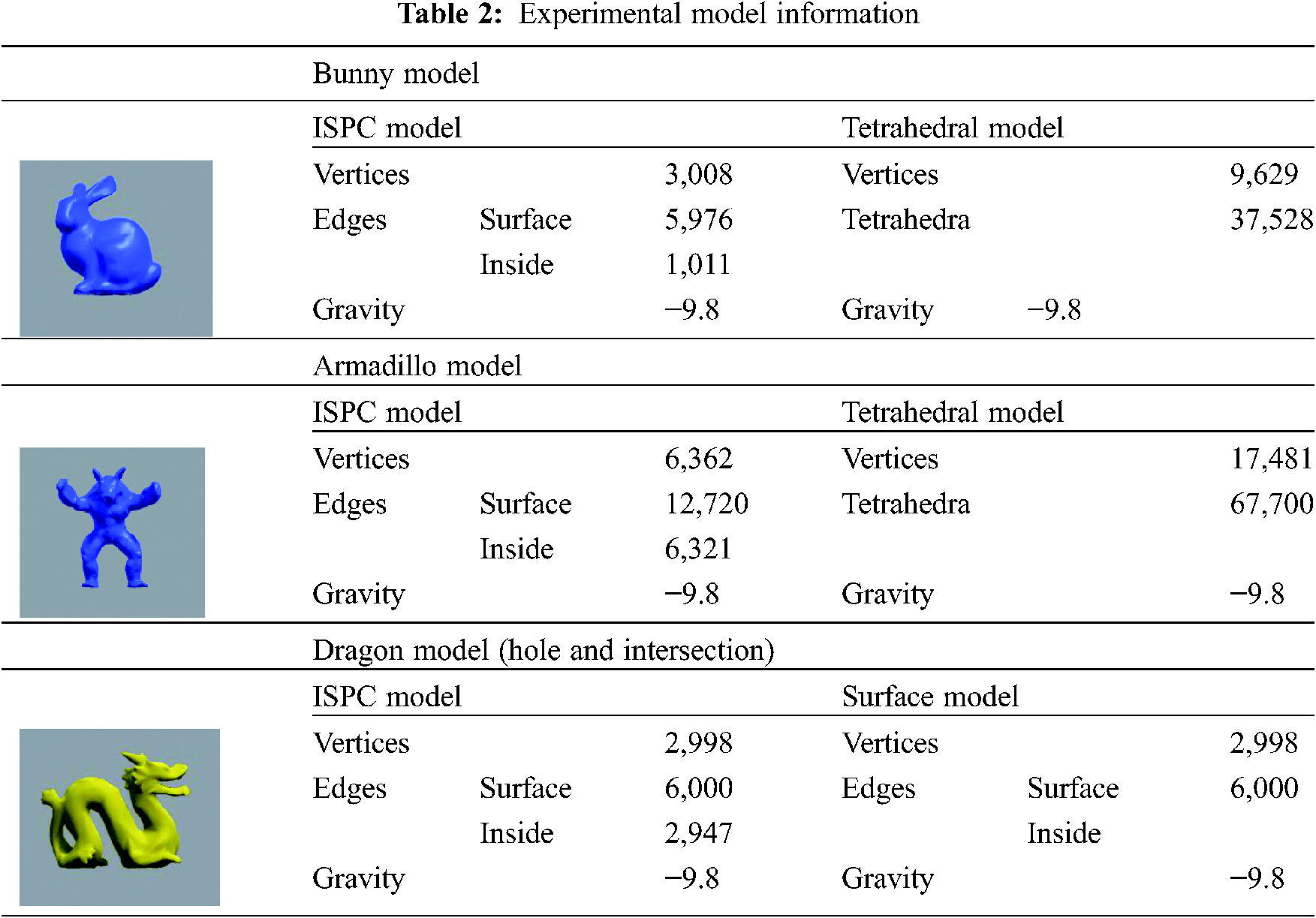
In the case of the Bunny and Armadillo models, since the surface models were completely modeled, it was easy to create the tetrahedral model using TetGen. The Dragon model is provided by Stanford University, and we reduced the number of mesh elements using the 3ds Max for real-time simulation. This Dragon model contains many holes in the surface mesh, so when the tetrahedral model is created through the TetGen program, various errors appear. In the case of the incomplete surface model in which the mesh is not closed, such as the Dragon Model in Fig. 4, an error occurred when we were trying to generate the tetrahedral model by TetGen. However, the proposed ISPC algorithm provided similar object behavior to the tetrahedral model in the Unity3D environment, even in the case of a surface object with no closed mesh or a large hole.

4.2 Result of Experimental Tests

In this paper, the experimental test was stopped when 15 elapsed based on the function to measure simulation time. The output data was set to accumulate every 1 s in order to reduce the error of the data through the experimental test. Fifteen times of experimental tests were performed, and the average of 10 experimental tests was used, excluding outliers, such as the maximum and minimum values. The graphs in Figs. 6 and 8 show the change of average FPS for the collision experimental test, in which the virtual objects of the tetrahedral model and the proposed ISPC model are falling from a certain height to the ground. The graphs in Fig. 10 show the change of average FPS for the same test as the ISPC model and surface model. The average FPS is obtained after adding up all the FPS values ​​at each time of the 10 experimental tests, except for outliers. The code for calculating FPS is as follows:

Deltatime=(time.deltaTime−Deltatime)×0.1f (12)

FPS=Deltatime/1.0f (13)

Unity3D Update function is called every frame to execute the corresponding code. In this code, Time.deltaTime means the execution time per frame. The x-axis of the graph is the result of outputting FPS at 1 s intervals, and the y-axis is the average of the results of the FPS changing per second.

4.2.1 Experimental Test for the Bunny Model

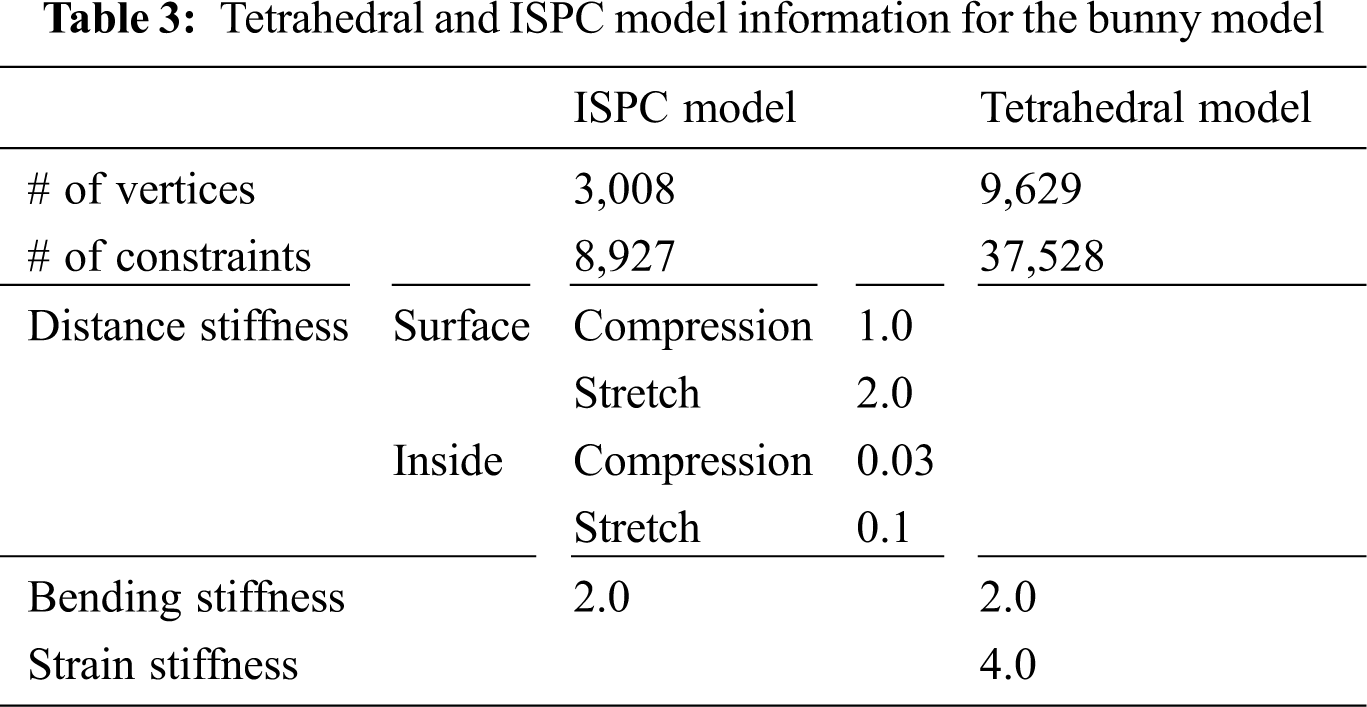
For the Bunny model, the ISPC and tetrahedral models were applied, and the results were compared. For experimental tests, the constraint parameters of the ISPC model, such as distance, bending, and internal shape-preservation, were adjusted to be similar to the behavior of the tetrahedral model. Tab. 3 shows the information of the models used for this experimental test, and Fig. 5 compares the behavior of these models. In this experimental test using the Bunny model, we can confirm similar behavior between the tetrahedral and the ISPC model by adjusting the stiffness of constraints.

Figure 5: The experimental test of ground collision for the Bunny model (left: Tetrahedral model using black color; right: ISPC model using blue color)

The result of comparing the FPS showed that the FPS of the ISPC model was about 115% faster than the FPS of the tetrahedral model, as shown in Fig. 6. The average FPS of the ISPC model was 47.30, while the average FPS of the tetrahedral model was 21.96.

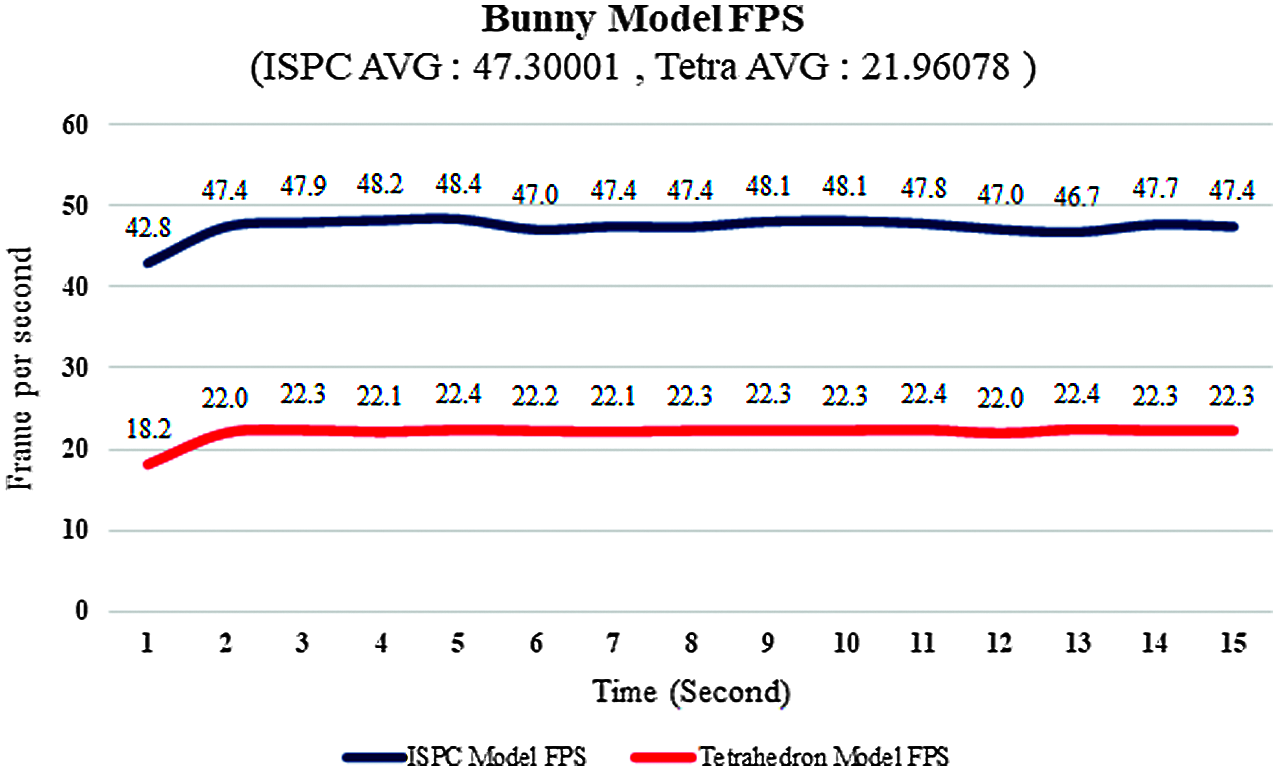
Figure 6: The FPS comparison for the bunny model between the ISPC and tetrahedral models

4.2.2 Experimental Test for the Armadillo Model

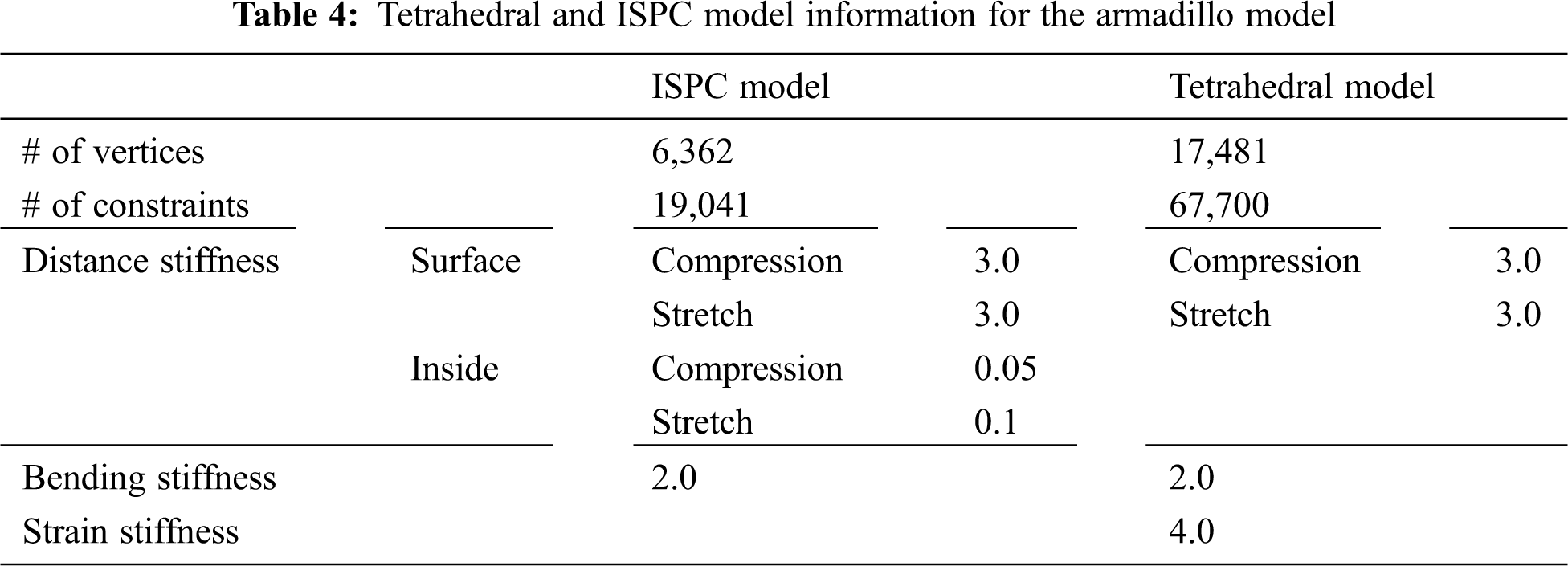
For the Armadillo model, the ISPC and tetrahedral models were applied, and the results were compared as well. For experimental tests, the constraint parameters of the ISPC Model, such as distance, bending, and internal shape-preservation, were adjusted to be similar to the behavior of the tetrahedral model, as for the Bunny model. Tab. 4 shows the information of the models used for this Armadillo model test, while Fig. 7 compares the behavior of these models.

Figure 7: The experimental test of ground collision for the armadillo model (left: Tetrahedral model using black color; right: ISPC model using blue color)

Similar to the Bunny model, the FPS of the ISPC model was about 285% faster than the FPS of the tetrahedral model, as shown in Fig. 8. The average FPS of the ISPC model was 29.09, and the average FPS of the tetrahedral model was 7.54 for the Armadillo model.

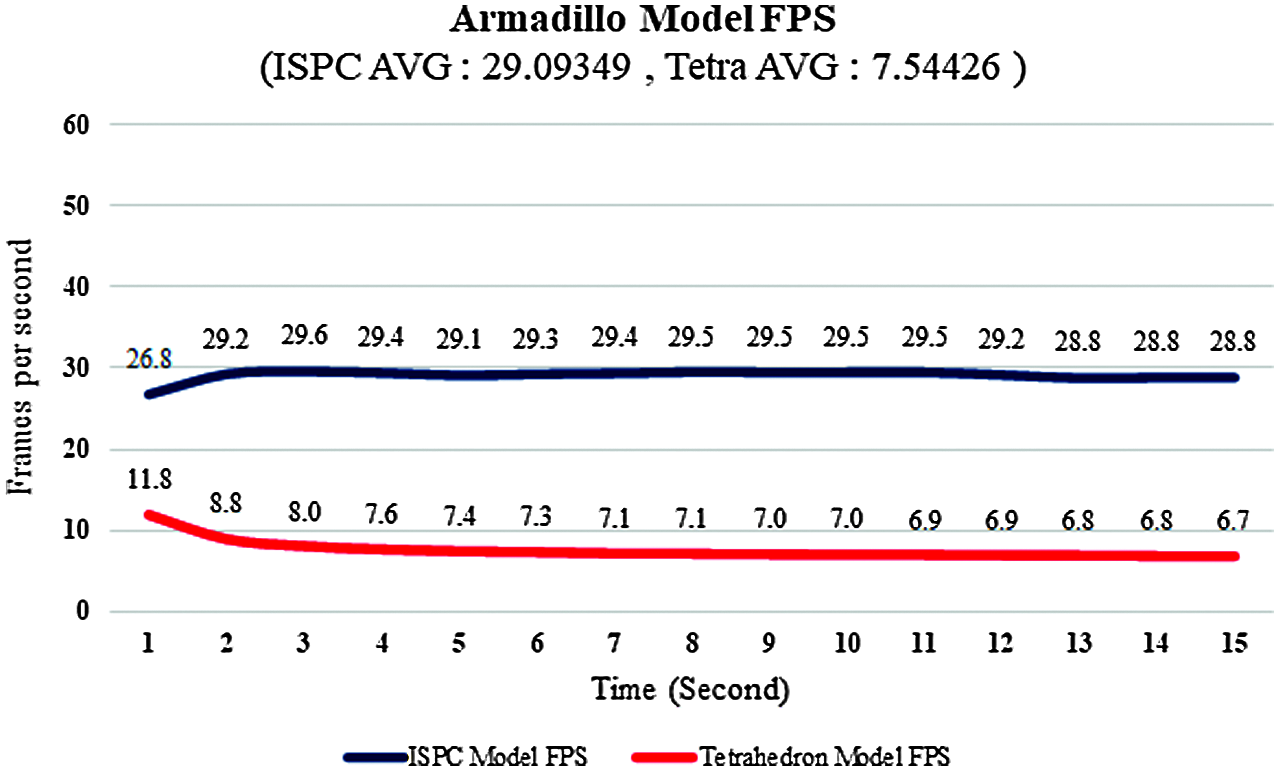
Figure 8: The FPS comparison for the armadillo model between the ISPC and tetrahedral models

4.2.3 Experimental Test for the Dragon Model

The experimental test with the Dragon model, which includes some holes in the model, was conducted. In the case of the surface model, no matter how high the stiffness value of the constraint is in setting up, when the interactions, such as gravity or collision, are applied to 3D virtual objects, the shape of the original model cannot be maintained. However, the proposed ISPC algorithm maintained the original shape of the object well, even under the collision situation, and it was confirmed that the behavior of the ISPC object simulation was similar to that of the tetrahedral model. Tab. 5 and Fig. 9 show the experimental test information and motion comparison of the Dragon model.

Figure 9: The experimental test of ground collision for the dragon model (left: ISPC model using purple color; right: Surface model using black color)

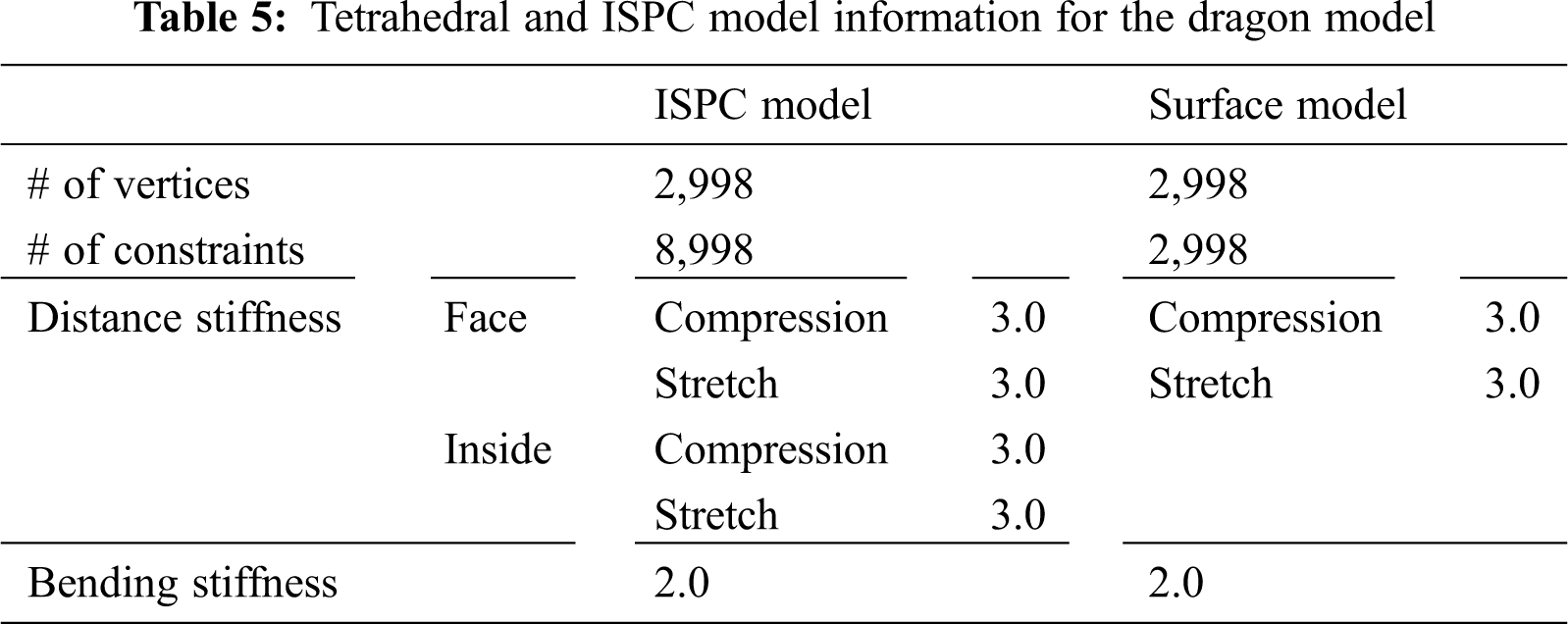
Fig. 10 shows the results of FPS comparison through the Dragon model for the surface model and the proposed ISPC model. As a result of comparing the FPS of the proposed ISPC model, the FPS of the surface model was about 5% higher, but it was confirmed that the difference in FPS was significantly smaller than that of the tetrahedral model, while maintaining the volume well.

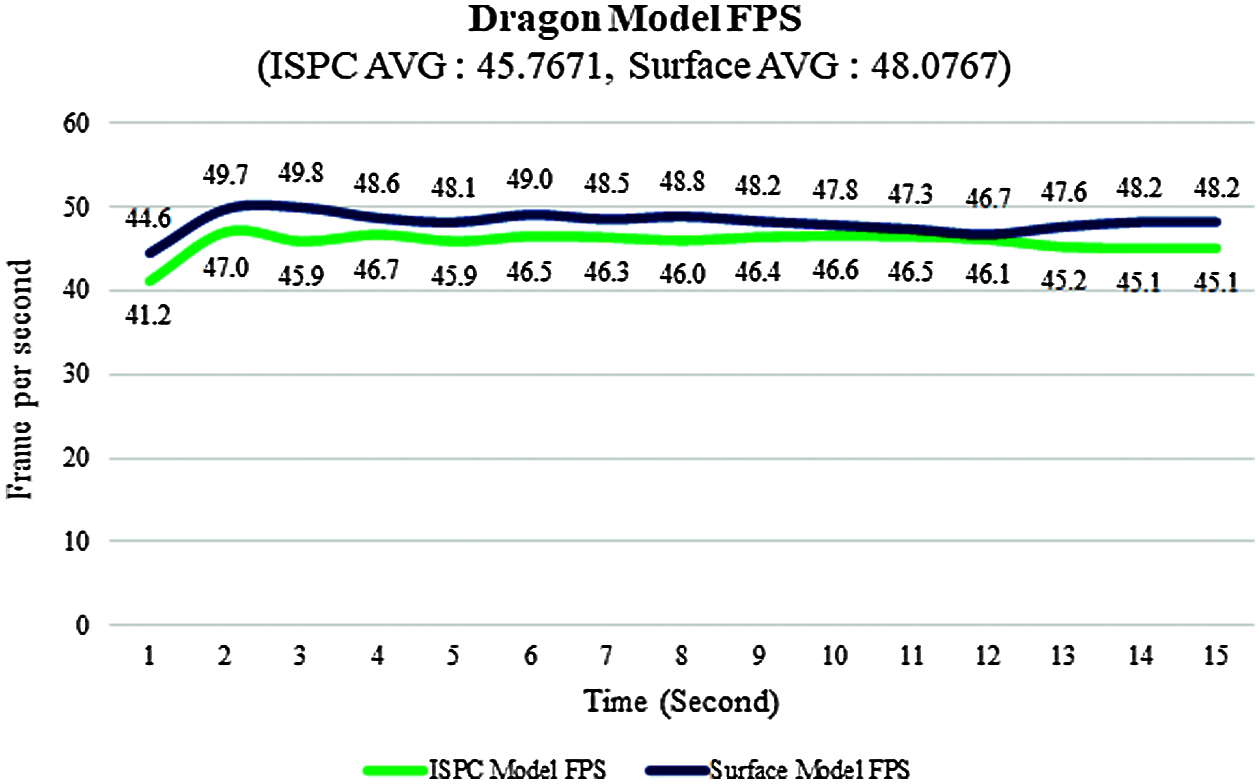
Figure 10: The FPS comparison for the dragon model between the ISPC and surface models

4.2.4 Experimental Test for Volume Preservation

Finally, to confirm the change in volume when pressure is applied to the ISPC and tetrahedral models, the experimental test of pressing two objects with a transparent glass plate was conducted. As a result of experimental test, it was confirmed that the proposed ISPC model as shown in Fig. 11 easily returns to the original shape as the result of the tetrahedral model by ISPC applied to the inside of the virtual object. In Fig. 11, the first row shows the front view results of the experimental test, while the second row shows the top view results.

Figure 11: Appearance of objects when heavy pressure is applied (left: Tetrahedral model using black color; right: Surface model using blue color)

4.2.5 Limitations of This Model

This model can generate a volumetric model similar to the tetrahedral model and can simulate it. However, since it creates a link inside the surface model and proceeds, it has a disadvantage in that it is vulnerable to accurate physics simulation compared to the tetrahedral model. Also, there is a disadvantage in that it is difficult to proceed with cutting simulation.

5  Conclusion

In this paper, in order to overcome the problem of generating the tetrahedral model from the surface model that might occur when trying to simulate a tetrahedral model using Unity3D, and the problem of real-time computation because it consists of many vertices, we proposed the ISPC algorithm to simply simulate the 3D virtual objects, applying the distance constraints to the inside of 3D objects. The tetrahedral model has the problem that generation errors easily occur depending on the completeness of the surface mesh and input parameter values. Therefore, users who are unfamiliar with the 3D modeling program may have difficulty in creating the simulation contents. In addition, when simulation through the tetrahedral model is possible, there is the disadvantage that real-time simulation cannot be performed on Unity3D, due to the heavy computational cost. To solve these problems, we applied the proposed ISPC algorithm, and obtained similar behavior to the result of the deformable object simulation for the tetrahedral model by adjusting the stiffness of constraints. Various physical properties, such as softness and rigidity, could be expressed with the proposed method. Also, the computational cost that could be represented using FPS was about 100% or more better than that of the tetrahedra model. Therefore, the proposed method can be a solution for the production of games or real-time simulation contents based on Unity3D.

The proposed ISPC algorithm can be effectively applied for interactive situations, such as collision and pressure, but in the case of precise simulation and cutting simulation, it has the disadvantage of being difficult to apply, which is mainly dealt with in the current simulation contents. In the future, we will provide the supplement of shortcomings of the ISPC model, and conduct the research on a new algorithm that can perform cutting simulation and volume preservation using constraints.

Funding Statement: This work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF-2019R1F1A1062752) funded by the Ministry of Education, was funded by BK21 FOUR (Fostering Outstanding Universities for Research)(No.: 5199990914048), and was supported by the Soonchunhyang University Research Fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. Si, X. Liao, Y. Qian and Q. Wang, “Mixed reality guided radiofrequency needle placement: A pilot study.” IEEE Access, vol. 6, pp. 31493–31502, 2018. [Google Scholar]

 2.  I. Berndt, R. Torchelsen and A. Maciel, “Efficient surgical cutting with position-based dynamics.” IEEE Computer Graphics and Applications, vol. 37, no. 3, pp. 24–31, 2017. [Google Scholar]

 3.  M. Müller, B. Heidelberger, M. Hennix and J. Ratcliff, “Position based dynamics.” Journal of Visual Communication and Image Representation, vol. 18, no. 2, pp. 109–118, 2007. [Google Scholar]

 4.  A. Munawar, N. Srishankar and G. S. Fischer, “An open-source framework for rapid development of interactive soft-body simulations for real-time training.” in 2020 IEEE Int. Conf. on Robotics and Automation (ICRAParis, France, pp. 6544–6550, 2020. [Google Scholar]

 5.  D. T. Lee and B. J. Schachter, “Two algorithms for constructing a delaunay triangulation.” International Journal of Computer & Information Sciences, vol. 9, no. 3, pp. 219–242, 1980. [Google Scholar]

 6.  H. Si, “TetGen, a delaunay-based quality tetrahedral mesh generator.” ACM Transactions on Mathematical Software (TOMS), vol. 41, no. 2, pp. 1–36, 2015. [Google Scholar]

 7.  J. Pan, L. Zhang, P. Yu, Y. Shen, H. Wang et al., “Real-time VR simulation of laparoscopic cholecystectomy based on parallel position-based dynamics in GPU.” in 2020 IEEE Conf. on Virtual Reality and 3D User Interfaces (VRAtlanta, GA, USA, pp. 548–556, 2020. [Google Scholar]

 8.  L. Thomas, K. A. Agüero and A. L. Apolinário, “Real-time 3D position-based dynamics simulation for hydrographic printing.” in 2020 33rd SIBGRAPI Conf. on Graphics, Patterns and Images (SIBGRAPIPorto de Galinhas, Brazil, pp. 23–30, 2020. [Google Scholar]

 9.  M. Vincent and O. Benoît, “GPU-Friendly data structures for real time simulation.” Advanced Modeling and Simulation in Engineering Sciences, vol. 8, no. 1, pp. 1–14, 2021. [Google Scholar]

10. M. Fratarcangeli, “Position-based facial animation synthesis.” Computer Animation and Virtual Worlds, vol. 23, no. 3–4, pp. 457–466, 2012. [Google Scholar]

11. S. Misra, K. T. Ramesh and A. M. Okamura, “Modeling of tool-tissue interactions for computer-based surgical simulation: A literature review.” Presence: Teleoperators and Virtual Environments, vol. 17, no. 5, pp. 463–491, 2008. [Google Scholar]

12. X. Zhang, H. Wu, W. Sun and C. Yuan, “An optimized mass-spring model with shape restoration ability based on volume conservation.” KSII Transactions on Internet and Information Systems (TIIS), vol. 14, no. 4, pp. 1738–1756, 2020. [Google Scholar]

13. D. Luo, Y. Zhang and R. Zhao, “Study on deformation technology of virtual surgery simulator based on liver puncture.” in 2018 3rd Int. Conf. on Robotics and Automation Engineering (ICRAEGuangzhou, China, pp. 176–179, 2018. [Google Scholar]

14. A. Talvas, M. Marchal, C. Duriez and M. A. Otaduy, “Aggregate constraints for virtual manipulation with soft fingers.” IEEE Transactions on Visualization and Computer Graphics, vol. 21, no. 4, pp. 452–461, 2015. [Google Scholar]

15. R. Wang, J. Yao, L. Wang, X. Liu, H. Wang et al., “A surgical training system for four medical punctures based on virtual reality and haptic feedback.” in 2017 IEEE Symp. on 3D User Interfaces (3DUILos Angeles, CA, USA, pp. 215–216, 2017. [Google Scholar]

16. M. Macklin and M. Müller, “Position based fluids.” ACM Transactions on Graphics (TOG), vol. 32, no. 4, pp. 1–12, 2013. [Google Scholar]

17. J. Bender, M. Müller, M. A. Otaduy, M. Teschner and M. Macklin, “A survey on position-based simulation methods in computer graphics.” in Computer Graphics Forum, vol. 33, no. 6, pp. 228–251, 2014. [Google Scholar]

18. S. J. Lee, M. Hong, S. Kim and S. J. Choi, “Effect analysis of virtual-reality vestibular rehabilitation based on eye-tracking.” KSII Transactions on Internet & Information Systems, vol. 14, no. 2, pp. 826–840, 2020. [Google Scholar]

19. M. Javaid and A. Haleem, “Virtual reality applications toward medical field.” Clinical Epidemiology and Global Health, vol. 8, no. 2, pp. 600–605, 2020. [Google Scholar]

20. X. Zhang, X. Yu, W. Sun and A. Song, “An optimized model for the local compression deformation of soft tissue.” KSII Transactions on Internet & Information Systems, vol. 14, no. 2, pp. 671–686, 2020. [Google Scholar]

21. M. Muller, N. Chentanez, T. Y. Kim and M. Macklin, “Strain based dynamics.” in Eurographics/ACM SIGGRAPH Symp. on Computer Animation, Copenhagen, Denmark, pp. 2, 2014. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.