DOI:10.32604/iasc.2022.022583

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.022583 |  |
| Article |
Performance Analysis of Two-Stage Optimal Feature-Selection Techniques for Finger Knuckle Recognition
Department of Information Technology, PSG College of Technology, Coimbatore, 641004, India
*Corresponding Author: P. Jayapriya. Email: jayapriy@gmail.com
Received: 12 August 2021; Accepted: 14 September 2021
Abstract: Automated biometric authentication attracts the attention of researchers to work on hand-based images to develop applications in forensics science. Finger Knuckle Print (FKP) is one of the hand-based biometrics used in the recognition of an individual. FKP is rich in texture, less in contact and known for its unique features. The dimensionality of the features, extracted from the image, is one of the main problems in pattern recognition. Since selecting the relevant features is an important but challenging task, the feature subset selection is an optimization problem. A reduced number of features results in enhanced classification accuracy. The proposed FKP system presents a mulitalgorithm fusion based on subspace algorithms at feature level fusion technique. In this paper, a new feature-selection algorithm, which is a Modified Magnetotatic bacterium Optimization Algorithm (MMBOA), is proposed for finger knuckle recognition to select relevant and useful features that increase the classification accuracy. The distinct characteristic of this bacterium influences the design of a new optimization technique. The hybrid features such as Eigen and Fisher (EiFi) are extracted from the finger knuckle. The fusion of this feature vector is optimized using newly proposed MMBOA_mr optimization algorithm. The results demonstrate a significant improvement compared with unimodal identifiers, and the proposed approach significantly outperforms with a recognition accuracy of 99.7% with 22 features with the reduction rate of 72%. Additionally, the proposed approach is compared with the state-of-the-art methods.
Keywords: FKP; Eifi feature extraction; feature selection; MMBOA; GWO; KNN
Authenticating a reliable user is important for e-commerce applications. In today’s real-life application, the world is afraid of the Coronavirus, which moves our biometric recognition system towards the contactless user identification system. Out of the various hand-based biometrics, Finger Knuckle print (FKP) is unique for an individual. Finger Knuckle represents the dorsum back surface of the hand. The texture and geometric shape features of the finger knuckle are used in the identification process of an individual to give the projected results. The advantage of using finger knuckle instead of other biometrics is its user-friendliness, invariant to emotions, low cost and user acceptance rate, which is incredibly high. The convex form lines and skin wrinkles on the finger dorsal surface are small in size, making them very unique in individual identification, which is typically not smashed as it is with the upper hand. Furthermore, the acquisition techniques require very little user interaction, resulting in high-speed recognition with low-resolution image cameras. As a result, using finger knuckle biometrics for identification will provide a distinct advantage in the field of physical biometrics. Woodard et al. [1] are the first scholars who changed the Researchers’ perspective towards the finger knuckle as the biometric identification. Here, the 3D finger knuckle print is used for recognition. However, it did not provide a practical implication since it is time consuming when it comes to the acquisition and processing of image in real time applications. Additionally, the authors, in this research, only use the Finger surface shape information for FKP recognition.
Ajay Kumar proposed a FKP recognition model that uses finger knuckle lines and creases are highly rich in texture, local orientation features, which are extracted using radon transform performs better results when compared with Gabor, and Eigen knuckles [2]. The subspace algorithms, such as PCA, ICA and LDA combinations, are used in FKP feature extraction. The geometric features are also extracted to obtain promising results [3].
Zhang et al. proposed a feature extraction scheme for FKP recognition. The classification of the image pattern is based on the feature extraction scheme and plays a key role in matching images and ROI’s accuracy. The local features such as local phase and local concurrency are integrated with the global features to enhance accuracy [4]. Local orientation and magnitude features are extracted using the Gabor filter [5]. The performance is much better for the large dataset. Features extracted from the triangular block of the finger knuckle image, which already small in size may cause the loss of some information. The combination of Local and global information is developed using the Gabor filter and Fourier transform respectively [6].
Feature Selection is a predictive model to select informative features and is considered as an input of the classification model. The dataset is large then it results to high dimensional data. Due to this phenomenon, the classification model is affected with negative impact in accuracy and computation cost [7]. The main goal of doing this preprocessing step is to reduce the computational cost and enhance better performance in recognition [8,9]. In feature selection, the selection of informative features results to an improvement of the classifier model by performance, speed and simplicity. As per literature, only a few optimization techniques are used in biometric recognition for feature selection such as Genetic algorithm (GA), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO). Optimization techniques are mostly used in iris, ear, palm print and in multimodal biometric recognition [10–15]. Even the number of algorithms related to bio-inspired and evolutionary algorithms is used in solving optimization problems. According to the “No free Lunch” theorem, no universal algorithm can solve the problem [16]. Therefore, it creates the required space to develop a new algorithm to provide the better solution.
Literature surveys show that many works have been done on Finger Knuckle recognition in feature extraction stage. However, Feature Selection is not much analyzed for finger knuckle recognition. For the first time, the MBOA optimization technique has been utilized for feature selection in FKP to provide promising results with reduced number of features. So far, the MBOA optimization technique is evaluated for the benchmarked dataset and this provides promising results. Salvatore Bellini, in 1963, identified the polyphyletic group of bacteria that move across the magnetic field line. The bacteria move towards an oxygen-concentrated region and the movement is performed with the help of magnetic crystals with magnetisms. It contains the fixed magnets, which align the bacteria moving towards the North Pole [17]. The traditional MBOA optimization technique is proposed by author [18,19]. The authors are likely to solve the optimization problems and promise fast convergence speed. In traditional MBOA, performance is based on the random replacement. The same author works with MBOA based on individual moments. Here, the solution is based on the local best cell moments and is tested in 13 benchmark functions that provide better performance [20]. The authors proposed a new moment-migration algorithm, which signifies that the moment of magnetosomes with good values can migrate to other solutions, which solve optimization problems. Due to this moment migration, the exploration problem is solved [21]. Based on the characteristics of the bacteria, the authors proposed a new optimization algorithm i.e., the Magnetotatic Bacteria Optimization Algorithm (MBOA). The MBOA is based on four stages: interaction distance, moment generation, moment regulation and moment replacement.
This paper is organized as follows; Section 2 presents the feature selection of the proposed optimization technique to select the discriminative features and feature extraction techniques. Section 3 provides the Experimental results and discussion of the proposed system, the Comparison of proposed feature selection with GWO method and also shows the comparison of proposed with other state of approaches and finally with conclusion in Section 4.
2 A Proposed MMBOA_mr Feature Selection for FKP Recognition
Finger knuckle recognition is based on the MMBOA_mr feature selection technique. Finger knuckle biometric exploits a new approach of choosing the optimal feature subset based on MMBOA_mr. The features are extracted based on the PCA and LDA combination and these feature vectors are fed to MMBOA_mr feature Selection.
The searching process is done iteratively to obtain the best subset features. It is based on the fitness function in terms of classification accuracy to validate the subset of features. The classification accuracy is taken as fitness value and is able to select the new feature subset. The bacteria contain multi cells and each cell contains the magnetosomes which is solution vector and the values of the vector are known for moment of the cells. The moment generation, moment regulation and moment replace are the factors which influences the feature reduction. Since the irrelevant features are eliminated the complexity of the system reduces the computational time and the search space.
The contributions of this work include:
• Finger Knuckle recognition is based on a new feature selection algorithm MMBOA_mr
• Ei and Fi features are extracted from the FKP image using PCA and LDA feature extraction techniques
• The MMBOA_mr feature selection technique is proposed for FKP recognition
• Performance of the proposed FKP recognition id evaluated using the performance metrics such as FAR, FRR, ERR and Accuracy.
Features extraction is the transformation of the original features to lower dimensionality with reduced number of features. The first step is to extract the features from the image. This research employs an appearance-based algorithm such as Principle Component Analysis (PCA) and Linear Discriminant Analysis (LDA). Both the PCA and LDA are linear transformations that reduce the computational cost and processing time.
In this paper, the combination Eigen and Fisher knuckle features are proposed to extract the features and it is known as EiFi features. The PCA and LDA are applied to the cropped images to extract the features. Fig. 1, shows the finger knuckle print and the segmented major knuckle print. In this work, the segmented major knuckle print is used for experimental analysis.

Figure 1: (a) Finger knuckle print, (b) Segmented major knuckle
2.1.1 Linear Discriminant Analysis (Fisher Features)
LDA describes the vectors in the classes by constructing the d-dimensional mean vector. Then it finds the scatter matrix within and between the classes. The next sort the Eigen vectors according to the Eigen value and largest Eigen value forms the matrix d × k, where each column represents the eigenvector. Based on the d × k, the sample is transformed into a new subspace [22]. LDA is defined as
The transformation depends on the number of classes (c), number of samples (s) and dimensionality d. The main aim of LDA is to maximize the measure between classes and minimize the measure within classes [3,22].
2.1.2 Principle Component Analysis (Eigen Features)
PCA identifies the subspace, in which the optimal solution lies. The size of the pixel is reduced to minimal without the loss of information. In this work, the feature vector of the finger knuckle image is the Eigen vectors of the covariance matrix (Q). The features extracted from the knuckle image contain n × m pixel. Before computing the covariance matrix, the vectors are normalized to make the system invariant to be illuminated. The covariance matrix is too large to compute Eigen vector. Various authors discussed different results while eliminating the first three Eigen vectors. Face recognition achieves better performance [23] and it results in poor performance [24]. In [2], the author uses a simplified model in reference to [25] where a set of projection coefficients, constructed from the finger knuckles during training phase, is used to refer to the testing phase. PCA fails to find the class separability. It typically aligns the transform axes with maximum variance and is not sure of the contained efficient features for recognition. Transformation depends on the number of classes (c), number of samples (s) and dimensionality denoted by d.
Feature Selection plays an important role in selecting the subset of features by eliminating the irrelevant and unnecessary features. Classification accuracy depends on the best subset of learning features [26]. The subset features should highly be correlated to the classes and uncorrelated with each other. As the dimension N of the feature increases, it expands the search space and computational cost [27]. The feature-selection evaluation procedure is classified into filters, wrappers and embedded [28]. Here, we used the wrapper approach MBOA where the evaluation procedure depends on the classifier. The quality of the learning algorithm is evaluated by the classification. The wrapper approach is based on the number of generations; whereby for each iteration, the best solution is found and highest accuracy-based subset features are selected [29].
2.2.1 Biological Basis for MBOA
MBOA is a magnetotactic bacteria optimization algorithm that is also a new bio inspired algorithm. The Magnetotactic bacteria represent a group of prokaryotes occurring in the natural seawater and fresh water. The magnetic lines, which are known as magnetosomes create the moment to find the optimal solution in their environment. Magnetosomes consist of magnetite colloids and mineral particles arranged narrowly in the geomagnetic field direction. The moment is based on the energy level of each cell and the chemical signals around the environment. The biological characteristics of the bacteria are that they organize themselves and adjust automatically to move along the earth’s magnetic field. The behavior of the bacteria is to find the best optimal oxygen-concentration and redox potentials in the water [30,31].
For survival, the magnetic lines in the magnetosomes that will bend to reduce the magnetostatic energy. The magnetosomes produce the moments, which support the minimization of energy. The optimization of minimized computational cost and storage achieves better performance in the recognition of finger knuckle biometric.
Here, the parameters are tuned with the number of iterations. The performance of the proposed algorithm varies according to the parameter tuning. Here, 30 iterations of 100 different generations, with the population size of 50, is performed and the results are discussed in Section 3. The parameters c1, c2, mp and B are used as objective function and the fitness value depends on the accuracy. The parameter setting for MMBOA_mr and GWO are shown in Tab. 1.

The parameter setting includes the values such as C1 = 30, C2 = 0.004, mp = 0.7 and B = 0.1 and are selected as best for the benchmark functions [21]. Here, constant variables setup as C1 = 1.5, C2 = 0.5, probability mp = 0.6 and parameter, magnetic field B = 1 for the Finger knuckle recognition and it plays a significant role on performance to reduce the computational cost without the loss of accuracy.
2.2.3 A Proposed FKP Feature Selection MMBOA_mr

Figure 2: Proposed FKP recognition
The combination of PCA and LDA feature extraction techniques are used to extract the features using the optimization technique to select the relevant features. Finally, to analyze the accuracy, the selected features are fed to the KNN classifier. The proposed FKP recognition architecture is displayed in Fig. 2. MBOA is a bio inspired optimization algorithm that regulates the moment of the magnetosomes cells. The regulating moment is mainly based on the continuous process following the three steps 1) MTS moment generation, 2) moment regulation, 3) moment replacement. Based on the original MBOA, novel MMBOA-mr is proposed to improve the performance of the single objective function. The multiple cells produce the moments based on the maximization of the magnetostatic energy. As such, this process is considered for optimization and minimization of the computational speed with minimal number of features. The feasible feature vector for finger knuckle recognition is obtained by continuous regulation of the moments by magnetosomes [21]. The overall work flow of the Feature Selection in MMBOA_mr is shown in Fig. 3.
The similitude between the Original MBOA and feature selection MMOBA_mr is the non-multi cells in the bacteria population where each cell (vector) is considered a feasible solution and the feature values are magnetosomes and moment of magnetosomes. Finally, the state of low concentration of magnetostatic energy is an obtained optimal solution
a) Initialization
The population P. randomly generates the feature vector (cell). The cell is generated using Eq. (5).
where i = 1, 2, 3 …. P (P is the size of the population), j = 1, 2, 3 … n, (dimension of the cell), max and mini are upper and lower bounds for the dimension j, rand (0, 1) is a random number from the uniform distribution (0, 1).

Figure 3: Work flow chart of MMBOA_mr
b) Interaction Distance
The distance between two cells is calculated as the interaction energy between the cells. The distance between the two cells are
Then P
c) Interaction Energy
The obtained Interaction distance
where ‘t’ is the current generation,
d) Moments Generation
Moment’s generation is produced using an interaction energy
In MBOA_mr, the magnetic field B is the constant value 1. Then, the moment generation will be
The total moments can be regulated as follows:
Here, l
e) Moment Regulation
The regular MBOA is not following the regulation setup for the moments. The proposed MMBOA_mr evaluates the population of the cells whereby the aspect of fitness value is based on the current generation (t) classification accuracy and regulates the moment as
If rand < mp
Otherwise
The worst features are omitted and the best features for each generation are included and calculated as per the fitness value. Some of the cell moments regulate the other cells, which improve the exploitation search (local minimum) as per Eq. (10). The exploration search is enhanced by identifying the best cell from the approximating the best one from the current generation as per Eq. (11).
f) Moment Replacement
After the moment migration, the population is evaluated according to the cell’s fitness. Based on the cost, the solutions are sorted in ascending order. The replacement probability is set as 0.5. The worst features are ignored using the formula below.
The remaining moments are replaced by the Eq. (13)
2.2.4 Pseudo Code of Modified MBOA_Moment Regulation (MMBOA_mr)
// Initialization
Initialize the random value as best value (Xbest)
Initialize the magnetic bacteria and memory as zero (X, F)
Initialize the population randomly (P) in search space
Initialize Parameters
Until stop criteria met to do
// Interaction Distance
Calculate the fitness of each cell
Normalize the fitness
// Interaction distance
Calculate the Interaction Distance D from Eq. (6)
// Moment Interaction Energy
For each cell do
If D > r
Calculate the Moment interaction Energy of the two cells from Eq. (7)
Else
E = rand (1, P)* R
End if
End for
// Moment Generations
Obtain moment generation from Eq. (8)
Evaluate the population according to the fitness
// Moment Regulation
Visualize the moments and next the regulation of the moment follows
Calculate the moment M of each cell at t generation from Eq. (10)
Regulate the moment of each cell at t generation Eq. (11)
Evaluate the population according to the fitness
// Moment Replacement
For each cell do
According to cost, the solution is sorted in ascending order
MTS replacement as in Eqs. (12) and (13)
End for
Archives best solution
2.2.5 K-Nearest Neighbor Classifier
The K-Nearest Neighbor (KNN) is a simple classifier. This supervised learning algorithm selects the minimum distance between the query samples and the trained samples. It is easy to implement using the K (K=1) value that defines the nearer number of neighbors. In this proposed work, KNN is used to ensure classification accuracy for the finger knuckle Recognition [32].
The performance of the proposed algorithm MMBOA_rm is discussed and presented. The implementation and testing are done using the poly u dataset. The Poly u finger knuckle dataset is used to prove the efficient recognition of an individual. The dataset with two sets: 70% for training and 30% for testing is used. The dataset has five images for the single user and is further divided into two sets for training and testing. For training 3 and for testing 2 images are given.
Feature Selection with stopping criteria for optimization is considered, a maximum of 30 generations with 100 iterations for each generation. It is done to prove the statistical implication and stability of the outcomes. After selecting the subsets of feature set, it is valued using the test set. This evaluation is done with the KNN classifier. The experiments are conducted with respect to different parameters and finally the adoptable results are discussed in below. Implementation is done in Matlab (2016) core™ i3-7100U, x-64 based processor, 64-bit operating system, and 4GB RAM. Based on the evaluation criteria, the different classifiers are implemented and compared to show the one that achieves better performance in the proposed work. The performance of the FKP recognition is generated with the metrics such as accuracy, FAR, FAR, EER
3.1 Evaluation of the Proposed Method
The FKP image features are extracted using PCA and LDA. It is represented as Eigen and fisher feature vectors. These two machine learning algorithms are used in feature extraction based on feature selection in various biometrics such as face, palm print, ear, finger vein [33–38]. Here, FKP image features are extracted using this appearance-based algorithm individually and the results are tabulated. The results show that the LDA performs better than PCA. Finally, the EiFi features are concatenated and recognition of the results outperforms well.
3.1.1 Performance Based on Classification Accuracy
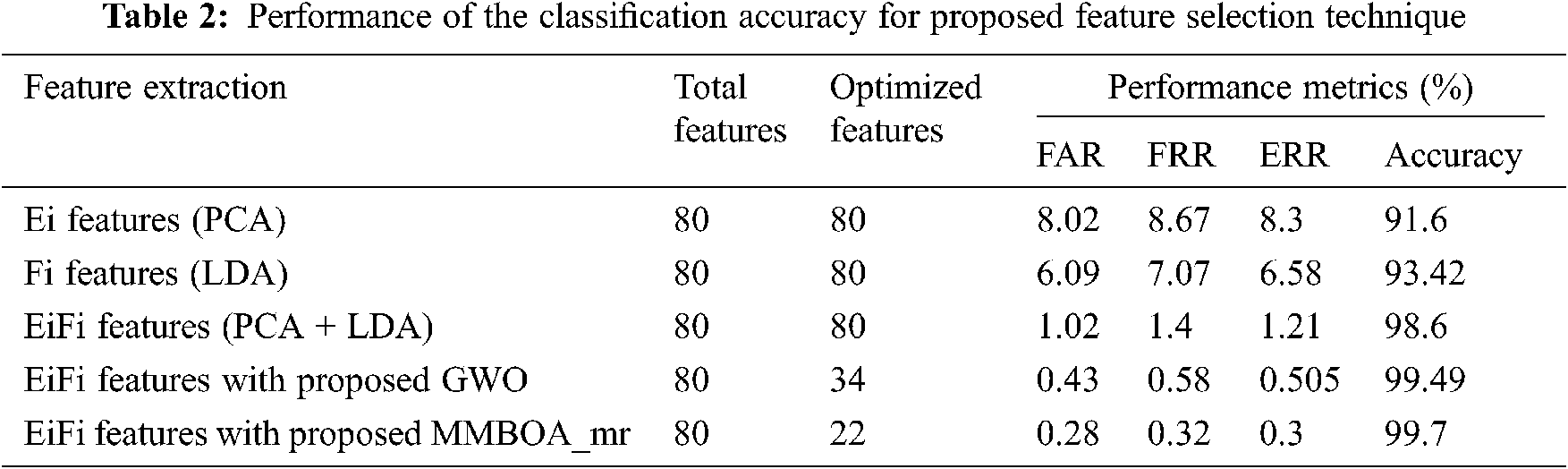
The KNN classifier is used to classify the genuine users due to its simplicity. In Tab. 2, the experimental results prove that the multi-algorithm feature level fusion with KNN reveals improved performance with better accuracy. The Ei knuckle feature outputs better accuracy of 91.16%. The Fi knuckle features achieve good performance for KNN classifiers with 93.42% accuracy. The results with the fusion of Eifi features show better and good results for KNN classifier with 99.67% accuracy. The FAR and FRR rate for the EiFi features based on the KNN classifiers gives lower rate of 0.361 and 0.28%. The EiFi features, with better accuracy, is given as an input to the proposed feature selection algorithms MMBOA_mr and GWO [39], which achieves 99.4% for GWO and 99.7% for MMBOA_mr accuracy with reduced number of features.
3.1.2 Performance of the Proposed MMBOA_mr with GWO Based on No of Generations/ Users
The proposed algorithm is compared with the Gray Wolf Optimizer (GWO). For Finger Knuckle recognition, the optimization algorithms for feature selection are used in limited study. Therefore, the comparison the Grey wolf Optimizer is implemented and the results compared with the proposed MBOA. Both the optimization algorithms such as MBOA and GWO show better results for the introduction of features. When GWO is compared with MBOA, MBOA outperforms well with minimum number of features and computational speed based on classification accuracy.
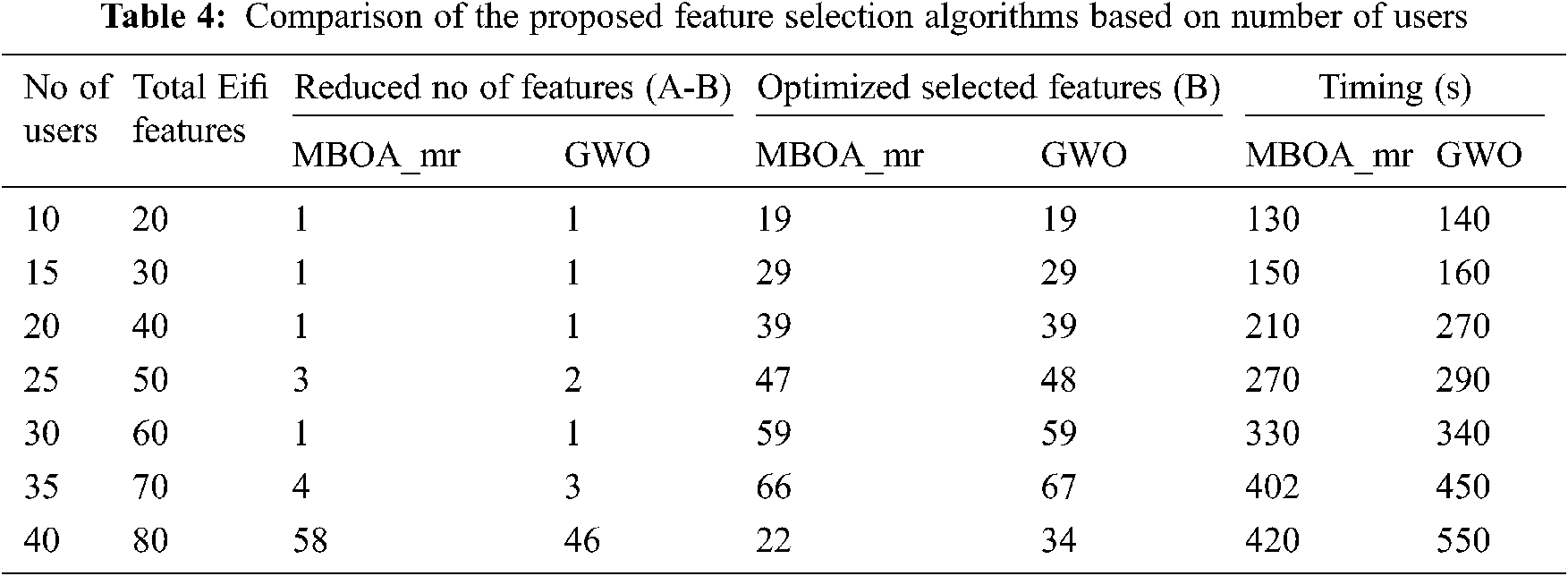
Performance comparison is based on these two algorithms: MMBOA_mr and GWO are shown in Tabs. 3 and 4. The results of both the algorithms show noteworthy enhancement in terms of classification accuracy based on feature selection. The GWO and MMBOA_mr algorithm show variations in accuracy. For 30 generations with 3000 iterations, algorithm shows nearly 99% accuracy. Regarding the number of features, GWO achieves 99.4% accuracy with 34 subset of features and MMBOA_mr achieves 99.7% accuracy with 22 subset of features. Figs. 4 and 5 show the comparative analysis of MMBOA_mr and GWO based on different features sets and execution time for the given users respectively.

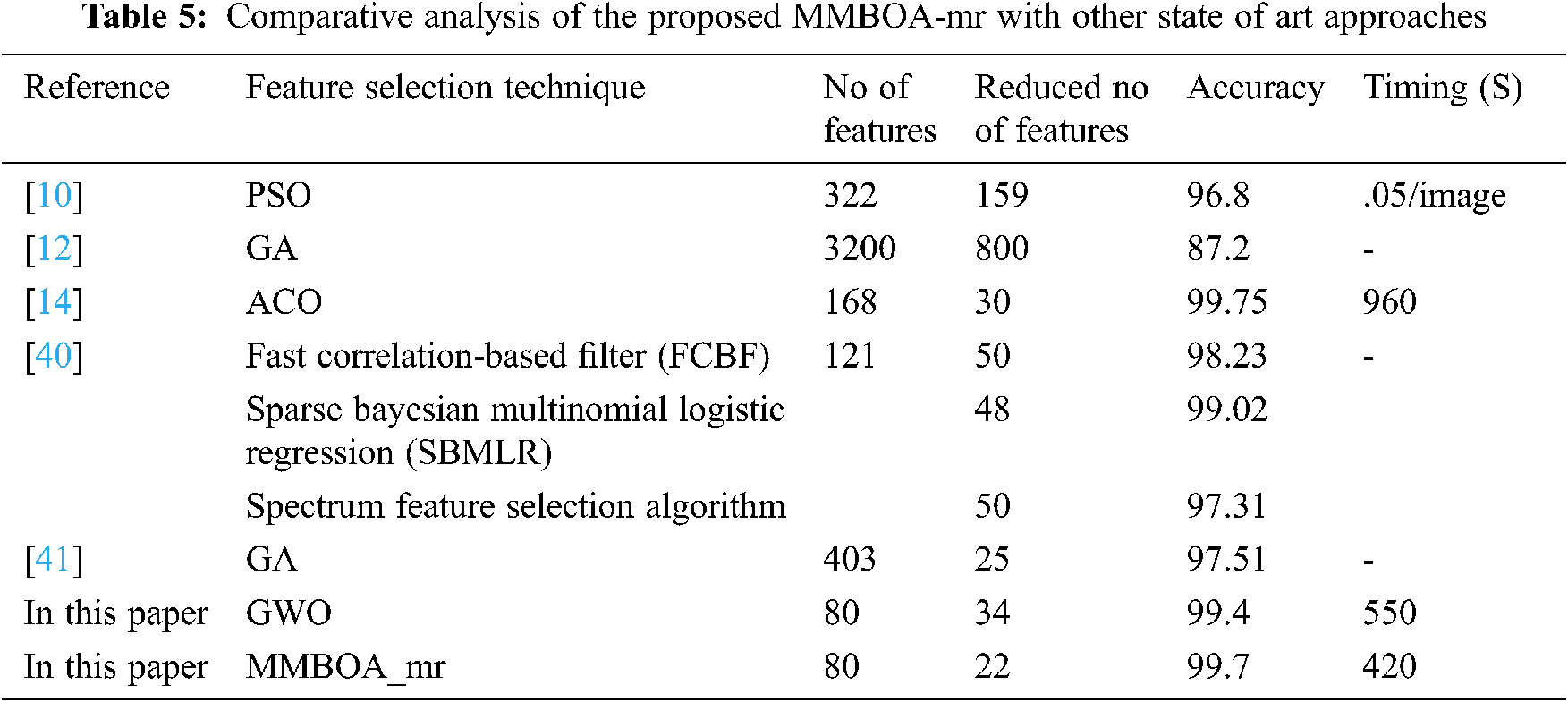
3.1.3 Comparison of the Proposed MMBOA_mr with Other Metaheuristic Algorithms
Feature selection in various biometrics such as the hand based, palm print, ear and face [10,12,14,40,41] are compared to the proposed feature selection method MMBOA_mr and GWO. The results are tabulated in Tab. 5 in terms of total number of features, subset of features and accuracy. In [40], the index finger knuckle with 121 features reduced to 50 and 48 for various feature selection methods with accuracy ranges from 97% to 98%. The proposed MMBOA_mr and GWO achieve 99% accuracy with 22 and 34 subsets of features.
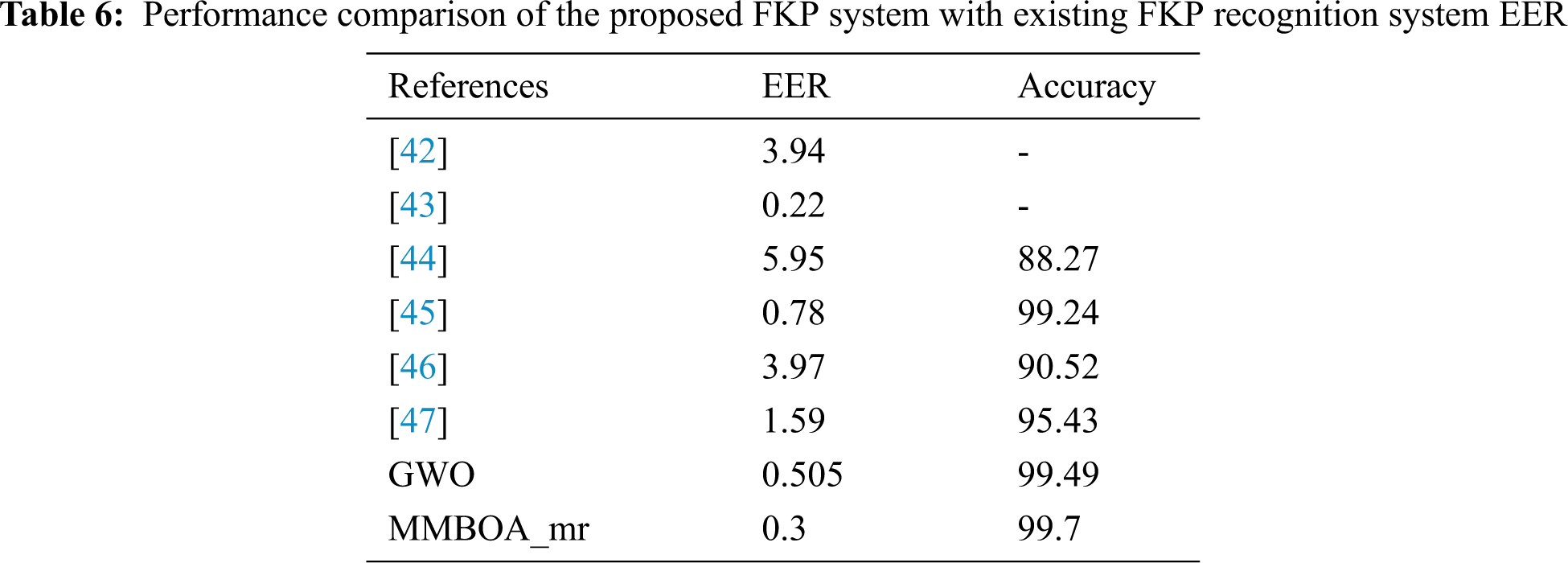
3.1.4 Comparison of the Proposed MMBOA_mr with Existing FKP Recognition System
In Tab. 6, the proposed FKP recognition based on feature selection is compared with other existing works to show the unimodal performance where some of the work concentrated on unimodal and here, the unimodal recognition values for EER and accuracy are considered [42–47]. The proposed unimodal FKP recognition achieves good results with optimized features.
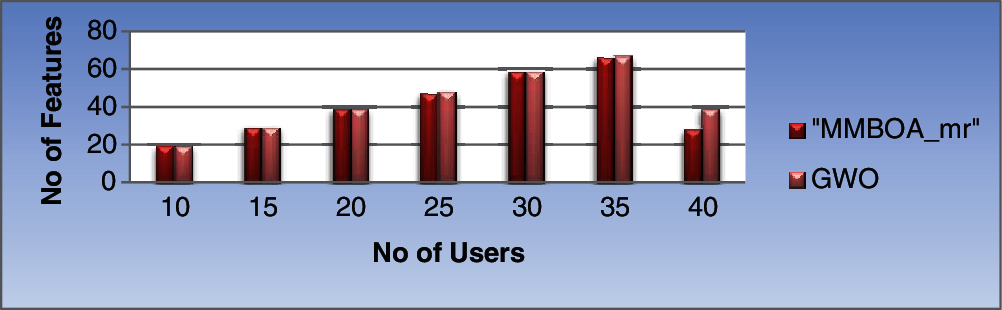
Figure 4: Performance comparison of selected features based on number of user
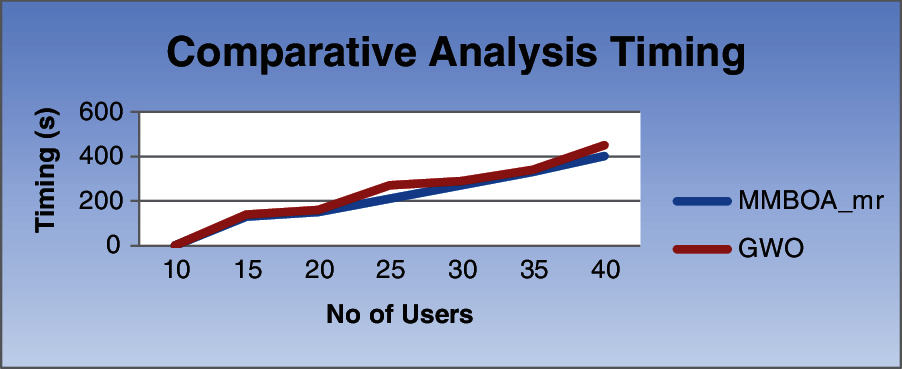
Figure 5: Comparison of execution time (s) for MMBOA_mr and GWO
3.1.5 Measure of Statistical Hypothesis Test
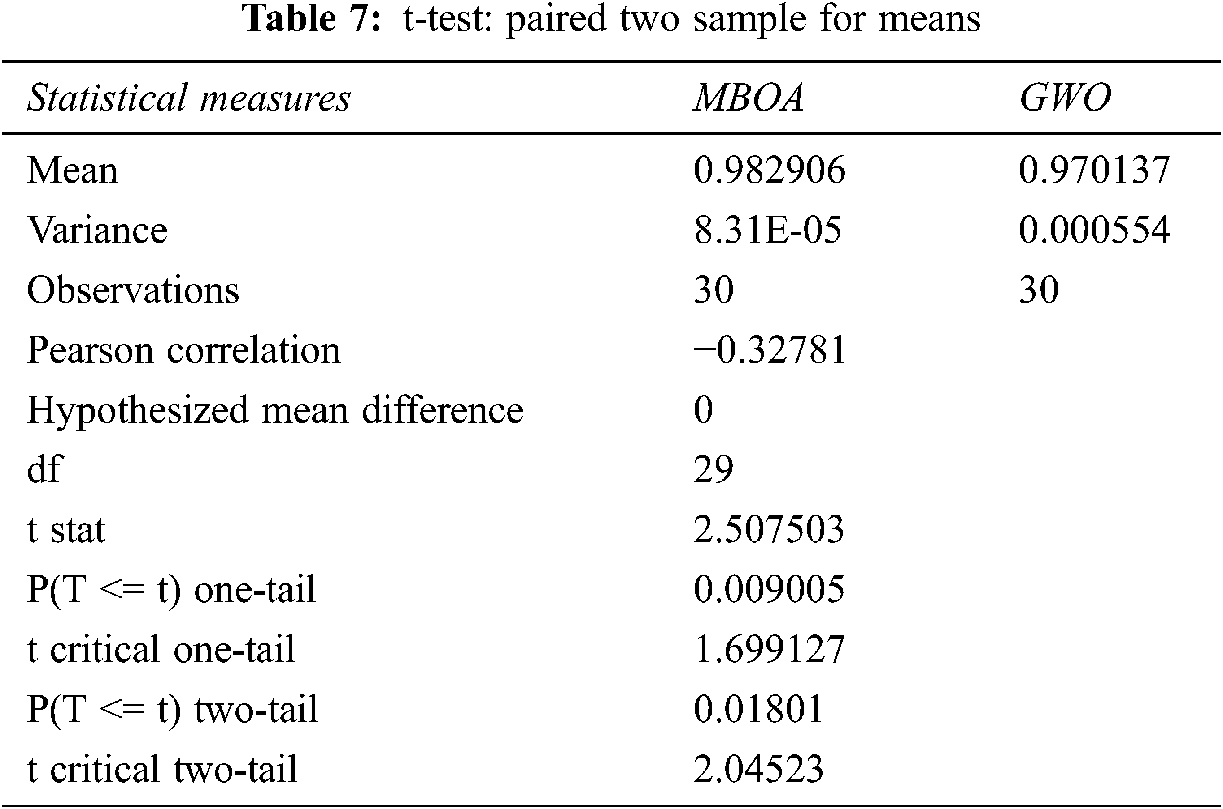
To evaluate the significant performance of the proposed algorithm, statistical test is done. Here, the MMBOA_mr and GWO algorithms are implemented with 30 runs. Here, the hypothesis test, t-test paired using two samples, is applied on the datasets that results 95% confidence level. The hypothesis test condition is depending on the p value. The hypothesis test is based on the conditional probability that is visualized for the given dataset. The assumption is that null hypothesis is true. It is defined as
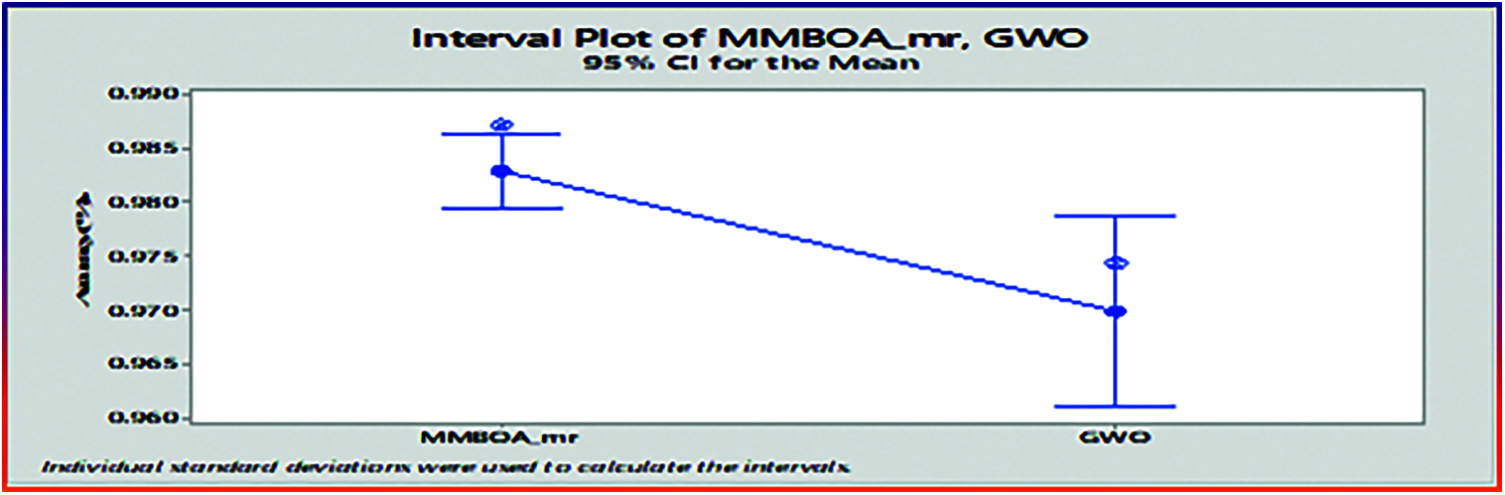
Figure 6: Comparison of average best accuracy for MMBOA_mr and GWO
For FKP recognition, this paper develops a novel feature-selection algorithm called Modified Magnetotatic Bacteria Optimization. The proposed FKP recognition extract features using hybrid EiFi feature extraction technique and Modified Magnetotatic Bacteria Optimization algorithm (MMBOA) for feature selection. MMBOA is able to provide the optimal subset of features for finger knuckle recognition that takes the least amount of time to compute and improves classification accuracy. MMBOA-KNN outperforms GWO-KNN in terms of accuracy and number of reduced features. Extensive experimental results and discussions indicate that our proposed methodology achieves significant enhancements than various existing finger Knuckle recognition algorithms. As demonstrated in the experiments, the proposed FKP recognition performs better and more efficiently than other state-of-the-art approaches, with higher accuracy of 99.7% and minimum EER of 0.3%.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. D. L. Woodard and P. J. Flynn, “Finger surface as a biometric identifier,” Computer Vision and Image Understanding, vol. 100, no. 3, pp. 357–384, 2005. [Google Scholar]
2. A. Kumar and Y. Zhou, “Personal identification using finger knuckle orientation features,” Electronics Letters, vol. 45, no. 20, pp. 1023–1025, 2009. [Google Scholar]
3. A. Kumar and C. Ravikanth, “Personal authentication using finger knuckle surface,” IEEE Transactions on Information Forensics and Security, vol. 4, no. 1, pp. 98–110, 2009. [Google Scholar]
4. L. Zhang, L. Zhang, D. Zhang and Z. Guo, “Phase congruency induced local features for finger-knuckle-print recognition,” Pattern Recognition, vol. 45, no. 7, pp. 2522–2531, 2012. [Google Scholar]
5. L. Zhang, L. Zhang, D. Zhang and H. Zhu, “Online finger-knuckle-print verification for personal authentication,” Pattern Recognition, vol. 43, no. 7, pp. 2560–2571, 2010. [Google Scholar]
6. L. Zhang, L. Zhang, D. Zhang and H. Zhu, “Ensemble of local and global information for finger-knuckle-print recognition,” Pattern Recognition, vol. 44, no. 9, pp. 1990–1998, 2011. [Google Scholar]
7. R. Sihwail, K. Omar, K. A. Z. Ariffin and M. Tubishat, “Improved harris hawks optimization using elite opposition-based learning and novel search mechanism for feature selection,” IEEE Access, vol. 8, pp. 121127–121145, 2020. [Google Scholar]
8. M. Ghaem and M. R. Feizi-Derakhshi, “Feature selection using forest optimization algorithm,” Pattern Recognition, vol. 60, pp. 121–129, 2016. [Google Scholar]
9. S. Huda, J. Abawajy, M. Alazab, M. Abdollalihian, R. Islam et al., “Hybrids of support vector machine wrapper and filter-based framework for malware detection,” Future Generation Computer Systems, vol. 55, pp. 376–390, 2016. [Google Scholar]
10. R. M. Ramadan and R. F. Abdel–Kader, “Face recognition using particle swarm optimization-based selected features,” International Journal of Signal Processing, Image Processing and Pattern Recognition, vol. 2, no. 2, pp. 51–65, 2009. [Google Scholar]
11. K. K. Patro, A. Jaya Prakash, M. Jayamanmadha Rao and P. RajeshKumar, “An efficient optimized feature selection with machine learning approach for ECG biometric recognition,” IETE Journal of Research, vol. 372, no. 1, pp. 1–12, 2020. [Google Scholar]
12. L. Ghoualmi, A. Draa and S. Chikhi, “An efficient feature selection scheme based on genetic algorithm for ear biometrics authentication,” in 12th Int. Sym. on Programming and Systems (ISPSAlgiers, Algeria, pp. 1–5, 2015. [Google Scholar]
13. F. G. Silva Teodoro, S. M. Peres and C. A. M. Lima, “Feature selection for biometric recognition based on electrocardiogram signals,” in Int. Joint Conf. on Neural Networks (IJCNNAnchorage, AK, USA, pp. 2911–2920, 2017. [Google Scholar]
14. H. R. Kanan and K. Faez, “An improved feature selection method based on ant colony optimization evaluated on face recognition system,” Applied Mathematics and Computation, vol. 205, no. 2, pp. 716–725, 2008. [Google Scholar]
15. A. Kumar, “Adaptive management of multimodal biometrics fusion using ant colony optimization,” Information Fusion, vol. 32, no. 1, pp. 49–63, 2016. [Google Scholar]
16. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]
17. D. Faivre and D. Schuler, “Magnetotactic bacteria and magnetosomes,” Chemical Reviews, vol. 108, no. 11, pp. 4875–4898, 2008. [Google Scholar]
18. H. W. Mo and L. F. Xu, “Magnetotactic bacteria algorithm for function optimization,” Journal of Software Engineering and Applications, vol. 5, no. 12, pp. 66–71, 2012. [Google Scholar]
19. H. W. Mo and L. F. Xu, “Magnetotactic bacteria optimization algorithm for multimodal optimization,” in IEEE Sym. on Swarm Intelligence (SISSingopore, pp. 240–247, 2013. [Google Scholar]
20. H. W. Mo and L. Liu, “Magnetotactic bacteria optimization algorithm based on best-target scheme,” in 2014 10th Int. Conf. on Natural Computation (ICNCXiamen, China, pp. 451–456, 2014. [Google Scholar]
21. H. Mo, L. Liu and J. Zhao, “A new magnetotactic bacteria optimization algorithm based on moment migration,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 14, no. 1, pp. 15–26, 2017. [Google Scholar]
22. A. M. Martnez and A. C. Kak, “PCA vs. LDA,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 23, no. 2, pp. 228–233, 2001. [Google Scholar]
23. A. Pentland, T. Starner, N. Etco, N. Masoiu, O. Oliyide et al., “Experiments with eigenfaces,” in Looking at People, Workshop of IJCAI, vol. 93, pp. 1–6, 1993. [Google Scholar]
24. H. Moon and P. J. Phillips, “Computational and performance aspects of PCA-based face-recognition algorithms,” Perception, vol. 30, no. 3, pp. 303–321, 2001. [Google Scholar]
25. K. Okada, J. Steffens, T. Maurer, H. Hong, E. Elagin et al., “The Bochum/USC face recognition system and how it fared in the FERET phase III test,” in Face Recognition. Berlin, Heidelberg: Springer, pp. 186–205, 1998. [Google Scholar]
26. P. Shunmugapriya and S. Kanmani, “A hybrid algorithm using ant and bee colony optimization for feature selection and classification,” Swarm and Evolutionary Computation, vol. 36, no. 1, pp. 27–36, 2017. [Google Scholar]
27. L. Brezočnik, I. Fister and V. Podgorelec, “Swarm intelligence algorithms for feature selection: A review,” Applied Sciences, vol. 8, no. 9, pp. 1521, 2018. [Google Scholar]
28. M. Naseriparsa, A. M. Bidgoli and T. Varaee, “A hybrid feature selection method to improve performance of a group of classification algorithms,” arXiv preprint arXiv: 1403. 2372, 2014. [Google Scholar]
29. M. Sebban and R. Nock, “A hybrid filter/wrapper approach of feature selection using information theory,” Pattern Recognition, vol. 35, no. 4, pp. 835–846, 2002. [Google Scholar]
30. C. Yang and Z. Chen, “Support vector machine optimization based on magnetic bacteria optimization algorithm,” International Journal of Hybrid Information Technology, vol. 8, no. 9, pp. 381–388, 2015. [Google Scholar]
31. S. T. E. F. A. N. Spring and D. A. Bazylinski, “Magnetotactic bacteria,” Prokaryotes, vol. 2, pp. 842–862, 2006. [Google Scholar]
32. E. Emary, H. M. Zawbaa and A. E. Hassanien, “Binary grey wolf optimization approaches for feature selection,” Neurocomputing, vol. 172, no. 1, pp. 371–381, 2016. [Google Scholar]
33. L. H. Chan, S. H. Salleh and C. Ting, “Face biometrics based on principal component analysis and linear discriminant analysis,” Journal of Computer Science, vol. 6, no. 7, pp. 693–699, 2010. [Google Scholar]
34. M. T. Sadeghi, M. Samiei and J. Kittler, “Fusion of PCA-based and LDA-based similarity measures for face verification,” EURASIP Journal on Advances in Signal Processing, vol. 2010, no. 1, pp. 1–2, 2010. [Google Scholar]
35. O. Nibouche, J. Jiang and P. Trundle, “Analysis of performance of palmprint matching with enforced sparsity,” Digital Signal Processing, vol. 22, no. 2, pp. 348–355, 2012. [Google Scholar]
36. C. Murukesh, A. Parivazhagan and K. Thanushkodi, “A novel ear recognition process using appearance shape model, fisher linear discriminant analysis and contourlet transform,” Procedia Engineering, vol. 38, pp. 771–778, 2012. [Google Scholar]
37. J. Yin, J. Zhou, Z. Jin and J. Yang, “Weighted linear embedding and its applications to finger-knuckle-print and palmprint recognition,” in 2010 Int. Workshop on Emerging Techniques and Challenges for Hand-Based Biometrics, Istanbul, Turkey, pp. 1–4, 2010. [Google Scholar]
38. J. D. Wu and C. T. Liu, “Finger-vein pattern identification using principal component analysis and the neural network technique,” Expert Systems with Applications, vol. 38, no. 5, pp. 5423–5427, 2011. [Google Scholar]
39. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
40. M. Hussain, A. Jibreen, H. Aboalsmah, H. Madkour, G. Bebis et al., “Feature selection for hand-shape based identification,” in Computational Intelligence in Security for Information Systems Conf., Basel, Switzerland, Springer Cham, pp. 237–246, 2015. [Google Scholar]
41. R. M. Luque, D. Elizondo, E. López-Rubio and E. J. Palom, “GA-based feature selection approach in biometric hand systems,” in Int. Joint Conf. on Neural Networks, San Jose, CA, USA, pp. 246–253, 2011. [Google Scholar]
42. A. Kumar and Y. Zhou, “Human identification using finger images,” IEEE Transactions Image Process, vol. 21, no. 4, pp. 2228–2244, 2012. [Google Scholar]
43. A. Kumar, “Can we use minor finger knuckle images to identify humans?,” in 2012 IEEE Fifth Int. Conf. on Biometrics: Theory, Applications and Systems (BTASArlington, VA, USA, pp. 55–60, 2012. [Google Scholar]
44. N. E. Chalabi, A. Attia and A. Bouziane, “Multimodal finger dorsal knuckle major and minor print recognition system based on pcanet deep learning,” ICTACT J. Image Video Process, vol. 10, no. 3, pp. 2153–2158, 2020. [Google Scholar]
45. J. C. Joshi, S. A. Nangia, K. Tiwari and K. K. Gupta, “Finger knuckle print based personal authentication using siamese network,” in 2019 6th Int. Conf. on Signal Processing and Integrated Networks (SPINNoida, India, pp. 282–286, 2019. [Google Scholar]
46. D. Thapar, G. Jaswal and A. Nigam, “Fkimnet: A finger dorsal image matching network comparing component (major, minor and nail) matching with holistic (finger dorsal) matching,” in 2019 Int. Joint Conf. on Neural Networks (IJCNNBudapest, Hungary, pp. 1–8, 2019. [Google Scholar]
47. A. Attia, Z. Akhtar and Y. Chahir, “Feature-level fusion of major and minor dorsal finger knuckle patterns for person authentication,” Signal Image and Video Processing, vol. 15, no. 4, pp. 851–859, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |