DOI:10.32604/iasc.2022.022335

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.022335 |  |
| Article |
Crow Search Algorithm with Improved Objective Function for Test Case Generation and Optimization
Institute of Engineering & Technology, Devi Ahilya Vishwavidyalaya, Indore, 452001, India
*Corresponding Author: Babita Pathik. Email: babitapathik@gmail.com
Received: 04 August 2021; Accepted: 07 September 2021
Abstract: Test case generation and optimization is the foremost requirement of software evolution and test automation. In this paper, a bio-inspired Crow Search Algorithm (CSA) is suggested with an improved objective function to fulfill this requirement. CSA is a nature-inspired optimization method. The improved objective function combines branch distance and predicate distance to cover the critical path on the control flow graph. CSA is a search-based technique that uses heuristic information for automation testing, and CSA optimizers minimize test cases generated by satisfying the objective function. This paper focuses on generating test cases for all paths, including critical paths. The control flow graph covers the information flow among all the classes, functions, and conditional statements and provides test paths. The number of test cases examined through graph path coverage analysis. The minimum number of test paths is counted through complexity metrics using the cyclomatic complexity of the constructed graph. The proposed method is evaluated as mathematical optimization functions to validate their effectiveness in locating optimal solutions. The python codes are considered for evaluation and revealed that our approach is time-efficient and outperforms various optimization algorithms. The proposed approach achieved 100% path coverage, and the algorithm executes and gives optimum results in approximately 0.2745 seconds.
Keywords: Test case generation; Crow Search Algorithm; improved objective function; control flow graph; branch distance; predicate distance
The generation or selection of test cases is critical for software testing to ensure its eminence as a product. Software testing is a process of ensuring that the actual result matches the desired result. It also ensures that the software is free from any kind of bugs or defects. There are various testing methods, such as manual testing or automation testing. Manual testing consumes 40%–70% of the time and expense associated with software development. The testing team performs software testing by examining the structure of the code deeply. It passes through each line of code to generate a test case suite and test data. Software testing determines the critical errors in the software products optimally so that error detection should be maximum. Simultaneously testing cost and time should be minimal [1,2]. Testing required some effort in terms of time and cost. Estimation is the process of approximating the needful value for business and industry purposes, even if there is any type of inconsistent data. Test estimation is a maintenance activity that predicts how long such a task would take to complete.
Numerous approaches for selecting test cases have been suggested to address the time constraint inherent in conventional testing. For developing test cases automatically, Search-Based Testing (SBT) is considered. There have been meta-heuristic techniques effectively utilized in the development of test data, including Genetic Algorithms (GA) [3,4], Ant Colony Optimization(ACO) [5,6], Particle Swarm Optimization (PSO) [7,8], Artificial Bee Colony (ABC) [9,10], hybrid Genetic Algorithm [11], Bat Algorithm [12,13]. Fitness functions (FF) drive a metaheuristic algorithm search process. The FF is measured through a mathematical equation that evaluates the feasibility of every solution in the search space by assigning a value. In SBT, FFs are primarily defined in terms of coverage criteria. A metric that determines how fine the generated test cases exercise the software under test is named as coverage criteria [14]. Path coverage, statement coverage, decision coverage, and branch coverage are all frequently used criteria [15]. For covering the target path, many researchers [10,16] employ a FF based on branch distance. Branch distance is estimated by examining the branching node's conditional statement and sometimes missed target [17]. The branch distance value alone is insufficient to produce the desired path. The branch distance is paired with heuristic information of approximation level to improve the searching. It indicates the distance between the target node and the node currently visited [16]. When there is a low probability of covering a path, this combined FF fails [18].
In this work, a CSA based approach is paired with an enhanced combination function to generate test cases for the critical path. The innovative aspect of this paper’s search strategy is introducing an improved objective function (IOF). IOF is a FF that combines branch distance with predicate distance. The objective behind considering CSA is the behavior of crow flock that resembles an optimization process [19]. Crows keep their extra food in explicit locations (hiding spots) in their environs and retrieve it once required. Crows are hungry birds as they flock together in search of better food supplies. From an optimization perspective, the crows represent searchers or agents. The environs represent searching space, and each location in the environs represents a feasible solution. The objective function is represented by food source quality, and the global solution to the problem is the finest food source in the environment.
We focus on finding the optimal test case suite of software. The selection of test cases is one of the significant parts of the test estimation. The aim is the critical path coverage so that test case selection will be effective, and any typical test case should not be skipped. The total test case selected is observed through Cyclomatic Complexity(CC) [20] by tracing paths on the CFG. In the proposed work, CSA is considered for generating test cases automatically and optimizing the test suite by applying FF. CSA with IOF is a novel approach that we considered in the paper. The main contributions of the paper are:
• Generate CFG for program code and trace the graph for complete path coverage without dropping any critical path.
• Compute the CC to approximate the number of test cases.
• Apply CSA search technique with path or branch based IOF.
Other content of the article organized as Section 2 summarizes the contributions done by researchers in this area. Section 3 elaborates on the background of the method opted in this paper. Section 4 comprises the proposed method, whereas Section 5 describes experimental setup and evaluation, Section 6 containing results and discussion. Section 7 concludes the work and mentions future works.
Generation of test data automatically using SBT is a motivating research area. The criteria for code-level testing is path coverage. This section focuses primarily on coverage of the branch or path code using AI-based heuristic search algorithms, using path/branch-based FFs. Some nature-inspired population based algorithms used by several researchers for test case generation are also mentioned here. The concepts and contributions are pithy here.
A hybrid and simple genetic algorithm are proposed by Garg D. and Garg P. [18] for path testing. An ExLB FF is suggested for path coverage. Although HGA provides better coverage through ExLB, it does not cover the target path. A genetic algorithm (GA) based algorithm is used for test data generation by Pachauri et al. [21]. The FF combines branch and path information for computation. The results of experiments reveal significantly better coverage percentages during the search, still difficult to get the targeted path. Babamir FS et al. [4] proposed a GA based testing technique to automate test data generation using different parameters for structural-oriented program structure. The FF proposed by the authors tries to cover program paths maximum possible way but does not achieve the targeted path. Jia YH et al. [7] developed a PSO based optimization algorithm for automatic test data generation. The criteria for software testing is condition-decision coverage that covers all conditional statements. This approach also does not cover the target path. PSO algorithm-based test case generation is suggested by Huang M et al. [8]. To improve the performance of PSO, they merged the group self-activity feedback (SAF) operator and Gauss mutation (G) changing inertia weight. That improved approach is efficient in test case generation for multi-path. Khan SA et al. [22] suggested Particle Swarm Optimization (PSO) technique for generating test case data for integration testing. Dahiya SS et al. [10] presented an automatic test generation for structural software using an artificial bee colony (ABC) based novel search technique. The FF generates test data with branch distance-based objective function. The technique is not suitable for large inputs and where constraints have many equality constraints. Sheoran S et al. [9] presented a novel approach using the ABC algorithm for data flow testing search. The approach prioritizes the definition-use paths that are not definition-clear paths. Aghdam ZK and Arasteh B. [23] presented an ABC algorithm for automatic test data generation. The experiment was evaluated with a FF that considers branch coverage criteria to optimize the solutions.
All the approaches discussed above cover a single path at a time that is a time-consuming process. Following are some approaches presented to address this gap by searching for multiple paths.
The Dynamic Multiple-Objective Sorting Algorithm is offered by Panichella A et al. [21] to handle many objectives. The FF combines approach level and branch distance in GA for branch coverage. Lv XW et al. [16] proposed the PSO approach with metamorphic relationships for generating test cases for multiple path coverage. The aim was to cover multiple paths efficiently with fewer iterations.
The attention of these mentioned works is on multiple path coverage, but they did not cover the critical path. In our proposed technique, we focus on covering many paths automatically along with the critical path in less time consumption.
A population based metaheuristic CSA is utilized for searching all crucial paths for test case generation. The common heuristics, e.g., branch distance, approximation level, have been considered. A graphical representation of source code called Control Flow Graph [24] is generated for path coverage. CFG is giving a moderate and sometimes exact prediction of test cases. The two important heuristic parameters are considered here: Branch distance and Predicate distance.
Testing with path coverage generates test cases by executing each path at least once in order to identify defects included within the path. First, we determine the total linear independent branches/paths by measuring the CC [15,18]. CC is a software metric measured to analyze the code's probable error. The complexity metric was first introduced by Thomas J. McCabe [20]. CFG, an intermediate graph of lines of code, is constructed for the calculation of CC. Then, using the McCabe formula, CC is determined from the source code’s CFG. CFG is the combination of nodes and edges that denote instructions and flow of control or data, respectively.
The mathematical equation to calculate the CC of a syntax drawn from the graph V(G) is:
Here M = CC of graph G
E = # edges in the graph
N = # nodes in the graph
The calculation of complexity is as follows:
Here P = no. of predicate node, the node with the conditional statement
CC is a metric of statistics about independent paths equivalent to the number of test case suites. Using Eqs. (1) or (2), we can find the CC, and both equations give the same amount of test case suite.
In this work, we consider two case studies for test cases by covering the multiple paths. The first one is a python program for Triangle Identification Problem [16,18] and generates test cases with 100% path coverage. The second example is a small python program to Identify Armstrong Numbers.
3.1.1 Triangle Identification Problem TIP)
This python program, given in Fig. 1a, identifies the type of triangle and classifies the angle. Triangle classification is done based on three sides of the triangle. This code segment has a conditional statement to decide whether a triangle is equilateral, isosceles, scalene, or it is not a triangle according to sides given to the program as input. It also classifies the angle of a triangle as acute or not given input. For the given program, a CFG is generated, as depicted in Fig. 1b.

Figure 1: TIP (a) Source code in python (b) CFG
Each node of the graph presents a complete statement, and each edge of the graph carries the data and control flow between two statements.
The linearly independent paths for the TIP program is obtained from its CFG as:
Path_1: 1 – 2 – 3 – 7 – 8 – S
Path_2: 1 – 2 – 4 – 5 – 7 – S
Path_3: 1 – 2 – 4 – 5 – 7 – 8 – S
Path_4: 1 – 2 – 4 – 6 – 7 – S
Path_5: 1 – 2 – 4 – 6 – 7 – 8 – S
Path_6: 1 – 9 – S
The outcomes of all these paths are given below:
Path_1: Equilateral and acute
Path_2: Isosceles
Path_3: Isosceles and acute
Path_4: Scalene
Path_5: Scalene and acute
Path_6: Can't form a triangle
The total number of the independent path can be confirmed with CC calculated by using Eq. (1).
where
The input to the program is given as three sides of triangles a, b, c as test data. If the value of a, b, c is less than or equal to zero, then a triangle cannot be formed. The probability is very low or zero for that test data generation. The probability of generating test data for these values is zero. Although the probability of the aimed crucial path is always less than that of other alternatives, but it must be higher than 0. The path with 0 probability is an infeasible solution. The probability of forming an equilateral triangle is on all equal test data. All the paths have higher probability except Path_1, which has the lowest probability than others according to probability measures. In the example given in Fig. 1, the Path_1 that results in “Equilateral and acute” is reflected as a critical path.
3.1.2 Identify Armstrong Number (IAN)
The part of the source code for Identification of an Armstrong number is shown in Fig. 2a. Input to this algorithm is a number to check whether it is an Armstrong number or not. In this program, a modulus, power, and division calculation are implemented within the for a loop. Whereas in TIP, only decision and selection statements are included.

Figure 2: IAN (a) Source code in python (b) CFG
The CFG for IAN is shown in Fig. 2b. The total number of the linearly independent path traced through path coverage is three for testing the IAN program. CC of the code can be calculated by equation no (1). According to the graph shown in Fig. 2b, Path 2 (dashed line) has a lower probability of covering. The other paths, i.e., Path 1 and Path 3, respond earlier than Path 2 because they have a higher probability of traversing if the input range is taken between [0,152]. Path 2 is considered a critical path.
Crows are a widespread genus of birds that are the most intelligent fowls among the creatures on the planet. They are capable of memorizing faces, using tools, communicating in complicated ways, and concealing and retrieving food. There are numerous examples of crow’s intelligence. These creatures have shown self-alertness and possess the ability to create tools. Additionally, they are capable of recalling the location of their meal up to several months later.
CSA is a unique population-based metaheuristic introduced by Askarzadeh A, 2016 [19], for solving engineering optimization issues. The primary source of inspiration of CSA is the behavior of crows, the memorization of hiding places used to store excess food, the following of one another during thefts, and the protection of their caches being stolen.
The fundamental principles of the algorithm include the organization of crows into flocks. These ideas resulted in the construction of a novel algorithm that is significantly different from existing algorithms that take their primary inspiration from the natural behavior of birds, such as Bird Swarm Algorithm (BSA), Bird Mating Optimizer (BMO), Chicken Swarm Optimization (CSO), Cuckoo Search (CS), and Peacock Algorithm (PA). The following are the CSA principles:
1. Crows live in large families (flocks).
2. Crows can remember and recognize the hiding place of food.
3. They follow each other to thieve their food.
4. Crows guard their stocks against theft by some probability.
The parameters for the algorithm are mentioned here:
The position of the hiding place of crow
Following is the matrix that describes the
The value of memory
The objective function OF(x) evaluates by using the fitness of ci. The input parameter x is the vector of decision variables. CSA technique researchers use the number of dimensions d in search space to evaluate fitness. Branch distance is determined for conditional nodes using test data. The value decides how close or distant the test data must be in order to satisfy the condition (true/false) [25]. In this research paper, we suggest an improved objective function with two heuristic values.
In this paper, we proposed a CSA based objective function that is modified for the fitness of the flocks. We analyze path coverage to check the criticality of a branch that should not be skipped. We apply CSA with the suggested FF to generate test cases. Fig. 3 showing the overall flow of the proposed method.
4.1 Test Case Selection with CSA
Each crow denotes one test path in the CSA stated in ALGORITHM 1 as given in Fig. 4. The next path is selected by updating the value by the statement with the equation below:
where
The memory for crow j indicate by
All of the values of the d-dimensional vector fall within the interval [cmin, cmax], then
In this work we initialize interval [cmin , cmax] = [1,8] means cmin = 1 and cmax = 8.

Figure 3: Flow diagram of the proposed approach
4.2 Branch Distance Calculation
The main purpose is to develop test cases for paths that have a very low probability of being covered during automated testing. Automatic test case generation becomes extremely challenging in this situation, as the test data is sparse and covers a wide range.
It is critical to direct the search process in order to obtain that kind of test data. In our proposed searching technique, we consider Branch Distance (BD) and Predicate Distance(PrD) for improved objective function (IOF). Fig. 5 showing all predicate nodes and brach distance.
The BD determines the degree to which the input deviates from the predicate [16]. It specifies whether the test data is close or far to satisfy the conditional statement of the code [25].
Here we consider TIP code for the explanation of the proposed technique. The conditional nodes in this example are node1, node2, node4, and node6. Suppose predicate node for a path is node1 and denoted as Pr1, then Branch Distance is shown as:

Figure 4: Algorithm for test case generation

Figure 5: Branch distance for the target of four conditional statements in TIP
Tab. 1 has the description of all predicates and their BD values. This BD is normalized [26] to map the value of function within the interval [0,1] through the following formula for input x:
where NBD is Normalized Branch Distance. This is the formula for Branch Distance Fitness (BDF).
In our objective function, the second fitness parameter we consider is predicate distance (PrD). PrD is the difference of nodes from the predicate node between the target(critical) path and other traversed path and denoted as:
where

4.4 Improved Objective Function
The path (
The value of IOF(
5 Experimental Setup and Evaluation
5.1 Predicate Distance Calculation
A matrix is generated from the CFG depicted in Fig. 1b, and it contains all of the test paths. This matrix is supposed to initialize the crow positions. The row denotes the paths for the crow, whereas the column denotes the nodes as crow position.
Paths =
All these paths are equalized in length by appending zero at the trailing position. We replace the letter ‘S’ with zero (0) to simplify the calculation of path distances. The final node ‘stop’ is the same in all the paths, which does not affect any computation. The nodes that exist on a path of the graph (CFG) are matched against the target path (critical). Predicate Distance is the number of unmatched nodes on these two paths. The critical path is Path_4, as discussed in section 3.1.1.
Now we calculate PrD of target path with every traverse path as:
Target path: Pt = [1 2 3 7 8 0 0] = P4
Pt: 1 2 3 7 8
PrD(P1 , Pt) = 0
PrD(P2 , Pt) = 2
PrD(P3, Pt) = 1
PrD(P4 , Pt) = 2
PrD(P5 , Pt) = 1
PrD(P6 , Pt) = 4
These values are going to be used to calculate fitness values through the CSA objective function.
5.2 CSA implementation for Generating Test Cases
The CSA is implemented on TIP with IOF function is described here:
Step 1: Initialize the crow population (number of test data)
N = 5
Dimension of search space is initialized with d = 3
Maximum Number of iterations Itr = 20
We initialize matrix of test data as the initial crow position as:
Crow =
Initially, the position of each crow is equivalent to the value of the memory.
So c1 = m1 = [2 2 5], c2 = m2 = [4 9 3], c3 = m3 = [3 7 5], c4 = m4 = [2 4 7], c5 = m5 = [1 3 3].
Fitness value evaluation:
Next, each crow’s position is evaluated through the improved objective function IOF(ci). The fitness value is initialized by using Eq. (9). Test case c1 [2 2 5] moves to the Path_2 and changes its position towards ‘Isosceles.’ BD is evaluated by using rule suggested by Tracey N et al.
BD(c1) = BD1 + BD2 + BD3 + BD4
BD1: (0-2)+(0-2)+(0-5) = -9<0 = 0
BD2: |(2-2)|+ |(2-5)| = 0+3 = 3+0.1 = 3.1
BD3: min(|(2-2)|, |(2-5)|, |(5-2)|) = min(0, 3.1, 3.1) = 0
BD4: (c-(a+b)) = (5-(2+2)) = 1+0.1 = 1.1
BD(c1) = 0+3.1+0+1.1 = 4.2
NBD(c1) = 1 – (1.001)-BD = 1 – (1.001)-4.2 = 0.0041
Fitness evaluation IOF(c1) = BD + PrD = 0.0041+2 = 2.0041 by Eq. (10)
Test case(c2) = [4 9 3] and Test case(c3) = [3 7 5] move to Path_5 and leads to same position ‘Scalene and acute’
BD(c2) = BD1 + BD2 + BD3 + BD4 = 0+11.2+1+0 = 12.2
NBD(c2) = 1- (1.001)-12.2 = 0.0121
Fitness evaluation IOF(c2) = BD + PrD = 0.0101 + 1 = 1.0121
BD(c3) = BD1 + BD2 + BD3 + BD4 = 0+9.2+2+0 = 11.2
NBD(c3) = 1- (1.001)-11.2 = 0.0111
Fitness evaluation IOF(c3) = BD + PrD = 0.0101 + 1 = 1. 0111
Test case(c4) = [2 4 7] is covering the Path_4 for ‘Scalene’
BD(c4) = BD1 + BD2 + BD3 + BD4 = 0+2.1+0+1.1 = 3.2
NBD(c4) = 1- (1.001)-3.2 = 0.0031
Fitness evaluation IOF(c4) = BD + PrD = 0.0031+2 = 2.0031
Likewise, for Test case(c5) = [1 3 3] to ‘Isosceles and acute’ by moving on Path_3
BD(c5) = BD1 + BD2 + BD3 + BD4 = 0+2.1+0+0 = 2.1
NBD(c5) = BDF = 1- (1.001)-2.1 = 0.0020
IOF = 0.0020+1 = 1.0020
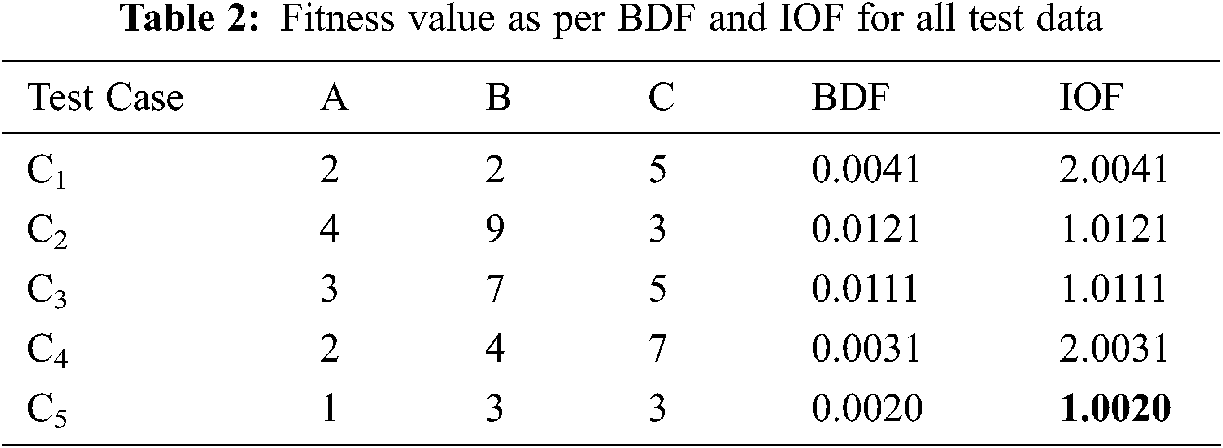
Tab. 2 consists of fitness values calculated above using BDF and IOF for all the randomly selected test cases and shown in the matrix as crow's initial positions.
The minimum fitness value observed is IOF(c5) = 2.0020
Step 2: We initialised AP = 0.5, fl = 0.7 r = random number ranges [0,1]
Next, the new position of crows to follow the path is computed by using Eqs. (5) and (6), given below:
Crow =
Now, again we evaluate fitness value for the first iteration. The value for the IOF for all new test cases given above is shown in Tab. 3. The fitness value is be replaced by step mentioned in the algorithm as: ‘if IOF (ci ) < IOF(mi )’ and test cases also updated accordingly.
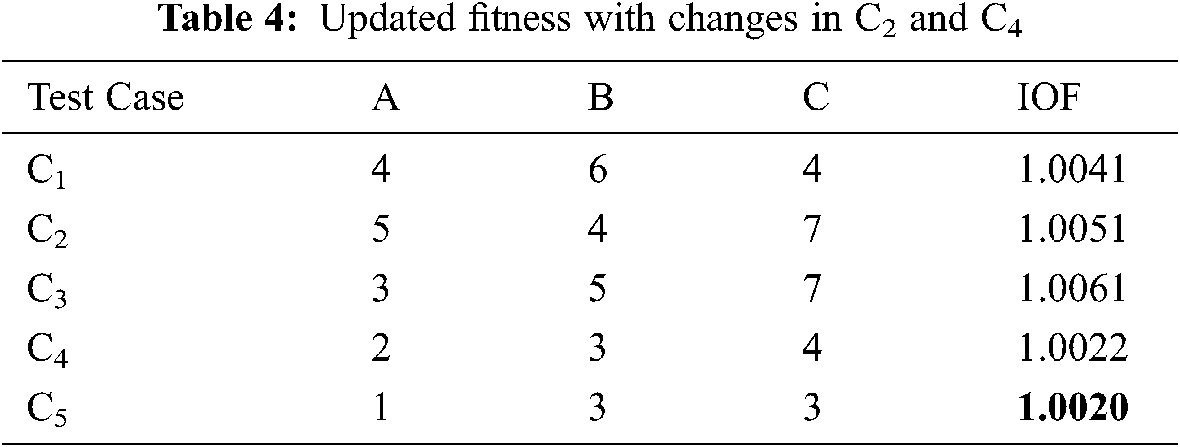
In Tab. 3, the fitness value of C1, C3, and C4 are lower than previous memory and only replaced in a new position. Repeat the same step for the second iteration, find a new crow position, and evaluate fitness value. The comparison is made with IOF(ci) and IOF(mi). The position of the crow is updated according to CSA.

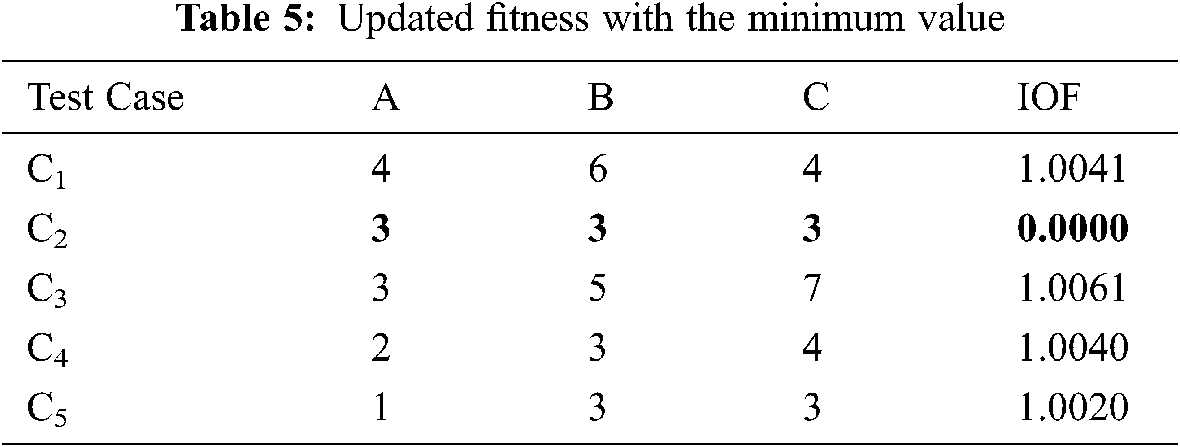
As shown in Tab. 4, the fitness value for test cases C2 and C4 have been updated. Again the process is repeated for the third iteration to find the new position of crow and their fitness value. The position as test cases and respective fitness values are updated and mentioned in Tab. 5. The CSA with IOF can achieve the target in few iterations. Although test on large numbers requires more iterations. From Tab. 5, we found a test case (C2) with [3 3 3] that leads to the critical path ‘Equilateral and acute’ triangle with minimum fitness value.
The proposed CSA based approach with improved objective function has its advantage over other metaheuristic algorithms in that the IOF covers almost every path by generating various test cases, including the critical path. The test case for the crucial path needs only a minimum number of iterations and reduced runtime.
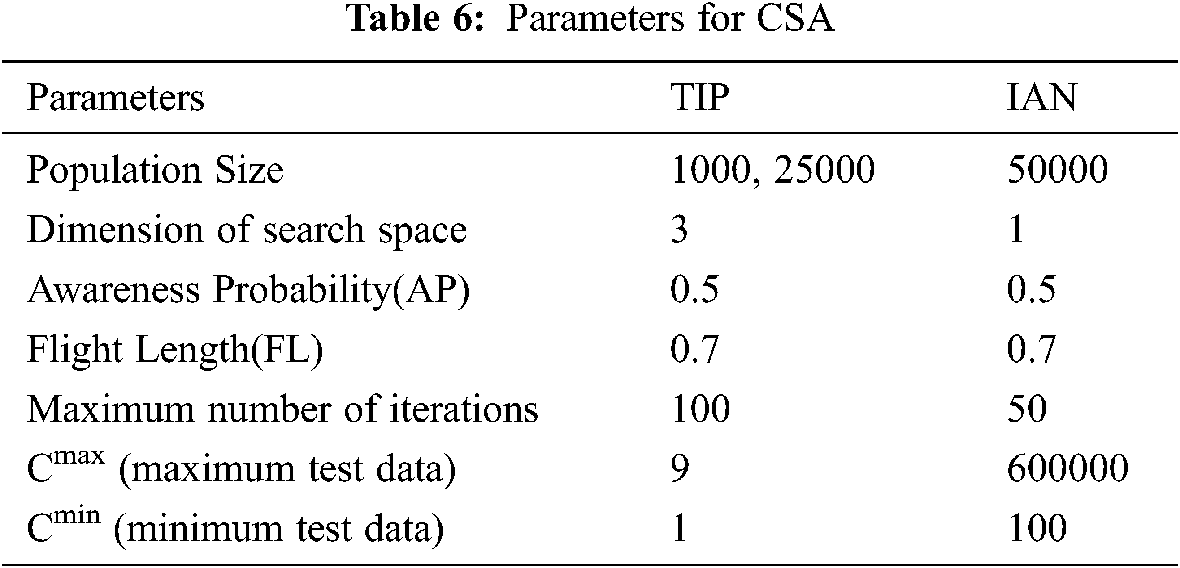
The parameter setting plays a key role in improving the performance of any optimization algorithm. Tab. 6 depicts the parameter setting of CSA for TIP and IAN. The values are based on some research work [3,16,18], general sources, and the nature of the programs. The system configuration is Windows 10, 8GB RAM, Intel Core i7,4690T central processing unit, 2.50 GHz, 64-bit OS, x64 based processor. CSA is implemented in an Anaconda environment.
A comparative analysis is done with the other metaheuristic algorithm such as PSO and APSO. These optimization algorithms are applied with BDF and Combined Fitness Function (CFF). The authors have considered the triangle classification problem and area calculation for empirical evaluation.
We also have considered the same problem for comparison purposes. To the best of our knowledge CSA algorithm with IOF is yet not applied for test case generation and optimization.
So here, we compared our results with the algorithm that considered the TIP problem with the population N =1000 and iterations Iter = 100 as parameter setting.
According to results shown in Tab. 7, the CSA with IOF giving test data for the target path in the 3rd iteration but within an average execution time of 0.2745 sec.

The results produced through the existing FFs and the suggested FF differ significantly in terms of how many iterations and the average time spent on implementation. CSA with ICF produces better results for considered TIP case study including IAN since this algorithm implements an efficient search strategy.
Fig. 6. has the details about the number of test cases generated for each test path for TIP in 100 iterations on 1000 population (test data) as given in Tab. 8.
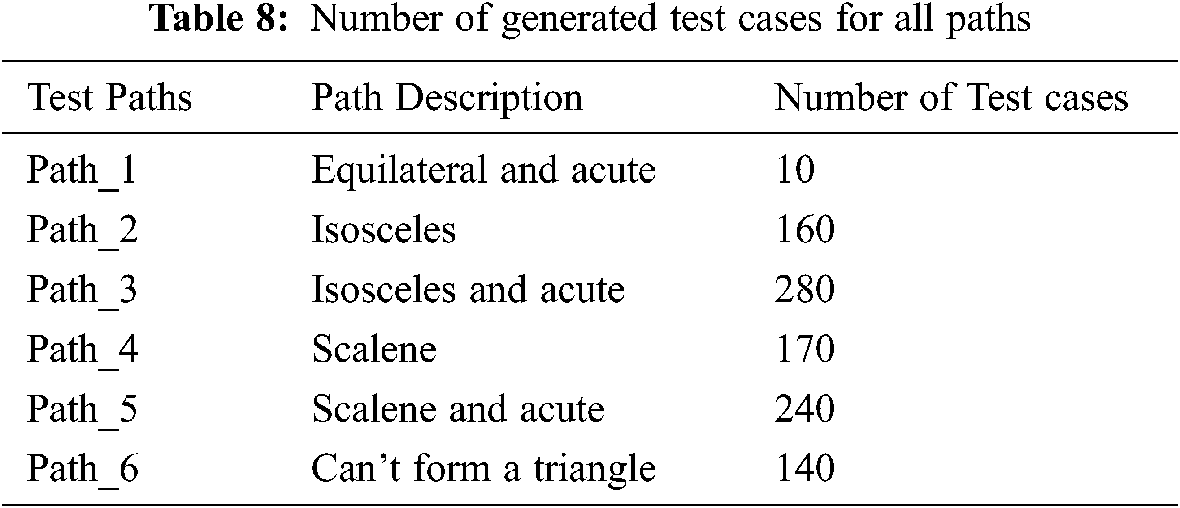

Figure 6: Test case generated with CSA
In this paper, the main objective was to cover the target path with a minimum time span. We adopt CSA based optimization technique by improvising its objective function. The fitness value is evaluated by using branch distance and predicate distance in IOF that guide the search algorithms to develop various test cases to cover a maximum number of paths automatically. The key idea was finding a test case for critical path minimum time and fewer iterations. A population-based metaheuristic algorithm is used. A heuristic path distance function IOF searched the target path efficiently. To carry out the experiments, we considered two case studies, TIP and IAN. We have achieved almost 100% complete path coverage for the case studies we considered using the suggested FF of CSA. The importance of the FF is that we reach our aimed path in fewer iterations and very little time span compared to the other existing heuristic algorithm with their branch distances FFs. We combine the predicate distance with branch distance as its heuristic distance to give the search technique a suitable direction.
Our future work is to cover additional test paths concurrently in evolutionary software systems. We will target to cover critical paths for regression testing and automate test case generation.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Z. Karimi and B. Arasteh, “An efficient method to generate test data for software structural testing using artificial bee colony optimization algorithm,” Int. Journal of Software Engineering and Knowledge Engineering, vol. 27, no. 06, pp. 951–966, 2017. [Google Scholar]
2. P. R. Srivastava, “Optimization of software testing using genetic algorithm,” in Proc. Information Systems, Technology and Management, Berlin, Heidelberg, Springer, pp. 350–351, 2009. [Google Scholar]
3. A. Pachauri and G. Mishra, “A path and branch based approach to fitness computation for program test data generation using genetic algorithm,” in Proc. IEEE Int. Conf. on Futuristic Trends on Computational Analysis and Knowledge Management (ABLAZEGreater Noida, India, pp. 49–55, 2015. [Google Scholar]
4. F. S. Babamir, A. Hatamizadeh, S. M. Babamir, M. Dabbaghian and A. Norouzi, “Application of genetic algorithm in automatic software testing,” in Proc. Int. Conf. on Networked Digital Technologies, Berlin, Heidelberg, Springer, pp. 545–552, 2010. [Google Scholar]
5. S. Sankar and V. Chandra, “An ant colony optimization algorithm based automated generation of software test cases,” in Proc. Int. Conf. on Swarm Intelligence, Cham, Springer, pp. 231–239, 2020. [Google Scholar]
6. S. Biswas, M. S. Kaiser and S. A. Mamun, “Applying ant colony optimization in software testing to generate prioritized optimal path and test data,” in Proc. ICEEICT, IEEE, pp. 1–6, 2015. [Google Scholar]
7. Y. H. Jia, W. N. Chen, J. Zhang and J. J. Li, “Generating software test data by particle swarm optimization,” in Proc Asia-Pacific Conf. on Simulated Evolution and Learning, Springer, pp. 37–47, 2014. [Google Scholar]
8. M. Huang, C. Zhang and X. Liang, “Software test cases generation based on improved particle swarm optimization,” in Proc Int. Conf. on Information Technology and Electronic Commerce, IEEE, pp. 52–55, 2014. [Google Scholar]
9. S. Sheoran, N. Mittal and A. Gelbukh, “Artificial bee colony algorithm in data flow testing for optimal test suite generation,” Int. Journal of System Assurance Engineering and Management, vol. 11, no. 2, pp. 340–349, 2020. [Google Scholar]
10. S. S. Dahiya, J. K. Chhabra and S. Kumar, “Application of artificial bee colony algorithm to software testing,” in Proc. Australian Software Engineering Conf., IEEE, pp. 149–154, 2010. [Google Scholar]
11. A. Alhroob, W. Alzyadat, A. T. Imam and G. M. Jaradat, “The genetic algorithm and binary search technique in the program path coverage for improving software testing using big data,” Intelligent Automation & Soft Computing, vol. 26, no. 4, pp. 725–733, 2020. [Google Scholar]
12. P. R. Srivastava, A. Bidwai, A. Khan, K. Rathore, R. Sharma et al., “An empirical study of test effort estimation based on bat algorithm,” Int. Journal of Bio-Inspired Computation, vol. 6, no. 1, pp. 57–70, 2014. [Google Scholar]
13. M. M. Öztürk, “A bat-inspired algorithm for prioritizing test cases,” Vietnam Journal of Computer Science, vol. 5, no. 1, pp. 45–57, 2018. [Google Scholar]
14. M. Shahid, S. Ibrahim and M. N. Mahrin, “A study on test coverage in software testing,” Advanced Informatics School (AISUniversiti Teknologi Malaysia, International Campus, Jalan Semarak. Kuala Lumpur, Malaysia, 2011. [Google Scholar]
15. R. Mall, “Fundamentals of software engineering,” in PHI Learning Pvt. Ltd., Delhi, India, 2018. [Google Scholar]
16. X. W. Lv, S. Huang, Z. W. Hui and H. J. Ji, “Test cases generation for multiple paths based on PSO algorithm with metamorphic relations,” IET Software, vol. 12, no. 4, pp. 306–317, 2018. [Google Scholar]
17. A. P. Gursaran, “Program test data generation branch coverage with genetic algorithm: Comparative evaluation of a maximization and minimization approach,” Int. Journal of Software Engineering & Applications, vol. 3, no. 1, pp. 207–218, 2012. [Google Scholar]
18. D. Garg and P. Garg, “Basis path testing using SGA & HGA with ExLB fitness function,” Procedia Computer Science, vol. 70, pp. 593–602, 2015. [Google Scholar]
19. A. Askarzadeh, “A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm,” Computers & Structures, vol. 169, no. 2, pp. 1–12, 2016. [Google Scholar]
20. T. J. McCabe, “A complexity measure,” IEEE Transactions on Software Engineering, vol. SE-2, no. 4, pp. 308–320, 1976. [Google Scholar]
21. A. Panichella, F. M. Kifetew and P. Tonella, “Automated test case generation as a many-objective optimisation problem with dynamic selection of the targets,” IEEE Transactions on Software Engineering, vol. 44, no. 2, pp. 122–158, 2018. [Google Scholar]
22. S. A. Khan and A. Nadeem, “Automated test data generation for coupling based integration testing of object oriented programs using particle swarm optimization (PSO),” in Genetic and Evolutionary Computing. Cham: Springer, pp. 115–124, 2014. [Google Scholar]
23. Z. K. Aghdam and B. Arasteh, “An efficient method to generate test data for software structural testing using artificial bee colony optimization algorithm,” Int. Journal of Software Engineering and Knowledge Engineering, vol. 27, no. 06, pp. 951–966, 2017. [Google Scholar]
24. S. Laokok and T. Suwannasart, “An approach for test case generation from a static call graph for object-oriented programming,” in Proc. Int. Multi Conf. of Engineers and Computer Scientists, Hong Kong, vol. 1, 2017. [Google Scholar]
25. Y. Chen, Y. Zhong, T. Shi and J. Liu, “Comparison of two fitness functions for GA-based path-oriented test data generation,” Proc. IEEE Int. Conf. on Natural Computation, vol. 4, pp. 177–181, 2009. [Google Scholar]
26. J. Wegener, A. Baresel and H. Sthamer, “Evolutionary test environment for automatic structural testing,” Information and Software Technology, vol. 43, no. 14, pp. 841–854, 2001. [Google Scholar]
27. N. Tracey, J. Clark, K. Mander and J. McDermid, “An automated framework for structural test-data generation,” in Proc. IEEE Int. Conf. on Automated Software Engineering (Cat. No. 98EX239Honolulu, HI, USA, pp. 285–288, 1998. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |