DOI:10.32604/iasc.2022.021954

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.021954 |  |
| Article |
Mathematical Design Enhancing Medical Images Formulated by a Fractal Flame Operator
1Institute of Electrical and Electronics Engineers (IEEE): 94086547, Kuala Lumpur, 59200, Malaysia
2Imam Ja'far Al-Sadiq University, Baghdad, 10064, Iraq
3Department of Mathematics, College of Science, Mustansiriyah University, Baghdad, 10052, Iraq
4Department of Applied Sciences, University of Technology, Baghdad, 10066, Iraq
5Department of Mathematics, Cankaya University, Ankara, 06530, Turkey
6Institute of Space Sciences, Magurele-Bucharest, R76900, Romania
7Department of Medical Research, China Medical University, Taichung, 40402, Taiwan
*Corresponding Author: Rabha W. Ibrahim. Email: rabhaibrahim@yahoo.com
Received: 21 July 2021; Accepted: 25 August 2021
Abstract: The interest in using fractal theory and its applications has grown in the field of image processing. Image enhancement is one of the feature processing tools, which aims to improve the details of an image. The enhancement of digital pictures is a challenging task due to the unforeseeable variation in the quality of the captured images. In this study, we present a mathematical model using a local conformable differential operator (LCDO). The proposed model is formulated by the theory of cantor fractal to generalize the definition of LCDO. The main advantage of utilizing LCDO for image enhancement is its capability to enhance the low contrast intensities using the coefficient estimate of LCDO. The proposed image enhancement algorithm is tested against different images with different qualities to show that it is robust and can withstand dramatic variations in quality. The quantitative results of Brisque, and Piqe were 30.38 and 35.53 respectively. The comparative consequences indicate that the proposed image enhancement model realizes the best image quality assessments. Overall, this model significantly improves the details of the given datasets, and can potentially help the medical staff during the diagnosis process. A MATLAB programming instrument utilized for application and valuation of the image quality measures. A comparison with other image techniques is illustrated regarding the visual review.
Keywords: Fractal theory; local fractional calculus; conformable differential operator; image processing; image enhancement; MRI
Kolwankar et al. [1–5] formulated the fractal operators for the usual fractional calculus of Riemann-Liouville operators. It was utilized to deal with non-differentiable structures appearing in both science and engineering [6]. Numerous other opinions and facts of the local fractional calculus were offered, such as the geometric fractal. Yang et al. formulated what is called “the cantor fractal” in the logical modifications of the definitions to the subject of local derivatives on fractals. Different studies and applications are indicated in the literature [7–12].
Anderson et al. [13] presented a unique conformable fractional calculus (CFC) that is connected with a control term called “the proportional-integral-derivative controller”. This controller is a loop device that is used in industrial, thermal study and economy to control the suggested systems. Furthermore, Ibrahim et al. [14] extended CFC to the complex plane to investigate the systematic solution of a class of complex differential equations. More extensions have been reported in the literature [15–17].
The image acquisition process sometimes generates poorly-illuminated images. To mitigate this issue, we suggest a new mathematical model that is based on combining the idea of fractal derivative and the conformable derivative to formulate the proposed LCDO for image enhancement. Applying the LCDO to enhance images based on estimating of the conformable differential operator. The coefficients are suggested by using the fractal sine function, which is a generalization of a fractal flame. We aim to provide an enhancement method to recover the interpretability or perception of data in pictures for human viewers, or to provide better input for other automated feature processing performances. The performance of the proposed image enhancement model was assessed using relevant image quality metrics, and compared with state-of-the art image enhancement techniques.
Medical imaging performances from time to time make pictures that: have objects, are low in difference, and/or do not obviously display the boundaries of the intuitive structures. To get these matters, we offer a novel mathematical modeling system, which is depended on the class of LCDO to improve the low contrast intensities of medical images. We aim to provide an enhancement technique for medical pictures so that physicians can offer scientific diagnoses earlier and additional positively.
The main contributions of this study are, as follows:
1-We present a unique low-light image enhancement method which can achieve better contrast enhancement on real low-light images.
2-We suggest a LCDO model using the coefficient estimation of a conformable differential operator for real low-light medical images enhancement.
3-The proposed LCDO can be applied as an efficient pre-processing step for any image processing approach.
Image enhancement methods are designed to enhance the visual appearance of an image such that the details of the image are significantly improved without altering the information of the image. In the literature, image enhancement can be categorized into spatial and frequency (regular) domain. Spatial domain image enhancement works on pixel values, while the image enhancement in frequency domain uses a transform approach of the images.
Recently, few image enhancement algorithms based on the concept of fractional calculus have been proposed. The fractional operators have the ability to keep the high frequency contour features, and to enhance the texture details. Roy et al. [18] proposed a new fractional calculus enhancement algorithm based on Laplacian operations. The method was proposed to remove the generated Laplacian noise from text inside video frames. Similarly, a fractional-based image enhancement design was proposed by Al-Shamasneh et al. [19]. The proposed model relies on pixel probability of the neighboring pixels to enhance kidney images obtained from self-collected MRI dataset. Moreover, Raghunandan et al. [20] proposed a low contrast license plate image enhancement model based on the Riesz fractional operator. The model achieved good results for the text images only. Alternatively, Al-Ameen et al. [21] proposed a tuned single-scale Retinex algorithm for improving the dynamic range of MRI scans. The proposed enhancement model is able to improve the brightness and contrast of the input MRI scans, but the preservation of fine details was not achieved. For poorly illuminated images, Fu et al. [22] proposed the fusion-based image enhancement method by applying different techniques to adjust the image illumination. This approach effectively improved the images illumination. However, the aim of the method is restricted to weakly illuminated images but not for images that suffer from degradations, and poor quality.
Despite the good results of this method, it was not shown to be able to preserve the fine details of medical images, which is required for the diagnosis process. Likewise, more image enhancement methods have been proposed deep learning approaches. Li et al. [23] proposed a deep learning approach to enhance dark images. This approach operated well without any paired training data for low-light enhancement jobs. The experimental results on various low light datasets show the effectiveness of this method. Using the same approach, Zhang et al. [24] have developed an adaptive fractional order image enhancement method based on the information of fractional order differential and the image segmentation. The image enhancement depends on the result of the image segmentation algorithm which is used to segment the image into the objects and the background. This technique makes the algorithm unable to preserve the contrast information of the image efficiently. Recently, [25] presented a mathematical model for medical image enhancement based on the class of fractional partial differential equations (FPDEs). The main advantage of FPDE is its ability to enhance the low contrast images. Similarly, [26] proposed a new medical image enhancement approach based on fractional calculus. This approach successfully improved the quality of the image while preserving the details, but it is not suitable for enhancing non-uniform illumination area inside the input images.
To overcome this problem, this investigation presents a new mathematical design based on LCDO for image enhancement, which is the main contribution of the study. The main advantage of LCDO is its ability to enhance the low contrast intensities through pixels’ illumination value based on a fractal conformable differential operator of the entire image. The proposed algorithm can enhance the image to a certain extent, and can display image information in a better way compared to the traditional image enhancement model.
This section briefly outlines the background of fractal theory and defines Fractal conformable differential operator. In terms of the LCDO, we introduce the fractal flame which is derived based on LCDO to get the enhanced image.
The conformable derivative of differential functions f(χ) is given by the formula
which has applications in various scientific applications and engineering (see [13]). Moreover, the conformable derivative satisfies the limit
and it is not conformable at the limit
Definition 1 Let α ∈ [0, 1]. A differential operator
Anderson et al. [13] showed that in the control theory, a proportional-derivative controller for controller output μ at time χ with two tuning parameters has the algorithm
where κp is the proportional gain, κd is the derivative gain, and
Definition 2 Consider the continuous functions κ0, κ1:[0, 1] × R → (0, ∞) such that
where κ1(α, χ) ≠ −κ0(α, χ),
and
Definition 3 The integral operator corresponds to
where k ∈ R,
As an example of κ1 and κ0, one can assume that
We shall use the definition of the local fractional calculus that given in [4]. Let
is finite and exists. We note that
For example
Thus, in general, for an analytic function f, we have the structure of fractal derivative as follows [5] -Theorem 9:
where f is defined in some fractal set. In our study, we shall use a fractal function defining by the fractal sine function
and fractal cosine function
The integral corresponds to the local fractional derivative operator is defined, as follows [4]:
3.3 Local Conformable Differential Operator (LCDO)
By combining the information in 3.1 and 3.2, we obtain the following LCDO:
Definition 4 For α ∈ [0, 1], consider the continuous functions in a fractal set
such that
where κ1(α, χ) ≠ −κ0(α, χ),
and
We have the following properties.
Proposition 1 Consider the LCDO in Definition 4. Assume the functions ϕ and ψ ≠ 0 are differentiated in a fractal set
The integral operator corresponding to C(α) is given by
where
Using the definition of LCDO, we have
Using the multiplication law of the fractal operator, we have
Finally, applying the division law of fractal derivative, we obtain
The last part can be obtained from Definition 3. This completes the proof.
3.4 Fractal Flame in Terms of LCDO
Our class is based on the fractal flame component. Note that the individual function has the following form:
where the parameter ωn is called the weight of the variation υn. Note that
υ0 = (x, y), υ1 = (sin(x), sin(y)) and
Using these components, the gamma correction is defined simply by
where υin is one of the component of the individual function, A is the image or video that must process and γ ∈ (0, 1) (encoding gamma). A gamma value γ < 1 is known as an encoding gamma, and the progression of encoding with this compressive power-law nonlinearity is titled gamma compression; contrariwise, a gamma value γ > 1 is named a decoding gamma, and the presentation of the spread-out power-law nonlinearity is so-called gamma growth. The logic behind utilizing LCDO as medical picture enhancement occurs in its ability to improve the low difference forces through the suggested fractional improved operator. Encoding gamma is utilized to enhance the treatment of bits when encoding a picture or the bandwidth utilized to move the picture, from the pleasing benefit of the non-linear method (power-law) in which one observes color, optic and light.
In a generalization study, γ indicates the slope of the input-output curve. Operating Θ j(x, y) by LCDO, where it defines on the fractal set
where
For example,
and
In the application part, we shall consider κ1(α, x) = 1 − α and κ0(α, x) = α.
Hence, we have the fractal conformable gamma corrections
where
where x presents the pixel value in the direction of x −axis (similarly, for y-axis), and C(α)υin refers to the fractal conformable variation of the individual function. The fractal conformable operators showed a significant improvement in the application of image processing (see [27–29]). In this effort, we combined these operators to bring a hybrid differential operator.
The following steps of the algorithm are presented to enhance the input image:
1. Consider the input image.
2. Experimentally obtain the fractal power (α) as tune image enhancement value.
3. Use the image to find the pixel probability value (x).
4. The values of α and x are used to enhance the input image as in Eq. (11).
5. The quality of enhanced image is evaluated by using two no-reference image quality assessment metrics (Brisque, and Piqe).
In the proposed enhancement model, the fractal power α is the parameter for the fine detail enhancement, and it is fixed experimentally as shown in Fig. 1. It is observed that when the value of α is equal to 0.5, the best score for BRISQUE is obtained (lower is better). Therefore, we consider 0.5 as the experimental value of α in this study.
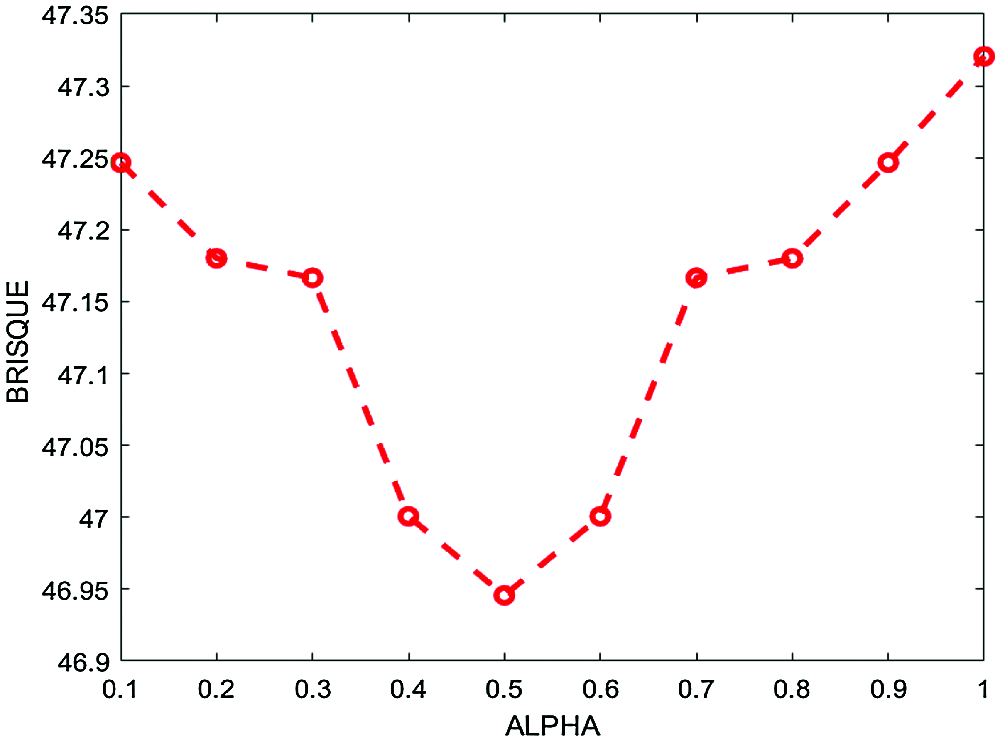
Figure 1: The average BRISQUE measure for altered values of the fractal power α
The histogram analysis of the input and the enhanced images are shown in Figs. 2b, 2d respectively. It is apparent from Fig. 2b that the probability distribution of the input image pixels looks compact, while the probability distribution of the pixels in the enhanced image Fig. 2d looks more scattered. This implies that the image's quality and contrast have been improved.


Figure 2: Sample output of the proposed algorithm along with histogram analysis. (a) Input image, (b) Histogram detail of input image, (c) Enhanced image, (d) Histogram detail of enhanced image
The proposed image enhancement model LCDO is tested using the different images with different qualities. The code of the proposed image enhancement algorithm was developed using MATLAB 2020b. In this study, the brain MRI benchmark (BRATS) dataset [26] has been used to test the proposed image enhancement algorithm.
To assess the suggested image enhancement design, we use two, no-reference image metrics, which are:
i) “The blind reference less image spatial quality evaluator (Brisque)”, which calculates the perceptual quality of images [30].
ii) “Perception based Image Quality Evaluator (Piqe)”, which calculates the image quality affected by arbitrary distortion [31].
It is noted that lower scores of Brisque, and Piqe indicate better quality of the enhanced images.
To demonstrate that the proposed enhancement model is efficient as a medical image enhancement tool, we implemented the following existing methods for the comparative study: the fractional entropy based enhancement method of kidney images by Al-Shamasneh et al. [19]. The image enhancement method for license plates by Raghunandan et al. [20], a method that is based on the Riesz fractional operator. The MRI brain images enhancement method by Al-Ameen et al. [21]. The fusion-based enhancement method of poorly illuminated images by Fu et al. [22]. And finally, the image enhancement model based on the class of fractional partial differential equations (FPDEs) [25].
The qualitative results of the proposed and the existing methods are illustrated in Fig. 3. It can be seen that all of the images have different trends with the dark and bright areas. When we compare the enhancement results of existing methods with the suggested method, the proposed method shows better enhancement results than the existing methods in terms of image quality. In the case of the existing method, it could be seen that FPDEs methods [25] (Fig. 3f) produce over-enhanced images, while the proposed method yields natural appearance by enhancing the dark areas and maintaining the bright areas of input images.


Figure 3: The brain MRI enhancement results of the proposed and existing enhancement models. (a) Input image, (b) Al-Shamasneh et al., (c) Raghunandan et al., (d) Z. Al-Ameen, (e) X. Fu et al., (f) FPDEs, (g) Proposed method
Overall, the brightening caused by the proposed model makes the structures of the medical images, which usually represent boundaries, well defined and clear. This is accredited to the model's capability to capture high frequency details efficiently. The proposed method introduces fair visual results for the weakly illuminated images. This is the contribution of the fractional integral entropy in this study.
The achieved quantitative results of the proposed enhancement method and the existing image enhancement models are stated in Tab. 1. Most of the image enhancement methods reported in the literature use the no-reference image quality metrics, therefore, the Brisque and Piqe scores have been used for the quantitative comparisons as presented in Tab. 1. The suggested method achieves the best Brisque and Piqe for almost all of the images from the two datasets.
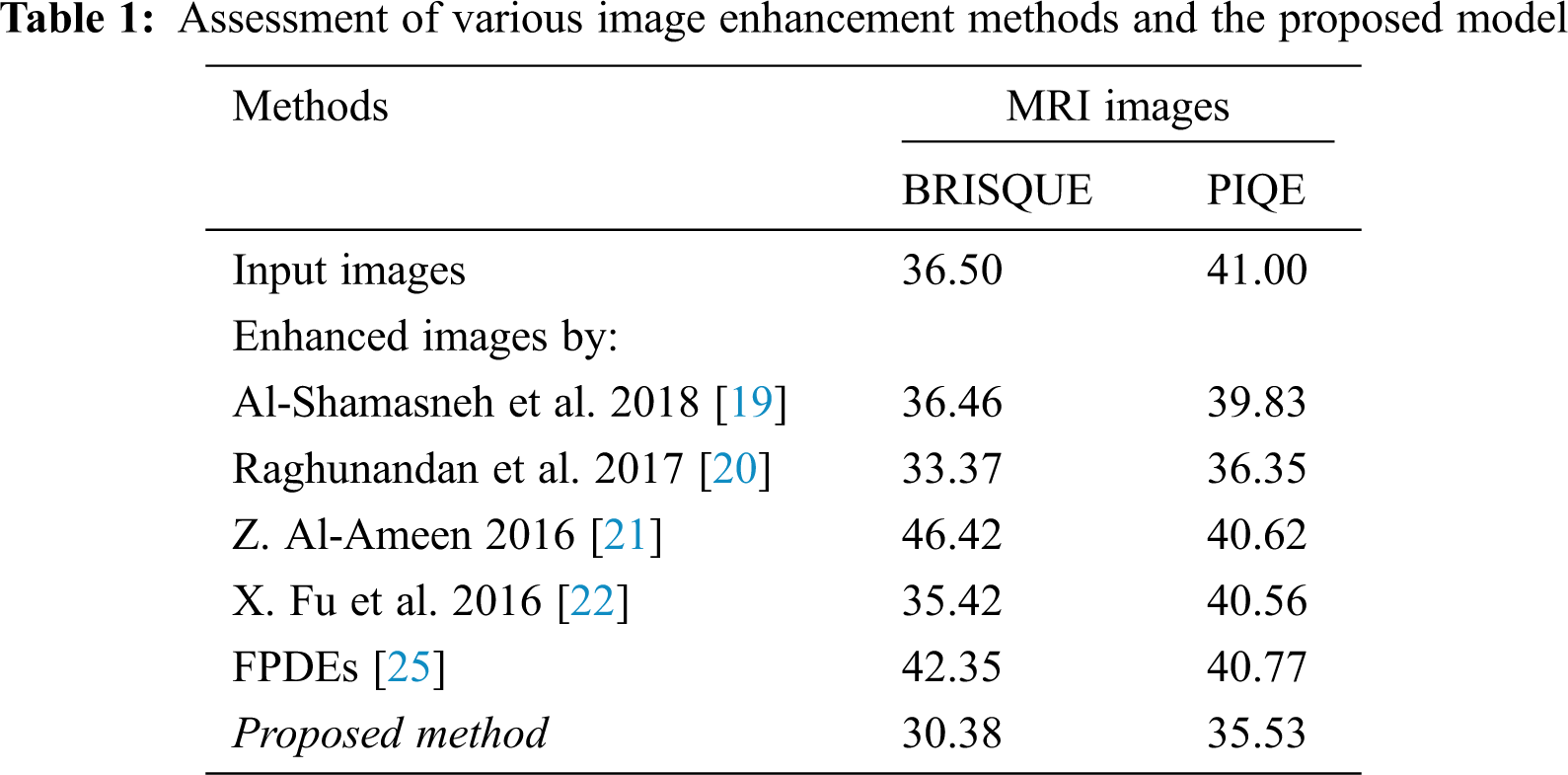
In summary, it can be said that the proposed method achieves the best results compared with the mentioned methods due to its consistent results across the different datasets.
In this study, we presented a novel method for image enhancement utilizing fractal flame, which is based on LCDO. The proposed method embraces the local fractional theory and the fractal conformable differential operator. This model applied the LCDO, which dynamically enhanced the fine details of the medical images. The proposed enhancement model enhanced the fine details in images of the input low light images. The experimental results indicate that the proposed LCDO approach outperforms existing methods under the general application of image enhancement. This gives the proposed model the advantage of being more scalable for low light image enhancement than the existing methods. Future works may adapt the present model for specific applications to achieve maximum enhancement benefit.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. M. Kolwankar and A. D. Gangal, “Fractional differentiability of nowhere differentiable functions and dimensions,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 6, no. 4, pp. 505–513, 1996. [Google Scholar]
2. X.-J. Yang, “Local fractional calculus of one-variable function”, Advanced Local Fractional Calculus and its Applications, Ed: World Science Publisher, New York, USA, 2012. [Google Scholar]
3. X.-J. Yang, D. Baleanu and H. Srivastava, “Local fractional similarity solution for the diffusion equation defined on cantor sets,” Applied Mathematics Letters, vol. 47, pp. 54–60, 2015. [Google Scholar]
4. X.-J. Yang, D. Baleanu and H. M. Srivastava,” In Local Fractional Integral Transforms and Their Applications,” Academic Press, New York, USA, 2015. [Google Scholar]
5. C. Cattani, H. M. Srivastava and X.-J. Yang, “Fractional Dynamics,” De Gruyter Open Poland, Berlin 224, Germany, 2016. [Google Scholar]
6. A. J. Mohammed, “Dimension for multi-fuzzy fractal sets using hyperbolic fuzzy dynamical system,” International journal of innovative computing, Information and Control, vol. 16, no. 1, pp. 1–14, 2020. [Google Scholar]
7. N. M. Al-Saidi and M. Said, “Biometric identification using local iterated function,” The European Physical Journal Special Topics, vol. 223, no. 8, pp. 1647–1662, 2014. [Google Scholar]
8. N. M. Al-Saidi and M. R. Md Said, “Improved digital signature protocol using iterated function systems,” International Journal of Computer Mathematics, vol. 88, no. 17, pp. 3613–3625, 2011. [Google Scholar]
9. N. M. Al-Saidi, S. S. Al-Bundi and N. J. Al-Jawari, “A hybrid of fractal image coding and fractal dimension for an efficient retrieval method,” Computational and Applied Mathematics, vol. 37, no. 2, pp. 996–1011, 2018. [Google Scholar]
10. A. Mohammed, “Performance evolution of a fractal dimension estimated by an escape time algorithm,” Boletim da Sociedade Paranaense de Matemática, vol. 38, no. 7, pp. 109–124, 2020. [Google Scholar]
11. N. M. Al-Saidi, D. Younus, H. Natiq, M. K. Ariffin, M. Asbullah et al., “A new hyperchaotic map for a secure communication scheme with an experimental realization,” Symmetry, vol. 12, no. 11, pp. 1881, 2020. [Google Scholar]
12. W. A. Hussein, N. M. Al-Saidi and H. Natiq, “A new 2d hénon-logistic map for producing hyperchaotic behavior,” in 2018 Third Scientific Conference of Electrical Engineering (SCEEUniversity of Technology, Iraq, IEEE, pp. 265–269, 2018. [Google Scholar]
13. D. R. Anderson and D. J. Ulness, “Newly defined conformable derivatives,” Advances in Dynamical Systems and Applications, vol. 10, no. 2, pp. 109–137, 2015. [Google Scholar]
14. R. W. Ibrahim and J. M. Jahangiri, “Conformable differential operator generalizes the Briot-Bouquet differential equation in a complex domain,” AIMS Mathematics, vol. 4, no. 6, pp. 1582–1595, 2019. [Google Scholar]
15. R. W. Ibrahim and D. Baleanu, “On quantum hybrid fractional conformable differential and integral operators in a complex domain,” Revista de la real academia de ciencias exactas, Físicas y Naturales. Serie A. Matemáticas, vol. 115, no. 1, pp. 1–13, 2021. [Google Scholar]
16. R. W. Ibrahim and D. Baleanu, “Geometric behavior of a class of algebraic differential equations in a complex domain using a majorization concept,” AIMS Mathematics, vol. 6, no. 1, pp. 806–820, 2021. [Google Scholar]
17. D. Veeman, H. Natiq, N. M. Al-Saidi, K. Rajagopal, S. Jafari et al., “A new megastable chaotic oscillator with blinking oscillation terms,” Complexity, vol. 2021, no. 5518633, pp. 1–12, 2021. [Google Scholar]
18. S. Roy, P. Shivakumara, H. A. Jalab, R. W. Ibrahim, U. Pal et al., “Fractional poisson enhancement model for text detection and recognition in video frames,” Pattern Recognition, vol. 52, pp. 433–447, 2016. [Google Scholar]
19. A. A. R. Al-Shamasneh, H. A. Jalab, S. Palaiahnakote, U. H. Obaidellah, R. W. Ibrahim et al., “A new local fractional entropy-based model for kidney MRI image enhancement,” Entropy, vol. 20, no. 5, pp. 344, 2018. [Google Scholar]
20. K. Raghunandan, P. Shivakumara, H. A. Jalab, R. W. Ibrahim, G. Kumar et al., “Riesz fractional based model for enhancing license plate detection and recognition,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 28, no. 9, pp. 2276–2288, 2017. [Google Scholar]
21. Z. Al-Ameen and G. Sulong, “Ameliorating the dynamic range of magnetic resonance images using a tuned single-scale retinex algorithm,” International journal of signal processing, Image Processing and Pattern Recognition, vol. 9, no. 7, pp. 285–292, 2016. [Google Scholar]
22. X. Fu, D. Zeng, Y. Huang, Y. Liao, X. Ding et al., “A fusion-based enhancing method for weakly illuminated images,” Signal Processing, vol. 129, no. 5, pp. 82–96, 2016. [Google Scholar]
23. C. Li, J. Guo, F. Porikli and Y. Pang, “LightenNet: A convolutional neural network for weakly illuminated image enhancement,” Pattern Recognition Letters, vol. 104, no. 1, pp. 15–22, 2018. [Google Scholar]
24. X. Zhang and H. Yan, “Image enhancement algorithm using adaptive fractional differential mask technique,” Mathematical Foundations of Computing, vol. 2, no. 4, pp. 347–359, 2019. [Google Scholar]
25. R. W. Ibrahim, H. A. Jalab, K. F. Khalid, A. Eatedal and N. A. Mohamad, “A medical image enhancement based on generalized class of fractional partial differential equations,” Quantitative Imaging in Medicine and Surgery, vol. 20, pp. 1–26, 2021. [Google Scholar]
26. H. A. Jalab, R. W. Ibrahim, A. M. Hasan, F. K. Karim, A. A. R. Al-Shamasneh et al., “A new medical image enhancement algorithm based on fractional calculus,” CMC-Computers Materials & Continua, vol. 68, no. 2, pp. 1467–1483, 2021. [Google Scholar]
27. P. N. Chowdhury, P. Shivakumara, H. A. Jalab, R. W. Ibrahim, U. Pal et al., “A new fractal series expansion based enhancement model for license plate recognition,” Signal Processing: Image Communication, vol. 89, no. 115958, pp. 1–12, 2020. [Google Scholar]
28. T. Subramaniam, H. A. Jalab, R. W. Ibrahim and N. F. Mohd Noor, “Improved image splicing forgery detection by combination of conformable focus measures and focus measure operators applied on obtained redundant discrete wavelet transform coefficients,” Symmetry, vol. 11, no. 11, pp. 1392, 2019. [Google Scholar]
29. R. W. Ibrahim, A. M. Hasan and H. A. Jalab, “A new deformable model based on fractional wright energy function for tumor segmentation of volumetric brain MRI scans,” Computer Methods and Programs in Biomedicine, vol. 163, no. 5, pp. 21–28, 2018. [Google Scholar]
30. A. Mittal, A. K. Moorthy and A. C. Bovik, “Blind/referenceless image spatial quality evaluator,” in 2011 Conf. Record of the Forty Fifth Asilomar Conf. on Signals, Systems and Computers (ASILOMARCA, USA, IEEE, pp. 723–727, 2011. [Google Scholar]
31. N. Venkatanath, D. Praneeth, M. C. Bh, S. S. Channappayya and S. S. Medasani, “Blind image quality evaluation using perception based features,” in 2015 Twenty First National Conf. on Communications (NCCBombay, India, IEEE, pp. 1–6, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |