DOI:10.32604/iasc.2022.016543

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.016543 |  |
| Article |
Deformation Expression of Soft Tissue Based on BP Neural Network
1Engineering Research Center of Digital Forensics, Ministry of Education, Jiangsu Engineering Center of Network Monitoring, School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science & Technology, Nanjing, 210044, China
3Faculty of Information Technology, University of Information Technology and Management, Rzeszow, 35-225, Poland
*Corresponding Author: Xiaorui Zhang. Email: zxr365@126.com
Received: 04 January 2021; Accepted: 13 August 2021
Abstract: This paper proposes a soft tissue grasping deformation model, where BP neural network optimized by the genetic algorithm is used to realize the real-time and accurate interaction of soft tissue grasping during virtual surgery. In the model, the soft tissue epidermis is divided into meshes, and the meshes generate displacements under the action of tension. The relationship between the tension and displacement of the mesh is determined by the proposed cylindrical spiral spring model. The optimized BP neural network is trained based on the sample data of the mesh point and vertical tension, so as to obtain the force and displacement of any mesh point on the soft tissue epidermis. The virtual experiment platform is built using a PHANTOM OMNI haptic hand controller and the 3D Max software, by which the simulation experiment of grasping the human abdomen is realized. The experimental results show that the proposed model has good visual interaction and real-time force feedback, which can meet the requirements of deformation simulation for soft tissue grasping in virtual surgery.
Keywords: Soft tissue grasping; genetic algorithm; BP neural network; surgical simulation
With the rapid development of the information technology, the intelligent era is coming. Various emerging technologies and applications are increasingly widespread. The aggravation of the global aging population [1], the shortage of medical staff [2,3], and the tediouness of surgical training task [4] have brought severe challenges to the traditional surgical training. The traditional surgical training has such shortcomings as few specimens, long cycle, slow effect, and high cost; therefore, the intellectualization of the virtual surgical training system is needed urgently. The emergence of virtual reality technologies and haptic interactive equipments has brought new opportunities to the virtual surgery training system, and its development and application have promoted the intellectualization of virtual surgery [5–7].
The key of the virtual surgery system is designing virtual soft tissue deformation model. In virtual surgery, the soft tissue model needs to simulate various deformation operations and to feedback the deformation operation, so as to simulate the operation process of real soft tissue. Generally, it is common to grasp the soft tissue with surgical instruments during the surgical simulation. For example, it is often necessary to grasp the wound when removing tumors in soft tissue.
With the rapid development of artificial intelligence technology, many researchers apply deep learning, neural network, and other optimization algorithms to deformable soft tissue models. In order to achieve the requirements of real-time performance and accuracy of the virtual models, Zhong et al. [8] proposed a cellular neural method for interaction of soft tissue deformation by virtue of real-time computing of cellular neural networks, where the soft tissue deformation is executed based on the potential energy propagation [9]. According to the law of conservation of energy, the external force applied to soft tissue is regarded as equivalent potential energy and propagates in soft tissue through nerve propagation based on CNN [10]. De et al. [11] also studied the neural network technology based on machine learning for soft tissue deformation. The calculation process is divided into off-line and on-line stages, in which the response of the FEM model under specified displacement is calculated in advance in the off-line stage, and the coefficients of neurons are optimized by training the radial basis function network (RBFN); the deformation field is reconstructed by using the trained RBFN in the online stage. Lorente et al. [12] further explored the method based on machine learning for calculating soft tissue deformation, by which liver deformation simulation was realized during respiration. In this method, a supervised machine learning model based on deformation data is used to construct the mapping function of input variables to approximate the known model output. The mapping function constructed in the training stage can generate exact output for unknown input in following testing stage, that is, the mapping function can reconstruct the overall deformation of soft tissue. Therefore, the performance of the machine learning model highly depends on the training data and the selected learning algorithm. Tonutti et al. [13] further studied the ability of machine learning method in real-time modeling of soft tissue deformation and experimental results showed that the position error is less than 0.3 mm, which exceeds the general threshold of surgical accuracy in images.
In this paper, a novel variable model of soft tissue deformation is proposed to model and simulate soft tissue grasping deformation in interactive surgical simulation. In this model, the grasping deformation of soft tissue is studied by using BP neural network optimized by the genetic algorithm, and the varieties of soft tissue in the direction of tension are determined. The paper is organized as follows: Section 2 introduces the establishment of the soft tissue grasping deformation model and determination of the functional relationship between key points and stress. Section 3 describes the construction of the virtual surgery simulation system based on the model proposed in this paper. In Section 4, we analyze and compare the experimental results through adjusting the stress range of the soft tissue model and the load of the model.
The soft tissue grasping deformation model consists of four major components: the establishment of a rectangular coordinate system, the study of key points, the functional relationship between key points and stress, and the establishment of the model. The following sections describe in detail the major components of the soft tissue grasping deformation model.
2.1 Establishment of a Rectangular Coordinate System
Under the action of given tension
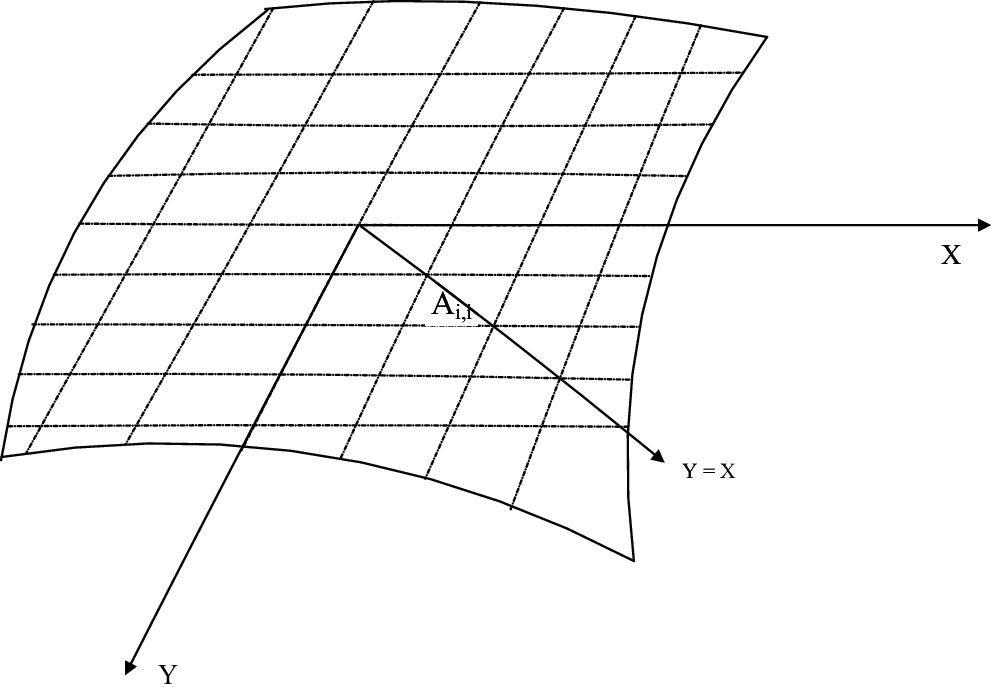
Figure 1: Division of soft tissue epidermis
The soft tissue epidermis can be divided into a series of areas. which denotes as,
where the number of regular block areas
Note that
The origin point
The four vertices of each block area are marked with spacial coordinates. In this way, the coordinates of the vertices of each block area in the four quadrants can be expressed as
where
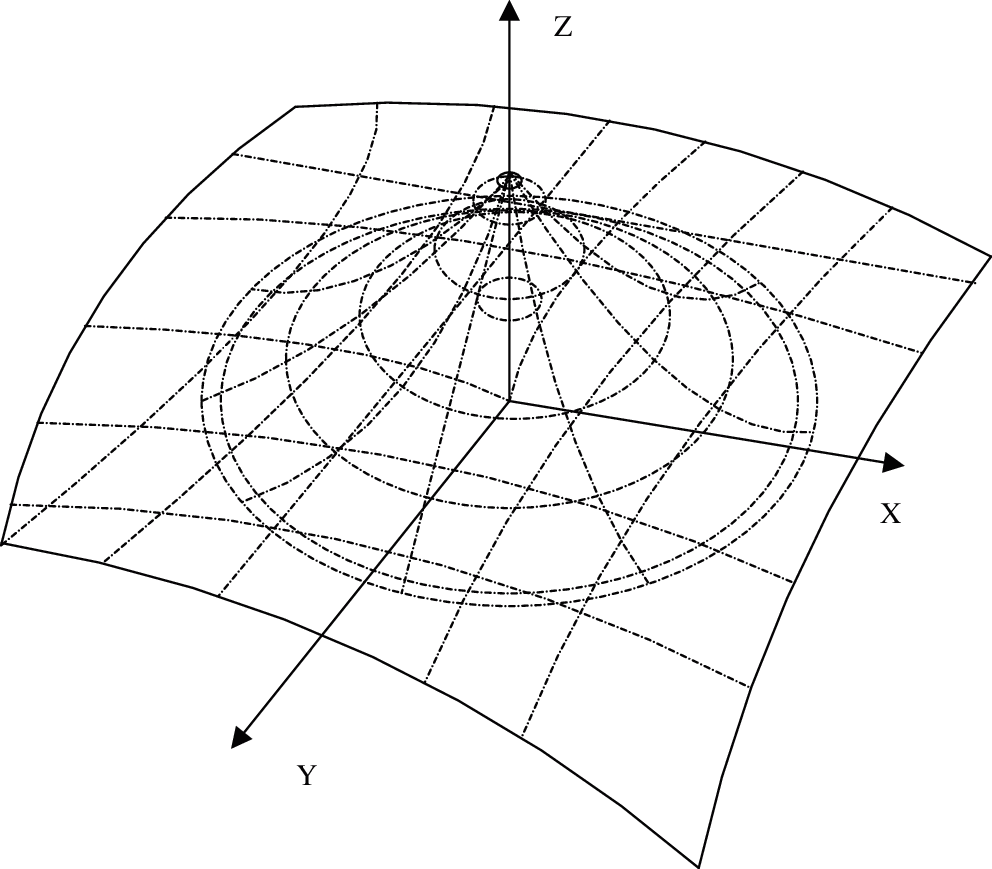
Figure 2: Deformation of key points in spacial coordinate system
2.3 The Functional Relationship Between Key Points and Stress
If any key point on the line
In order to study the relationship between the
In Eq. (4), spring tension is proportional to the elongation of deformation, that is, the tension
The database is used to help the genetic algorithm optimize the
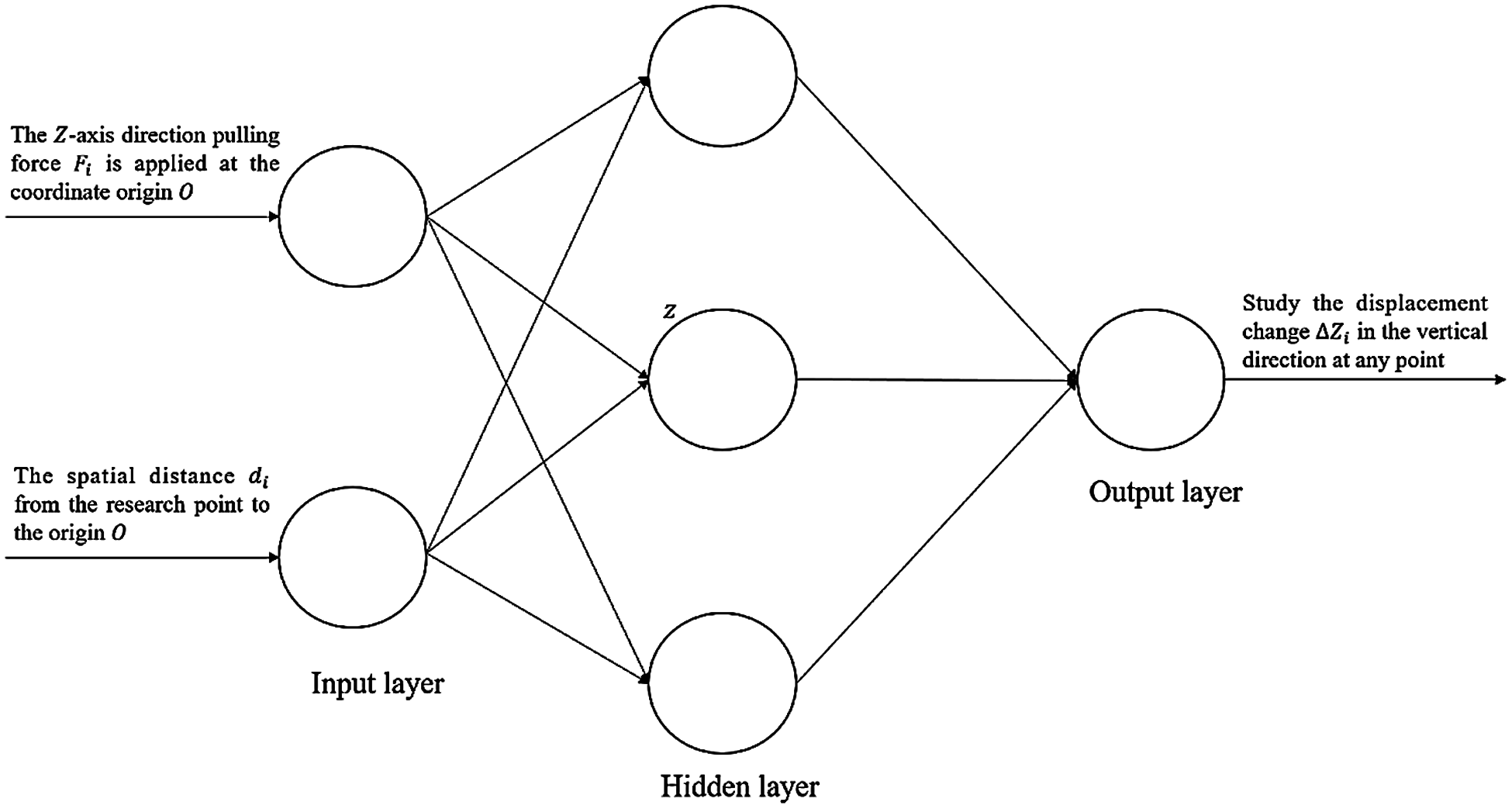
Figure 3: Schematic diagram of neural network training
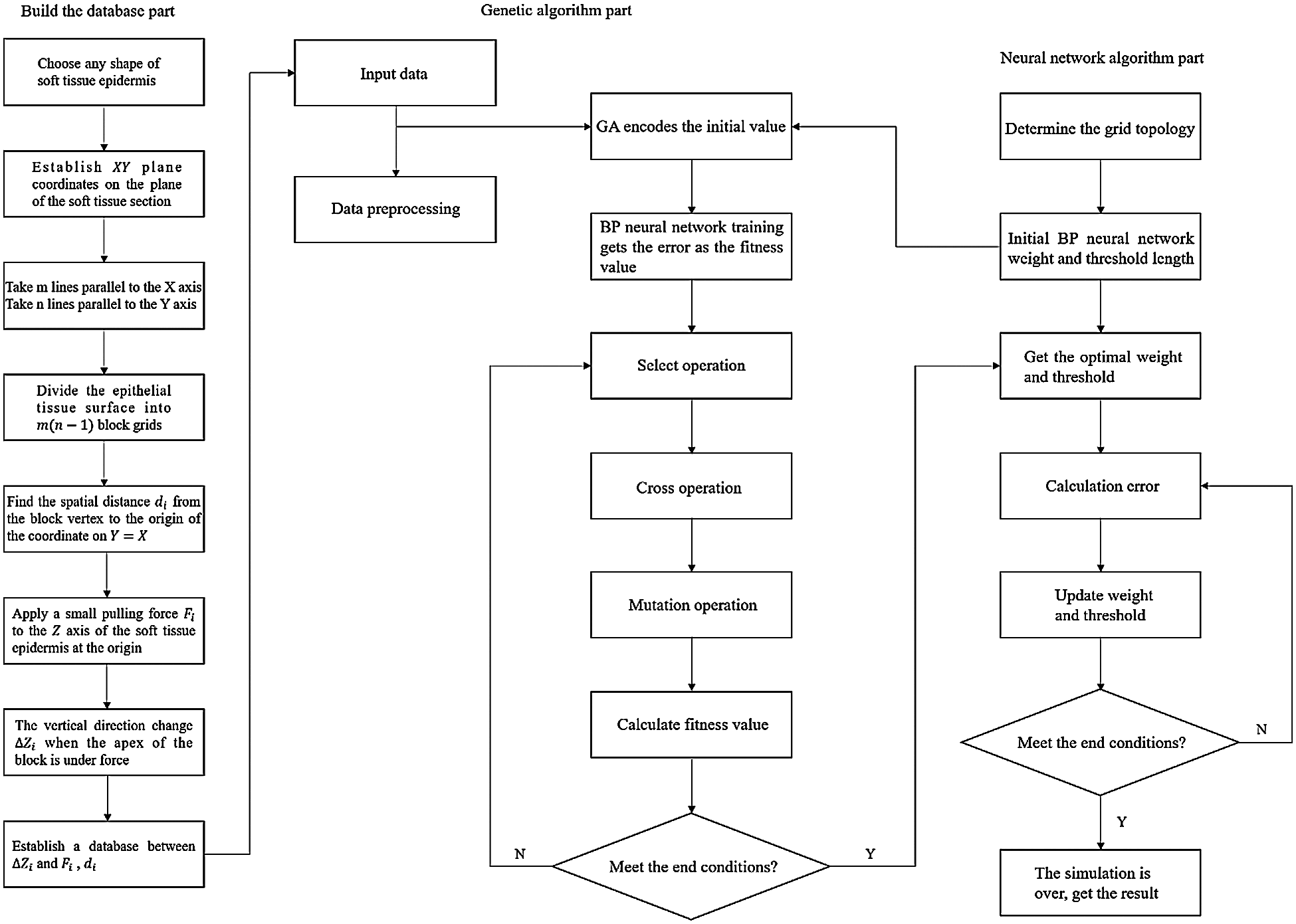
Figure 4: Flow chart of the genetic algorithm
If a tension
In order to test the usability of the virtual platform, operate the PHANTOM OMNI hand controller to grasp the modeled lower abdomen. The process of simulated grasping operation is shown in Fig. 5. Experiments show that this model is effective, can grasp the modeled soft tissues, and can provide visual and tactile feedback.
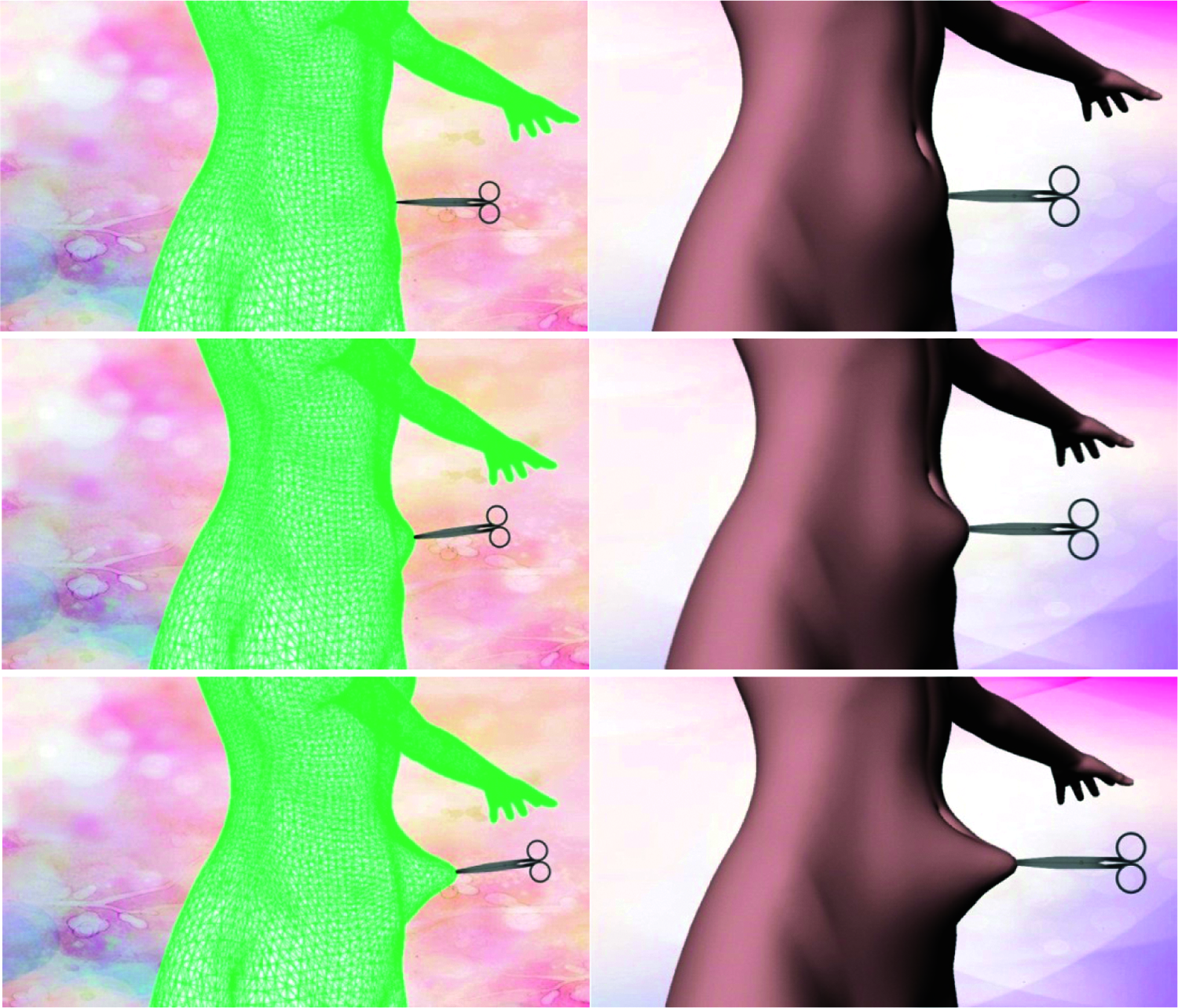
Figure 5: Grasping process diagram
In the grasping process, the color map is used to display the deformation characteristics of the soft tissue, which more intuitively and clearly shows the deformation of the soft tissue under local stress. The colors from blue to red indicate the strength of the force, blue indicates no force, and red indicates the area that is deformed by the force, as shown in Fig. 6.
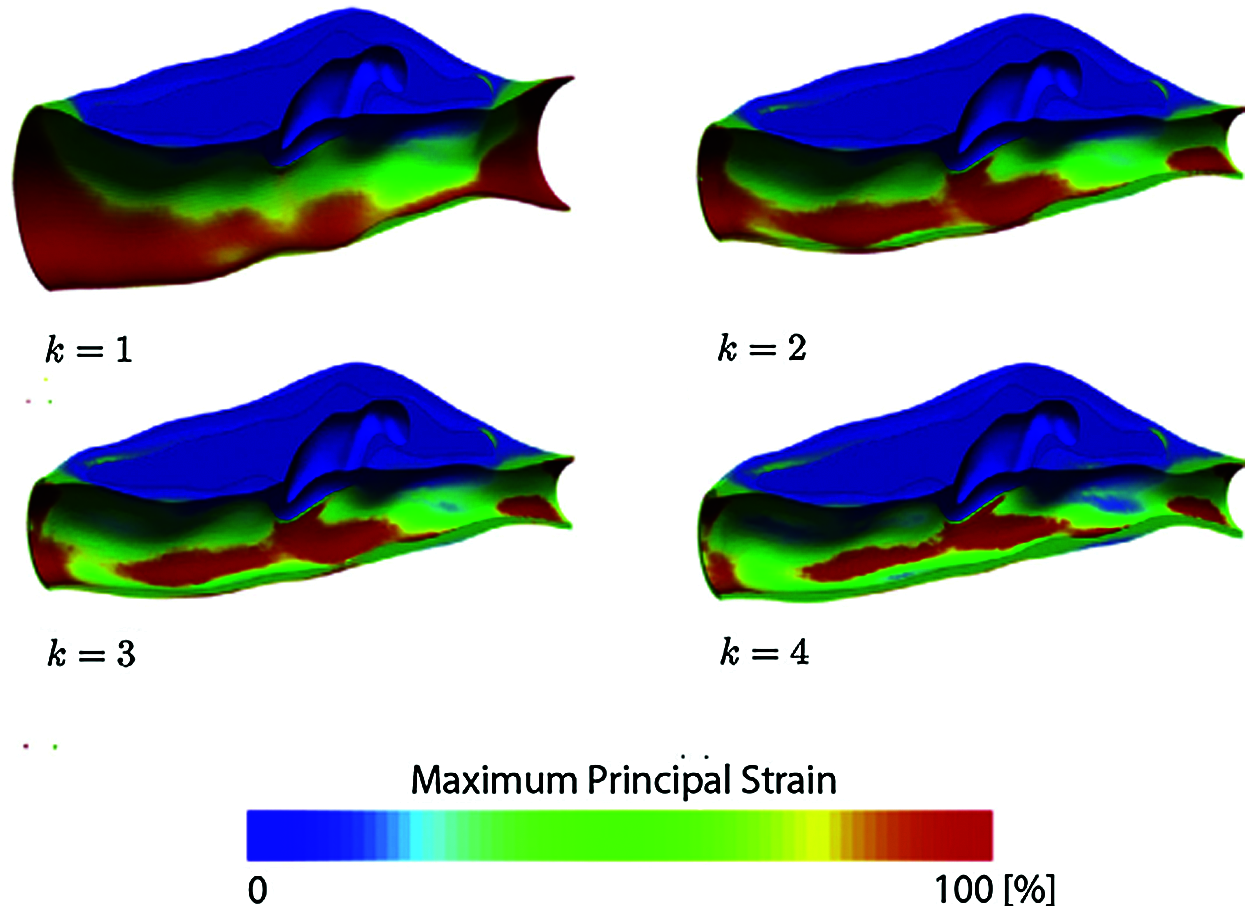
Figure 6: Virtual soft tissue stress and deformation map (
The virtual surgery simulation system is composed of three modules, including the input module, information processing module, and output module. The input module mainly uses force-tactile interaction devices to input the tension force, including the magnitude, direction, and duration of the force. The information processing module is a soft tissue model programmed by 3D MAX software, which relies on the computer operating system for processing, including force signal processing and model shape processing. The output module is for feeding back the information to the operator after the signal processing by the input module, including the feedback force from the force-tactile interactive device and the deformation of the model displayed on the displayer. The pipeline of the simulation test is shown in Fig. 7.
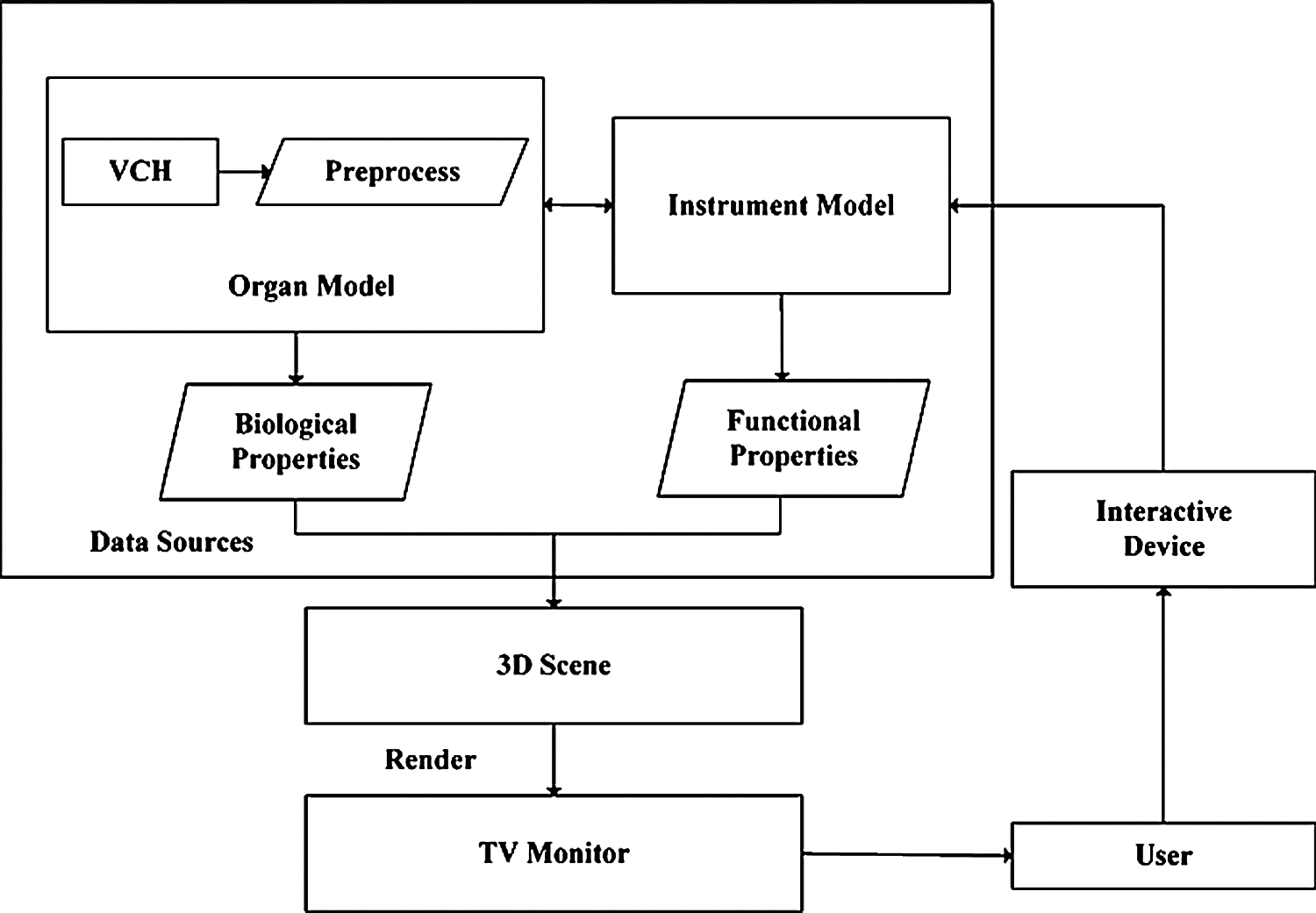
Figure 7: Pipeline of the simulation test
In order to realize the algorithm, a virtual simulation platform is first established. Our platform consists of a computer and a haptic interaction facility called PHANTOM OMNI. The computer is based on Windows 10 with an Intel (R) Xeon (R) CPU, E5-1650 v3 @ 3.5 GHz processor, and NVIDIA GeForce GT 720M graphics. The simulation is carried out on VC++ 2019 and 3DS MAX 2019 software with OpenGL graphics libraries. The PHANTOM OMNI allows the operators to touch and operate on the virtual object simulated by our method. The experimental environment is shown in Fig. 8.

Figure 8: Experiment environment
A three-dimensional model of 65536 lower abdomens and forceps is used, which is shown in Fig. 9. Import the 3D model into the 3D MAX software, and render the entire 3D model surface with the colorful lower abdomen CT data obtained from the First Affiliated Hospital of Southeast University, including 36,542 color rendering triangles. The rendering effect is shown in Fig. 10.

Figure 9: Three-dimensional model

Figure 10: Three-dimensional rendering effect
3.1 Collision Detection Validation
The top-K algorithm in the bounding box hierarchy method has better performance and high real-time detection accuracy [14,15], therefore, the study selects it as the collision detection method. The basic idea of the bounding box hierarchy method is to use a slightly larger bounding box and more simple geometric structure characteristics than the simulation model to approximately represent the complex simulation object, and gradually approach the object by constructing a tree-like hierarchy until the geometric characteristics of the object is completely obtained. If the collision of the object is detected, the bounding box is intersected. Since finding the intersection of the object is easy by the intersection ratio of the bounding box, it is possible to quickly exclude many disjoint objects. The overlapping parts of the bounding boxes are further tested for intersection, thereby speeding up the algorithm.
4 Experimental Results and Analysis
4.1 Simulation Deformation Time
Under the same experimental conditions, 50 grasping operations were performed on the virtual abdomens. The virtual abdomens are constructed by the model proposed in this paper and the spring-mass model [16], respectively. Additionally, we also select fresh living soft tissues for 50 real grasping operations, and the deformation time of the 50 grasping operations is shown in Fig. 11, where the deformation time is from the beginning of the grasping operation on the abdomen to the end of the model deformation. The blue grid points denote the results of the proposed model in this paper, green grid points denote the results based on the Spring-mass model and red grid points denote the results based on living soft tissues.
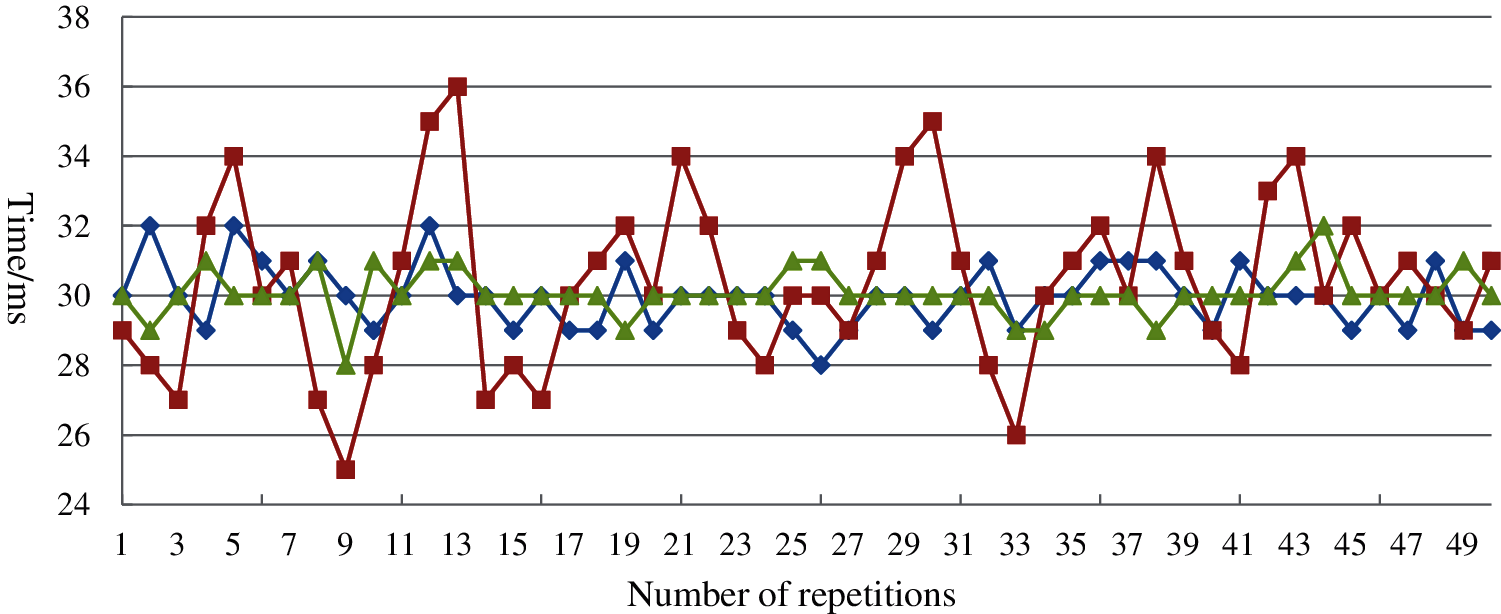
Figure 11: Response time for grasping
4.2 Stress Range of Soft Tissue Model
The soft tissue has the maximum stress range during the deformation process after being stressed. In order to make the deformation of this model more accurate, it is necessary to determine its maximum stress. This paper used real living soft tissues to grab and obtain real data, which is shown in Fig. 12. Based on the obtained real data, we improved the parameter settings of the proposed model.
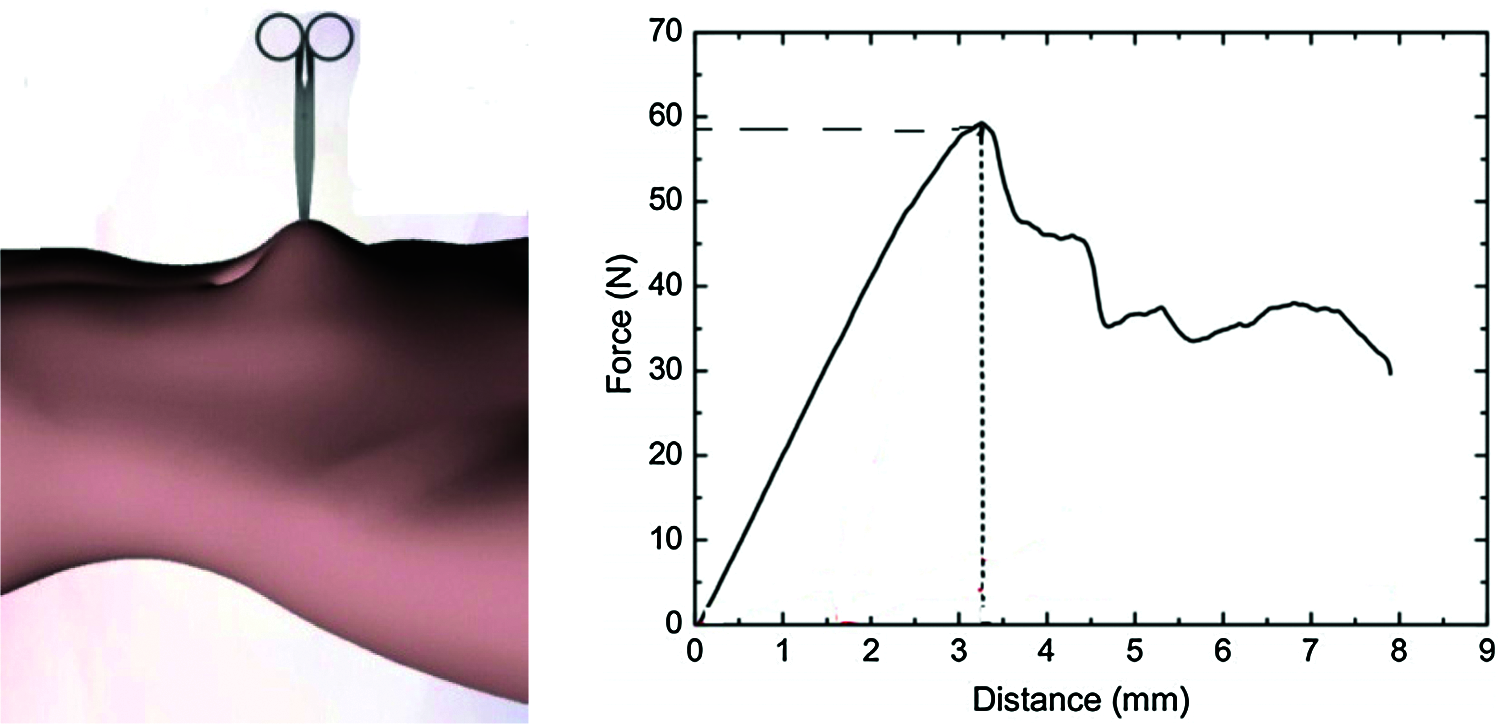
Figure 12: Stress change graph over time
The stability of model deformation is an important metric of the performance of the model. In order to verify the stability of the proposed model, the traditional spring-mass model [16] and the proposed model are simulated, respectively. The proposed model achieves stable at about 50ms for the soft tissue deformation of 12 cm, but traditional spring-mass model has a slight increase after 75 ms without reaching a steady state. As shown in Fig. 13, the proposed model has better stability after the grasping operation.
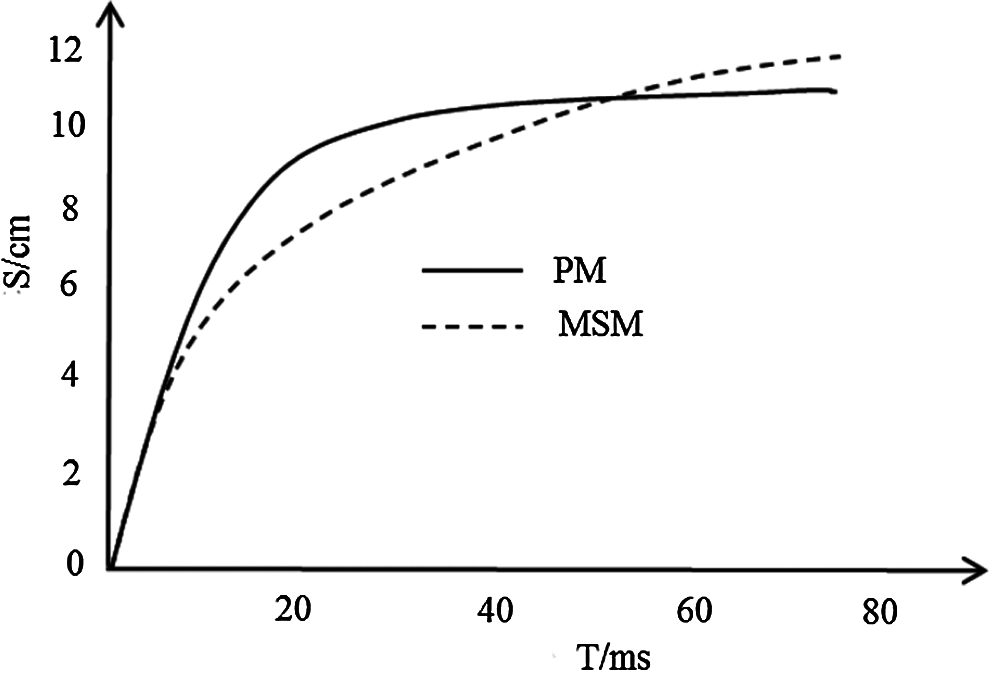
Figure 13: Displacement change graph
The finite element model with better load performance [17–21] and the model proposed in this paper are simulated, respectively, and the deformation results are shown in Fig. 14. The load-displacement of the local deformation of the proposed model is also in good agreement with the finite element model, and the maximum deviation between the load and displacement is about 5%. The experimental results show that the proposed model is excellently similar to the finite element model in the load performance.
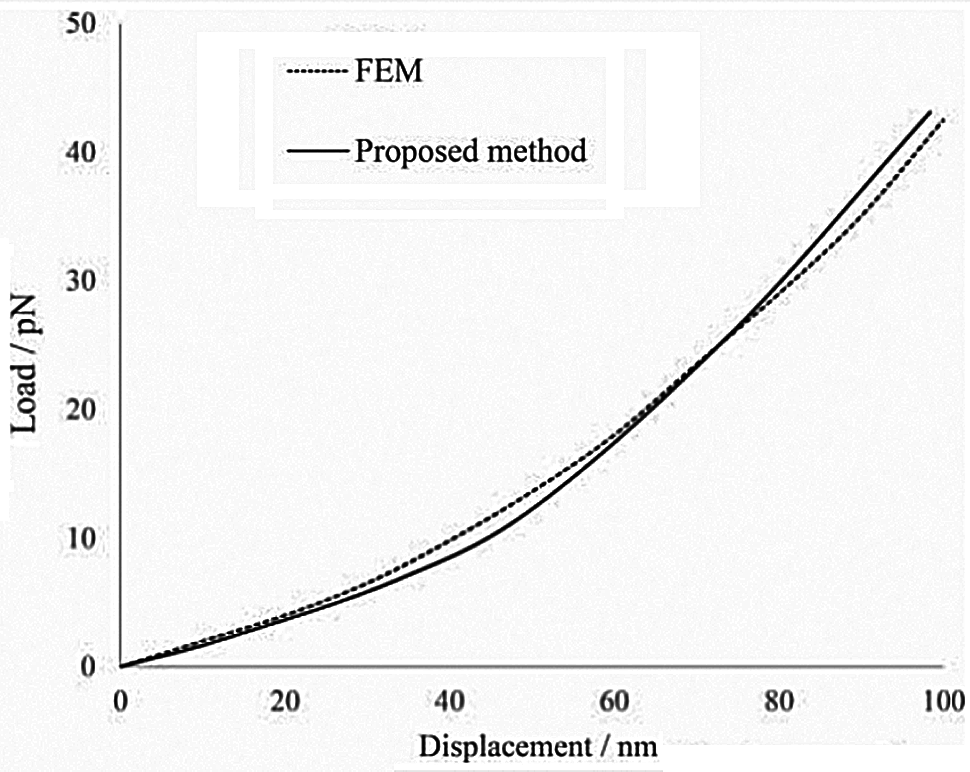
Figure 14: Load-displacement behaviors of the proposed model and FEM model
This study proposed a soft tissue grasping deformation model to simulate the grasping deformation process on the human abdomen soft tissue by virtual human-computer interaction. Using 3DS MAX 2019 with OpenGL graphics libraries and VC++ 2019 software, the abdominal soft tissue model training system for grasping operation was built through the PHANTOM OMNI force-tactile interactive device. The proposed model combines the displacement and deformation of any point of the irregular cross-section elastic cylinder under grasping action, where the BP neural network optimized by the genetic algorithm is used to calculate the deformation of the elastic tissues intuitively, accurately and quickly. A real-time deformation simulation system was constructed to improve the fidelity of virtual force tactile interaction. The real-time performance and accuracy of the proposed model are verified by comparative experiments. The experimental results show that the proposed model has better stability and on-site perception.
Funding Statement: This work was supported, in part, by the Natural Science Foundation of Jiangsu Province under Grant Numbers BK20201136, BK20191401; in part, by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund; in part, by the Collaborative Innovation Center of Atmospheric Environment and Equipment Technology (CICAEET) fund; NUIST Students’ Platform for Innovation and Entrepreneurship Training Program; NUIST Undergraduate Excellent Graduation Design (Thesis) Support Program Project.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. P. Juha and L. Puustjärvi, “Towards web-assisted self-care in developing countries: A challenge for health posts and pharmacies,” in Proc. IST-Africa Week, South Africa, pp. 1–10, 2016. [Google Scholar]
2. D. Wang, J. Jiao, Y. Zhang and X. Zhao, “Computer haptics: Haptic modeling and rendering in virtual reality environments,” Journal of Computer Aided Design & Computer Graphics, vol. 28, no. 6, pp. 881–895, 2016. [Google Scholar]
3. X. R. Zhang, P. P. Wang, W. Sun and N. I. Badler, “A novel twist deformation model of soft tissue in surgery simulation,” Computers Materials & Continua, vol. 55, no. 2, pp. 297–319, 2018. [Google Scholar]
4. X. Shao, X. Nie and B. Wang, “GPU-based real-time 3D visual hull reconstruction and virtual-reality interaction,” Journal of Computer Aided Design & Computer Graphics, vol. 29, no. 1, pp. 52–61, 2017. [Google Scholar]
5. M. Freutel, H. Schmidt, L. Dürselen, A. Ignatius and F. Galbusera, “Finite element modeling of soft tissues: material models, tissue interaction and challenges,” Clinical Biomechanics, vol. 29, no. 4, pp. 363–372, 2014. [Google Scholar]
6. X. R. Zhang, X. F. Yu, W. Sun and A. G. Song, “Soft tissue deformation model based on marquardt algorithm and enrichment function,” Computer Modeling in Engineering & Sciences, vol. 124, no. 3, pp. 1131–1147, 2020. [Google Scholar]
7. X. R. Zhang, J. L. Duan, J. Liu and N. I. Badler, “An integrated suture simulation system with deformation constraint under a suture control strategy,” Computers Materials & Continua, vol. 60, no. 3, pp. 1055–1071, 2019. [Google Scholar]
8. Y. Zhong, B. Shirinzadeh, G. Alici and J. Smith, “A cellular neural network methodology for deformable object simulation,” IEEE Transactions on Information Technology in Biomedicine, vol. 10, no. 4, pp. 749–762, 2006. [Google Scholar]
9. J. Zhang, Y. Zhong, J. Smith and C. Gu, “Energy propagation modeling of nonlinear soft tissue deformation for surgical simulation,” Simulation, vol. 94, no. 1, pp. 3–10, 2018. [Google Scholar]
10. J. Zhang, Y. Zhong, J. Smith and C. Gu, “Neural dynamics-based poisson propagation for deformable modelling,” Neural Computing and Applications, vol. 31, no. 2, pp. 1091–1101, 2019. [Google Scholar]
11. S. De, D. Deo, G. Sankaranarayanan and V. S. Arikatla, “A physics-driven neural networks-based simulation system (phynness) for multimodal interactive virtual environments involving nonlinear deformable objects,” Presence: Teleoperators and Virtual Environments, vol. 20, no. 4, pp. 289–308, 2011. [Google Scholar]
12. D. Lorente, F. Martínez-Martínez, M. J. Rupérez, M. A. Lago, M. Martínez-Sober et al., “A framework for modelling the biomechanical behaviour of the human liver during breathing in real time using machine learning,” Expert Systems with Applications, vol. 71, no. 1, pp. 342–357, 2017. [Google Scholar]
13. M. Tonutti, G. Gras and G. Z. Yang, “A machine learning approach for real-time modelling of tissue deformation in image-guided neurosurgery,” Artificial Intelligence in Medicine, vol. 80, no. 8, pp. 39–47, 2017. [Google Scholar]
14. S. Gottschalk, M. C. Lin and D. Manocha, “OBBTree: A hierarchical structure for rapid interference detection,” in Proc. SIGGRAPH, New Orleans, USA, pp. 171–180, 1996. [Google Scholar]
15. M. L. Yiu and N. Mamoulis, “Efficient Processing of Top-k Dominating Queries on Multi-Dimensional Data,” in Proc. VLDB, Vienna, Austria, pp. 483–494, 2007. [Google Scholar]
16. R. Blickhan, “The spring-mass model for running and hopping,” Journal of Biomechanics, vol. 22, no. 11–12, pp. 1217–1227, 1989. [Google Scholar]
17. X. R. Zhang, H. L. Wu, W. Sun and S. K. Jha, “A fast and accurate vascular tissue simulation model based on point primitive method,” Intelligent Automation & Soft Computing, vol. 27, no. 3, pp. 873–889, 2021. [Google Scholar]
18. J. Goldak, A. Chakravarti and M. Bibby, “A new finite element model for welding heat sources,” Metallurgical and Materials Transactions B, vol. 15, no. 2, pp. 299–305, 1984. [Google Scholar]
19. A. A. Ahmed and B. Akay, “A survey and systematic categorization of parallel k-means and fuzzy-c-means algorithms,” Computer Systems Science and Engineering, vol. 34, no. 5, pp. 259–281, 2019. [Google Scholar]
20. Z. Wang, Y. Huang and F. Xiong, “Three-dimensional numerical analysis of blast-induced damage characteristics of the intact and jointed rockmass,” Computers Materials & Continua, vol. 60, no. 3, pp. 1189–1206, 2019. [Google Scholar]
21. X. R. Zhang, X. F. Yu, W. Sun and A. Song, “An optimized model for the local compression deformation of soft tissue,” KSII Transactions on Internet and Information Systems, vol. 14, no. 2, pp. 671–686, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |