DOI:10.32604/iasc.2022.020543

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.020543 |  |
| Article |
Hybrid Online Model for Predicting Diabetes Mellitus
1E.G.S Pillay Engineering College, Nagapattinam, 611002, Tamilnadu, India
2A.V.C College of Engineering, Mannampandal, 609305, Tamilnadu, India
*Corresponding Author: C. Mallika. Email: cmallikachinna@gmail.com
Received: 28 May 2021; Accepted: 28 July 2021
Abstract: Modern healthcare systems have become smart by synergizing the potentials of wireless sensors, the medical Internet of things, and big data science to provide better patient care while decreasing medical expenses. Large healthcare organizations generate and accumulate an incredible volume of data continuously. The already daunting volume of medical information has a massive amount of diagnostic features and logged details of patients for certain diseases such as diabetes. Diabetes mellitus has emerged as along-haul fatal disease across the globe and particularly in developing countries. Exact and early diagnosis of diabetes from big medical data is vital for the deterrence of disease and the selection of proper therapy. Traditional machine learning-based diagnosis systems have been initially established as offline (non-incremental) approaches that are trained with a pre-defined database before they can be applied to handle prediction problems. The major objective of the proposed work is to predict and classify diabetes mellitus by implementing a Hybrid Online Model for Early Detection of diabetes disease (HOMED) using machine learning algorithms. Our proposed online (incremental) diabetes diagnosis system exploits (i) an Adaptive Principal Component Analysis (APCA) technique for missing value imputation, data clustering, and feature selection; and (ii) an enhanced incremental support vector machine (ISVM) for classification. The efficiency of HOMED is estimated on different performance metrics such as accuracy, precision, specificity, sensitivity, positive predictive value, and negative predictive value. Experimental results on Pima Indian diabetes dataset (768 samples: 500 non diabetic and 268 diabetic patients) reveal that HOMED considerably increases the classification accuracy and decreases computational complexity with respect to the offline models. The proposed system can assist healthcare professionals as a decision support system.
Keywords: Adaptive principal component analysis; clustering; diabetes; missing value imputation; support vector machine
Diabetes is one of the most common chronic endocrine sickness or set of metabolic disorders where people suffer from high blood sugar (glucose) in their body. The pathologic sources of diabetes are the failure of the pancreas to secrete adequate insulin and the body’s cells do not react well to insulin. Continuously, there is substantial growth in the number of persons suffering from diabetes in several healthcare organizations. It has reached the dubious distinction of becoming the 5th leading cause of disease-related death [1]. Besides contributing to cardiovascular diseases, diabetes also upturns the risks of increasing blindness, blood vessel damage, nerve damage, and kidney disease. Of late, research revealed that around 552 million individuals are estimated to get affected owing to diabetes mellitus by 2030 [2]. As stated by the International Diabetes Federation (IDF), this number is anticipated to the extent of 628 million by 2045 and is claimed to cause one death every 6 s due to diabetes related issues [3,4]. Furthermore, 46.5% of those with diabetes have not been diagnosed [5]. The only way for the diabetic patient to live with this disease is to maintain the blood glucose as normal as possible deprived of severe low or high levels, and this is realized when the patient uses an appropriate treatment which may comprise consuming oral diabetes drugs or using some form of insulin, exercising, and nourishment [6]. Moreover, treating diabetes mellitus is also a challenging, costly, and complex endeavor for healthcare professionals. There is several significant information to log about the diseases and patients that helps the physician in making an optimal decision to enhance patient life expectancy. This brings the traditional analysis methods to a halt or depreciates the learning process as the learning algorithm becomes prone to over-fitting owing to the massive redundant and irrelevant features in a high-dimensional dataset.
As such diabetes has become a significant issue in the healthcare industry to find solutions to combat the disease, which include using cutting-edge techniques and tools in information and communication technologies for the early diagnosis of diabetes in order to reduce the human fatal rate. One of the widely recognized and influential approaches in any disease diagnosis is the application of machine learning techniques. Machine learning deals with the development of technologies that enable machines to learn. In this usage, “learning” denotes developing a data model, often with the objective of making predictions about new data that are assumed to come from the similar population that produced the data employed for the model. The challenge is to develop systems that can consider a set of patterns (i.e., the available information) and inevitably make new inferences from the early statistics, with or without human involvement. In this work, we propose a hybrid online model for early detection of diabetes disease using an adaptive principal component analysis technique for missing value imputation, data clustering, feature selection, and an incremental support vector machine algorithm for classification.
The primary challenge in mining clinical datasets for extracting hidden knowledge is handling missing data. One way of dealing with missing values is just neglecting that portion of the data from the further study [7]. However, eliminating the data variable with missing value is the bad practice for predicting disease [8]. Removing rows of data due to the deficiency of a few variables causes a loss of significant information observed that would have been useful for analyses. This could cause unfair evaluations. Missing value can also be predicted from medical records by means of Natural Language Processing (NLP) and rule-based algorithms [9]. On the other hand, trying to calculate missing data by a close estimation according to the data context is known as data imputation.
Several authors tried to develop methods for filling in missing data components. An example includes ‘mean value imputation’ [10,11], carrying forward the last observation, and probability-based techniques such as multiple imputations (MI) and hot-deck imputation. However, there is an opportunity that these approaches may result in biased results and therefore they are considered suboptimal [12]. Additionally, these methods do not directly utilize information gained from the perceived values. Classification of the disease helps the clinicians in predicting the risk elements that cause diabetes, taking preventive actions, and efficient therapy at an early stage. Accessibility of huge categorized clinical data associated with diabetes is an advantage for scientists to combat diabetes. But, using a conventional approach to estimate and process huge data will initiate complications, since most of the data have a higher degree of complexity and uncertainty [13,14].
The clustering problem has been addressed in numerous disease diagnosis systems [15,16]. This reveals its extensive application and effectiveness as one of the phases in investigative medical data analysis. Clustering is the common technique in machine learning approaches that cluster data based on likelihood metric. The proposed APCA uses the Gaussian Mixture Model (GMM) to perform clustering. In this model-based approach, the expectation-maximization (EM) algorithm is employed to calculate the model parameters.
Feature selection is very decisive for enhancing the enactment of the classification process, particularly in the case of high-dimensional data classification [17]. It is an important preprocessing technique to eliminate redundant and inappropriate features. In this work, a PCA-based dimensionality reduction method is selected to transform the original set of features, thus solving the correlation problem, which makes it problematic for the classification method to obtain associations between the data. Our proposed APCA aids to filter out inappropriate features, thus decreasing the training time, cost, and also improve the performance of the model [18].
From the machine learning perception, classification is the problem of categorizing a group of elements into different classes, according to the training result of a subset of observations whose fitting class is identified [19,20]. Several researchers in the healthcare sector have intensified efforts to enhance classification in order to gain improved results when detecting or diagnosing related diseases. A large number of notable studies have been carried out for predicting and classifying diabetes at the earliest but still with a lack of accuracy. SVM is extensively used in disease diagnosis systems for their effectiveness and consistency. It is a powerful classification method that has been employed in many studies on disease classification [21].
There are several methods employed in data mining, particularly for supervised machine learning approaches; hence, applying a suitable method has been a challenge among researchers in designing the diabetes diagnosis systems [22]. Even though these data mining approaches can be employed to predict diabetes mellitus over large real-life datasets, the majority of the techniques developed by supervised learning in the previous research do not support the incremental (online) methods for predicting diabetes disease. Additionally, standard supervised learning often cannot be carried out on line and hence they need to compute all the training data again to perform the classification process. Therefore, to enhance the classification accuracy and to reduce the computation complexity of disease prediction, a new hybrid approach is developed using intelligent clustering, feature selection, and classification techniques [23]. Furthermore, since clinical datasets require continuous data updating, it is necessary to incrementally update the once trained models to decrease computation time in data classification and is more effective in terms of memory requirement.
The main objective of this work is to develop an effective and accurate aboriginal diagnostic system for detecting diabetes, notwithstanding the existence of numerous recognized prevailing approaches, which have already been implemented or are in use for the diagnosis of diabetes. The contributions of this paper are two-fold:
• We propose an APCA technique for missing value imputation, data clustering and feature selection.
• We devise an enhanced ISVM to predict and classify the diabetes mellitus.
• The efficiency of HOMED is estimated on different performance metrics such as accuracy, precision, specificity, sensitivity, positive and negative predictive values.
We conduct extensive experimentation on Pima Indian diabetes dataset. The experimental results reveal that HOMED considerably increases the classification accuracy and decreases computational complexity with respect to the offline models [24]. The proposed system can assist healthcare professionals as a decision support system.
There are several research studies, which have been employed for the classification of diabetes mellitus. In this section, we discuss the past related research which focuses on predicting and classifying diabetes dataset that machine learning algorithms reselected as the key technique. Wang et al. [25] suggested an artificial neural network (ANN) as a classification technique for diabetes mellitus. According to this study, the authors proved that computational intelligence techniques deliver a more accurate result as related to regression models. Varma et al. developed a decision tree modeling for classifying diabetes. However, conventional decision tree models are disadvantaged by a problem of sharp cutoffs [26]. The authors also proposed a fuzzy computation technique for eliminating the crisp boundaries in order to improve the performance of the decision tree. This work used 336 samples, which were analyzed by means of MATLAB, and lead to 75.8% accuracy.
Osman et al. [27] developed a unified method of the K-means clustering and SVM algorithms to classify diabetes data. The authors also introduced an unsupervised learning approach based on K-means clustering, and diagnose diabetes using the supervised SVM classifier. The suggested approach considered the medical data collected from pancreas cell and laboratory test results (i.e., glucose level in urine and blood). The clustering is employed to gather all similar instances in feature data, which improves and raises the likelihood and accuracy of diagnosis prediction. The clustering output will then be applied as input to the SVM classifier. Kandhasamy et al. employed Decision Random Forest (RF), SVM, and KNN Classifier for classifying diabetes. The performance of the proposed system was evaluated by a confusion matrix, specificity, and sensitivity. Zou et al. [28] introduced a diabetes prediction model using machine learning algorithms. The authors used a random forest, decision tree, and neural network for diabetes prediction. Random forest and decision tree are implemented using the Weka tool, whereas the neural network is implemented by MATLAB.
Kumar et al. [29] developed SVM-based technique to classify the most discriminatory gene target for diabetes mellitus. Barkana et al. [30] carried out analysis is related to the performance of descriptive statistical features to specify retinal vessel segmentation due to diabetes mellitus problems known as diabetic retinopathy. This study was assessed using ANN, SVM, and Fuzzy Logic classifiers. Several research studies are carried out with different machine learning techniques for early prediction and classification of diabetes mellitus but still with a lack of accuracy. In the chorus, mining the diabetes data is one of the crucial problems. To resolve this issue, this research develops a new hybrid online model using APCA and ISVM for the early detection of diabetes disease with high accuracy.
Focusing on the classification and prediction of diabetes diseases, HOMED exploits the outcomes of clinical laboratory assessments as input, extracts a reduced dimensional feature subset, and delivers diagnosis of diabetes. At first, the input data are pre-processed for eliminating the irrelevant and unwanted data and for missing value imputation. Then, the most effective and best features are extracted by the proposed APCA and they are utilized for the further classification process. From the extracted optimal features, diabetes mellitus can be classified and predicted by the ISVM algorithm. As the health records are continuously gathered from the new observations, it is useful to incrementally update the earlier model of classification by considering only new input in order to decrease the time complexity in the classification process. Hence, we propose a model to support incremental updates to re-learn the data which can be more effective in terms of space complexity. Fig. 1 depicts the overall structure of the proposed HOMED system.
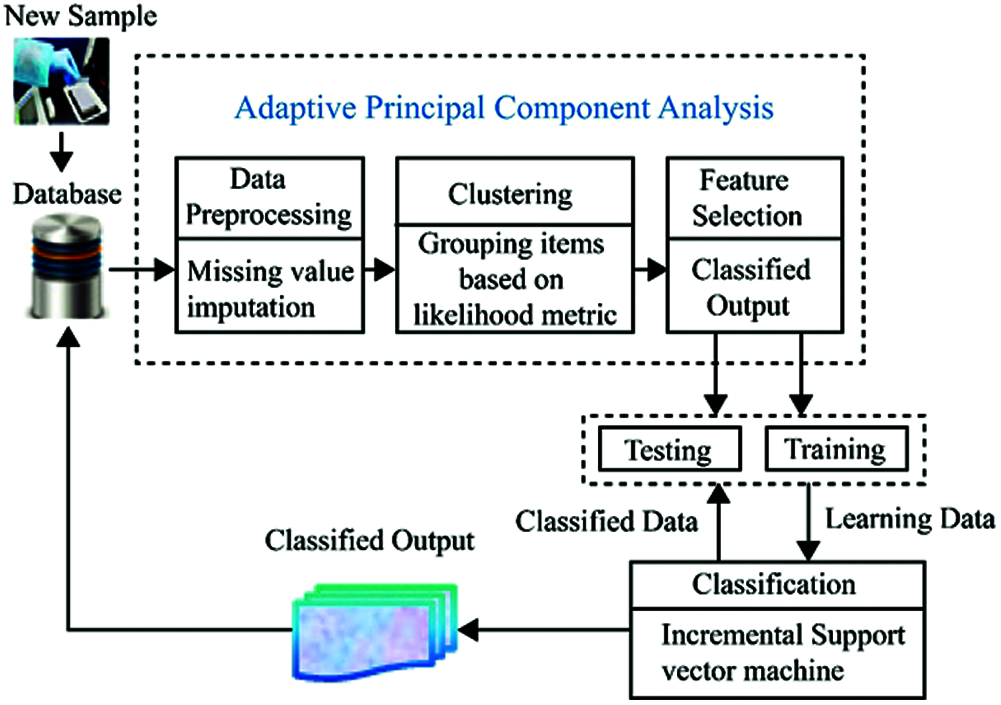
Figure 1: System architecture of HOMED
3.1 Adaptive Principal Component Analysis
The proposed APCA technique is implemented to perform missing data imputation, clustering, and dimensionality reduction. APCA exploits a weighted adaptive data imputation technique for missing value imputation. Also, it adopts an EM algorithm to group data points into appropriate clusters. The key notion is to decrease the number of data dimensions while maintaining as much as possible the variations in the original dataset.
In this work, we propose a weighted adaptive input imputation technique for the missing value. This technique can be carried out for each class of the designated data for the training process. Here, we construct a small size weighted vector as M
Vector and current object x is expressed as given in Eq. (1).
where
and
The calculated values are imputed as the missing data in the same dimensions and the ultimate pre-processed data can be used for further process.
The clustering process groups the data with related characteristics into the diabetes group. This task also aids to predict diabetes albeit the data is unsupervised or the class labels are not present. Therefore, it improves the consistency of classifier performance. The proposed APCA employs EM technique for clustering owing to its effective iterative nature in calculating the maximum probability. Since it is difficult to exploit the log-likelihood directly, EM algorithm maximizes the expectation of the entire log-likelihood as an alternative. The entire data in EM algorithm are designated as (x, z), where z is the missing value designating the mixture component origin label of each data and is expressed as Eq. (4)
where
where
EM algorithm begins with the initial parameter and then estimates the expectation (E step) and the maximization (M step) iteratively:
• E step: In this step, the expected value of the entire log-likelihood function is considered. The calculation is related to the conditional distribution of z given x under the current estimation of the parameters
That is, compute the posterior likelihoods
• M step: In this step, the parameter
In general, principal component analysis is a statistical method for multivariate analysis and is employed as a feature extraction method in data compression to preserve the vital information and is easy to visualize [31]. The proposed APCA technique finds patterns in data and signifies the data in a way that highlights resemblances and dissimilarities. The key concept is to decrease the data dimensions while retaining as much as possible the variations in the original dataset [32]. APCA has four objectives regarding feature reduction.
• To mine the maximum information from the data.
• To reduce the dimensionality of the data by only preserving the most characterizing information.
• To simplify the data description.
• To provide the structure analysis of the observations.
The analysis provides conclusions about the used variables and their relationships. Feature extraction is carried out by transforming the data into a new set of variables which is known as principal components (PCs). The PCs are uncorrelated and organized in such a way that the first few PCs preserve most of the variations of the entire dataset [33]. The first principal component denotes the dimension in which the data have the maximum variation (variance) and the second PC denotes the dimension in which it has the second-largest variation (variance). If the data have linear relations and are correlated, as data often are in clinical records, APCA will achieve a compression as well as preserves a high amount of the information in the initial dataset. The defined solution hoards compressed data, which is derived by applying ideas from statistics to enable an analysis while keeping its important features. In this work, we implement an algorithm for APCA developed by Hall et al. that appraises eigenvalues and eigenvectors incrementally [34].
3.2 Incremental Support Vector Machine Classification
SVM is a maximum-margin classification method that has found several popular applications in various scientific meadows including engineering [35], information retrieval, disease diagnoses business and finance [36], etc. A central and critical idea in the SVM design is that it can deliver a good generalization irrespective of the distribution of training data by exploiting the principle of structural risk minimization. This idea offers a trade-off between the quality of a suitable training sample (generalization-empirical error) and the complexity of the classification method (accuracy in the training set). Hence, the SVMs belong to a class of algorithms which are called large-margin classification. The size of the gap is decided upon by the training data which are between the margins [37]. These data are the known as support vectors. Traditional SVMs approach has been initially established as offline classifiers that are trained with predefined samples before they can be employed for classification problems. Cauwenberghs et al. [38] developed ISVM by evaluating the variations of the Karush–Kuhn–Tucker (KKT) conditions for incremental learning when a new data was appended to the previous dataset.
Employing a partition of the dataset, ISVM trains an SVM which reserves only the support vectors at every phase of training and generates the training dataset for the next phase with these support vectors. Therefore, the central idea of ISVM is to keep the KKT conditions on all available training samples while adding a new sample. Suppose the present working set is X and the new set is I. First, X is clustered by APCA; therefore, X is grouped to
3.3 Dataset for the Experiments
For experimentation, we have used an Intel Core i5 processor with Windows 10 operating system. All the algorithms are simulated using MATLAB R2009b. The dataset for the experimentation is obtained from the National Institute of Diabetes and Digestive and Kidney Diseases [39]. This dataset consists of 768 clinical records of Pima Indian heritage, a population living near Phoenix, Arizona, USA. There are eight features related to this dataset (i.e., plasma glucose concentration, 2-h serum insulin, the number of times pregnant, diastolic blood pressure, function of diabetes nutrition, triceps skin fold thickness, body mass index (BMI), and age). Tab. 1 shows the statistical report of each instance in this dataset. The range of binary variables is limited to ‘0’ or ‘1’. The target variable ‘1’ represents a positive result for diabetes disease (i.e., diabetic), ‘0’ is a negative result (i.e., non-diabetic). After preprocessing of dataset, there are 392 existing cases with no missing values.

The range of binary variables is limited to ‘0’ or ‘1’. The target variable ‘1’ denotes a positive result for diabetes disease (i.e., diabetic), ‘0’ is a negative result (i.e., non diabetic). The number of cases in class ‘1’ is 268, and the number of cases in class ‘0’ is 500.
The experimental results of the proposed method prompted on Pima Indian datasets are described in this section. The efficiency and accuracy of any predictive and diagnostic model are of vital significance and should be confirmed before such a model is used for implementation. We compare HOMED with other five existing classification methods viz. support vector machine [39], Random forest Naïve Bayesian [40], decision tree [41] and K-nearest neighbor [42]. The performance assessment of the diabetes classification methods is carried out using several performance metrics including accuracy, precision, specificity, sensitivity, positive predictive value, and negative predictive value.
• Accuracy: Accuracy is defined as a rate of correct classification. It is the ratio of the number of true classified samples (sum of the true positive and true negative) against the total number of samples. It can be expressed as:
• Sensitivity: Sensitivity is the proportion of the number of correctly classified positive samples (TP) to the total number of positive samples (TP + FN):
• Specificity: It is the ratio of the number of true negative samples (TN) to the total number of positive samples (TP + FN):
• Precision: Precision is the ratio of the number of true positives (TP) samples predicted as class 1 to the total number of samples (TP + FP) predicted as class 1:
Tab. 2 shows the results of the classification technique. The results show that the KNN classifier can predict 63.04% properly while Naive Bayesian can predict 67.89% properly. The decision tree classifier performed 73.18%, random Forest 75.39%, and support vector machine 77.73% respectively.
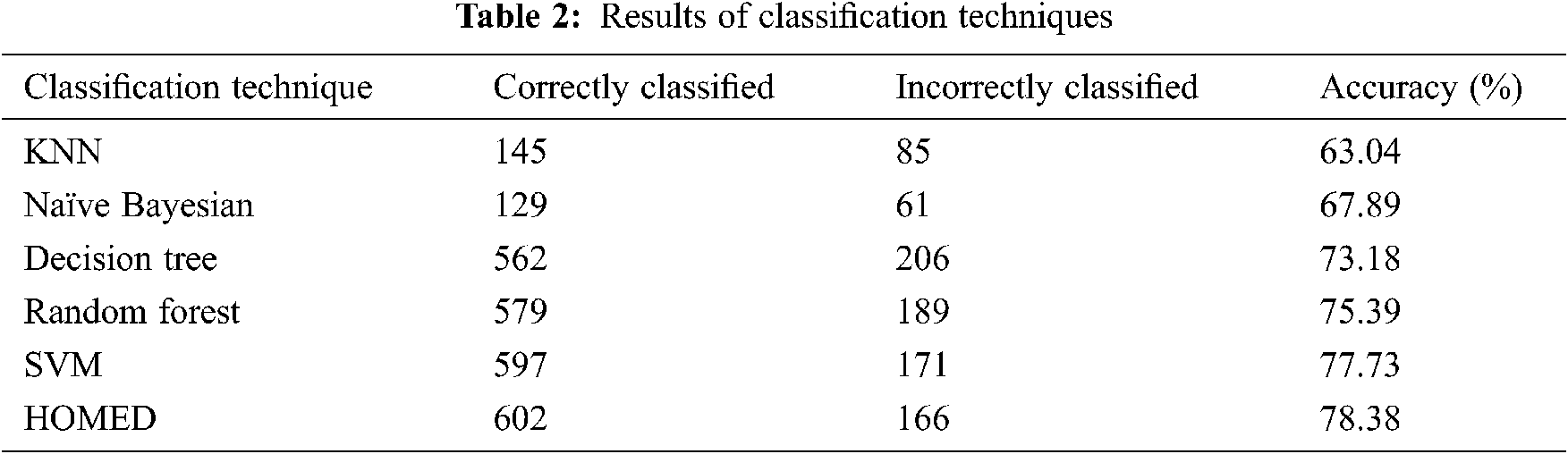
Furthermore, the proposed HOMED classifier proved to be the most accurate classifier for the accuracy of 78.38% as shown in Fig. 2.
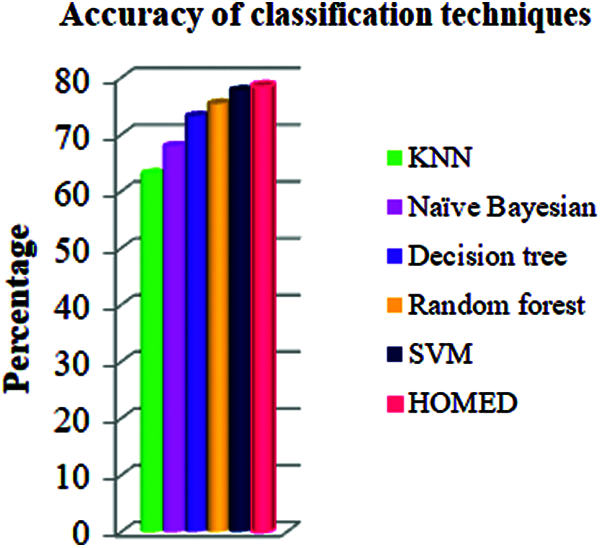
Figure 2: Accuracy of different classifiers
The performance of the proposed technique is compared with other methods in terms of different performance metrics as given in Tab. 3. From the results shown in this table, our HOMED proves to have a better precision (81.2%) in relation to the other classification systems. Compared to KNN (74.8%), Naïve Bayesian (77.0%), Decision tree (79.7%), Random forest (7.91%), and SVM (78.1%), our classification, clustering, and missing value imputation techniques aid to enhance the precision of the classifier [43]. HOMED achieves 98.71% specificity, 93.20% sensitivity, 79.55% negative predicted value, and 89.56% positive predicted value as shown in Tab. 3.

Our proposed HOMED proves to have a better specificity, sensitivity, positive predictive value, and negative predictive value compared to KNN, Naïve Bayesian, Decision tree, Random forest, and SVM. Our classification, clustering, and missing value imputation techniques aid to enhance the performance measures of the HOMED classifier. Fig. 3 demonstrates the efficiency of HOMED for predicting diabetes disease.
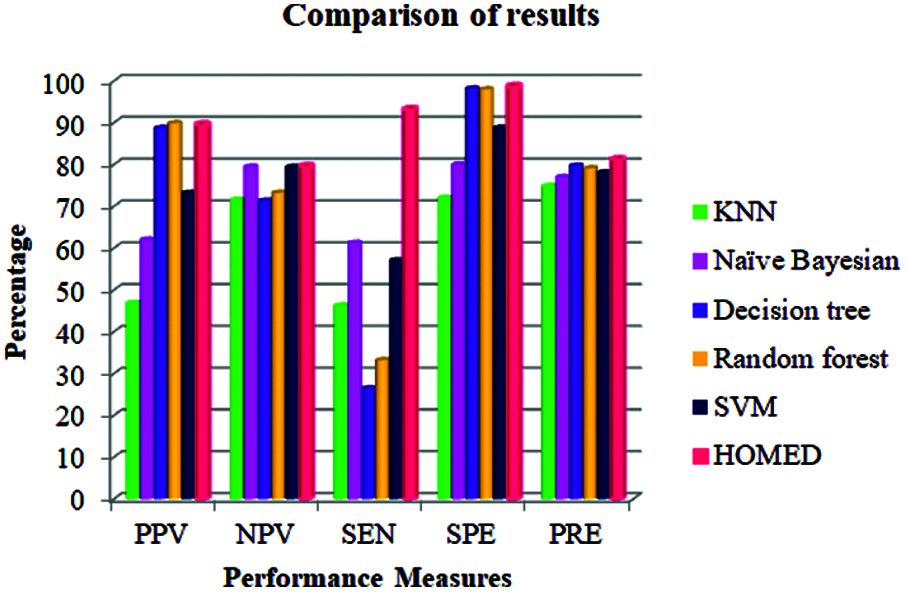
Figure 3: Performance measures of different classifiers
Diabetes is one of the heterogeneous groups of chronic endocrine sickness where people suffer from high sugar (glucose) in the blood. In order to support the lives of the people, we are trying to predict and avert the complications of diabetes at the early stage using predictive analysis by enhancing the performance of the diabetes diagnosis system. Our proposed work also carries out the feature extraction in the dataset and chooses the optimum features according to the correlation values. The major objective of the proposed work is to predict and classify diabetes mellitus by implementing a hybrid online model for the early detection of diabetes disease using machine learning algorithms. Our proposed online (incremental) diabetes diagnosis system exploits an APCA technique for missing value imputation, data clustering, feature selection, and an enhanced incremental support vector machine for classification. The efficiency of HOMED is estimated on different performance metrics such as accuracy, precision, specificity, sensitivity, positive predictive value, and negative predictive value. Experimental results on Pima Indian diabetes dataset reveal that HOMED considerably increases the classification accuracy and decreases computational complexity with respect to the offline models. The proposed system can assist healthcare professionals as a decision support system.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. B. A. Hamburg and G. E. Inoff, “Relationships between behavioral factors and diabetic control in children and adolescents: A camp study,” Psychosomatic Medicine, vol. 44, no. 4, pp. 321–339, 1982. [Google Scholar]
2. D. R. Whiting, L. Guariguata, C. weil and J. Shaw, “IDF diabetes atlas: Global estimates of the prevalence of diabetes for 2011 and 2030,” Diabetes Research and Clinical Practice, vol. 94, no. 3, pp. 311–321, 2011. [Google Scholar]
3. K. Kaul, J. M. Tarr, S. I. Ahmad, E. M. Kohner, R. Chibber et al., “Introduction to diabetes mellitus,” Advances in Experimental Medicine and Biology: Diabetes, vol. 771, no. 1, pp. 1–11, 2013. [Google Scholar]
4. R. B. Lukmanto and E. Irwansyah, “The early detection of diabetes mellitus (DM) using fuzzy hierarchical model,” Procedia Computer Science, vol. 59, no. 1, pp. 312–319, 2015. [Google Scholar]
5. K. Ioannis, T. Olga, S. Athanasios, M. Nicos et al., “Machine learning and data mining methods in diabetes research,” Computational Structural Biotechnology Journal, vol. 15, no. 1, pp. 104–116, 2017. [Google Scholar]
6. J. P. Kandhasamy and S. Balamurali, “Performance analysis of classifier models to predict diabetes mellitus,” Procedia Computer Science, vol. 47, no. 1, pp. 45–51, 2015. [Google Scholar]
7. C. A. Manly and R. S. Wells, “Reporting the use of multiple imputations for missing data in higher education research,” Research in Higher Education, vol. 56, no. 1, pp. 397–409, 2015. [Google Scholar]
8. K. L. Masconi, T. E. Matsha, R. T. Erasmus and A. P. Kengne, “Effects of different missing data imputation techniques on the performance of undiagnosed diabetes risk prediction models in a mixed-ancestry population of South Africa,” PLOS ONE, vol. 10, no. 9, pp. 1–12, 2015. [Google Scholar]
9. H. Hegde, N. Shimpi, I. Glurich and A. Acharya, “Tobacco use status from clinical notes using natural language processing and rule based algorithm,” Technology and Health Care, vol. 26, no. 3, pp. 1–12, 2018. [Google Scholar]
10. C. D. Newgard and R. J. Lewis, “Missing data,” JAMA Guide to Statistics and Methods, vol. 314, no. 9, pp. 940–941, 2015. [Google Scholar]
11. P. Li, E. A. Stuart and D. B. Allison, “Multiple imputation,” JAMA Guide to Statistics and Methods, vol. 314, no. 18, pp. 1966–1967, 2015. [Google Scholar]
12. I. Eekhout, H. C. W. de Vet, J. W. R. Twist, J. P. Brand, M. R. de Boer et al., “Missing data in a multi-item instrument were best handled by multiple imputation at the item score level,” Journal of Clinical Epidemiology, vol. 67, no. 3, pp. 335–342, 2014. [Google Scholar]
13. J. A. Sanz, M. Galar, A. Jurio, A. Brugos, M. Pagola et al., “Medical diagnosis of cardiovascular diseases using an interval valued,” Applied Soft Computing, vol. 20, no. 2, pp. 103–111, 2014. [Google Scholar]
14. T. Nguyen, A. Khosravi, D. Creighton and S. Nahavandi, “Classification of healthcare data using genetic fuzzy logic system and wavelets,” Expert Systems with Applications, vol. 42, no. 4, pp. 2184–2197, 2015. [Google Scholar]
15. K. Polat, “Classification of Parkinson’s disease using feature weighting method on the basis of fuzzy C-means clustering,” International Journal of Systems Science, vol. 43, no. 4, pp. 597–609, 2012. [Google Scholar]
16. C. H. Chen, “A hybrid intelligent model of analyzing clinical breast cancer data using clustering techniques with feature selection,” Application Soft Computing, vol. 20, no. 3, pp. 4–14, 2014. [Google Scholar]
17. M. Zhu and J. Song, “An embedded backward feature selection method for MCLP classification algorithm,” Procedia Computer Science, vol. 17, no. 4, pp. 1047–1054, 2013. [Google Scholar]
18. S. Seyed, G. Mohammad and S. Kamran, “Combination of feature selection and optimized fuzzy apriori rules: The case of credit scoring,” The International Arab Journal of Information Technology, vol. 12, no. 2, pp. 138–145, 2015. [Google Scholar]
19. J. Han, M. Kamber and J. Pei, Data Mining: Concepts and Techniques (The MORGAN Kaufmann Series in Data Management Systems). Burlington, MA, USA: Science Direct, 2000. [Google Scholar]
20. M. Rahman and T. Habib, “A preprocessed counter propagation neural network classifier for automated textile defect classification,” Journal of Industrial and Intelligent Information, vol. 4, no. 3, pp. 209–217, 2016. [Google Scholar]
21. N. C. Long, P. Meesad and H. Unger, “A highly accurate firefly based algorithm for heart disease prediction,” Expert System Application, vol. 42, no. 2, pp. 8221–8231, 2015. [Google Scholar]
22. J. F. G. Molina, L. Zheng and M. Sertdemir, “Incremental learning with SVM for multimodal classification of prostatic adenocarcinoma,” PLOS ONE, vol. 9, no. 4, pp. e93600, 2014. [Google Scholar]
23. W. Yu, T. Liu and Rivaled, “Application of support vector machine modeling for prediction of common diseases: The case of diabetes and pre-diabetes,” BMC Medical Informatics and Decision Making, vol. 10, no. 1, pp. 1–16, 2010. [Google Scholar]
24. O. Erkaymaz and M. Ozer, “Impact of small-world network topology on the conventional artificial neural network for the diagnosis of diabetes,” Chaos Solution Fractals, vol. 83, no. 1, pp. 178–185, 2016. [Google Scholar]
25. C. Wang, L. Li, L. Wang, Z. Ping, M. T. Flory et al., “Evaluating the risk of type 2 diabetes mellitus using artificial neural network: An effective classification approach,” Diabetes Research and Clinical Practice, vol. 100, no. 1, pp. 111–118, 2013. [Google Scholar]
26. K. V. Varma, A. A. Rao, T. S. M. Lakshmi and P. N. Rao, “A computational intelligence approach for a better diagnosis of diabetic patients,” Computers & Electrical Engineering, vol. 40, no. 5, pp. 1758–1765, 2014. [Google Scholar]
27. A. H. Osman and H. M. Aljahdali, “Diabetes disease diagnosis method based on feature extraction using K-SVM,” Int. J. Adv. Computer. Science Application, vol. 8, no. 1, pp. 236–244, 2017. [Google Scholar]
28. Q. Zou, K. Qu, Y. Luo, D. Yin, Y. Ju et al., “Predicting diabetes mellitus with machine learning techniques,” Frontiers in Genetics, vol. 9, no. 3, pp. 515, 2018. [Google Scholar]
29. A. Kumar, D. J. S. Sharmila and S. Singh, “SVMRFE based approach for prediction of most discriminatory gene target for type II diabetes,” Genomics Data, vol. 12, no. 5, pp. 28–37, 2017. [Google Scholar]
30. B. D. Barkana, I. Saricicek and B. Yildirim, “Performance analysis of descriptive statistical features in retinal vessel segmentation via fuzzy logic, ANN, SVM, and classifier fusion,” Knowledge-Based Systems, vol. 118, no. 1, pp. 165–176, 2017. [Google Scholar]
31. B. C. Moore, “Principal component analysis in linear systems: Controllability, observability, and model reduction,” IEEE T Automatic Control, vol. 26, no. 1, pp. 17–32, 1981. [Google Scholar]
32. M. Nilashi, M. D.Esfahani and M. Z.Roudbarak, “A multi-criteria collaborative filtering recommender system using clustering and regression techniques,” Journal of Soft Computing Decision Support System, vol. 3, no. 5, pp. 24–30, 2016. [Google Scholar]
33. M. Nilashi, D. Jannach, O. Ibrahim and N. Ithnin, “Clustering and regression-based multi-criteria collaborative filtering with incremental updates,” Information Sciences, vol. 293, no. 6, pp. 235–250, 2015. [Google Scholar]
34. P. M. Hall, A. D. Marshall and R. R. Martin, “Incremental eigen analysis for classification,” BMVC, vol. 98, no. 3, pp. 286–295, 1998. [Google Scholar]
35. M. Farahm, M. I. Desa and M. Nilashi, “A comparative study of CCR-(e-SVR) and CCR-(e-SVR) models for efficiency prediction of large decision-making units,” Journal of Soft Computing Decision Support System, vol. 2, no. 1, pp. 8–17, 2015. [Google Scholar]
36. N. C. Long, P. Meesad and H. Unger, “A highly accurate firefly based algorithm for heart disease prediction,” Expert System Application, vol. 42, no. 21, pp. 8221–8231, 2015. [Google Scholar]
37. W. W. Wu, “Beyond business failure prediction,” Expert System Application, vol. 37, no. 3, pp. 2371–2376, 2010. [Google Scholar]
38. G. Cauwenberghs and T. Poggio, “Incremental and decremented support vector machine learning,” Advances in Neural Information Processing System, vol. 55, no. 4, pp. 409–415, 2001. [Google Scholar]
39. N. H. Barakat, “Intelligible support vector machines for diagnosis of diabetes mellitus,” IEEE Transactions on Information Technology in Biomedicine, vol. 14, no. 4, pp. 1114–1120, 2010. [Google Scholar]
40. V. Wan and W. Campbell, “Support vector machines for speaker verification and identification,” Proc. of the 2000. IEEE Signal Processing Society Workshop, Sydney, NSW, Australia, vol. 2, no. 2, pp. 221–235, 2000. [Google Scholar]
41. K. Y. Yeung, R. E. Bumgarner and A. E. Raftery, “Bayesian model averaging: Development of an improved multi-class, gene selection and classification tool for microarray data,” Bioinformatics, vol. 21, no. 4, pp. 2394–2402, 2005. [Google Scholar]
42. J. R. Quinlan and R. L. Rivest, “Inferring decision trees using the minimum description length principle,” Information Computation, vol. 80, no. 3, pp. 227–248, 1989. [Google Scholar]
43. M. Maniruzzaman, N. Kumar, M. M. Abedin, M. S. Islam, H. S. Surietal et al., “Comparative approaches for classification of diabetes mellitus data: Machine learning paradigm,” Computer Methods Programs. Biomedicine, vol. 152, no. 1, pp. 23–34, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |