DOI:10.32604/iasc.2022.020006

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.020006 |  |
| Article |
Lyapunov-Redesign and Sliding Mode Controller for Microprocessor Based Transfemoral Prosthesis
1Advanced Robotics & Automation Lab, Department of Mechatronics Engineering, University of Engineering & Technology, Peshawar, 25100, Pakistan
2Physical Rehabilitation Training Coordinator, International Committee of the Red Cross, Sana'a, Yemen
*Corresponding Author: Izhar ul Haq. Email: izhar@uetpeshawar.edu.pk
Received: 05 May 2021; Accepted: 30 July 2021
Abstract: Transfemoral prostheses have evolved from mechanical devices to microprocessor-based, electronically controlled knee joints, allowing amputees to regain control of their limbs. For improved amputee experience at varying ambulation rates, these devices provide controlled damping throughout the swing and stance phases of the gait cycle. Commercially available microprocessor-based prosthetic knee (MPK) joints use linear controllers, heuristic-based methods, and finite state machine based algorithms to track the refence gait cycle. However, since the amputee experiences a variety of non-linearities during ambulation, such as uneven terrains, walking backwards and climbing stairs, therefore, traditional controllers produces error, abnormal movements, unstable control system and require manual-tuning. As a result, novel controllers capable of replicating and tracking reference gait cycles for a range of reference signals are needed to reduce the burden on amputees and improve the rehabilitation process. Therefore, the current study proposes two non-linear control techniques, the Lyapunov-redesign controller and the sliding mode controller for real-time tracking of various signals, such as walking on level ground at a normal speed and ambulation on uneven terrains. State-space model of MPK was developed along with the mathematical modelling of non-linear controllers. Simulations and results are presented using MATLAB to verify the ability of proposed non-linear controllers for constantly and dynamically tracking and maintaining desired motion dynamics. Furthermore, for selected reference signals, a linear controller was applied to the same mathematical model of MPK. During tracking of reference angel in case of general gait cycle, an accuracy of 99.95% and 99.96% was achieved for sliding mode controller and Lyapunov-redesign controller respectively. Whereas, for the same case, linear controller had an accuracy of 95.5% only. Therefore, it can be concluded that the performance of non-linear controllers was better than their linear counterparts while tracking various reference signals for microprocessor based prosthetic knee.
Keywords: Active prosthesis; non-linear controller; sliding mode controller; lyapunov-redesign controller; PID; gait cycle; microprocessor based prosthetic knee
Microprocessor-based prosthetic knee (MPK) joints provide relief to patients suffering from traumatic effects of amputation. MPK provides better and more promising results than mechanical counterparts, such as enhanced balance, less emphasis on walking mechanics, and less energy input from amputees in controlling these devices [1,2].
With the rapid advancement of above-knee prosthesis, it is necessary to provide a cost-effective solution to reduce the high cost of MPKs [3,4]. Various control strategies, such as linear quadratic regulator (LQR) [5], PID and fuzzy logic control [6], have been endorsed in the literature for MPK joints spanning from C-leg [7] to rheo-knee [8], with each displaying some viable outcomes and a few limitations [3]. All commercial MPKs therefore employ a finite state machine-based approach to control MPKs, and state-of-the-art machine techniques. While these techniques increase the cognitive burden of the amputee according to the literature, they cause unnatural movements [9]. As a result, novel controllers capable of robustly replicating and tracking reference gait cycles are needed to reduce the burden of amputees, improve the rehabilitation process, and give them confidence.
Alzaydi et al. [6] developed a fuzzy-based walking controller to track the behavior of healthy limbs during normal walking. Herr et al. [10] developed MPK based on magnetorheological damper (MRD) and designed an open-loop controller utilizing a finite state machine based technique to detect various phases of the gait cycle for controlling the resistance of the knee joint. The authors in [11] developed MRD based prosthetic knee and proposed a combination of computed control law and PD control law to track the angle of the knee joint in real time. In [12], the authors proposed a running controller for the actively powered prosthesis to enable amputees to run with a bio-mechanically appropriate gait. Lawson et al. [13] proposed a piece-wise controller for detecting various phases of the gait cycle to control the torque and damping of the knee joint. Park et al. [14] developed a knee prosthesis that can operate in active or semi-active modes controlled through polynomial prediction function. Jung et al. [15] proposed a semi-active type MRD based prosthetic knee joint controlled through a linear current controller. The authors in [16] discussed that for a continuous phase controller manual tuning is cumbersome, therefore, extremum seeking controller (ESC) capable of simultaneously tuning the feedback control gains of a powered knee prosthesis was developed. Various experiments were performed to verify the effectiveness of the proposed ESC across different walking speeds. Chang et al. [17] developed a data-driven model to track lower limb cadence trajectory and estimate the uncertainties by utilizing past input-output data. In [18] a model-free adaptive control method to estimate the angel of knee joint for applications such as exoskeleton and MPK was developed and simulated in MATLAB. The results indicated that the controller has an acceptable accuracy while tracking the trajectory of the knee joint. The authors in [19] developed a model-free robust adaptive controller capable of handling known non-linearities in robotic applications. Simulations suggested that tracking performances of the proposed autotuned adaptive gain is better than manually tuned constant gains.
The efficacy of linear controllers and data-driven models has been successfully demonstrated in the literature. However, because the amputee encounters various non-linearities during ambulation, such as irregular terrains and changes in loading conditions, linear controllers may result in error and unstable control systems. This is due to the fact that linear controllers lack formal guarantees (when applied to non-linear systems) and require hand-tuning [20,21].
1.4 Contribution and Organization
The main objective of this study was to develop robust non-linear controllers for MPKs to address the limitations of linear controllers. The proposed non-linear controller will not only aid amputees in level-ground walking but will also allow for self-selected ambulation on uneven terrains. Furthermore, the proposed controllers resulted in adapting amputee's walking pattern and gait cycle according to ideal gait cycle. The chosen MPK's physical model included intrinsic sensing capabilities for detecting the actual phase of the gait cycle [22]. A state-space model of MPK was developed, and non-linear controllers were used to track the reference gait cycle. MATLAB simulations and results are presented to validate the ability of proposed nonlinear controllers to track and maintain desired motion dynamics constantly. Furthermore, the results are compared with the linear controller for selected reference signals. Lyapunov-redesign controller achieved an accuracy of 99.96% and 98.90% while tracking knee angle for a general gait cycle and partial gait cycle for uneven terrains, whereas, SMC had an accuracy of 99.95% and 98.70% while tracking the same reference signals. Contrarily, fine-tuned linear PID demonstrated an accuracy of 95.5% and 94% only, therefore, it can be concluded that non-linear controllers outperform linear PID while tracking reference signals for MPK.
The remainder of the article is organized as follow: Section 2 describes the state-space modelling of the system, which is followed by the design of nonlinear controllers in Section 3. Section 4 presents the findings and discussions, whereas Section 5 presents the conclusion and future considerations.
2 State-Space Model of the System
Schematic of MPK consisting of flexion/extension of knee joint is presented in Fig. 1. The angular displacement and angular velocity of knee joint are important control parameter in MPKs as tracking of gait cycle is dependent on these two variables. The state-space model for MPK presented in Fig. 1 is developed to apply and validate non-linear controller strategies. State-space representation is actually a mathematical model of a physical system as a set of input, output and state variables related by differential equations [23].
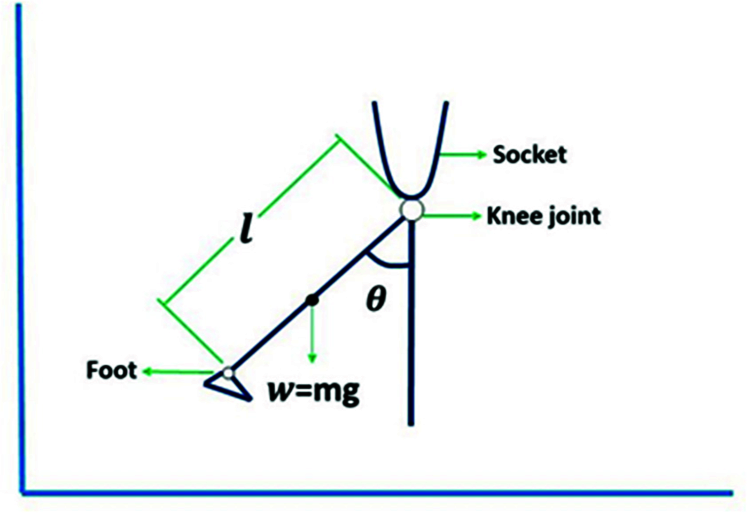
Figure 1: Schematic model of microprocessor-based prosthetic knee
The proposed control strategy shown in Fig. 2 consists of a non-linear controller that takes the angular position and angular velocity of the knee joint as input, followed by a single-link manipulator based MPK as a dynamic model whose angular position and velocity are to be tracked according to the reference gait cycle. To demonstrate the efficacy and robustness of the proposed non-linear controller to external disturbances, noise is also introduced as an input to the control mechanism.
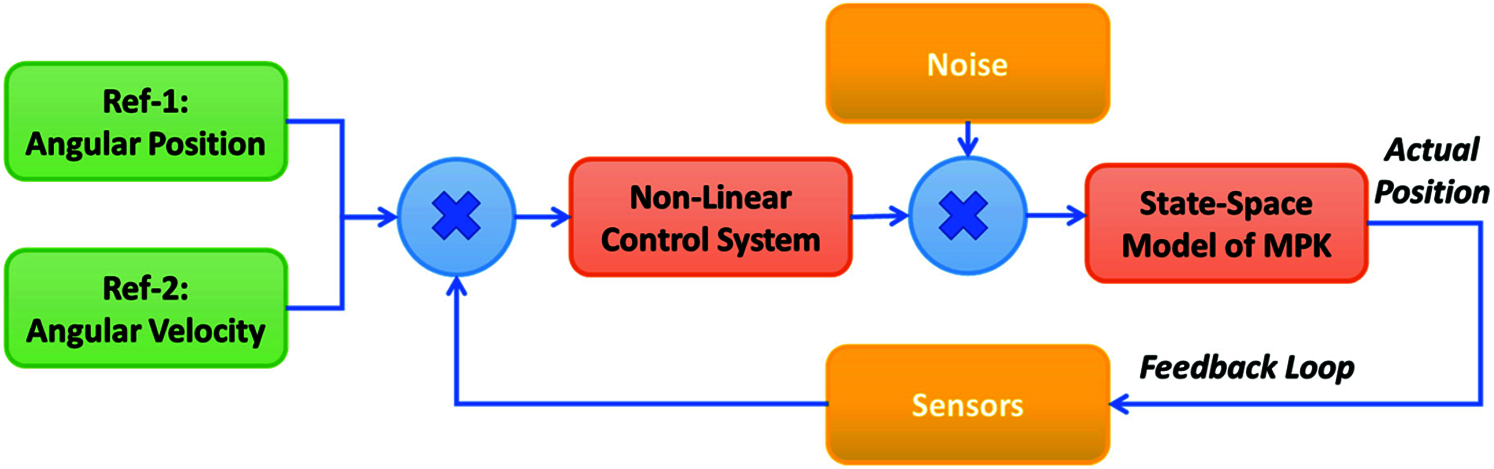
Figure 2: Control mechanism for microprocessor-based prosthetic knee
For developing a state-space model of the system, the following variables are assumed:
where θ and
The complete state-space model of the MPK after simplification can then be described as:
where g, m, l, b, u, I, and φ(t) are gravitational acceleration, mass of the joint, length from the knee joint to foot, damping constant, input torque of the actuator, inertia of knee joint and external disturbances respectively.
3 Design and Stability Analysis of Non-Linear Controllers
Based on the state-space model discussed in Eq. (7), two different non-linear controllers, namely Lyapunov-redesign and SMC, were designed and their stability analyses were performed to ensure that MPK performed as designed because if the system deviates from the desired behavior, it may lead to gait instability and dissatisfaction of the amputee. The development of the Lyapunov-redesign controller for MPK is discussed in the following section.
3.1 Design of Lyapunov-Redesign Controller
Lyapunov-redesign Control is based on the energy function, and the stability of a given non-linear system is determined by the time rate of change of the energy function. According to the Lyapunov stability criterion, if the rate of change of the energy function is zero or negative definite, the system is converging and stable [25].
From Eqs. (3) and (4), it could be written that
As, from Lyapunov-redesign control theory when the controller is stable, the error converges as discussed in [26] and can be formulated as:
where K1 is the controller gain, and its value must be positive to keep the controller stable. By substituting the values of
Now, by comparing Eq. (10) with (12)
By rearranging Eq. (13) and solving for u
where, u is the input torque (control input) that may be controlled with the help of Eq. (14), leading to track the concerned variable such as angular displacement and angular velocity to their desired reference signals.
Stability of Lyapunov-Redesign Controller
Even if the system is efficiently controlled, unstable Lyapunov-redesign control can result in unbounded system output that does not provide the desired ouputs. As a result, controller stability is as important as controller design [26]. The following steps can be used to test the Lyapunov-redesign controller's stability:
• Supposing a semi-positive definite energy function
• Computing time derivative of the energy function
• If the rate of change of energy function is negative or equal to zero, then the controller is stable, whereas if the rate of change of energy function is positive, then the system is deemed to be unstable [26].
To select an optimal candidate for the Lyapunov-redesign energy function in order to test the stability of the controller, a semi-positive definite energy function having mass (m) and length (l) of MPK as key parameters are assumed.
By taking time-derivative of Eq. (15), V1 can be simplified as:
Substituting Eq. (10) in (16) and simplification yields:
In Eq. (17), m, l and K1 are always positive with the added fact that the square of e2 also results in a positive value. Thus,
3.2 Design of Sliding Mode Controller
The Sliding Mode Controller (SMC) is a nonlinear control method that modifies the dynamics of a nonlinear system by applying a discontinuous control signal (or, more precisely, a set-valued control signal) that causes the system to slide along a cross-section (sliding surface) of the system's normal behavior [27]. SMC is well suited to nonlinear systems containing disturbances and uncertainties, such as MPK. SMC is a technique in which the control inputs are alternating between two limits [27]. The desired performance of closed-loop dynamics is expressed at s = 0, which happens through a proper design of a controller. Let us assume a sliding surface:
where a, s and e2 are the coefficient of the controller, sliding surface and error of angular velocity, respectively. By taking the time derivative of Eq. (18), it can be written as:
where
where as from the theory of SMC, it could be analyzed that when the system attains stability, the error converges and system slides on the supposed sliding surface. Thus from the theory of the SMC [27], the rate of change of sliding surface could also be formulated as:
where α and γ are the controller coefficients used to control the rate of convergence and chattering (disturbance) [27] and K2 is the controller gain which must be positive to ensure the controller is stable. Furthermore, sgn is the signum function used to ensure an ideal switching. By comparing Eq. (20) with Eq. (21), it could be written as:
By solving for u Eq. (21) yields:
Stability of Sliding Mode Controller
Similar to the Lyapunov redesign controller it is essential to exercise stability of SMC. Let us assume a semi-positive definite energy function that includes the sliding surface parameter:
By taking the time derivative of Eq. (24), it can be written as:
Substituting Eq. (21) in Eq. (25) yields:
By simplifying Eq. (26)
whereas |γ| = γ as γ > 0. Therefore, Eq. (27) can be simplified as
As K2 > 0, so Eq. (28) will result in a negative value which concludes that the developed SMC for MPK is stable.
Simulations in MATLAB have validated the developed Lyapunov-redesign and sliding mode controller is capable of successfully tracking various reference signals in MPK. Tab. 1 summarises key parameters of MPK such as the mass of knee joint (m) and length of joint (l) [28]. Results for a sinusoidal signal, normal walking gait cycle, and specific partial gait cycles have been plotted and compared with linear controller to acquire a realistic view of the developed controllers.

4.1 Sinusoidal Reference Signal
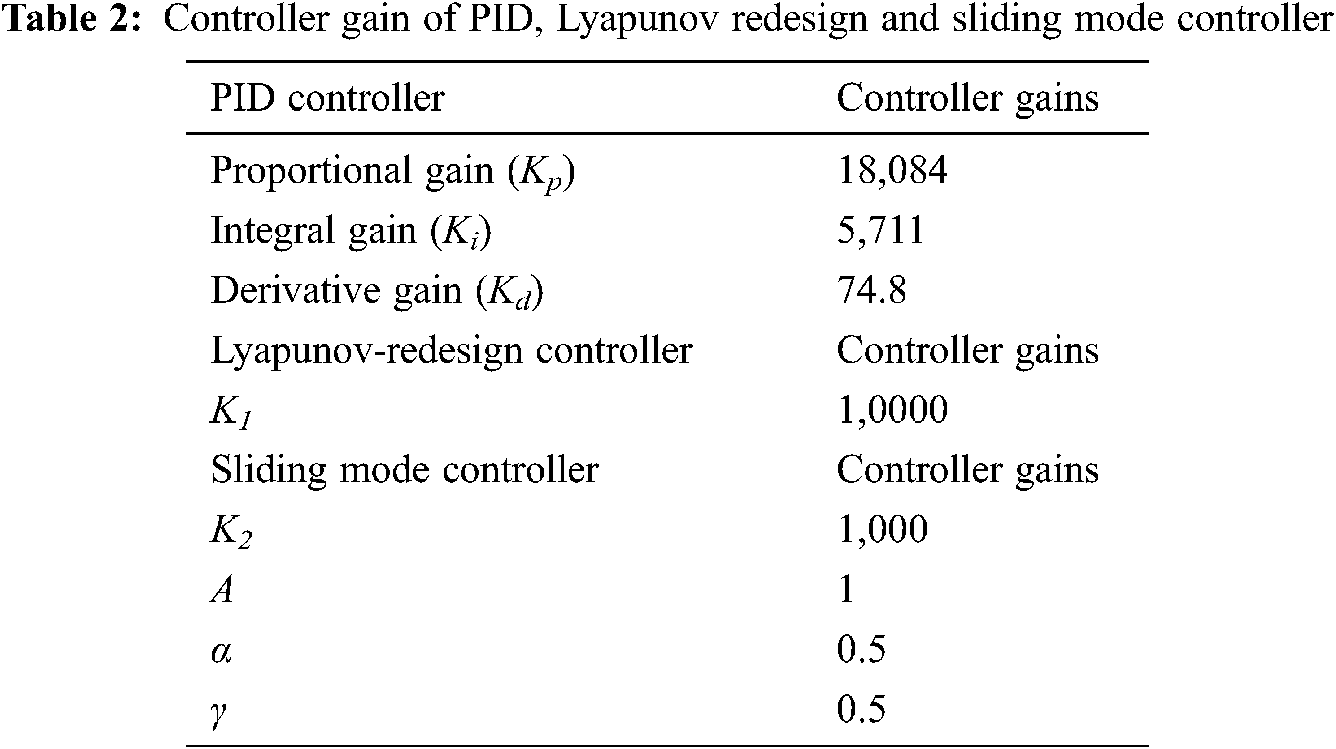
The reference signal to be tracked for an MPK varies frequently with time. Therefore, to test the adaptability and robustness of the proposed controllers, the authors have implemented them on a sinusoidal signal which modifies its behavior at every instant. The hit and trial approach was used to fine-tune the parameters of the linear controller (PID), Lyapunov-redesign, and SMC as described in Tab. 2 to follow the reference sinusoidal signals, and the obtained results are plotted in Fig. 3.

Figure 3: Tracking sinusoidal reference signal (a) Angular position (b) Angular velocity (c) Error plot of angular position (d) Error plot of angular velocity
From Fig. 3a, it may be observed that linear and the non-linear controllers produced comparable results while following angular position as fine-tuning of the controller parameters were performed. Similarly, Fig. 3b presents that the linear controller produced slightly poor results as compared to SMC and Lyapunov-redesign controller for an angular velocity reference signal due to the inherited system non-linearities. A comparison of three controllers in terms of error plot for angular position and angular velocity is presented in Figs. 3c and 3d respectively from where it can be analyzed that both non-linear controllers produced comparatively better results than PID controller.
The Lyapunov redesign and SMC were then implemented on the actual normal walking gait cycle, after their validation on the sinusoidal signal. The reference angular position of the knee during normal walking presented in Fig. 4 is adopted from [29], whereas, reference angular velocity can be obtained by taking the time derivative of reference angular position. The parameters tuned for individual controllers in the previous section were used, as in real-life it is not possible to recalibrate controller parameters for individual reference signals.

Figure 4: Tracking general gait cycle (a) Angular position (b) Torque (c) Error plot of angular position
From Fig. 4a, it can be concluded that both nonlinear controllers achieved steady state in a shorter time and produced comparable, while the linear controller had relatively poor results because of ripples and a long transitional period. Additionally, control input (torque) and error difference between the desired (reference) and actual outputs have also been plotted in Figs. 4b and 4c respectively. This helps to analyze that both nonlinear controllers produce comparatively better results than linear controller. Lyapunov-redesign controller tracked knee angel with an accuracy 99.96%, whereas, SMC had a comparable accuracy of 99.95%. However, linear controller was the least accurate with only 95.50% accuracy.
4.3 Partial Gait Cycles for Knee Extension/Flexion at Normal Walking Speed
This subsection validates non-linear controllers for the knee extension and flexion phase for a normal speed walking, whereby the reference signals for angular position and angular velocity has been adopted from [30,31]. In Figs. 5a–5c it can be analyzed that the linear controller produced poor results while tracking the referral signal, since it had significant steady-state error, undershoot and overshoot. SMC and Lyapunov redesign controllers were, by contrast, relatively fast in their stability and had no large ripples over the simulation cycle, making it more suitable both for partial and complete gait cycles. Furthermore, in Fig. 5d, error difference between reference and actual outputs is shown, indicating the comparatively better results for both non-linear controllers. While tracking angular position Lyapunov-redesign and sliding mode controller achieved an accuracy of 99.20% and 98.80% respectively, whereas, linear controller was only 92.20% accurate.

Figure 5: Tracking partial gait cycle for knee flexion/extension (a) Angular position (b) Angular velocity (c) Torque (d) Error plot of angular position
4.4 Partial Gait Cycle for Knee Extension/Flexion at Uneven Terrains
Lyapunov-redesign and SMC have been validated for both knee flexion and knee extension for uneven terrain. The reference angular position and velocity were obtained from [30,31], Fig. 6 shows and compares the results for uneven terrain. Nonlinear controllers gave good results over uneven terrains, as illustrated in Figs. 6a and 6b. When compared to both SMC and Lyapunov-redesign controllers, PID failed to precisely track the reference, resulting in a large steady-state error. The developed non-linear controllers reached steady-state values more quickly, whereas PID lagged at first exhibited wobbles and large ripples, proving PID is inappropriate for uneven terrains, as discussed in the literature [28,29]. In addition, in Figs. 6c and 6d the control input (torque) and the error difference between the reference and actual output have been shown for easy comparison between non-linear controllers and the PID controller. An accuracy of 98.90% was observed for Lyapunov-redesign controller, whereas, SMC was 98.70% accurate. However, PID only achieved 94% accuracy proving that it is inappropriate for non-linear systems.

Figure 6: Tracking partial gait cycle for knee flexion/extension for uneven terrains (a) Angular position (b) Angular velocity (c) Torque (d) Error plot of angular position
Due to advancements in the field of bio-mechatronics, lower-limb implants, particularly transfemoral prostheses, are quickly progressing. Microprocessor-based knee prostheses perform better and are more viable than mechanical knee prosthesis, which provide little assistance to amputees. Several control techniques have been reported in the literature, including finite-state controllers, optimal controllers, and PID controllers. However, there are certain key shortcomings that need to be addressed. This study presents non-linear controllers for a single-link manipulator based MPK, such as the Lyapunov-redesign controller and the Sliding Mode Controller, to address the limitations of linear controllers. The suggested non-linear control techniques have been validated for a variety of reference signals, including the general gait cycle, sinusoidal reference signal, and partial gait cycle for natural speed in both knee-flexion and extension phase. The results are plotted in MATLAB and compared to a linear PID controller, confirming that non-linear controllers outperform PID controls for all reference signals. Eventually, for microprocessor-based prosthetic knee joints, nonlinear controllers are the way of the future. In addition, the present study provides a platform for implementation of non-linear controllers through hardware-in-loop technique.
Funding Statement: This work was supported by Advanced Robotics & Automation Lab, National Center for Robotics & Automation.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Geeroms, L. Flynn, R. J. Fabian, B. Vanderborght and D. Lefeber, “Ankle-knee prosthesis with powered ankle and energy transfer for CYBERLEGs α-prototype,” in Rehabilitation Robotics, 13th Int. Conf., ICORR 2013, Seattle, WA, USA, pp. 1–6, 2019. [Google Scholar]
2. P. Theeven, B. Hemmen, F. Rings, G. Meys, P. Brink et al., “Functional added value of microprocessor–controlled prosthetic knee joints in daily life performance of medicare functional classification level–2 amputees,” Journal of Rehabilitation Medicine, vol. 43, no. 10, pp. 906–915, 2011. [Google Scholar]
3. R. Seymour, B. Engbretson, K. Kott, N. Ordway, G. Brooks et al., “Comparison between the C-leg® microprocessor-controlled prosthetic knee and non-microprocessor control prosthetic knees: A preliminary study of energy expenditure, obstacle course performance, and quality of life survey,” Prosthetics and Orthotics International, vol. 31, no. 1, pp. 51–61, 2007. [Google Scholar]
4. J. Thiele, C. Schöllig, M. Bellmann and M. Kraft, “Designs and performance of three new microprocessor-controlled knee joints,” Biomedical Engineering, vol. 64, no. 1, pp. 119–126, 2019. [Google Scholar]
5. S. R. Adarsh and S. Selvakumar, “Model identification and control of prosthetic leg,” in First Int. Conf. on Advances in Physical Sciences and Materials, Coimbatore, India, pp. 12109, 2020. [Google Scholar]
6. A. A. Alzaydi, A. Cheung, N. Joshi and S. Wong, “Active prosthetic knee fuzzy logic-pID motion control, sensors and test platform design,” International Journal of Scientific & Engineering Research, vol. 2, no. 12, pp. 1–7, 2011. [Google Scholar]
7. J. W. Michael and J. H. Bowker, In Atlas of Amputations and Limb Deficiencies: Surgical, Prosthetic, and Rehabilitation Principles, 3rd ed, vol. 86, Rosemont, IL, USA, American Academy of Orthopaedic Surgeons, 2004. [Google Scholar]
8. C. L. Semasinghe, J. L. Prasanna, H. M. Kandamby, R. K. Ranaweera, D. G. Madusanka et al., “Transradial prostheses: Current status and future directions,” in Manufacturing & Industrial Engineering Symposium, MIES 2016, Colombo, Sri Lanka, pp. 1–7, 2016. [Google Scholar]
9. R. Fluit, E. C. Prinsen, S. Wang and H. van der Kooij, “A comparison of control strategies in commercial and research knee prostheses,” IEEE Transactions on Biomedical Engineering, vol. 67, no. 1, pp. 277–290, 2019. [Google Scholar]
10. H. Herr and A. Wilkenfeld, “User-adaptive control of a magnetorheological prosthetic knee,” Industrial Robot, vol. 30, no. 1, pp. 42–55, 2003. [Google Scholar]
11. B. Aeyels, L. Peeraer, J. V. Sloten and G. J. V. D. Perre, “Development of an above-knee prosthesis equipped with a microcomputer-controlled knee joint: First test results,” Journal of Biomedical Engineering, vol. 14, no. 3, pp. 199 –202, 1992. [Google Scholar]
12. A. H. Shultz, B. E. Lawson and M. Goldfarb, “Running with a powered knee and ankle prosthesis,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 23, no. 3, pp. 403–412, 2014. [Google Scholar]
13. B. E. Lawson, J. Mitchell, D. Truex, A. Shultz, E. Ledoux et al., “A robotic leg prosthesis: Design, control, and implementation,” IEEE Robotics & Automation Magazine, vol. 21, no. 4, pp. 70–81, 2014. [Google Scholar]
14. J. Park, G. H. Yoon, J. W. Kang and S. B. Choi, “Design and control of a prosthetic leg for above-knee amputees operated in semi-active and active modes,” Smart Materials and Structures, vol. 25, no. 8, pp. 85009, 2016. [Google Scholar]
15. J. H. Kim and J. H. Oh, “Development of an above knee prosthesis using MR damper and leg simulator,” in IEEE Int. Conf. on Robotics and Automation, Seoul, South Korea, pp. 3686–3691, 2001. [Google Scholar]
16. S. Kumar, A. Mohammadi, D. Quintero, S. Rezazadeh, N. Gans et al., “Extremum seeking control for model-free auto-tuning of powered prosthetic legs,” IEEE Transactions on Control Systems Technology, vol. 28, no. 6, pp. 2120–2135, 2019. [Google Scholar]
17. C. H. Chang, V. H. Duenas and A. Sanyal, “Model free nonlinear control with finite-time estimation applied to closed-loop electrical stimulation induced cycling,” in American Control Conf. (ACC) 2020, Denver, CO, USA, pp. 5182–5187, 2020. [Google Scholar]
18. Y. Zhang, J. Wang, W. Li and J. Wang, “A model-free control method for estimating the joint angles of the knee exoskeleton,” Advances in Mechanical Engineering, vol. 10, no. 10, pp. 1–10, 2018. [Google Scholar]
19. M. Jin, J. Lee and N. G. Tsagarakis, “Model-free robust adaptive control of humanoid robots with flexible joints,” IEEE Transactions on Industrial Electronics, vol. 64, no. 2, pp. 1706–1715, 2016. [Google Scholar]
20. D. P. Atherton and S. Majhi, “Limitations of PID controllers,” in Proc. of the American Control Conf., San Diego, CA, USA, pp. 3843–3847, 1999. [Google Scholar]
21. H. Zhao, J. Horn, J. Reher, V. Paredes and A. D. Ames, “First steps toward translating robotic walking to prostheses: A nonlinear optimization based control approach,” Autonomous Robots, vol. 41, no. 3, pp. 725–742, 2017. [Google Scholar]
22. J. Martin, A. Pollock and J. Hettinger, “Microprocessor lower limb prosthetics: Review of current state of the art,” Journal of Prosthetics and Orthotics, vol. 22, no. 3, pp. 183–193, 2010. [Google Scholar]
23. C. Huemmer, R. Maas, C. Hofmann and W. Kellermann, “A Bayesian network approach to linear and nonlinear acoustic echo cancellation,” Journal on Advances in Signal Processing, vol. 1, pp. 1–11, 2015. [Google Scholar]
24. M. O. Ajayi, Modelling and control of actuated lower limb exoskeletons: A mathematical application using central pattern generators and nonlinear feedback control techniques, Ph.D. dissertation, Tshwane University of Technology, Pretoria, South Africa, 2015. [Google Scholar]
25. A. Hamza, I. Ahmad and M. Uneeb, “Fuzzy logic and lyapunon based non-linear controllers for HCV infection,” IET Systems Biology, vol. 15, no. 2, pp. 53–71, 2021. [Google Scholar]
26. S. Sastry, In Nonlinear Systems: Analysis, Stability, and Control, vol. 10, Springer Science & Business Media, New York, USA, 2013. [Google Scholar]
27. E. Hossain, R. Perez, S. Padmanaban, L. M. Popa, F. Blaabjerg et al., “Sliding mode controller and lyapunov redesign controller to improve microgrid stability: A comparative analysis with CPL power variation,” Energies, vol. 10, no. 12, pp. 1959, 2017. [Google Scholar]
28. E. J. Rouse, L. M. Mooney and H. M. Herr, “Clutchable series-elastic actuator: Implications for prosthetic knee design,” The International Journal of Robotics Research, vol. 33, no. 13, pp. 1611–1625, 2014. [Google Scholar]
29. B. J. West and N. Scafetta, “Nonlinear dynamical model of human gait,” Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, vol. 67, no. 5, pp. 51917, 2003. [Google Scholar]
30. G. Bovi, M. Rabuffetti, P. Mazzoleni and M. Ferrarin, “A multiple-task gait analysis approach: Kinematic, kinetic and EMG reference data for healthy young and adult subjects,” Gait & Posture, vol. 33, no. 1, pp. 6–13, 2011. [Google Scholar]
31. M. H. Schwartz, A. Rozumalski and J. P. Trost, “The effect of walking speed on the gait of typically developing children,” Journal of Biomechanics, vol. 41, no. 8, pp. 1639–1650, 2008. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |