DOI:10.32604/iasc.2022.016919

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.016919 |  |
| Article |
Improved Anomaly Detection in Surveillance Videos with Multiple Probabilistic Models Inference
1School of Computer and Electronic Information, Nanjing Normal University, Nanjing, 210023, China
2Department of Computer Science, University of Massachusetts Boston, Boston, 02125, USA
*Corresponding Author: Genlin Ji. Email: glji@njnu.edu.cn
Received: 15 January 2021; Accepted: 23 July 2021
Abstract: Anomaly detection in surveillance videos is an extremely challenging task due to the ambiguous definitions for abnormality. In a complex surveillance scenario, the kinds of abnormal events are numerous and might co-exist, including such as appearance and motion anomaly of objects, long-term abnormal activities, etc. Traditional video anomaly detection methods cannot detect all these kinds of abnormal events. Hence, we utilize multiple probabilistic models inference to detect as many different kinds of abnormal events as possible. To depict realistic events in a scene, the parameters of our methods are tailored to the characteristics of video sequences of practical surveillance scenarios. However, there is a lack of video anomaly detection methods suitable for real-time processing, and the trade-off between detection accuracy and computational complexity has not been given much attention. To reduce high computational complexity and shorten frame processing times, we employ a variable-sized cell structure and extract a compact feature set from a limited number of video volumes during the feature extraction stage. In conclusion, we propose a real-time video anomaly detection algorithm called MPI-VAD that combines the advantages of multiple probabilistic models inference. Experiment results on three publicly available datasets show that the proposed method attains competitive detection accuracies and superior frame processing speed.
Keywords: Video anomaly detection; probabilistic model; surveillance video; real-time processing
The detection of abnormal events in surveillance videos is a significant task because watching the videos frame by frame manually consumes lots of time. The availability of large volumes of surveillance videos gives rise to a great demand for processing. However, this could be extremely challenging due to the uniqueness and unbounded nature of abnormal events in the real world. Besides, as it is infeasible to enumerate all kinds of abnormal events, we are unable to find a sufficiently representative set of anomalies. Based on the characteristics of the labeled data in the training set, video anomaly detection can typically be classified into the following three categories: supervised [1] where both normal and abnormal samples are labeled, semi-supervised [2–6] where only normal samples are provided, and unsupervised [7,8] where no training data is given. We aim to tackle semi-supervised video anomaly detection when only normal samples are required in the training set. An intuitive approach is to model the normality distribution of training data, and any sample which does not adhere to the normality distribution is identified as abnormal.
Probabilistic models are used for statistical data analysis, e.g., path planning [9]. Probabilistic models are widely used for establishing normality distribution of training data, such as Markov random field [5], conditional random field [6], probabilistic event logic [10], and local statistical aggregates [11]. The problem formulation of video anomaly detection based on multiple probabilistic models inference is presented as follows: (1) In the model training stage, given the training data Xtrain = {x1, x2, …, xn} containing only normal video samples, the goal is to build a few probabilistic models
•
•
If
There are too many abnormal events in the real world, and we divide them into four fine-grained categories: appearance anomaly, global motion anomaly, local motion anomaly, and long-term abnormal activities. For example, skaters, cyclists, and disabled people moving with the help of a wheelchair are local motion anomalies on the sidewalk, and they have a similar appearance to a normal pedestrian. The probabilistic models only using appearance features in [2,10,11] cannot detect these local motion anomalies. Long-term abnormal activities like loitering can be detected by Markov models [2,4]. However, Markov models are not sensitive to the other three kinds of abnormal events. To sum up, the above video anomaly detection models have some limitations such as high missed and false detection rates. Inspired by this observation, we characterize all four kinds of abnormal events using both appearance and motion features to ensure detection accuracy. Specifically, we employ multiple probabilistic models to learn appearance and motion features in surveillance videos respectively, and then integrate multiple probabilistic models into an anomaly inference algorithm to infer all kinds of abnormal events as much as possible. The main contributions of this paper are as follows:
(1) We theoretically formulate video abnormal detection based on multiple probabilistic models inference as a statistical hypothesis testing problem.
(2) We propose a novel video anomaly detection algorithm based on multiple probabilistic models inference called MPI-VAD.
(3) To strike the trade-off between detection accuracy and computational complexity, we employ a variable-sized cell structure to help extract the appearance and motion feature from a limited number of video volumes.
The rest of the paper is organized as follows. Section 2 introduces the related work regarding two types of abnormal event detection methods - Accuracy First Methods and Speed First Methods. Section 3 presents our proposed MPI-VAD in detail. Section 4 describes the experiment settings and results from evaluation of MPI-VAD on three publicly available datasets: UMN, CUHK Avenue and USCD Pedestrian. Finally, Section 5 concludes our work and discusses possible improvements in the future work.
Over the past decade, despite important advances in improving video anomaly detection accuracy, there is a lack of methods designed for real-time processing that impairs its applicability in practical scenarios. Real-time video anomaly detection means that a frame processing time is shorter than the time of a new frame received. Taking a 30 FPS video sequence as an example, video anomaly detection could attain real-time processing performance when a frame processing time is less than 33.3 milliseconds. According to the trade-off between detection accuracy and computational complexity, existing video anomaly detection methods can be divided into two main categories: Accuracy First Methods, which focus on improving the detection accuracy no matter the required frame processing times, and Speed First Methods, which are primarily concerned about reducing frame processing times to satisfy practical applications for real-time processing.
Accuracy First Methods: They usually achieve higher detection accuracy at the expense of increased computational complexity and frame processing times. An important characteristic of these methods is to select sufficient video volumes to be processed, such as dense scanning [2], multi-scale scanning [12], and cell-based methods [13]. Roshtkhari et al. [2] generate millions of features by an overlapped multi-scale scanning techniques to enhance detection precision. Bertini et al. [12] compute a descriptor based on three-dimensional gradients from overlapped multi-scale video volumes. Zhu et al. [3] adopt histograms of optical flow (HOF) to detect anomalies in crowded scenes. Cong et al. [14] adopt multi-scale HOF (MHOF), which preserves temporal contextual information and is a highly descriptive feature specifically for accuracy improvement. Although these local feature descriptors extracted from video volumes have shown promising performance, it takes long processing times to compute such feature descriptors. Leyva et al. [13] employ a variable-sized cell structure-based methods to extract features from a limited number of video volumes.
Speed First Methods: Though the above methods attain high detection accuracy, their frame processing times are extremely long, and some essential efforts should be made to reduce the computational complexity. Lu et al. [15] and Biswas et al. [16] manage to handle a few features even though they employ multi-scale scanning techniques. Lu et al. [15] employ multi-scale temporal gradients as the prime feature to speed up feature extracting. Biswas et al. [16] adopt the compressed motion vectors of a video sequence itself in a histogram-binning scheme as features. Adam et al. [17] analyze the optical flow for individual regions in the scene to meet real-time processing requirement; unfortunately, they only detect the appearance anomaly and cannot detect local motion anomaly and long-terms abnormal activities in surveillance videos. A common characteristic of these methods is that they are fast to extract features but not highly descriptive. These methods usually reduce frame processing times by employing low-complexity descriptors. In a word, these previously proposed methods mostly reduce the computational complexity at the expense of slightly lower detection accuracy. Our proposed method achieves a trade-off between detection accuracy and computational complexity.
In this section, we firstly employ a variable-sized cell structure to extract appearance and motion features from a limited number of video volumes. Secondly, multiple probabilistic models are built on a compact feature set in the model training stage. Finally, we integrate multiple probabilistic models into MPI-VAD in order to detect four fine-grained categories of abnormal events.
In order to select the video volumes for analysis, we firstly construct a variable-sized cell structure for the whole scene (shown in Fig. 1). Local feature descriptors based on foreground occupancy and optical flow information are extracted from a limited number of video volumes (shown in Fig. 1). Each video volume u ∈ R3 has dimensions mx × my × mt, where mx and my respectively correspond to the horizontal and vertical dimensions of the cell, and mt denotes the number of consecutive frames.

Figure 1: Feature extraction process in surveillance videos
Foreground feature can efficiently describe the abnormal object presence such as trucks and wheelchairs. For each video volume u associated with the cell at position (i, j), the corresponding foreground occupancy F(i, j) ∈ R is computed as follows:
where N is the total number of pixels in video volume u, and u(n) indicates whether the n-th pixel belongs to the foreground region. If foreground occupancy F(i, j) of a video volume u exceeds a threshold θ, the video volume u can be considered active, and only active video volumes are further analyzed.
Optical flow information can properly describe the motion anomaly such as crowd panic, fights and other sudden variations. To filter salient regions in active video volumes, we detect STIPs on the absolute temporal frame differences via the FAST detector (shown in Fig. 1). Optical flow energy Op(xp, yp, tp) and an MHOF descriptor wp(xp, yp, tp) are generated from each spatio-temporal support region centered in the STIP(xp, yp, tp). Optical flow energy Op(xp, yp, tp) is computed as:
where N is the total number of pixels in a spatio-temporal support region, and
3.2 Multiple Probabilistic Models
Our method for building multiple probabilistic models of normal event patterns in the model training stage is illustrated in Fig. 2. Multiple probabilistic models are built on a compact feature set based on foreground occupancy and optical flow information.
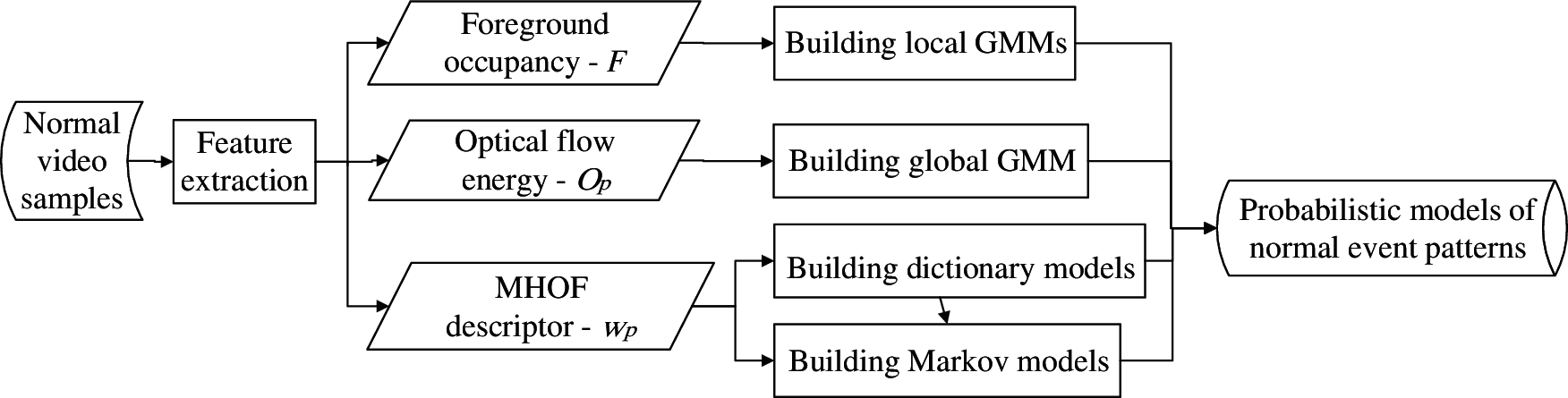
Figure 2: Our method for building multiple probabilistic models of normal event patterns in the model training stage
Multiple probabilistic models are applied to detect various abnormal events in complex scenes, including appearance anomaly, global motion anomaly, local motion anomaly, and long-term abnormal activities. Foreground occupancy and optical flow energy are respectively analyzed with the distinct Gaussian Mixture Models. The MHOF descriptors are simultaneously analyzed with dictionary models and Markov models.
(1) GMMs for Foreground Occupancy: Gaussian Mixture Model (GMM) is widely used in various fields, e.g., iris segmentation [18]. To detect appearance anomaly like variable-sized objects, we use GMMs to learn foreground occupancy of normal video samples. The foreground occupancy of each cell is analyzed by a GMM with parameters
where N is a normal distribution. Expectation-Maximization (EM) algorithm is used to train these local GMMs. The parameters of the models are determined exhaustively as follows:
where F represents all the foreground occupancy to be processed, whose posterior likelihood is to be maximized by iterating the Akaike Information Criterion (AIC); and
Considering the spatially immediate neighborhood of local cells, we construct a final probability density function to calculate the posterior likelihood of F(i, j) from the current cell, as follows:
where γ is an exception-modified Kronecker delta function.
(2) GMM for Optical Flow Energy: Different from multiple GMMs for foreground occupancy in the scene, to detect global motion anomaly, we only employ a global GMM with parameters
where N is a normal distribution; and Op represents all the optical flow energy to be processed and
(3) Dictionary Models for MHOF Descriptors: We are interested in capturing the local motion anomaly in the scene considering the fact that the activities may vary within the scene. For example, when both sidewalk and road exist in a scene, the activities on the sidewalk may largely differ from the activities in the road. Hence, we create an individual dictionary for each cell in the scene instead of creating a global dictionary as proposed in [2,19,20]. Each cell is assigned a dictionary generated from the set S of MHOF descriptors within the cell. We firstly use k-means to define the cluster centroid zi ∈ R8 in a dictionary, as follows:
The generated dictionary is associated with a normal distribution with parameters θDIC = {μDIC, σDIC}, respectively representing the mean and standard deviation of the distribution, as follows:
where dp = ‖wp − zi‖2, denoting the l2 distance of the word wp ∈ S to the cluster centroid zi. When we calculate the posterior likelihood of the observed words wp ∈ S, dp ≈ 0 and pDIC(dp|θDIC) → 1; otherwise wp∉S, dp ≫ 0 and pDIC(dp|θDIC) → 0. Maximum likelihood estimation is used to train the dictionary models.
(4) Markov Models for MHOF Descriptors: Finite-State Markov Chain (FSMC) is used to capture long-term abnormal activities like loitering. Because the activities in the scene vary significantly across different regions, we use multiple local Markov models for different regions to detect anomalous events in a scene, instead of creating a global Markov model as in [4]. Let us consider the current state Xl given by the matching label l of the local dictionary, the probability density function of the FSMC is given, as follows:
where L is the number of states defined by the total number of labels in the local dictionary. The matching label index l is defined as:
and the associated state transition matrix A is defined as:
The probability of words i and j both occurring is calculated by the concurrence of the two words. The order of occurrence of words i and j does not matter if the number of analyzed frames is limited; thus we make matrix A symmetrical.
After building multiple probabilistic models of normal event patterns, a novel video anomaly detection algorithm based on multiple probabilistic models inference — MPI-VAD (shown in Algorithm 1) is proposed to detect four fine-grained categories of abnormal events in the detection stage. MPI-VAD integrates the multiple probabilistic models into video anomaly detection and synthetically considers the detection results from different probabilistic models inference. MPI-VAD works in two cascaded phases — mask generation and multiple mask joint analysis, as follows:
In the first phase –– mask generation, the mechanism evaluates the posterior likelihood of appearance and motion features from video volumes. We generate three likelihood binary masks: foreground occupancy mask MaskFG, optical flow energy mask MaskOFE and MHOF descriptors mask MaskMHOF. The posterior likelihood of the foreground occupancy F is calculated as follows:
The likelihood binary mask MaskFG is generated by thresholding γFG, as follows:
where εFG is a posterior likelihood threshold used to determine whether the video volume corresponding to foreground occupancy F is abnormal; 1 denotes abnormal and 0 denotes normal. Similarly, we calculate the posterior likelihood of the optical flow energy Op and MHOF descriptors wp. The posterior likelihood of the optical flow energy Op is calculated as follows:
The likelihood binary mask MaskOFE is generated by thresholding γOFE, as follows:
where εOFE is a posterior likelihood threshold used to determine whether the spatio-temporal support region corresponding to optical flow energy Op is abnormal. The posterior likelihood of the MHOF descriptors wp is calculated as follows:
The likelihood binary mask MaskMHOF is generated by thresholding γMHOF, as follows:
where εMHOF is a posterior likelihood threshold used to determine whether the spatio-temporal support region corresponding to MHOF descriptor wp is abnormal.
In the second phase –– multiple mask joint analysis, the above multiple likelihood binary masks are jointly analyzed to determine whether abnormal events occurred in surveillance videos. Specifically, if a video volume is identified as anomalous in any individual likelihood binary mask, the corresponding cell at time t is marked as anomalous, as follows:
In order to make the anomaly inference mechanism more resilient to noise, we use the two consecutive frames at times {t − 1, t} to determine the abnormality of the frame at time t, as follows:
The binary mask

We have implemented MPI-VAD in MATLAB and tested it on a 3.2 GHz CPU with 16 GB RAM. We have verified the effectiveness of MPI-VAD on three publicly available benchmark datasets, i.e., UMN, CUHK Avenue, and USCD Pedestrian. Tab. 1 shows the details of the above three benchmark datasets.

We construct the variable-sized cell structure according to cell growing rate α and initial vertical dimension y0. For MOG background subtraction, the background learning rate is set to 0.01 on all these datasets. The number of frames for background modeling is set to 200 on CUHK Avenue, USCD Ped1 and Ped2, but 300 on UMN. For FAST detector, the number of the strongest points is set to 40. When applying EM algorithm to train the GMMs, we limit the number of iterations k to 10 since we empirically observe that AIC usually does not provide additional information when k is set to more than 10. These parameters are tailored to the characteristics of video sequences in practical surveillance scenarios.
Fig. 3 shows detection samples containing the detected abnormal events, which are marked with red masks. We evaluate the performance of MPI-VAD against several state-of-the-art methods. Experiment results show that MPI-VAD achieves competitive detection accuracy compared to no real-time methods and outperforms other real-time methods.

Figure 3: Detection samples of MPI-VAD
Two evaluation criteria are adopted to measure the accuracy of video abnormal detection, i.e., Frame-level criterion and Pixel-level criterion. The two evaluation criteria consider the matching degree between the detection results and the ground truth with different granularities.
(1) Frame-level criterion: Once a frame is detected to contain anomalous pixels, it is identified as an anomalous frame. This criterion focuses on abnormal event detection accuracy in the temporal dimension of videos. However, it does not consider the detection accuracy in the spatial dimension. Thus normal pixels in an anomalous frame are misidentified as anomalous.
(2) Pixel-level criterion: The criterion focuses on abnormal event detection accuracy in the temporal and spatial dimensions. If 40% of the detected pixels are true anomalous pixels in a frame, the anomalous frame is considered to be successfully detected.
The Receiver Operating Characteristic (ROC) curve is drawn to measure the detection accuracy. ROC curve is a curve of True Positive Rate (TPR) vs. False Positive Rate (FPR), as follows:
Based on a ROC curve, two values are calculated as quantitative indexes: 1) Area Under Curve (AUC): area under the ROC curve. 2) Equal Error Rate (EER): the FPR value when the condition FPR + TPR = 1 is satisfied. Notice that AUC and EER are similar performance evaluation metrics, specifically, EER → 0 when AUC → 1. We also consider whether a method could attain real-time processing performance according to a frame processing time.
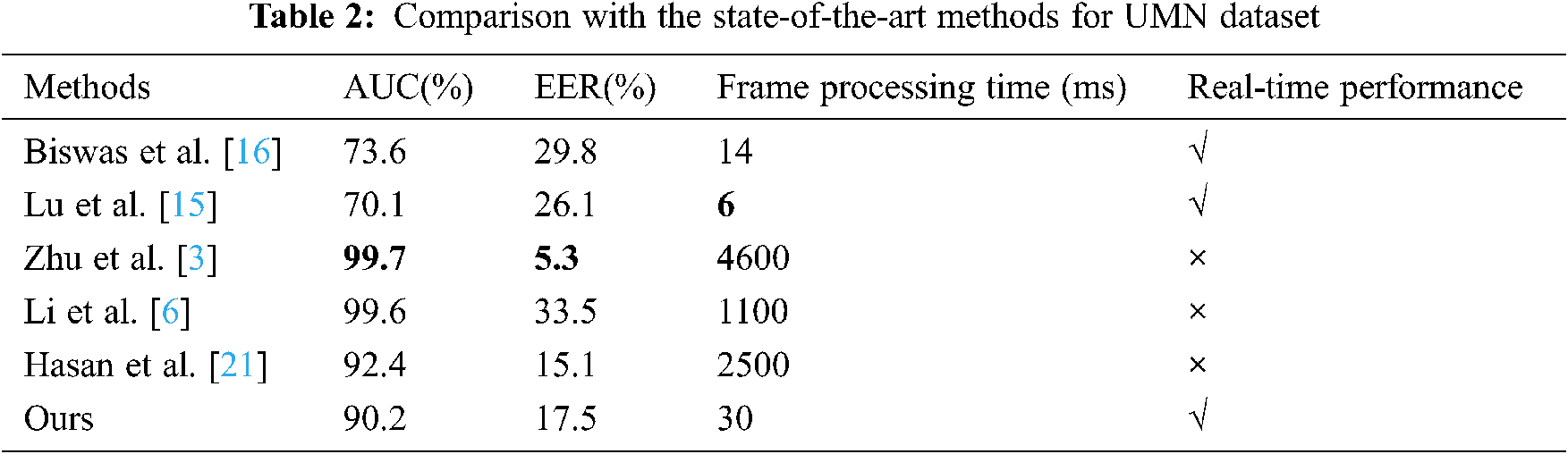
For the UMN dataset, we report frame-level ROC curves in Fig. 4 and evaluate the corresponding results in terms of the AUC and EER in Tab. 2. From Fig. 4, we notice that the detection accuracy of MPI-VAD is inferior to the methods proposed by Zhu et al. [3] and Li et al. [6]. From Tab. 2, we find that our method achieves the second shortest frame processing time and real-time performance.
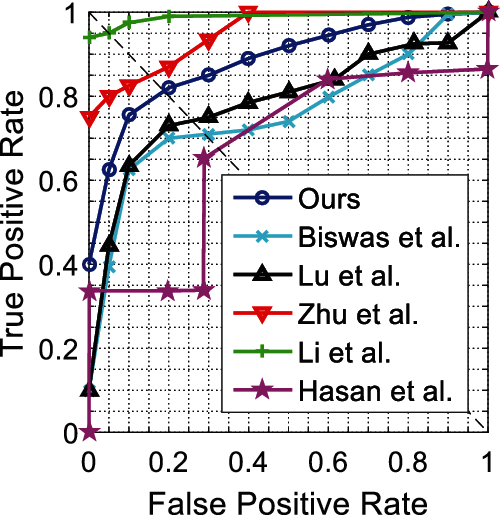
Figure 4: Frame-level ROC curves for UMN
For CUHK Avenue dataset, Fig. 5 shows frame-level ROC curves, and our method attains the best performance. From Tab. 3, we can observe that our method achieves the highest AUC and meets real-time performance. The shorter frame processing time attained by [15] is mainly due to the method do not employ optical flow estimation nor background subtraction to extract motion features and instead uses multi-scale temporal gradients with low computational cost.
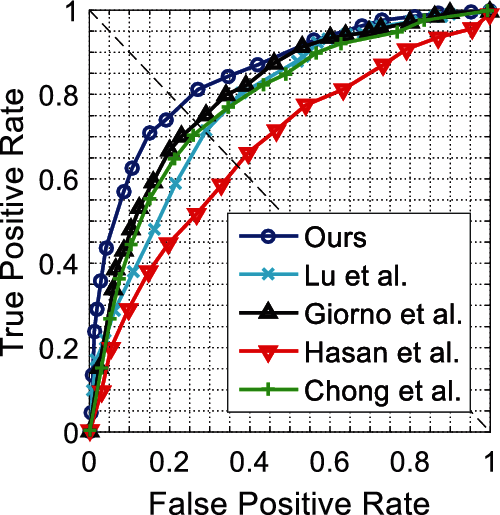
Figure 5: Frame-level ROC curves for CUHK Avenue

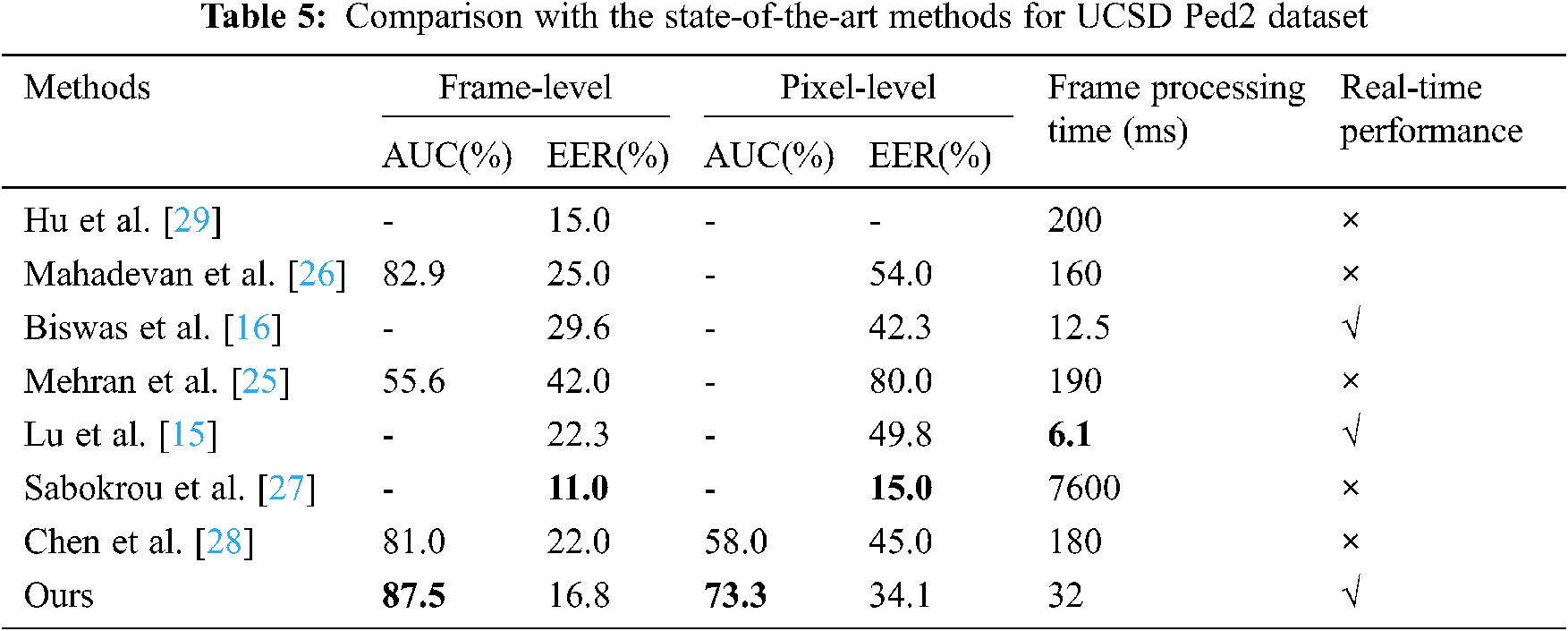
Figs. 6 and 7 show ROC curves for the UCSD Ped1 dataset. We evaluate the experiment results in terms of the AUC and EER at the frame-level and pixel-level in Tab. 4. As expected, no real-time methods [20,23–27] tend to attain higher AUC and lower EER than real-time methods [15]. The method [23] achieves the highest frame-level AUC, and the method [24] achieves the lowest pixel-level EER, while their frame processing times are much longer than ours; however, our method achieves competitive detection accuracy and best real-time performance. Figs. 8 and 9 show ROC curves for UCSD Ped2 dataset, and Tab. 5 evaluates the corresponding results in terms of the AUC and EER. From Tab. 5, we find our method outperforms the fastest real-time methods [15], and attains the highest detection accuracy compared to no real-time methods [25–28].
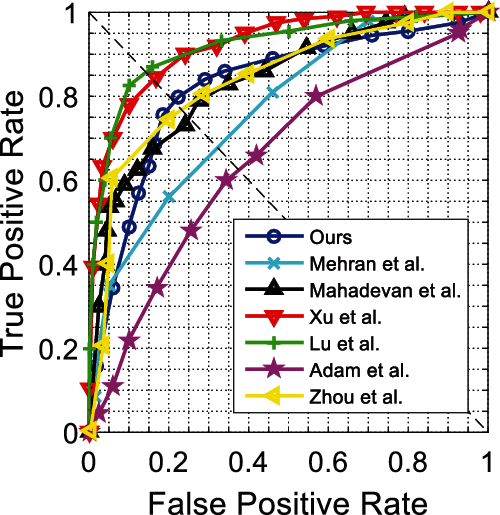
Figure 6: Frame-level ROC curves for Ped1
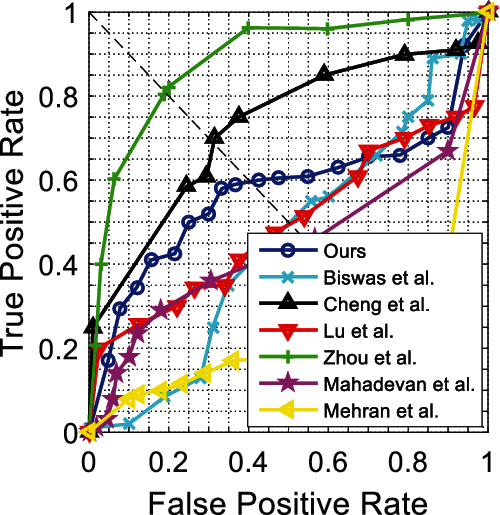
Figure 7: Pixel-level ROC curves for Ped1
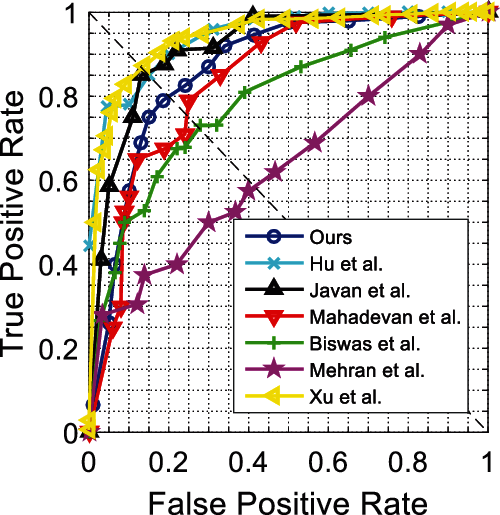
Figure 8: Frame-level ROC curves for Ped2
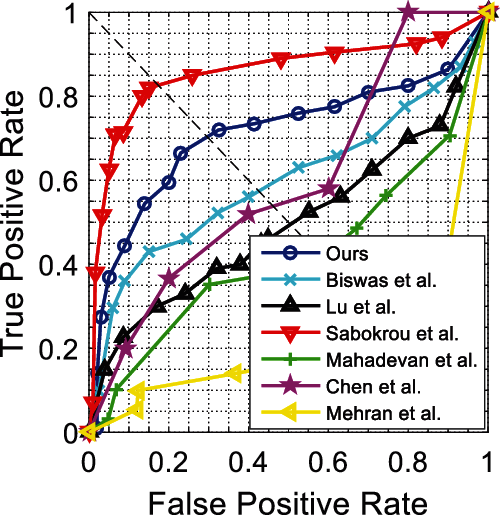
Figure 9: Pixel-level ROC curves for Ped2

In this paper, we integrate multiple probabilistic models into video anomaly detection and propose a novel video anomaly detection algorithm called MPI-VAD. Attributed to the multiple probabilistic models inference, MPI-VAD is able to detect various abnormal events in complex surveillance scenes. Our method employs a variable-sized cell structure to extract appearance and motion features from a limited number of video volumes and then achieves the trade-off between detection accuracy and computational complexity. We evaluate MPI-VAD on three publicly available datasets and attain competitive detection accuracies and real-time frame processing performance. However, MPI-VAD takes quite a long time to train multiple probabilistic models. Thus our future work will focus on reducing the required time.
Funding Statement: This work was supported by the National Science Foundation of China under Grant No.41971343.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. W. Sultani, C. Chen and M. Shah, “Real-world anomaly detection in surveillance videos,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 6479–6488, 2018. [Google Scholar]
2. M. J. Roshtkhari and M. D. Levine, “An on-line, real-time learning method for detecting anomalies in videos using spatio-temporal compositions,” Computer Vision and Image Understanding, vol. 117, no. 10, pp. 1436–1452, 2013. [Google Scholar]
3. X. Zhu, J. Liu, J. Wang, C. Li and H. Lu, “Sparse representation for robust abnormality detection in crowded scenes,” Pattern Recognition, vol. 47, no. 5, pp. 1791–1799, 2014. [Google Scholar]
4. Y. Benezeth, P.-M. Jodoin, V. Saligrama and C. Rosenberger, “Abnormal events detection based on spatio-temporal co-occurences,” in Procedings of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Miami, Florida, USA, pp. 2458–2465, 2009. [Google Scholar]
5. J. Kim and K. Grauman, “Observe locally, infer globally: a space-time MRF for detecting abnormal activities with incremental updates,” in IEEE Conf. on Computer Vision and Pattern Recognition, Miami, Florida, USA, pp. 2921–2928, 2009. [Google Scholar]
6. W. Li, V. Mahadevan and N. Vasconcelos, “Anomaly detection and localization in crowded scenes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 36, no. 1, pp. 18–32, 2014. [Google Scholar]
7. R. T. Ionescu, S. Smeureanu, B. Alexe and M. Popescu, “Unmasking the abnormal events in video,” in Proc. of the IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 2914–2922, 2017. [Google Scholar]
8. A. Del Giorno, J. A. Bagnell and M. Hebert, “A discriminative framework for anomaly detection in large videos,” in Proc. of the European Conf. on Computer Vision, Amsterdam, The Netherlands, pp. 334–349, 2016. [Google Scholar]
9. H. Gao, W. Huang and X. Yang, “Applying probabilistic model checking to path planning in an intelligent transportation system using mobility trajectories and their statistical data,” Intelligent Automation & Soft Computing, vol. 25, no.3, pp. 547–559, 2019. [Google Scholar]
10. W. Brendel, A. Fern and S. Todorovic, “Probabilistic event logic for interval-based event recognition,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, pp. 3329–3336, 2011. [Google Scholar]
11. V. Saligrama and Z. Chen, “Video anomaly detection based on local statistical aggregates,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Providence, RI, USA, pp. 2112–2119, 2012. [Google Scholar]
12. M. Bertini, A. Del Bimbo and L. Seidenari, “Multi-scale and real-time non-parametric approach for anomaly detection and localization,” Computer Vision and Image Understanding, vol. 116, no. 3, pp. 320–329, 2012. [Google Scholar]
13. R. Leyva, V. Sanchez and C. T. Li, “Video anomaly detection with compact feature sets for online performance,” IEEE Transactions on Image Processing, vol. 26, no. 7, pp. 3463–3478, 2017. [Google Scholar]
14. Y. Cong, J. Yuan and Y. Tang, “Video anomaly search in crowded scenes via spatio-temporal motion context,” IEEE Transactions on Information Forensics and Security, vol. 8, no. 10, pp. 1590–1599, 2013. [Google Scholar]
15. C. Lu, J. Shi and J. Jia, ”Abnormal Event Detection at 150 FPS in MATLAB,” inProc. of the IEEE Int. Conf. on Computer Vision, Sydney, Australia, pp. 2720–2727, 2013. [Google Scholar]
16. S. Biswas and R. V. Babu, “Real time anomaly detection in H.264 compressed videos,” in proceedings of the national conference on computer vision,” in Pattern Recognition, Image Processing and Graphics, Jodhpur, India, pp. 1–4, 2013. [Google Scholar]
17. A. Adam, E. Rivlin, I. Shimshoni and D. Reinitz, “Robust real-time unusual event detection using multiple fixed-location monitors,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 30, no. 3, pp. 555–560, 2008. [Google Scholar]
18. F. Mallouli, “Robust em algorithm for iris segmentation based on mixture of Gaussian distribution,” Intelligent Automation & Soft Computing, vol. 25, no.2, pp. 243–248, 2019. [Google Scholar]
19. L. Kratz and K. Nishino, “Anomaly detection in extremely crowded scenes using spatio-temporal motion pattern models,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Miami, Florida, USA, pp. 1446–1453, 2009. [Google Scholar]
20. K.-W. Cheng, Y.-T. Chen and W.-H. Fang, “Gaussian process regression-based video anomaly detection and localization with hierarchical feature representation,” IEEE Transactions on Image Processing, vol. 24, no. 12, pp. 5288–5301, 2015. [Google Scholar]
21. M. Hasan, J. Choi, J. Neumann, A. K. Roy-Chowdhury and L. S. Davis, “Learning temporal regularity in video sequences,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 733–742, 2016. [Google Scholar]
22. Y. S. Chong and Y. H. Tay, “Abnormal event detection in videos using spatiotemporal autoencoder,” in Proc. of the Int. Symposium in Neural Networks, Sapporo, Hakodate, and Muroran, Hokkaido, Japan, pp. 189–196, 2017. [Google Scholar]
23. K. Xu, T. Sun and X. Jiang, “Video anomaly detection and localization based on an adaptive intra-frame classification network,” IEEE Transactions on Multimedia, vol. 22, no. 2, pp. 394–406, 2020. [Google Scholar]
24. S. Zhou, W. Shen, D. Zeng, M. Fang, Y. Wei et al., “Spatial-temporal convolutional neural networks for anomaly detection and localization in crowded scenes,” Signal Processing: Image Communication, vol. 47, pp. 358–368, 2016. [Google Scholar]
25. R. Mehran, A. Oyama and M. Shah, “Abnormal crowd behavior detection using social force model,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, Miami, Florida, USA, pp. 935–942, 2009. [Google Scholar]
26. V. Mahadevan, W. Li, V. Bhalodia and N. Vasconcelos, “Anomaly detection in crowded scenes,” in Proc. of the IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, San Francisco, CA, USA, pp. 1975–1981, 2010. [Google Scholar]
27. M. Sabokrou, M. Fayyaz, M. Fathy, Z. Moayed and R. Klette, “Deep-anomaly: Fully convolutional neural network for fast anomaly detection in crowded scenes,” Computer Vision and Image Understanding, vol. 172, pp. 88–97, 2018. [Google Scholar]
28. T. Chen, C. Hou, Z. Wang and H. Chen, “Anomaly detection in crowded scenes using motion energy model,” Multimedia Tools and Applications, vol. 77, no. 11, pp. 14137–14152, 2018. [Google Scholar]
29. Y. Hu, Y. Zhang and L. S. Davis, “Unsupervised abnormal crowd activity detection using semiparametric scan statistic,” in Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Portland, OR, USA, pp. 767–774, 2013. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |