DOI:10.32604/iasc.2022.020090

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.020090 |  |
| Article |
Implementation of a High-Speed and High-Throughput Advanced Encryption Standard
1Department of ECE, Karpagam Institute of Technology, Coimbatore, India
2Department of ECE, Karpagam College of Engineering, Coimbatore, India
*Corresponding Author: T. Manoj Kumar. Email: srimanojkumar@gmail.com
Received: 08 May 2021; Accepted: 02 July 2021
Abstract: Data security is an essential aspect of data communication and data storage. To provide high-level security against all kinds of unauthorized accesses, cryptographic algorithms have been applied to various fields such as medical and military applications. Advanced Encryption Standard (AES), a symmetric cryptographic algorithm, is acknowledged as the most secure algorithm for the cryptographic process globally. Several modifications have been made to the original architecture after it was proposed by two Belgian researchers, Joan Daemen and Vincent Rijment, at the third AES candidate Conference in 2000. The existing modifications aim to increase security and speed. This paper proposes an efficient pipelined architecture for the key expansion process, effectively reducing the propagation delay to generate the required subkeys. Along with the pipeline structure, the fork and join architecture is also used in the key expansion part of the AES architecture, and it significantly reduces the time taken to generate the required subkeys. The proposed architecture is simulated and implemented on Xilinx Virtex4 XC4VLX200 FPGA. The result indicates that the proposed architecture achieves an improvement of about 37% in throughput compared with the original architecture. Also, the proposed architecture can convert the given plain text to cipher with a minimal propagation delay.
Keywords: Advanced encryption standard; cryptography; FPGA; propagation delay; key expansion; S-box; encryption; decryption
Information is regarded as the most valuable asset today, and a large amount of information is processed and shared per second in this technological world. However, the information must be processed and shared securely to avoid piracy issues or alteration of the information by an unintended user. Cryptographic researches aim to prevent unauthorized access to any information. Also, unauthorized change and availability of the original information motivate the researchers to keep our information securely.
Researchers use cryptographic algorithms to keep information secure while the information is transmitted and received on an insecure channel. Sometimes, information must be secure where it is stored. Cryptographic algorithms perform encryption operations on the original plain text before transmitting and perform decryption operations after receiving the encrypted text from the insecure channel. A secret key is used for both encryption and decryption operations. In terms of the usage of secret keys, cryptographic algorithms can be classified as symmetric and asymmetric algorithms. Also, the algorithms can be classified as block and stream cipher algorithms based on the number of bits. Cryptographic algorithms rely on statistical and analytical techniques that depend on the key of the cryptographic process. Algorithms used for secure communication must withstand the cryptanalytic attacks that aim to find the secret key through the techniques and mathematical operations used to convert the plain text to ciphertext. In 2001, the National Institute of Standards and Technology (NIST) published a symmetric algorithm called Rijndael, and it has been taken as the AES after the Third AES Candidate Conference. AES is available as FIPS 197 in the federal register. Rijndael is designed by two Belgian researchers, Joan Daemen and Vincent Rijment. In the last two decades, researchers have proposed many cryptographic efficient algorithms. However, AES is still the most secure cryptographic algorithm, and it is cost-effective and easy to implement in both hardware and software. AES is a non-Feistel cipher that has the same rounds of operations in both encryption and decryption processes.
In terms of secrecy, the AES cryptographic algorithm is efficient. Also, it has flexibility in both hardware and software implementations. Besides, it executes faster than the other cryptographic algorithms. According to the number of rounds presented in the algorithms, the subkeys required also vary. The generation of these subkeys is a sequential process, and it takes a significant amount of time to generate all the subkeys. This paper proposes an efficient architecture that reduces the time taken to generate the subkeys, and a pipelined architecture is introduced to decrease the amount of propagation delay to generate the subkeys. The proposed architecture can also be implemented in hardware and software effectively. Especially, the algorithm’s security is not compromised since all the originally statistical and mathematical operations are preserved in the proposed architecture. The primary motivation of this design is to provide a high-speed and secure AES algorithm.
The rest of the paper is organized as follows. Section 3 reviews the existing AES algorithms and the mathematical operations involved in the encryption and decryption operations. Section 4 introduces the proposed modifications to the existing algorithm. Section 5 presents the results and discussion of the new design. Section 6 concludes this paper and gives further research work.
3.1 Advanced Encryption Standard
AES is a symmetric cryptographic algorithm in which a single secret key is used for both encryption and decryption operations. AES has three different versions, and each version operates at different bit levels of a secret key. Based on the number of bits in the secret key, AES can be classified into AES-128, AES-192, and AES-256 [1–5]. Tab. 1 indicates the AES rounds and the corresponding bit size of the secret key. Every round of the AES algorithm uses a different subkey that is generated from the main key. Though the key sizes are different for each version, the number of bits from the original data to be communicated securely remains the same for all versions [6,7].
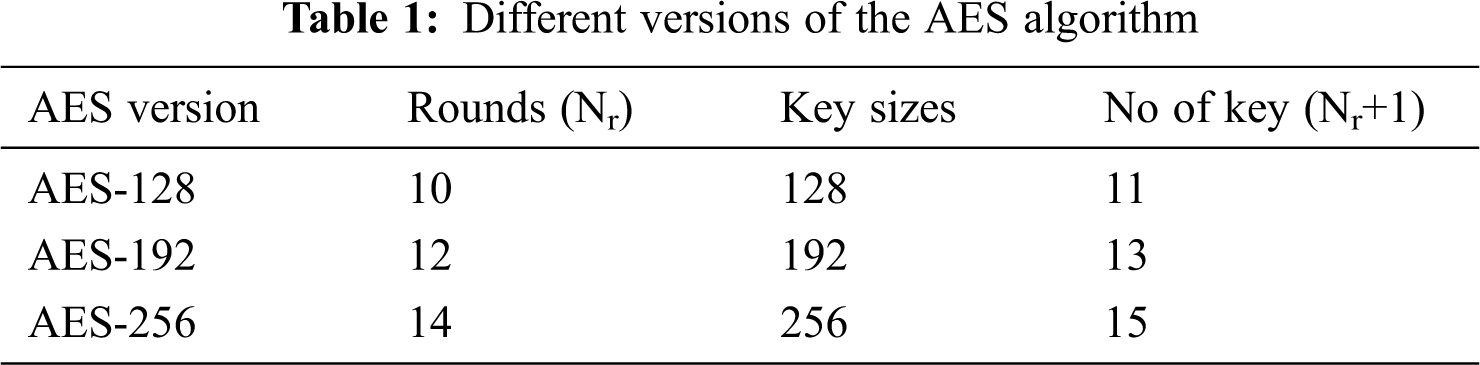
It should be noted that the data block size is 128 bits for all three versions of the AES algorithm. The number of rounds denotes the encryption operations for a single data block with different subkeys obtained from the key expansion process. The diffusion and confusion process for each round remains the same [8,9]. The first main key is used for pre-round transformation, and the remaining subkeys are used in each round [10–12]. So, the number of keys required is always significantly more than the number of rounds in AES versions.
AES is a non-Feistel block cipher cryptographic algorithm that encrypts a 128-bit block of the plain original text into a 128-bit block of encrypted ciphertext based on a secret key. The length of key differs for different versions of the AES algorithm, as mentioned in Tab. 1. The same algorithm used to encrypt the plain text can also be used to recover the plain text from the ciphertext with the help of the secret key used in the encryption process. Except for the last round of all AES versions, all the other rounds have the following four operations in both encryption and decryption processes. Before proceeding to the encryption process, the 128-bit plain text is grouped into a state matrix with a size of 4 × 4, and each element in the matrix is represented as a word (2 bytes).
Substitution is a process in which a byte is replaced by another byte. The only non-linear process involved in the AES algorithm is substitution. Each byte in the state matrix is considered a polynomial in the Galois Field 28 and transformed into another byte by matrix multiplication and affine transformation. Substitution can also be performed directly through the Rijndael S-box. In decryption, inverse S-box is used in the substitution process. The substitution step introduces the actual confusion to the original data, which forms the vital step in preserving the original data from unauthorized accesses [13,14].
In this operation, the rows in the state array are shifted cyclically. The second, third, and fourth rows are respectively shifted left by one, two, and three times, whereas the first row remains unchanged. For decryption operation, rows are shifted to the right. Row shift is the first process of diffusion in the AES algorithm, and this process is invertible [15,16].
Like row shift operation, the mix column operation is performed at the column level [17]. Several techniques have been proposed for this operation, and one straightforward operation is matrix multiplication. Eq. (1) gives the operation involved in the mix column operation.
where S’1, S’2, S’3, and S’4 are the output of the mix column operation; S1, S2, S3, and S4 are the output of the row shift operation and are taken as the input of the mix column operation.
Add round key is the most vital operation in the AES algorithm. Because all the previous three steps are invertible, without this operation, AES encryption becomes meaningless. The secret key works at the add round key operation. In this operation, the main key or several subkeys are first arranged as a state matrix with a size of 4 × 4, and matrix addition between keys and plain text is performed. As a result of the add round key operation, the ciphertext is obtained [18].
All the above four operations are repeated for n times, where n is the number of rounds in the AES version. For every iteration, different subkeys are used. Therefore, for n rounds, n subkeys must be derived. Derivation of several subkeys from a single main key is the key expansion process. The operations in the key expansion process or key schedule must be carefully implemented because the relation between subkeys should not be exploited easily. The key expansion process in the AES algorithm is a non-linear process that follows a mathematical procedure to derive different keys from a single key. Many researchers have developed different architectures for this process to improve the security of the keys obtained. As for the proposed architecture in this paper, the time consumption to generate subkeys from the primary key is reduced.
3.3 Existing Key Expansion Architecture
The key expansion process of AES-128 is discussed in this section. In this process, the main secret key of 128 bits is divided into four words, each with a length of 32 bits. For AES-128, ten subkeys must be derived from the main secret key, and these subkeys are used in the process of producing ciphertext from the plain text. The process of key expansion is illustrated in Fig. 1. Mathematical operations are performed on the main key to derive the subkeys. Interdependency with the previous subkey makes the key expansion process efficient. The mathematical operation is performed at the word level, and consecutive four words are combined to form a subkey. For example, W4, W5, W6, and W7 are combined to form the first subkey. The key expansion algorithm creates a total of 4 (Nr+1) words just with an EXOR operation between the previous word and a word from the previous subkey.
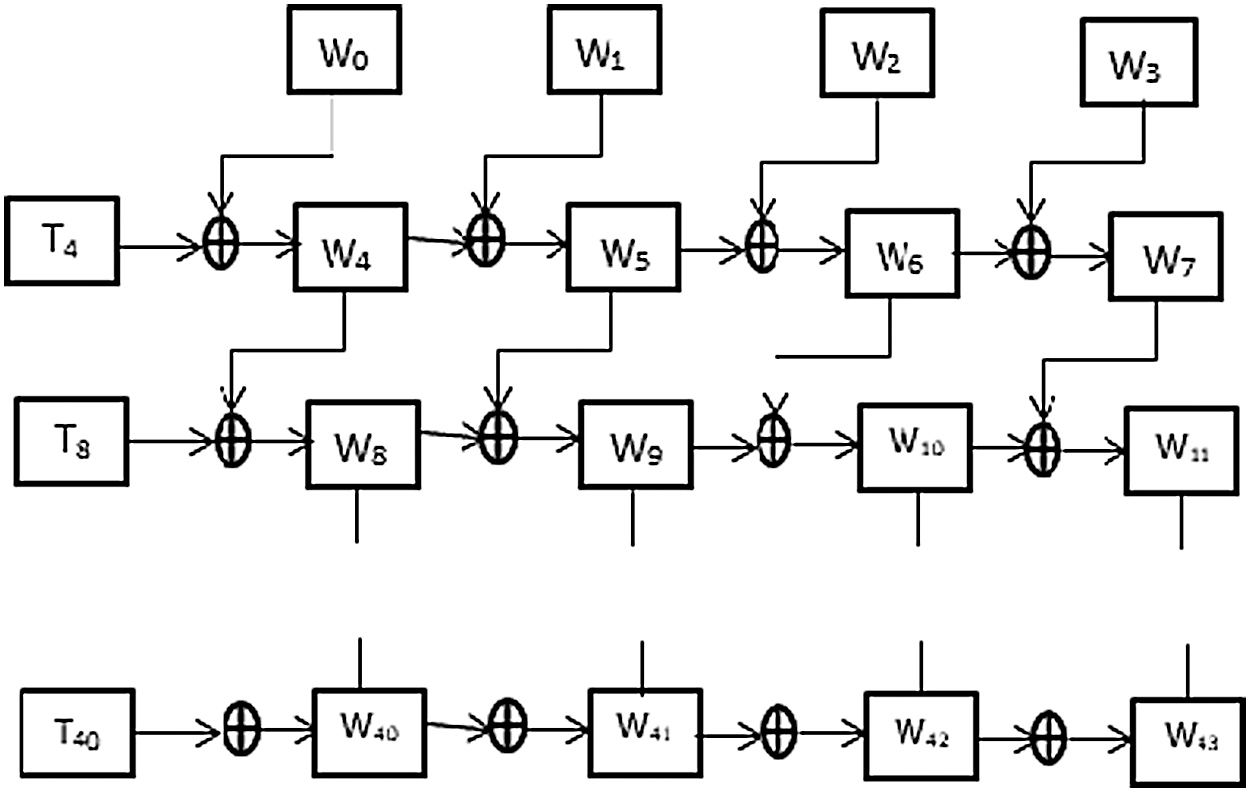
Figure 1: Conventional key expansion architecture
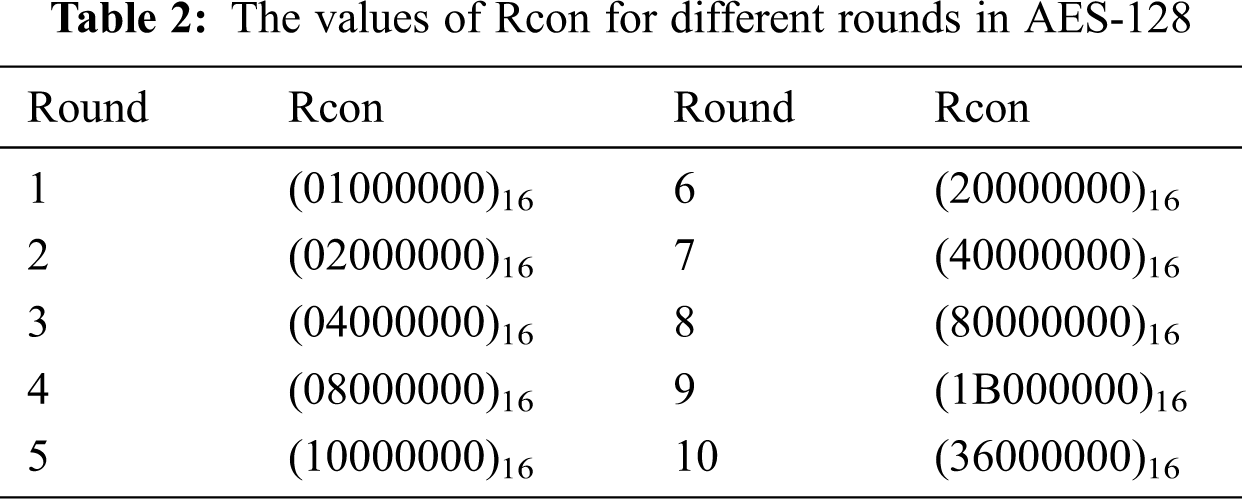
Temporary word is the most important in the key expansion process. The only non-linear process involved in the generation of subkeys is the generation of the temporary word. The first word of every subkey is generated as a result of the EXOR operation between its corresponding temporary word and a word from the previous subkey. Three operations are performed in a word to create a temporary word, as shown in Eq. (2). Substitution, rotation, and EXOR are the three operations that are performed in the process of creating a temporary word. For AES-128, the temporary words of W4, W8, W12, W16, W20, W24, W28, W32, W36, and W40 need to be created. Only when i ≠ 4Nr, temporary words are not needed, where ‘i’ denotes the word number, and ‘Nr’ denotes the round number in AES.
The Rotword operation is the same as the row shift operation, but it is applied to only one row. The Subword operation is similar to the Subbyte operation. The value of Rcon differs for each round and it is listed in Tab. 2.
The studies of the efficient implementation of the AES algorithm are going on for the past two decades. Several architectures that are efficient in terms of speed, area, and throughput have been proposed. Zhang et al. [6] presented an efficient high-speed architecture for the hardware and software implementation of the AES algorithm. In this architecture, CFA is used to reduce the area. In each round of the encryption and decryption operations, a fully sub-pipelined encryptor is used, achieving a throughput of 21.56 Gbps on the Xilinx XCV1000 device. Hammad et al. [7] also used CFA in the AES encryptor to increase the execution speed of the AES algorithm. The architecture is a multi-stage sub pipelined architecture that allows a high throughput of 39.053 Gbps for nine pipeline stages with an operational frequency of 305.1 MHz. Fan et al. [8] proposed a sequential and fully pipelined AES architecture using Xilinx ISE 7.1 synthesizer and proposed an efficient, low-cost add round key architecture for real-time key generation. The pipelined AES architecture achieves a throughput of 28.4 Gbps with an operational frequency of 222 MHz. Kumar et al. [9] proposed an architecture that uses CFA in the S-box substitution and found that the offline key expansion and pipelining in a composite field implementation can reduce the area. So, the throughput can be improved through parallel processing and pipelining. The area can be reduced by introducing these concepts in specific transformations like S-Box and Mix Column because these transformations affect the overall throughput. Kamal et al. [10] implemented an area-efficient AES architecture. It requires 2732 slices of a Xilinx Virtex-II XC2V1000bg575 device and runs at a maximum clock speed of 98.95 MHz, and achieves a throughput of 29.32 Mbps.
4 The Proposed Key Expansion Architecture for AES
In the conventional key expansion architecture, all the subkeys are generated sequentially. The interdependency between the subkeys is essential to making efficient cryptanalytic-prone subkeys. Therefore, the interdependency between the subkeys must be preserved. Meanwhile, in the conventional architecture, the words of Wi-1 and Wi-4 are required to create the current word of With. Because of this interdependency, all the required subkeys are generated sequentially. The sequential process is usually time-consuming since the last step is executed only after all the previous steps have been executed. In this case, there is a lot of time delay in generating all the required subkeys. Thus, this research work aims to decrease the time delay required for generating the required subkeys.
The proposed architecture makes two types of modifications to the conventional key expansion structure to reduce the time delay. Each word in the subsequent subkey always depends on a word of the previous subkey, which makes deep confusion necessary. Therefore, the interdependency between subkeys should be preserved to ensure that it is less possible to track the main key with the subkey generated.
4.1 Pipeline Architecture in the Key Expansion Process
In the proposed architecture, the generation of the temporary word differs from that of conventional architectures. In conventional architectures, the last word from the previous subkey is mathematically operated to form the temporary word. Due to this, pipeline architecture is difficult to be implemented. Instead of obtaining the temporary word from the last word of the previous subkey, it is possible to obtain the temporary word from the first word of the previous subkey. Based on this modification, the temporary word can be obtained earlier than that of the conventional architecture. Also, pipeline architecture can be implemented for the subkey generation process to speed up the process.
In the conventional architecture, W8 is dependent on W4 and T8, but T8 is generated from W7. Therefore, it is not possible to generate W8 until W7 is generated. Based on the newly proposed modification, the temporary word W8 can be generated once W4 is available. Since T8 is dependent on W4, it can be generated at the same time as W5, and there is no need to wait until the generation of W7 is completed. Likewise, W9 can also be generated before W7. This effectively speeds up the process of generating subkeys. Based on the circuit with the block structure shown in Fig. 2, the interdependency between the subkeys can be prevented, and the propagation delay for generating subkeys is significantly reduced. Eq. (3) gives the pipeline organization for the subkey generation process.
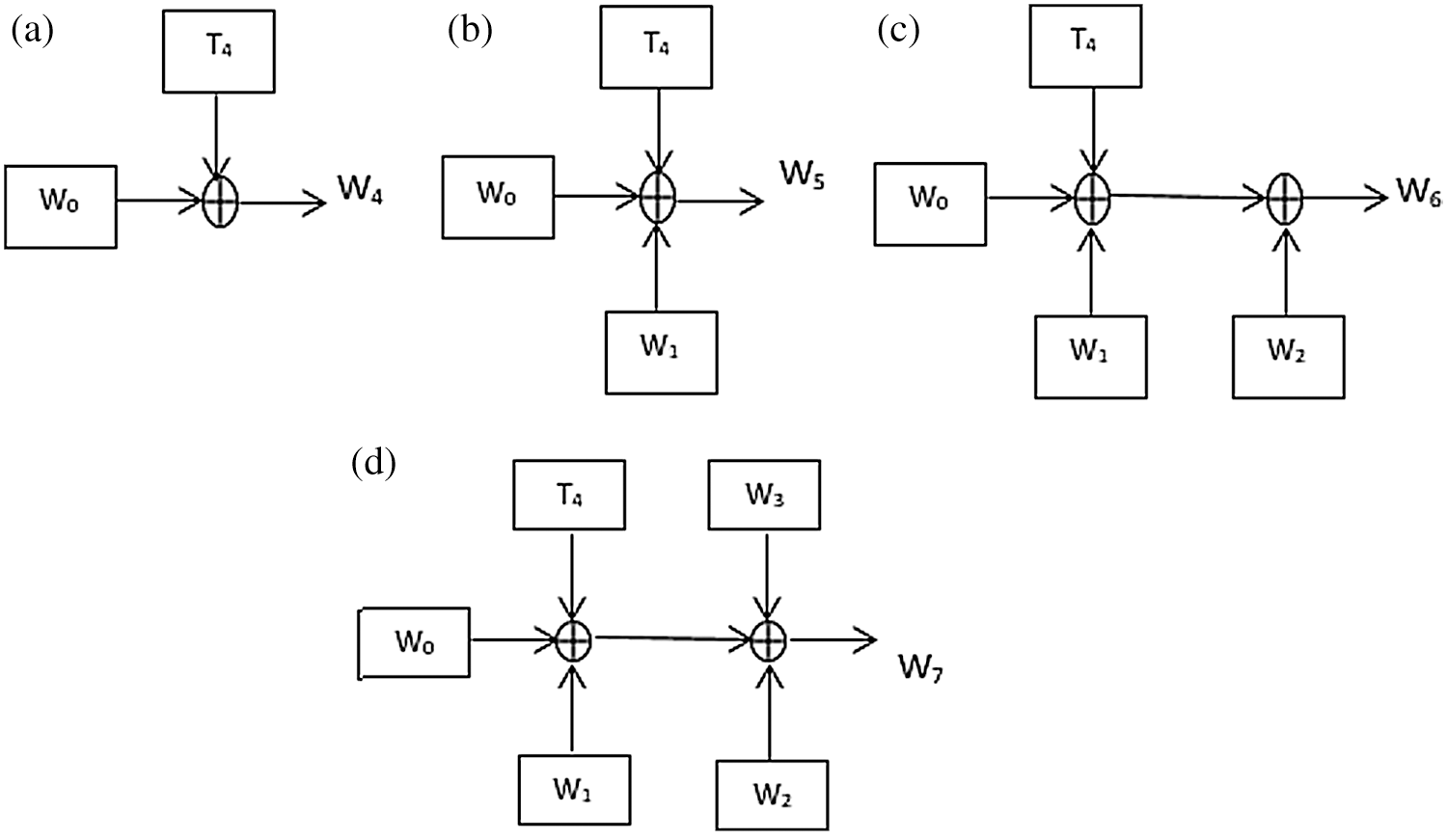
Figure 2: (a, b, c, d): The pipeline architecture for the key expansion process of AES-128
4.2 Fork-Join Model of Key Expansion Architecture
In the new proposed architecture, the second modification is splitting the entire architecture into two blocks and executes them in parallel. As for AES-128, ten subkeys are used in ten iterations of the encryption process. Therefore, in the AES-128 architecture, the generation of the first five subkeys can be grouped into one block, and the generation of the remaining five subkeys can be grouped into another block. The first subkey is generated from the main key. The second, third, fourth, and fifth subkeys are generated from the previous subkeys as in the conventional architecture. In the standard AES architecture, the sixth subkey is generated from the previous subkey (the fifth subkey). As shown in Fig. 3, the main key instead of the fifth subkey is used to generate the sixth key in the new architecture. Because of this modification, the sixth subkey and the first subkey can be generated simultaneously. Since the seventh, eighth, ninth, and tenth subkeys are respectively dependent on the sixth, seventh, eighth, and ninth subkeys, the seventh, eighth, ninth, and tenth subkeys are also available once the second, third, fourth, and fifth subkey are generated. Both blocks can generate subkeys in parallel since they generate subkeys from the main key.
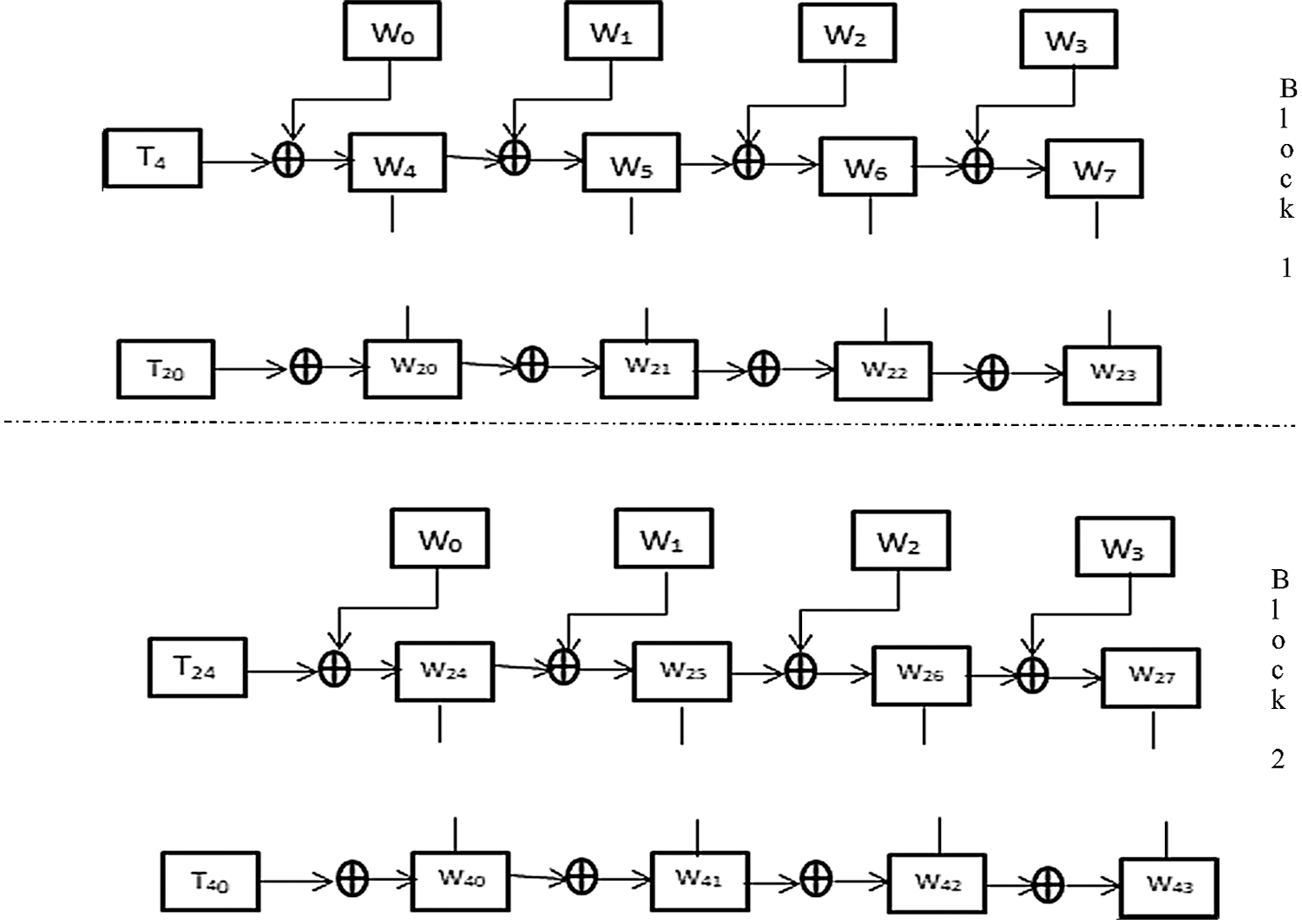
Figure 3: The fork and join model of the key expansion process for AES-128
For AES-128, it is necessary to create ten temporary words that form an integral part in forming the first word in all subkeys. Therefore, before employing the fork and join model for the key expansion process, the temporary word for the generation of the first word of the sixth subkey must be carefully created so that it does not depend on the subkeys in the first block. To address this issue, t24 is designed by using the third word of the main secret key. In the proposed architecture, t24 is generated from W2, whereas in existing architecture t24 is generated from W23. Also, the sixth subkey is entirely dependent on the main key instead of the fifth subkey. All the other operations are the same as that of the standard AES temporary word generation process. AES-192 has 12 subkeys because the AES-192 architecture has 12 iterations in both encryption and decryption processes. In AES-192, the entire key expansion architecture can be split into two blocks with each block generating six subkeys. The seventh subkey and seventh temporary word can be derived from the main key instead of the sixth subkey as in the conventional architecture. Likewise, in the AES-256 architecture, each block generates seven subkeys, and the eighth subkey is derived from the main key instead of the seventh subkey. Also, the temporary word of the eighth subkey is derived from the main key.
The proposed key expansion architecture can replace the conventional key expansion architecture without changing the other parts of the AES algorithm. The proposed architecture with a modified key expansion structure for AES-128 is first simulated to verify whether all the subkeys are correctly generated. After verification, this proposed architecture is used in the key expansion process, and the entire AES-128 algorithm is simulated, synthesized, and implemented in Modelsim 10.4d and Xilinx Virtex 4XC4VLX200 FPGA, respectively. Meanwhile, the time consumption to generate the ciphertext of 128 bits is calculated.
Figs. 4 and 5 show the simulation results of the existing and proposed architecture for the key expansion process. During simulation, the same main key is given as the input for both architectures. It can be seen from the simulation result that the first five subkeys generated from both the architecture remain the same. There is a change in the remaining subkeys because the interdependency between the keys in the second part of the architecture is changed. It results in the vast difference between the subkeys obtained in the second part of both architectures. Since there is no change in the first five subkeys generated up to five iterations, the encrypted data also remains. The final output of the encryption process from both architectures is different because the subkeys generated from the second part are different.
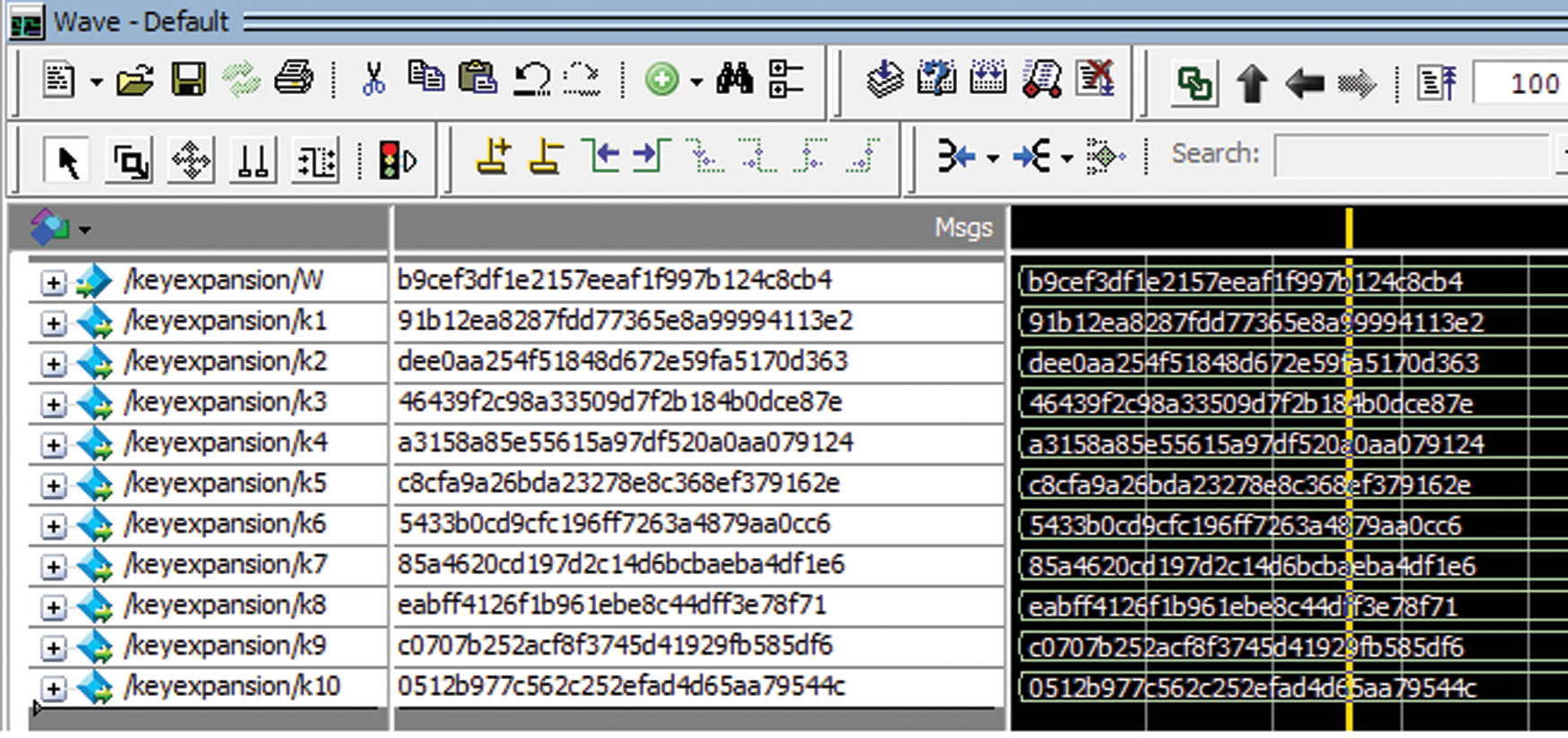
Figure 4: Simulation results of the existing architecture
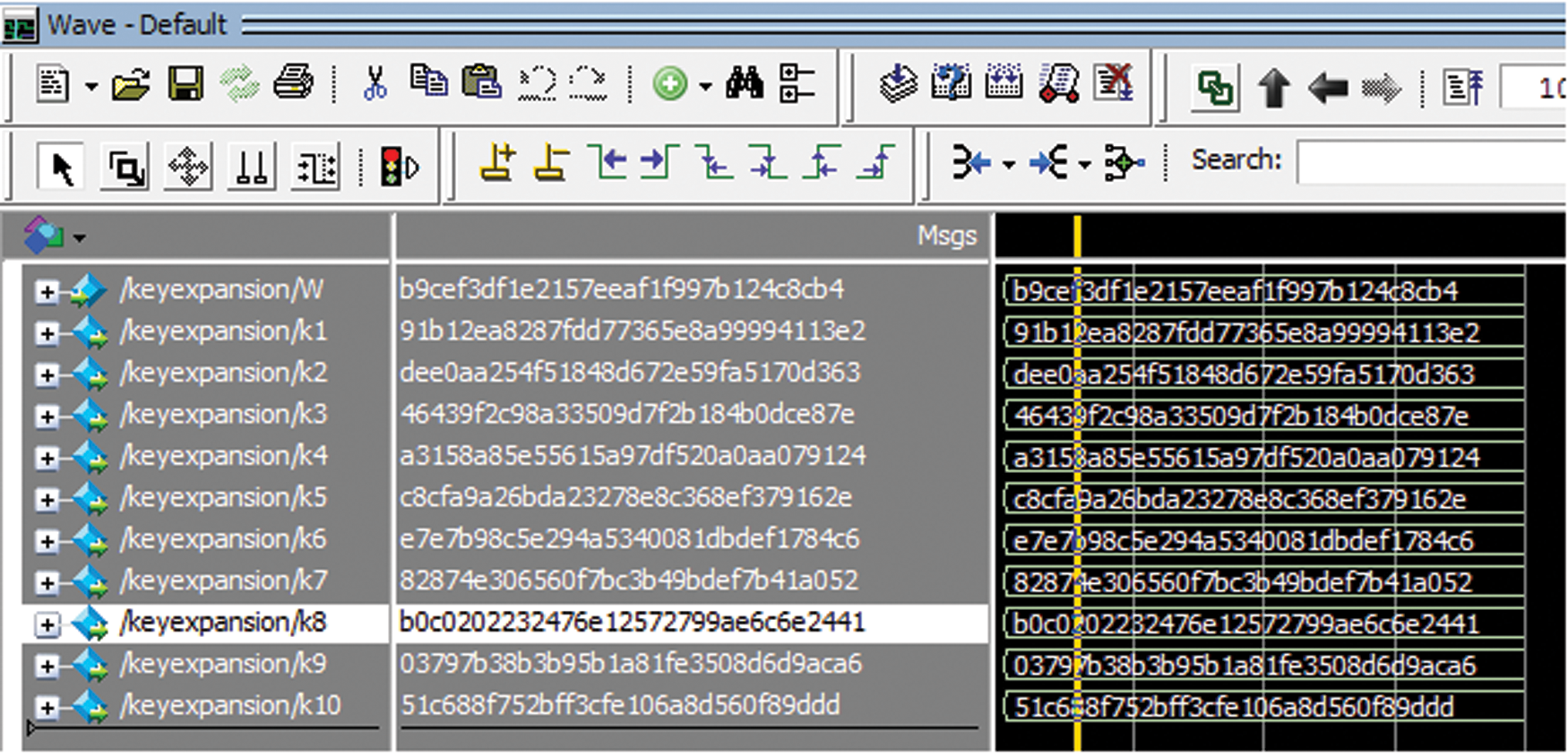
Figure 5: Simulation results of the proposed architecture
Since the final output is different, it is impossible to decrypt the encrypted data of the standard AES algorithm with the proposed algorithm. Therefore, it is necessary to use the same algorithm for both encryption and decryption operations. That is, the receiver must be aware of the modification introduced to the AES algorithm used for encryption. Suppose that the receiver tries to decrypt the ciphertext with the standard AES algorithm and its secret key. In this case, because of the modified subkey values, it is not possible to decrypt correctly. Also, the security is enhanced because even if the intruders obtain the secret key but are not aware of the modifications introduced in the algorithm, the intruder cannot decipher the encrypted data. However, the modifications introduced to the AES algorithm have to be declared to the public since being an open-source algorithm is an important criterion to be considered as AES.
This proposed architecture is implemented in the AES algorithm replacing the conventional architecture for the key expansion process. Because of the multi-stage pipeline architecture, the proposed architecture has the potential to achieve better results than the conventional architecture. Literature [3] is a synthesis report of a conventional AES architecture. The same conventional architecture is modified with a 4-stage pipeline in [4], which results in better throughput and shows significant improvement in the propagation delay for AES execution by sacrificing area. The work in [5] solves the area problem by implementing a sub-pipelined S-box model, and a conventional key expansion process is used in the AES pipelined architecture. By introducing pipeline and parallel block architecture in the key expansion of the proposed architecture, the efficiency (throughput) can be improved, and the propagation delay is also reduced. The throughput of an algorithm can be obtained by Eq. (4).
After the proposed architecture is implemented in the Virtex-4 FPGA, the time cost of the algorithm to encrypt a text is calculated, and the result is compared with that of the existing architecture. Tab. 3 lists the efficiency of the proposed architecture in terms of propagation delay and throughput. From Figs. 6 and 7, it can be seen that the throughput of this improved architecture is better than that of the existing architectures.
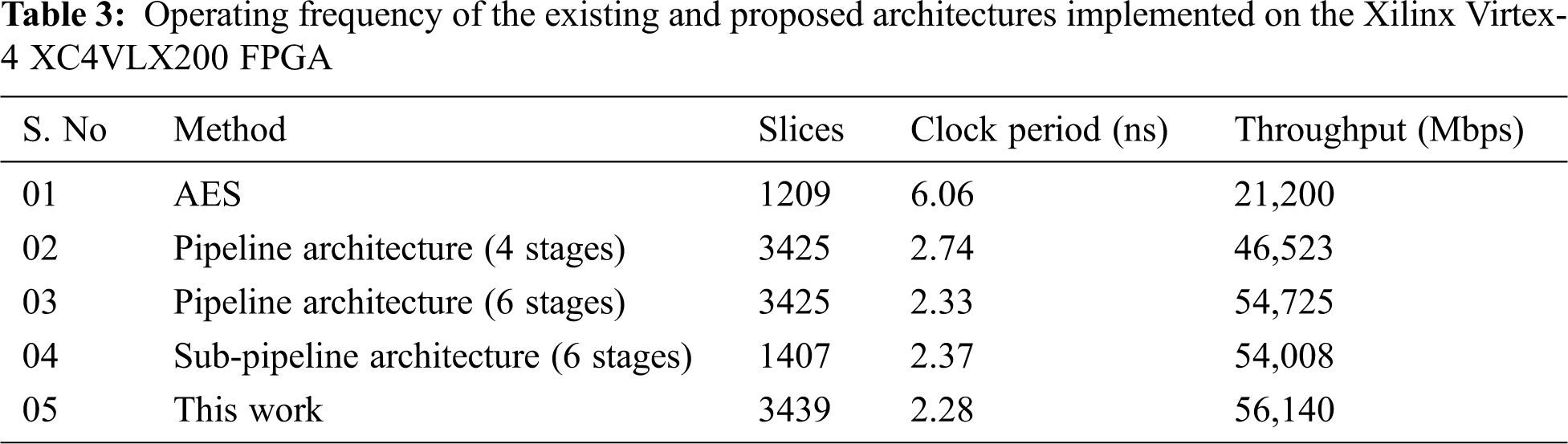

Figure 6: Area comparisons of the proposed and existing architectures
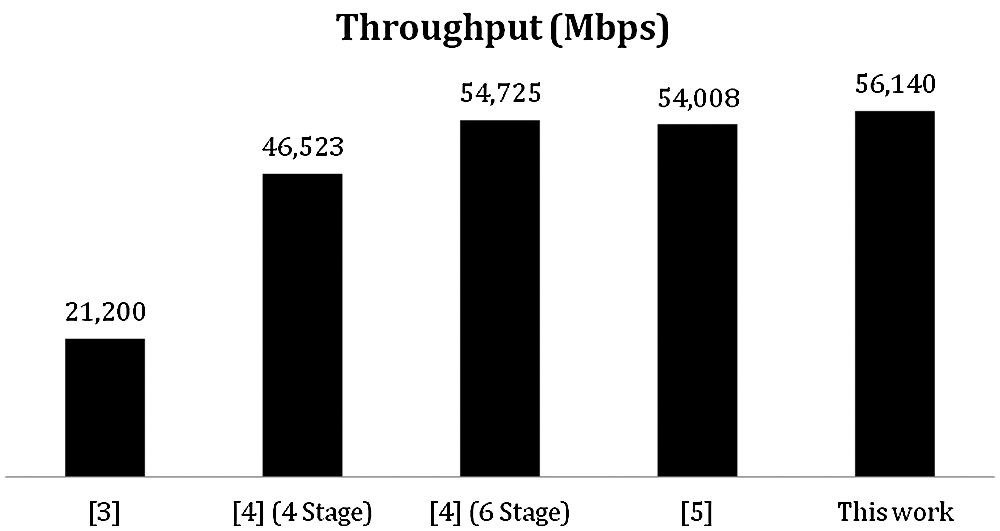
Figure 7: Throughput comparisons of the proposed and existing architectures
The throughput efficiency of the proposed architecture is compared to that of the other existing architectures, and the result is listed in Tab. 4. The proposed architecture shows an improvement of about 2.53% in throughput compared to the results obtained from the 6-stage pipeline architecture. Compared with the 6-stage sub-pipeline structure, the proposed architecture shows an improvement of about 3.8% in throughput and a greater improvement in speed. Also, the number of slices utilized by the new architecture is increased by about 59.09% compared to that of the 6-stage sub-pipeline and 0.5% compared to that of the 6-stage pipeline architecture. The clock period can be related to the propagation delay to generate output after the input data is given. With a lower clock period, the circuit generates an output in less time. Therefore, if a circuit has less propagation delay, then it is considered a high-speed circuit. A circuit is said to speed efficient if it takes a small amount of time to provide the output. However, to achieve high throughput, there is a little sacrifice in the area to implement this structure. The security is ensured because the non-linearity process in the S-box remains unchanged.

The proposed architecture can be expanded to AES-192 and AES-256, and similar improvements can be achieved. Security is the most crucial aspect of a cryptographic algorithm. The proposed architecture does not compromise the security of the algorithm because the modification of the existing architecture is made to the process of subkey generation. The basic AES operations of the algorithm remain unchanged. In the proposed architecture, the entire plain text will be processed by different numbers of iterations like that of the standard AES algorithm. The secret key and the length of the subkey used in the proposed architecture also remain the same. Also, in the subkey generation process, the interdependency between the subkey is preserved in each block. So, the security of the proposed algorithm is the same as that of the standard AES.
In this paper, a speed-efficient AES algorithm is proposed and implemented on FPGA. In the proposed architecture, the CFA-based pipeline architecture for key schedule operation is used. Also, the parallel execution of the subkey generation process is implemented in the proposed architecture. The proposed architecture aims to improve the execution speed of the algorithm without compromising the security and the area of the original AES algorithm. The structure is implemented on the Xilinx Vitex-4 FPGA. The analysis indicates that the proposed architecture achieves a higher speed than that of existing architectures with the same area. The critical path delay is reduced by 2.15% by this new pipelined structure. Because of the pipeline architecture and parallel block execution of the subkey generation process, this new architecture achieves an improvement of about 2.53% in throughput. However, the operating frequency can be further increased without affecting the area consumption. Also, some optimization techniques like the pipeline architecture in S-box can be exploited to extend this research work. Besides, the implementation of the basic AES operations can be improved to achieve a better area-efficient algorithm.
Acknowledgement: We would like to thank TopEdit (www.topeditsci.com) for the English language editing of this manuscript.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Daemen and V. Rijmen, “AES proposal: Rijndael,” Federal Information Processing Standard Publication, vol. 197, pp. 1–45, 2001. [Google Scholar]
2. T.Manoj Kumar and P. Karthigaikumar, “FPGA implementation of an optimized key expansion module of AES algorithm for secure transmission of personal ECG signals,” Design Automation for Embedded Systems, vol. 22, no. 1–2, pp. 13–24, 2018. [Google Scholar]
3. P. Karthigaikumar and K. Baskaran, “An ASIC implementation of low power and high throughput blowfish crypto algorithm,” Microelectronics Journal, vol. 41, no. 6, pp. 347–355, 2010. [Google Scholar]
4. F. R. Rezaeian, B. Rashidi and S. S. Masoud, “FPGA based fast and high-throughput 2-slow returning 128-bit AES encryption algorithm,” Microelectronic Journal, vol. 45, no. 8, pp. 1014–1025, 2014. [Google Scholar]
5. S. S. Priya, P. Karthigaikumar, N. M. Sivamangai and P.Kirti Gaurav Das, “An efficient hardware architecture for high throughput AES encryptor using MUX-based sub pipelined S-box,” Wireless Personal Communications, vol. 94, no. 1, pp. 2259–2273, 2017. [Google Scholar]
6. X. Zhang and K. K. Parhi, “High speed VLSI architectures for the AES algorithm,” IEEE Transactions on Very Large-Scale Integration (VLSI) Systems, vol. 12, no. 9, pp. 957–967, 2004. [Google Scholar]
7. I. Hammad, K. El-Sankary and E. El-Masry, “High speed AES encryptor with efficient merging techniques,” IEEE Embedded Systems Letters, vol. 2, no. 3, pp. 67–71, 2010. [Google Scholar]
8. C. P. Fan and J. K. Hwang, “FPGA implementations of high throughput sequential and fully pipelined AES algorithm,” International Journal of Electrical Engineering, vol. 15, no. 6, pp. 447–455, 2008. [Google Scholar]
9. S. Kumar, V. K. Sharma and K. K. Mahapatra, “Low latency VLSI architecture of s-box for AES encryption,” in Proc. Int. Conf. on Circuits, Power and Computing Technologies, Noorul Islam Centre For Higher Education, Thuckalay, India, pp. 694–698, 2013. [Google Scholar]
10. A. A. Kamal and A. M. Youssef, “An area optimized implementation of the advanced encryption standard,” in Proc. Int. Conf. on Microelectronics, The University of Edinburgh, UK, pp. 159–162, 2008. [Google Scholar]
11. M. Stefan, “A simple power-analysis (SPA) attack on implementations of the AES key expansion,” Information Security and Cryptology, vol. 2587, no. 1, pp. 343–358, 2003. [Google Scholar]
12. S. Sheikhpoura, A. Mahania and N. Bagherib, “Reliable advanced encryption standard hardware implementation: 32- bit and 64-bit data-paths,” Microprocessors and Microsystems, vol. 81, 103740, 2021. [Google Scholar]
13. T. Manoj Kumar and P. Karthigaikumar, “A novel method of improvement in advanced encryption standard algorithm with dynamic shift rows, sub byte and mixcolumn operations for the secure communication,” International Journal of Information Technology, vol. 12, no. 1, pp. 825–830, 2020. [Google Scholar]
14. B. Langenberg, H. Pham and R. Steinwandt, “Reducing the cost of implementing the advanced encryption standard as a quantum circuit,” IEEE Transactions on Quantum Engineering, vol. 1, pp. 1–12, 2020. [Google Scholar]
15. H. Indriyawati, T. Winartib and V. Vydia, “Web-based secure degree certificate legalization system using advanced encryption standard algorithm,” International Journal of Information Technology and Business, vol. 2, no. 2, pp. 14–18, 2020. [Google Scholar]
16. N. M. Mangai, P. Karthigaikumar, S. T. Vinod and D. A. Chandy, “FPGA implementation of elephant recognition in infrared images to reduce the computational time,” Journal of Ambient Intelligence and Humanized Computing, vol. 1, no. 1, pp. 1–16, 2018. [Google Scholar]
17. A. Paul, “Real-time power management for embedded m2m using intelligent learning methods,” ACM Transactions on Embedded Computing Systems, vol. 13, no. 5s, pp. 1–22, 2014. [Google Scholar]
18. T. Manoj Kumar, P. Karthigaikumar and V. Ramachandran, “An optimized s-box circuit for high speed AES design with enhanced PPRM architecture to secure mammographic images,” Journal of Medical Systems, vol. 3, no. 31, pp. 1, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |