Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.018358
Article

Optimization Based Vector Quantization for Data Reduction in Multimedia Applications

V. R. Kavitha1,*, M. Kanchana2, B. Gobinathan3, K. R. Sekar4 and Mohamed Yacin Sikkandar5

1Department of CSE, Prathyusha Engineering College, Thiruvallur, 602025, Tamil Nadu, India
2School of Computing, SRM Institute of Science and Technology, Kattankulathur, 603203, Tamil Nadu, India
3Jaya Sakthi Engineering College, Chennai, 602024, Tamil Nadu, India
4School of Computing, SASTRA Deemed University, Thanjavur, 613401, Tamil Nadu, India
5Department of Medical Equipment Technology, College of Applied Medical Sciences, Majmaah University, Al Majmaah, 11952, Saudi Arabia
*Corresponding Author: V. R. Kavitha. Email: vr.kavitha.cs@gmail.com
Received: 06 March 2021; Accepted: 13 April 2021

Abstract: Data reduction and image compression techniques in the present Internet and multi-media age are essential to increase image and video capacity in relation to memory, network bandwidth use and safe data transmission. There have been a different variety of image compression models with varying compression efficiency and visual image quality in the literature. Vector Quantization (VQ) is a widely used image coding scheme that is designed to generate an efficient coding book that includes a list of codewords that assign the input image vector to a minimum distance of Euclidea. The Linde–Buzo–Gray (LBG) historically widely used model produces the local optimal codebook. The LBG model’s codebook architecture is seen as an optimization challenge that can be resolved using metaheuristic algorithms. In this perspective, this paper introduces a new DPIO algorithm for codebook generation in VQ. The model presented uses LBG to initialise the DPIO algorithm to construct the VQ technique and is called the DPIO-LBG process. The performance of the DPIO-LBG model is validated with benchmark data and the effects of different performance aspects are investigated. The simulation values showed the DPIO-LBG model to be efficient interfaces of compression efficiency and image quality reconstructed. The presented model produces an efficient codebook with minimum computational time and a better signal to noise ratio (PSNR).

Keywords: Multimedia; data reduction; image compression; vector quantization; optimization algorithm

1  Introduction

The progressive Internet use contributes to the generation of multimedia information to be kept in the memory or forwarded by the device that congestions the network with minimal bandwidth for the channel. By minimising the amount of data to be transmitted, transmission quality can be improved. A slight delay can be sustained at this stage when the recipient accepts the recovery data with some loss. Recently, photographs are the main multimedia suppliers. Data reduction methods are employed to improve the efficiency of transmission and to ensure the superiority of the reconstructed picture. However, the compression ratio and recovered image quality are the primary parameters for every technique of compression. Furthermore, the supremacy of the restored image must be restricted to increase the CR of an image.

Before sending the data the compression process is used without delay or loss. This refers to the processing of source coding from the transmitter side to optimise transmission speed [1] in a state of change and reception tolerated decompression. The loss compression approach will achieve better CR and rebuild fidelity from both the sender and the receiver sides. The two goals called CR and reconstruction fidelity, therefore, are conflicting. The highest CR results in lower fidelity to reconstruction. Digital images are then the data carrier that has been widely used to routinely transfer data over the Internet, which is how the compression process is modelled. Vector quantization (VQ) is extensively used compared to other state-of-the-art image compression models due to the satisfying rate distortion feature and improved real-world efficiency of the application and used to conceal picture watermarkers as well as image data [2]. In addition, block truncation coding (BTC) is commonly used to compress the digital image and provides the encoded bits [3] with the VQ compression method operating mechanism. The encoder and decoder are actually supplied with a related codebook consisting of large codebooks. The actual image is calculated blockwise when compressed. In addition, Euclidean distance is calculated to evaluate the similarity between the current picture block and each code-word in a codebook. When the non-overlapping blocks are displayed, code-word index measure, index table with index values are created as the image compressed VQ code.

In the event of the VQ decompression, a process for search table was computed in a codebook to identify the codeword which shows the index value due to an index table that refers to an image block. A codeword is followed by reformed picture block pixel steps. It should be noted that a binary representation length, for the maximum index value of compressed code for a block, refers to CR size and reconstruction quality. Furthermore, the main drawback of VQ encoding is the negation of the association between nearby image blocks. For the improvement of VQ defects and the maximum compression functionality, Side Match VQ (SMVQ) has been established as an extended VQ [4] with a connection between neighbouring image blocks. Unlike VQ, codebook and subcodebooks are used to generate SMVQ encoding index values. The developers have currently planned SMVQ-based picture compression models and used SMVQ for extended applications such as image data hiding. In [5], the transmitter separated the image as a different set of blocks which are not overlapped and which are VQ-encoded by left and top blocks. In [6], it was suggested that the adaptive block classificator achieve minimal distortions. The recovery scheme designed in [7] has been developed to solve the problems in the error of the present block. Previous studies show that the Linde–Buzo–Gray (LBG) codebook design is considered to be an optimization problem, which needs to be solved through metaheuristic algorithms. This paper presents a novel Discrete Pigeon Inspired Optimization (DPIO) codebook generation algorithm in VQ. The presented model uses LBG to initialise the DPIO algorithm to construct the VQ technique and is called DPIO-LBG. The efficiencies of the DPIO-LBG model are evaluated on the basis of a benchmark dataset and outcomes of various aspects are analysed. The simulation values showed the DPIO-LBG model to be efficient interfaces of compression efficiency and image quality reconstructed.

2  Related Works

This segment discusses the recently proposed techniques of compression on the basis of VQ. Karri et al. [8] introduced the new BA-LBG method for Bat Algorithm (BA) for LBG. An efficient codebook with a limited working time, and with tuneable pulse emission rate as well as bats, the optimal peak signal-to-noise relation (PSNR) is the automatic zoom-function. Rasheed et al. [9] have created a new method to compress high-resolution images with a DFT and a Matrix Minimization (MM) model. It consists of modifying the picture using DFT, which produces real and imaginative elements. The measuring process is performed with the intensity of maximum frequency coefficients for these components. The initial component matrix undergoes a low-frequency (LFC) and high-frequency coefficients insulation (HFC).

Chiranjeevi et al. [10] proposed a metaheuristic optimization system for Cuckoo search (CS), which uses the levy flight algorithm rather than Gaussian, to optimise the LBG codebook. CS applies the maximum time for local and global codebook convergence. A novel VQ codebook model relating to swarm clustering was introduced in Fonseca et al. [11]. It also depends on the search mechanism of the Fish School (FSS). FSS is then used in the LBG scheme as a swarm clustering solution known as FSS-LBG. Additionally, the extension of the current FSS breeding process is used to increase the scanning capacity and to achieve better results through the PSNR of restored images.

Ammah et al. [12] proposed a DWT-VQ (Discrete Wavelet Transform-VQ) model to compress images and preserve the perceptual quality at a medically supported stage. Speckle noises in the ultrasound picture are greatly reduced here. When the picture is not ultrasound, the effect is insignificant, but the edge is preserved. The photos are then filtered using DWT. Then, the threshold system is used to emit coefficients. In Lu et al. [13] a Deep Convolutionary Neural Network (DCNN) was introduced to encode, quantize and decode image compression. A Fully Convolutionary VQ framework (VQNet) is developed in particular to measure the feature vectors in which representative VQNet vectors are optimised with alternate system parameters. Second, the current DCNN approaches are trained when large datasets are fine-tuned and effective. In Kasban et al. [14], the image background is isolated from an image background using an automatic histogram-dependent threshold and the image background is compressed by feasible CR using image pyramid and Lossy VQ-compression is implemented using a Generalized Lloyd Algorithm (GLA) model to produce a codebook. Next, ROI undergoes compression with minimal CR and data loss with the aid of Huffman Code (HC).

3  The Proposed DPIO-LBG Model

In the DPIO-LBG model, the codebook generated by the LBG technique is optimized by the use of DPIO algorithm in the designing of VQ for image compression process. The detailed processes involved in the presented DPIO-LBG model are discussed in the subsequent sections.

3.1 Vector Quantization

The fundamental concept of VQ has been defined in the following. Here, VQ is treated as a lossy data compression model in block coding. Assume the size of actual image Y={yij} be M×M pixels which have segmented various blocks with the sizes of n×n pixels. Besides, Nb=[ Nn ]×[ Nn ] blocks show a set of input vectors X=(xi,i=1,2,…,Nb) . Assume L as n×n and input vector χi,χi∈ℜL in which ℜL indicates an L-dimensional Euclidean space. The codebook C is composed of NcL -dimensional codewords, which shows that, C={c1,c2,…,cNC},cj∈ℜL,∀j=1,2,…,Nc . The input vector is depicted as a row vector χi=(xi1,xi2,…,xiL) and jth codeword of a codebook is depicted as cj=(cj1,cJ2cjL) . The VQ models allocate input vector to a codeword, and replaces the corresponding input vectors which are subjected to compression [15]. The optimization of C by means of Mean Square Error (MSE) is developed by reducing the distortion function D. Actually, low value of D is considered as better quality of C as depicted below:

D(C)=1Nb∑j=1Nc⁡∑i=1Nb⁡μij⋅‖xi−cj‖2 (1)

And referred to as:

∑j=1Nc⁡μij=1,∀i∈{1,2,…,Nb} (2)

μij={1ifχiisinthejthcluster;0otherwise (3)

and

Lk≤cjk≤Uk,k=1,2,…,L (4)

where Lk denotes the lower value of k th element in training vectors, and Uk implies the higher value of kth element from input vectors. The ‖x−c‖ refers the Euclidean distance among vector χ as well as codeword c. Fig. 1 illustrates the flowchart of VQ technique.

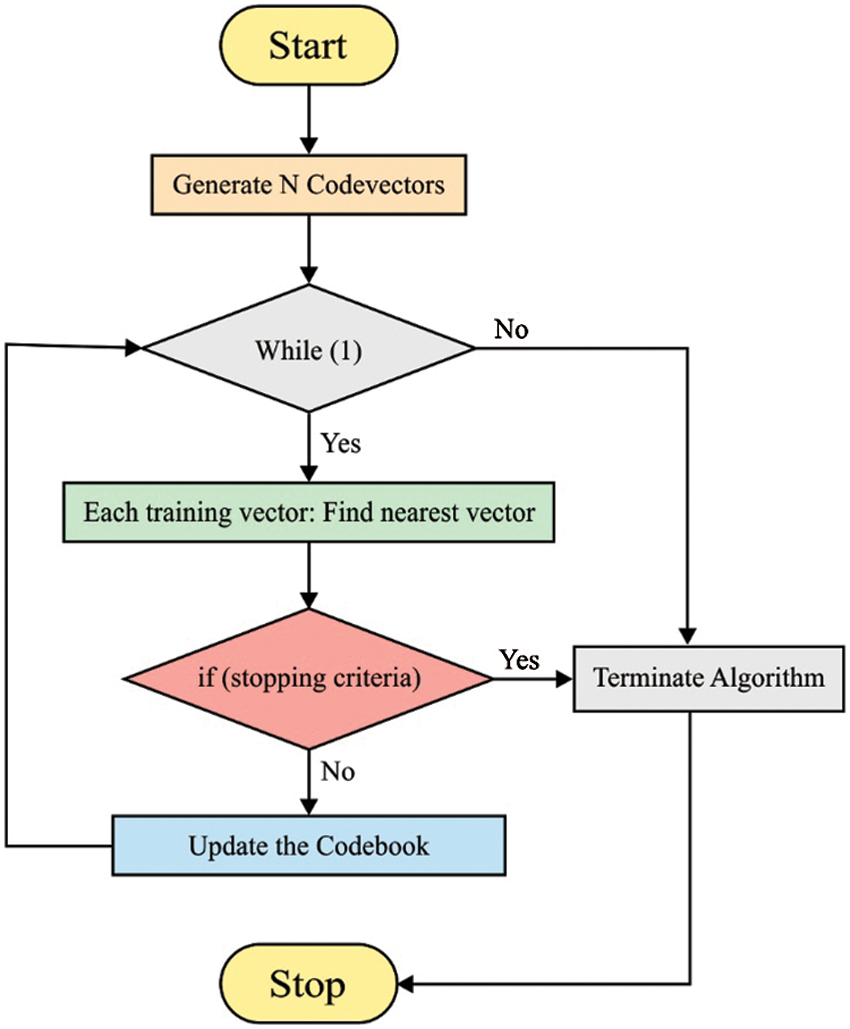
Figure 1: Flowchart of VQ

The 2 essential conditions are used for optimal VQ.

(1) The portion Rj,j=1,…,Nc should convince

Rj⊃{x∈χ:d(x,cj)<d(x,ck),∀k≠j}. (5)

(2) The codeword cj has to be applied by centroid of Rj :

cj=1Nj∑i=1Nj⁡xi,xi∈Rj, (6)

where Nj denotes the overall values of vectors from Rj .

3.2 LBG Algorithm

A widely employed VQ is Generalized Lloyd Algorithm (GLA) also named LBG. The noise gets reduced next to the recursive execution of the LBG model; however, it offers the local codebook. It uses pre-defined conditions for input vectors while computing the codebook. From the input vectors, xi,i=1,2,…,Nb , the distance function d , and initial codewords cj(0), j=1,…,Nc . Fig. 2 illustrates the general process involved in LBG model. The LBG uses 2 conditions to generate best codebook on the basis of given method:

•   Divide the input vectors as numerous groups with the help of minimum distance rule [15]. The partition results are recorded in a Nb×Nc binary indicator matrix U where the elements are considered as shown below:

μij={1ifd(xi,cj(k))=mind(xi,cp)0otherwise (7)

•   Estimate the centroid of a partition. Substitute the previous codewords using centroids:

cj(k+1)=∑i=1Nb⁡μijxi∑i=1Nb⁡μij,j=1,…,Nc. (8)

•   Follow steps (1) and (2) till no cj, j=1,…,Nc changes exist.

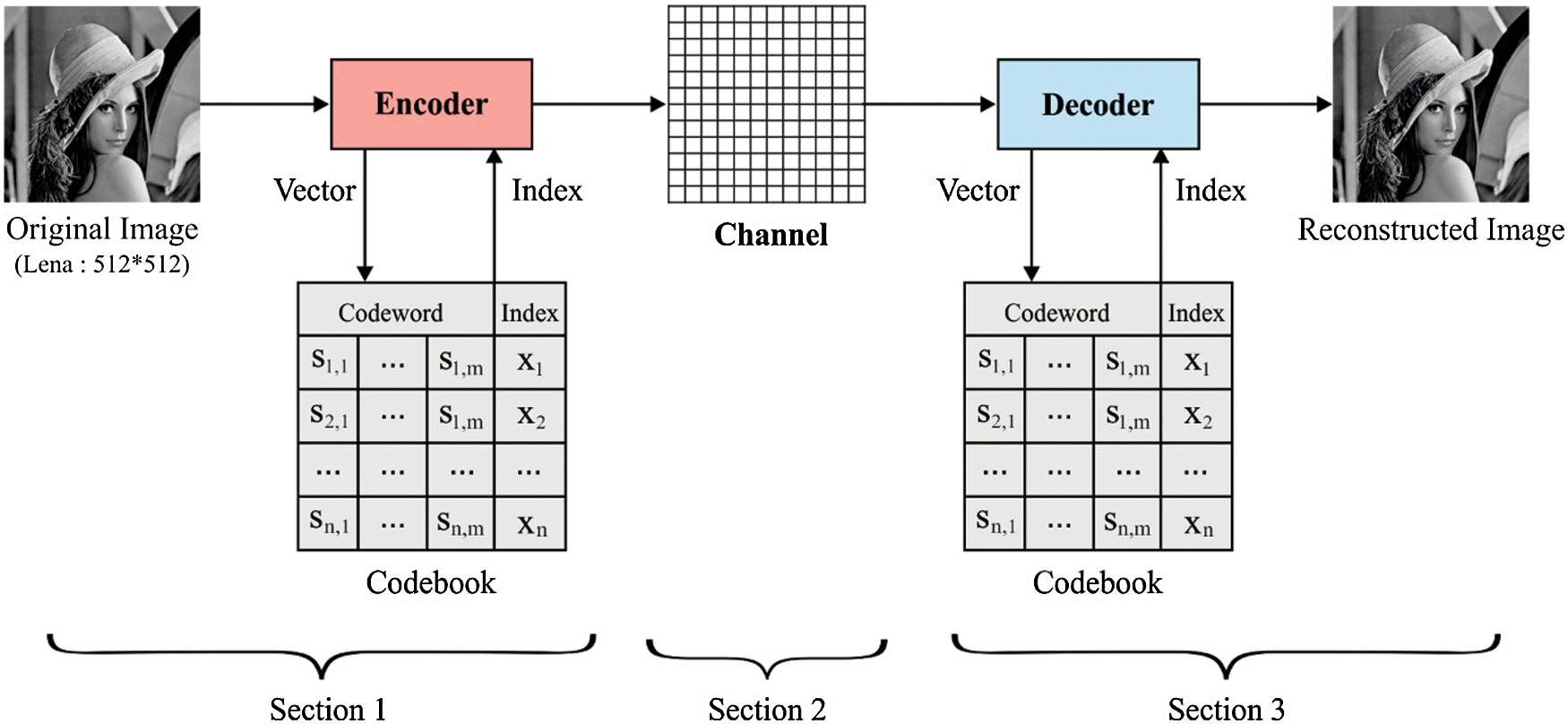
Figure 2: General process involved in LBG model

3.3 Procedure of DPIO Algorithm

Actually, PIO method reflects the homing behavior of pigeons which is evolved from developed SI method. Particularly, 2 operators have been developed with the help of ideal principles related to homing features of pigeons namely, (1) Map and Compass operator that showcases the homing characteristics assisted by sun and magnetic elements; (2) Landmark operator represents the homing nature oriented landmark of well-known area. Magnetoreception is defined as a sensing operator that enables to predict of a magnetic field to learn the direction and location. Pigeons detect the earth field with the help of magnetoreception to grasp the map in their brains. Then, the altitude of sun is a compass to change the direction [16]. Map and compass operator is used to refer the homing nature. Consider that search space is N -dimensional, then i-th pigeon of swarm is illustrated as N -dimensional vector Xi=(xi,1,xi,2,…,xi,N) . Here, the velocity of pigeon showcases the location of pigeon and depicted by alternate N -dimensional vector yi=(vi,1,vi,2,…,vi,N) . The previously consulted location of i-th pigeon is defined as Pi=(pi,1,pi,2,…,pi,N) . The global best position of a swarm is g=(g1,g2,…,gN) , and the superscripts depict the iteration value, and a pigeon flies on the basis of given expression:

vi,jt;=vi,jt−1e−Rt+r(gjt−1−χi,jt−1) (9)

χi,jt=xi,jt−1+vi,jt (10)

where j=1,2,…,N;i=1,2,…,M , and M denotes the size of a swarm; R refers a map and compass factor which is applied to manage the effect of advanced velocity on present velocity; r indicates the random value; and t=1,2,… , estimates the iteration value. Eq. (9) is applied to determine the velocity of pigeons and distance of new position from global best knowledge. Followed by, pigeon moves to the new place as per given in Eq. (10).

If the pigeon is flying in well-known region suited nearby the home, then it moves by a landmark. Landmark operator is modeled to reflect the homing nature. Moreover, the count of pigeons is reduced to a certain extent. The better portion would fly to the defined place, and worse portion would fly to random portion.

cjt=∑i=1M⁡(xi,jt−1f(χit−1))M∑i=1M⁡(f(χit−1)) (11)

xi,jt=xi,jt−1+r(cjt−χi,jt−1) (12)

where j=1,2,…,N;i=1,2,…,M , and M implies the size of better portion; Eq. (11) has been applied to estimate the center of pigeons. Followed by, pigeon moves to a better place as per the Eq. (12).

In PIO, 2 features have been applied namely, search process and portioning of swarm that has contributed to greater efficiency. Since the search process has been classified as 1st and 2nd stage, PIO models apply different forms of searching operator in varied phase that tries to manage the explorative and exploitative ability. Hence, division of swarm limits the residual swarm size and classifies swarm as a successful and unsuccessful group, followed by PIO models that develop various search principles for diverse groups. Classification of swarm is a type of division that has been assumed as essential characteristics of SI. The 3D path planning for UAV, node self-development for marine Wireless Sensor Networks (WSN), controlling variable optimization automatically by landing mechanism, and robust attitude management intends to reuse thevehicles. Fig. 3 demonstrates the flowchart of PIO model.

In DPIO algorithm [17], the 2 elements χ1,j and χ2,j from 2 position vector X1 and X2 , minus operator ⊖ , has been applied for generating velocity vj in j-th dimension is depicted as (13):

vj=x2,j ⊖ x1,j={x2,j,χ2≠χ1,je∈nc(j),x2=x1,j (13)

where nc(j) denotes the upcoming visiting city of j and e defines a city that is randomly selected from nc(j) . By the application of (13), the simulation of minus operator among 2 location X2 and X1 is meant to be velocity V in which the element vj is similar to χ2,j ⊖ χ1,j . For j-th velocity element vj , when χ2j is unequal to χ1,j , then vj=χ2,j , else, velocity component is selected randomly from nc(j) . Different ways are developed to make nc(j) for a city j:(1) Empty, which refers that nc(j) is null; (2) Full defines that nc(j) encloses alternate cities; and (3) Heuristic shows that nc(j) is nearby city list deployed from k nearest cities, in which k denotes the parameter which implies length of c(j) . Based on the pigeon condition, it selects the applicable way to move in nc(j) .

Followed by, pigeon applies (3) to determine the center and employ center as the instance for flying. Certainly (3) is not suitable for discrete data in X . However, the mode restricts the exemplar to prominently used samples, and it is varied from each other. Here, every component has a chance to be decided and prominent for having maximum probability to be decided. In order to perform this, a new selection operator has been followed. From the list of position elements (x1,j,x2,j,…,xm,j) in j-th dimension, selection operator ∪ , which has to be determined as component cj in j-th dimension, is depicted as (14). Likewise, the position component xj as well as velocity component vj , is the meaning of exemplar unit cj shows an edge from city j to city cj.

cj=Ui=1mxi,j=xk,j, (14)

where k denotes randomly selected solution from (1,2,…,m)

From the position χ and velocity component vj , the plus operator ⊕, which is applied to generate a novel location as depicted in (15).

χ⊕vj=min(inverse(x,vj),insert(x,vj),swap(x,v)) (16)

where inverse (x,vj),insert(x,vj) , and swap (x,vj) denotes the inverse, block insert, as well as swap operator correspondingly. The inverse (x,vj) operator generates a novel solution by inversing the cities from xj and vj . The insert (x,vj) operator generates a novel solution by changing the ensemble of cities which results in vj to xj . A swap (x,vj) operator generates novel solution by interchanging the location of xj and vj . Especially, for edge ej,vj is depicted by velocity component vj , it applies inverse operator, blocks insert operator as well as swap operator for generating 3 neighbor solutions.

Under the application of new operators described, the flying operators are explained in (17).

x=x⊕(P ⊖ x)=((((x⊕(p1 ⊖ x1))⊕(p2 ⊖ x2)),…)⊕(pn ⊖ xn)) (17)

In DPIO mechanism, map and compass operator as well as landmark operators are employed to generate novel solution, however the semantic of exemplar component pj and visiting city list nc in minus operator (13) are based on the pigeon state. When the pigeon is involved in first stage, then pj defines the j-th component of personal best solution of arbitrarily decided pigeon and Full strategy has been applied nc . When the pigeon is next stage, then pj refers the j-th element of ‘center’ generated by selection operator as well as Heuristic principle has been applied for developing nc.

For map and compass operator, there are 2 important variations among and actual one:

a) In the actual stage, the global best solution has been applied for assisting the pigeon’s movement. In pigeon learns from global best solution, and also learns from optimal solution of diverse pigeon in various dimension. It is a type of comprehensive learning principle and is effectively utilized for TSP.

b) Unlike the actual state, actual velocity is not applied. Rather, the minus operator generates novel velocity from subsequent visiting city list in 2 similar operands. In case of map and compass operators, Full strategy has been utilized for developing consecutive visiting city lists. The principle behind this method is operated in 2 factors: (1) mostly, edges in actual velocity are previously in recent location. At this point, to include the edges from actual velocity with recent position is unknown; (2) to generate novel velocity from the accessible cities improves the diversity.

For landmark operator, there are 2 essential variations from new one:

a) The semantics of center-based model is dissimilar. In DPIO, exemplar element is a randomly decided component from present swarm.

b) In DPIO model, heuristic data has been applied to enhance the intensification capability. In particular, in the landmark operator, Heuristic principle has been applied for developing the upcoming visiting city list.

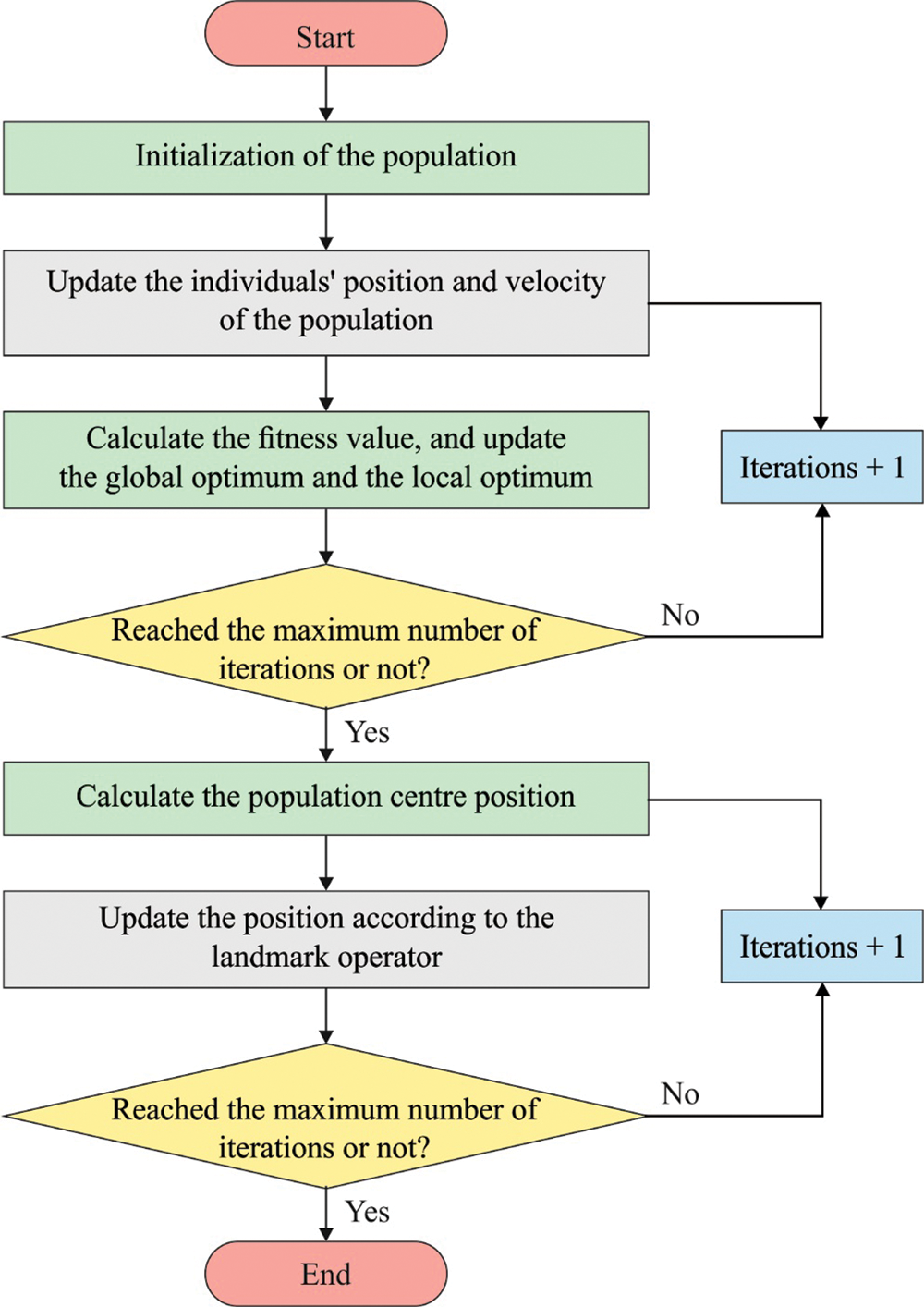
Figure 3: Flowchart of PIO model

3.4 Application of DPIO-LBG Model for Data Reduction

The working principle involved in the presented DPIO-LBG model is given as follows. Primarily, the input images are partitioned into a set of non-overlapping blocks are quantized using LBG technique. A codebook which is generated by LBG model undergoes training by the DPIO model. It is applied to fulfill the requirements of global convergence and ensure it. The index numbers are transmitted on the communication media and reconstructed in the receiving end by the use of the decoder. The reconstructed index numbers and the equivalent codewords are sorted effectively to generate the reconstructed image size identical to the provided input image.

Step 1: Parameter initialization

During this step, the construction of codebook by LBG method is considered as the initial solution and the rest of the solutions are generated randomly. Then, the obtained solutions define a codebook of Nc codewords.

Step 2: Selection of best solution

The fitness value of the solutions is processed and the solution with maximum fitness location is considered as the optimum solution.

Step 3: Generation of effective solutions

The position and velocity of the pigeons are updated using compass and map operations. If the randomly produced number R exceeds the value of ~a, then the worse positions and velocities are updated with the recently determined ones and sustain the optimal solutions unchanged.

Step 4: Finding Optimal solutions

Sort the generated solutions based on the application of fitness function and pick up the optimal solution.

Step 5: Stopping condition

Repeat steps 2–3 till the termination criteria get fulfilled.

4  Performance Validation

The simulation of the DPIO-LBG algorithm takes place using MATLAB R2014a. To perform experimental analysis, a collection of 4 grayscale images (such as Lena, Baboon, Goldhill, and Barba) is used with 8-bit resolution. The images are present in the bmp format with the pixel size of 512 * 512 except the Goldhill image which has the pixel size of 720 * 576. As explained earlier, the images are split into non-overlapping blocks with a pixel size of 4 * 4. The blocks are treated as the input vector to the presented system. For validating the experimental results, many codebooks are generated with varying sizes of 8, 16, 32, 64, and 128 are employed. Besides, the results are examined under the presence of varying bit rates and block sizes for ensuring image quality and time complexity. The sample grayscale images are provided in Fig. 4.

Figure 4: Sample images (a) LENA (b) BABOON (c) GOLDHILL (d) BARBA

Tab. 1 and Fig. 5 examines the PSNR analysis of the DPIO-LBG algorithm with existing methods under varying bit rates of 0.1875, 0.2500, 0.3125, and 0.3750. The obtained results denoted that the DPIO-LBG algorithm has outperformed all the compared methods by obtaining a higher PSNR value under all the applied bit rates and codebook sizes. From the table, it is evident that the DPIO-LBG algorithm has achieved a higher PSNR of 25.8 dN under the presence of 0.1875-bit rate and codebook size of 8 on the applied LENA image. At the same time, the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG algorithms have resulted in a lower PSNR of 24.2, 24.1, 24.0, 24.0, and 24.0 dB respectively. Similarly, under the bit rate of 0.2500, the presented DPIO-LBG algorithm has exhibited effective PSNR of 26.7 dB whereas the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG algorithms have gained a slightly lower PSNR of 25.5, 25.2, 25.1, 25.1, and 25.0 dB respectively.

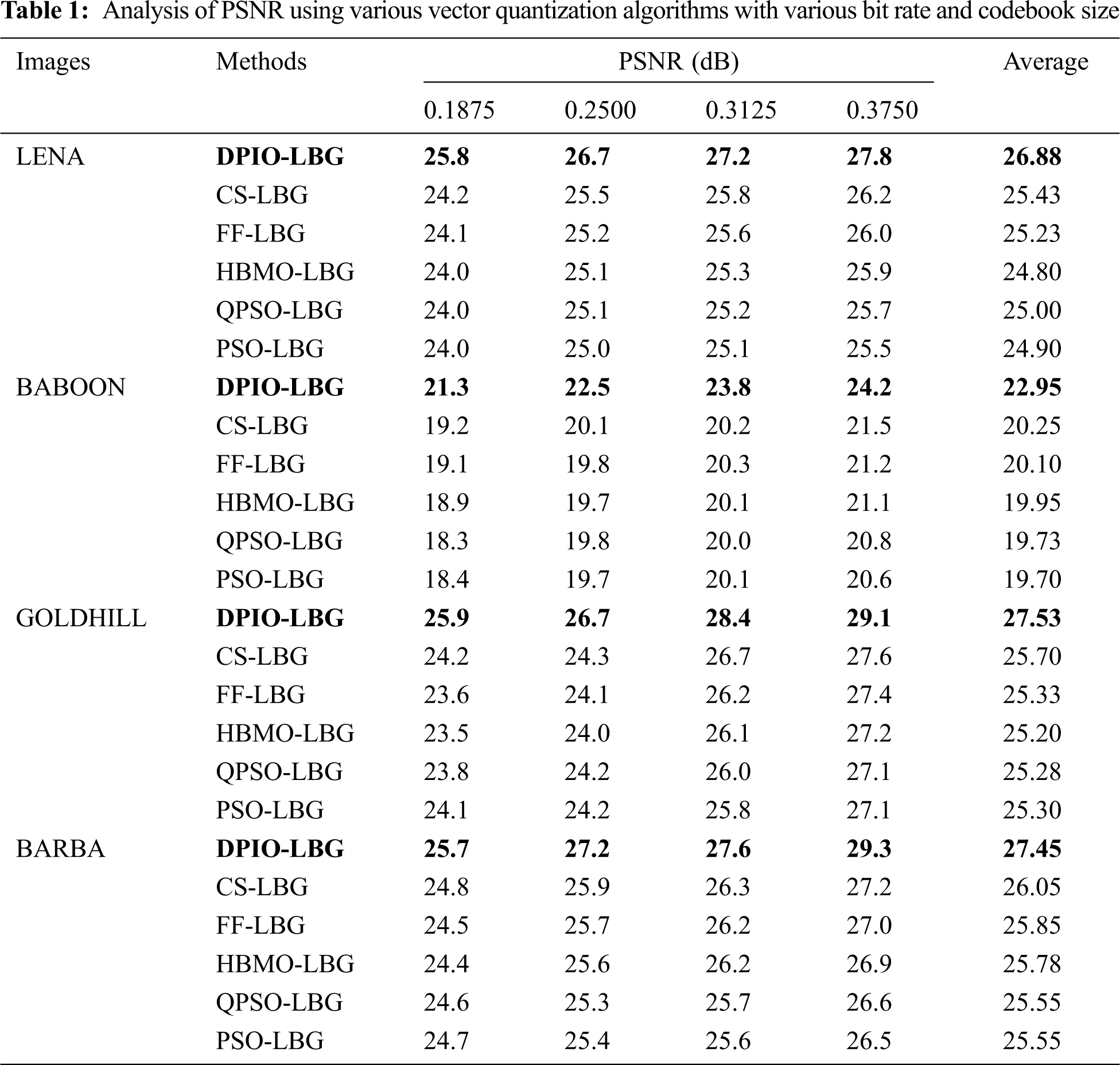
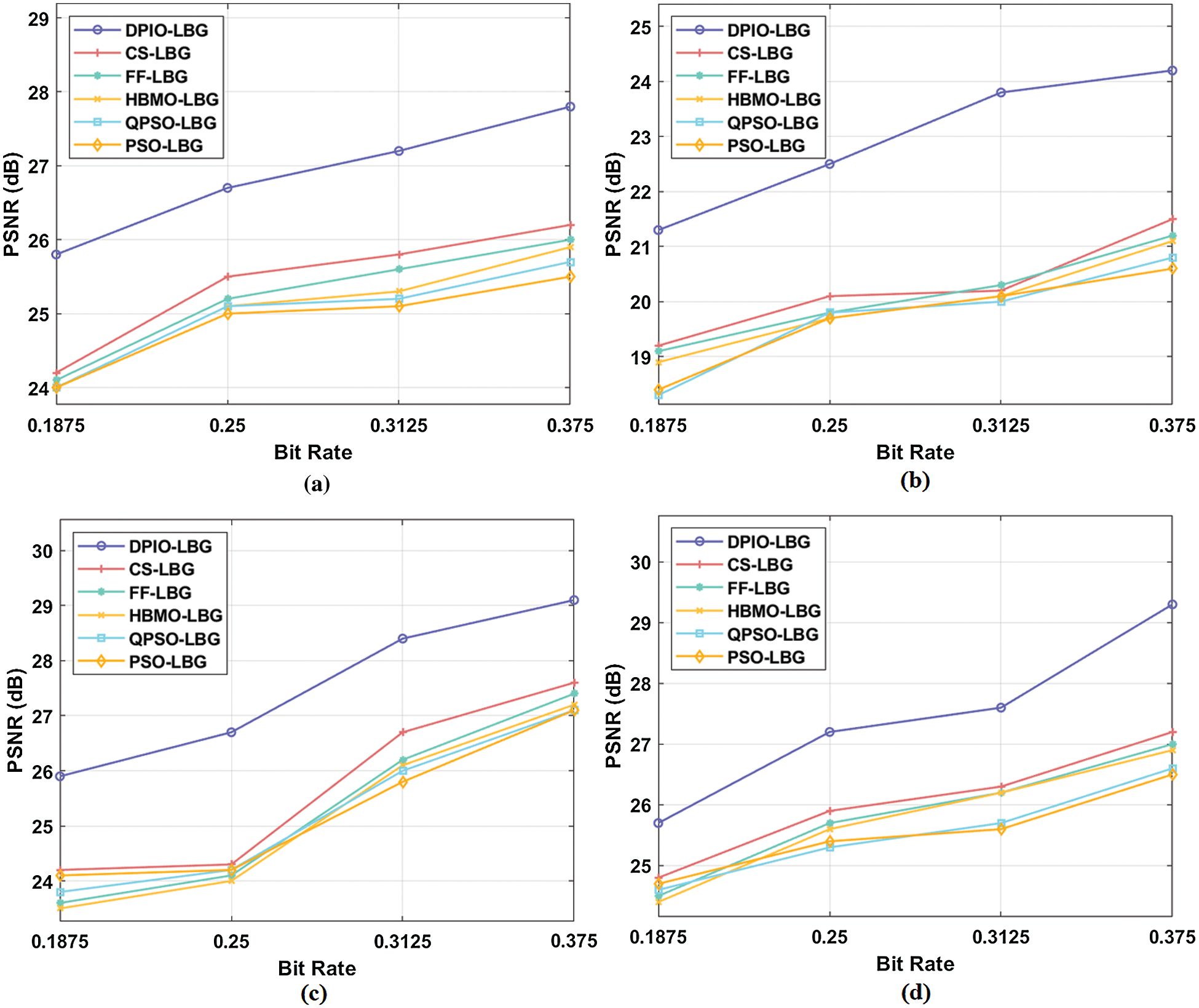
Figure 5: PSNR analysis (a) Bitrate of 0.1875 and codebook size of 8 (b) Bitrate of 0.2500 and codebook size of 16 (c) Bitrate of 0.3125 and codebook size of 32 (d) Bitrate of 0.3750 and codebook size of 64

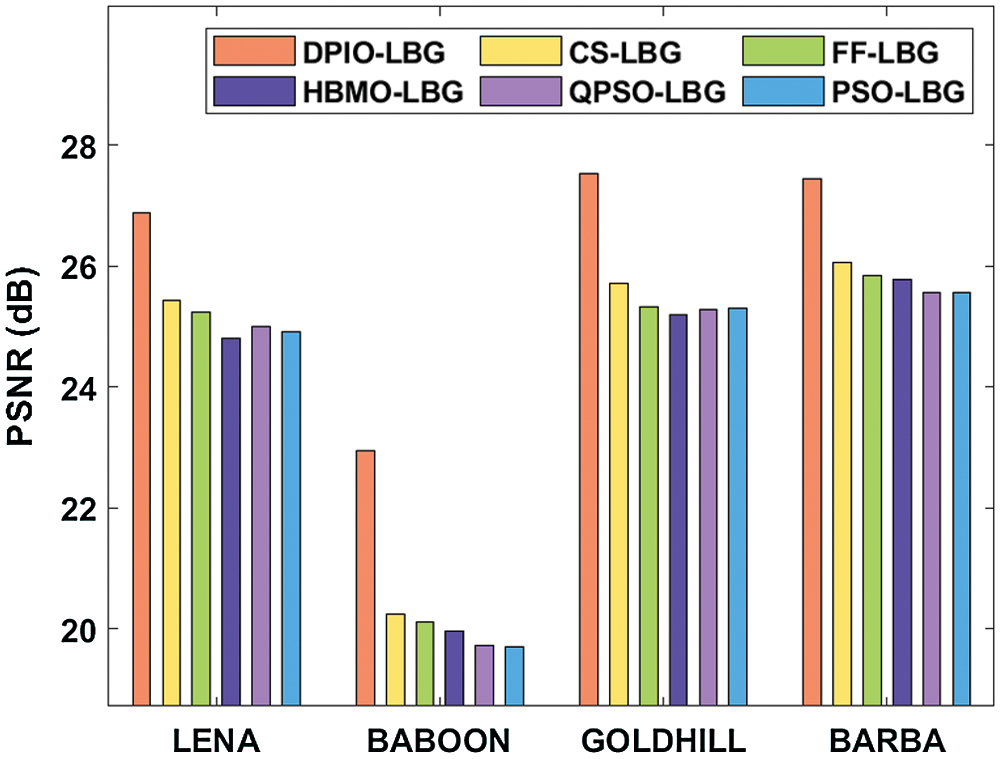
Figure 6: Average PSNR analysis of the DPIO-LBG model

Along with that, under the bit rate of 0.3125, the presented DPIO-LBG algorithm has displayed effective PSNR of 27.2 dB whereas the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG algorithms have obtained a slightly lower PSNR of 25.8, 25.6, 25.3, 25.2, and 25.1 dB respectively. Simultaneously, under the bit rate of 0.3750, the presented DPIO-LBG algorithm has revealed better PSNR of 27.8 dB whereas the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG algorithms have obtained a certainly decreased PSNR of 26.2, 26.0, 25.9, 25.7, and 25.5 dB respectively. Likewise, the presented DPIO-LBG model has exhibited superior PSNR values on the other applied test images. Fig. 6 demonstrates the average PSNR analysis of the presented DPIO-LBG model on the applied four test images. The figure exhibited that the DPIO-LBG algorithm has surpassed the compared methods on the applied test images. For instance, on the applied LENA image, the presented DPIO-LBG algorithm has reported maximum PSNR value of 26.88 dB whereas the PSO-LBG algorithm has obtained a minimum PSNR value of 24.90 dB. Simultaneously, on the applied BABOON image, the presented DPIO-LBG algorithm has attained a higher PSNR value of 22.95 dB whereas the PSO-LBG algorithm has achieved a certainly lower PSNR value of 19.70 dB. Concurrently, on the applied GOLDHILL image, the presented DPIO-LBG algorithm has obtained a superior PSNR value of 26.88 dB whereas the PSO-LBG algorithm has obtained a minimum PSNR value of 24.90 dB. At last, on the applied BARBA image, the presented DPIO-LBG algorithm has revealed maximum PSNR value of 27.45 dB whereas the QPSO-LBG and PSO-LBG algorithms have accomplished a lower and identical PSNR value of 24.90 dB.

Tab. 2 and Fig. 7 observes the CT analysis of the DPIO-LBG model with existing methods under varying bit rates of 0.1875, 0.2500, 0.3125, and 0.3750. The attained outcomes denoted that the DPIO-LBG model has demonstrated all the compared methods by achieving a higher CT value under all the applied bit rates and codebook sizes. From the table, it can be evident that the DPIO-LBG model has reached a minimum CT of 682.5 s under the presence of 0.1875-bit rate and codebook size of 8 on the applied LENA image.

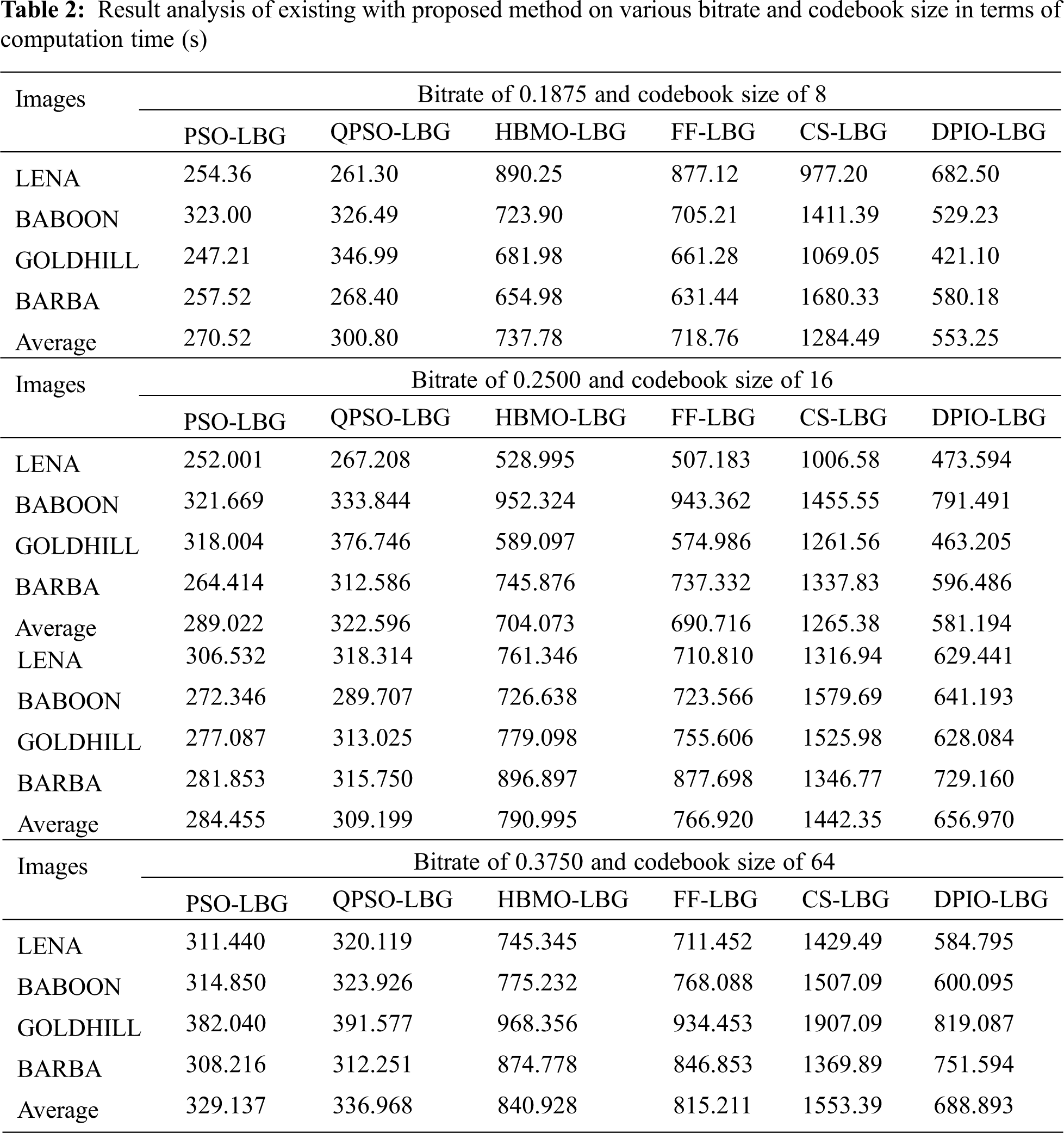
Simultaneously, the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG methodologies have resulted in a higher CT of 977.2, 877.12, 890.25, 261.30, and 254.36 s correspondingly. Likewise, under the bit rate of 0.2500, the proposed DPIO-LBG algorithm has exhibited effective CT of 473.594 s while the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG algorithms have gained a slightly higher CT of 1006.58, 507.183, 528.995, 267.208, and 252.001 s correspondingly. Along with that, under the bit rate of 0.3125, the presented DPIO-LBG algorithm has showcased a lower CT of 629.441 whereas the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG algorithms have obtained a slightly higher CT of 1316.94, 710.810, 761.346, 318.314, and 306.532 s respectively. At the same time, under the bit rate of 0.3750, the presented DPIO-LBG algorithm has revealed minimum CT of 584.795 s but the CS-LBG, FF-LBG, HBMO-LBG, OPSO-LBG, and PSO-LBG techniques have reached a certainly superior CT of 1429.49, 711.452, 745.345, 320.119, and 311.440 s respectively. Also, the presented DPIO-LBG model has exhibited superior CT values on the other applied test images.

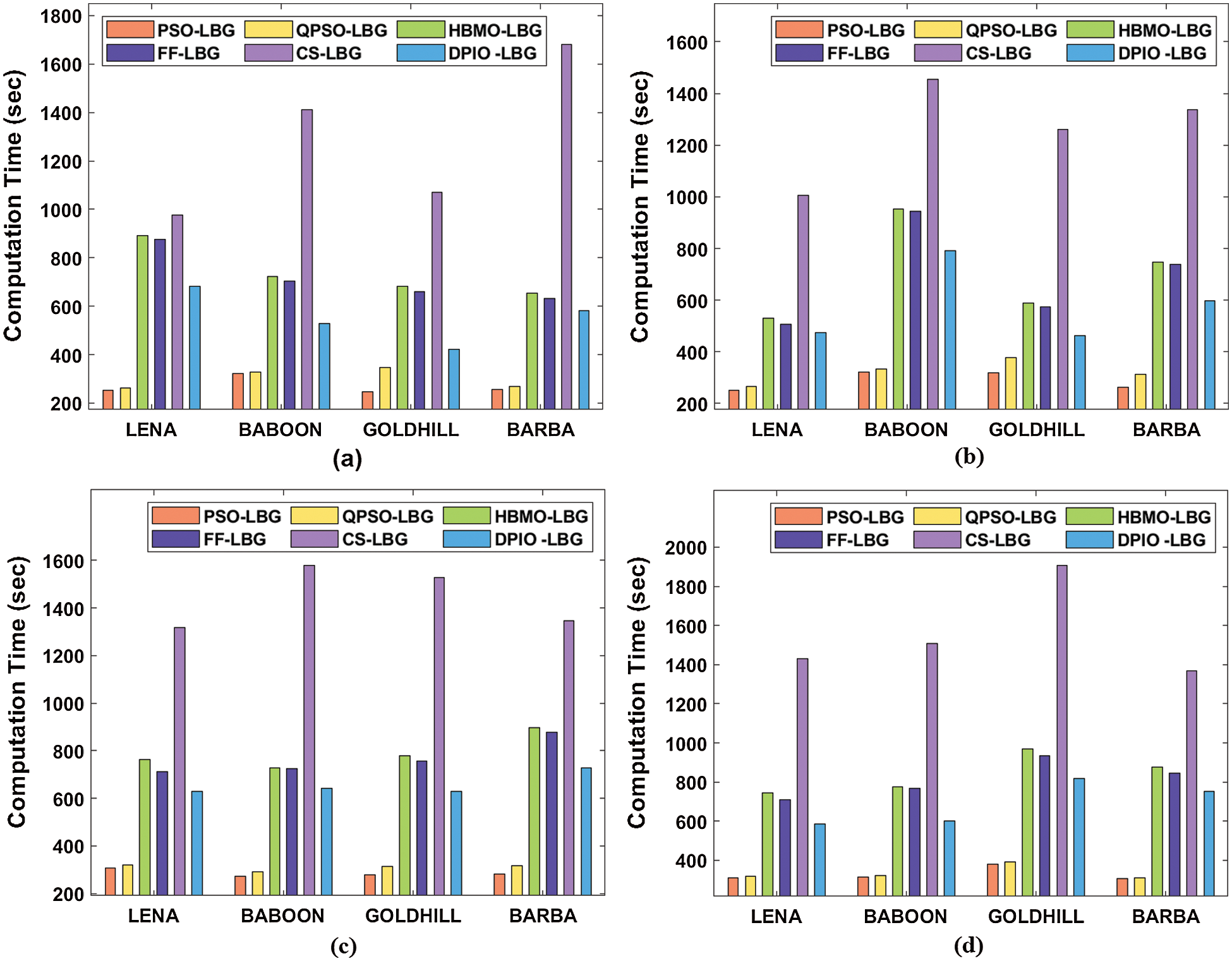
Figure 7: Computation time analysis (a) Bitrate of 0.1875 and codebook size of 8 (b) Bitrate of 0.2500 and codebook size of 16 (c) Bitrate of 0.3125 and codebook size of 32 (d) Bitrate of 0.3750 and codebook size of 64

5  Conclusion

This study introduced a new DPIO codebook generation algorithm called DPIO-LBG. Input images are primarily divided into non-overlapping blocks that are then quantified using LBG technology. The codebook of the LBG model is trained by using the DPIO algorithm. It is implemented to meet and ensure the criteria of global convergence. The index numbers are transmitted on the contact media and reconstituted using the decoder at the receiving end. The presented model uses LBG to initialise the DPIO algorithm for the VQ technique. The efficiencies of the DPIO-LBG model are evaluated on the basis of a benchmark dataset and outcomes of various aspects are analysed. The simulation values showed the DPIO-LBG model to be efficient interfaces of compression efficiency and image quality reconstructed. The model presented produces an efficient codebook with the lowest calculation time and a better PSNR. In the future, the efficiency of the proposed model can be enhanced by using dictionary encoding techniques.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. S. Taubman and M. W. Marcellin, JPEG 2000: Image Compression Fundamentals Standards and Practice, 1sted., vol. 11. USA: Springer International, pp. 1–286, 2001. [Google Scholar]

 2.  C. Qin and Y. C. Hu, “Reversible data hiding in VQ index table with lossless coding and adaptive switching mechanism,” Signal Processing, vol. 129, no. 2, pp. 48–55, 2016. [Google Scholar]

 3.  C. Qin, P. Ji, C. Chang, J. Dong and X. Sun, “Non-uniform watermark sharing based on optimal iterative BTC for image tampering recovery,” IEEE MultiMedia, vol. 25, no. 3, pp. 36–48, 2018. [Google Scholar]

 4.  T. Kim, “Side match and overlap match vector quantizers for images,” IEEE Transaction on Image Processing, vol. 1, no. 2, pp. 170–185, 1992. [Google Scholar]

 5.  S. S. Kambel and A. S. Deshpande, “Image compression based on side match vector quantization,” International Journal of Engineering Science and Computing, vol. 6, no. 5, pp. 5777–5779, 2016. [Google Scholar]

 6.  S. Lin and S. C. Shie, “Side-match finite-state vector quantization with adaptive block classification for image compression,” IEICE Transactions on Information and Systems, vol. 83, no. 8, pp. 1671–1678, 2000. [Google Scholar]

 7.  C. C. Chang, F. C. Shiue and T. S. Chen, “Pattern-based side match vector quantization for image compression,” The Imaging Science Journal, vol. 48, no. 2, pp. 63–76, 2000. [Google Scholar]

 8.  C. Karri and U. Jena, “Fast vector quantization using a Bat algorithm for image compression,” Engineering Science and Technology, An International Journal, vol. 19, no. 2, pp. 769–781, 2016. [Google Scholar]

 9.  M. H. Rasheed, O. M. Salih, M. M. Siddeq and M. A. Rodrigues, “Image compression based on 2D discrete Fourier transform and matrix minimization algorithm,” Array, vol. 6, no. 2, pp. 100008–100024, 2020. [Google Scholar]

10. K. Chiranjeevi and U. R. Jena, “Image compression based on vector quantization using cuckoo search optimization technique Ain Shams,” Engineering Journal, vol. 9, no. 4, pp. 1417–1431, 2018. [Google Scholar]

11. C. S. Fonseca, F. A. Ferreira and F. Madeiro, “Vector quantization codebook design based on fish school search algorithm,” Applied Soft Computing, vol. 73, no. 2, pp. 958–968, 2018. [Google Scholar]

12. P. N. T. Ammah and E. Owusu, “Robust medical image compression based on wavelet transform and vector quantization,” Informatics in Medicine Unlocked, vol. 15, pp. 100183, 2019. [Google Scholar]

13. X. Lu, H. Wang, W. Dong, F. Wu, Z. Zheng et al., “Learning a deep vector quantization network for image compression,” IEEE Access, vol. 7, pp. 118815–118825, 2019. [Google Scholar]

14. H. Kasban and S. Hashima, “Adaptive radiographic image compression technique using hierarchical vector quantization and Huffman encoding,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 7, pp. 2855–2867, 2019. [Google Scholar]

15. M. H. Horng, “Vector quantization using the firefly algorithm for image compression,” Expert Systems with Applications, vol. 39, no. 1, pp. 1078–1091, 2012. [Google Scholar]

16. Z. Cui, J. Zhang, Y. Wang, Y. Cao, X. Cai et al., “A pigeon-inspired optimization algorithm for many-objective optimization problems,” Science China Information Sciences, vol. 62, no. 70212, pp. 1218, 2019. [Google Scholar]

17. Y. Zhong, L. Wang, M. Lin and H. Zhang, “Discrete pigeon-inspired optimization algorithm with metropolis acceptance criterion for large-scale traveling salesman problem,” Swarm and Evolutionary Computation, vol. 48, no. 1, pp. 134–144, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.