DOI:10.32604/iasc.2022.020132

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.020132 |  |
| Article |
A Hybrid Multi-Criteria Collaborative Filtering Model for Effective Personalized Recommendations
Faculty of Information Technology, Al-Ahliyya Amman University, Amman, 19328, Jordan
*Corresponding Author: Qusai Y. Shambour. Email: q.shambour@ammanu.edu.jo
Received: 09 May 2021; Accepted: 10 June 2021
Abstract: Recommender systems act as decision support systems in supporting users in selecting the right choice of items or services from a high number of choices in an overloaded search space. However, such systems have difficulty dealing with sparse rating data. One way to deal with this issue is to incorporate additional explicit information, also known as side information, to the rating information. However, this side information requires some explicit action from the users and often not always available. Accordingly, this study presents a hybrid multi-criteria collaborative filtering model. The proposed model exploits the multi-criteria ratings, implicit similarity, similarity transitivity and global reputation concepts to expand the space of potential recommenders. This expansion will enhance the prediction accuracy and coverage of the proposed model when applied to sparse data situations. To show effectiveness of the proposed model, a set of experiments are conducted on two real-world multi-criteria datasets, Yahoo! Movies and TripAdvisor. The experimental results demonstrate the superiority of the proposed model compared to a number of existing collaborative filtering-based recommendation methods under a variety of evaluation metrics.
Keywords: Recommender systems; collaborative filtering; multi-criteria; implicit similarity; global reputation
Recommender systems have been successfully employed in various fields to help users in selecting desired items or services according to their preferences from a wide range of potential options [1–4]. Collaborative Filtering (CF) approaches are the most used recommendation techniques in literature for generating personalized recommendations as they are instinctive, reasonably easy to implement, steady, and highly understandable [5]. In CF based approaches, recommendations in a given domain are generated as a weighted average of the observed ratings by the active user’s nearest neighbours. Regardless of their significant advances, CF based approaches are known to be very sensitive in terms of its predictive performance and coverage when dealing with sparse rating datasets. This is due to the fact that the lack of ratings prevents such approaches from effectively identifying suitable neighbours, which leads to the generation of less reliable and accurate recommendations [5].
In order to overcome the data sparsity limitations, the industry and the academia propose the exploitation of supplementary sources of information about users or items besides the rating information. This additional source of information, also known as side information, can be obtained from various sources such as users profile (demographic information), relations between users (explicit trust social networks), items contents (content-based information or item reviews), properties of items (semantic relations between items), social media, temporal information and user’s knowledge [6–10]. The inclusion of side information are effective in alleviating the impact of the above challenge by making the CF-based approaches able to successfully identify more suitable neighbours, which leads to the generation of more reliable and accurate recommendations. Regardless of its significant advantages, the inclusion of side information is not always convenient due to a number of reasons: (1) recommendation approaches who depends on side information are domain specific approaches that have some difficulty to be directly applied to others domains without adjustments [11]; (2) the side information is not always obtainable and is often not easy to collect such information. For example, in explicit trust-based CF approaches, the side information in the trust social network involves manual labor and user efforts in providing his/her trustworthiness to other users which is a highly effort demanding task to do [12]; and (3) the side information can be incomplete, not satisfactorily reliable or even not representative [13].
Another significant aspect that has a considerable effect on the performance of CF-based approaches, in terms of predictive accuracy, is the incorporation of multi-criteria (MC) ratings of an item. Multi-criteria CF approaches recommend valuable items to users by providing users with the ability to rate items based on a number of criteria. The multi-criteria ratings can guarantee a more advanced comprehension of users’ preferences by considering the knowledge about the essential aspects that make users concerned to choose particular items. For an example, in a hotel multi-criteria recommender system, suppose that user u and v rate a particular hotel with 4 out of 5 as an overall rating. Specifically, user u rate the hotel based on its cleanliness and quality of rooms, while user v rate the same hotel based on its location and quality of check-in. Despite the fact that both users look alike as they provide the same overall ratings, however, they aren’t alike in reality as they like different aspects of the same hotel. For that reason, the additional information extracted from users’ multi-criteria ratings would aid to precisely model users’ preferences, and consequently produce further accurate recommendations [7,10,14,15].
The key contributions of this study are described below:
1. It develops a hybrid multi-criteria collaborative filtering (HMCCF) model for alleviating the sparsity problem in CF-based recommender systems by addressing the lack of rating information without the need for side information from external knowledge sources.
2. The HMCCF model utilizes multi-criteria ratings, implicit similarity, similarity transitivity and global reputation concepts to expand the neighbourhood of user or item using implicit information derived from the existing user-item multi-criteria rating matrix.
3. The experimental results of the HMCCF model, compared to a number of benchmark CF-based recommendation algorithms using two real-world MC datasets, demonstrate its effectiveness in terms of prediction accuracy and coverage when confronted with sparse rating information.
The rest of the paper is structured along five sections. Section 2 describes related works, and the key components related to the proposed HMCCF model are presented in detail in Section 3. Section 4 introduces experimental evaluation including datasets, evaluation measures, benchmark algorithms and the evaluation results. Finally, Section 5 draws conclusions and directions for the future work.
Although recommender systems are an efficient solution to deal with the information overload problem, they also come up with a number inherent problems, mainly data sparsity, due to the vast number of users and items available in most recommender systems [16].
Data Sparsity refers to a scenario in which users often give only a limited number of ratings for a limited number of items, leaving most of the available items without any ratings, which leads to a sparse user-item rating matrix. For example, if none of the nearest neighbors of user u have rated movie x, then it is not feasible to make a rating prediction of that movie for user u. Thus, sparsity creates challenges in the computation of similarity when the number of co-rated items between two users is very small [16], and faces a lot of problems in the formulation of proper neighbours, which result in producing low quality recommendations. The sparsity of a user-item rating dataset is defined as:
Up to date, a number of research papers have been published in the literature focusing in mitigating the impact of data sparsity by incorporating additional information to the rating information to be able to make personalized recommendations. Shambour et al. [7] propose an item-based MC CF algorithm that utilizes the semantic information of items in addition to the multi-criteria ratings of users to reduce the impact of sparsity and new item problems of the item-based CF techniques. Experimental results show the efficiency of the proposed algorithm when compared to standard item-based CF techniques. Tian et al. [17] propose a recommendation method that incorporates the explicit trust relationship between users with the rating information to improve recommendation accuracy by dealing with sparsity problems. A number of experiments conducted using the Epinions dataset to demonstrate the improvement of prediction accuracy of the proposed method over two benchmark recommendation algorithms, as well as, in effectively coping with data sparsity problem. Zhang et al. [18] propose a hybrid CF algorithm, which exploits the tag information in addition to the rating information, in the process of similarity calculation between users or items, to lessen the data sparsity problem. Experimental evaluation on the MovieLens dataset demonstrates the improvements of performance of the proposed algorithm in terms of alleviating the data sparsity problem when compared with another four baseline CF-based approaches. In the research proposed by Yang et al. [19], the authors integrate the product attribute information from users reviews in addition to the rating information to alleviate the data sparsity problem and get a more efficient performance in product recommendations. Experimental evaluation on a sparse dataset from Amazon show the feasibility of the proposed recommendation approach by outperforming a number of baseline algorithms. Natarajan et al. [20] develop a recommendation model that utilizes the Linked Open Data (LOD) knowledge base to find and collect information about new entities for a cold start issues. The proposed model also uses a matrix factorization model with LOD to handle the data sparsity problem. Experimental evaluations on MovieLens and Netflix datasets show the supremacy of the proposed model in comparison with other existing methods in terms of improving recommendation accuracy when confronted with sparsity and cold start problems.
All the presented recommendation approaches are based on the presence and the inclusion of side information beside the rating information, and they prove to be an effective solution to the data sparsity. However, this is not always convenient due to a number of reasons such as: (1) the recommendation approach that depends on side information is a domain specific approach, which limits its applicability in other application domains [11]; (2) the side information is not always available and is often requires manual labor and user efforts, which is often cumbersome for users [12]; and (3) the side information can be not complete, satisfactorily reliable or even not representative [13].
The strength of the proposed approach in this paper lies in (1) its capability to alleviate the sparsity within the actual core of the MC-based CF framework without the need for side information from external knowledge sources, and (2) its widespread scope in terms of its applicability to a wide variety of recommendation domains as it does not require any domain-specific side information in addition to the actual ratings of users to make reliable recommendations.
3 A Hybrid Multi-Criteria Collaborative Filtering Model
This section illustrates the building of the HMCCF recommendation model that fuses the users’ and items’ implicit similarity information in a unified MC-based CF framework.
The proposed HMCCF recommendation model follows the similarity-based approach presented by Adomavicius et al. [15]. In the proposed model, a raw user-item MC rating matrix Rm*n with m users and n items is the input, and a predicted rating for unrated item a user is the output, as shown in Fig. 1. Formally, let U = {u1, u2, …, um}, be set of m users, and I = {i1, i2, …, in}, be a set of n items. Based on the MAUT principles [21], each item is expressed by means of a diverse set of criteria. Specifically, let {c1, c2, …, ck}, be a list of criteria where an item i is rated upon, each criteria ck (k = 1,…, d) represents each aspect of an item with a rating value
where
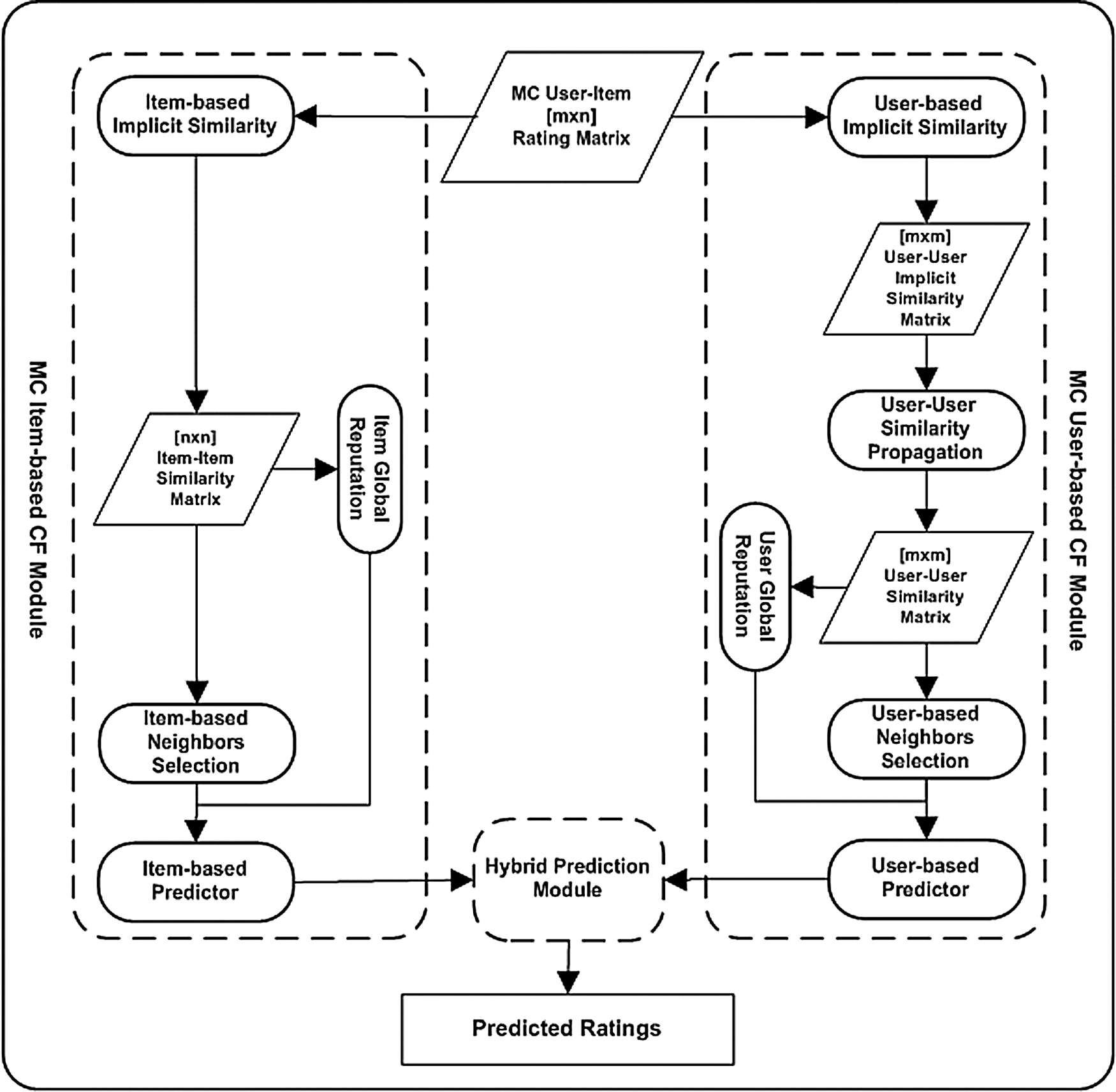
Figure 1: The illustration of the HMCCF recommendation model
3.1 The MC User-Based CF Module
This module makes use of users’ implicit similarities in the user-user implicit similarity matrix to produce MC user-based predictions. The module consists of five main steps:
Step 1: User-based Implicit Similarity
An improved user-based similarity metric is proposed here that takes into account three impact factors of similarity: the absolute difference between rating values, the proportion of the co-rated items between users, and the rating preference of users. This metric can find more accurate neighbours and, consequently, enhancing the prediction accuracy.
At first, this step calculates the direct implicit similarity of every pair of users. This study measures the implicit similarity between users by computing the prediction accuracy of a given user as a past recommender to another user. For example, if user v delivers high accurate recommendations to user u in the past, then users u and v should acquire a high implicit similarity value. For implicit similarity derivation, the Resnick’s prediction method [22] is use to calculate the predicted rating. For any user u, the predicted rating of item i by the solely neighbourhood user v, Pu,i, is specified as follows:
where
The Absolute Difference of Ratings (ADF) method [23] is utilized to calculate the implicit similarity value of user u with regard to user v based on the predictions error of their co-rated items, as shown below.
where
According to literature [7,10,24,25], the number of commonly rated items between users is an important impact factor to consider when measuring the similarity between users. The more co-rated items between users, the more valuable information that can be exploited from the rating data, and the more accurate is the similarity computation. Consequently, a asymmetry factor [24] is used in our model to emphasis the significance of the co-rated items in measuring the implicit similarity between users u and v, and vice versa. The difference amount of the rated items among user u and user v demonstrates the asymmetry of user similarity. If the quantity of rated items of user u is less that the quantity of rated items of user v, then the impact of user u on user v is weaker than that of user v on user u. For the active user u, the asymmetry factor between users u and v is given as follows:
where
Additionally, due to the fact that diverse users may have different rating behaviors in which some users like to provide high ratings while others may have a preference of providing low ratings, a rating preference factor [24,25] is used in our model to signify the rating preference of each user. Therefore, in order to consider the influence of users preferences and obtain a more objective result based on their ratings, the mean and variance of the ratings of both users is employed to consider the rating preferences when measuring the implicit similarity between users u and v.
where
Finally, for any pair of users u, v ∈ U, the implicit similarity between user u and user v, USimu,v, is given as:
Step 2: User-User Similarity Propagation
After computing the direct implicit similarity, a similarity network is created as a directed graph where the nodes reflect users and the edges represent the degree of similarity among users. Because of the limited number of ratings that are often exist in most recommendation systems [26], the underlying similarity network is very sparse, hence, a similarity transitivity is needed to propagate the similarity in the network. In this way, new indirect connections are established between users who have no direct link in the similarity network, but are connected via intermediary users, to calculate their similarities. Assume that user z has rated an item of interest for user u, however, user u does not have any common items with user z and hence their similarity can’t be computed. As a result, it will be hard to know if the rating of user z will be useful for user u. However, by utilizing the similarity transitivity, an indirect link between users u and z can be established through intermediary users, for example user v, who have direct links with users u and z. By doing this, the number of neighbors as potential recommenders will be significantly increase to any given user. For example, suppose that user u (source user) has a direct link with user v (intermediate user) and user v has a direct link with user z (target user), it can be inferred by using similarity propagation that user u can have similar preferences with user z to some extent.
This study uses the following aggregation function that emphasizes the significance of the co-rated items in measuring the propagated similarity between users. For any u, v, z ∈ U, the propagated similarity value that specifies to what extent user u implicitly similar to user z, is computed as follows:
where user u has direct similar adjacent neighbours that are adjacent neighbours to user z, iSimu,v is the direct implicit similarity value among users u and v. iSimv,z is the direct implicit similarity value among users v and z. AFu,v is asymmetry factor among users u and v. AFv,z is asymmetry factor among users v and z.
Step 3: User Global Reputation
The average of all similarity values acquired from other associated users in the user-user similarity matrix, is defined as a user global reputation. For user u, the global reputation is specified as below:
where user a is an neighboring user that is connected to user u, USima,u is the value of user-user similarity among users a and u. T is the total number of neighboring users that are connected to user u.
Step 4: User-based Neighbour Selection
In this step, the users with the utmost similarity values to the active user (
Step 5: User-based Predictor
The deviation-from-mean function [22,27] is used as a user-based predictor to determine the user-based predicted rating of target item p for the active user u,
where,
3.2 The MC Item-Based CF Module
This module makes use of items’ implicit similarities in the item-item similarity matrix to produce MC item-based predictions. The module consists of four major steps:
Step 1: Item-based Implicit Similarity
In this step, the direct implicit similarity between every pair of items is computed based on the MC user-item rating matrix. This study measures the implicit similarity between items by measuring the prediction accuracy of a given item, as a past recommender, to another item. For example, if an item p delivers accurate recommendations to item q in the past, then items p and q should attain a high implicit similarity value. For implicit similarity derivation, the Resnick’s prediction method [22] is used to calculate the predicted rating. The predicted rating for the user u on item p by the solely neighbourhood item q, Pu,p, is specified as follows:
where
The Absolute Difference of Ratings (ADF) method [23] is also used here to calculate the implicit similarity of item p with regard to item q based on the predictions error of their co-rated users.
where
To take into account the ratio of the common users who have rated both items when calculating the implicit similarity between items, the asymmetry factor is again used to tackle this issue. The asymmetry factor among items p and q, is formulated as follows:
where
Step 2: Item Global Reputation
The item global reputation is characterized as the average of all similarity values acquired from other associated items in the item-item similarity matrix. The global reputation value for item p, is given as below:
where item x is an neighboring item for item p, ISimtx,p is the value of item-item implicit similarity among items x and p. T is the total number of neighboring items for item p.
Step 3: Item-based Neighbour Selection
In this step, the items with the utmost similarity values to the target item (
Step 4: Item-based Predictor
The deviation-from-mean function [22,27] is used as an item-based predictor to determine the item-based predicted rating value of the active user u ∈ U on target item p ∈ I,
where,
3.3 The Hybrid Prediction Module
The switching hybridization [28] is enabled to fuse both of the MC user-based CF and the MC item-based CF approaches into a single system. When one of the approaches is unable to produce a rating perdition, the switching method is applied and the other approach is executed. When both approaches are able to produce rating predictions, the weighted harmonic mean method [29] is employed to combine the predictions of the two approaches to guarantee that a high prediction rating is attained on condition that predictions generated from both approaches are also high. Formally, the rating prediction for an active user u on un-rated item p, is specified as below.
This section evaluates the performance of the proposed HMCCF recommendation model. It includes the experimental datasets, evaluation metrics, benchmark algorithms and the experimental results and analysis.
4.1 Datasets and Evaluation Metrics
Two real-world multi-criteria dataset are employed to assess the effectiveness of the HMCCF model. The Yahoo! Movies MC dataset [30] contains 34,800 multi-criteria ratings of 965 movies made by 1716 users. Each user provides ratings on four criteria: story, acting, direction and visuals on the scale from 1 to 5. Furthermore, users provide an overall rating for each movie. The sparsity level of the Yahoo! Movies MC dataset is 93.7%. The TripAdvisor MC dataset [31]. This dataset contains 28,829 multi-criteria ratings on 693 hotels made by 1039 users. Each user provides ratings, besides an overall rating, on seven criteria: value for money, quality of rooms, location of the hotel, cleanliness of the hotel, quality of check-in, overall quality of services and particular business services, on the scale from 1 to 5. The sparsity level of the TripAdvisor MC dataset is 93.7%.
In order to evaluate the performance of the HMCCF model concerning the prediction accuracy and coverage, the standard Mean Absolute Error (MAE), the Root Mean Squared Error (RMSE) and the Coverage metrics are used. The MAE is a commonly used metric for measuring the predictive accuracy in recommender systems. MAE measures accuracy by dividing the summation of the absolute differences between the actual ratings and predicted ratings by the total number of predicted ratings. Therefore, a smaller value of MAE represents a better prediction accuracy. RMSE is defined as the square root of the division of the sum of squares of the absolute differences between the actual ratings and predicted ratings by the total number of predicted ratings. The coverage metric measures the capability of a given recommender system to produce recommendations. The coverage is defined as the rate of items for which a prediction can be produced to the number of available items for recommendations [32].
To illustrate the performance of the HMCCF model that is a hybrid of MC user-based CF and MC item-based CF approaches, a five user-based CF and item-based CF benchmark algorithms have been implemented, including four traditional single-criteria and multi-criteria CF algorithms and a state-of-the-art multi-criteria recommendation algorithm:
(1) the single-criteria user-based CF algorithm (SC-UCF), which utilizes Pearson Correlation between users as a similarity measure in order to generate recommendations [27].
(2) the single-criteria item-based CF algorithm (SC-ICF), which utilizes Pearson Correlation between items as a similarity measure to generate recommendations [33].
(3) the multi-criteria user-based CF recommendation algorithm (MC-UCF) [15], which utilizes the multi-criteria ratings between users to generate recommendations.
(4) the multi-criteria item-based CF recommendation algorithm (MC-ICF) [15], which utilizes the multi-criteria ratings between items in order to generate recommendations.
(5) the multi-criteria user-based trust-enhanced CF recommendation algorithm (MC-TeCF) [10], which utilizes the multi-criteria ratings and implicit trust relations among users to generate recommendations.
4.3 Evaluation Results and Analysis
The aim of this section is to carry out a set of experiments to confirm the superiority of the HMCCF model by comparing it with well-known benchmark CF-based recommendation algorithms. We conducted a set of experiments to validate the effect of the HMCCF model against the benchmark algorithms in terms of prediction accuracy and data sparsity.
4.3.1 Comparison Results of Prediction Accuracy with Benchmark Algorithms on Different Datasets
Four experiments are conducted using the Yahoo Movies! and Tripadvisor datasets to compare the performance of the prediction accuracy of the HMCCF model with respect to the five benchmark CF-based recommendation algorithms. The number of neighbours are varied when computing the corresponding MAE and RMSE for all recommendation algorithms. As shown in the following figures, the results indicate that the HMCCF model outperformed the other algorithms by attaining the best prediction accuracy (i.e., lowest MAE and RMSE) at different sizes of neighbourhood. In Fig. 2, the MAE of the HMCCF on the Yahoo! Movies dataset is 35%, 32%, 21%, 14% and 7% better than SC user-based CF, SC item-based CF, MC user-based CF, MC item-based CF, and MC trust-enhanced CF benchmark algorithm respectively. Whereas, in Fig. 3, the RMSE of the HMCCF is 34%, 33%, 26%, 20% and 7% better than SC user-based CF, SC item-based CF, MC user-based CF, MC item-based CF, and MC user-based trust-enhanced CF benchmark algorithms, respectively.
In Fig. 4, the MAE of the HMCCF on the TripAdvisor dataset are is 54%, 45%, 39%, 28% and 13% better than SC user-based CF, SC item-based CF, MC user-based CF, MC item-based CF, and MC user-based trust-enhanced CF benchmark algorithms, respectively. Whereas, in Fig. 5, the RMSE of the HMCCF is 53%, 45%, 41%, 28% and 10% better than SC user-based CF, SC item-based CF, MC user-based CF, MC item-based CF, and MC user-based trust-enhanced CF benchmark algorithms, respectively. As a result, all the results justify that the HMCCF model is a considerable enhancement with reference to prediction accuracy in comparison with the other benchmark recommendation algorithms.
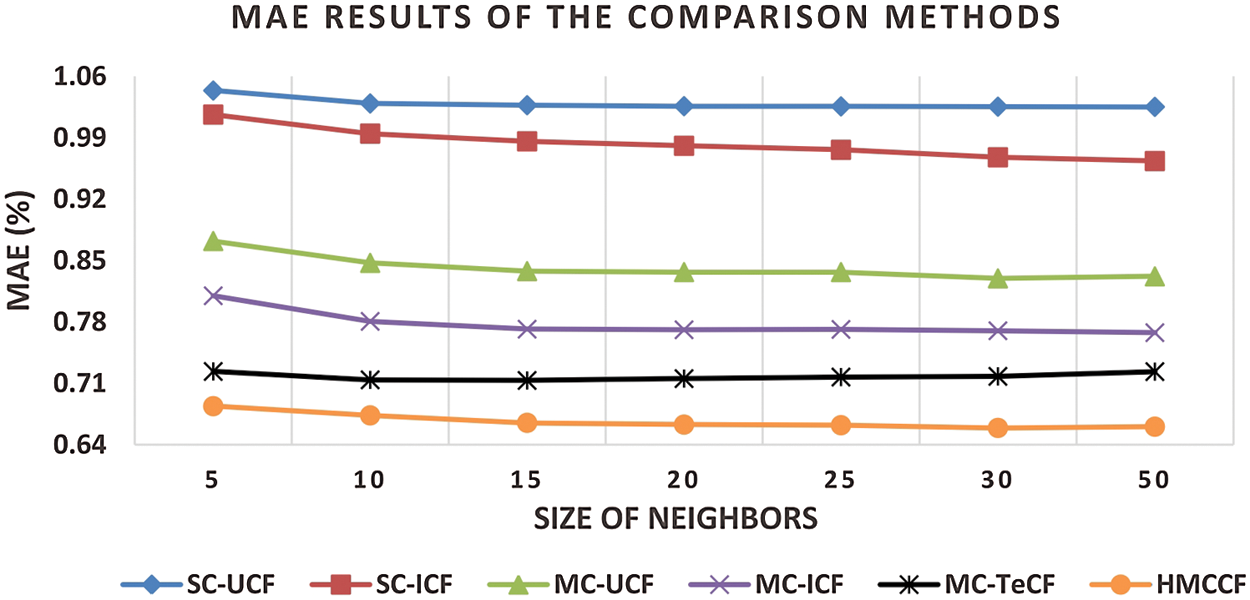
Figure 2: MAE results on varied numbers of neighbours on the Yahoo movies dataset
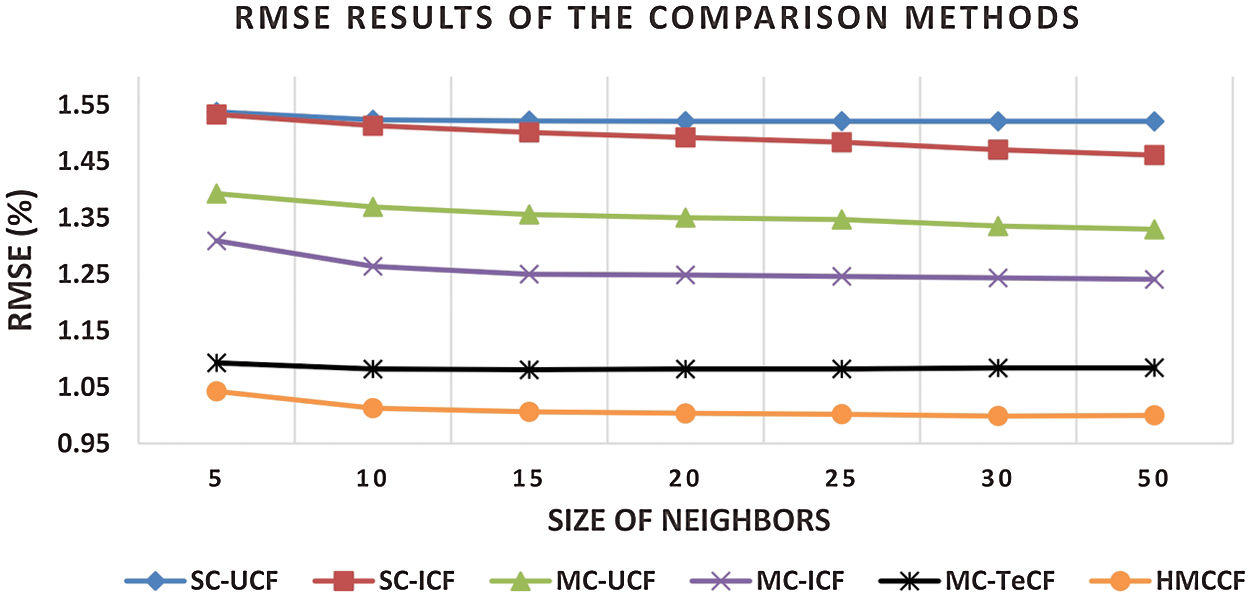
Figure 3: RMSE results on varied numbers of neighbours on the Yahoo movies dataset
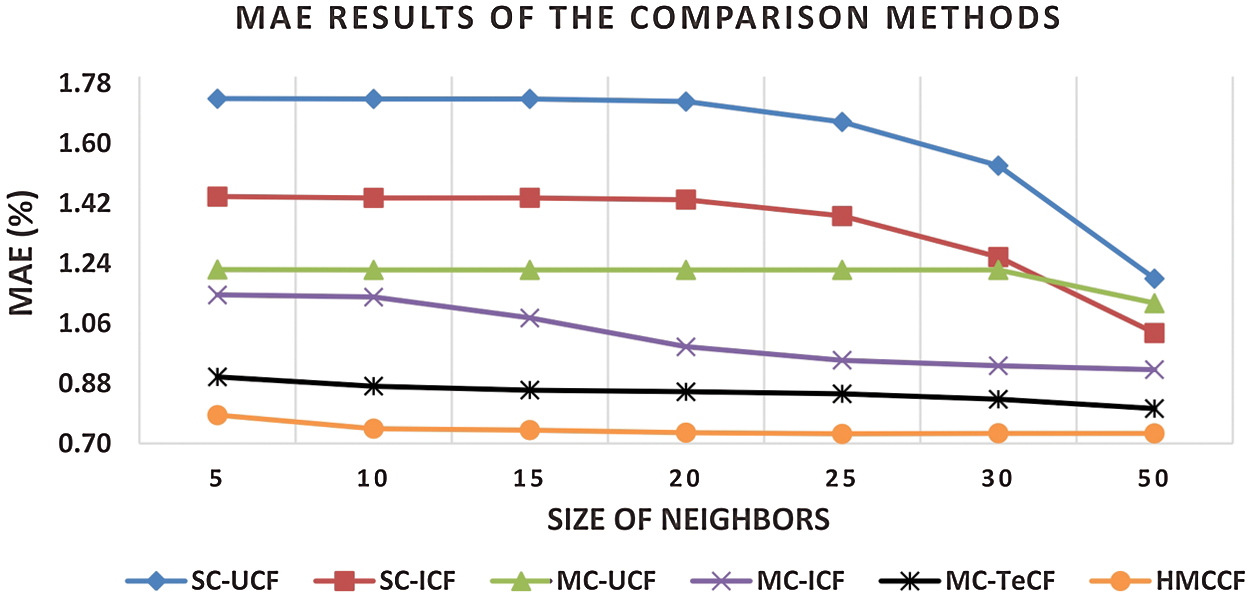
Figure 4: MAE results on varied numbers of neighbours on the TripAdvisor dataset
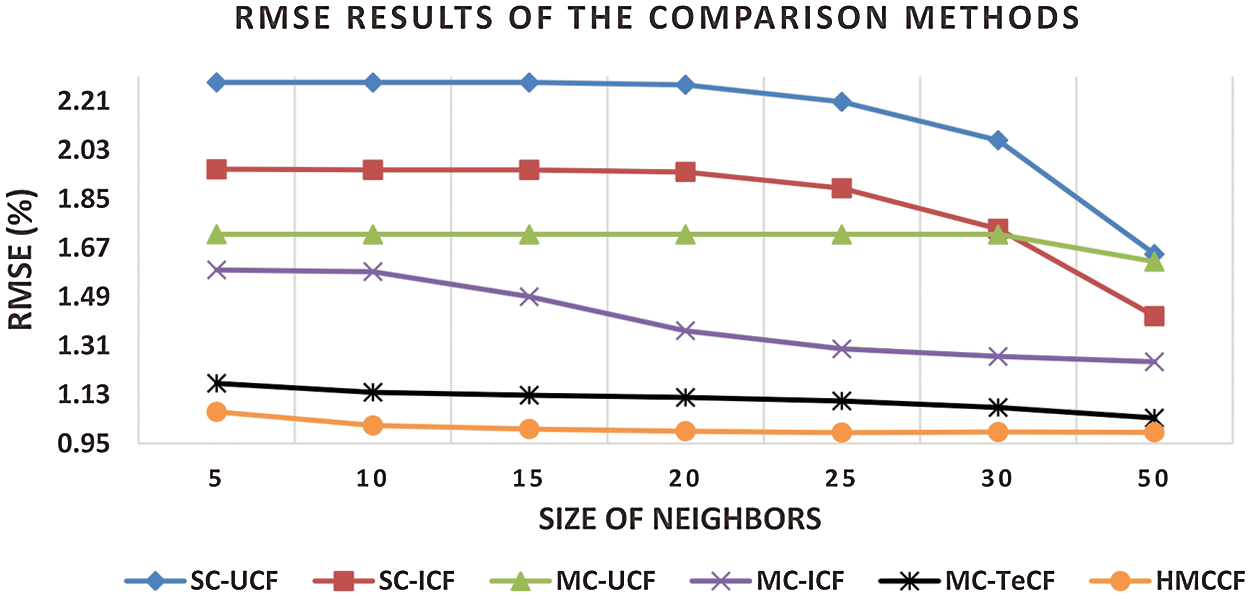
Figure 5: RMSE results on varied numbers of neighbours on the TripAdvisor dataset
4.3.2 Comparison Results of Prediction Accuracy and Coverage with Benchmark Algorithms for Varying Levels of Sparsity
Two experiments are conducted on six datasets with different levels of sparsity to verify whether the proposed HMCCF model is indeed superior to the other benchmark algorithms in alleviating the sparsity problem in terms of prediction accuracy and coverage. The sparsity metric is used to create six sparse datasets with various sparsity levels from the Yahoo Movies! dataset. Ratings are randomly removed from these sparse data sets to make them having increasing levels of sparsity ranging from the lowest level of 98.0% to highest level of 99.8% (i.e., 98%, 98.5%, 98.8%, 99%, 99.5%, and 99.8%).
As shown in Figs. 6 and 7, the results signify that the HMCCF model outperformed the other algorithms, particularly in the extremely sparse datasets, by achieving better results of prediction accuracy (i.e., lower MAE and RMSE) and prediction coverage (i.e., higher coverage) at all ranges of sparsity. Fig. 6 shows that the HMCCF provided a major improvement of 68.23%, 67.85%, 64.56%, 61.86% and 29.75% over the SC user-based CF, SC item-based CF, MC user-based CF, MC item-based CF, and MC user-based trust-enhanced CF benchmark algorithms, respectively. While, as shown in Fig. 7, the prediction coverage of the HMCCF is 56.65%, 57.20%, 48.83%, 44.77% and 9.92% better than SC user-based CF, SC item-based CF, MC user-based CF, MC item-based CF, and MC user-based trust-enhanced CF benchmark algorithms, respectively.
It can be noted that the HMCCF model works robustly with extremely sparse datasets, for example, the average percentages of improvement on the 99.8% spare dataset are 63.8%, 50.4% and 90.45% over the benchmark algorithms in terms of MAE, RMSE and coverage, respectively. Hence, referring to both prediction accuracy and coverage, it can be confirmed that the HMCCF model is a significant enhancement in lessening the data sparsity problem.
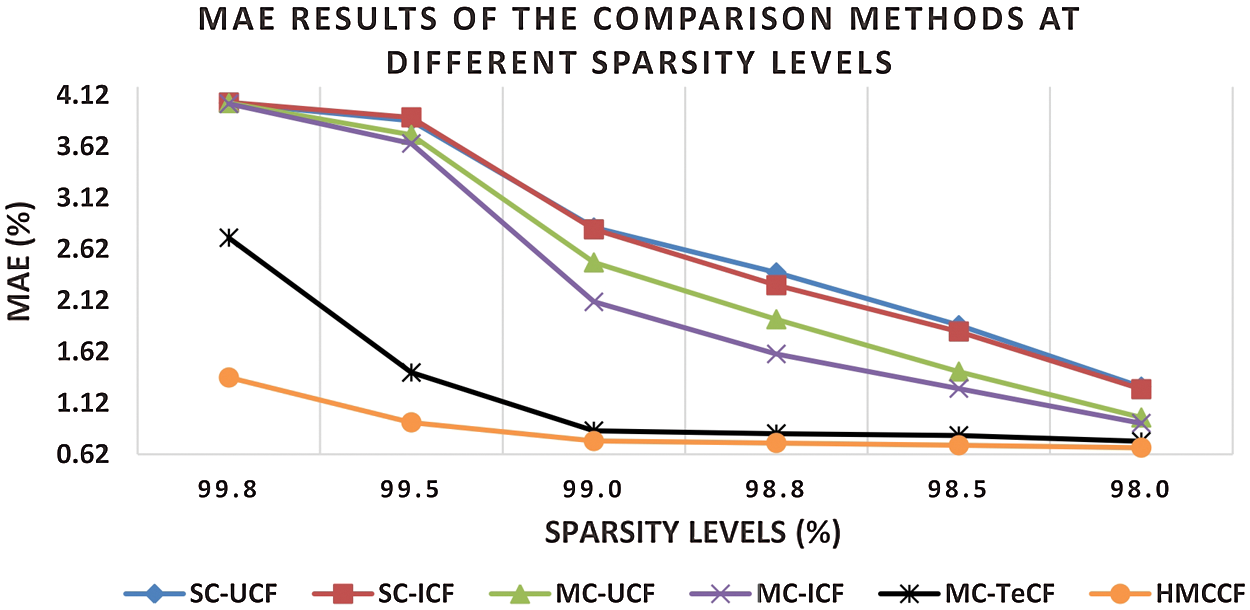
Figure 6: MAE results on varied levels of data sparsity
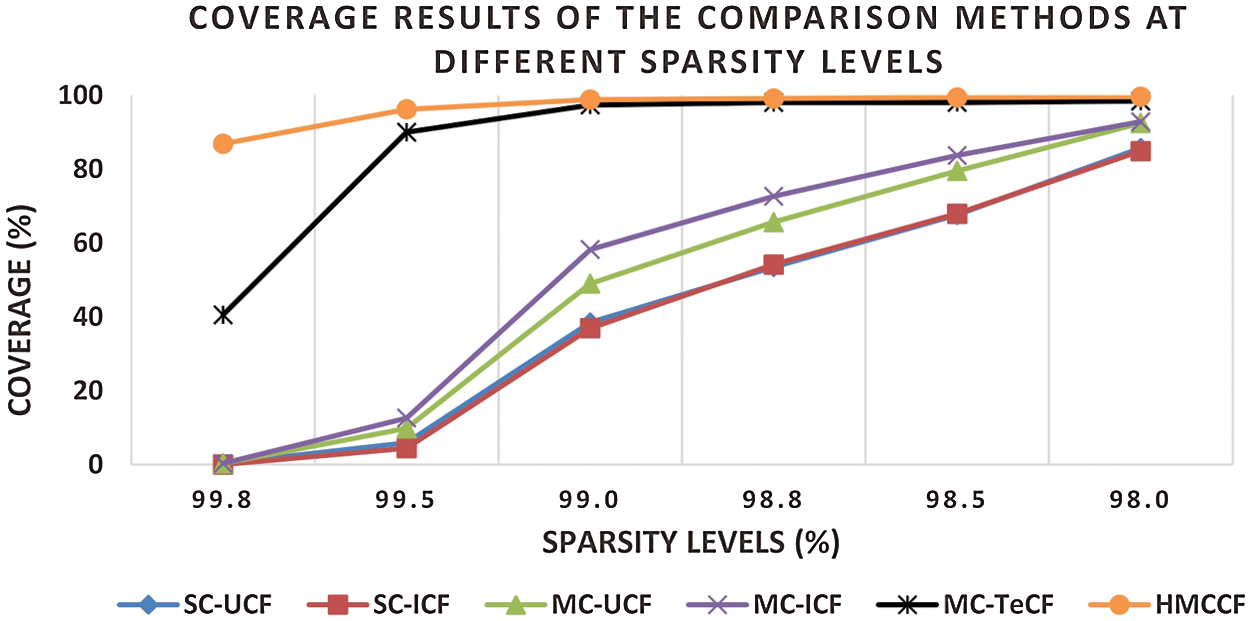
Figure 7: Coverage results on varied levels of data sparsity
This research article addresses the data sparsity problem in CF-based recommender systems without the need for side information from external knowledge sources. It proposes a hybrid multi-criteria CF model that exploits the multi-criteria ratings, implicit similarity, similarity transitivity and global reputation concepts to expand the space of potential recommenders (i.e., neighbours) using implicit information derived from the existing user-item MC rating matrix. The HMCCF model applies a switching hybrid strategy, which switches between the user-based and item-based approaches within the MC-based CF framework to attain more effectual results in respect of predictive accuracy and coverage, in particular, when confronted with data sparsity problem. The HMCCF model exploits the implicit similarities and similarity propagation between users, the implicit similarities among items, and the users’ and items’ global reputation, to alleviate the influence of the data sparsity problem.
Furthermore, the strength of the proposed HMCCF lies in its ability to alleviate the problems of the CF-based recommender systems within the actual core of the MC-based CF framework without the need for side information from external knowledge sources, and its applicability to a wide variety of recommendation domains as it does not require any domain-specific side information in addition to the actual ratings of users to make reliable recommendations. A number of experiments are conducted on two real-world multi-criteria dataset to show the effectiveness of the proposed model. The experimental results, compared with benchmark CF-based recommendation algorithms, show the superiority of the proposed model in respect of prediction accuracy and coverage when faced with data sparsity.
Future enhancement that need to be addressed is how to learn the relationship between overall ratings and MC criteria-based ratings using an improved aggregation function. Accordingly, a number of high-performance machine learning and deep learning methods can be applied and tested for learning the aggregation function that may further improve the accuracy of predictions.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Q. Shambour and J. Lu, “Government-to-business personalized e-services using semantic-enhanced recommender system,” in Electronic Government and the Information Systems Perspective, vol. 6866. Berlin, Heidelberg: Springer, pp. 197–211, 2011. [Google Scholar]
2. Q. Y. Shambour, M. M. Abu-Alhaj and M. M. Al-Tahrawi, “A hybrid collaborative filtering recommendation algorithm for requirements elicitation,” International Journal of Computer Applications in Technology, vol. 63, no. 1–2, pp. 135–146, 2020. [Google Scholar]
3. Q. Shambour, N. Turab and O. Adwan, “An effective e-commerce recommender system based on trust and semantic information,” Cybernetics and Information Technologies, vol. 21, no. 1, pp. 103–118, 2021. [Google Scholar]
4. Q. Shambour and J. Lu, “An effective recommender system by unifying user and item trust information for b2b applications,” Journal of Computer and System Sciences, vol. 81, no. 7, pp. 1110–1126, 2015. [Google Scholar]
5. C. C. Aggarwal, “Neighborhood-based collaborative filtering,” in Recommender Systems: The Textbook. Cham: Springer International Publishing, pp. 29–70, 2016. [Google Scholar]
6. J. K. Tarus, Z. Niu and G. Mustafa, “Knowledge-based recommendation: A review of ontology-based recommender systems for e-learning,” Artificial Intelligence Review, vol. 50, no. 1, pp. 21–48, 2018. [Google Scholar]
7. Q. Shambour, M. Hourani and S. Fraihat, “An item-based multi-criteria collaborative filtering algorithm for personalized recommender systems,” International Journal of Advanced Computer Science and Applications, vol. 7, no. 8, pp. 274–279, 2016. [Google Scholar]
8. S. M. Al-Ghuribi and S. A. M. Noah, “Multi-criteria review-based recommender system-the state of the art,” IEEE Access, vol. 7, pp. 169446–169468, 2019. [Google Scholar]
9. M. Y. H. Al-Shamri, “User profiling approaches for demographic recommender systems,” Knowledge-Based Systems, vol. 100, no. 6, pp. 175–187, 2016. [Google Scholar]
10. Q. Shambour, “A user-based multi-criteria recommendation approach for personalized recommendations,” International Journal of Computer Science and Information Security, vol. 14, no. 12, pp. 657, 2016. [Google Scholar]
11. H. N. Kim, A. El-Saddik and G. S. Jo, “Collaborative error-reflected models for cold-start recommender systems,” Decision Support Systems, vol. 51, no. 3, pp. 519–531, 2011. [Google Scholar]
12. P. Victor, M. Cock and C. Cornelis, “Trust and recommendations,” in Recommender Systems Handbook. US: Springer, pp. 645–675, 2010. [Google Scholar]
13. J. Bobadilla, F. Ortega, A. Hernando and J. Bernal, “A collaborative filtering approach to mitigate the new user cold start problem,” Knowledge-Based Systems, vol. 26, no. 6, pp. 225–238, 2011. [Google Scholar]
14. N. Manouselis and C. Costopoulou, “Analysis and classification of multi-criteria recommender systems,” World Wide Web, vol. 10, no. 4, pp. 415–441, 2007. [Google Scholar]
15. G. Adomavicius and Y. O. Kwon, “New recommendation techniques for multicriteria rating systems,” IEEE Intelligent Systems, vol. 22, no. 3, pp. 48–55, 2007. [Google Scholar]
16. G. Adomavicius and A. Tuzhilin, “Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions,” IEEE Transactions on Knowledge and Data Engineering, vol. 17, no. 6, pp. 734–749, 2005. [Google Scholar]
17. H. Tian and P. Liang, “Improved recommendations based on trust relationships in social networks,” Future Internet, vol. 9, no. 1, pp. 9, 2017. [Google Scholar]
18. C. Zhang, M. Yang, J. Lv and W. Yang, “An improved hybrid collaborative filtering algorithm based on tags and time factor,” Big Data Mining and Analytics, vol. 1, no. 2, pp. 128–136, 2018. [Google Scholar]
19. X. Yang, S. Zhou and M. Cao, “An approach to alleviate the sparsity problem of hybrid collaborative filtering based recommendations: The product-attribute perspective from user reviews,” Mobile Networks and Applications, vol. 25, no. 2, pp. 376–390, 2020. [Google Scholar]
20. S. Natarajan, S. Vairavasundaram, S. Natarajan and A. H. Gandomi, “Resolving data sparsity and cold start problem in collaborative filtering recommender system using linked open data,” Expert Systems with Applications, vol. 149, no. 3, pp. 113248, 2020. [Google Scholar]
21. J. Dyer, “Maut—Multiattribute utility theory,” in Multiple Criteria Decision Analysis: State of the Art Surveys. New York: Springer, pp. 265–292, 2005. [Google Scholar]
22. P. Resnick, N. Iacovou, M. Suchak, P. Bergstrom and J. Riedl, “Grouplens: An open architecture for collaborative filtering of netnews,” in Proc. of the 1994 ACM Conf. on Computer Supported Cooperative Work, Chapel Hill, North Carolina, United States, pp. 175– 186, 1994. [Google Scholar]
23. A. Gazdar and L. Hidri, “A new similarity measure for collaborative filtering based recommender systems,” Knowledge-Based Systems, vol. 188, pp. 1–47, 2020. [Google Scholar]
24. Y. Wang, J. Deng, J. Gao and P. Zhang, “A hybrid user similarity model for collaborative filtering,” Information Sciences, vol. 418–419, no. 1, pp. 102–118, 2017. [Google Scholar]
25. J. Feng, X. Fengs, N. Zhang and J. Peng, “An improved collaborative filtering method based on similarity,” PLoS ONE, vol. 13, no. 9, pp. e0204003, 2018. [Google Scholar]
26. M. Papagelis, D. Plexousakis and T. Kutsuras, “Alleviating the sparsity problem of collaborative filtering using trust inferences,” in Trust Management, vol. 3477. Heidelberg: Springer, pp. 224–239, 2005. [Google Scholar]
27. J. Herlocker, J. A. Konstan and J. Riedl, “An empirical analysis of design choices in neighborhood-based collaborative filtering algorithms,” Information Retrieval, vol. 5, no. 4, pp. 287–310, 2002. [Google Scholar]
28. R. Burke, “Hybrid web recommender systems,” in The Adaptive Web: Methods and Strategies of Web Personalization. Berlin, Heidelberg: Springer, pp. 377–408, 2007. [Google Scholar]
29. J. O'Donovan and B. Smyth, “Trust in recommender systems,” in Proc. of the 10th Int. Conf. on Intelligent User Interfaces, San Diego, California, USA, pp. 167–174, 2005. [Google Scholar]
30. K. Alodhaibi, “Decision-guided recommenders with composite alternatives,” Doctor of Philosophy, George Mason University, Virginia,2011. [Google Scholar]
31. D. Jannach, M. Zanker and M. Fuchs, “Leveraging multi-criteria customer feedback for satisfaction analysis and improved recommendations,” Information Technology & Tourism, vol. 14, no. 2, pp. 119–149, 2014. [Google Scholar]
32. M. Ge, C. Delgado-Battenfeld and D. Jannach, “Beyond accuracy: Evaluating recommender systems by coverage and serendipity,” in Proc. of the Fourth ACM Conf. on Recommender Systems, Barcelona, Spain, pp. 257–260, 2010. [Google Scholar]
33. M. Deshpande and G. Karypis, “Item-based top-n recommendation algorithms,” ACM Transactions on Information Systems, vol. 22, no. 1, pp. 143–177, 2004. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |