Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.019473
Article

Deep Learning Based Stacked Sparse Autoencoder for PAPR Reduction in OFDM Systems

A. Jayamathi1 and T. Jayasankar2,*

1Department of Electronics and Communication Engineering, K.S.R. College of Engineering, Tiruchengode, 637215, India
2Department of Electronics and Communication Engineering, University College of Engineering, BIT Campus, Anna University, Tiruchirappalli, 620024, India
*Corresponding Author: T. Jayasankar. Email: jayasankar27681@gmail.com
Received: 14 April 2021; Accepted: 20 May 2021

Abstract: Orthogonal frequency division multiplexing is one of the efficient and flexible modulation techniques, and which is considered as the central part of many wired and wireless standards. Orthogonal frequency division multiplexing (OFDM) and multiple-input multiple-output (MIMO) achieves maximum spectral efficiency and data rates for wireless mobile communication systems. Though it offers better quality of services, high peak-to-average power ratio (PAPR) is the major issue that needs to be resolved in the MIMO-OFDM system. Earlier studies have addressed the high PAPR of OFDM system using clipping, coding, selected mapping, tone injection, peak windowing, etc. Recently, deep learning (DL) models have exhibited improved performance on channel estimation, signal recognition, channel decoding, modulation identification, and end-to-end wireless system. In this view, this paper presents a new Hyperparameter Tuned Deep Learning based Stacked Sparse Autoencoder (HPT-SSAE) for PAPR Reduction Technique in OFDM system. The proposed model aims to substantially reduce the peaks in the OFDM signal. The presented HPT-SSAE model is utilized to adaptively create a peak-canceling signal based on the features of the input signal. In the HPT-SSAE model, the constellation mapping and demapping of symbols take place on every individual subcarrier adaptively using the SSAE model in such a way that bit error rate (BER) and the PAPR of the OFDM systems are cooperatively diminished. Besides, to enhance the performance of the SSAE model, the hyperparameter tuning process takes place using monarch butterfly optimization (MBO) algorithm. A comprehensive set of simulations were performed to highlight the supremacy of the HPT-SSAE model. The obtained experimental values showcased the betterment of the proposed model over the compared methods interms of bit error rate (BER), complementary cumulative distribution function (CCDF), and execution time.

Keywords: OFDM; PAPR; autoencoder; hyperparameter; deep learning

1  Introduction

Advanced development in new wireless communication technologies has resulted in an increasing need for higher data rate owing to the familiarity of multimedia services, like real-time streaming media, games, and other social media services. Since these requirements result in maximum bandwidth technologies [1], improved Quality of Service (QoS) becomes important. For instance, in Minoli et al. [2], it is estimated that the 5G mobile network achieves 1000 times the system capacity, 10 times the spectral effectiveness, high data rate, 25 times the average cell throughput, and other enhancements of the current generation 4G system. Orthogonal frequency division multiplexing (OFDM) forms the basis of 4G wireless communication system; for example, it can be involved in the IEEE 802.16 Worldwide Interoperability for Microwave Access (WiMAX) and Long-Term Evolution (LTE) standard. LTE is presented as the widely used standard to achieve interoperable Public Safety communication in United States and other countries [3]. One of the distinct method of multicarrier modulation (MCM) is termed as OFDM (orthogonal frequency-division multiplexing) in which the total frequency selective fading channel is separated into numerous orthogonal narrowband flat-fading sub channels.

The integration of OFDM with Multiple-Input Multiple-Output (MIMO) wireless communication system leads to the design of MIMO-OFDM system [4], a significant technique for wireless communication systems due to maximum data rate. Besides, the OFDM reduces the computational complexity of the MIMO transceiver through the transformation of a frequency selective MIMO channel to a collection of parallel frequency flat MIMO channels [5]. But the transmission of signals in the OFDM method whereas the outcome is the superposition of many subcarriers through an Inverse Fast Fourier Transform (IFFT) function encompasses high peak-to-average power ratio (PAPR). It is a major limitation that exists in the design of OFDM systems. When a transmitting device has maximum PAPR, the average power gets considerably minimized with reference to persistent saturation energy.

With the recently available commercial wireless system, the PAPR problem is highly important in uplink [6] due to the fact that it is the limiting connection with respect to range and coverage. Since the mobile terminals are restricted to inbuilt batteries, the effectiveness of the power amplification device is essential. Fig. 1 shows the structure of OFDM system [7].

Figure 1: Structure of OFDM systems

An inclination in 5G allows high frequency bands to attain extra unused spectrum, and several researches have been carried out to accomplish it [8]. In the forthcoming 5G smartphones where beam forming concept is utilized, the reduction in PAPR is essential assuming the minimum power efficiency of mm Wave PAs and insignificant battery efficiency is studied in Huo et al. [9]. Furthermore, in case of tactical communication, the coverage is a serious point, and vehicle-to-vehicle broadband data transmission necessitates a robust output power. The issue that exists is that power amplifier (PA) connected to maximum power scope is highly expensive. Consequently, a real-time design of OFDM needs to address all ways to minimize the high PAPR. Several works have resolved the issue using distinct mechanisms like clipping and filtering, selected mapping, coding, peak windowing, clipping, tone injection, and Partial Transmit Sequence (PTS). Each of these techniques possesses their individual merits and demerits. However, the PTS model is considered an effective method owing to its improved performance in PAPR reduction. Recently Machine Learning (ML) models have been emerged in the design of OFDM systems to accomplish superior PAPR reduction.

This paper develops a novel Hyperparameter Tuned Deep Learning based Stacked Sparse Autoencoder (HPT-SSAE) for PAPR Reduction Technique in OFDM system. The goal of the proposed HPT-SSAE model is to train the network in such a way as to minimize PAPR with no degradation of the BER. The presented HPT-SSAE model is employed to dynamically generate a peak-canceling signal depending upon the characteristics of the input signal. For further improving the efficiency of the SSAE model, the hyperparameters can be tuned by the use of monarch butterfly optimization (MBO) algorithm. Extensive experimental analysis of the HPT-SSAE model takes place to point out the betterment of the HPT-SSAE model. In short, the contribution of the paper is given as follows.

•   Propose a new HPT-SSAE based PAPR Reduction Technique for OFDM system

•   Aims to substantially reduce the peaks in the OFDM signal

•   Employ SSAE model for the peak cancelling signal generation

•   Perform hyperparameter tuning of SSAE model using MBO algorithm

•   Validate the results of the HPT-SSAE model interms of different measures.

2  Literature Review

Al-Jawhar et al. [10] presented a novel PTS model for decreasing the high PAPR of the filtered OFDM systems. It has analyzed different parameters namely frequency localization, bit error rate (BER), and computation difficulty under the existence of with and without PTS. In Amhaimar et al. [11], a low complex PTS model is presented based on a Swarm Intelligence (SI) based Fireworks Algorithm (FWA). The FWA is an iterative technique that begins to execute till the stopping condition is satisfied and it involves four major parameters such as mutation operation, mapping rule, explosive operator, and selection approach. The obtained experimental values stated that the presented model has accomplished higher accuracy of PAPR and convergence rate compared to the traditional methods.

In Wang et al. [12], an effective DL based tone reservation network (TRNets) has been presented for OFDM system for enhancing the outcome of the TR scheme. Particularly, TRNet will reserve a portion of the tones for the generation of a peak-canceling signal. The feed forward neural network (FFNN) is applied for the adaptive generation of a peak-canceling signal based on the nature of an input signals. In Kim et al. [13], a new PAPR reducing network (PRNet) is presented depending upon the autoencoder (AE) model of the DL. Here, the constellation mapping and demapping of the symbols that take place on every individual subcarrier is computed in an adaptive way by the use of DL model in such a way to minimize the BER and PAPR of the OFDM systems.

Sohn et al. [14] designed a novel PAPR reduction technique which makes use of the time-domain kernel matrix for the generation of the PAPR-reduction signals. In addition, the generation considerable of the clipping noise is relaxed where the clipping noise includes a set of non-correlated parabolic pulse and employ the presented model. Depending upon the instantaneous observation of clipping noises, the presented model designs an easier time domain kernel matrix and applies a curve fitting technique for the optimization of the respective scaling factors. In Singh et al. [15], a novel Firefly (FF) technique is employed for searching the optimum combination of the phase vectors. The presented model offers an improved tradeoff amongst the enhanced PAPR results and computation difficulty over the PTS model for several sub-blocks.

For reducing the high PAPR, a PTS model depending upon the adaptive particle swarm optimization (PSO) algorithm is presented [16]. It effectively searches for the optimum integration of the phase rotation factors to reduce the computation complexity. In Xiao et al. [17], a new SFLAHC-PTS model is presented for the minimization of the PAPR of the signal. The presented model is an enhanced version of the PTS model that inherits the merits of the shuffled frog leaping optimization and hill-climbing algorithms for tuning the classical PTS model and reduces the computational complexity.

In Wang et al. [18], an effective scaling SCR (S-SCR) method is presented where the scaling factor is an optimized vector with peak regeneration constraint. For additional enhancements of the convergence rate and elimination of many peaks at every round, a multiple scaling SCR (MS-SCR) method is presented. In Kumar et al. [19], a PTS along with hybrid optimization technique called PS-GW is defined for obtaining minimum outcome on PAPR and computation complexity. The PS-GW algorithm is an integration of the PSO and Gray Wolf Optimization (GWO) algorithms that identifies the optimum combination of phase rotational factors in an efficient way. This method is based on the idea that the volume of exploitation in PSO is improved with the capacity of examination in GWO for the creation of two variations in quality.

3  The Proposed HPT-SSAE Model

A paper for publication should be divided into multiple sections: a Title, Full names of all the authors including their affiliations, a concise Abstract, a list of Keywords, Main text (including figures, equations, and tables), Acknowledgments, Funding Statement, Conflict of Interests, References, and Appendix. The suggested length of a manuscript is 10 pages. Each page in excess of 15 will be charged an extra fee. The transmission of signal using transceiver depending upon OFDM systems is a commonly employed technique. It partitions the efficient spectrum channels as to a set of orthogonal subchannels with equivalent bandwidth, every individual sub-channel autonomously manages the individual data utilizing separate subcarrier. In addition, the OFDM signals are the total of every independent subcarrier. With the multi-carrier signal transmission system, the input data of binary sequence undergo mapping to a set of symbols through a modulation technique. Next, the N symbols X=[X0,X1,XN−1]T are appended to the IFFT element for the independent modulation of every individual subcarrier and attain the OFDM signal in time domain x=[x0,x1,.xN−1]T. The complicated covering of the OFDM signal in the discrete time domain with oversampling factor L is defined by

x[n]=1N∑k=0N−1⁡Xke(j2πnk/LN),0≤n≤LN−1, (1)

where N indicates the subcarrier count and Xk is the n th complex symbol performed and sent through the k th sub-carrier.

In Eq. (1), the signal in the time domain produced by IFFT comprises N autonomously modulated and orthogonal sub-carriers with high PAPR in case of adding it to the outcome of the IDFT block [20]. The PAPR of the OFDM signals from discrete time can be represented as the ratio of maximal to average power (or excepted power E{⋅}) of the difficult OFDM signal, as represented in Eq. (2):

PAPR{x[n]}=max{|x[n]|2}E{|x[n]|2},0≤n≤LN−1, (2)

3.1 Architecture of SSAE Model

SSAE is a NN comprised of multiple SAEs connected in an end-to-end way. The output of the preceding layer of sparse self encoder is utilized as the input of the subsequent layer of self-encoder, therefore higher-level feature illustrations of an input data are achieved. A greedy layerwise pretraining model is utilized for the sequential training of all layers of SSAE for accessing the optimization connection weights as well as bias values of the whole SSAE network. Fig. 2 illustrates the representation of AE.

Figure 2: Representation of AutoEncoder

Afterward, the error backpropagation (BP) technique is utilized for fine-tuning the SSAE till the outcome of error function among the input as well as output data fulfills the predictable necessities, in order to get the better parameter model. The error function Jsparse(W,b) is determined by:

∂∂wijrJsparse(W,b)=12nr∑r=1nr∂∂wijrJsparse(W,b,X(n),Y(n))+λwijr (3)

∂∂brJsparse(W,b)=12nr∑r=1nr∂∂brJsparse(W,b,X(n),Y(n)) (4)

So, the upgraded model of the weight as well as bias are given as follows:

wijk=wijk−η∂∂wijkJ(W,b) (5)

br=br−η∂∂brJ(W,b) (6)

where X(n) and Y(n) are correspondingly signified as the n th actual vector and its equivalent reformation vector, and η implies the upgrade rate of learning.

Assume that there are sparse restraints from the SSAE model, it requires utilizing several rates of learning for various parameters like decreasing the frequency of upgrade to infrequent features. Fig. 3 demonstrates the architecture of SSAE [21]. But, the typical Gradient Descent (GD) technique contains Stochastic Gradient Descent (SGD) and mini-batch GD that utilize a similar learning rate to each network parameter which requires to upgraded, creating it complex to select the proper learning rate and simply attain the local minimal.

In the SSAE, the encoding of the input data takes place at the constellation plane by the use of the encoder of SSAE, comprised of Lf=5 sub-blocks. Therefore, the outcome of the encoding unit can be defined by f(r)=ϕLf(|WLffϕLf−1(…ϕ1(|W1fr+b1f|norm)…)b1f|norm) , where Wlff and blff indicates the weights and biases values of the lf -th FC of the encoding unit correspondingly. Next, the encoded symbols are passed via the IFFT operation that produces the transmitting signal. Afterward, the signal is sent via the wireless channel prior to the arrival at the receiving end. At last, the received signal gets passed to an FFT operation and undergoes decoding by the use of SSAE. It is considered that the decoding unit contains a set of Lg=5 sub-blocks are as same as the encoding unit. Therefore, the outcome of the decoding unit, g(y) , is defined by g(y)=ϕLg(|WLggϕLg−1(…ϕ1(|W1gy+b1g|norm)…)+bLgg|norm) where y is the input of decoding unit and WLgg and blgg are the weight and bias values of the lg -th FC of the decoding unit.

Figure 3: Structure of SSAE

The recreated symbol at the receiving end r^ , is represented as:

r^=g∘FFT∘H∘IFFT∘f(r), (7)

where H signifies the effect of the wireless channel like multipath fading and thermal noise.

3.2 Hyperparameter Optimization of SSAE Model

In order to tune the parameters of the SSAE model, MBO technique is used. The MBO technique is a population based technique which belongs to the classification of SI techniques that are stimulated by the nature of specific species with swarm tendencies like bees, butterflies, etc. As above mentioned, the MBO was currently proposed by Wang et al. [22], which is depends on their concept of intelligent characteristics of butterfly, which is native to North America. It is featured by the attractiveness of the formation that comprises black and orange colors. The migratory performance of these butterflies is inspired to resolve the optimization problem. There are numerous guidelines and basic ideas that should be followed to attain the optimum result to the applied problem:

1.    Each butterfly from the population is either existing in land1 (the home beforehand migration) or in land2 (the home afterward migration).

2.    All children of every butterfly is made by the migration operator, nevertheless either the parent is existing in land1 or 2.

3.    The population shouldn’t alter and must be continuous forever, thus between 2 (novel child or parent) would be detached by a fitness function.

4.    The butterfly is chosen depending upon fitness function are moved to the succeeding round and hasn’t been altered by the migration operator.

The butterfly starts migration initially in April if they exit land1 and head to land2, and the inverse migration starts in September. The overall monarch butterflies in the lands denote the entire population that is termed as NP.

3.1.1 Migration Operator

The migration procedure of the butterfly is demonstrated as:

Xi.kt+1=Xr1.kt (8)

where Xi.kt+1 denotes K th component of Xi at t+1 generation, that illustrate the position of butterfly i , and Xr1.kt denotes Kth component of novel generation position. Now, r denotes arbitrary number estimated as:

R=rand∗peri (9)

where peri denotes migration period time. Alternatively, when r>p , after that the Kth components of novel generation position are estimated as [23]:

Xi.kt+1=Xr2.kt (10)

where Xr2.kt denotes K th components of Xr2 at t generation of butterfly r2 . Henceforth P denotes ratio of monarch butterfly in land1.

3.1.2 Butterfly Adjustment Operator

With these techniques, the tradeoff among the way of migration from land1 to land2 is attained by adapting the ratio of P value. When P is greater, it implies that the butterfly count would be chosen from land1 is larger than l land22, and vice versa. The location of butterfly is adapted when the created rand is lesser to or equivalent to P . The succeeding formula illustrates the upgraded location of butterflies position:

Xj.kt+1=Xbest.kt (11)

where Xj.kt+1 denotes K th components of Xj at t+1 generation, that illustrate the butterfly j position, and Xbest.kt denotes K th components of Xbest at the present round t at land1 and land22. Now, when the random>P, afterward it can be upgraded as:

Xj.kt+1=Xr3.kt (12)

where BAR denotes the adaptation rate of butterfly and dx represents walk step of j butterfly which is estimated with executing Lévy flight as:

(Dx=Le´⁡vy(Xjt)) (13)

α in Eq. (6) denotes weighted factor which is estimated as:

α=Smax/t2 (14)

where Smax indicates maximal length of butterfly enters step 1 and t denotes present generation. Fig. 4 showcases the flowchart of MBO technique [24].

Alternatively, when the rand is larger than BAR, the novel position is upgraded as:

Xj.kt+1=Xj.kt+1+α∗(dxk−0.5) (15)

3.2 Network Training on PAPR Reduction

The HPT-SSAE model undergoes effective training process to decrease PAPR and avoid the degradation of BER. Initially, the HPT-SSAE is required for reconstructing the broadcast signal from the received signal ensured that the BER remains same. Next, the HPT-SSAE produces a transmission signal which exhibits minimum PAPR [25]. To attain the first goal, the encoding unit of the HPT-SSAE model undergo training for determining the appropriate constellation mapping from input data, rk , to the output, Xk , and the decoding unit of the HPT-SSAE needs decoding of the received signal. Afterward, the suitable loss function for achieving this aim can be equated in Eq. (16):

L1(r,r^)=||r−g(FFT(H∘IFFT(f(r;θf))+ϵ);θg)||2, (16)

where f(⋅;θf) and g(⋅;θg) are the parametric depiction of the encoding and decoding units correspondingly, and ϵ indicates the noise at the receiver. Here, the weight matrices, bias, and activation layer are defined using simpler matrix functions of hidden node variables, i.e., θ={W,b} . By the training, θf and θg , i.e., the weights as well as biases of the HPT-SSAE are determined by minimizing the loss function therefore the constellation is robust to a random channel H is obtained through the encoding unit and an effective method of decoded the constellation mapping is attained using the decoding unit. At the same time, the loss function L1(r) employed for achieving minimum PAPR can be represented in Eq. (17):

L2(r)=PAPR{x[n]}PAPR{IFFT(f(r;θf))}. (17)

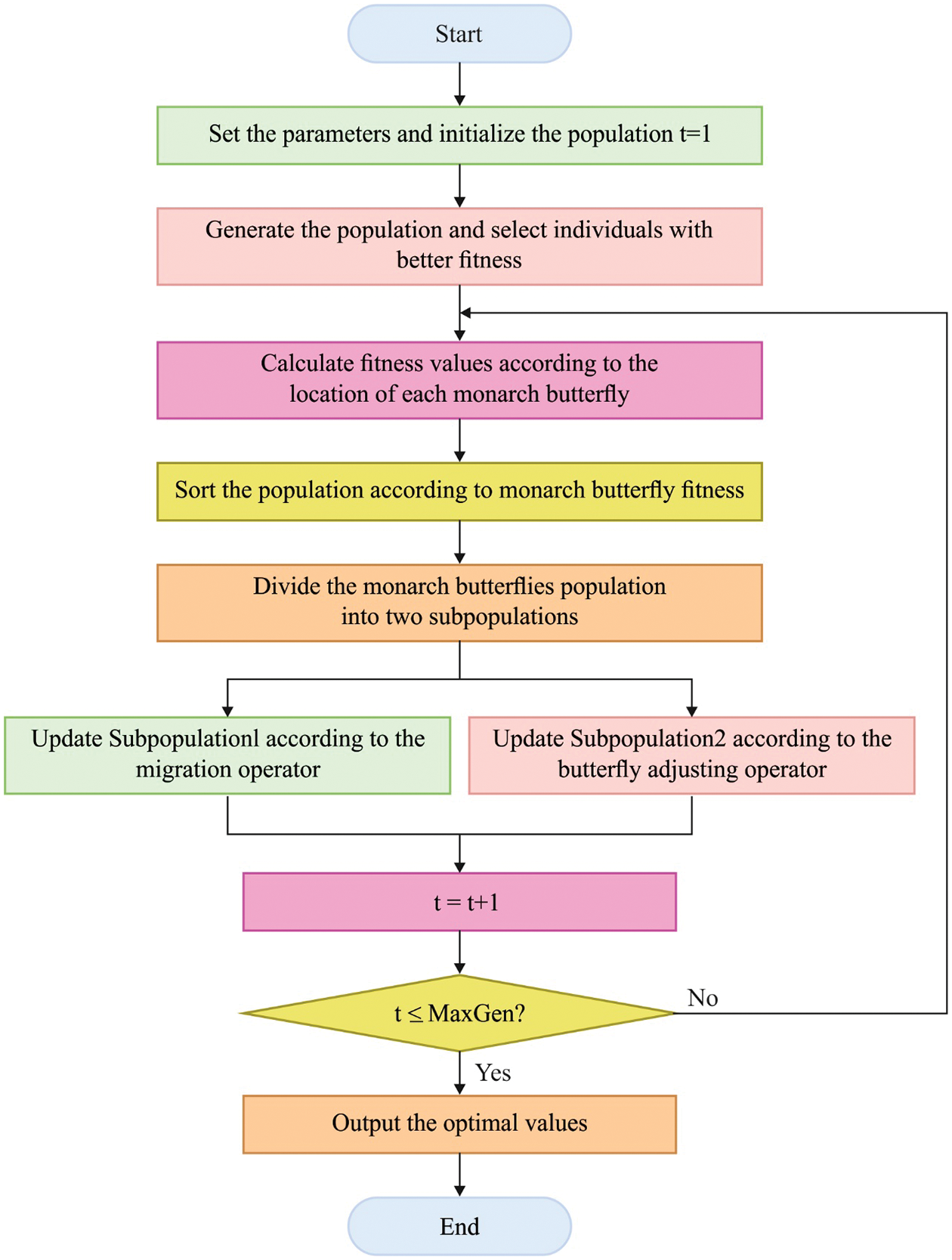
Figure 4: Flowchart of MBO algorithm

Here, the training process takes place on two levels. During the initial level of training, the correct corruption level, η=E[|ϵ|2]E[|r|2] defining the ratio of noise power to signal power is found by loss function L1 . Later, in the next level of the training process, the weight and bias of the HPT-SSAE ( θf and θg ) are learnt through the consideration of the joint loss function, L(r,r^) , integrating L1 and L2 such that the minimization of PAPR and BER takes place. Then, the L(r,r^) is defined by:

L(r,r^)=L1(r,r^)+λL2(r). (18)

where λ represents the weight parameter determining that loss is significant i.e., L1 or L2 , is dominant.

4  Experimental Validation

In this section, a detailed set of simulations were performed to highlight the better performance of the HPT-SSAE model with other existing methods such as original OFDM, with GA, and with FSO algorithms. The results are examined under different subcarriers such as 128, 256, and 512.

Fig. 5 illustrates the BER, SER, and CCDF analysis of the HPT-SSAE model under the presence of 128 subcarriers. From the figure, it is evident that the HPT-SSAE model has accomplished effective performance under distinct aspects. For instance, on measuring the results interms of BER, the experimental outcome indicated that the OFDM model has shown insignificant performance over all the other methods by attaining higher BER. At the same time, the with-GA algorithm has accomplished slightly reduced BER over the OFDM model whereas even improved BER has been obtained by the with-FSO algorithm. But the presented HPT-SSAE model has resulted in effective performance and achieved a minimum BER. The HPT-SSAE model has reached the least BER of 10–0.73 whereas the OFDM, with-GA, and with-FSO algorithms have demonstrated an increased BER of 10–0.44, 10–0.56, and 10–0.62 respectively.

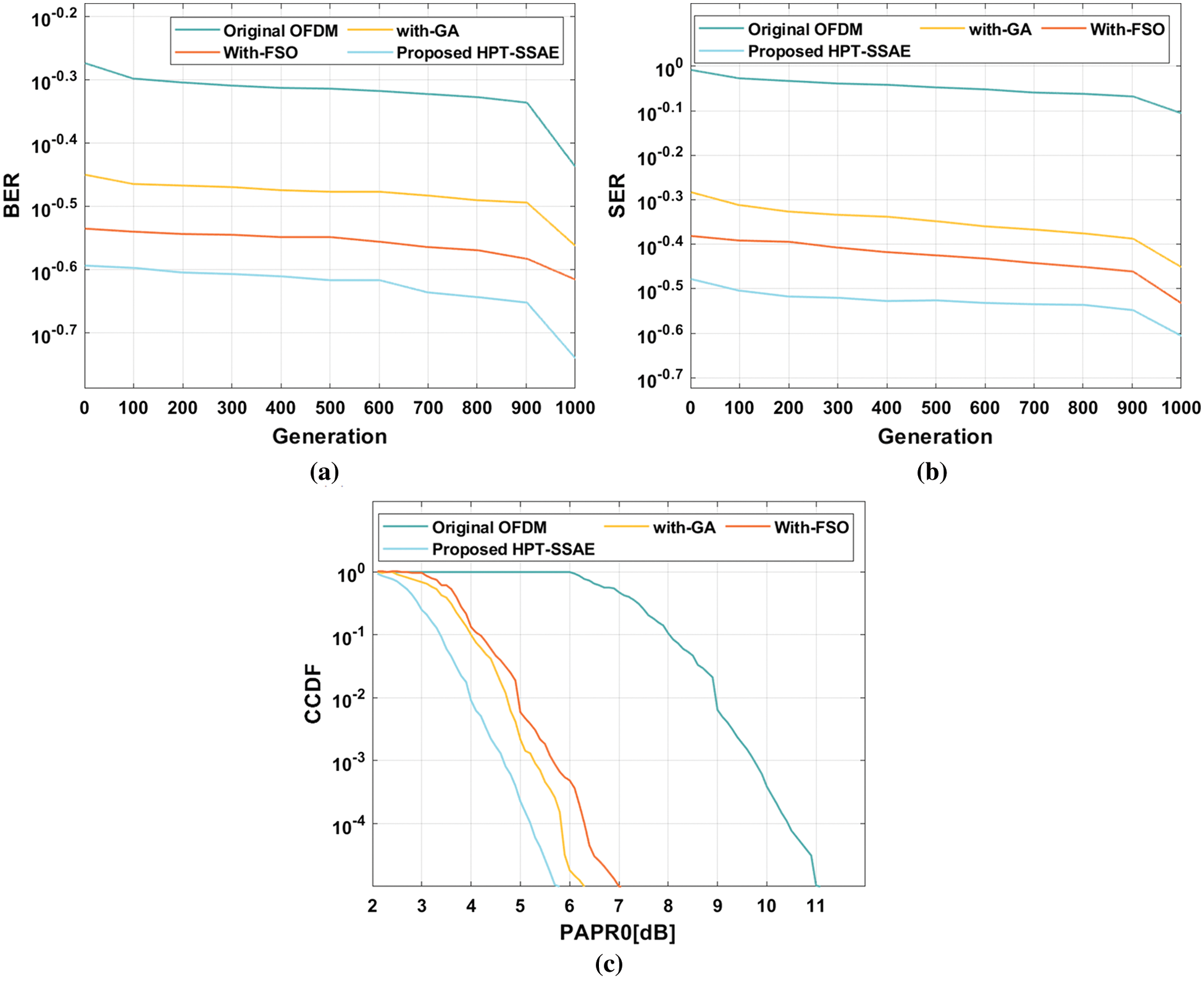
Figure 5: Result analysis of 128 subcarriers (a) BER (b) SER (c) CCDF

Moreover, on determining the results with respect to SER, the experimental result represented that the OFDM technique has shown insignificant performance over all the other models by attaining higher SER. Simultaneously, the with-GA method has accomplished slightly decreased SER over the OFDM approach whereas even increased SER has been achieved by the with-FSO model. But the proposed HPT-SSAE model has resulted in effective performance and achieved a minimum SER. The HPT-SSAE model has reached the least SER of 10–0.61 whereas the OFDM, with-GA, and with-FSO techniques have outperformed an improved SER of 10–0.11, 10–0.45, and 10–0.53 correspondingly. Lastly, on determining the outcomes interms of CCDF, the experimental result indicated that the OFDM model has depicted insignificant performance over all the other techniques by obtaining superior CCDF. Likewise, the with-GA algorithm has accomplished somewhat reduced CCDF over the OFDM model whereas even higher CCDF has been reached by the with-FSO algorithm. But the proposed HPT-SSAE model has resulted in effective performance and achieved a lesser CCDF. The HPT-SSAE approach has achieved a minimum CCDF of 5.8 dB whereas the OFDM, with-GA, and with-FSO methods have outperformed an increased CCDF of 11 dB, 6.2 dB, and 7 dB correspondingly.

Fig. 6 showcases the BER, SER, and CCDF analysis of the HPT-SSAE technique under the presence of 256 subcarriers. From the figure, it is clear that the HPT-SSAE model has accomplished effective performance under different aspects. On evaluating the results with respect to BER, the experimental outcome referred that the OFDM model has exhibited insignificant performance over all the other methods by attaining higher BER. In line with, the with-GA methodology has accomplished somewhat reduced BER over the OFDM method whereas even increased BER has been reached by the with-FSO algorithm. But the presented HPT-SSAE model has resulted in effective performance and achieved a minimal BER. The HPT-SSAE model has reached a minimum BER of 10–1.56 whereas the OFDM, with-GA, and with-FSO techniques have demonstrated a maximum BER of 10–0.56, 10–0.98, and 10–1.35 respectively. On measuring the outcomes interms of SER, the experimental result represented that the OFDM technique has illustrated insignificant performance over all the other methods by achieving superior SER. Similarly, the with-GA method has accomplished somewhat reduced SER over the OFDM model whereas even improved SER has been reached by the with-FSO algorithm. But the presented HPT-SSAE manner has resulted in effective performance and achieved a minimal SER. The HPT-SSAE technique has reached the least SER of 10–0.75 whereas the OFDM, with-GA, and with-FSO algorithms have demonstrated an increased SER of 10–0.42, 10–0.57, and 10–0.62 correspondingly. At last, on determining the results with respect to CCDF, the experimental outcome shown that the OFDM model has displayed insignificant performance over all the other methods by attaining higher CCDF. Concurrently, the with-GA method has accomplished slightly decreased CCDF over the OFDM approach whereas even improved CCDF has been attained by the with-FSO model. However, the proposed HPT-SSAE methodology has resulted in effective performance and achieved a minimal CCDF. The HPT-SSAE model has reached the least CCDF of 5.2 dB whereas the OFDM, with-GA, and with-FSO techniques have demonstrated a maximum CCDF of 11 dB, 7.2 dB, and 6 dB respectively.

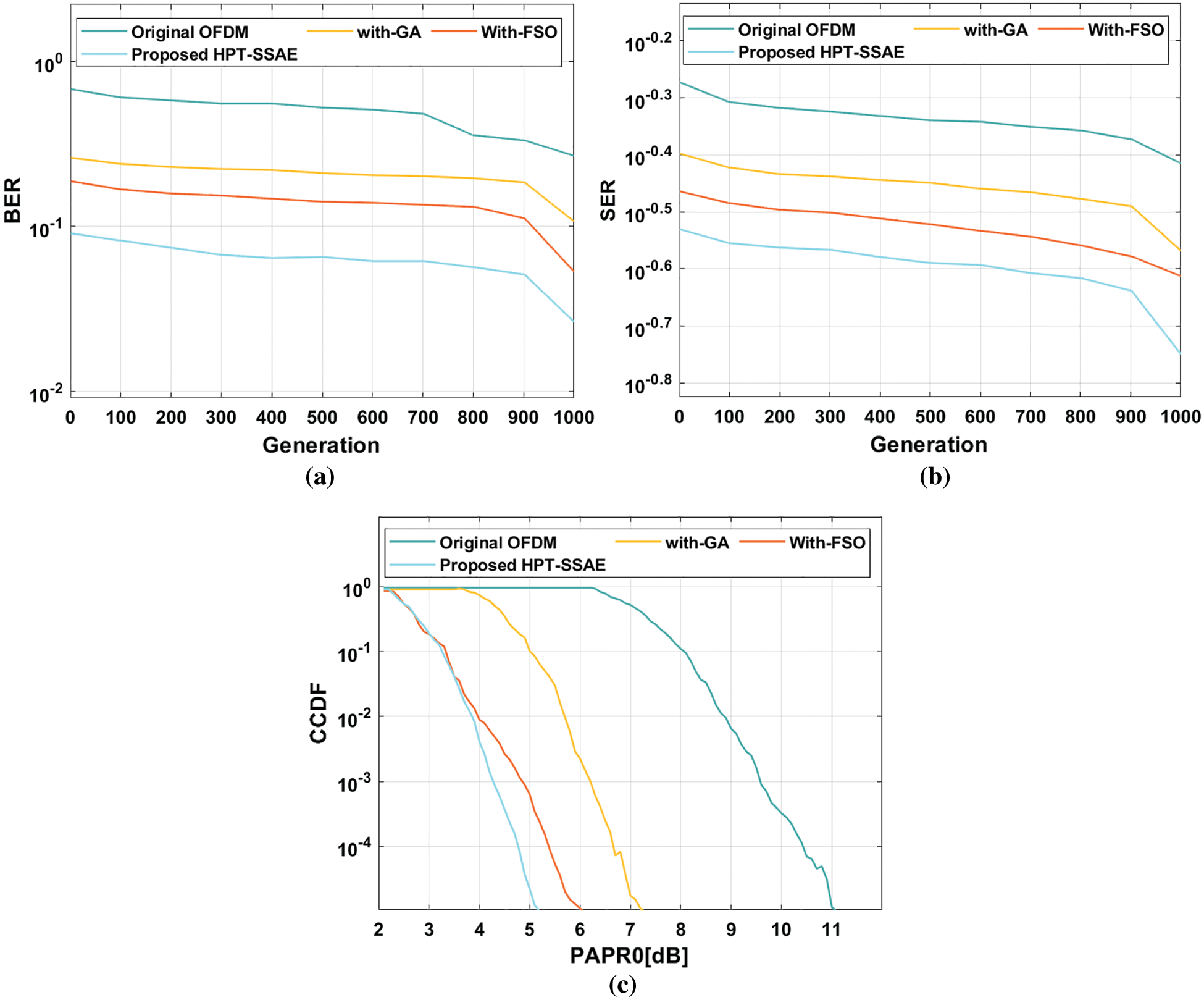
Figure 6: Result analysis of 256 subcarriers (a) BER (b) SER (c) CCDF

Fig. 7 demonstrates the BER, SER, and CCDF analysis of the HPT-SSAE technique under the presence of 512 subcarriers. From the results, it is evident that the HPT-SSAE model has accomplished effective performance under distinct aspects. For instance, on measuring the results interms of BER, the experimental outcome indicated that the OFDM model has shown insignificant performance over all the other methods by attaining higher BER. At the same time, the with-GA algorithm has accomplished slightly reduced BER over the OFDM model whereas even improved BER has been obtained by the with-FSO algorithm. But the presented HPT-SSAE model has resulted in effective performance and achieved a minimum BER. The HPT-SSAE model has reached a minimum BER of 10–2.11 whereas the OFDM, with-GA, and with-FSO algorithms have demonstrated an increased BER of 10–0.90, 10–1.15, and 10–1.35 respectively. On calculating the outcomes with respect to SER, the experimental result referred that the OFDM model has shown insignificant performance over all the other methods by attaining higher SER. At the same time, the with-GA algorithm has accomplished somewhat reduced SER over the OFDM model whereas even superior SER has been achieved by the with-FSO algorithm. But the projected HPT-SSAE model has resulted in effective performance and achieved a minimal SER. The HPT-SSAE algorithm has reached the least SER of 10–0.8 whereas the OFDM, with-GA, and with-FSO algorithms have outperformed a higher SER of 10–0.42, 10–0.58, and 10–0.62 correspondingly. Finally, on evaluating the results interms of CCDF, the experimental outcome indicated that the OFDM model has outperformed insignificant performance over all the other techniques by attaining higher CCDF. At the same time, the with-GA algorithm has accomplished slightly reduced CCDF over the OFDM approach whereas even improved CCDF has been obtained by the with-FSO algorithm. However, the proposed HPT-SSAE method has resulted in effective performance and achieved a minimal CCDF. The HPT-SSAE approach has reached the least CCDF of 5.3 dB whereas the OFDM, with-GA, and with-FSO techniques have showcased a higher CCDF of 11 dB, 5.8 dB, and 7 dB correspondingly.

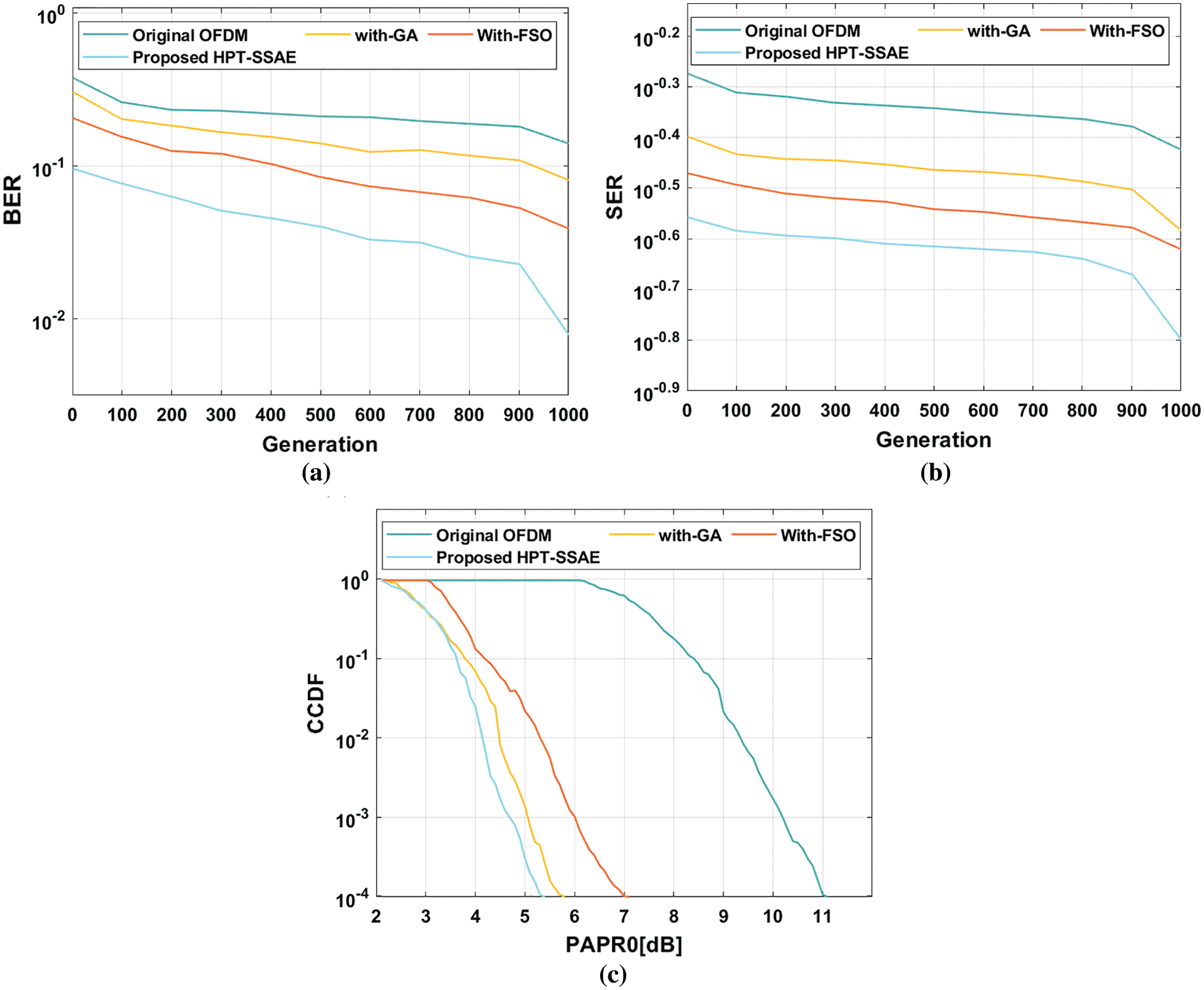
Figure 7: Result analysis of 512 subcarriers (a) BER (b) SER (c) CCDF

5  Conclusion

For addressing the PAPR problem in OFDM systems, this paper has introduced a new HPT-SSAE model for PAPR reduction. The HPT-SSAE model is intended for the substantial reduction in the peaks in the OFDM signal with no degradation of the BER. The presented HPT-SSAE model is exploited to create a peak canceling signal dynamically depending upon the features of the input signal. In the HPT-SSAE model, the constellation mapping and demapping of symbol take place on every individual subcarrier dynamically using the SSAE model. In order to further enhancement in the efficiency of the SSAE model, the hyperparameters can be tuned by the use of MBO algorithm. Extensive experimental analysis of the HPT-SSAE model takes place to point out the betterment of the HPT-SSAE model. The obtained experimental outcomes pointed out that the HPT-SSAE model highlighted the superior performance over the other compared methods interms of different measures.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Khan, P. Kumar, D. N. K. Jayakody and M. Liyanage, “A survey on security and privacy of 5G technologies: Potential solutions, recent advancements, and future directions,” IEEE Communications Surveys & Tutorials, vol. 22, no. 1, pp. 196–248, 2018. [Google Scholar]

 2.  D. Minoli and B. Occhiogrosso, “Practical aspects for the integration of 5G networks and IoT applications in smart cities environments,” Wireless Communications and Mobile Computing, vol. 2019, no. 6, pp. 1–31, 2019. [Google Scholar]

 3.  C. Mannweiler, C. Sartori, B. Wegmann, H. Flinck, A. Maeder et al., “Evolution of mobile communication networks. Towards cognitive autonomous networks: Network management automation for 5G and beyond,” in Communication Technology Networks, 1st ed., United States: Wiley Publication, pp. 29–92, 2020. [Google Scholar]

 4.  K. Zhang and H. J. Suh, “An analysis of multiuser diversity technology in the MIMO-OFDM system,” Journal of the Korea Institute of Electronic Communication Sciences, vol. 14, no. 6, pp. 1121–1128, 2019. [Google Scholar]

 5.  L. Kansal, V. Sharma and J. Singh, “Multiuser massive MIMO-OFDM system incorporated with diverse transformation for 5G applications,” Wireless Personal Communications, vol. 109, no. 4, pp. 2741–2756, 2019. [Google Scholar]

 6.  K. Anoh, C. Tanriover and B. Adebisi, “On the optimization of iterative clipping and filtering for PAPR reduction in OFDM systems,” IEEE Access, vol. 5, pp. 12004–12013, 2017. [Google Scholar]

 7.  F. Sandoval, G. Poitau and F. Gagnon, “Hybrid peak-to-average power ratio reduction techniques: Review and performance comparison,” IEEE Access, vol. 5, pp. 27145–27161, 2017. [Google Scholar]

 8.  T. S. Rappaport, S. Shu, M. Rimma, Z. Hang, A. Yaniv et al., “Millimeter wave mobile communications for 5G cellular: It will work!,” IEEE Access, vol. 1, pp. 335–349, 2013. [Google Scholar]

 9.  Y. Huo, X. Dong and W. Xu, “5G cellular user equipment: From theory to practical hardware design,” IEEE Access, vol. 5, pp. 13992–14010, 2017. [Google Scholar]

10. Y. A. Al-Jawhar, K. N. Ramli, M. A. Taher, N. S. M. Shah, S. A. Mostafa et al., “Improving PAPR performance of filtered OFDM for 5G communications using PTS,” ETRI Journal, vol. 43, no. 2, pp. 1–28, 2020. [Google Scholar]

11. L. Amhaimar, S. Ahyoud, A. Elyaakoubi, A. Kaabal, K. Attari et al., “PAPR reduction using fireworks search optimization algorithm in MIMO-OFDM systems,” Journal of Electrical and Computer Engineering, vol. 2018, no. 3, pp. 1–12, 2018. [Google Scholar]

12. B. Wang, Q. Si and M. Jin, “A novel tone reservation scheme based on deep learning for PAPR reduction in OFDM systems,” IEEE Communications Letters, vol. 24, no. 6, pp. 1271–1274, 2020. [Google Scholar]

13. M. Kim, W. Lee and D. H. Cho, “A novel PAPR reduction scheme for OFDM system based on deep learning,” IEEE Communications Letters, vol. 22, no. 3, pp. 510–513, 2017. [Google Scholar]

14. I. Sohn and S. C. Kim, “Neural network based simplified clipping and filtering technique for PAPR reduction of OFDM signals,” IEEE Communication Letters, vol. 19, no. 8, pp. 1438–1441, 2015. [Google Scholar]

15. M. Singh and S. K. Patra, “On the PTS optimization using the firefly algorithm for PAPR reduction in OFDM systems,” IETE Technical Review, vol. 35, no. 5, pp. 441–455, 2018. [Google Scholar]

16. M. H. Aghdam and A. A. Sharifi, “PAPR reduction in OFDM systems: An efficient PTS approach based on particle swarm optimization,” ICT Express, vol. 5, no. 3, pp. 178–181, 2019. [Google Scholar]

17. W. Xiao, H. Deng and S. Jiang, “PAPR reduction in VLC-OFDM system using a combination of shuffled frog leaping algorithm and hill-climbing algorithm,” Wireless Personal Communications, vol. 97, no. 3, pp. 3757–3771, 2017. [Google Scholar]

18. J. Wang, X. Lv and W. Wu, “SCR-based tone reservation schemes with fast convergence for PAPR reduction in OFDM system,” IEEE Wireless Communications Letters, vol. 8, no. 2, pp. 624–627, 2019. [Google Scholar]

19. P. R. Kumar, P. V. Naganjaneyulu and K. S. Prasad, “Hybrid PS-GW optimised PTS scheme for PAPR reduction in OFDM system,” IET Communications, vol. 13, no. 18, pp. 2996–3002, 2019. [Google Scholar]

20. N. Krishnaraj, M. Elhoseny, E. L. Lydia, K. Shankar and O. A. L. Dabbas, “An efficient radix trie-based semantic visual indexing model for large-scale image retrieval in cloud environment,” Journal of Software: Practice and Experience, vol. 51, no. 3, pp. 489–502, 2021. [Google Scholar]

21. B. Yan and G. Han, “Effective feature extraction via stacked sparse autoencoder to improve intrusion detection system,” IEEE Access, vol. 6, pp. 41238–41248, 2018. [Google Scholar]

22. Y. Feng, J. Yang, C. Wu, M. Lu and X. J. Zhao, “Solving 0-1 knapsack problems by chaotic monarch butterfly optimization algorithm with Gaussian mutation,” Memetic Computing, vol. 10, no. 2, pp. 135–150, 2018. [Google Scholar]

23. M. Alweshah, S. Al-Khalaileh, B. B. Gupta, A. Almomani, A. I. Hammouri et al., “The monarch butterfly optimization algorithm for solving feature selection problems,” Neural Computing and Applications, vol. 116, no. 10, pp. 147, 2020. [Google Scholar]

24. L. Sun, S. Chen, J. Xu and Y. Tian, “Improved monarch butterfly optimization algorithm based on opposition-based learning and random local perturbation,” Complexity, vol. 2019, pp. 1–21, 2019. [Google Scholar]

25. M. H. Kavita and P. H. Uday, “Efficient selective mapping PAPR reduction technique,” Procedia Computer Science, vol. 45, pp. 620–627, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.