DOI:10.32604/iasc.2022.019330

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.019330 |  |
| Article |
A Dynamic Adaptive Firefly Algorithm for Flexible Job Shop Scheduling
Department of Mechanical Engineering, Delhi Technological University, Delhi, India
*Corresponding Author: K. Gayathri Devi. Email: itzgaya@gmail.com
Received: 10 April 2021; Accepted: 06 June 2021
Abstract: An NP-hard problem like Flexible Job Shop Scheduling (FJSP) tends to be more complex and requires more computational effort to optimize the objectives with contradictory measures. This paper aims to address the FJSP problem with combined and contradictory objectives, like minimization of make-span, maximum workload, and total workload. This paper proposes ‘Hybrid Adaptive Firefly Algorithm’ (HAdFA), a new enhanced version of the classic Firefly Algorithm (FA) embedded with adaptive parameters to optimize the multi objectives concurrently. The proposed algorithm has adopted two adaptive strategies, i.e., an adaptive randomization parameter (α) and an effective heterogeneous update rule for fireflies. The adaptations proposed by this paper can help the optimization process to strike a balance between diversification and intensification. Further, an enhanced local search algorithm, Simulated Annealing (SA), is hybridized with Adaptive FA to explore the local solution space more efficiently. This paper has also attempted to solve FJSP by a rarely used integrated approach where assignment and sequencing are done simultaneously. Empirical simulations on benchmark instances demonstrate the efficacy of our proposed algorithms, thus providing a competitive edge over other nature-inspired algorithms to solve FJSP.
Keywords: Adaptive firefly algorithm; combined objective optimization; integrated approach; flexible job-shop scheduling problem
Flexible Job Shop Scheduling (FJSP) differs from the classic job shop scheduling problem in being flexible. This flexibility assists the manufacturer in handling customized orders from customers. In FJSP, more than one machine is available to process different operations of jobs. This availability makes FJSP an NP-hard problem that even a slight change in the setup will increase the complexity. In FJSP, two sub-problems have to be tackled: assignment and sequencing. First, suitable machines have to be assigned to each operation, and then those operations have to be sequenced to process. These sub-problems can be addressed by two methods, i.e., a hierarchical and an integrated approach. As for a hierarchical approach, a researcher first solves the assignment and then performs the sequencing. However, as for an integrated approach, both assignment and sequencing issues are solved concurrently. Most researchers prefer a hierarchical approach, as it is easy to implement. Very few researchers have attempted an integrated approach. Since the Integrated approach solves both of the problems concurrently, it tends to solve the FJSP more efficiently. Therefore, this paper tries to solve the FJSP by an integrated approach.
Mati et al. [1] proposed an integrated greedy heuristic where the assignment and the sequencing issues are tackled simultaneously to solve a problem with more than two jobs. Buddala et al. [2] solved the FJSP by teaching–learning-based optimization (TLBO) through the integrated methodology to minimize make-span. As a new methodology, metaheuristics can solve the FJSP in less time. Nature-inspired algorithms are gaining momentum to solve the FJSP, and it is proved to give better optimal results than the classical approaches. New Nature-inspired algorithms, such as Firefly algorithm (FA), Crow search, Grey wolf optimization, LeapFrog algorithm, Social Spider Optimization, Cuckoo Search, etc., have been implemented to solve various engineering problems. Among these algorithms, the Firefly algorithm has the advantage of getting good optimal results quickly with fewer parameters. When an update rule is given for the Firefly algorithm, it achieves much better convergence, thereby obtaining the optimal results in less time [3–5]. The combination of two or more metaheuristic techniques contributes to much better results. Xia et al. [6] integrated Particle Swarm Optimisation with Simulated Annealing (SA) for minimization of the three objectives. Li et al. [7] developed a two-tuple scheme to solve FJSP by an integrated approach. They fine-tuned the control parameters for their proposed adaptive evolutionary algorithm. Kato et al. [8] solved multi-objective FJSP. Specifically, they used Particle Swarm Optimization (PSO) for the assignment subproblem and Random Restart Hill Climbing (RRHC) for the scheduling subproblem, and they found the obtained results to be conclusive. A new (2 + ∈)-approximation algorithm without any condition was proposed by Zhang et al. [9] for a two-stage flexible flow shop scheduling problem. Ding et al. [10] proposed an improved PSO with an enhanced encoding-decoding strategy. Naifar et al. [11] presented Leader Tree Guided Optimization, and they found two new optimal results for Hurink benchmark instances. Tian et al. [12] incorporated different variants of the Genetic Algorithm (GA) with PSO and a local search, and the algorithm was tested on Lawrence Benchmark instances. An et al. [13] solved a multi-objective problem by developing a non-dominated sorting Biogeography method with a hybrid Variable neighborhood search (VNS). Zhu et al. [14] studied the FJSP with job precedence constraints by evolutionary multi-objective grey wolf optimizer (EMOGWO). Vijayalakshmi et al. [15] hybridized Cuckoo search with PSO to solve a multi-objective problem in Wireless Sensor Network. Mohammad et al. [16] have presented a novel algorithm which mimics the knowledge gaining and sharing of human life. This algorithm is known as Gaining Sharing Knowledge based algorithm. The authors have implemented the algorithm for continuous optimization of 30 benchmark problems and demonstrated the efficacy of their algorithm.
Fister et al. [17] did a comprehensive review of the firefly algorithm, which provided a good insight into the firefly algorithm with its modified versions. Ong et al. [18] compared the prey-predator algorithm with the Firefly algorithm and conducted a Mann–Whitney test to demonstrate the algorithm’s efficiency. Udaiyakumar et al. [19] solved the instances of Lawrence benchmark by FA for combined objective optimization. Bottani et al. [20] solved Flexible Manufacturing System’s (FMS) loading problem by discrete FA with bi-objective. Khadwilard et al. [21] utilized the design of experiments for parameter tuning in FA and implemented it for Job shop scheduling. Rohaninejad et al. [22] solved the capacitated Job Shop Problem by Tabu search and FA following hierarchical and integrated approaches to minimize tardiness and overtime cost.
In our extensive literature study, we found that among the different objectives that can be solved for FJSP, minimizations of make-span, the maximum workload, and the total workload are contradictory. We also observed that very few papers had handled these three objectives simultaneously. Likewise, we learned that very few studies had exploited the integrated approach to solve the subproblems–sequencing and assignment of machines simultaneously. Similarly, FA has been applied to diverse fields of optimization, especially engineering. The Firefly algorithm in discrete form and hybrid form has been exploited to solve FJSP previously. However, the Firefly algorithm with adaptive features in its control parameters is a relatively new scheme to solve FJSP. In our proposed HAdFA, we have applied two adaptive features: i) Randomness parameter (α), where the α changes dynamically at every iteration, and ii) A modified update rule for fireflies with a heterogeneous update strategy. By applying the adaptive features in classic FA, premature convergence is avoided, and the search mechanism is enhanced, leading to the exploration of new optimal solutions. Additionally, the Adaptive FA (AdFA) has been hybridized with enhanced simulated annealing to accelerate the local search and overcome local optima entrapment issues. Besides, regarding the literature study we have done, no previous works have solved the benchmark instances used in this work with the proposed adaptive features.
The remainder of this article is organized as follows. Section 2 introduces the problem model and the hypothesis. AdFA and HAdFA algorithms are explained in Section 3. Section 4 describes the results obtained by HAdFA when it is applied to well-known benchmark instances of Brandimarte taken from Operations Research (OR) library and Du et al. and Rajkumar et al. Some final concluding remarks are provided in Section 5.
The main advantage of the FJSP is its flexibility. Any available machine can process any operation for different types of jobs. This paper formulates the FJSP by a set of notations. The assumptions made in our FJSP problem are as follows:
1. No disruption of operation is allowed during the process;
2. Jobs are not dependent on each other;
3. None of the jobs has been assigned any priority;
4. Jobs can be processed at starting time;
5. Processing time is not inclusive of any setup time or transfer time.
m: Total number of machines
n: Number of jobs in total
J: The entire set of jobs to process
i, u = job list; i, u = 1, 2, …. n
Ji: The ith job of J
Oi: The set of all operations from Ji
ni = Number of operations of job i in total
g,v: index of operations of Ji, g, v = 1, 2, … ni
Oig: the gth operation of Oi
Mig: Number of machines in total that are free to process
k: the index of machines, k = 1, 2 … m
Mig: the set of available machines for operation Oig
Bigk: The time taken by operation Oig to start on machine k
Figk: The time taken by operation Oig to finish on machine k
Pigk: The time taken by operation Oig to process on machine k
Fk: Finishing time of Mk
ω1, ω2, ω3: weight variables
Xigk, Diugvk: decision variable
The three objectives to be minimized are
1. The time taken for processing all jobs known as the Make-span (MSmax) of the jobs given in Eq. (1).
2. The machine with the maximum workload, known as the Maximum machine workload (WLmax) given in Eq. (2).
3. The total workload of entire machines (WLtotal) given in Eq. (3)
The Combined Objective Function (COF) is formulated as
They are subjected to:
Eq. (4) ascertains operation precedence constraint; Eqs. (5) and (6) ascertains non-violation of resource constraint; Eq. (7) indicates a limitation that, when two operations are performed on the same machine, the predecessor has to be processed before successor; Eq. (8) ascertains that, a machine can process only one operation at a time. Among the different approaches to solve a combined objective problem, we take the weighted sum approach. In the weighted sum approach, weights are assigned to each multi-objective, and then the multi-objective is converted to a single objective. The conversion of the weighted sum of the three objectives into a single is given by Eq. (9)
This is subjected to:
In Eq. (10), COF is the combined objective function. ω1, ω2, ω3 are weights given for the three objectives. The value of weights depends upon the problem: for an objective that needs more consideration, a higher weight value is given; else, a small value is given. The advantage of the weighted sum approach is that the user can amend the weights of the objectives according to the requirement of the problem. We have assigned ω1 = 0.7, ω2 = 0.15, and ω3 = 0.15 in this study.
Among the recently developed Swarm intelligence techniques, the Firefly algorithm works on the firefly’s bioluminescence feature. Bioluminescence is a form of communication between fireflies. The flashing of light helps the fireflies find their mates or prey or protect themselves from a predator. The fireflies move in a swarm. Depending upon the intensity of the flashlight, the swarm may move to brighter and more attractive positions. The movement of a firefly to better flashing firefly is correlated to the objective function, which makes optimization of the objective function important.
The following points depict the basic working mechanism of FA: (1) All fireflies are unisexual; therefore, the fireflies may get attracted to each other regardless of their gender. (2) If a firefly finds another firefly brighter than it, then the former will move towards it. If a firefly can’t find a brighter firefly, then it roams around randomly until it finds one. (3) The brightness of fireflies increases proportionally to the objective for a maximization problem and vice versa for the minimization problem.
In standard FA, the above rules are incorporated into the algorithm’s procedure. Specifically, the algorithm is initialized by generating an initial population of fireflies. Then, it calculates the objective function and repeats the calculation for generations.
β is the attractiveness of a firefly, which controls the convergence of fireflies and is given by Eq. (11); the term α (Randomness parameter) allows random exploration, and the adjustment of α can enhance exploration [23]. The attractiveness (α) of a firefly can be calculated by
where β0 is the attractiveness when r is 0; r is the distance between two fireflies; γ is the light absorption coefficient.
The distance rij for two fireflies Xi and Xj is given by Eq. (12)
where D is the problem dimension.
If a firefly Xj is brighter than Xi, then Xi starts moving towards Xj. This movement of the firefly is called updating of a position of the firefly, and it is given by Eq. (13).
where xid and xjd are the dth dimension value of firefly Xi and Xj, respectively;
3.1 Adaptive Firefly Algorithm (AdFA)
The three parameters that play an essential role in FA are the randomization parameter α, the attractiveness β, and the absorption coefficient γ. The performance and efficiency of FA depend upon the parameters. In standard FA, the algorithm has a limitation of premature convergence. Also, the parameters in standard FA cannot be modified at each iteration as they are fixed. This restriction makes the standard FA have a limited diversification search area and limited algorithm speed. Hence, the firefly’s capability to search effectively can be enhanced by fine-tuning the parameters α, β, γ, and movement. Different parameter adjustment strategies have been proposed by [24–26]. In any swarm-based algorithms, the balance of global exploration and local exploitation is essential. The fireflies have to explore the entire search space and do not cluster on local optima, especially during the preliminary stages of optimization. In the later stages of optimization, the convergence has to be towards global optima to find optimal solutions efficiently.
Randomization parameter α has a significant role in moving a firefly from the current position to the optimum position of the search space. Therefore, setting up α is an important step to get better convergence. A fixed α decreases linearly to the generation that leads to premature convergence. From existing studies, it is observed that fixed α does not work well for all applications. If a large α is set, then there is a chance that α may skip the optimal solution during the search, reducing the search efficiency. Otherwise, if a small α is set, then the convergence becomes a problem when it moves towards the global optimum. Therefore, it is suggested that to gain a balance between the exploration of search space and exploitation, α has to be decreased dynamically with respect to the generation number.
So, considering the importance of α and its effect on the exploration and convergence of the algorithm, we have adopted the randomization parameter (α) strategy proposed by [27], which is given by Eq. (14)
where c denotes the integer number for determining the randomness speed decay, tmax denotes the maximum number of iterations, and ti is the current iteration. c = 5 is set in this study. The randomization parameter is set in the initialization stage, and it changes dynamically during optimization. By applying Eq. (14), the randomness parameter is modified at each step during the optimization process after an initial value is set up, thereby increasing the convergence speed.
Another adaptation we have made is in the movement step. Cheung et al. [28] proposed an adaptive movement strategy by two mechanisms: distance-based adaptive mechanism and gray-based coefficients. We have adopted the second mechanism, i.e., gray-based coefficients, where the search is enhanced by applying a heterogeneous update rule.
Two updating equations are defined based on the heterogeneous rule given by Cheung [28], and they are randomly selected during the search course. The updating equation is given in Eqs. (15a) & (15b)
where Gmax is the number of generations in maximum; η is a gray coefficient, and
By implementing these adaptations in classic FA, local optima entrapment and premature convergence are prevented in the proposed AdFA. Fireflies’ search abilities are enhanced, and they exchange valuable information and their flight paths adaptively. A proper balance has been achieved between exploration and exploitation. These modifications will help the fireflies acquire beneficial information from other fireflies, and they change the directions of flight adaptively. The movement update rule helps the search of conditions. These modifications can improve the FA and contribute to better optimal solutions. The pseudo-code of the Adaptive Firefly Algorithm (AdFA) is given in Tab. 1.

Adaptive FA is a modification of classic FA where randomization α strategy and heterogeneous update rule are used. The adaptive FA has excellent convergence speed, but it has the disadvantage of falling into local optima. To address this problem and improve the solution set, we have hybridized AdFA with SA. SA is an approximation algorithm that is based on the annealing process of metals. With the metropolis criterion, it is ensured that SA does not fall into local optima and it can search in a wide area. Simulated annealing is further explained in detail in subsequent content. This paper has implemented a modified FA with an adaptive strategy embedded with enhanced SA to prevent premature convergence and local optima entrapment. The experimentations should be carried out along with an adequate comparison with standard methods to show the effectiveness of the designed model for the scheduling and controlling complications involved in the function/working of the FJSP. At every repeated step of the algorithm, the comparatively weak schedules showing inferior performance are detached out of the populace, and they are substituted with the fresh individuals. The output of the algorithm is augmented with a local searching routine.
The simulated annealing method is a probabilistic search technique with effective local searchability. The neighborhood structure and annealing rate function have a substantial influence on the algorithm. The working and description of the algorithm are given in the following subsections, and improvement observed in optimal solutions is discussed in relevant sections.
3.2.1 Population Initialisation
The initial population should have good quality because a good search space ensures enough diversity. The population of fireflies determines the search space of fireflies to explore the optimal solutions. An initial population of fireflies is generated randomly where sorting of jobs and a machine is randomly selected for each operation.
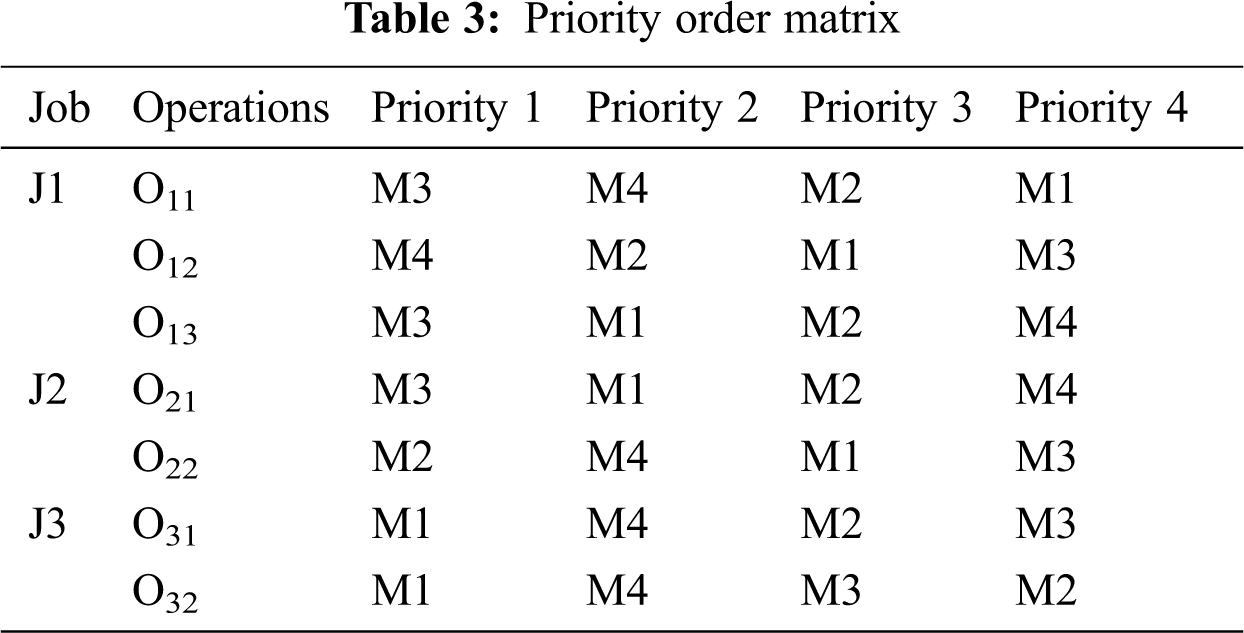
For encoding purposes, we have employed ‘real number encoding’ in this paper. An integrated approach to solve routing and scheduling simultaneously is attempted [29]. The integer portion is assigned to the operations of each job, and the fractional portion is allocated to the operation sequence on each machine. The encoding system is explained with an example. Tab. 2 shows the three jobs and four machines matrix with processing times on different machines. A priority table of machines is designed according to the operation’s processing times in increasing sequence, as shown in Tab. 3. Priority values 1–4 are given, starting from the least processing time to the most processing time. For example, job 1, O11, has M4 with the least processing time of 3. Hence, the priority for this case is 1; M3 has the next higher processing time of 4, so the priority for this case is 2; M2 has the next processing time of 5, so the priority for this case is 3; finally, M4 has the highest processing time, so the priority for it is 4. If the processing times are the same, then priority will be given to the machine with a lower number.
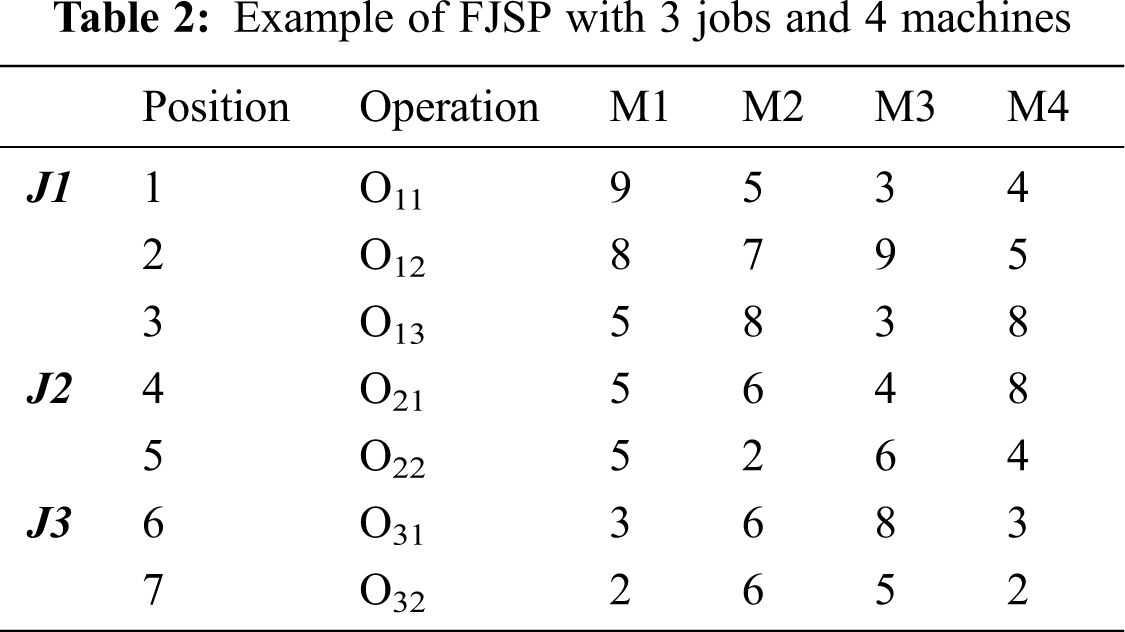
Tab. 4 illustrates the stochastic representation of firefly position. Random initialization of fireflies is generated. The maximum value corresponds to the firefly position should be equal to the total number of machines available (tnm). “One” is the least value that can be used. Therefore, in the range of (1, 1 + tnm), firefly position values with positive integers are generated.
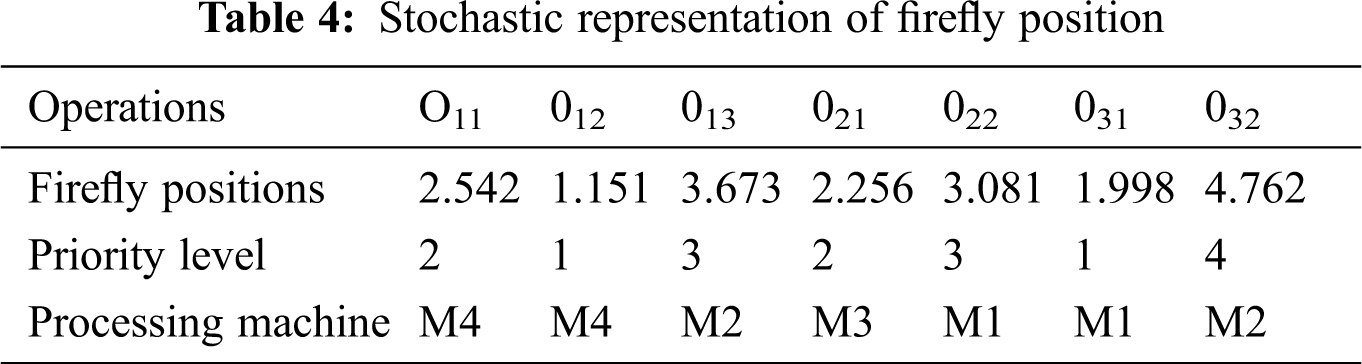
In Tab. 4, O11 has a value of 2.542, and 2 is the integer value. According to the priority table matrix listed in Tab. 3, O11 is assigned to M4, the second priority machine. In the same way, all operations are assigned to the machines. After the assignment of machines to operations, the operation has to be sequenced according to the fractional part. For example, M4 is assigned to O11 and O12. Comparing the fractional part of the corresponding operations, O11 has 0.542 and O12 has 0.151. It can be seen that the fractional part of O12 is smaller than that of O11. So, O12 has to be sequenced first and O11 later. Tab. 5 shows the initial sequencing of the machines done by this method. If the fractional parts have the same values, then the operation processing sequence is chosen randomly.

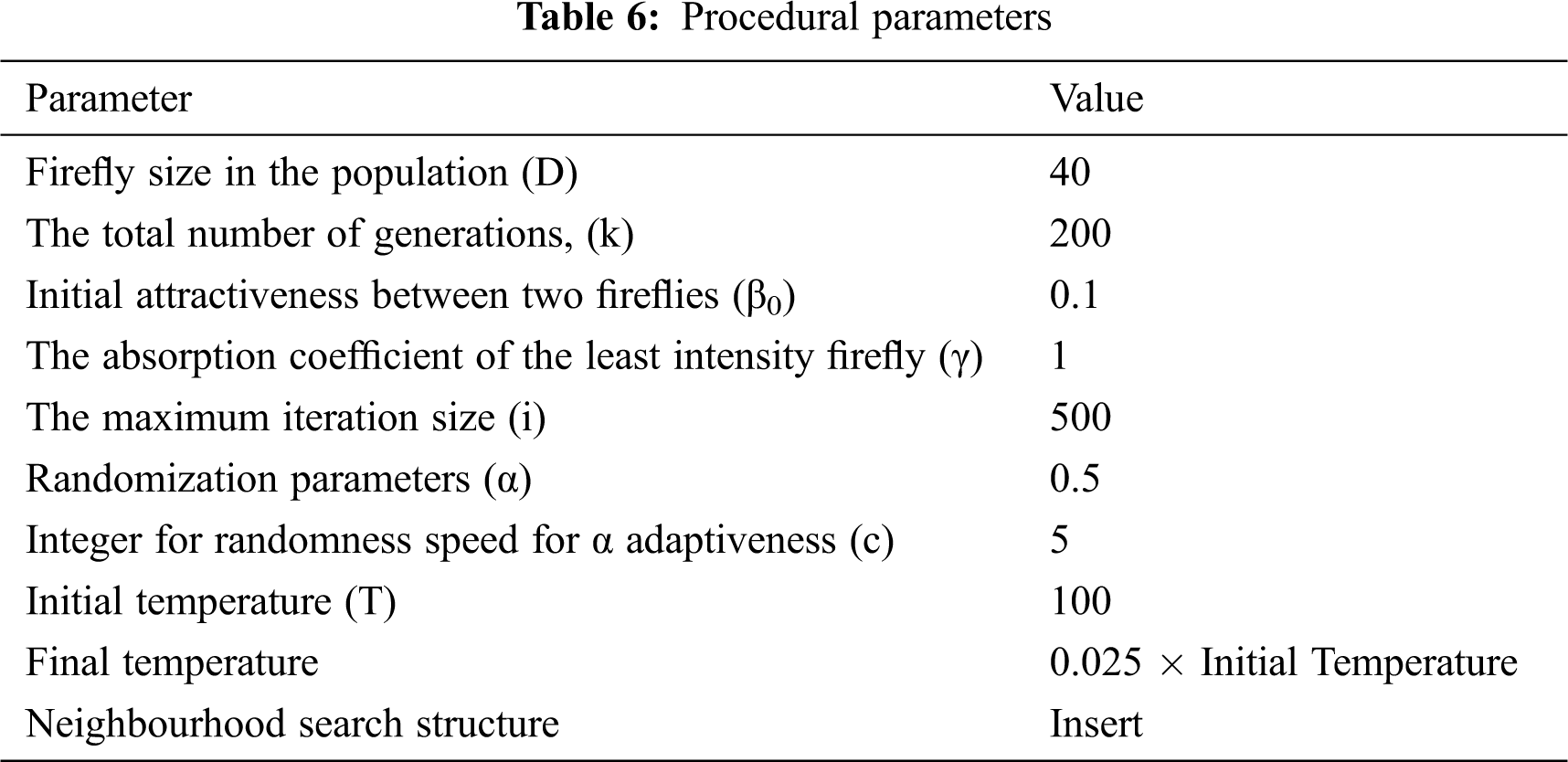
In this step, the minimization of the objective function is measured. The flashlight intensity of the firefly is correlated to the objective function considered. As for our problem, the combined objective function is given in Eq. (9) is to be solved. The procedural parameters are listed in Tab. 6. After careful analysis of different swarm sizes and iterations, we set Firefly size to 40 and the number of iterations to 500. After these values are set, there is no substantial change in obtaining an optimal solution. Our program is editable, thus we can change the number of fireflies and iterations according to user requirements.
Once fireflies are assigned intensity values, the fireflies will start to explore the solution universe, searching for brighter fireflies. In FA, the fireflies will be attracted to each other according to their brightness, i.e., the objective function. A less bright firefly will get attracted to a much brighter firefly. A new heterogeneous update rule is employed to calculate this movement and is given in Eqs. (15a) and (15b). If the current new solution is best than the previous one, the current best solution replaces the preceding inferior solution. Reiterate the preceding steps till the termination criteria. We have taken a maximum number of generations (200) as termination criteria.
The initial population for SA is a combination of the best solution from AdFA and the randomly generated initial solutions. The SA prevents the solutions from falling into local optima. The parameters for SA are established as pre-defined. After the initial temperature (T = T0) is set, the SA starts searching for global optima of the combined objective function in the neighborhood. Search for global optima is achieved by the continuous decrease of annealing rate of temperature. When the termination criterion is reached, the algorithm stops after giving the optimal solution. It has been demonstrated that with sufficient randomness and very slow cooling, SA can converge to its global optima. Since the minimization problem is dealt with in this paper, any movement that decreases the objective value will be retained. If the value is increased, then the movement can be maintained by a transition probability from the Boltzmann function exp (−KT), where T is the temperature that controls the annealing. SA has very few parameters that need to be fine-tuned. They are explained in the following subsections.
As the local search efficiency is directly affected by the neighborhood structure, proper care has to be taken. A random neighborhood insert is adopted in this paper, and any two vectors are selected. The larger position number is inserted into the previous position of the smaller position number, while the smaller position number and the subsequent number sequence are postponed.
Annealing rate has a significant influence on SA. Annealing rate directly influences the speed and accuracy of the annealing method. An improved annealing rate function inspired by the Hill function is adopted to enhance the exploitation of optimal solutions, as shown in Eq. (16).
where T0 is the temperature threshold, and it has a relationship with the initial temperature of the annealing method; n is the Hill coefficient, and n ≥ 1; β ∈ (0, 1) is the annealing rate coefficient; t is the iteration number.
4 Experiments and Computational Results
This section elaborates and discusses the performance metrics of the proposed AdFA and HAdFA. The proposed algorithms have been executed and tested with Matlab R2016b and above, and a computer equipped with Intel Core™i7 and running Windows 10 operating system. All the test results have been run 20 times to check the stability of the algorithm. The experiments aim to conclude that the recommended algorithm is a capable approach for flexible job shop applications. The efficiency of the proposed AdFA and HAdFA algorithms has been tested on standard benchmark instances taken from the OR library.
For our study, we have implemented the AdFA and HAdFA algorithms. Different weights have to be given to the combined objective function as we have used the weighted sum approach. After carefully reviewing the literatures of FJSP and some trial-and-error methods, we have found that the most optimal weights to solve MK01–MK10 instances are ω1 = 0.7, ω2 = 0.15, ω3 = 0.15. The weights are given according to the importance of the objectives that need to be solved. We have focussed more on make-span (MSmax), and equal weight has been assigned to total workload (WLtotal) and maximum workload (WLmax). For Du test instances, different weights have been assigned and discussed in the relevant section. The procedural parameters for FA are few. However, we have applied two adaptive strategies to FA and hybridized the Adaptive FA with SA. So, few extra parameters have to be defined. The parameters specified for our study are shown in Tab. 6. In Tab. 6, c = 5 is a parameter for α adaptive strategy, which is an integer number to determine the randomness of speed decay. Though an additional parameter is introduced for each adaptive strategy, there is no difference in computational time; nevertheless, we obtain a better optimal result. Hence, it can be concluded that the adaptive strategy helps the algorithm explore search space efficiently, and the local search is done efficiently. SA parameters are also given in Tab. 6.
Brandimarte’s benchmark set (BRdata) consists of 10 test instances with 10 to 20 jobs for 15 to 20 machines with a maximum of 240 operations. Brandimarte’s benchmark is chosen, as it is the standard benchmark to test the performance of any heuristic technique, and it is one of the most solved problems in the FJSP.
4.2.1 Performance Comparison of AdFA and HAdFA
The BRdata test problems are run for the Combined Objective Function. We have run the test instances for three algorithms, i.e., the discrete Firefly Algorithm (DFA) [30], the adaptive firefly algorithm AdFA and the proposed hybrid algorithm HAdFA. Tab. 7 shows the optimal results of MSmax, WLtotal, WLmax, and COF. The last column in Tab. 7 presents the percentage improvement (PI) for COF of each problem. Eq. (17) shows the formula for PI. We can find a significant improvement obtained by the algorithm of hybridizing Adaptive Firefly with the local search technique of SA. The F1 column is MSmax, F2 column is WLmax, and F3 column is WLtotal.
From Tab. 7, it can be observed that best makespan values are obtained for large scale problems especially MK10 has new makespan value of 201. Though there is not much difference in makespan value between DFA with AdFA and HAdFA for small and mid size problems, large scale problems show considerable improvement. Also, the COF shows a significant enhancement in all cases. This demonstrates the importance of adaptive parameters and local search when introduced to classic FA. It is also observed that there is a significant improvement of 2.22%, 5.79%, 1.58%, 2.27%, and 1.47% in COF for MK 01, MK02, MK05, MK06, and MK07, respectively. Though MK03, MK04, MK08 and MK09 show a little improvement in optimal values, this slight difference will significantly impact the computational time.
A Wilcoxon signed rank test is adopted to analyse the significant differences in the results for each test instance. It’s a non parametric analysis used for performance comparison of two metaheuristics. A confidence level of α = 0.05 is taken. The analysis was done for average makespan of 10 Brandimarte instances for 25 runs. The results show that the HAdFA performs better than Adaptive FA for 8 instances with p-value < 0.0001 except MK01, MK03 and MK08 for which p-value is ‘0‘ that indicates there is no significant difference in both algorithms. For MK07 and MK09 AdFA performs better than HAdFA.
4.2.2 Performance Comparison of HAdFA with other Techniques
Next, the proposed HAdFA is compared with other recent techniques taken from literature, and the comparison is shown in Tab. 8. Very few studies have been done for combined objective function as ours. We have compared the proposed HAdFA with Search Method (SM) by Xing et al. [31], HTSA by Li et al. [32], MODE by Balaraju et al. [33], BEG-NSGA-II by Deng et al. [34], and ADCSO by Jiang et al. [35]. In Tab. 8, the column AI is the algorithm improvement calculated by Eq. (18).
where MSbest is the best make-span value obtained by the techniques taken for comparison, and MSHadFA is the make-span value of the proposed HAdFA. The row Time(s) indicates the computational time in seconds.
The results shown in Tab. 8 indicate that our technique achieves the best output for MK01–MK03 and MK10, and it outperforms other approaches, especially in mid-scale problems. A maximum improvement of 13% can be seen for MK06. All the problems have been run 25 times. It can be observed from Tab. 8 that the computational time has been drastically reduced. Though the computational time depends on the operating system, coding technique, and other factors, our computational time has been reduced drastically. If we make the direct comparison between BEG-NSGA IId and HAdFAg, coded in Matlab on an Intel processor, it can be perceived that HAdFA takes just 0.3–2.252 s to compute for all MK problems. In comparison, BEG-NSGA II takes about 0.36 to 12.38 s. Even HAdFA takes just 1.765 s for a larger instance of MK10. Lesser computational time proves that our technique is superior to other methods, thereby proving that HAdFA has high efficacy to reduce the computational effort of FJSP. From the computational analysis shown in Tab. 8, it can be inferred that our algorithm works effectively for both mono-objective optimization and multi-objective optimization. There is a substantial improvement in both computational times and the optimal results. As the actual optimal schedule for Brandimarte instances is very challenging to be represented as Gantt charts, we have respectively shown two sample Gantt charts in Figs. 1 and 2, and these charts are obtained from HAdFA for MK01 and MK06 for make-span. The hatched lines indicate idle time.
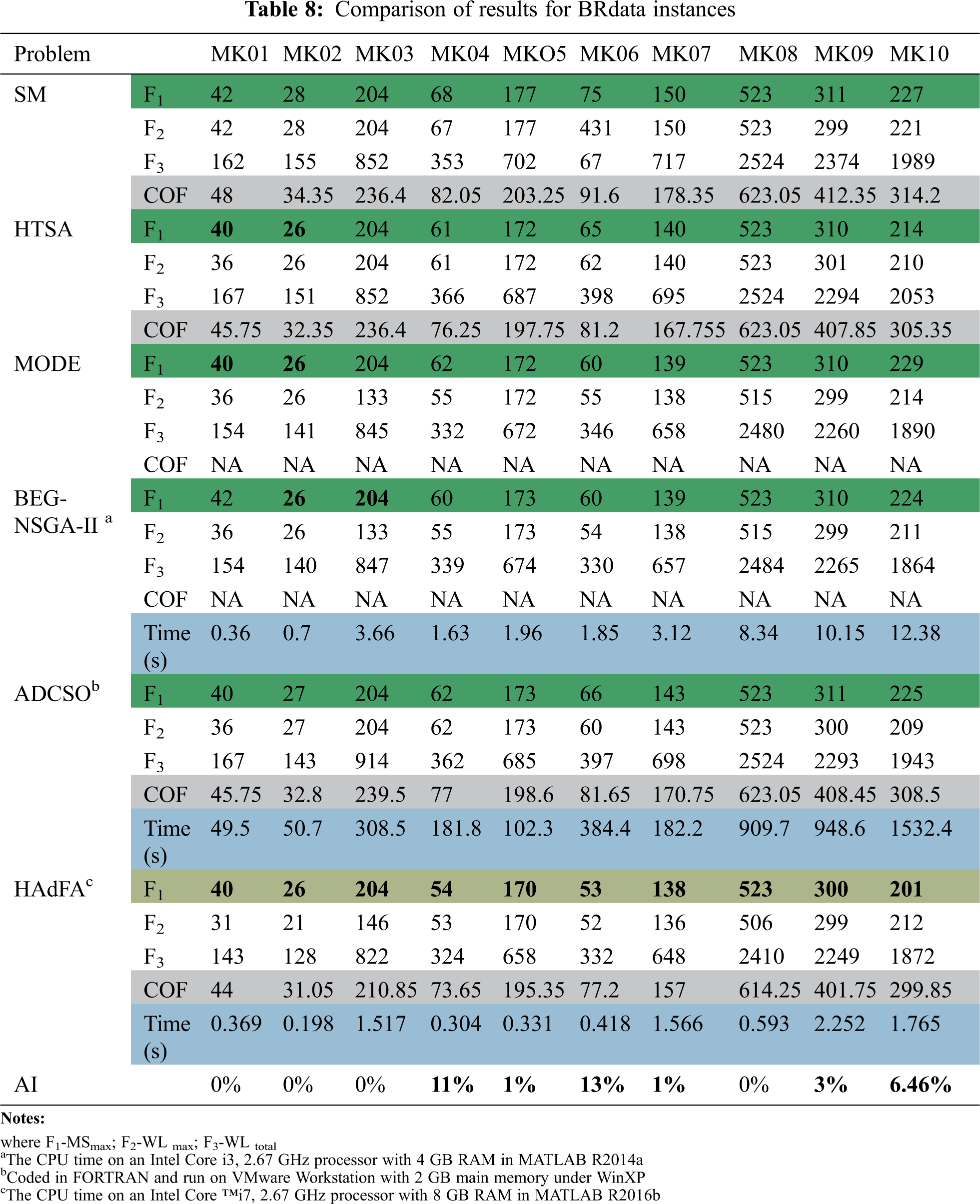

Figure 1: Gantt chart of problem MK01 for make-span (MSmax = 40)

Figure 2: Gantt chart of problem MK06 for make-span (MSmax = 53)
4.3 Experiment 2-Du Test Instances and Rajkumar Instance
For further study, the proposed AdFA and HAdFA have been tested on three problem instances taken from [36,37]. The computational results obtained by AdFA and HAdFA are given in Tab. 9. Tab. 9 also shows the COF obtained for different weights and performance comparison with other algorithms, including GA by Du et al. [36], GRASP technique by Rajkumar et al. [37], Discrete FA (DFA), and Hybrid Discrete FA (HDFA) by Karthikeyan et al. [38]. The ‘-’ indicates that the data is unavailable. The time taken for computation is given in seconds. It is validated that the proposed AdFA and HAdFA perform superiorly to the other algorithms in reference to the results shown in Tab. 9. The computational time has been reduced drastically in comparison to other algorithms. The computational time of AdFA and HAdFA has significantly less difference. There is a significant improvement in COF values. Figs. 3–5 depicts the Gantt chart of solutions. J (11), J (12), and so on represent the job number and operation in Gantt charts. Hatched lines show the machine’s idle time.
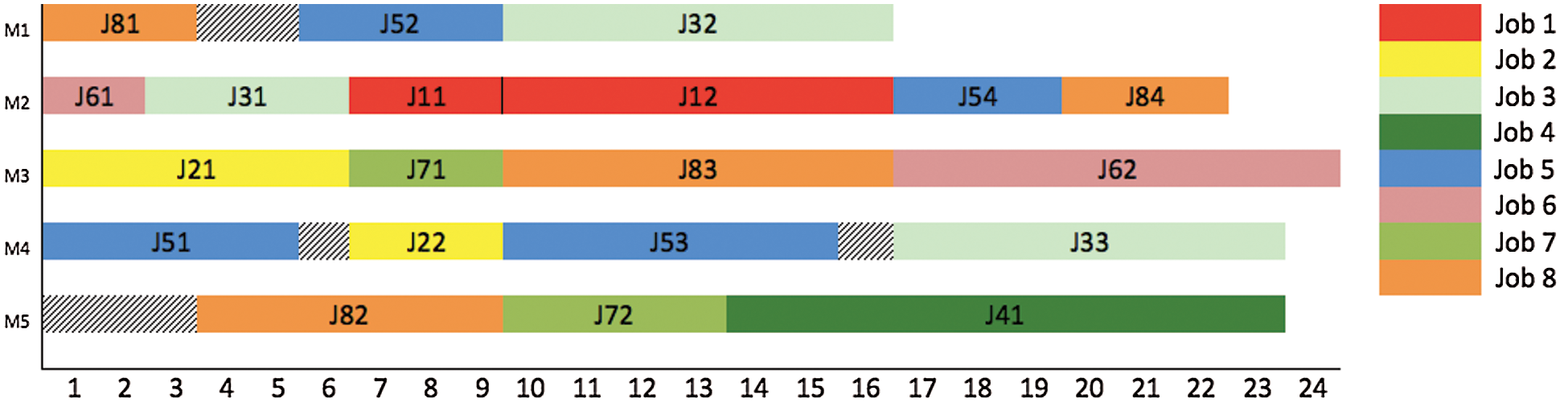
Figure 3: Gantt chart of problem 8 × 5 with 20 operations

Figure 4: Gantt chart of problem 12 × 5 with 30 operations
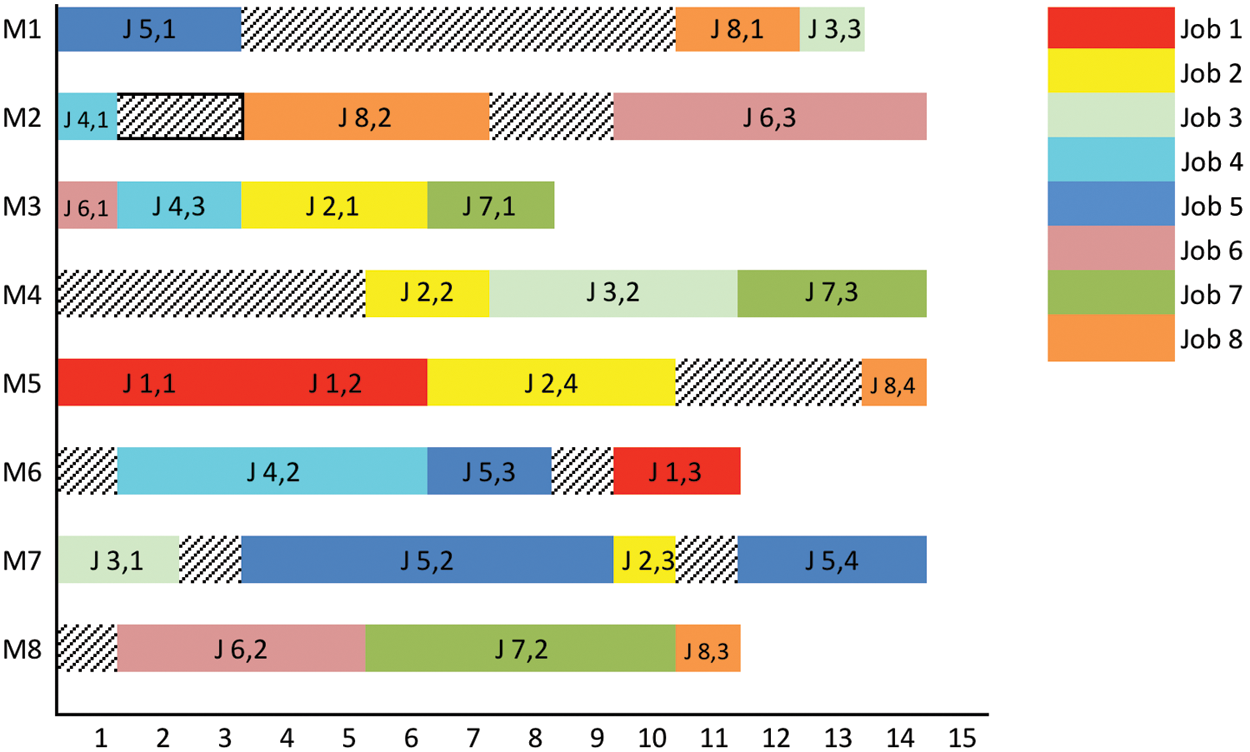
Figure 5: Gantt chart of problem 8 × 8 with 27 operations
In this article, a new novel Hybrid Adaptive Firefly algorithm (HAdFA) has been proposed to optimize the scheduling of FJSP. We have modified the classic FA by adopting and employing adaptive strategies to update the randomization parameter (α) dynamically. Also, a heterogeneous update rule is exploited to enhance the searchability of fireflies. By implementing a heterogeneous update rule, the exploitation is done efficiently, preventing premature convergence. We have hybridized the Adaptive Firefly with simulated annealing to analyze further if there is an improvement in optimal solutions. The performance of both AdFA and HAdFA has been tested on the renowned benchmark instance of Brandimarte and three test instances of Du et al. and Rajkumar et al. Combined objective optimization of three objectives has been done, including minimizing make-span, total workload, and critical workload. A less used integrated approach with real number encoding has been implemented to solve the FJSP. All the problems have been programmed in Matlab. The computational results and statistical analysis showed that our technique outperforms other meta-heuristics in getting better optimal results, and new solutions are found in some cases. Likewise, the computational time has been reduced considerably. The algorithm works effectively in both mono-objective and multi-objective optimization. It has also been observed that with an increased number of iterations and swarm size, the performance of the algorithm also increases.
Moreover, to the best of our knowledge, there are no studies that have employed the Firefly algorithm with adaptive parameters to solve Brandimarte instances and Du-Rajkumar problems for the combined objectives of MSmax, WLmax, WLtotal. For a future study of the algorithm, we intend to
• Test it for other benchmark instances and real-world problems.
• To use the hierarchical method to solve the subproblems of assignment and sequencing.
• Include some random breakdown or preventive maintenance or job insertion.
• Explore dynamic and real-time scheduling problems.
• Other combinatorial optimization problems can also be attempted.
Acknowledgement: We appreciate the linguistic assistance provided by TopEdit (https://www.topeditsci.com) during the preparation of this manuscript.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Y. Mati, N. Rezg and X. Xie, “An integrated greedy heuristic for a flexible job shop scheduling problem,” in Proc. IEEE Conf. on Systems, Man and Cybernetics, Singapore, vol. 4, pp. 2534–2539, 2001. [Google Scholar]
2. R. Buddala and S. S. Mahapatra, “An integrated approach for scheduling flexible job-shop using teaching-learning-based optimization method,” Journal of Industrial Engineering, vol. 15, no. 1, pp. 181–192, 2019. [Google Scholar]
3. X. S. Yang and M. Karamanoglu, “Swarm intelligence and bio-inspired computation: An Overview,” in Swarm Intelligence and Bio-Inspired Computation. Amsterdam, Netherlands: Elsevier, pp. 3–23, 2013. [Google Scholar]
4. G. Lindfield and J. Penny, The firefly algorithm. In: Introduction to Nature-Inspired Optimization. Amsterdam, Netherlands: Elsevier, pp. 85–100, 2017. [Google Scholar]
5. S. Carbas, “Design optimization of steel frames using an enhanced firefly algorithm,” Engineering Optimisation, vol. 48, no. 12, pp. 2007–2025, 2016. [Google Scholar]
6. W. Xia and Z. Wu, “An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems,” Computers & Industrial Engineering, vol. 48, no. 2, pp. 409–425, 2005. [Google Scholar]
7. Y. Li, J. Wang and Z. Liu, “An adaptive multi-objective evolutionary algorithm with two-stage local search for flexible job-shop scheduling,” International Journal of Computational Intelligence Systems, vol. 14, no. 1, pp. 54–66, 2020. [Google Scholar]
8. E. R. R. Kato, G. D. de A. Aranha and R. H. Tsunaki, “A new approach to solve the flexible job shop problem based on a hybrid particle swarm optimization and random-restart hill climbing,” Computers and Industrial Engineering, vol. 125, no. 4, pp. 178–189, 2018. [Google Scholar]
9. M. Zhang, Y. Lan and X. Han, “Approximation algorithms for two-stage flexible flow shop scheduling,” Journal of Combinatorial Optimisation, vol. 39, no. 1, pp. 1–14, 2020. [Google Scholar]
10. H. Ding and X. Gu, “Improved particle swarm optimization algorithm based novel encoding and decoding schemes for flexible job shop scheduling problem,” Computers and Operations Research, vol. 121, pp. 104951, 2020. [Google Scholar]
11. F. Naifar, M. Gzara and M. T. Loukil, “A new leader guided optimization for the flexible job shop problem,” Journal of Combinatorial Optimisation, vol. 39, no. 2, pp. 602–617, 2020. [Google Scholar]
12. X. Tian and X. Liu, “Improved hybrid heuristic algorithm inspired by tissue-like membrane system to solve job shop scheduling problem,” Processes, vol. 9, no. 2, pp. 1–18, 2021. [Google Scholar]
13. Y. An, X. Chen, Y. Li, Y. Han, J. Zhang et al., “An improved non-dominated sorting biogeography-based optimization algorithm for the (hybrid) multi-objective flexible job-shop scheduling problem,” Applied Soft Computing, vol. 99, pp. 106869, 2021. [Google Scholar]
14. Z. Zhu and X. Zhou, “An efficient evolutionary grey wolf optimizer for multi-objective flexible job shop scheduling problem with hierarchical job precedence constraints,” Computers and Industrial Engineering, vol. 140, no. 19, pp. 106280, 2020. [Google Scholar]
15. K. Vijayalakshmi and P. Anandan, “Global levy flight of cuckoo search with particle swarm optimization for effective cluster head selection in wireless sensor network,” Intelligent Automation & Soft Computing, vol. 26, no. 2, pp. 303–311, 2020. [Google Scholar]
16. A. W. Mohamed, A. A. Hadi and A. K. Mohamed, “Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm,” International Journal of Machine Learning and Cybernetics, vol. 11, no. 7, pp. 1501–1529, 2020. [Google Scholar]
17. I. Fister, X. S. Yang and J. Brest, “A comprehensive review of firefly algorithms,” Swarm Evolutionary Computation, vol. 13, no. 3, pp. 34–46, 2013. [Google Scholar]
18. H. C. Ong, S. L. Tilahun, W. S. Lee and J. M. T. Ngnotchouye, “Comparative study of prey predator algorithm and firefly algorithm,” Intelligent Automation & Soft Computing, vol. 24, no. 2, pp. 359–366, 2018. [Google Scholar]
19. K. C. Udaiyakumar and M. Chandrasekaran, “Optimization of multi objective job shop scheduling problems using firefly algorithm,” Applied Mechanics Materials, vol. 591, pp. 157–162, 2014. [Google Scholar]
20. E. Bottani, P. Centobelli, R. Cerchione, L. Del Gaudio and T. Murino, “Solving machine loading problem of flexible manufacturing systems using a modified discrete firefly algorithm,” International Journal of Industrial Engineering Computations, vol. 8, no. 3, pp. 363–372, 2017. [Google Scholar]
21. A. Khadwilard, S. Chansombat, T. Thepphakorn, P. Thapatsuwan, W. Chainate et al., “Application of firefly algorithm and its parameter setting for job shop scheduling,” The Journal of Industrial Technology, vol. 8, no. 1, pp. 49–58, 2012. [Google Scholar]
22. M. Rohaninejad, A. S. Kheirkhah, B. Vahedi Nouri and P. Fattahi, “Two hybrid tabu search-firefly algorithms for the capacitated job shop scheduling problem with sequence-dependent setup cost,” International Journal of Computer Integrated Manufacturing, vol. 28, no. 5, pp. 470–487, 2015. [Google Scholar]
23. X. Yang, Nature-Inspired Metaheuristic Algorithms, 2nd ed., United Kingdom: Luniver Press, 2010. [Google Scholar]
24. S. Yu, S. Su, Q. Lu and L. Huang, “A novel wise step strategy for firefly algorithm,” International Journal of Computer Mathematics, vol. 91, no. 12, pp. 2507–2513, 2014. [Google Scholar]
25. S. Yu, S. Zhu, Y. Ma and D. Mao, “A variable step size firefly algorithm for numerical optimization,” Applied Mathematics and Computation, vol. 263, pp. 214–220, 2015. [Google Scholar]
26. H. Wang, X. Zhou, H. Sun, Yu, J. Zhao et al., “Firefly algorithm with adaptive control parameters,” Soft Computing, vol. 21, no. 17, pp. 5091–5102, 2017. [Google Scholar]
27. M. Sababha, M. Zohdy and M. Kafafy, “The enhanced firefly algorithm based on modified exploitation and exploration mechanism,” Electronics, vol. 7, no. 8, pp. 132, 2018. [Google Scholar]
28. N. J. Cheung, X. M. Ding and H. Bin Shen, “Adaptive firefly algorithm: Parameter analysis and its application,” PLOS One, vol. 9, no. 11, pp. e112634, 2014. [Google Scholar]
29. M. R. Singh and S. S. Mahapatra, “A quantum behaved particle swarm optimization for flexible job shop scheduling,” Computers & Industrial Engineering, vol. 93, no. 7, pp. 36–44, 2016. [Google Scholar]
30. W. Lunardi, L. Cherri and H. Voos, “A mathematical model and a firefly algorithm for an extended flexible job shop problem with availability constraints,” Lecture Notes in Computer Science, Springer, vol. 1, no. 2015, pp. 548–560, 2018. [Google Scholar]
31. L.-N. Xing, Y.-W. Chen and K.-W. Yang, “An efficient search method for multi-objective flexible job shop scheduling problems,” Journal of Intelligent Manufacturing, vol. 20, no. 3, pp. 283–293, 2009. [Google Scholar]
32. J. Q. Li, Q. K. Pan and Y. C. Liang, “An effective hybrid tabu search algorithm for multi-objective flexible job-shop scheduling problems,” Computers & Industrial Engineering, vol. 59, no. 4, pp. 647–662, 2010. [Google Scholar]
33. G. Balaraju, S. Venkatesh and B. S. P. Reddy, “Multi-objective flexible job shop scheduling using hybrid differential evolution algorithm,” International Journal of Internet Manufacturing and Services, vol. 3, no. 3, pp. 226–243, 2014. [Google Scholar]
34. Q. Deng, G. Gong, X. Gong, L. Zhang, W. Liu et al., “A bee evolutionary guiding nondominated sorting genetic algorithm ii for multiobjective flexible job-shop scheduling,” Computational Intelligence and Neuroscience, vol. 2017, no. 1, pp. 1–20, 2017. [Google Scholar]
35. T. hua Jiang and C. Zhang, “Adaptive discrete cat swarm optimisation algorithm for the flexible job shop problem,” International Journal of Bio-Inspired Computation, vol. 13, no. 3, pp. 199–208, 2019. [Google Scholar]
36. X. Du, Z. Li and W. Xiong, “Flexible job shop scheduling problem solving based on genetic algorithm with model constraints,” in Proc. IEEE 2008, Singapore, pp. 1239–1243, 2008. [Google Scholar]
37. M. Rajkumar, P. Asokan, N. Anilkumar and T. Page, “A GRASP algorithm for flexible job-shop scheduling problem with limited resource constraints,” International Journal of Production Research, vol. 49, no. 8, pp. 2409–2423, 2011. [Google Scholar]
38. S. Karthikeyan, P. Asokan and S. Nickolas, “A hybrid discrete firefly algorithm for multi-objective flexible job shop scheduling problem with limited resource constraints,” International Journal of Advanced Manufacturing Technology, vol. 72, no. 9–12, pp. 1567–1579, 2014. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |