DOI:10.32604/iasc.2022.018558

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2022.018558 |  |
| Article |
Dynamic Hyperparameter Allocation under Time Constraints for Automated Machine Learning
Korea Institute of Science and Technology Information (KISTI), Daejeon, 34140, Korea
*Corresponding Author: Sunil Ahn. Email: siahn@kisti.re.kr
Received: 12 March 2021; Accepted: 15 April 2021
Abstract: Automated hyperparameter optimization (HPO) is a crucial and time-consuming part in the automatic generation of efficient machine learning models. Previous studies could be classified into two major categories in terms of reducing training overhead: (1) sampling a promising hyperparameter configuration and (2) pruning non-promising configurations. These adaptive sampling and resource scheduling are combined to reduce cost, increasing the number of evaluations done on more promising configurations to find the best model in a given time. That is, these strategies are preferred to identify the best-performing models at an early stage within a certain deadline. Although these time and resource constraints are significant for designing HPO strategies, previous studies only focused on parallel exploration efficiency using resource awareness. In this study, we propose a novel diversification strategy for HPO, which exploits the dynamic hyperparameter space allocation for a sampler according to the remaining time budget. We provide a simple yet effective method to accelerate the maturity of the sampler that is independent of the sampling algorithm. Compared to previous resource awareness solutions, our solution achieves better performance via both time and resource awareness. We demonstrate the performance gains of our solution on several well-known HPO benchmarks. Furthermore, we implement them to our high-performance computing AI convergence platform. Considering the different types of users, both a fully automated HPO service based on graphic processing unit (GUI) interfaces and HPO job management via python application programming interface (API) on the Jupyterlab are served on the platform, publicly.
Keywords: Hyperparameter optimization; HPO; machine learning; automated machine learning; AutoML
Automated machine learning (AutoML) is the automated process of the whole machine learning (ML) pipeline, which includes data collection, preprocessing, feature extraction, feature selection, model training, validation, and model outcome integration in various business processes without human intervention; it aims to reduce the demand for human experts and achieve optimal performance on a given task or dataset. Recently, several businesses in the artificial intelligence (AI) space have started employing AutoML owing to data heterogeneity, model sensitivity, and/or service efficiency; AutoML can be used in several applications such as speech recognition and image recognition. For example, Google AutoML provides several services according to the type of user dataset, such as natural language, vision, and tables. By contrast, Amazon SageMaker offers data preprocessing that enables the user to easily build, train, integrate, and deploy AutoML models using a given dataset at any scale. In addition, several studies have focused on developing and employing model compression, which is particularly relevant in large data applications, by reducing the size of neural networks without diminishing the model’s accuracy, to develop ML models that reflect realistic solutions (e.g., real-time diagnostics, inferences on a mobile device). The most crucial part of AutoML is automated model generation, owing to the critical selection process of a wide range of hyperparameters that greatly affects the model’s architecture, regularization, and optimization. Thus, data scientists often spend a significant amount of time tuning hyperparameters for obtaining the best-performing model. Over the past decade, a variety of automated hyperparameter optimization (HPO) techniques have been proposed, which aim to improve a model’s performance by choosing the right set of hyperparameters by finding the global optimum configuration,
Previous studies applied the Bayesian optimization on the HPO problem, including sequential model-based Bayesian optimization (SMBO) algorithms such as the Spearmint [1], sequential model-based algorithm configuration (SMAC) [2], and tree-structured Parzen estimator (TPE) [3]. The objective function
To the best of our knowledge, only the recent research by Liaw et al. [7] considered both time and resource awareness for HPO. They tried to make an optimal trade-off between evaluating multiple configurations and training the most promising ones by a certain deadline using dynamic resource reallocation. The gradual exploitation by allocating more parallel resources in the exploitation process could maximize the accuracy of a promising model under both time and resource constraints. In brief, their scheme concentrates more resources on the promising model after a certain amount of time has elapsed. However, as their solution is an extended version of ASHA, time awareness is used for the parallelization scheme with respect to resource allocation, and not for samplers including their search space. Here lies the novelty of our study. Since most previous studies were designed to select the current best configuration among the static hyperparameter space, they tend to fail several times in finding the promising configurations in the early stage of the process if the hyperparameter space is too wide because the sampler might not be mature enough. Unfortunately, nowadays ML models are getting bigger and deeper, and a hyperparameter space tends to be wide. In worst cases, one could spend expensive computing resources and time without any profit because a considerable number of finished evaluations is necessary to mature the sampler. The parallel evaluations can spend more configurations simultaneously, but they cannot affect the maturity of the sampler when they are in training.
In this study, we first design a sampling strategy under time awareness. We propose a novel diversification strategy that exploits the dynamic hyperparameter space allocation. According to the remaining time, the application-level scheduler dynamically restricts the hyperparameter space by using shrinking and gradual expanding. Such a simple yet effective method accelerates the maturity of a sampling model that is independent of the type of sampling algorithm. It can combine with ASHA for efficient parallel evaluation as pruners, to have the solution achieve a better performance via both time and resource awareness at a certain time compared to existing solutions.
The rest of this paper is organized as follows. Section 2 explains the related works with respect to the overall HPO schemes that motivated our proposed scheme. Section 3 shows the system architecture and diversification strategies of the proposed scheme, and the performance evaluation of the said scheme is compared to the schemes of the previous studies via well-known HPO benchmarks in Section 4. Section 5 introduces the systemic implementation of the proposed scheme as a practical web service on the HPC AI convergence platform, including challenging issues and design principles. Section 6 concludes the study.
In conventional ML, hyperparameters are a set of values that affect how the ML algorithms, including supported vector machine, random forest, and deep learning, fit a model, and they are set prior to the learning process. Moreover, recent HPO studies have conducted in-depth analyses of various model configurations using hyperparameters, which includes the simultaneous handling of multiple algorithms, using different data sampling, and finding an excellent network architecture of a deep learning model to automatically build the best-performing model that is selected as the best configuration among possible candidates. Strictly, these are not a set of hyperparameters but many researchers exploit such configurations for HPO problems. Therefore, in this study, we also consider them as hyperparameters for convenience. We also cite previous studies that have discussed major challenges of HPO such as sampling configuration, pruning configuration, and parallelization.
The hyperparameter configuration space, also known as the search space, organizes all the hyperparameters, and is where the configurations are sampled. In addition, the goal of a sampling algorithm is to find the best-performing configuration out of all the possible candidates. Their strategies could be classified into the following: a non-adaptive solution and an adaptive solution. The grid search is one of the most simple and intuitive non-adaptive solution in which a set of parameters is selected at regular intervals through a manually specified subset in the search space to build a model. Since the grid search defines the search space as a grid of all possible hyperparameter values and evaluates all possible position in the grid, it is difficult to find the optimal value probabilistically. Random Search [8], on the other hand, defines the search space as a bounded domain of hyperparameters and randomly draws a hyperparameter in that defined domain. Therefore, it increases the possibility of finding the optimal value faster by reducing unnecessary repetitive searches, which shows some of the advantages of employing non-adaptive solutions that includes short sampling time and effective parallelization. However, due to its stateless nature, the frequency of the non-promising sampling increases in proportion as the size of the search space increases. To solve this problem, a pruning configuration algorithm such as HyperBand, SH, and ASHA can be combined with the sampling algorithm. We described them in detail in the next chapter.
Although the adaptive solution samples a configuration that is expected to perform better than its original performance based on the sampling history to date and the corresponding evaluation score, several Bayesian optimization (BO)-based algorithms have been proposed and improved in the past decade, such as Spearmint, SMAC, and TPE. BO-based algorithms consist of a surrogate model, which estimates the evaluation score instead of evaluating the sampled configuration, and an acquisition function, which suggests a new sample for discovering promising configurations using the results of the surrogate model. The surrogate model usually employs the Gaussian process (GP), random forest [9], and TPE algorithms. Various acquisition functions such as the probability of improvement (PI), expected improvement (EI), upper confidence bound (UCB), and GP-Hedge have been proposed for improving sampling efficiency. For example, the GP-Hedge [10] provides a diversification strategy by exploiting multiple acquisition functions in solving a single acquisition problem, which is the significant variations observed in the performance of different task types. In recent studies, adaptive diversification algorithms such as S-Div, Hedge, and e-greedy have been proposed to avoid the worse cases of diversification and to increase the efficiency of such effects. However, a major drawback of the BO-based algorithms is the large sampling time, which continuously increases as the number of sampling configurations and sampling dimensions increase.
In addition, most adaptive samplers suffer from low accuracy, which suggests that the sampling results are insufficient; this results in a lower performance than the performance of those from a random draw in worst cases. We referred this as a sampling maturity problem and describe it in detail in the proposed scheme.
If we build all models using an entire set of hyperparameter candidates, a large computing time is required. For example, to optimize nine types of hyperparameters for the LeNet-1 model using the Modified National Institute of Standards and Technology (MNIST) dataset, 20,000 models need to be generated in Cho et al. [11]. If we assume that a training environment takes an average of 6.3 min, then the total evaluation time is approximately 88 days. Even if an adaptive sampling algorithm such as BO is used, it is difficult to find a promising configuration within a wide search space or to execute an expensive evaluation. Moreover, it should be noted that finding a promising configuration repeatedly in worst cases is impossible unless given enough time and resources. To alleviate the limitation, several pruning configuration algorithms based on the perspective of the multi-armed bandit problem have been proposed in which various configurations are sampled and trained at the same time. In particular, the step of each model training can be divided into several detailed steps, and the current state is stored in the memory once the training of a certain model is partially completed. Subsequently, the next model is trained, and this process is repeated. The evaluation scores are estimated after each model is completely trained based on the change in the intermediate score during training. Moreover, more resources such as dataset and computing resources are allocated to the promising configuration, which are expected to have high performance according to the estimated performance. Meanwhile, non-promising configurations are pruned. Such bandit-based algorithms can reduce the total time needed in discovering optimum values in most general tasks.
The number of parameters employed in ML models increases as the tasks, which are to be performed by ML, become increasingly sophisticated and complex. Increasing the number of parameters inevitably requires a larger amount of data to mature a model. Therefore, to understand an ML model with a complex structure such as deep learning, a given dataset should be iteratively learned. In other words, given a dataset, we might consider it as the cost of training the ML model. For example, if the cost of training a dataset is R, then the cost of repeated training for 10 epochs will be 10R. Success halving algorithm (SHA) is a strategy to obtain a learning curve value based on this training iteration and to terminate the half group with poor performance. That is, some configurations will end before 10R. By contrast, Hyperband selects the pruning rate, also known as the early-stopping rate, by running different variants of SHA. In addition, many hybrid approaches that combine adaptive sampling and pruning have been proposed in several studies. Bertrand et al. [12] suggest a combination strategy between BO and hyperband called the Bayesian optimization and hyperband (BOHB) in which a subset of the hyperparameter space would be evaluated as a hyperband and a surrogate model will then learn it. Subsequently, the probability distribution is calculated by the expected performance improvement for the undiscovered subsets. This method searches for an optimal solution about twice as fast as the existing BO. BOHB [13] exploits the TPE to BO to improve the efficiency of computation. Instead of using a random selection of a hyperparameter subset, BOHB uses BO to select a subset. BOHB also proposes a parallelization scheme that prunes a set of non-promising configurations.
In the past years, several studies have been proposed to realize a successful parallelization of HPO. Since a sampler suggests almost similar combinations within the same sampling history whether it is parallelized or not, simple parallelization cannot affect the HPO performance. Therefore, in parallel BO algorithms, various methods have been proposed to diversify the sampling results. For example, Contal et al. [14] combines UCB and pure exploration, Gonz´alez et al. [15] exploits penalized acquisition function, Wang et al. [16] suggests divide and conquer strategy, and Kathuria et al. [17] provides the diversity of a batch.
Population-based training (PBT) [18] is a hybrid evolutionary approach that exploits partial training and selective mutation. It periodically trains neural network weights in parallel with hyperparameters by using the information from the rest of the population to refine and mutate them. However, it is designed to optimize neural networks and is not suited with the general approach used in HPO. ASHA suggests parallelism and aggressive early-stopping for maturing hyperparameter optimization functionality in distributed computing settings. ASHA promotes promising configurations to the higher step of training asynchronously. Thus, it improves the suitability for the large-scale regime of hyperparameter optimization. Also, ASHA can be intrinsically combined with any sampler, even a non-adaptive random sampler, but preferably with a light sampler such as TPE. The proposed scheme is a method of improving the sampling method of HPO, which is combined with ASHA considering the utility of parallelization and built on the HPC-based platform.
In this section, we first look at the factors that may affect the maturity of the sampler for HPO problems and then discuss the strategies to effectively control them.
3.1 Definitions and Assumptions
We refer to a study as a set of trials in which each individual trial evaluates the objective function, which contains the ML model training and validation processes via the testing dataset, using a specific hyperparameter configuration. Each trial exploits different configurations sampled by its own sampling algorithm to optimize the objective function. We assume that each study has a static budget, including the number of computing resources and the time limit to finish the optimization process. Although each trial runs independently if parallelized, all trials could be finished simultaneously by their scheduler.
A sampler, which selects a configuration from the hyperparameter space, completely relies on the previous evaluations of the objective function. Thereby, it is theoretically identical to the problem of designing a recommended model that predicts a promising new configuration based on identifying the correlation among configurations and an evaluation score of the objective function using the finished evaluations dataset. Unlike general ML modeling, where a large number of datasets are prepared in advance and models are designed based on them, samplers in HPO problems should predict values in real-time with almost no data. Thus, intuitive descriptors, which can affect the maturity of a sampler, are defined as
Alternatively, we can alleviate this problem by temporarily limiting the search space the sampler has to search by decreasing k in
3.3 Gradual Expanding Search Space (GES)
We now introduce the GES running under the recognition of the time budget for the early maturing of a HPO sampler. GES divides the training steps of a model into multiple steps according to the given budget and partially restricts a given search space per each step. As shown in Algorithm 1, GES first operates by exploiting both the hyperparameter importance among well-known parameters and their initial default parameter values, providing a guided search that utilizes well-known criteria, while conventional samplers commonly set the search direction through random observations. In particular, if the type of task or the nature of the data is similar, we can expect a faster search rather than searching from the scratch.

The budget is used as an important criterion for gradual expanding. GES divides the entire search space into several steps based on the budget, referring to them as the search dimension D. For example, when optimizing four parameters such as {
Since the sampling operates independent of both pruning and parallelization, the sampler performance would be evaluated in a single processor non-pruning environment. The features of the proposed scheme are analyzed using a simple test function, and then the performance of the HPO framework is compared on several well-known regression datasets.
4.1 Test Function: Beale Function
The Beale function is multimodal with sharp peaks at the corners of the input domain. The global minimum
As shown in Fig. 1(a), during 100
4.2 Test Function: Hartmann 6-Dimensional Function
The 6-dimensional Hartmann function has six local minima, and the function is usually evaluated on the hypercube

Figure 1: Optimization with the Beale test function. The top figures are the KDE joint plots, and the bottom figures show the scatter plot for each sampling. (a) shows the TPE samples with a wider spread than others, while (b) shows discrete sampling like grid search. In (c), most of the sampling is biased towards the optimal value. (a) TPE, (b) TPE+GES with random default, (c) TPE+GES with optimal default

Figure 2: The Beale function optimization history plot. Each line shows the average error among all studies, each dashed line shows the median value, and the shaded area represents the error between q1(25%) and q3(75%) among all studies with different seeds

Figure 3: The Hartmann 6-dimension function optimization history plot. (a) shows optimization when the budget is 20, while 100 in (b). In (b), semi-optimal default value for each parameter is set to 0.5
We use UCI regression datasets for the HPO benchmark. Test dataset has been generated randomly by selected 20% of the entire dataset before model training, and a 5-fold cross-validation has been applied. In Fig. 4, each study has 50 trials as a budget to discover the best-performing hyperparameter set for the XGBoost algorithm and has been repeated with 100 different sampling seeds. All datasets can be found at https://archive.ics.uci.edu/ml/datasets.php. Tab. 1 shows the hyperparameter space of the XGBoost algorithm on each dataset. We compare five different strategies for sampling a promising configuration such as Bayesian optimization (BO:Skopt), covariance matrix adaptation evolution strategy (CMA-ES: CMA), random search (RS), tree-structured Parzen estimator (TPE), and TPE with GES (TPE+GES). In GESTPE, the search rate is set to 0.5, and the search dimension is 4. Hyperparameters have been ordered according to the parameter importance derived by provenance data on our platform, and default values on the XGBoost document webpage have been applied for the gradual expanding.


Figure 4: Performance evaluation for XGBoost comparing existing solutions such as BO, CMA, RS, TPE, and our scheme via well-known HPO regression benchmarks. (a) Boston House Prices, (b) Power Plant, (c) Concrete, (d) Parkinsons, (e) ENB2021:y1, (f) ENB2021:y2, (g) Naval: gt_c_decay, (h) Naval: gt_t_decay, (i) Protein, (j) Yacht Hydrodynamics, (k) Slice Localization Those changes can be founded in the MS word and pdf file with the red color. If you have any question, please contact me freely.
Overall, the proposed method using GES showed the best performance in all simulations. Both TPE and BO differ according to the type of dataset used, but they performed well in most problems. Since the sampling seed sequence is the same, TPE initially operates in the same way as RS, but after the sampler learns the relationship between parameters to some extent, it can be inferred that the result is superior to RS. CMA showed lower performance compared with other samplers owing to the difficulty in maturing within a given search range.
Tab. 2 shows the results of the average time consumed for each task. In the test environment, a single NVIDIA P100 was used, and all values are the average values of 100 studies performed by each sampling algorithm. As we previously mentioned, the opportunities to sample a new configuration were equally provided for each algorithm since each simulation was performed with the same budget for each trial unit. However, if we measure the simulation results in terms of absolute execution time (seconds), there is a relatively large difference in how each algorithm spends its sampling budget. If we check the approximate time consumed by the average of all the datasets, CMA consumed almost the same time as a random search, TPE consumed approximately 1.5 times more time, and BO and the proposed GESTPE consumed approximately 2 times more time. Promising configurations tend to consume more time owing to the characteristics of the Boost Tree algorithm. Although the performance of TPE and BO slightly differ depending on the type of dataset, they showed almost similar sampling performance, and the overall consumption time of TPE was lower. However, even if an algorithm finds the best configuration in the early stage than other algorithms, the HPO task cannot be completed until the given budget has been exhausted; therefore, it may include the iteration time at the stage where performance improvement is rarely achieved. This phenomenon can be confirmed in the same way in GESTPE, the proposed method, and the chart confirming how the time consumption occurred in the worst-case dataset is as follows. For example, as shown in Fig. 5(a), GESTPE consumed approximately 4.5 times more time than random search; however, GESTPE consumed more promising configurations than other algorithms. Similarly, in Fig. 5(b), BO spent approximately 3.95 times as much time as a random search. However, GESTPE, the proposed method, showed the best performance in this dataset. Excluding such worst cases, GESTPE consumed almost the same time as the TPE algorithm, whereas BO consumed more time. This is because the BO-series sampling algorithms internally perform a Gaussian process for sampling. As the sampling history (sampling rows) and sampling dimension increase (sampling columns), the time required for such internal calculations increases significantly.
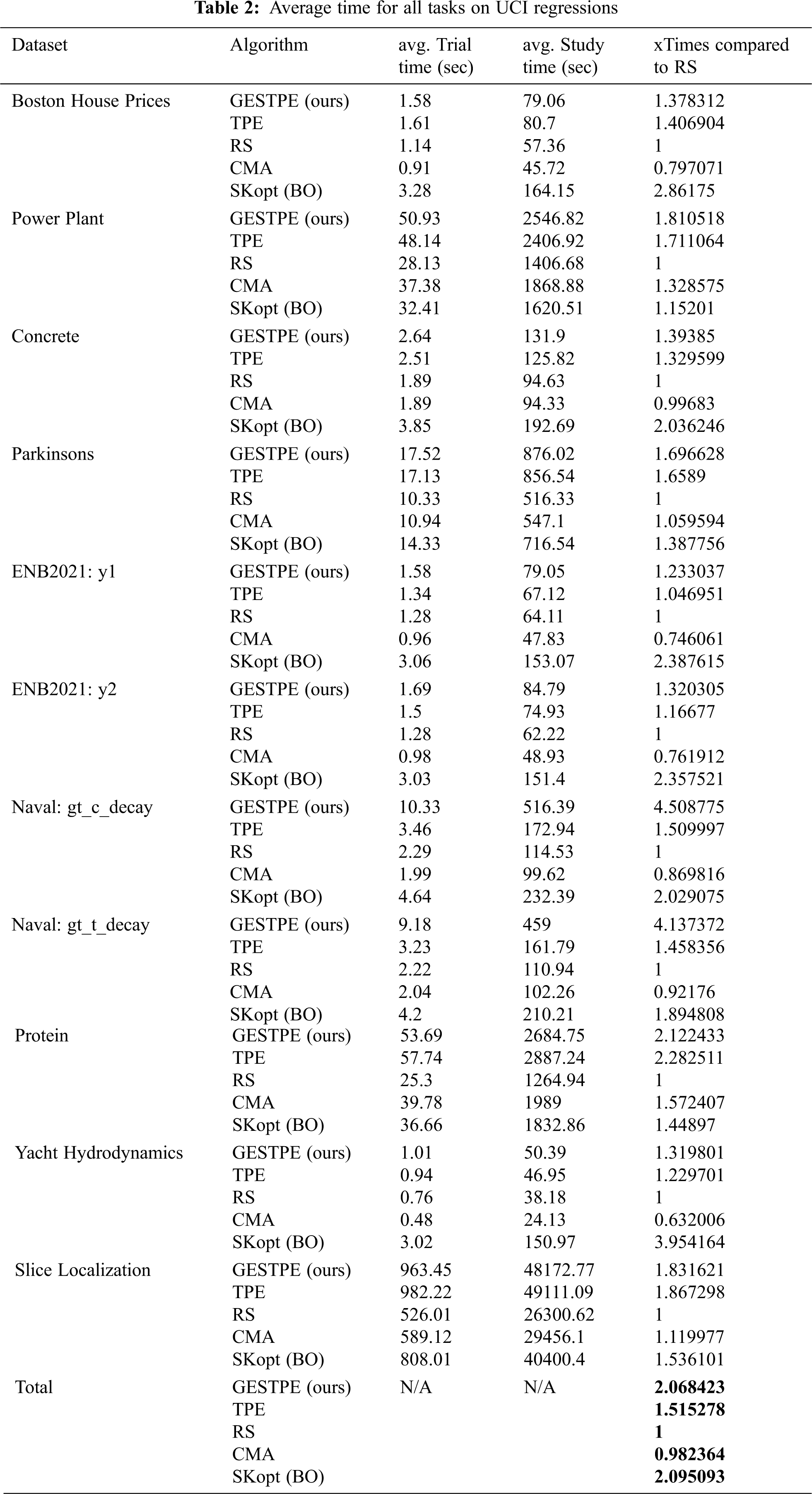

Figure 5: The worst cases of optimization history plot by time. (a) the worst case in GES+TPE, (b) the worst case in SkOpt (BO)
We describe the systemic implementation of the proposed scheme to provide a practical web service on our HPC AI convergence platform. We first introduce several challenging issues and then suggest design principles to solve them.
Before designing and developing the HPO scheme on the online platform, it is important to consider the users . If the goal is to automatically design high-performance AI models that anyone can easily build, the HPO should be simple and not complex. For example, in the case of novice users who want to automatically generate AI models using an AutoML service, if they first need to learn how to select valid hyperparameters according to a given task and data type and how to determine the search range of these parameters, the utilization of the service will significantly drop owing to the complexity of the process. Meanwhile, if the goal is to automatically maximize a pre-defined objective function, HPO should be ready for the model developer without any concern of infrastructures. If possible, HPO schemes such as parallel training and hyperparameter search should be provided as simple APIs like python-APIs or rest-APIs to facilitate an easier means of developing a best-performing AI model under the same development circumstance. For example, users should be able to do everything in a Jupyter notebook if possible.
As mentioned above, the quality and quantity of configurations consumed have a close influence on the maturity of the sampler. In terms of quantity, a certain number of evaluations is required to mature the sampler, and the cost depends on some parameters regarding training complexity such as epochs, learning rate, the number of layers, and the length of layers. In terms of quality, the larger the hyperparameter space, the more configurations the sampler requires to mature.
To date, various sampling algorithms have been proposed to select a better (promising) configuration, but none of them perform well. That is, the performance of the sampler may vary depending on a given task and dataset type. In addition, in most cases, the ML modeling is closely related to data generation and pre-processing except in the case in which a given dataset starts from a defined competition (i.e., in Kaggle competition). Thus, the HPO process might be repeated several times. In other words, when data or new features are added, the whole HPO process has to be done from scratch.
The entire search range changes depending on how the hyperparameter space (search space) is set, resulting in a rapid change in the amount of computation required to obtain the desired level of the model. For example, the best model using the MNIST dataset can achieve an accuracy of up to 99%; therefore, it is not difficult to develop a model that achieves more than 90% accuracy. However, in the case of HPO, there is a high possibility that it will take a few hours to find a model with 99% performance efficiency or none at all, even after wasting a few days of GPU time, depending on how the search range is specified. In addition, if the search range is too wide, it takes a significant amount of time for the sampler to mature, and in some cases, even if a large number of resources are consumed, the desired level of results may not be obtained at all.
Effectively performing HPO optimization using parallel resources is perhaps the most crucial metric for achieving a practical AutoML. In particular, the parallelization efficiency in HPO goes beyond reducing the overall exploration time by simultaneously evaluating multiple configurations, making it possible to determine whether to create a model that satisfies the requirements during a single project because the resources given to us are always finite. As shown in the case of task dependency, it is virtually impossible to wait for months for an HPO task that might be repeated several times from scratch.
One of the most difficult aspects of designing an ML model is the estimation of the number of resources and effort required to develop the desired level of the model. Since HPO is the best-effort solution to find the semi-optimal hyperparameter configuration, the result of the optimization is expected to be the given number of configurations for the evaluation or a given time for using resources.
5.7 Implementation for HPC Resources
We introduce, in detail, the suggested principles to help deal with the above challenges in the high-performance computing (HPC) AI convergence platform.
First, note that to use the HPO services in the platform, we have provided the GUI interfaces for novice users and the Python APIs for expert users, which are considered as different types of HPO users. In the platform, users can have personal storage managed by Jupyterlab so that they can easily upload their own dataset via the web interface. The system supports a CSV-formatted structured dataset or a CSV file containing relative file paths in the GUI-based HPO interface. After a dataset is selected for the hyperparameter to optimize, the task types, algorithm to be modelled, and resource budgets, such as seconds and the number of nodes for the training models, are chosen. These selections are managed by a metadata file. Subsequently, Python scripts and a job file are automatically generated. We exploit the SLURM workload manager to schedule jobs in which submitted jobs can be managed by web interfaces. Also, users can submit their HPO jobs on Jupyterlab directly via Python APIs. With the well-known HPO framework OPTUNA [22], users can optimize their objective functions and then submit them with job submit APIs. Each job can be managed by both web pages and Jupyterlab. That is, users need not learn the parallelization methods for HPC resources even if they are working in Jupyterlab. Automatically-generated SLURM scripts related to the HPO task will run under massive parallel HPC resources via MPI processes using a pre-defined singularity image and databases to manage the hyperparameter history of the job.
Second, diversification is achieved through the ensemble of sampling algorithms in our HPO scheme, to handle the issue with the sampler maturity. Since the internal characteristics of the sampling algorithm are very different, the ensemble rule is set in consideration of a given time constraint. For example, BO-based algorithms, such as GP, generally propose configurations that are expected to have higher performance compared with the configurations generated by the other algorithms. However, the computational amount increases as the consumed configurations increase, which is a drawback of these algorithms. Since the common TPE algorithm infers each parameter independently, it is very fast compared to other tightly coupled hyperparameter-based algorithms such as GP or CMA-ES. However, in general, there are a lot of configurations required to achieve the desired level of results in the TPE algorithm. In the case of CMA-ES, an effective sampling can be performed with sufficient configurations. However, it is difficult to expect high performance in early-stage sampling. Therefore, in the platform, we propose a progressive scheme that sequentially applies BO, TPE, and CMA-ES in consideration of parallel resources. Through this method, the task dependency of the sampler could be removed and diversification is performed.
Third, we suggest several methods in handling both the sampler maturity and search space sensitivity. In terms of configuration quality, the proposed scheme consisted of the GES strategy, which limits the hyperparameter search range according to a given time to accelerate the maturity of the sampler and dynamically allocate the hyperparameter space. Such a heuristic method can help the sampler to quickly grasp the relationship between reduced dimensions of hyperparameters and their evaluation score. Subsequently, it can gradually expand the search range to find the global optimum effectively. While in terms of configuration quantity, we add some parameters into the hyperparameter space, which are strongly correlated with evaluation time. For example, epoch, learning rate, or even sampling rates of datasets can be added to increase the number of finished evaluations in a certain time period. As previously stated, the gain of the hyperparameter optimization efficiency can be obtained even by adjusting the sampling of a dataset. When considering a given time, it may be the better choice to conduct quick searches several times than trying to train the dataset fully with a specific configuration. Additionally, guided sampling can be used. If a user knows some good configurations in advance, the user can add them in the early stage of the HPO process. It helps to quickly estimate an approximation close to the desired evaluation score in the most common situation where time constraints exist.
Fourth, ASHA is used for pruners in the proposed scheme since it is more important to increase the usability of each resource in a massively parallel computing environment such as HPC. As mentioned above, nowadays, the complexity of the AI model to be optimized increases gradually, and the number of resources required to solve it increases rapidly; therefore, the utilization of each computing resource should be maximized through aggressive early stopping. This is also related to the sampler maturity issue. Synchronous pruning algorithms such as HyperBand and Success Halving (SH) determine the number of resources to allocate through comparison of median values between them even though their samplers select a set of non-promising configurations. In other words, since such synchronous promotion largely depends on the maturity of the sampler, we adopted the asynchronous method as pruners.
Finally, the proposed scheme determines all detailed strategies based on a certain deadline allowed for a HPO job. By using several diversification methods considering both time and resource awareness, we believe that the proposed scheme has been implemented into our platform as a practical HPO service.
5.8 Case Study: AutoML Service
This section discusses a case study in which a ML model is developed using several HPO services in the HPC AI convergence platform. Fig. 6 shows the simplified AutoML service for beginner users, provided with an interface that uses a web-based GUI. The AutoML service has an easy-to-use web interface for creating and learning ML models based on user data; it includes the processes for uploading a dataset, defining data schema, selecting algorithms, and assigning a number of resources to use (number of nodes and execution time). Such job information is managed in the portal database. Based on this information, programming codes and job scripts regarding model training, optimization, and/or parallelization have been generated internally. An HPC-based scheduler will then run this job.

Figure 6: AutoML service on the HPC AI convergence platform
On the top left of Fig. 6, The “Select CSV file from uploaded dataset” is a pop-up menu that allows you to select a dataset previously registered in the portal or uploaded previously. You can also upload files via other options. The upper right figure shows a menu to check the data type and schema information of the uploaded or selected dataset. The sample data and type of each column are automatically selected, but users can modify them when they want to. Next, as shown on the lower left figure, after selecting a prediction target (y), feature lists (X) and training and test ratio need to be selected. Finally, on the lower right figure, you can select the type of HPO tasks. To date, only regression or classification tasks can be selected. You can select an algorithm or even multiple, to train and optimize a model.
Currently, the supported algorithms are: multiple linear regression (MLR), support vector machine, random forest, boost tree, XGBoost, LightGBM, and deep learning (PyTorch-based). The job submission is completed by setting the budget such as the time deadline (seconds) and the number of nodes. The use-case diagram is shown in Fig. 7. Submitted jobs can be managed in the portal as shown in Fig. 8. You can check the current status of a submitted job, and the time and resources information. You can cancel or delete jobs, as well as directly access the Jupyter notebook of the job, which is mounted in the user's home directory.

Figure 7: Use-case diagram: The AutoML service on our platform

Figure 8: HPO job list in the portal
As shown in Fig. 9, the job details include three menus: Overview, Trials Detail, and Resubmit. First, the overview shows detailed information of the best model among all trials on a study of a job. You can check at a glance not only the best score, algorithm used, and hyperparameter information, but also the performance evaluation chart using the model performance, optimization history, and parameter importance information of each algorithm. The best model can be downloaded directly, or can be easily deployed as a service by using the model bookmark and deployment tools. Next, Fig. 10 shows Trials Detail, so you can find and download the history information of each trial. Based on the trial score, top-10 models among all algorithms or top-3 models per each algorithm can be individually downloaded or registered to the portal via the bookmark function. Each trial score and hyperparameter information can be checked on the chart, and the algorithm can be checked by color. Finally, in Resubmit, intermediate or advanced users can analyze the correlation between hyperparameters through a parallel coordinate chart as well as re-specify the hyperparameter search space and resubmit the job again. The AutoML service in our platform excludes detailed information except for algorithm selection. For beginning users, it is not easy to define the search range of hyperparameters according to tasks and algorithms; therefore, the platform takes advantage of the pre-searched range of hyperparameters and their initial values by referring to previous research [23] and provenance data of the platform. An example of the HPO hyperparameter detailed analysis and job resubmit interface are shown in Fig. 11. Based on the results of the trial, filtering functions are provided in All, Best-10, and Best-100, and the correlation between the hyperparameter and the result value can be easily grasped through the parallel coordinates chart. The hyperparameter search category can be changed by users directly. Finally, it can be submitted again as another HPO job.

Figure 9: Example of the HPO job view: overview

Figure 10: Example of the HPO job view: Trials Detail

Figure 11: Example of the HPO job view: Resubmit
Additionally, the sdroptim library contains a scheduler and the GES algorithm for performing MPI-based parallel tasks, and the sdroptim_client library is a code that automatically generates ML programming codes and SLURM task scripts using the data schema and task metadata entered by the user. As shown in Fig. 12, various HPO analysis and task management tools shown in web-based AutoML service were developed to be used in Jupyter notebooks as well.

Figure 12: Example of the HPO job on Jupyter notebook
AutoML can save the significant amount of time and resources required to build high-performance models by automating time-consuming processes in model optimization such as hyperparameter tuning. In addition, since the performance of most AI models greatly depends and is highly sensitive to the selection of the hyperparameters of the model, it is worth noting that AutoML showcases its efficiency on the selection of hyperparameters. Moreover, various methods have been proposed for efficient hyperparameter optimization over the past decade, mainly focusing on finding the best combination within a given input algorithm and hyperparameter search category. In other words, an AutoML problem should prepare an appropriate hyperparameter search space in advance. In addition, recent studies on large-scale parallelization of hyperparameter optimization have focused on assessing the exploration efficiency in improving the productivity within a given resource constraint. However, studies that consider the time constraint are few. From the user's perspective, time constraint plays a crucial role in setting the direction for solving this problem. Thus, these perspectives must be reflected for practical AutoML service. Since most of the HPO sampling strategies proposed till date are based on the sampling history datasets, their samplers can understand configuration datasets as well as recommend a new promising configuration set only after sufficient sampling has been made. In other words, the amount of metadata composed of evaluated configurations tend to determine the performance of the sampler. Unfortunately, the amount of time and resources we can use is always limited; therefore, we need a method to adjust the amount of metadata in a given time according to the type and size of the problem.
In this study, we propose a novel diversification strategy for HPO, which exploits dynamic hyperparameter space allocation for a sampler according to the remaining time budget. In the proposed scheme, the search range of a specific model selects mainly used hyperparameters for a given task and uses their well-known initial values as default values. The optimal value is searched by expanding the dimension of the search space in process of time. Substantially, the goal of AutoML is to address entry barriers for novice users or to automate repeat procedures for intermediate and/or high-level users; therefore, its interface should be as simple as possible. Also, the details for optimizing a model, such as programming codes and job scripts, should be automatically generated and easily managed. The performance evaluations show that our solution outperforms existing studies. We developed an easy-to-use AutoML service on our HPC AI convergence platform, considering several challenging issues for designing the practical hyperparameter optimization service.
In the future, we plan to develop a wider range of efficient AutoML services including automated feature engineering (AFE) as well as existing HPO problems and building them into our platform. In particular, for an ML model that uses large-scale structured data such as scientific data, not only the performance but also explainability and interpretability that provide the basis for model prediction are important. Therefore, we plan to expand the existing service to be an explainable one. Moreover, we further plan to study complex tasks from previous simple regression or classification tasks, which require simultaneous multiple model optimization (i.e., automated design of generative models [24] and pre-trained model [25] for the AutoML).
Funding Statement: This research was supported by the KISTI Program (No. K-20-L02-C05-S01) and the EDISON Program through the National Research Foundation of Korea (NRF) (No. NRF-2011-0020576).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Snoek, H. Larochelle and R. P. Adams, “Practical Bayesian optimization of machine learning algorithms,” Advances in Neural Information Processing Systems, vol. 25, no. 1, pp. 2951–2959, 2012. [Google Scholar]
2. F. Hutter, H. H. Hoos and K. Leyton-Brown, “Sequential model-based optimization for general algorithm configuration,” in Proc. LION, Rome, Italy, pp. 507–523, 2011. [Google Scholar]
3. J. S. Bergstra, R. Bardenet, Y. Bengio and B. Kégl, “Algorithms for hyper-parameter optimization,” Advances in Neural Information Processing Systems, vol. 24, no. 1, pp. 2546–2554, 2011. [Google Scholar]
4. L. Li, K. Jamieson, G. DeSalvo, A. Rostamizadeh and A. Talwalkar, “Hyperband: A novel bandit-based approach to hyperparameter optimization,” Journal of Machine Learning Research, vol. 18, no. 185, pp. 1–52, 2017. [Google Scholar]
5. Z. Karnin, T. Koren and O. Somekh, “Almost optimal exploration in multi-armed bandits,” in Proc. ICML, Atlanta, GA, USA, pp. 1238–1246, 2013. [Google Scholar]
6. L. Li, K. Jamieson, A. Rostamizadeh, E. Gonina, M. Hardt et al., “A system for massively parallel hyperparameter tuning,” in Proc. MLSys, Austin, TX, USA, pp. 230–246, 2020. [Google Scholar]
7. R. Liaw, R. Bhardwaj, L. Dunlap, Y. Zou, J. Gonzalez et al., “HypserSched: Dynamic resource reallocation for model development on a deadline,” in Proc. SoCC, Santa Cruz, CA, USA, pp. 61–73, 2019. [Google Scholar]
8. J. Bergstra and Y. Bengio, “Random search for hyper-parameter optimization,” Journal of Machine Learning Research, vol. 13, no. 10, pp. 281–305, 2012. [Google Scholar]
9. Y. Amit and D. Geman, “Shape quantization and recognition with randomized trees,” Neural Computation, vol. 9, no. 7, pp. 1545–1588, 1997. [Google Scholar]
10. M. D. Hoffman, E. Brochu and N. de Freitas, “Portfolio allocation for Bayesian optimization,” in Proc. UAI, Barcelona, Spain, pp. 327–336, 2011. [Google Scholar]
11. H. Cho, Y. Kim, E. Lee, D. Choi, Y. Lee et al., “Basic enhancement strategies when using Bayesian optimization for hyperparameter tuning of deep neural networks,” IEEE Access, vol. 8, no. 1, pp. 52588–52608, 2020. [Google Scholar]
12. H. Bertrand, R. Ardon and I. Bloch, “Hyperparameter optimization of deep neural networks: Combining hyperband with Bayesian model selection,” in Proc. CAp, Grenoble, France, pp. 1–5, 2017. [Google Scholar]
13. S. Falkner, A. Klein and F. Hutter, “Bohb: Robust and efficient hyperparameter optimization at scale,” in Proc. ICML, Stockholm, Sweden, pp. 1436–1445, 2018. [Google Scholar]
14. E. Contal, D. Buffoni, A. Robicquet and N. Vayatis, “Parallel Gaussian process optimization with upper confidence bound and pure exploration,” in Proc. ECMLPKDD, Prague, Germany, pp. 225–240, 2013. [Google Scholar]
15. J. Gonz'alez, D. Zhenwen, P. Hennig and N. Lawrence, “Batch Bayesian optimization via local penalization,” in Proc. AISTATS, Cadiz, Spain, pp. 648–657, 2016. [Google Scholar]
16. Z. Wang, C. Gehring, P. Kohli and S. Jegelka, “Batched large-scale Bayesian optimization in high-dimensional spaces,” in Proc. AISTATS, Lanzarote, Spain, pp. 745–754, 2018. [Google Scholar]
17. T. Kathuria, A. Deshpande and P. Kohli, “Batched Gaussian process bandit optimization via determinantal point processes,” Advances in Neural Information Processing Systems, vol. 29, no. 1, pp. 4206–4214, 2016. [Google Scholar]
18. M. Jaderberg, V. Dalibard, S. Osindero, W. M. Czarnecki, J. Donahue et al., “Population based training of neural networks,”U.S. Patent Application No. 16/766, 631,2021. [Google Scholar]
19. N. Decastro-garcia, A. L. M. Castaneda, D. E. Garcia and M. V. Carriegos, “Effect of the sampling of a dataset in the hyperparameter optimization phase over the efficiency of a machine learning algorithm,” Complexity, vol. 2019, no. 6, pp. 1–16, 2019. [Google Scholar]
20. K. Ozaki, LightGBM tuner: New optuna integration for hyperparameter optimization, 2020. [Online]. Available: https://medium.com/optuna/lightgbm-tuner-new-optuna-integration-for-hyperparameter-optimization-8b7095e99258. [Google Scholar]
21. F. Hutter, H. Hoos and K. Leyton-Brown, “An efficient approach for assessing hyperparameter importance,” in Proc. ICML, Beijing, China, pp. 754–762, 2014. [Google Scholar]
22. T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, “Optuna: A next-generation hyperparameter optimization framework,” in Proc. KDD, Anchorage, AK, USA, pp. 2623–2631, 2019. [Google Scholar]
23. P. Probst, A. Boulesteix and B. Bischl, “Tunability: Importance of hyperparameters of machine learning algorithms,” Journal of Machine Learning Research, vol. 20, no. 53, pp. 1–32, 2019. [Google Scholar]
24. J. Cheng, Y. Yang, X. Tang, N. Xiong, Y. Zhang et al., “Generative adversarial networks: A literature review,” KSII Transactions on Internet and Information Systems, vol. 14, no. 12, pp. 4625–4647, 2020. [Google Scholar]
25. F. Lin, X. Ma, Y. Chen, J. Zhou and B. Liu, “Pc-san: Pretraining-based contextual self-attention model for topic essay generation,” KSII Transactions on Internet and Information Systems, vol. 14, no. 8, pp. 3168–3186, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |