Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.019023
Article

Segmentation of the Left Ventricle in Cardiac MRI Using Random Walk Techniques

Osama S. Faragallah1,*, Ghada Abdel-Aziz2, Hala S. El-sayed3 and Gamal G. N. Geweid4,5

1Department of Information Technology, College of Computers and Information Technology, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
2Department of Computer Science and Engineering, Faculty of Electronic Engineering, Menoufia University, Menouf 32952, Egypt
3Department of Electrical Engineering, Faculty of Engineering, Menoufia University, Shebin El-Kom 32511, Egypt
4Department of Electrical Engineering, Faculty of Engineering, Benha University, Benha 13512, Egypt
5Department of Biomedical Engineering, College of Engineering & Computer Sciences, Marshall University, Huntington, WV 25755, USA
*Corresponding Author: Osama S. Faragallah. Email: o.salah@tu.edu.sa
Received: 29 March 2021; Accepted: 30 April 2021

Abstract: As a regular tool for assessing and diagnosing cardiovascular disease (CVD), medical professionals and health care centers, are highly dependent on cardiac imaging. The purpose of dividing the cardiac images is to paint the inner and outer walls of the heart to divide all or part of the limb’s boundaries. In order to enhance cardiologist in the process of cardiac segmentation, new and accurate methods are needed to divide the selected object, which is the left ventricle (LV). Segmentation techniques aim to provide a fast segmentation process and improve the reliability of the process. In this paper, a comparative study is made on basic random walk (BRW), extended random walk with priors (ERW), and high-speed random walk (HSRW) techniques. In the presented paper, we have applied three different types of medical image segmentation techniques to many Cardiovascular Magnetic Resonance images (CMRIs) in our experimental evaluation to lead statistically significant conclusion and confirm that our results are generalized. We have used 125 sets of CMRIs generated from five groups of patients with different types of cardiovascular disease to get the precise capacity of the productivity of the introduced method. In this paper, several performance metrics are used for instance correspondence coefficient D, distance, and PSNR. In the presented paper, a short-axis 3D multilayer CMRIs database has been taken and applied on many case studies to decide the outcomes of several segmentation methods. Throughout the experiments, the performance time for three segmentation methods are also calculated and utilized in the comparison process as another important performance factor. The experimental results show that ERW technique is the furthermost accurate segmentation technique among all the approaches.

Keywords: Cardiovascular disease (CVD); basic random walk (BRW); high speed random walk (HSRW); extended random walk (ERW)

1  Introduction

Cardiovascular disease (CVD) has recently been the leading cause of death and according to the latest statistics, the biggest health problem in the world [1,2]. The detection of cardiovascular disease is necessary since there may be a shortage of experienced surgeons when necessary.

Providentially, any problem in cardiac function or the complete cardiac cycle is reflected in the change of shape of the left ventricle (LV) [1]. This special property can be used to control cardiac function, and this will lead to the diagnosis of a probable medical condition that affects the heart. The analysis of the function of the human heart requires a detailed description of the shape of the left ventricle [2]. Blood is pumped over the carotid arteries into the area of the head and neck. The carotid arteries are in pairs on the right and left sides of the neck [2]. The Vertebral Arteries (AV) are the vessels on both sides of the vertebra that supply the human brain. The carotid arteries consist of vessels that extend from the area of the “Aortic Arch” to the “Circle of Willis” area [3]. The CCA begins at the aorta and when it reaches the cervical area, these two vessels separate as the external carotid and the internal carotid artery [4]. ECA is responsible for pumping blood to regions outside the skull such as the face. The Circle of Willis is in the lower part of the brain. Some arteries come together in this region. In the Circle of Willis, the ICAs branches to the brain with smaller arteries that provide more than 80% oxygen-rich blood to the brain [1,3].

To assist the cardiac specialist to detect heart disease based on segmenting technique, a new and precise approach is needed to detect certain objects that affect the LV. The purpose of the segmentation method is to obtain a faster detection process and increase the process of dependability [5]. In the field of biomedical diagnosis, image processing is considered an important part in the recognition of cardiovascular disease (CVD) by segmentation of the cardiac image. The major aim of the segmentation of cardiac images is to delimit the external and internal walls of the heart to segment all or part of the heart’s boundaries [6]. Consequently, precise segmentation of heart imaging is of great importance for the diagnosis and intervention planning because it allows specialists to accurately visualize the required cardiac cavities [3,4,6]. The information obtained from segmented CMRIs facilitates physical measurements by obtaining a variety of measurements useful for evaluating and identifying CVDs. The efficiency of the segmentation of medical images decides the precise diagnoses needed, guided surgical procedure or medical treatment.

Random walking methods are considered a major research area in the field of medical segmentation [7]. Edge-based methods are called border-based methods. These methods depend on the dissatisfaction of the properties of the image between different regions as a function of the high intensity gradient values. Gamal Geweid, Reza Fazel-Razai et al, have actively presented a geographical method that can afford a closed curvature in the form of a compromise between the uniformity of the curvature and the high gradient [8]. The main obstacle to these methods is that they need worthy initialization and are extremely sensitive to distortion. Techniques based on regions are considered best suited for segmenting structured images based on fusion regions and growth.

The feature of regional methods is that they consider the characteristics of the region. Chan-Vese technique [9], which is an actual curve without boundaries, was presented in 2001 by Chan and Vese. Another technique of Chan-Vese has been enhanced and introduced in 2010 by Wang, Huang and Xu. However, for these techniques, they do not require a large image protection to differentiate the two areas [10]. Tannenbaum and Lankton proposed a technique of active curves in 2008 located at the regional level. To arrive at a solution adapted to this technique, the initialization of the segmentation contour must be sufficiently close to the desired final curve [11]. Shi et al. [12] presented a real-time technique in 2008 to approximate the evolution of the curve based on quantity levels. Li, Kao, Gore and Ding introduced a minimization of fitting technology by region in 2008 [13]. In 2009, Bernard, Friboulet, Thevenaz and Unser presented a linear filter approach for the rapid development of the deformable model [14]. This method is a level technique that relies on the B-spline. However, these techniques do not consider the data provided by object borderlines [15,16].

The graph-based segmentation methods have the advantage of taking into consideration the pixel statistics of the image by viewing the image as a graph [17]. Random walk segmentation can be defined as a multi-label image segmentation method based on electrographic potentials [18,19]. The Random Walk method for segmenting the image was introduced by Grady [20,21]. The Random-Walk technique can capture both ranges and borderlines. In methods of random walk, the seeds are affected. The highest probability for all pixels that are located on the label provides the greatest probable segmentation results. This method is presented in an isolated space by combinatorial similarities of the theory of continuous potential. Other random walk techniques, for instance the segmentation of multi-label random walking images, using previous models presented by Grady in 2006 [20,21]. Correction and Regularized Random Walk Ranking, Random Walks’ fast, parameter estimation and random segmentation, based on pre-calculation of the eigenvector was introduced by Grady, Sinop, and Yuan in 2008, 2007 and 2018 [19,22,23]. These techniques are introduced to improve the technique of random walking. The random-walk technique was registered as a US patent in 2017 [21].

The rest of this paper is structured as follows: Section 2 presents the BRW image segmentation method. Section 3 introduces the random walk with pre-computations technique. In Section 4, the Random walk with prior model is illustrated. Section 5 shows the experimental results. Finally, section 6 concludes the paper.

2  Random Walking with Seeds

The Random Walking with Seed is considered as basic random walk (BRW) image Segmentation and was introduced by Leo Grady in [20]. In BRW, the electrical potentials of the graph theory are used to get object details. The theoretical properties of the BRW technique have been developed with different possible theories and related compounds of the electrical circuit. In general, the beginnings of segmentation can be separated into three main levels [24]. In the first level, the user sets the sequential points to the border or very close to it. The minimum path method is used to find the final boundary. In the second level, the technique needs the definition of the initial border, and then the cost function representing the property data of the image is minimized [25]. In the third level, the technique needs the seeds in certain regions. Random Walk technique uses the third level of initialization. Seeds determine locations with predefined labels. The probability xi , that the random walker beginning with the node vi first ranges a seed denoted S , can be calculated by obtaining the circuit-theoretic based on the Dirichlet technique [16]. All seeds with other labels are stranded and the S -labeled are considered the possibility of unity.

The function which provides a solution for the Dirichlet problem by satisfying the boundary constraints to minimize the Dirichlet integral is called a harmonic function. The connections established between the random walks and the electrical potentials of the graph theory lead to an appropriate method for estimating random walking probabilities. Fig. 1 describes the harmonic function and segmentation resulting from a 4 × 4 chart of unit weights using three seed nodes with different labels, which are ( L1 , L2 and L3 ). Alternatively, the potential of each seed may be set to a voltage source of the unit connected to ground, and the other nodes are grounded. Calculated electrical potentials denote the possibility that a random walking of each electrode will touch the seed point that is presently fixed to one [20].

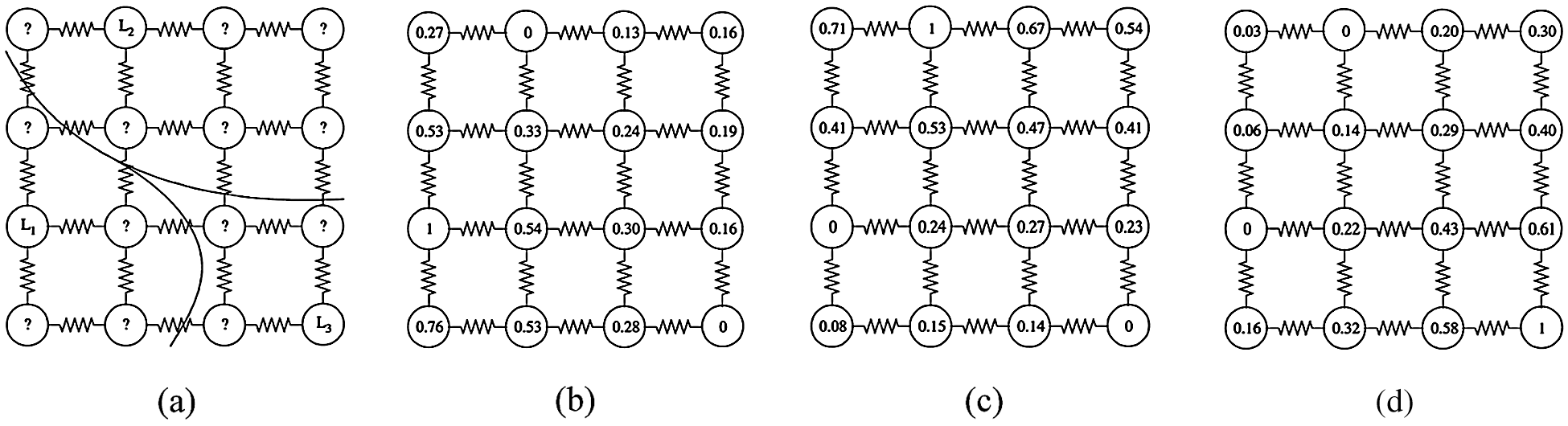
Figure 1: Segmentation resulted from graph theoretic electrical potentials (harmonic function). (a) Initial seeds and the obtained segmentation. (b) Random walk probability corresponding to seed L1 . (c) Random walk probability corresponding to seed L2 . (d) Random walk probability corresponding to seed L3

The BRW technique marks an untagged pixel by implementing this computation of the possibilities that the random walker will first reach each of the starting pixels from that untagged node. The BRW technique must solve a system of linear equations with positive and sparse symmetry to find the probability. The final segmentation is obtained when each node is assigned a label with the corresponding most likely seed destination. Random walk segmentation technique contains a pair U=(V,E) with nodes peaks ?∈V and boundaries e∈E,E⊆V×V . A boundary e , connecting two nodes, ?i and ?j , is signified by eij . This graph is a weighted chart which gives a rate to each boundary named a weight. An edge weight eij in the image, is signified as w(eij) or wij . A node degree is di=∑w(eij) for all edges eij located on ?i , wij>0 [17].

2.1 Edge Weights

To represent the image construction and the weight of edges using BRW prejudices, a function should be used to map the change in image intensity to edge weight. The weighting function plays a significant role for a robust segmentation of BRW technique for image segmentation in every condition. For mapping the change in image intensity to edge weight, the Gaussian weighting function is utilized and represented as:

wij=exp⁡(−β(Ii−Ij)2) (1)

where Ii shows the image density at pixel ?i . Performance of the weighting function is based on the unrestricted parameter β [11].

2.2 Construct Optimization Laplacian Matrix

The Dirichlet optimization problem has the similar explanation as the wanted random walking possibilities. This problem can be known as the problem of obtaining a harmonic function according to its border ranges. This function can be used to adapt the boundary conditions and reduces the integral of Dirichlet [26]. The creation of the Laplace matrix is done by using neighbor weights for each node in the graph. The combinatory matrix of Laplace as:

Lij={diifi=j,−−wijifviandvjareadjacentnodes,0otherwise, (2)

where Lij is indexed by vertices viandvj.

2.3 Partition the Laplacian Matrix

In this section, we divided the nodes into two groups, VM and VU which denote the marked and unmarked nodes where VM⋃VU=V and VM∩VU=∅. The seed points are found in the group VM notwithstanding of their label. The values in L and x are rearranged such that labeled vertices are first, unlabeled vertices are second and B is the complementary matrix. If seeds are provided, divide L and x into:

L=[LMBBTLU],andx=[xMxU], (3)

where and xM and xU represent the potentials of the labeled and unlabeled vertices, respectively.

The composition of Dirichlet D[xU] :

D[xU]=12[xMTxUT][LMBBTLU][xMxU]=12[xMTLMxM+2xUTBTxM+xUTLUxU] (4)

Differentiating D[xU] according to xU and obtaining the critical pixel at borderline conditions:

LUxU=−BTxM (5)

where xM and xU represent the labeled and unlabeled potentials for all nodes, respectively. The steps of BRW method is presented in Fig. 2. The above-mentioned methods can be taken within circuit theory. The diagram denotes an electric circuit, the boundaries of the graph represent resistors, the random walk probability represents the potentials, and the weights represent the conductance.

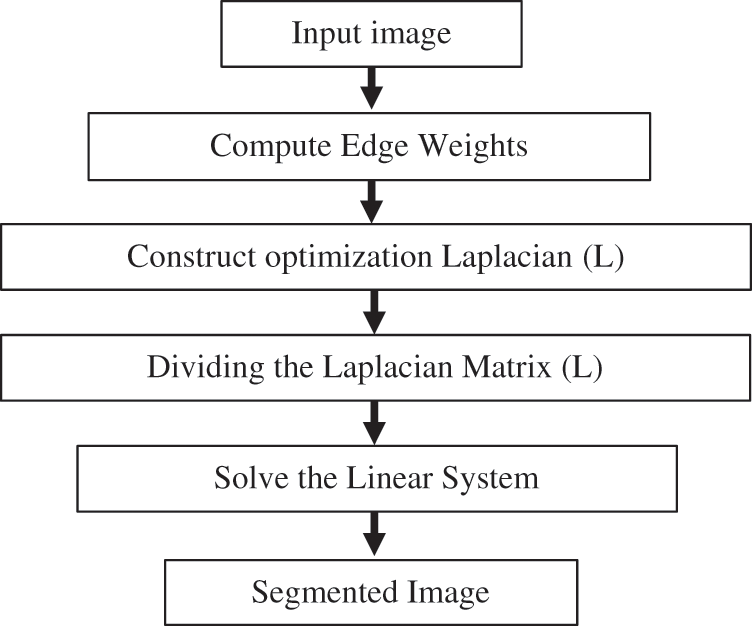
Figure 2: BRW method steps (online calculations)

3  High-Speed Random Walker

Random Walking through pre-computations is considered a fast method of estimating random walker. The steps of HSRW method is conclude in Fig. 3. This method is denoted as High-Speed Random Walking Approach (HSRW). In this technique, the goal is to transfer the offline computing load that is done before the user interaction. Offline pre-calculation is difficult because the starting positions are not known. The pre-calculation of a small number of eigenvectors of the Laplace matrix of the graph, whatever the locations of the seed data gives a better and rapid segmentation solution. An offline process is significant in medical segmentation because, usually in several situations, a lot of substantial time after the acquisition of the images is lost before segmentation. Especially the medical images frequently take weeks or days on the servers before interaction. Random walker solution can be approximated using eigenvectors calculations of the Laplacian matrix. Before defining the seeds, calculations can be achieved by computing Eigen-Vector couples of eigenvalues. This can be done offline to obtain the solution of Eq. 5. The Eigen-Vector pairs of eigenvalues decomposition of L are:

L=QΛQT (6)

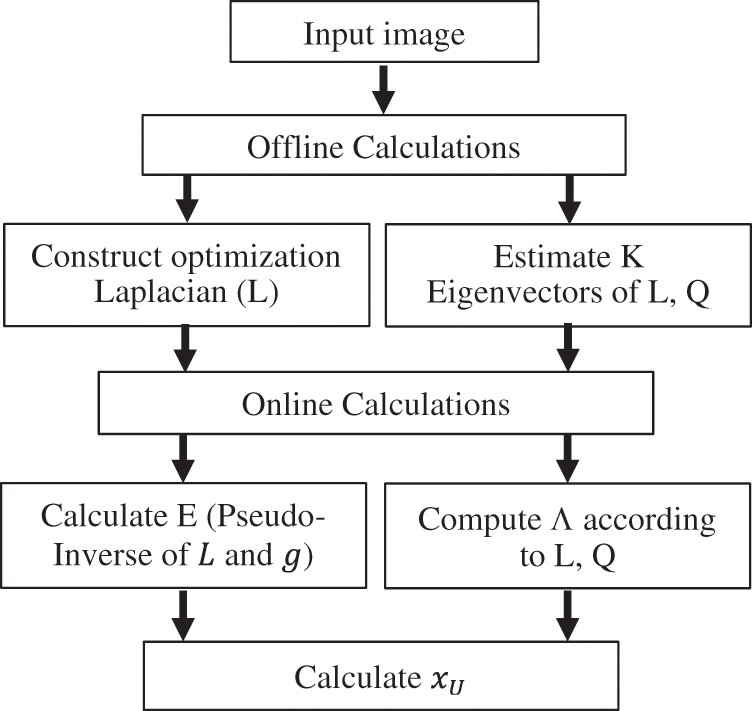
Figure 3: HSRW method stages

where, Λ represents the diagonal matrix of laplacian k minimum eigenvalues of L, and Q denotes a column of the k resultant eigenvectors. Using accumulative K, the explanation will come closer to the precise result. Decomposition of f according to labeled/unlabeled nodes using the feature f as follow:

Lx=f,andf=[fMfU] (7)

Then, when one performs a decomposition of the eigenvector of L , using Eq. (7) as follows:

QΛQTx=f (8)

If E is the pseudo-inverse of L and g is defined as the eigenvector of the Laplace matrix with the zero eigenvalue, then it is a stable vector. Then, decompose the E, in according to labeled and unlabeled nodes, and decompose the g in according to labeled and unlabeled nodes:

E=QΛ−1QT,E=[EMRRTEU],RT=QUΛ−1QMT,g=[gMgU],andEL=(I−ggT) (9)

From Eq. (7), approximates x using E :

ELx=(I−ggT)x=Ef=QΛ−1QTf (10)

when fU=0 , to find fM :

LMxM+BxU=fM (11)

Replacement of Eqs. (2) and (3) in Eqs. (5) and (7) provides:

−gUgMTxM+xU−gUgUTxU=RTfM (12)

Multiply B by Eq. (12), and then subtract it from Eq. (11):

(LM+BgUgMT)xM+BgUgUTxU=(I−BRT)fM (13)

when(BgUgMT)isaverysmallamountandgUgMT≈0,

letα=gUTxU,P=(I−BRT), then:

LMxM+BgUα=PfM, (14)

where fM=fM^+fM¯α

From Eq. (14), can be divided into:

PfM^=LMxMandPfM¯=BgU (15)

By definition of g and from Eq. (7):

gTf=gTLx=0,gTf=[gMTgUT][fMfU] ,

gMTfM=−gUTfU=0andgMT[fM^+fM¯α]=0 (16)

Then, α, can be found as:

α=−gMTfM^gMTfM¯, (17)

From Eq. (9)

xU=RTfM+gUα+gUgMTxMandxU≈RTfM+gUα (18)

4  Random Walk with Priors

In statistical pattern recognition and classical machine learning, the test points are decided to be classified without taking the relationship between them in consideration. On the other hand, in many situations the modern spatial techniques, such as ACM, LSM and the random walk, the desired object to be segmented may be reasonably featured by the image intensity distribution. So, the spatial technique is preferable to be able to concentrate on the intensity information in the image and use this information to guide the segmentation process. The BRW method is a multi-label image segmentation technique which has good theoretical characteristics. But practically, this technique may be problematic in some segmentation tasks. A main drawback of BRW technique is that there is no concentration on intensity integration in the system because the technique is based on only intensity gradients not the absolute intensity information of the image. Extended random walk method with priors is a comprehensive technique (ERW) that utilizes images prior in the segmentation technique. The aim of ERW is to fuse the density translated in the probability intensity prior model with the spatial interconnection of the random walk segmentation concept in order to obtain the best segmentation results, regardless of the intensity gradients variability. Every label is represented as a floating auxiliary node added to the graph and connected to the other nodes. When, λis is the prior probability density value when the intensity at node, vi , present in the intensity distribution of label S .

xis=λis∑q=1kλiq (19)

where λ is the vector containing prior probabilities of graph nodes, and γ is the weight of the vector. Once the starting values are assumed and the previous possibilities are achieved, the Laplace operator is enhanced with supplementary nodes. The Laplace matrix, after increasing with the prior, is separated into groups according to the labeled, unlabeled and supplementary nodes, in the similar approach as Eq. (3),

L=[LMB0BTLU+γIU−γλ0−γλγIU] (20)

The random walk possibility xU is computed as follows:

(LU+γIU)xU=−BTxM+γλ (21)

Fig. 4 illustrates the ERW method conclude steps when the prior value λi which signifies the probability intensity using the density of node vi , λ denotes the vector containing prior probabilities of graph nodes, and γ is the weight of the vector and it is constant.

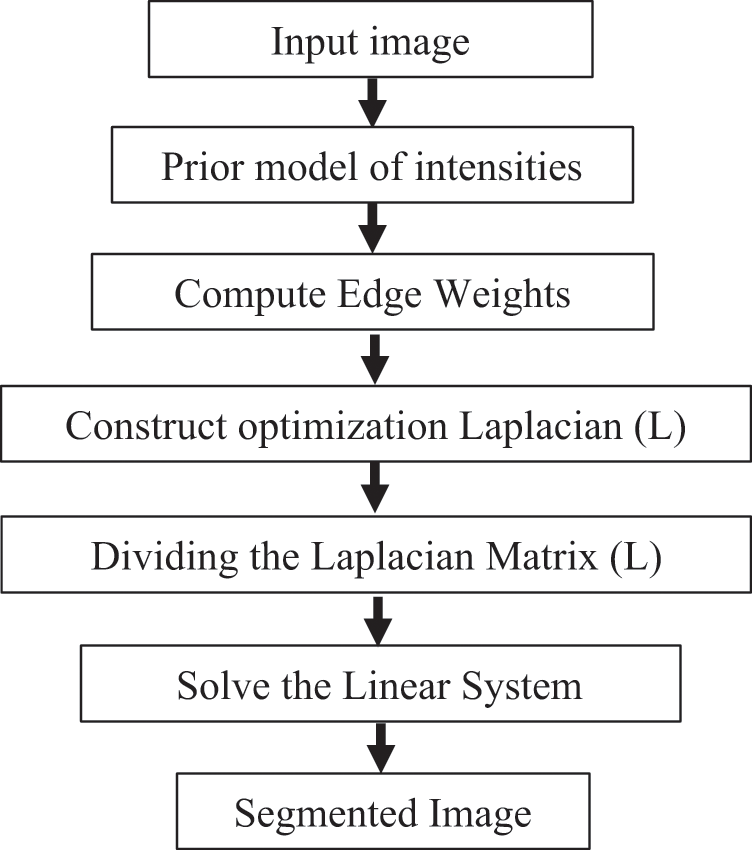
Figure 4: ERW technique steps (online calculations)

5  Results

The BRW, HSRW, and ERW medical imaging segmentation schemes are executed on MATLAB, and examined on a short-axis of 3D multi-slices CMRI dataset [27]. Several segmentation performance metrics are utilized such as Dice Metric (DM), the Haussdorff distance (HS), and the Peak signal to noise ratio (PSNR). The BRW, HSRW, and ERW segmentation schemes are executed on a short-axis of 3D multi-slices CMRI datasets. The same multilayer CMRI dataset is segmented using various random walk methods. The presented results were obtained through using BRW, HSRW and ERW methods on five different groups of patients; each group contains 25 subject of multilayer CMR dataset. Experimental results illustrate that the BRW method can achieve a good segmentation of the LV cavity. The results of the HSRW algorithm have very comparable similarities to BRW, but with a slightly less efficiency and a much higher execution rate. Pre-calculations reduce the performance online time in offline mode. The average time of HSRW equals to 0.09 seconds for each slide. Raising the rate of K will improve the comparison and makes the process of segmentation more precise, but also reduces the execution time. The ERW technique results illustrate that this method has the greatest efficiency of segmentation. Figs. 5 to 7 show the resulting images of the BRW segmentation method on five sets of sample data. HSRW with pre-calculation segmentation method is applied on the same sets of sample data and illustrated in Figs. 8 to 10. Figs. 11–13 show the high efficiency segmentation using the ERW method with an earlier model for the same sets of sample data. The results of the Random Walk segmentation overcame the potential restrictions of the prior art CMR methods. The performance of segmentation is fast compared to segmentation methods based on edge and region. BRW precedes into account the properties of regions and edges, as shown in Figs. 5–7. Looking at the image as a graph, the technique makes it possible to integrate pixel relations with neighboring pixels. As a result, segmentation produces good quality BRW technique sections when their qualitative accuracy is compared to the ground truth, and this is also evident from the Tab. 1 measurements in the diastolic and systolic phases in Tab. 2 as well as in the complete cardiac cycle noticed. Figs. 8–10 illustrate the HSRW results. There are no dissimilarities observed in furthermost cases of CMR slides in the figures, but the correspondence measurements of the DM, PSNR and HS coefficients present that the results of the HSRW technique are worse than those of the BRW method. This presents that HSRW is an effective estimation of the random walk influence as mentioned in Tab. 1 and throughout the cardiac cycle in Tab. 2. The values of PSNR and DM are lower, whereas HS is higher than the BRW method, but with slight dissimilarities between HSRW and BRW methods throughout the blood circulation. The impact of execution eigenvectors pre-calculations is perfect when the execution time is faster than the BRW method and, in fact, more efficient than other segmentation method for LV heart segmentation. With the identical dataset, the ERW method shows a significant enhancement in efficiency, as presented in Figs. 11–13. From the scores, we can see that the segmentation is smoother and cleaner. The ERW method considers boundaries and areas, such as BRW, using the relations between adjacent pixels in the image. It also considers the additional regional advantage by including the assumptions that affect the results of the segmentation. Mean segmentation quality measurements are computed from the segmented images using correspondence measurements for instance DM, HS, and PSNR and verified for each method in the diastolic and systolic stages as presented in Tab. 1. Based on results, it can be determined that methods of random walk are enhanced in diastolic diagnosis and that their outcomes in the systolic stage are also of good efficiency. The results of the random walk segmentation methods in the complete blood circulation are shown in Tab. 2. The cardiac cycle similarity amounts indicate that DM and PSNR capacities of ERW are improved than the corresponding capacities in the case of the HSRW and BRW approaches; however, the HS measurements are lower than the equivalent measurements, as illustrated in Tab. 2. This designates that the ERW technique is the furthermost accurate segmentation technique among all the approaches stated above. The ERW technique has the uppermost value of PSNR, and the HSRW method has the lowermost value that denotes the uppermost speed in segmentation process.

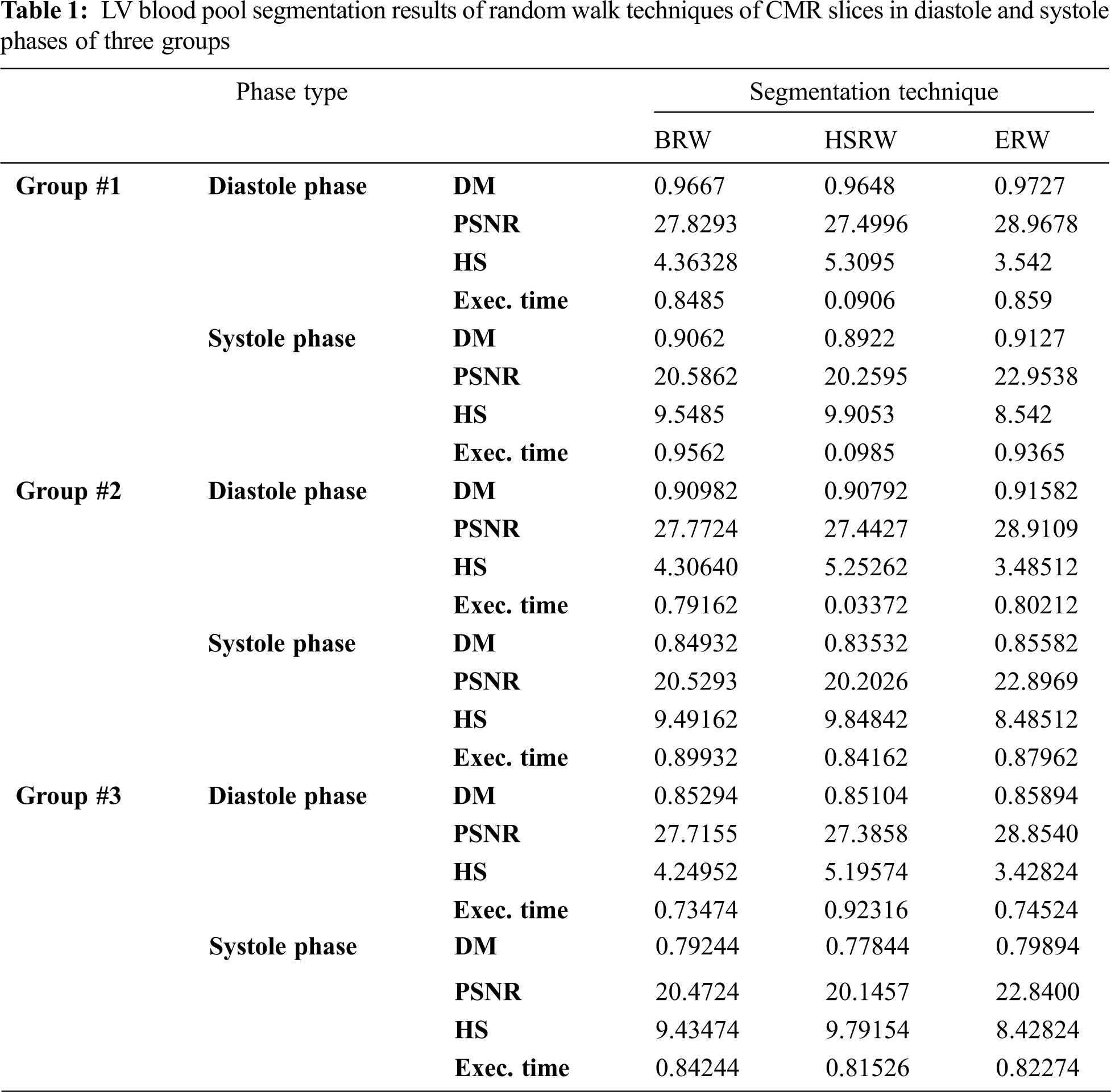
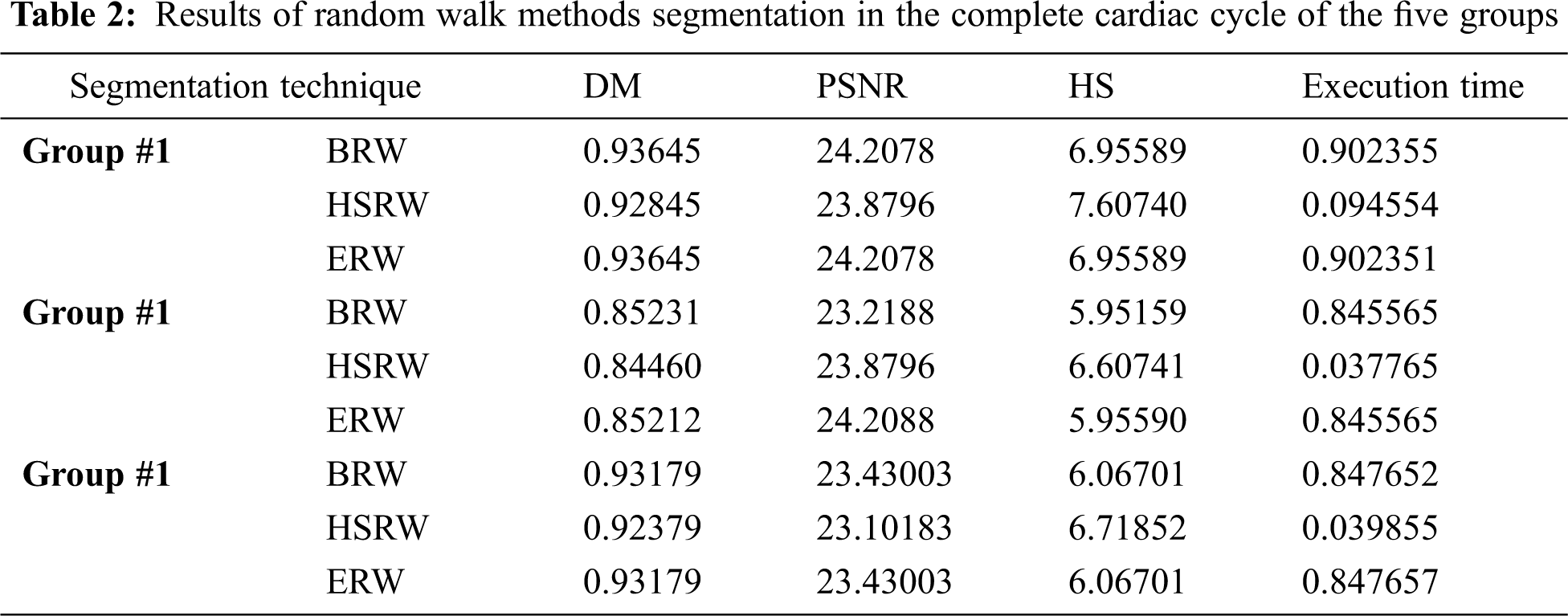
Figure 5: BRW results for the first samples set

Figure 6: BRW results for the second samples set

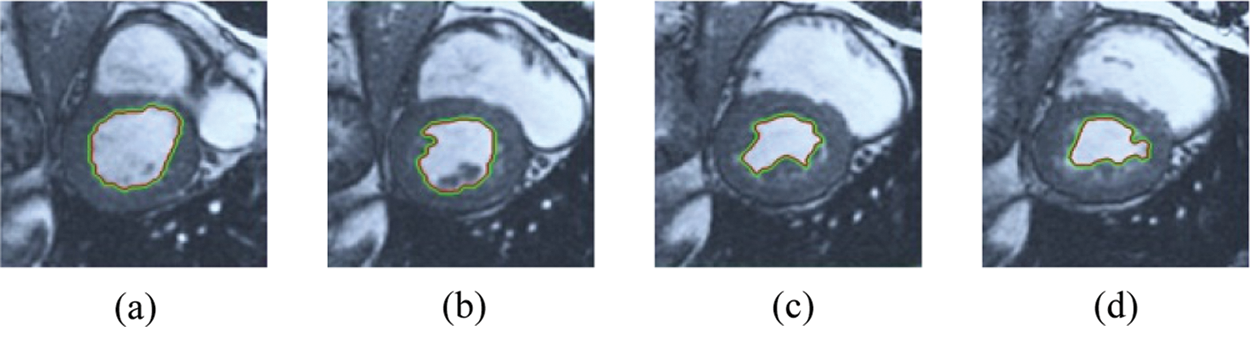
Figure 7: BRW results for the third samples set

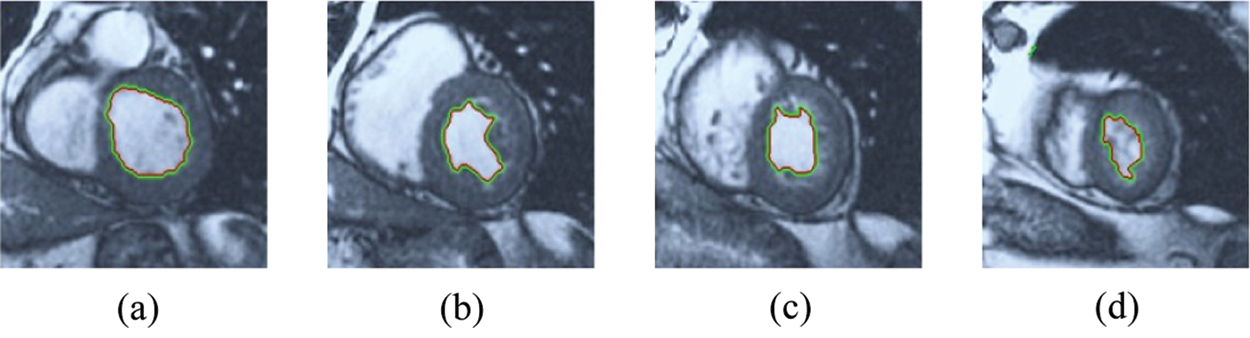
Figure 8: HSRW results for the first samples set

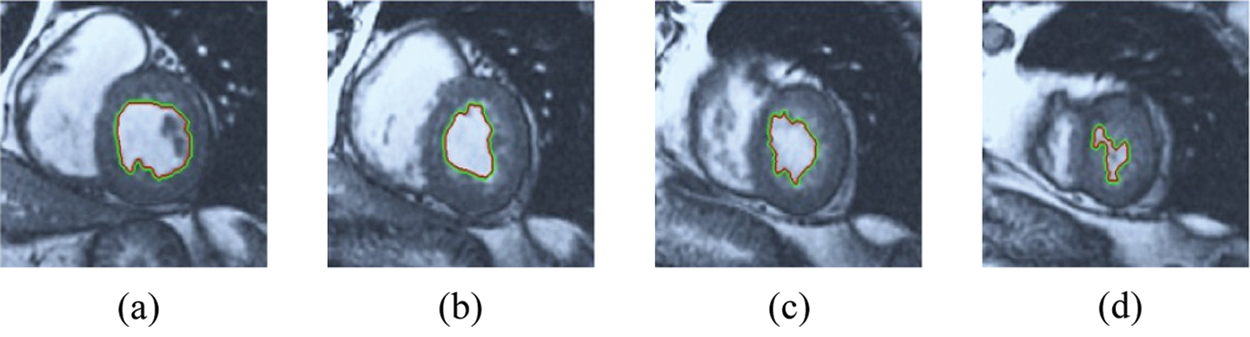
Figure 9: HSRW results for the second samples set

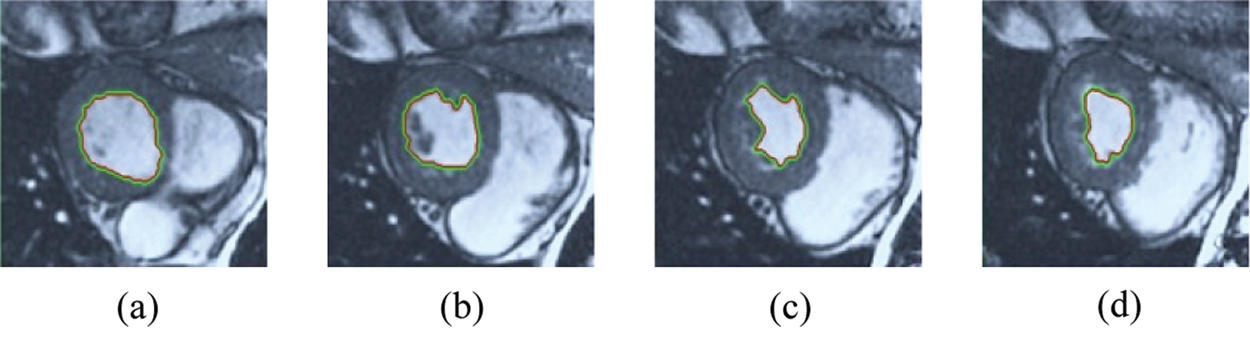
Figure 10: HSRW results for the third samples set

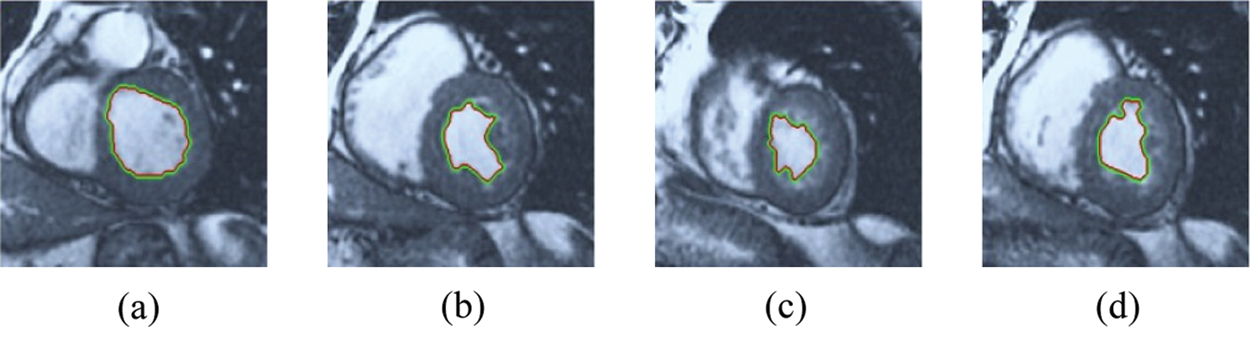
Figure 11: ERW results for the first samples set

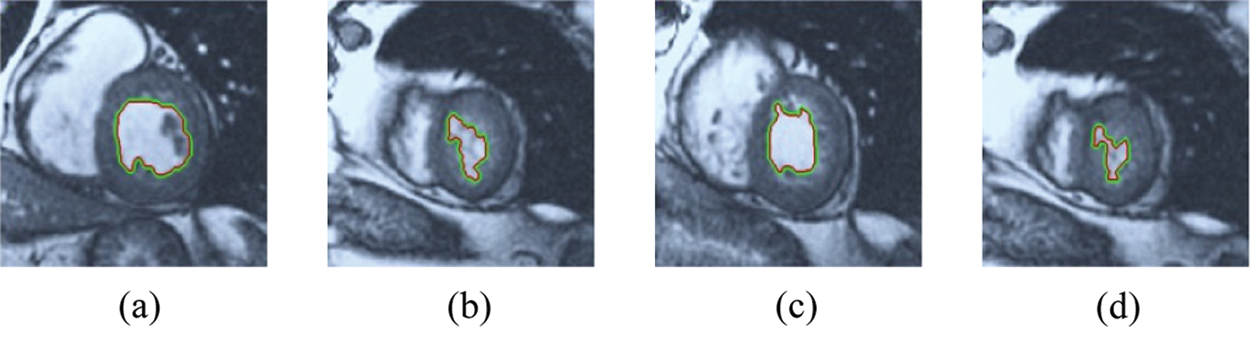
Figure 12: ERW results for the second samples set

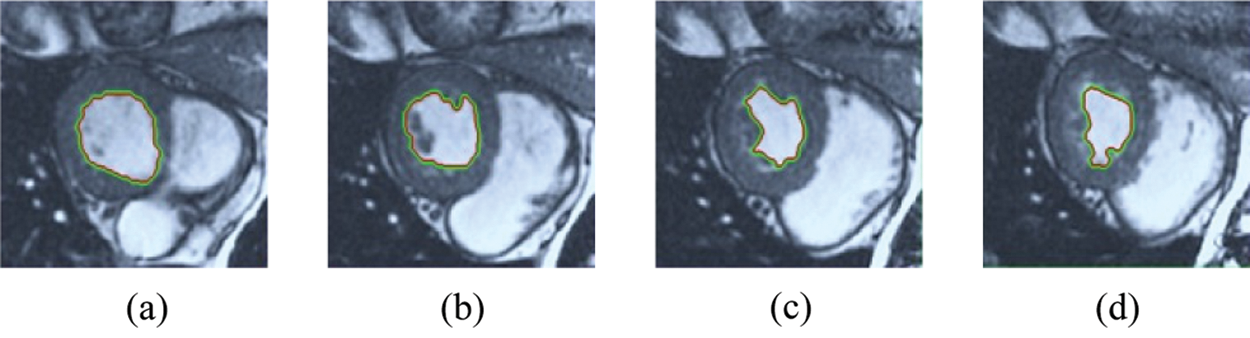
Figure 13: ERW results for the third samples set

6  Conclusions

In this research, a comparative study of three random walk techniques (BRW, RWP, and HSRW) was conducted to get the most precise segmentation method. These three techniques of medical image segmentation were applied to 125 sets of cardiovascular magnetic resonance (CMR) generated from five groups of patients with different types of cardiovascular disease to find the precise measurement of the effectiveness of the segmentation method. The performances of the examined segmentation approaches are estimated using MATLAB on a short-axis of 3D multi-slices CMRI datasets using various image efficiency performance metrics like similarity coefficient, PSNR, and the distance from Hausdorff. In addition, the performance time of each scheme is obtained for investigating to calculate segmentation procedure speed. The paper results conclude that the BRW method provides good performance, but the ERW method is the most precise of the extreme similarity measurements because of the priority consideration. In HSRW, the correspondence results are very similar to the equivalent match amounts in BRW with slightly smaller match prices, but considerably less execution time. The Pre-calculations in HSRW offline approach decreases execution time in the online approach.

Acknowledgement: This study was funded by the Deanship of Scientific Research, Taif University Researchers Supporting Project number (TURSP-2020/08), Taif University, Taif, Saudi Arabia.

Funding Statement: This study was funded by the Deanship of Scientific Research, Taif University Researchers Supporting Project number (TURSP-2020/08), Taif University, Taif, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Newman, J. Berger, C. Rockman, Y. Guo, H. Weintraub et al., “Diabetes mellitus is a cardiovascular disease (CVD) risk equivalent for peripheral arterial disease and carotid artery stenosis,” Journal of the American College of Cardiology, vol. 13, pp. 2278, 2018. [Google Scholar]

 2.  F. Bozkurt, C. Köse and A. San, “Comparison of seeded region growing and random walk methods for vessel and bone segmentation in CTA images,” in IEEE 10th Int. Conf. on Electrical and Electronics Engineering (ELECOpp. 561–567, 30 November 2017. [Google Scholar]

 3.  V. Tavakoli and A. A. Amini1, “A survey of shaped-based registration and segmentation techniques for cardiac images,” Computer Vision and Image Understanding, vol. 117, no. 9, pp. 966–989, September 2013. [Google Scholar]

 4.  M. Gadermayr, C. Disch, M. Müller, S. Merhof and B. Gess, “A comprehensive study on automated muscle segmentation for assessing fat infiltration in neuromuscular diseases,” Magnetic Resonance Imaging, vol. 48, no. 1, pp. 20–26, 2018. [Google Scholar]

 5.  A. Ezak, M. Goyal, J. S. McPhee, H. Degens and M. H. Yap, “Semantic segmentation of human thigh quadriceps muscle in magnetic resonance images,” arXiv preprint arXiv:1801.00415, 2018. [Google Scholar]

 6.  A. W. McAlpine, Heart and coronary arteries: an anatomical atlas for clinical diagnosis, radiological investigation, and surgical treatment. Springer Science & Business Media, Springer-Verlag Berlin Heidelberg, 2012. [Google Scholar]

 7.  D. Golden, M. Le, J. Lieman-Sifry and H. K. Lau, “Automated segmentation utilizing fully convolutional networks,” United States patent application US 15/879, vol. 742, 2018. [Google Scholar]

 8.  G. G. N. Geweid, M. A. Elsisy, O. S. Faragallah and R. F. Razai, “Automatic tumor detection in medical images using a non-parametric approach based on image pixel intensities,” Expert Systems with Applications, vol. 15, pp. 139–154, 2019. [Google Scholar]

 9.  T. Chan and L. Vese, “Active contours without edges,” IEEE Trans. Image Process, vol. 10, no. 2, pp. 266–277, 2001. [Google Scholar]

10. D. Mandal, A. Chatterjee and M. Maitra, “Particle swarm optimization based fast Chan-Vese algorithm for medical image segmentationm,” Metaheuristics for Medicine and Biology, vol. 704, pp. 49–74, 2017. [Google Scholar]

11. S. Soomro, A. Munir and K. N. Choi, “Hybrid two-stage active contour method with region and edge information for intensity inhomogeneous image segmentation,” PLoS One, vol. 13, no. 1, pp. e0191827, 2018. [Google Scholar]

12. Y. Shi and W. C. Karl, “A real-time algorithm for the approximation of level-set based curve evolution,” IEEE Trans. Image Process, vol. 17, no. 5, pp. 645–656, 2008. [Google Scholar]

13. C. Li, C. Y. Kao, J. C. Gore and Z. Ding, “Minimization of region-scalable fitting energy for image segmentation,” IEEE Transactions on Image Processing, vol. 17, no. 10, pp. 1940–1949, 2008. [Google Scholar]

14. O. Bernard, D. Friboulet, P. Thevenaz and M. Unser, “Variational B-spline level-set: A linear filtering approach for fast deformable model evolution,” IEEE Trans. Image Process, vol. 18, no. 6, pp. 1179–1191, 2009. [Google Scholar]

15. M. H. Soomro, G. Giunta, A. Laghi, D. Caruso, M. Ciolina et al., “Segmenting MR images by level-set algorithms for perspective colorectal cancer diagnosis,” European Congress on Computational Methods in Applied Sciences and Engineering, vol. 27, pp. 396–406, 2017. [Google Scholar]

16. W. Li, J. Xie, M. Xin and J. Mo, “An overlapping network community partition algorithm based on semi-supervised matrix factorization and random walk,” Expert Systems with Applications, vol. 91, no. 1, pp. 277–285, 2018. [Google Scholar]

17. X. Chen and L. Pan, “A survey of graph cuts/graph search based medical image segmentation,” IEEE Reviews in Biomedical Engineering, vol. 11, pp. 112–124, 2018. [Google Scholar]

18. L. Grady and G. Funka-Lea, “Multi-label image segmentation for medical applications based on graph theoretic electrical potentials,” in Proc. Workshop Computer Vision and Math. Methods in Medical and Biomedical Image Analysis, pp. 230–245, May 2004. [Google Scholar]

19. L. Grady and A. K. Sinop, “Fast approximate random walker segmentation using eigenvector precomputation,” IEEE Conf. CVPR, Anchorage, AK, USA, pp. 1–8, 2008. [Google Scholar]

20. L. Grady, “Random walks for image segmentation,” IEEE Transactions On Pattern Analysis and Machine Intelligence, vol. 28, no. 11, pp. 1768–1783, November 2006. [Google Scholar]

21. S. H. Baloch, E. Siampli and L. Grady, “Parameter estimation for mesh segmentation using random walks,” United States patent application US 9/262, vol. 704, 2017. [Google Scholar]

22. A. K. Sinop and L. Grady, “A seeded image segmentation framework unifying graph cuts and random walker which yields a new algorithm,” in IEEE 11th Int. Conf. on Computer Vision, Brazil: Rio de Janeiro, pp. 1–8, 2007. [Google Scholar]

23. Y. Yuan, C. Li, J. Kim, W. Cai and D. D. Feng, “Reversion correction and regularized random walk ranking for saliency detection,” IEEE Transactions on Image Processing, vol. 27, no. 3, pp. 1311–1322, 2018. [Google Scholar]

24. H. Hu, Z. Gao, L. Liu, H. Liu, J. Gao et al., “Automatic segmentation of the left ventricle in cardiac MRI using local binary fitting model and dynamic programming techniques,” PLoS One, vol. 9, no. 12, pp. 1–17, 2014. [Google Scholar]

25. A. R. Hareendranathan, M. Noga, P. Boulanger, H. Becher and K. Punithakumar, “Random walker framework for sensor-based echocardiography fusion,” IEEE Access, vol. 6, pp. 8519–8525, 2018. [Google Scholar]

26. A. Thomas, M. Mateos, J. Pfefferer and A. Rösch, “Error estimates for Dirichlet control problems in polygonal domains: quasi-uniform meshes,” Mathematical Control & Related Fields, vol. 8, no. 1, pp. 217–245, 2018. [Google Scholar]

27. P. Radau, Y. Lu, K. Connelly, G. Paul, A. J. Dick et al., “Evaluation framework for algorithms segmenting short axis cardiac MRI,” The MIDAS Journal – Cardiac MR Left Ventricle Segmentation Challenge, pp. 1–2, 2009. Available: http://hdlhandlenet/10380/3070. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.