DOI:10.32604/iasc.2021.018823

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.018823 |  |
| Article |
Robust Sound Source Localization Using Convolutional Neural Network Based on Microphone Array
1School of Information and Communication Engineering, Nanjing Institute of Technology, Nanjing, 211167, China
2School of Information Science and Engineering, Southeast University, Nanjing, 210096, China
3University of Oulu, Oulu, 900014, FI, Finland
*Corresponding Author: Xiaoyan Zhao. Email: xiaoyanzhao205@163.com
Received: 22 March 2021; Accepted: 23 April 2021
Abstract: In order to improve the performance of microphone array-based sound source localization (SSL), a robust SSL algorithm using convolutional neural network (CNN) is proposed in this paper. The Gammatone sub-band steered response power-phase transform (SRP-PHAT) spatial spectrum is adopted as the localization cue due to its feature correlation of consecutive sub-bands. Since CNN has the “weight sharing” characteristics and the advantage of processing tensor data, it is adopted to extract spatial location information from the localization cues. The Gammatone sub-band SRP-PHAT spatial spectrum are calculated through the microphone signals decomposed in frequency domain by Gammatone filters bank. The proposed algorithm takes a two-dimensional feature matrix which is assembled from Gammatone sub-band SRP-PHAT spatial spectrum within a frame as CNN input. Taking the advantage of powerful modeling capability of CNN, the two-dimensional feature matrices in diverse environments are used together to train the CNN model which reflects mapping regularity between the feature matrix and the azimuth of sound source. The estimated azimuth of the testing signal is predicted through the trained CNN model. Experimental results show the superiority of the proposed algorithm in SSL problem, it achieves significantly improved localization performance and capacity of robustness and generality in various acoustic environments.
Keywords: Microphone array; sound source localization; convolutional neural network; gammatone sub-band steered response power-phase transform spatial spectrum
The aim of microphone array-based sound source localization (SSL) is to determine the location information by applying a series of signal processing on multichannel received signals. It plays an important role in numerous application fields including speech enhancement, speech recognition, human-computer interaction, autonomous robots, smart home monitor system, etc [1–5].
Over the past decades, many microphone array-based SSL approaches have been presented. In generally, the traditional approaches for SSL can be divided into two categories [6]. The first category is the indirect approach, which first computes a set of time difference of arrivals (TDOAs) between microphone pairs, and then estimates the sound source location through TDOAs and geometry of array [7]. The second category is the direct approaches, which achieve the sound source location by searching the extremum value of a cost function, including multiple signal classification (MUSIC) algorithm [8], maximum-likelihood estimators [9], steered response power (SRP) [10] and so on. The steered response power-phase transform (SRP-PHAT) [11] is one of the most popularly used traditional SSL algorithm. In certain acoustic environments, the traditional SSL approaches perform fairly well. However, the approaches suffer from the drawback of lack of robustness to noise and reverberation, resulting in performance deterioration in adverse acoustic environments. Therefore, robust SSL is still a challenging and worth studying task.
With the development of artificial neural network (ANN), the usage of deep learning for SSL task have been proposed in recent years. The usage of deep learning for SSL task can be performed in two ways. The first way is to apply deep learning techniques in traditional methods, while the second way considers SSL problem as a classification task and use deep learning to map the input features to the azimuth. For first way, the related research is as follows. Wang et al. [12,13] adopted deep neural networks (DNN) to predicted the time-frequency (T-F) masking, which is used to weight the traditional method. Pertila et al. [14] predicted the T-F masking by convolutional neural network (CNN) and then estimated the azimuth by SRP-PHAT weighted by T-F masking. Salvati et al. [15] used CNN to predict the weighting factors of incoherent frequency bands, which are used to fuse the narrowband response power to realize SRP beamformer.
The second way of applying deep learning to SSL task has been more widely studied, and a variety of input features types are involved by the approaches, such as inter-aural level difference (ILD), inter-aural phase difference (IPD), cross-correlation function (CCF), generalized cross correlation (GCC) and so on. The related research is as follows. An SSL approach based on CNN with multitask learning has been proposed in [16], in which the IPD and ILD are combined as the input features. DNN was utilized in [17] to map the combination of CCF and ILD to source azimuth. The approach in [18] taken CCF as input feature to train DNN model of each time-frequency (T-F) unit. In [19], CCFs of all sub-bands are arranged into a two dimensional feature matrix to train a CNN model. The methods in [20,21] jointed ILDs and CCF as input features, an SSL algorithm fusing deep and convolutional neural network is presented in [20], and a method based on DNN and cluster analysis is present in [21] to improve the localization performance in the mismatched HRTF condition. The approach in [22] taken GCC as the input feature of multi-layer perceptron (MLP) model. A probabilistic neural network-based SSL algorithm proposed in [23] also taken GCC as the input feature. A CNN-based SSL method has been proposed in [24], in which GCC-PHAT was extracted as the input feature. The approach in [25] taken the cross correlations in different frequency bands on mel scale as input features, and trained the CNN model to estimate the map of sound source direction of arrival. A SSL algorithm using a DNN for phase difference enhancement has been proposed in [26], in which the input feature is the sinusoidal functions of the IPD. A DNN-based SSL method has been proposed in [27], which extracted SRP-PHAT spatial spectrum as input feature. The approaches in [28,29] extracted the phase information of short-time Fourier transform (STFT) from the multichannel signals as the input feature of CNN. The method in [30] extracted the real and imaginary part of the spectrograms as the input features to fed to a DNN model. A SSL approach based on convolutional recurrent neural networks has been proposed in [31], which taken the phase and magnitude component of the spectrogram of microphone signal as the input features. The approach in [32] utilized CNN to learn the mapping regularity between raw microphone signals and the direction without feature extraction.
In this paper, we focus on SSL in far-field and come up with a novel robust SSL approach. As our previous work described in [27], the SRP-PHAT spatial power spectrum of the array signals contains spatial location information robustly. Furthermore, considering the feature correlation of consecutive sub-bands, the Gammatone sub-band SRP-PHAT spatial spectrum is adopted as the localization cue in this paper. The “weight sharing” characteristics of CNN [33–35] make it have greater advantages in processing tensor data compared to traditional DNN, and it is widely employed in various applications of deep learning. Therefore, we introduce CNN to establish the mapping regularity between the input feature and the azimuth of sound source by taking its advantage of the powerful modeling capability. The probability that testing signal belongs to each azimuth is predicted through the trained CNN model, and then the azimuth with maximum probability is taken as the estimated azimuth. Experimental results demonstrate that the proposed algorithm improves the localization performance significantly and has capacity of robustness and generality in various acoustic environments.
The rest of the paper is organized as follows. Section 2 illustrates the proposed SSL algorithm based on CNN, which include system overview, feature extraction, the architecture of CNN and the training of CNN. The simulation results and analysis are presented in Section 3. The conclusions follow in Section 4.
2 Sound Source Localization Algorithm Using CNN
The proposed algorithm treats the sound source localization problem as a multi-classification task, and constructs the mapping regularity between spatial feature matrix and the azimuth of sound source through CNN model. Fig. 1 illustrates the overall architecture of the proposed SSL system. The CNN-based microphone array SSL system includes two phases, the training phase and the localization phase. The signals received by microphone array are used as the system input. The Gammatone sub-band SRP-PHAT spatial spectrum are calculated through the microphone signals decomposed in frequency domain by Gammatone filters bank, and assembled into a spatial feature matrix as CNN input. In the training phase, a CNN model which reflects mapping regularity between the spatial feature matrix and the azimuth of sound source is learned. To enhance the robustness and generalization ability of CNN model, signals in diverse reverberation and noise environments are taken together as training data. In the localization phase, the probability that testing signal belongs to each azimuth is predicted through the trained CNN model, and the azimuth with maximum probability is taken as the estimated azimuth.
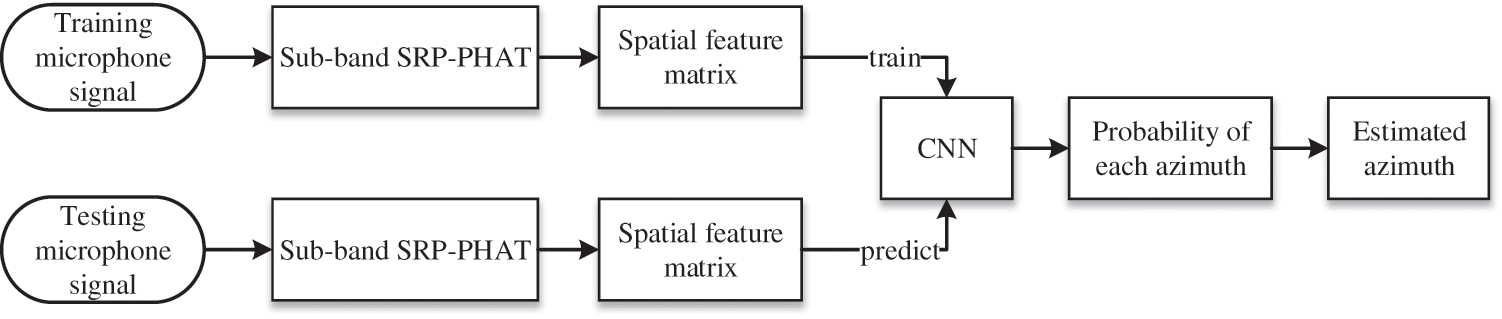
Figure 1: Overall architecture of the proposed SSL system based on microphone array
The physical model for signal received by mth microphone in indoor scenarios can be formulated
where s(t) denotes the clean sound source signal, hm(rs, t) represents the room impulse response from the source position rs to the mth microphone, “*” denotes the linear convolution, vm(t) is additive noise for the mth microphone, and M is the number of microphones. The room impulse response hm(rs, t) is related to the source position, microphone position, and acoustic environment.
As our previous work described in [27], the SRP-PHAT spatial power spectrum of the array signals contains spatial location information, and it is dependent of the room impulse response and is independent of the content of the sound source signal in theory. The SRP-PHAT function of microphone array signals is expressed as:
where P(r) represents the response power when the array is steered to the position r, Δτmn(r) is the propagation delay difference from the steering position r to the mth microphone and the nth microphone, Δmn(r) is only related to the azimuth of the steering position r in the far-filed case, Xm(ω) is the Fourier transforms of xm(t). From Eq. (2), we note that the phase information of the microphone array signals is exploited through SRP-PHAT function.
Gammatone filter bank, which has different central frequencies and bandwidths, is used to simulate the time-frequency analysis to acoustic signals by human auditory system. The impulse response of the ith Gammatone filter is defined as:
where c denotes the gain coefficient, n denotes the filter order, bi denotes the decay coefficient, fi denotes the central frequency of the ith filter, and φ denotes the phase. The frequency response of the Gammatone filter bank is depicted in Fig. 2.
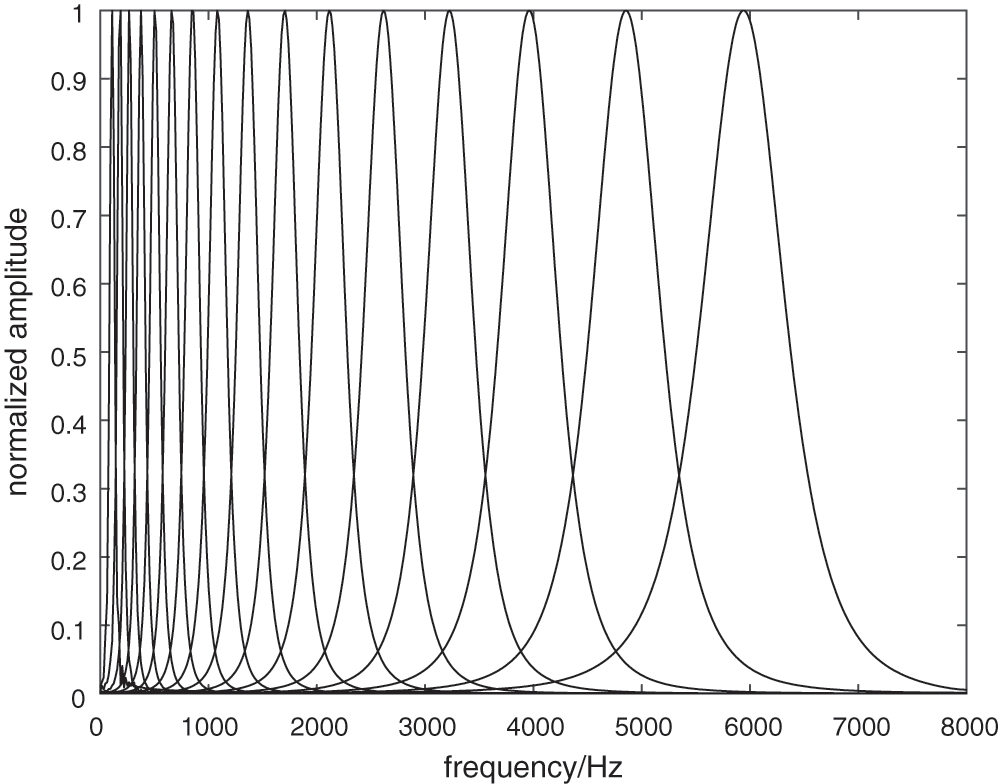
Figure 2: Frequency response of the Gammatone filter bank
The feature parameter extracted from the array signals is the basis of sound source localization. Considering the spatial location information contained in the SRP-PHAT spatial spectrum and the time-frequency analysis capability of the Gammatone filter, the SRP-PHAT spatial spectrum in each band of Gammatone filter bank is exploited as the feature for sound source localization in this paper.
The microphone signals are decomposed into consecutive sub-bands in frequency domain by Gammatone filters bank. The central frequencies of Gammatone filters ranges from 100 to 8000 Hz on the equivalent rectangular bandwidth (ERB). The SRP-PHAT function of a Gammatone sub-band is defined as:
where Pi(r) denotes the SRP-PHAT function of ith Gammatone sub-band, and Gi(ω) is the Fourier transforms of gi(t). We note that Eq. (4) of calculating Gammatone sub-band SRP-PHAT function is equivalent to weighting frequency components in Eq. (2) by Gammatone multichannel bandpass filter.
The microphone signals are divided into 32 ms frame length without frame shift. Then the sub-band SRP is calculated by Eq. (4). Afterwards, all Gammatone sub-band SRPs within a frame are arranged into a matrix, which can be expressed as follows:
where P(k) is the feature matrix of kth frame, and Pi(rl, k) is the ith Gammatone sub-band SRP-PHAT at rl in kth frame which is calculated by Eq. (4), I is the channel number of Gammatone filter, L is the number of steering positions. In this paper, the channel number of Gammatone filter is 32. In the far-filed case, the argument rl is simplified to the azimuth with a distance of 1.5 m from the steering position to the microphone array, and the azimuth ranges from 0° to 360° with a step of 5°, corresponding to 72 steering positions. Thus the dimension of SRP-PHAT feature matrix is 32
CNN is introduce to train a set of SRP-PHAT feature matrices constructed in Section 2.2. To improve the robustness and generality of model, training signals with known azimuth information in diverse environments are used together to train the CNN model. The training azimuth ranges from 0° to 360° with a step of 10°, corresponding to 36 training positions.
As depicted in Fig. 3, the CNN architecture of our algorithm includes one input layer, three convolutional-pooling layers, a fully connected layer, and an output layer. The data of input layer is the feature matrix P(k) of size 36 × 72 which is described in Section 2.2. For the three convolutional layers, the size of convolution kernel is 3 × 3, the stride is 1, and the number of convolution kernels is 24, 48, and 96 respectively. In order to ensure the same size of input and output feature, the output of 2D convolution is zero-filled. Rectified Linear Unit (ReLU) activation function is performed after each 2D convolution operation. For each of pooling layers, the maximum pooling operation of size 2 × 2 with stride of 2 is adopted. After three convolution-pooling operations, the two-dimensional feature matrix with size of 36 × 72 becomes a three-dimensional feature data with size of 5 × 9 × 96. The fully connected layer is followed the last convolutional-pooling layer. We have introduced the Dropout method to avoid overfitting. For the output layer, the softmax regression model is utilized to convert the feature data to the probability that array signal belongs to each azimuth. The azimuth with maximum probability is taken as the estimated source azimuth.

Figure 3: The CNN architecture of the proposed algorithm
The training of CNN includes forward propagation process and back propagation process. Forward propagation is the process of transferring features layer by layer. In the forward propagation process, the output of network under the current model parameters is calculated for the input signal. The output of the dth convolutional layer is expressed as follows:
where Sd denotes the output of the dth layer, “*” denotes the convolution operator, Wd denotes the weight of the convolution kernel in dth layer, bd denotes the bias of the dth layer, and ReLU is the activation function. In order to improve the stability of the network, the batch normalization (BN) operation is performed before the activation operation of the ReLU function in our method.
The output of the dth pooling layer is expressed as follows:
The expression of the output layer is as follows:
where D represents the output layer, WD and bD denote the weight and bias of the fully connected layer respectively, SD is a vector with size of J, and J is the number of class labels, J = 36 in this paper.
The cross-entropy loss function E(W, b) is minimized in the back propagation process as follows:
where the subscript j represents the jth training azimuth position,
The stochastic gradient descent with momentum (SGDM) algorithm is adopted to minimize the loss function. The momentum is set to 0.9, the L2 regularization coefficient is set to 0.0001, the mini-batch is set to 200, and the initial learning rate is set to 0.01. The learning rate is reduced by 0.2 times every 6 epochs.
Over-fitting often occurs during the construction of complex network models. Cross Validation and DropOut are utilized to prevent over-fitting in the training phase. The training data is divided into training set and validation set randomly according to the ratio of 7:3 for cross validation. The DropOut method is introduced in the fully connected layer, and the Dropout ratio is set to 0.5.
3 Simulation and Result Analysis
Simulation experiments are conducted to evaluate the performance of the proposed algorithm. The dimensions of the simulated room are given as 7 m × 7 m × 3 m. A uniform circular array with a radius of 10 cm is located at (3.5 m, 3.5 m, 1.6 m) in the room. The array consists of six omnidirectional microphones. The clean speech sampled at 16 kHz which are taken randomly from the TIMIT database are adopted as the sound source signals. The Image method [36] is used to generate the room impulse response between any two points. The microphone signal is derived by convolving the clean speech with the room impulse response and then adding scaled Gaussian white noise. The microphone signals are segmented into 32-ms frame length without frameshift and windowed by Hamming window. Voice activity detection is performed before sound source localization.
The source is placed in the far-field, and the azimuth ranges from 0° to 360°with a step of 10°, corresponding to 36 training positions. During the training phase, the SNR is varied from 0 to 20 dB with a step of 5 dB, and the reverberation time T60 is set to two levels as 0.5 and 0.8 s. The microphone array signals in different reverberation and noise environments are taken together as training data to enhance the generalization ability of the CNN model.
The localization performance is measured by the percentage of correct estimates, which is defined as follows:
where Nall is the total number of testing frames, nc is the number of correct estimate frames, and the correct estimate is defined that the estimated azimuth is equal to the true azimuth. The performance of the proposed algorithm is compared with two related algorithms, namely the SRP-PHAT [11] and SSL based on deep neural network (SSL-DNN) [27].
3.2 Evaluation in Trained Environments
In this section, the localization performance is investigated and analyzed in the situation that the test signals are generated in the same setting as the training signals. Fig. 4 depicts the localization performance as a function of SNR for SRP-PHAT, SSL-DNN and the proposed algorithm under various reverberation environments.
From Fig. 4, it can be seen that the performance of SRP-PHAT deteriorates significantly as the SNR decreases and the reverberation time increases, and the proposed algorithm is superior to the SRP-PHAT method significantly. The reason is that the proposed algorithm exploits the Gammatone sub-band SRP-PHATs as the feature matrix which consider the feature correlation of consecutive sub-bands, and meanwhile the DNN model can extract efficient spatial location information from them. Furthermore, at the same reverberation time, the performance improvement of the proposed algorithm compared with SRP-PHAT method is greatest at moderate SNR (10 dB); for high SNR (above 10 dB), the performance improvement increase gradually as the SNR decreases; for low SNR (below 10 dB), the performance improvement increases gradually as the SNR increases. For example, in the T60 = 0.8 s scenario, the performance improvement increases from 21.25% to 28.23% as the SNR increases from 0 to 10 dB, and it decreases from 28.23% to 25.09% as the SNR increases from 10 to 20 dB. In addition, the performance improvement of the proposed algorithm compared with the SRP-PHAT method is more significant at higher reverberation time in the same SNR scenario. For example, when SNR = 20 dB, the performance is increased by 17.49% and 25.09% respectively with T60 = 0.5 s and T60 = 0.8 s.
From Fig. 4, it can also be seen that the proposed algorithm outperforms the SSL-DNN method in most environments, and the performance improvement is more significant at higher reverberation time. In addition, at the same reverberation time, the performance improvement of the proposed algorithm compared with the SSL-DNN method increase gradually as the SNR increases. For example, in the T60 = 0.8 s scenario, the improvement of the percentage of correct estimates of the proposed algorithm compared with the SSL-DNN algorithm increases from 1.07% to 9.34% as the SNR increases from 0 to 20 dB. In the low SNR and moderate reverberation environments, the percentage of correct estimates of the proposed method is close to or slightly lower than that of the SSL-DNN method.

Figure 4: Performance comparison of different algorithms in trained environments. (a) Percentage of correct estimates with T60 = 0.5 s (b) Percentage of correct estimates with T60 = 0.8 s
3.3 Evaluation in Untrained Environments
In this section, we investigate the robustness and generality of the proposed algorithm in untrained environment. For the testing signals, the untrained SNR is varied from −2 to 18 dB with a step of 5 dB, and the untrained reverberation time T60 is set to two levels as 0.6 and 0.9 s. Figs. 5 and 6 depict the performance comparison of different algorithms under untrained noise and untrained reverberation environments, respectively.
As shown in Figs. 5 and 6, we have found that the regularity of data variation in untrained environment are consistent with those described in Section 3.2, which reflects that the proposed algorithm is the robustness and generality to untrained noise and reverberation. Specifically, compared with SRP-PHAT method, the percentage of correct estimates is increased about 18% to 30% by the proposed method in diverse environments. Compared with SSL-DNN method, in low SNR and moderate reverberation environments, the proposed method and SSL-DNN method have similar localization performance; in other scenario, the percentage of correct estimates is increased about 5% to 10% by the proposed method.

Figure 5: Performance comparison of different algorithms in untrained noise environments. (a) Percentage of correct estimates with T60 = 0.5 s (b) Percentage of correct estimates with T60 = 0.8 s

Figure 6: Performance comparison of different algorithms in untrained reverberation environments. (a) Percentage of correct estimates with T60 = 0.6 s (b) Percentage of correct estimates with T60 = 0.9 s
In this work, a robust SSL algorithm using convolutional neural network based on microphone array has been presented. Considering the feature correlation of consecutive sub-bands, the sub-band SRP-PHAT spatial spectrum based on Gammatone filter bank is exploited as the feature for sound source localization in the proposed algorithm. CNN is adopted to establish the mapping relationship between the spatial feature matrix and the azimuth of sound source due to its advantage on processing tensor data. Experimental results show that the proposed algorithm provides better localization performance in both the trained and untrained environments, especially in high reverberation environments, and achieves superior capacity of robustness and generality.
Funding Statement: This work is supported by Nanjing Institute of Technology (NIT) fund for Research Startup Projects of Introduced talents under Grant No. YKJ202019, NIT fund for Doctoral Research Projects under Grant No. ZKJ2020003, the National Nature Science Foundation of China (NSFC) under Grant No. 61571106, NSFC under Grant No. 61703201, Jiangsu Natural Science Foundation under Grant No. BK20170765, Innovation training Program for College Students in Jiangsu Province under Grant No. 202011276110H, and NIT fund for “Challenge Cup” Cultivation support project under Grant No. TZ20190010.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. M. Kim and H. H. Kim, “Direction-of-arrival based SNR estimation for dual-microphone speech enhancement,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 22, no. 12, pp. 2207–2217, 2014. [Google Scholar]
2. X. Li, L. Girin, R. Horaud and S. Gannot, “Estimation of the direct-path relative transfer function for supervised sound-source localization,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 24, no. 11, pp. 2171–2186, 2016. [Google Scholar]
3. D. Salvati, C. Drioli and G. L. Foresti, “Sound source and microphone localization from acoustic impulse responses,” IEEE Signal Processing Letters, vol. 23, no. 10, pp. 1459–1463, 2016. [Google Scholar]
4. S. Zhao, S. Ahmed, Y. Liang, K. Rupnow, D. Chen et al., “A real-time 3D sound localization system with miniature microphone array for virtual reality,” in 7th IEEE Conf. on Industrial Electronics and Applications, Singapore, pp. 1853–1857, 2012. [Google Scholar]
5. T. Long, J. D. Chen, G. Huang, J. Benesty and I. Cohen, “Acoustic source localization based on geometric projection in reverberant and noisy environments,” IEEE Journal of Selected Topics in Signal Processing, vol. 13, no. 1, pp. 143–155, 2019. [Google Scholar]
6. D. Salvati, C. Drioli and G. L. Foresti, “A low-complexity robust beamforming using diagonal unloading for acoustic source localization,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 26, no. 3, pp. 609–622, 2018. [Google Scholar]
7. J. Benesty, “Adaptive eigenvalue decomposition algorithm for passive acoustic source localization,” Journal of Acoustical Society of America, vol. 107, no. 1, pp. 384–391, 2000. [Google Scholar]
8. S. Zhao, T. Saluev and D. L. Jones, “Underdetermined direction of arrival estimation using acoustic vector sensor,” Signal Processing, vol. 100, pp. 160–168, 2014. [Google Scholar]
9. C. Zhang, D. Florencio, D. E. Ba and Z. Zhang, “Maximum likelihood sound source localization and beamforming for directional microphone arrays in distributed meetings,” IEEE Transaction on Multimedia, vol. 10, no. 3, pp. 538–548, 2008. [Google Scholar]
10. L. O. Nunes, W. A. Martins, M. V. S. Lima, L. W. P. Biscainho, M. V. M. Costa et al., “A steered-response power algorithm employing hierarchical search for acoustic source localization using microphone arrays,” IEEE Transaction on Signal Processing, vol. 62, no. 19, pp. 5171–5183, 2014. [Google Scholar]
11. J. H. Dibiase, “A high-accuracy, low-latency technique for talker localization in reverberant environments using microphone arrays,” Ph.D. dissertation. Brown University, Providence, RI, 2001. [Google Scholar]
12. Z. Q. Wang, X. L. Zhang and D. L. Wang, “Robust TDOA estimation based on time-frequency masking and deep neural networks,” in 19th Annual Conf. of the International Speech Communication, Hyderabad, India, pp. 322–326, 2018. [Google Scholar]
13. Z. Q. Wang, X. L. Zhang and D. L. Wang, “Robust speaker localization guided by deep learning-based time-frequency masking,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 27, no. 1, pp. 178–188, 2019. [Google Scholar]
14. P. Pertila and E. Cakir, “Robust direction estimation with convolutional neural networks based steered response power,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, pp. 6125–6129, 2017. [Google Scholar]
15. D. Salvati, C. Drioli and G. L.Foresti, “Exploiting CNNs for improving acoustic source localization in noisy and reverberant conditions,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 2, no. 2, pp. 103–116, 2018. [Google Scholar]
16. C. Pang, H. Liu and X. Li, “Multitask learning of time-frequency CNN for sound source localization,” IEEE Access, vol. 7, pp. 40725–40737, 2019. [Google Scholar]
17. N. Ma, T. May and G. J. Brown, “Exploiting deep neural networks and head movements for robust binaural localization of multiple sources in reverberant environments,” IEEE/ACM Transactions on Audio, Speech and Language Processing, vol. 25, no. 12, pp. 2444–2453, 2017. [Google Scholar]
18. N. Ma, J. A. Gonzalez and G. J. Brown, “Robust binaural localization of a target sound source by combining spectral source models and deep neural networks,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 26, no. 11, pp. 2122–2131, 2018. [Google Scholar]
19. L. Zhou, K. Y. Ma, L. J. Wang, Y. Chen and Y. B. Tang, “Binaural sound source localization based on convolutional neural network,” Computers, Materials & Continua, vol. 60, no. 2, pp. 545–557, 2019. [Google Scholar]
20. S. Jiang, W. L., P. Yuan, Y. Sun and H. Liu, “Deep and CNN fusion method for binaural sound source localization,” The Journal of Engineering, vol. 2020, no. 13, pp. 511–516, 2020. [Google Scholar]
21. J. Wang, J. Wang, Z. Yan, W. X. and X. X., “DNN and clustering based binaural sound source localization in mismatched HRTF condition,” in IEEE Int. Conf. on Signal, Information and Data Processing, Chongqing, China, pp. 1–5, 2019. [Google Scholar]
22. X. Xiao, S. K. Zhao, X. H. Zhong, D. L. Jones, E. S. Chng et al., “A learning-based approach to direction of arrival estimation in noisy and reverberant environments,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Brisbane, QLD, Australia, pp. 2814–2818, 2015. [Google Scholar]
23. Y. X. Sun, J. J. Chen, C. Yuen and S. Rahardja, “Indoor sound source localization with probabilistic neural network,” IEEE Transactions on Industrial Electronics, vol. 65, no. 8, pp. 6403–6413, 2018. [Google Scholar]
24. H. Zhu and H. Wan, “Single sound source localization using convolutional neural networks trained with spiral source,” in 5th Int. Conf. on Automation, Control and Robotics Engineering, Dalian, China, pp. 720–724, 2020. [Google Scholar]
25. S. Sakavicius and A. Serackis, “Estimation of sound source direction of arrival map using convolutional neural network and cross-correlation in frequency bands,” in 2019 Open Conf. of Electrical, Electronic and Information Sciences, Vilnius, Lithuania, pp. 1–6, 2019. [Google Scholar]
26. J. Pak and J. W. Shin, “Sound localization based on phase difference enhancement using deep neural networks,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 27, no. 8, pp. 1335–1345, 2019. [Google Scholar]
27. X. Y. Zhao, S. W. Chen and L. Zhou, “Sound source localization based on SRP-PHAT spatial spectrum and deep neural network,” Computers, Materials & Continua, vol. 64, no. 1, pp. 253–271, 2020. [Google Scholar]
28. S. S. Mane, S. G. Mali and S. P. Mahajan, “Localization of steady sound source and direction detection of moving sound source using CNN,” in 10th Int. Conf. on Computing, Communication and Networking Technologies, Kanpur, India, pp. 1–6, 2019. [Google Scholar]
29. S. Chakrabarty and E. A. P. Habets, “Broadband DOA estimation using convolutional neural networks trained with noise signals, ” in IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. New Paltz, NY, USA, 136–140, 2017. [Google Scholar]
30. G. L. Moing, P. Vinayavekhin, T. Inour, J. Vongkulbhisal, A. Munawar et al., “Learning multiple sound source 2Dlocalization, ” in 21st Int. Workshop on Multimedia Signal Processing. Kuala Lumpur, Malaysia, 1–6, 2019. [Google Scholar]
31. S. Adavanne, A. Politis, J. Nikunen and T. Virtanen, “Sound event localization and detection of overlapping sources using convolutional recurrent neural networks,” IEEE Journal of Selected Topics in Signal Processing, vol. 13, no. 1, pp. 34–48, 2019. [Google Scholar]
32. J. J. Tong and Y. F. Zhang, “Robust sound localization of sound sources using deep convolution network,” in 15th Int. Conf. on Control and Automation, Edinburgh, United Kingdom, pp. 196–200, 2019. [Google Scholar]
33. K. Yang, J. Jiang and Z. Pan, “Mixed noise removal by residual learning of deep CNN,” Journal of New Media, vol. 2, no. 1, pp. 1–10, 2020. [Google Scholar]
34. D. J. Zeng, Y. Dai, F. Li, J. Wang and A. K. Sangaiah, “Aspect based sentiment analysis by a linguistically regularized CNN with gated mechanism,” Journal of Intelligent & Fuzzy Systems, vol. 36, no. 5, pp. 3971–3980, 2019. [Google Scholar]
35. R. Chen, L. Pan, Y. Zhou and Q. Lei, “Image retrieval based on deep feature extraction and reduction with improved CNN and PCA,” Journal of Information Hiding and Privacy Protection, vol. 2, no. 2, pp. 9–18, 2020. [Google Scholar]
36. J. B. Allen and D. A. Berkley, “Image method for efficiently simulating small-room acoustics,” Journal of Acoustical Society of America, vol. 65, no. 4, pp. 943–950, 1979. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |