Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.018120
Article

Measurement-based Quantum Repeater Network Coding

Si-Yi Chen1, Gang Xu2, Xiu-Bo Chen1, Haseeb Ahmad3 and Yu-Ling Chen4,*

1Information Security Center, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
2School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
3Department of Computer Science National Textile University, Faisalabad, 37610, Pakistan
4State Key laboratory of Public Big Data, College of Computer Science and Technology, Guizhou University, Guiyang, 550025, China
*Corresponding Author: Yu-Ling Chen. Email: Ylchen3@gzu.edu.cn
Received: 25 February 2021; Accepted: 02 April 2021

Abstract: Quantum network coding can effectively improve the aggregate throughput of quantum networks and alleviate bottlenecks caused by topological constraints. Most of previous schemes are dedicated to the efficient teleportation of unknown quantum states in a quantum network. Herein a proposal for transmission of deterministic known states over quantum repeater network based on quantum measurements. We show that the new protocol offers advantages over three aspects. Firstly, the senders in our protocol obtain the knowledge of the quantum state to be transmitted, which enables the autonomy of quantum network transmission. Secondly, we study the quantum repeater network coding for long-distance deterministic quantum state communication. Quantum repeater network initialization requires entanglement distribution only among neighboring nodes, greatly saving entanglement resources, channel overhead and storage costs. Thirdly, based on Pauli measurements and local complementation, new protocol realizes parallel coding operations to mitigate latency issues sufficiently. Combining quantum network coding and quantum remote state preparation technology, our protocol provides an important solution for deterministic known states transmission over large-scale quantum network in the future.

Keywords: Quantum repeater network coding; graph state; Pauli measurements; local complementation

1  Introduction

With the rapid development of quantum information technology, the establishment of globalized quantum networks is an inevitable trend in the future. Hayashi et al. [1] first proposed the quantum network coding protocol “XQQ”. Due to the quantum non-cloning theorem, Hayashi used approximate cloning to replicate the quantum state, which led to partial distortion of the original quantum state. In order to improve the fidelity, then Hayashi [2] adopted quantum teleportation as the information transmission method. This method [2] was able to achieve perfect cross-transmission of two quantum states over the butterfly network. In 2011, perfect quantum network encoding [3] was proposed over arbitrary network model with classical communication assistance. Subsequently, Nishimura [4] pointed out that future work on quantum network coding should be extended to general network structures. In recent years, Li et al. [5,6] have conducted profound studies on the solvability of quantum network coding for multi-unicast problem in general network structures.

However, considering the large-scale distributed quantum networks in future, quantum network coding protocols mentioned above [1–6] have not considered about the communication cost seriously. By taking the addition of auxiliary quantum repeaters at nodes regardless of expensive quantum resources [1–6], the communication cost will greatly increase. How to effectively use quantum network resources has become a hot research topic recently. As a solid foundation for future large-scale quantum communication networks, quantum repeater technology successfully performs communication tasks in long-range complex topologies. For the study of quantum repeater network coding, scholars start with three different information transmission methods [7–9] in butterfly network. There are universal gate operations [7], entanglement swapping [8], and quantum measurement [9] respectively. In 2017, Nguyen et al. [10] proposed a large-scale quantum network coding protocol (LQNC), which aimed at a quantum repeater network with M-pairs communicating parties and N intermediate nodes. In 2018, Li et al. [11] studied the quantum repeater network multicast problem. Compared to the general repeater networks protocol with graph transformation [12], this protocol [11] showed the more general version.

Although the existing quantum repeaters network coding are dedicated to releasing quantum resource consumption in general network communication [13,14], few studies addressed the scalability of transmitted information types. In the above protocols, each sender only acts as a communication tool to transmit unknown quantum states, without considering the senders’ transport needs. In this paper, a quantum repeater network coding protocol is proposed to support active remote transmission of known quantum states. By distributing entangled resources among adjacent nodes, each sender can send a certain quantum state to the receiver. It not only gives the sender the right to determine the transmitted quantum state, but also saves channel overhead and alleviates the shortage of quantum resources. The new protocol combines quantum network coding with quantum controlled remote state preparation techniques. Firstly, we use cluster states as entanglement resources and distribute entanglement among neighbor nodes. Then, based on quantum measurement techniques, especially Pauli measurement, repeater coding operations are designed to extend the entanglement relationship. Finally, local complementation operation is used to construct a quantum controlled remote state preparation channel for both communicating parties. The deterministic quantum network communication can be achieved simply by introducing the existing quantum remote preparation scheme [15]. Overall, our protocol provides an important solution for building large-scale quantum network communication in the future.

2  Preliminary

We assume that the reader already has a basic knowledge of quantum information theory, but if the reader does not have a background in this area, please refer to the literature [16] for prior learning. Here we focus on quantum repeater networks and the knowledge of quantum graph state covered in new protocol.

2.1 Quantum Repeater

Quantum repeater can solve the problem of exponential decay of photon signal in optical fiber, and it is one of the important ways to realize Super-far-distance quantum communication in the future. Specifically, the original point-to-point transmission will be changed to segmented transmission, that is, the whole communication line will be reasonably segmented to enjoy the polynomial scaling with the total distance. Then these segments are cascaded by quantum repeater, which makes it possible to build a full quantum network.

The basic principle of quantum repeater is the combination of segmenting entanglement distribution and entanglement swapping to expand the communication distance. Fig. 1 shows us the principle of quantum repeater. In quantum repeater network, due to the long distance between Alice and Bob, the photon signal has the problem of exponential decay in the fiber. Therefore, we need to add quantum repeaters (R1, R2, R3) between Alice and Bob. Firstly, the initialization process is carried out by pre sharing the entangled resource between adjacent repeaters. Secondly, in order to extend the entanglement relationship, local operations with the assistance of classical communication (LOCC) should be performed on the entangled states. Finally, by exploiting quantum information communication methods (e.g., quantum teleportation, quantum remote state preparation), perfect quantum repeater network communication can be achieved.

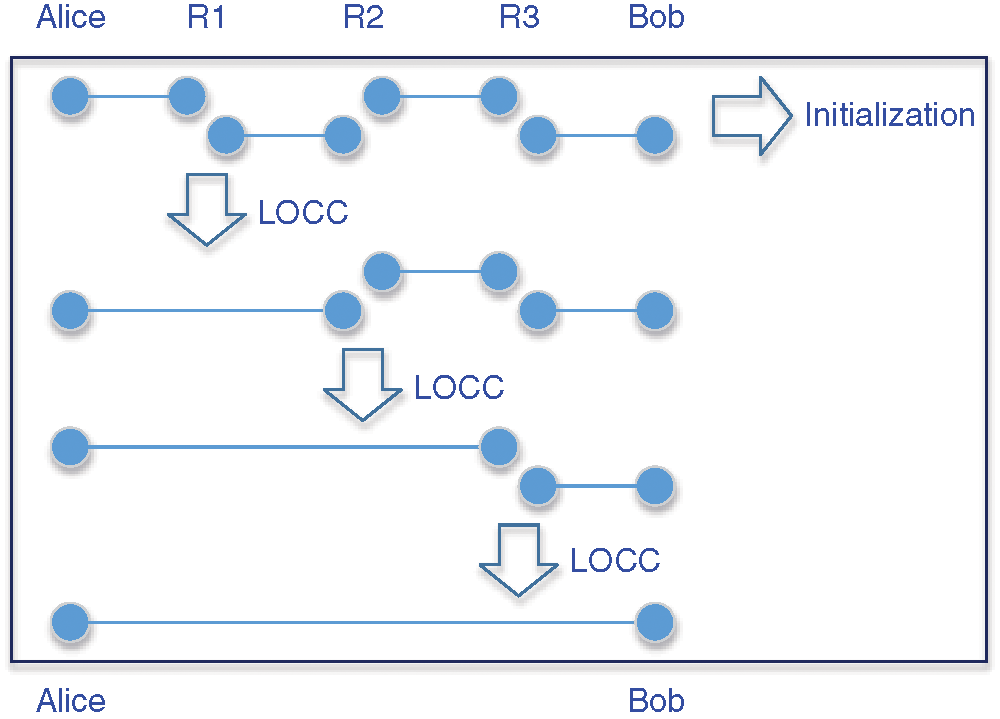
Figure 1: The Principle of Quantum Repeater

2.2 Quantum Graph State

This section introduces the quantum graph states, the local complementation of graph states and Pauli measurements involved in encoding and decoding operations, as well as quantum remote state preparation.

2.2.1 Graph State

Graph state is a special class of quantum entangled states. Any simple graph can have a corresponding graph state. Now we introduce the concept of a graph. A graph G=(V,E) is defined by a set of vertices V={1,2,...,m} and a set of edges E={(i,j)|i,j∈V} . If there is an edge between vertex i and j , they can be called as neighboring vertices. The set of neighbors of a vertex i∈V is denoted by Ni .

Graph state has another construction definition. Given a simple graph G=(V,E) , the corresponding graph state |G⟩ can be defined as:

|G⟩=∏(a,b)∈ECZab|+⟩⊗|V| (1)

This definition explains the process of constructing a graph state. Firstly, each vertex represents an initial qubit |+⟩=|0⟩+|1⟩2 . Secondly, the edges between neighboring vertices a,b represent the the controlled-Z gate operation CZab performed on vertices a,b qubits. In particular, the graph G is undirected, i.e., the edges (a,b ) and (b,a ) are identical.

When the graph G is a simple chain or grid structure, the corresponding graph states are called cluster states. They were originally introduced by Briegel et al. [17]. There are some examples about cluster states shown in Tab. 1. As an important class of entanglement resources, cluster states are widely used in quantum computing and quantum information processing. In this paper, cluster states are used as entanglement resources for network coding.

2.2.2 Graph State Properties

Graph states are a class of entangled quantum states that embody multi-particle entanglement structures, which have many peculiar properties.

(1) Local Complementation (LC)

In graph theory, when two graphs are isomorphic, there is an equivalence relation between them. For graph states, there also exist an equivalence relation between different graph states. Here equivalence relations include LU equivalence and LC equivalence.

LU equivalence relationship of a graph state means: if there is a local unitary operator U=⊗i=1nUi for two n-qubits graph states |G1⟩ and |G2⟩ , satisfying U|G1⟩=|G2⟩ , where Ui is the unitary operator acting on a single qubit, then the |G1⟩ and |G2⟩ is said to be LU-equivalent.

LC equivalence is a subclass of the LU equivalence relation. If there exists a local Clifford operator L=⊗i=1nLi for two n-qubits graph state |G1⟩ and |G2⟩ , satisfying L|G1⟩=|G2⟩ , where Li is the Clifford operator acting on a single qubit, then the |G1⟩ and |G2⟩ is the LC equivalence. The effect of a local Clifford operator acting on a graph state can be depicted by Local Complementation (LC) on the graph.

Local Complementation (LC): Given a simple graph G=(V,E) , a local complementation on vertex i∈V is applied through unitary transformation Uiτ:=e−iπ4Xi⊗j∈Nieiπ4Zj . From the perspective of graph transformation, edges are added between all the adjacent vertices of the original vertex i∈V . If the original neighbors have been connected already, the original edges are cancelled. Meanwhile the other parts remain unchanged. It is recorded as τi(G) or LC(i) .

Fig. 2 gives an example about LC. In Fig. 2, the left one is the original graph and the right one is LC(a) . In the original graph, the set of neighbors of vertex a is Na={b,c,d} . The original vertex b and c, d are not adjacent, we need to connect (b,c), (b,d). Since the original vertex c, d had an edge already, we need to cancel the connection. The rest of original graph remains unchanged. Therefore, LC(a) is shown as the right one, which is applied through unitary transformation Uaτ:=e−iπ4Xa⊗eiπ4Zb⊗eiπ4Zc⊗eiπ4Zd .

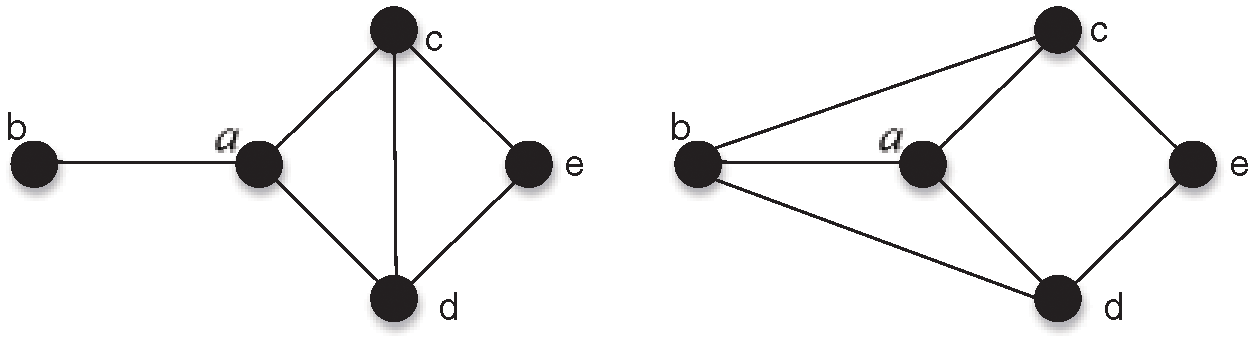
Figure 2: An Example LC(a) in graph state

(2) Pauli Measurement

Pauli measurement on a graph state satisfies a set of graph rules [18,19]. In this paper, the Pauli-measurements involved are Y-measurements and Z-measurements. Here we focus on the transformation rules for these two Pauli measurements.

Z-measurement: Z-measurement on a vertex of the graph state is easiest by simply removing that vertex and corresponding edges from the graph. Given a graph state G=(V,E) , when we apply Z-measurement with a∈V , the resulting state is given by

Pz,±(a)|G⟩=|z,±⟩(a)⊗Uz,±(a)|G′⟩ (2)

Uz,+(a)=I,Uz,−(a)=∏b∈Naσz(b) (3)

Pz,±(a) is the projective measurement on a vertex a∈V with σz and the measured results will be ±1 . The resulting graph is given by

G′=G−{a} (4)

Y-measurement: To make a Y-measure on a vertex of a graph state, you need to do a local complement operation on the vertex and then remove the vertex and corresponding edges from the graph. Given a graph state G=(V,E) , when we apply Y-measurement with a∈V , the resulting state is given by:

Py,±(a)|G⟩=|y,±⟩(a)⊗Uy,±(a)|G′⟩ (5)

Uy,+(a)=∏b∈Na(−iσz(b))1/2,Uy,−(a)=∏b∈Na(iσz(b))1/2 (6)

Py,±(a) is the projective measurement on a vertex a∈V with σy and the measured results will be ±1 . The resulting graph is given by

G′=G−E(Na,Na) (7)

Here we give an example. The rules for the structure of the graph changed by Pauli Measurement (Z-measurement, Y-measurement) of the vertex a (vertex a is noted in white) are summarized in Tab. 2, where we use the Nielsen et al. [16] notation to formalize the transformation.

2.3 Quantum Remote State Preparation

Quantum remote state preparation (RSP) is a kind of remote transmission method for certain quantum states. RSP and quantum teleportation (QT) both use quantum entanglement channel and classical communication to realize quantum communication. They are two important transmission modes in quantum information theory. The difference between them is whether the sender has the right to know the transmission state. In quantum teleportation, the sender has the physical sample of the quantum state to be transmitted, but he may not know the specific expression of the state. While in remote state preparation, the sender clearly knows the expression of the quantum state to be transmitted, but he may not have the physical sample of the state.

Before introducing our quantum network coding protocol, we give a brief review of a protocol for quantum controlled remote state preparation (CRSP) based on GHZ state [15]. There are three legal participants in the protocol [15]: Alice, Bob and Charlie. Suppose Alice wants to help his colleague Bob prepare an arbitrary single quantum state

|ξ⟩=x|0⟩+yeiθ|1⟩ (8)

Where, real coefficients x,y≥0 , θ∈[0,2π) and x2+y2=1 . Alice knows the specific expression of the state, but Bob doesn’t. Meanwhile Charlie will control the whole remote preparation process. To accomplish the above tasks, Alice, Bob and Charlie share a 4-bit GHZ state in advance:

|G⟩A1A2BC=12(|0000⟩+|1111⟩)A1A2BC (9)

Alice, Bob and Charlie have particles A1A2 , B and C , respectively.

The specific steps of the quantum controlled remote state preparation protocol [15] are as follows:

Step1. Alice applies the projective measurement on the qubit A1 with {|ξ1⟩,|ξ2⟩} :

|ξ1⟩A1=x|0⟩+y|1⟩,|ξ2⟩A1=x|1⟩−y|0⟩ (10)

According to the measurement results, Alice uses the corresponding measurement basis to measure the qubit A2 .

If the measurement result is |ξ1⟩A1 , Alice operates U1 on A2 :

U1=12(1e−iθ1−e−iθ) (11)

Then Alice applies the projective measurement on the qubit A2 with:

|η1⟩A2=12(|0⟩+e−iθ|1⟩),|η2⟩A2=12(|0⟩−e−iθ|1⟩) (12)

If the measurement result is |ξ2⟩A1 , Alice operates U2 on A2 :

U2=12(e−iθ1e−iθ−1) (13)

Then Alice applies the projective measurement on the qubit A2 with:

|η1′⟩A2=12(e−iθ|0⟩+|1⟩),|η2′⟩A2=12(e−iθ|0⟩−|1⟩) (14)

It is worth noting that Alice uses feedforward measurement technology here. In other words, the choice of measurement basis for the qubit A2 mainly depends on the previous measurement results of the qubit A1 . Here the projective measurement results of the qubits A1 and A2 are represented by PMA1 and PMA2 respectively. After that, Alice informs Bob and Charlie of the measurement results (PMA1 and PMA2 ) through classical communication. Since these results are meaningless to any outsider, they can be transmitted publicly. Now the qubits BC held by Bob and Charlie collapses into the following entangled state

|μ±⟩BC=x|00⟩BC±ye−iθ|11⟩BC,|ν±⟩BC=x|11⟩BC±ye−iθ|00⟩BC (15)

The relationship between the measurement results and the joint collapse state is shown in Tab. 3.

According to the measurement results PMA1 and PMA2 , Charlie uses the measurement basis {|+⟩,|−⟩} to measure the qubit C . And then Charlie informs Bob of the measurement result PMC through classical communication.

Once the message from Alice and Charlie is received, Bob can perform a corresponding unitary operation on the qubit B to recover the single quantum state |ξ⟩ . The corresponding relationship between Bob’s unitary operation and the measurement results of Alice (PMA1 and PMA2 ) and Charlie (PMC ) is shown in Tab. 4.

3  Measurement-based Quantum Repeater Network Coding

Existing quantum repeater network coding aim to teleport unknown quantum information. They extend the entanglement relations by gate operations [7], entanglement exchange [8], or quantum measurement techniques [9], and construct quantum teleportation channels between source-target nodes to transfer unknown quantum states. In this paper, considering the need for deterministic known quantum state transmission, we propose to construct a quantum controlled remote state preparation channel between source-target nodes. It contributes to deterministic quantum state transmission in quantum repeater network.

3.1 The Proposed Protocol

The main task of our protocol is to construct a quantum controlled remote preparation channel between the source-target nodes in quantum repeater network. The flowchart of the entire protocol is shown in Fig. 3.

Figure 3: The flow chart of measurement-based quantum repeater network coding

As shown in Fig. 3, a deterministic quantum state transmission over quantum repeater network requires setting up quantum repeaters at the source nodes S1,S2 , intermediate node R1,R2 , and target node T1,T2 in initialization process. The source nodes S1,S2 pre-share a three-particle linear cluster state |G1,2,3>=12(|0+0>+|1−1>)1,2,3 and |G4,5,6>=12(|0+0>+|1−1>)4,5,6 with their adjacent intermediate node R1 respectively; the intermediate nodes R1,R2 pre-share two pairs of two-particle cluster states |G7,8>=12(|0+>+|1−>)7,8 and |G9,10>=12(|0+>+|1−>)9,10 ; the target nodes T1,T2 pre-share a two-particle cluster state |G11,12>=12(|0+>+|1−>)11,12 and |G13,14>=12(|0+>+|1−>)13,14 with their adjacent intermediate node R2 respectively. The initial state of the whole protocol is:

|Ψinit⟩=|G1,2,3⟩|G4,5,6⟩|G7,8⟩|G9,10⟩|G11,12⟩|G13,14⟩ (16)

The following are the steps for coding a deterministic quantum state network based on quantum repeaters.

Step 1. Generate two 7-particle linear cluster states by connecting (3,7), (4,9), (8,11), and (10,13) in parallel at the intermediate nodes R1,R2 via the Controlled-Z operation:

|Ψ1>=|G1,2,3,7,8,11,12>|G4,5,6,9,10,13,14>=((|00>−|11>)(|+00+0>+|+00−1>+|+01−0>+|+01+1>)+(|00>−|11>)(|−10+0>+|−10−1>−|−11−0>−|−11+1>)+(|01−>+|10+>)(|00+0>+|00−1>+|01−0>+|01+1>)+(|01+>+|10−>)(|10+0>+|10−1>−|11−0>−|11+1>))1,2,3,7,8,11,12⊗((|00>−|11>)(|+00+0>+|+00−1>+|+01−0>+|+01+1>)+(|00>−|11>)(|−10+0>+|−10−1>−|−11−0>−|−11+1>)+(|01−>+|10+>)(|00+0>+|00−1>+|01−0>+|01+1>)+(|01+>+|10−>)(|10+0>+|10−1>−|11−0>−|11+1>))4,5,6,9,10,13,14 (17)

Step 2. Apply Y-measure with 3, 6, 13, 11 particles by R1,R2 simultaneously. It removes the redundant particles and connect the neighbor qubits directly.

|Ψ2>=|G1,2,7,8,12>|G4,5,9,10,14>=(|+0⟩(|+0+⟩+|−1−⟩)+|−1⟩(|−0+⟩+|+1−⟩))1,2,7,8,12⊗(|+0⟩(|+0+⟩+|−1−⟩)+|−1⟩(|−0+⟩+|+1−⟩))4,5,9,10,14 (18)

Step 3. Perform local complement operations on 2, 5 particles by S1,S2 .

Step 4. Perform local complement operations on 7, 9 particles by R1 .

Step 5. Perform local complement operations on 8, 10 particles by R2 .

Step 6. Apply Z-measure with the particles 7, 9, thus generating two required 4-particles GHZ states.

|Ψfinal⟩=|GHZ⟩1,2,12,8|GHZ⟩4,5,14,10=12(|0000⟩+|1111⟩)1,2,12,8⊗12(|0000⟩+|1111⟩)4,5,14,10 (19)

Now the source nodes S1,S2 , the corresponding target nodes T1,T2 and the intermediate node R2 successfully construct a quantum remote state preparation channel [15]. According to [15], the intermediate node R2 can remotely control the task of determining the quantum state network communication.

3.2 The Performance Analysis

In this section, we give a detailed performance analysis of the new protocol in terms of security, and communication rate.

3.2.1 Security

Since the quantum repeater network coding protocol does not require sending quantum particles during the entire transmission process, the eavesdropper Eve can only steal secret message particles at the source node. This situation can be ensured by means of quantum detection listening [20–25]. The technique of quantum detection listening was inspired by BB84 QKD [26], which has been proven to be absolutely safe. It is assumed that the X-basis and Z-basis measurements are used with equal probability to detect particles. If the state of the detected particle is |0>, eavesdropper Eve has a 1/2 probability of using Z-basis to measure it, and the state of the particle is not |0> after the measurement, so it will not be detected. When eavesdropper Eve has a 1/2 probability of using base X to measure, she still has a 1/2 probability of getting the result |0>, so the probability of eavesdropper Eve randomly choosing the base to measure without changing the quantum state is 12+12×12 .

3.2.2 Communication Rate

In the asymptotic scenario [27,28], the extensive use of network is allowed. Under the assumption that there is a communication protocol Pn , where the sender Si uses n times network to transmit n(ri−δi) qubits with fidelity 1−ϵi for δi,ϵi⟶0 to the receiver ti , the rate k-tuple (r1,r2,…,rk ) is achievable and the set of all achievable rate pairs is called the achievable rate region. ∑i=1kri represents the value of 1-flow with fidelity 1 transmission, while 1- maxflow represents the upper bound of 1- flow value. The new protocol proposed in this paper achieves the value of 1-maxflow since it realizes the perfect transmission of quantum state over the quantum network per use of network and classical communication.

4  Conclusion

In this paper, a quantum repeater network coding protocol that supports active remote transmission of known quantum states is proposed by combining quantum remote preparation techniques. The new protocol uses clustered states as entanglement resources and designs repeater coding operations based on quantum measurements. Compared to the previous quantum network coding protocols, the new protocol only distribute entanglement resources among neighbor node. Each sender at the source node can determine the transmitted quantum state and each node complete the coding operation in parallel, which achieve an optimized remote transmission of known quantum states in the quantum network.

Funding Statement: This work is supported by the NSFC (Grant Nos. 92046001, 61671087, 61962009), the Fundamental Research Funds for the Central Universities (Grant No. 2019XD-A02), the Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data (Grant Nos. 2018BDKFJJ018), and the Scientific Research Foundation of North China University of Technology.

Conflicts of Interest: We declare that we have no conflicts of interest to report regarding the present study.

References

 1.  M. Hayashi, K. Iwama, H. Nishimura, R. Raymond and S. Yamashita, “Quantum network coding,” in Proc. of the 24th Annual Conf. on Theoretical Aspects of Computer Science, Berlin, BE, Germany, pp. 610–621, 2007. [Google Scholar]

 2.  M. Hayashi, “Prior entanglement between senders enables perfect quantum network coding with modification,” Physical Review A, vol. 76, no. 4, pp. 1–5, 2007. [Google Scholar]

 3.  H. Kobayashi, F. L. Gall, H. Nishimura and M. Roetteler, “Constructing quantum network coding schemes from classical nonlinear protocols,” in Proc. IEEE Int. Symp. Information Theory, pp. 109–113, 2011. [Google Scholar]

 4.  H. Nishimura, “Quantum network coding—how can network coding be applied to quantum information?,” in Proc. IEEE Int. Symp. Netw Coding, pp. 1–5, 2013. [Google Scholar]

 5.  J. Li, X. B. Chen, X. M. Sun, Z. P. Li and Y. X. Yang, “Quantum network coding for multi-unicast problem based on 2D and 3D cluster states,” Science China-Information Sciences, vol. 59, no. 4, pp. 1–15, 2016. [Google Scholar]

 6.  J. Li, X. B. Chen, G. Xu, Y. X. Yang and Z. P. Li, “Perfect quantum network coding independent of classical network solutions,” IEEE Communications Letters, vol. 19, no. 2, pp. 115–118, 2015. [Google Scholar]

 7.  T. Satoh, F. Le Gall and H. Imai, “Quantum network coding for quantum repeaters,” Physical Review A, vol. 86, no. 3, pp. 032331, 2012. [Google Scholar]

 8.  T. Satoh, K. Ishizaki, S. Nagayama and R. Van Meter, “Analysis of quantum network coding for realistic repeater networks,” Physical Review A, vol. 93, no. 3, pp. 032302, 2016. [Google Scholar]

 9.  T. Matsuo, T. Satoh, S. Nagayama and R. Van Meter, “Analysis of measurement-based quantum network coding over repeater networks under noisy conditions,” Physical Review A, vol. 97, no. 6, pp. 062328, 2018. [Google Scholar]

10. H. V. Nguyen, Z. Babar, D. Alanis, P. Botsinis, D. Chandra et al., “Towards the quantum internet: Generalised quantum network coding for large-scale quantum communication networks,” IEEE Access, vol. 5, no. 99, pp. 17288–17308, 2017. [Google Scholar]

11. D. D. Li, F. Gao, S. J. Qin and Q. Y. Wen, “Perfect quantum multiple-unicast network coding protocol,” Quantum Information Processing, vol. 17, no. 1, pp. 1204, 2018. [Google Scholar]

12. T. Shang, J. Li, Z. Pei and J. W. Liu, “Quantum network coding for general repeater networks,” Quantum Information Processing, vol. 14, no. 9, pp. 3533–3552, 2015. [Google Scholar]

13. Z. Z. Li, G. Xu, X. B. Chen, Q. Z. Guo, X. X. Niu et al., “Efficient quantum state transmission via perfect quantum network coding, Science China-Information Sciences,” Science China-Information Sciences, vol. 62, no. 1, pp. 191–204, 2019. [Google Scholar]

14. S. Y. Ma, X. B. Chen, M. X. Luo, X. X. Niu and Y. X. Yang, “Probabilistic quantum network coding of M-qudit states over the butterfly network,” Optics Communications, vol. 283, no. 3, pp. 497–501, 2010. [Google Scholar]

15. H. Y. Jia, “Research on graph state: Remote preparation and applications in quantum cryptographic protocols,” Ph.D. dissertation. Beijing University of Posts and Telecommunications, China, 2012. [Google Scholar]

16. M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]

17. H. J. Briegel and R. Raussendorf, “Persistent entanglement in arrays of interacting particles,” Physical Review Letters, vol. 86, no. 5, pp. 910–913, 2001. [Google Scholar]

18. M. Hein, J. Eisert and H. J. Briegel, “Multiparty entanglement in graph states,” Physical Review A, vol. 69, no. 6, pp. 307, 2004. [Google Scholar]

19. D. Schlingemann, “Cluster states, algorithms and graphs,” Quantum Information & Computation, vol. 4, no. 4, 2004. [Google Scholar]

20. G. Xu, K. Xiao, Z. Li, X. X. Niu and M. Ryan, “Controlled secure direct communication protocol via the three-qubit partially entangled set of states,” Computers, Materials & Continua, vol. 58, no. 3, pp. 809–827, 2019. [Google Scholar]

21. Z. G. Qu, S. Y. Wu, L. Sun and X. J. Wang, “Analysis and improvement of steganography protocol based on bell states in noise environment,” Computers, Materials & Continua, vol. 59, no. 2, pp. 607–624, 2019. [Google Scholar]

22. Z. Dou, G. Xu, X. B. Chen and K. G. Yuan, “Rational non-hierarchical quantum state sharing protocol,” Computers, Materials & Continua, vol. 58, no. 2, pp. 335–347, 2019. [Google Scholar]

23. V. S. Naresh and S. Reddi, “Multiparty quantum key agreement with strong fairness property,” Computer Systems Science and Engineering, vol. 35, no. 6, pp. 457–465, 2020. [Google Scholar]

24. Z. G. Qu, S. Y. Chen and X. J. Wang, “A secure controlled quantum image steganography algorithm,” Quantum Information Processing, vol. 19, no. 10, pp. 661, 2020. [Google Scholar]

25. X. B. Chen, Y. R. Sun, G. Xu and Y. X. Yang, “Quantum homomorphic encryption scheme with flexible number of evaluator based on (k, n)-threshold quantum state sharing,” Information Sciences, vol. 501, no. 1, pp. 172–181, 2019. [Google Scholar]

26. H. B. Charles and B. Gilles, “Quantum cryptography: Public key distribution and coin tossing,” in Proc. IEEE Int. conf. computers Systems & Signal Processing, Bangalore, India, 1984. [Google Scholar]

27. D. Leung, J. Oppenheim and A. Winter, “Quantum network communication – the butterfly and beyond,” IEEE Transactions on Information Theory, vol. 56, no. 7, pp. 3478–3490, 2010. [Google Scholar]

28. E. T. Campbell and J. Fitzsimons, “An introduction to one-way quantum computing in distributed architectures,” International Journal of Quantum Information, vol. 8, pp. 219–258, 2011. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.