Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.017154
Article

Blockchain-Based Decision Tree Classification in Distributed Networks

Jianping Yu1,2,3, Zhuqing Qiao1, Wensheng Tang1,2,3,*, Danni Wang1 and Xiaojun Cao4

1College of Information Science and Engineering, Hunan Normal University, Changsha, 410081, P.R. China
2Hunan Provincial Key Laboratory of Intelligent Computing and Language Information Processing, Hunan Normal University, Changsha, 410081, P.R. China
3Hunan Xiangjiang Artificial Intelligence Academy, Changsha, 410000, P.R. China
4Department of Computer Science, Georgia State University, Atlanta, 30303, USA
*Corresponding Author: Wensheng Tang. Email: tangws@hunnu.edu.cn
Received: 22 January 2021; Accepted: 11 March 2021

Abstract: In a distributed system such as Internet of things, the data volume from each node may be limited. Such limited data volume may constrain the performance of the machine learning classification model. How to effectively improve the performance of the classification in a distributed system has been a challenging problem in the field of data mining. Sharing data in the distributed network can enlarge the training data volume and improve the machine learning classification model’s accuracy. In this work, we take data sharing and the quality of shared data into consideration and propose an efficient Blockchain-based ID3 Decision Tree Classification (BIDTC) framework for distributed networks. The proposed BIDTC takes advantage of three techniques: blockchain-based ID3 decision tree, enhanced homomorphic encryption, and stimulation smart contract to conduct classification while effectively considering the data privacy and the value of user data. BIDTC employs the data federation scheme based on homomorphic encryption and blockchain to achieve more training data sharing without sacrificing data privacy. Meanwhile, smart contracts are integrated into BIDTC to incentivize users to share more high-quality data. Our extensive experiments have demonstrated that the proposed BIDTC significantly outperforms existing schemes in constructed consortium blockchain networks.

Keywords: Blockchain; classification algorithm; decision tree; homomorphic encryption

1  Introduction

Much data is produced by social networks, engineering sciences, biomolecular research, commerce, and security logs [1]. To extract the information hidden in such big data, machine learning techniques such as statistical model estimation and predictive learning have emerged [2]. Classification is a critical supervised machine learning technique that can learn from the training data and label test data as different predefined classes [3]. Many classification algorithms such as Iterative Dichotomiser 3 (ID3), Support Vector Machine (SVM), and K-Nearest Neighbor (KNN) have been intensively studied [4,5]. Most of the existing classification schemes are based on centralized settings where a large training dataset is available in a single host. However, in a distributed computing system such as Internet of Things (IoT), the data is likely scattered around the system, which makes it difficult to have a large centralized dataset for training and classifications [6–8]. For example, the work in Ang et al. [6] proposed the ensemble approach PINE to classify concepts of interest in a distributed computing system. PINE combines reactive adaptation, proactive handling of upcoming changes, and adaptation across peers to achieve better accuracy. A distributed classification algorithm (P2P-RVM) for the peer-to-peer networks was proposed in Khan et al. [7], which is based on the relevance vector machines. To solve the distributed multi-label classification problem, the work in Xu et al. [8] proposed a quantized distributed semi-supervised multi-label learning algorithm, where the kernel logistic regression function is used, and the common low-dimensional subspace shared by multiple labels is learned. The work in Vu et al. [9,10] tries to consider data privacy by use of encrypted traffic. Similarly, the flow-based relation network classification model RBRN was proposed in Zheng et al. [11] to overcome the imbalanced issues of encrypted traffic. However, in these existing approaches, either the data privacy or the value of the user data was not taken into consideration.

It is challenging to optimize the classification accuracy while effectively taking the data privacy and data value into consideration in a distributed system. As each user node in a distributed network system has a limited amount of data for model training, the classification accuracy may be limited due to the insufficient training data at the node. Data sharing among nodes can be employed to enlarge the training dataset and improve classification accuracy. However, such data sharing gives rise to data privacy leakage, which is of great importance for many security-sensitive IoT applications. In this work, we propose an efficient Blockchain-based ID3 Decision Tree Classification (BIDTC) framework to take data sharing and the quality of shared data into consideration during the classification process. The proposed BIDTC employs a blockchain-based distributed storage and fully homomorphic encryption scheme for data sharing among the distributed nodes. By adopting the blockchain-based data federation classification and the smart contract-based stimulation scheme, the proposed BIDTC allows an individual node to have an enlarged training dataset in the distributed environment. As the decision tree-based classification is widely adopted and requires a short training time for knowledge acquisition in various applications [12,13], the proposed BIDTC integrates the decision tree-based classification with the blockchain-based scheme.

The organization of the rest of the paper is as follows. The related literature is summarized in Section 2. Section 3 proposes a blockchain-based data sharing architecture for training the classification model. A blockchain-based ID3 decision tree classification algorithm for the distributed environment is presented in Section 4. Experimental evaluations and the analysis of the results are presented in Section 5. Finally, Section 6 concludes the paper.

2  Related Work

The related work is summarized in this section, which mainly includes the literature work in the decision tree-based classification, fully homomorphic encryption, and blockchain technologies.

2.1 Decision Tree-based Classification

The decision tree technique is widely used in data analysis and prediction [14–21]. For example, in [16], the C4.5 decision tree algorithm is applied to achieve precision marketing prediction. The C5.0 decision tree classifier is proposed in [17] for the general and Medical dataset, in which the Gain calculation function is modified by adopting the Tsallis entropy function. A service decision tree-based post-pruning prediction approach is proposed to classify the services into the corresponding reliability level after discretizing the continuous attribute of services in service-oriented computing [18]. The ID3 is one of the standard algorithms for the decision tree learning process, which calculates the entropy to select the condition attributes [19–21].

2.2 Fully Homomorphic Encryption

Several privacy-involved machine learning classification has been proposed recently [22,23]. For example, fully homomorphic encryption (FHE) is proposed for classification without leaking user privacy, especially in the outsourcing scenarios of the distributed environment [24]. An ElGamal Elliptic Curve (EGEC) Homomorphic encryption scheme for safeguarding the confidentiality of data stored in a cloud is proposed in Vedara et al. [25]. In Ren et al. [26], a practical homomorphic encryption scheme is proposed to allow the IoT systems to operate encrypted data. A privacy-preserving distributed analytics framework is presented for big data in the cloud by using the FHE cryptosystem [27]. In order to reduce the excessive interactions and ciphertext transformation, the work in Smart et al. [28] proposed the SIMD to improve the efficiency of homomorphic operations by encrypting multiple small plaintexts into a ciphertext. In [29], a private decision tree classification algorithm with SIMD-based fully homomorphic encryption is proposed.

2.3 Blockchain

The blockchain is a distributed ledger database and has attracted much recent attention in the academic community [30]. The blockchain paradigm takes advantage of key technologies such as peer-to-peer networking, the distributed ledger, the consensus mechanism, and the smart contracts, which has many applications in fields such as Internet of Things (IoT), finance, and manufacture [31]. In Wang et al. [32], a blockchain-powered parallel healthcare system (PHS) framework is proposed to support comprehensive healthcare data sharing and care auditability. A blockchain-based framework for supply chain provenance is proposed in Cui et al. [33], and the analysis for this framework is performed to ensure its security and reliability. A theoretical framework for trust in IoT scenarios and the blockchain-based trust provision system are investigated in Bordel et al. [34]. The blockchain technique is deployed to create a secure and reliable data exchange platform across multiple data providers in Nguyen et al. [35]. In Wang et al. [36], a blockchain-based data secure storage mechanism for sensor networks is proposed. The blockchain-based privacy-aware content caching in cognitive Internet of vehicles is presented in Qian et al. [37], in which the privacy protection and secure content transaction are examined.

3  Data Sharing for Classification

The dataset owned by a single node in a distributed system is usually limited and insufficient for training a classification model with high accuracy. In order to improve the classification accuracy, data sharing among nodes is needed. In addition, both the value and the privacy of the shared data are of great importance in the applications such as healthcare and finance. To jointly take the data sharing, data privacy, and the value of data into consideration, we propose a blockchain-based data sharing architecture for classification, as shown in Fig. 1.

Figure 1: The architecture of the blockchain-based data sharing

There are double chains and different types of nodes in the proposed data sharing architecture. As shown in Fig. 1, a node in the blockchain network can be a data provider, data requestor, storage server, or ledgering node. The data providers in the blockchain network can share valuable data with encryption throughout the whole network. The sharing procedure will be recorded by the ledgering node and finally be written into the corresponding blockchain. If one of the data requestors demands more training datasets to improve the classification accuracy, it can send the request message to a storage server in the blockchain network. As a result, better performance of classification can be achieved by data requestors, and the financial profits can be obtained by data providers when the predefined blockchain-based smart contracts are executed, as shown in Fig. 1.

3.1 Double Blockchains

In the proposed blockchain-based data sharing architecture, the consortium chain is employed to store and share the training datasets among multiple nodes in the blockchain network. The data in the consortium chain is mainly from several related nodes such as institutions or companies [38]. In Fig. 1, we propose double blockchains according to the various transactions in the system. One chain for Transaction I is used to store the block data and share the encrypted data by data providers. The other chain is for Transaction II, which is used to store the block data for improving the classification performance by enlarging the volume of the related training dataset. The chain with Transaction II enables some nodes to make financial profits through the blockchain-based pre-negotiated smart contracts between the data providers and the data requestors.

3.2 Roles of Node

As shown in Fig. 1, every node in the consortium blockchain network has one or multiple roles: data provider, data requestor, storage server, or ledgering node. The data provider needs to encrypt the plaintext data M to generate ciphertext data C, then upload the ciphertext file and the corresponding encryption algorithm to a data storage server. At the same time, the data provider can obtain the download address of the file and calculate the hash value of ciphertext data to verify the data integrity. The access policies for the uploaded data can be defined by data providers. The data owned by data providers can be packed as a transaction and added to a blockchain (after the confirmation by ledgering nodes in the focused consortium blockchain network). Note that the storage server is not a physical centralized storage node/device. It can be a virtual/logic node like cloud-based storage existing in the consortium blockchain network.

The data requestors can issue a request to the ledgering nodes for some shared data. The ledgering nodes verify the different identities of access policies corresponding to the requested data. Once approved, the data requestors can download the requested encrypted data from the storage servers and train the classification models on the federated training datasets. In the meantime, the smart contracts for the transactions associated with data sharing between the data requestors and the data providers can be executed automatically.

3.3 Data Storage and Sharing

Each node that has valuable data can obtain some rewards from data sharing. The implementation process requires two phases associated with the two chains of the blockchain network. In phase I, the data providers share their valuable encrypted data to the storage servers. Such sharing is recorded and validated by the ledgering nodes running the consensus algorithm. The data requestors can then issue requests for specific shared data and receive the shared data along with the encryption algorithm after authentication. In phase II, the data requestors encrypt their local data using the obtained encryption algorithm and federate the obtained encrypted training data with their local encrypted data, then train the classification models on the newly federated training data. Correspondingly, the data requestors will pay the predetermined electronic currency to the data providers according to the blockchain-based smart contracts.

4  Blockchain-based Improved ID3 Decision Tree Classification

In this section, we present a new Blockchain-based ID3 Decision Tree Classification (BIDTC) framework for the blockchain-based data sharing architecture. The proposed BIDTC takes into account the relation between the current condition attributes, the other condition attributes in the learning process, and the stimulation mechanism in smart contracts.

4.1 An Improved ID3 Decision Tree Classification

The original ID3 classification algorithm only takes the current condition attributes and decision attributes into consideration during the process of calculating the gain. Here, we present an improved ID3 algorithm to take advantage of all the attributes from the system that includes the relationship between the current condition attributes and the other condition attributes. In specific, we denote A = (A1,A2,…,AN) as a set of N conditions attributes with values of (R1,R2,…,RN) , respectively. Assuming that the occurrence of attribute Ai (i = 1, 2, …, N) is Ni , the frequency of Ai can be defined as below.

F(Ai)=NiN (1)

Then the weight of the attribute Ai can be calculated as Eq. (2).

WAi=F(Ai)∑i=1N⁡F(Ai) (2)

Assume that Ỷ is a decision attribute with M possible values RY=(Ỷ1,Ỷ2,…,ỶM) , Ai (i=1, 2, …, N) has Ui possible values, and Ri is set as Ri∈{1,2,…,N}=(a1,a2,…,aUi) . Then, the relationship degree between the condition attribute Ai and the decision attribute Ỷ can be defined as Eq. (3).

RD(Ai,Ỷ)=∑k=1Ui⁡||Akj|−∑j=2M⁡|Akj||Ui (3)

The |Akj| in Eq. (3) is the number of instances that the k-th value of Ai belongs to the j-th class of decision attribute Ỷ. According to Eq. (3), we can calculate the weighted degree as Eq. (4).

WRD(Ai,Ỷ)=RD(Ai,Ỷ)∑i=1N⁡RD(Ai,Ỷ) (4)

Assuming that the training data samples are in S={(xi,Ỷi)|xi∈R1∗R2∗…∗RN,Ỷi∈Ry´} , where xi has a corresponding output class label Ỷi . Let Pj be the percentage of training samples belonging to the class j of decision attribute Ỷ . Then, the class involved entropy E(Ỷ) for the attribute Ỷ is defined as follows.

E(Ỷ)=−∑j=1M⁡Pj∗log2Pj (5)

Similarly, the condition entropy E(Ỷ|Ai) for each attribute Ai can be defined in Eq. (6).

E(Ỷ|Ai)=∑k=1Ui⁡E(Ỷ|ak)=−∑k=1Ui⁡(∑j=1M⁡Pkj∗log2Pkj) (6)

Therefore, the formula of calculating the information gain of the condition attribute Ai can be defined as follows.

Gain(Ỷ|Ai)=E(Ỷ)−E(Ỷ|Ai) (7)

The ID3 decision tree algorithm starts with the dataset at the root node and recursively partitions the data into lower-level nodes based on the split criterion. Only nodes that contain multiple different classes need to be split further. Eventually, the decision tree-based algorithm stops the growth of the tree based on a certain stopping criterion. We can set two stopping criteria for the algorithm. The criterion I is whether all samples in the training dataset are labeled as a single class or not. Criterion II is whether the attribute set A is empty (or all attribute values of S are the same) or not. Accordingly, we propose an improved blockchain-based ID3 decision tree algorithm as the following steps.

Step 1. Check the stopping Criteria I and II. If Criterion I is true, mark the current node as a class Ỷ leaf node; if Criterion II is true, mark the Tree as a leaf and set the most common value of Y´ in S as the label. Otherwise, go to step 2.

Step 2. Calculate the information gain Gain(Ỷ|Ai) of each condition attribute Ai according to Eq. (7); and set the parameter sW =0 and pW =0. For attribute value ai∈Ri , calculate the weight of each attribute using the training set Si of each value ai .

Step 3. For attribute values in Aj∈A∖{Ai} , calculate the relationship degree using Eq. (3) and calculate the weighted relationship degree as Eq. (4). Then the new value of pW is obtained as: pW←pW∗WRD(Aj,Ỷ) and the new value of sW is set: sW←sW+|Si||S|∗pW . The value of the comprehensive information gain can be achieved as: Gain(Ỷ|Ai)←Gain(Ỷ|Ai)∗sW.

Step 4. Determine the best splitting attribute Abest that has the maximum comprehensive information gain: Abest←arg⁡maxAGain(Ỷ|A) , and go to Step 1.

4.2 Enhanced Homomorphic Encryption

To consider both privacy and efficiency, we adopt the vector homomorphic encryption (VHE) method [39] for the proposed BIDTC framework. Assuming that the data requestor and the data provider are denoted as R and P , respectively, we present the setup, training, and classification processes of BIDTC as follows.

Phase 1. P.Setup(λ,Dt) : The data providers identify the security parameter λ and the training data Dt,(t=1,2⋅⋅⋅) , where t represents the sequence number of the transferring data. With the key generation algorithm KeyGen(λ) , the data providers obtain the VHE public, private keys, and the H matrix. The data providers will encrypt the Dt (Dt={x1t,x2t,⋅⋅⋅,xnt}) to Dt′(Dt′={c1t,c2t,⋅⋅⋅,cnt}) by using the encryption algorithm Encrypt(pk,xi) . Then, the data providers send the Encrypt(pk,xi) , Dt′ and matrix H to the corresponding storage servers.

Phase 2. R.Training_Classifier_ID3(D∪′) : The data requestors encrypt the local dataset D to D′ by using the encryption algorithm Encrypt(pk,xi) , which will be combined with the received dataset Dt′ to generate a new dataset D∪′ . Then the classification model will be trained by performing the improved ID3 algorithm on the federated training dataset D∪′ .

Phase 3. R.Testing_ID3(VD′) : The data requestors encrypt the local testing dataset VD={x1,x2,⋅⋅⋅,xm} to obtain the encrypted testing dataset VD′={c1,c2,⋅⋅⋅,cm} by using the same encryption operations as mentioned above. The classification accuracy will be calculated by the data requestors when completing the classification task on the testing dataset VD′ .

4.3 Stimulation Scheme with Smart Contract

In this section, we develop a stimulation scheme with smart contracts for the proposed BIDTC framework.

In the blockchain network, the transactions in a smart contract can be executed automatically, and the corresponding inputs, outputs, and states affected by executing the smart contracts are negotiated and agreed on by all participating nodes [40,41]. Here, we propose a stimulation scheme to incentivize the providers to share more valuable data. For each transaction of data sharing, there are two types of transaction fees: basic transaction fee and additional transaction fee. We assume that the basic transaction fee the data providers can receive from the data requestors is Δ ethers. The additional transaction fee depends on the percentage increase of the classification accuracy due to the data sharing. Let Δacc denote the percentage increase of the classification accuracy between the original classification model and the newly constructed one (i.e., after the data sharing). If the Δacc>0 , then the data requestors will pay an additional transaction fee to the data providers, according to Tab. 1. If the classification accuracy is not increased when comparing with the original model, the data requestors will not pay an additional transaction fee to the data providers for the data sharing.

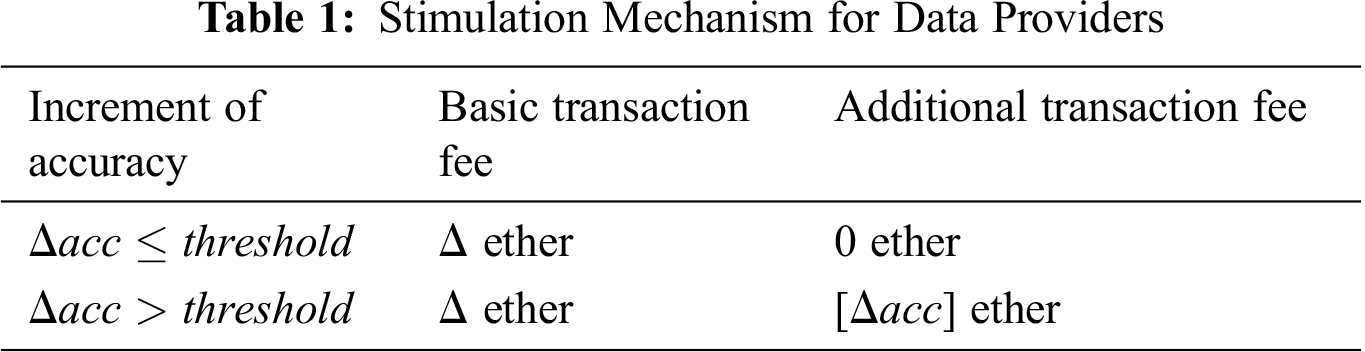
The higher quality of the data shared by the providers, the better classification accuracy, and the more financial profits the data providers can obtain during the procedure of the sharing of the training data. Therefore, the data providers in various blockchain networks have incentives to share more valuable datasets.

4.4 The Proposed BIDTC Framework

The proposed Blockchain-based ID3 Decision Tree Classification (BIDTC) framework takes advantage of three techniques: blockchain-based ID3 decision tree, enhanced homomorphic encryption, and stimulation smart contract to conduct the classification in the distributed environment while effectively considering the data privacy and the value of the user data. Fig. 2 shows the overall process of the proposed BIDTC framework, whose primary operations are listed below.

     i)  The distributed blockchain network is set up, and the Ethereum-based consortium chains are constructed. The distributed blockchain network consists of a large number of data providers, the ledgering nodes, and the data requestors.

    ii)  The data providers encrypt their local training data by using the vector homomorphic encryption, then upload the encrypted data to a storage server in the blockchain network. The ledgering nodes with the consensus algorithm can validate the transactions involved with sharing data. All the transactions will be stored in the consortium chain.

   iii)  The data requestors train the local training dataset with the ID3-based algorithm and obtain a classification model. This model is then validated on the testing dataset, and the accuracy (say acc0 ) is obtained. The data requestors can then issue requests to the blockchain network for more shared training data. With the authentication by the ledgering nodes, the data requestors can receive the encrypted training data shared by the providers. At the same time, a smart contract is bounded between the data providers and the corresponding data requestors. Once receiving the encrypted training data, the data requestors encrypt the local training data by using the same encryption scheme from the data providers, federate it with the received encrypted training dataset and perform the improved ID3 algorithm to obtain a new classification model and accuracy (say acc1 ).

    iv)  The smart contracts and the stimulation scheme will be triggered when the accuracy difference: Δacc=acc1−acc0 is above a certain threshold.

Figure 2: The flow diagram of the proposed blockchain-based scheme

5  Performance Evaluation

In this section, we conduct simulations to validate the proposed blockchain-based BIDTC framework and analyze the performance.

5.1 Experiment Settings

We simulated the blockchain-based BIDTC network with Python 3.7. The simulation platform is built on a machine with Ubuntu 16.04 LTS, Intel Core 3.40 GHz i5-8250U CPU, and 8.0 GB of RAM. In the consortium blockchain network, each node is deployed based on the Geth 1.7.2 (Go Ethereum). The configuration file genesis. json includes the identifier of the chain id , the random number nounce , and the timestamp . The Remix-based coding and testing for smart contracts are implemented in a browser-based IDE environment. The account address, the balance, and the indexes of datasets are defined in the structs, as shown in Fig. 3.

Figure 3: The illustration of the deployment for blockchain-based smart contracts

We carry out the experiments using the MNIST dataset [42]. We set 60000 samples as the training dataset and 10000 samples as the testing dataset. The training dataset is further divided into four equal parts and stored in four random nodes, namely, Node A , Node B , Node C , and Node D .

5.2 Experimental Results

As the data privacy is built-in encrypted data sharing, here, we focus on evaluating the accuracy and speed of the proposed BIDTC. The confusion matrix includes True Positives ( TP ), True Negatives ( TN ), False Positives ( FP ), and False Negatives ( FN ). The TP represents the sample that is actually positive and predicted to be positive; the TN represents the sample that is actually negative and predicted to be negative; the FP represents the sample that is actually negative and predicted to be positive; and the FN represents the sample that is actually positive and predicted to be negative. If there are M classes, we can calculate the classification accuracy according to the following formula.

AC=∑i=1MTPi+TNiTPi+FNi+TNi+FPiM (8)

As Eq. (8) shows, the classification accuracy AC equals the rate between all the true classified samples and all the classified samples in the corresponding testing dataset. The speed of the classification can be measured based on the time consumed in training the model and classifying the testing samples.

5.2.1 Classification Accuracy versus Data Volume

Fig. 4 shows the classification accuracy for the four random nodes. From Fig. 4, we can see that the classification accuracy of all four nodes is improved significantly when increasing their training data volume. The initial values of the classification accuracy of the four nodes are different in Fig. 4. Specifically, Fig. 4a has the maximum accuracy of 0.84, and Fig. 4b has the minimum accuracy of 0.8. This is because the quality of the training dataset in Node A is the highest among the four nodes, while Node B has the worst data quality. We use Qi to denote the dataset quality of Node i . The quality relationship among the four nodes: QA>QD>QC>QB is further verified in Fig. 5, where each node works as a data requestor and federates more training data from the other three data providers. From Fig. 5, we can see that the classification accuracy improves as the amount of the data federation increases, and the nodes with high-quality datasets can achieve a greater gain of the classification accuracy.

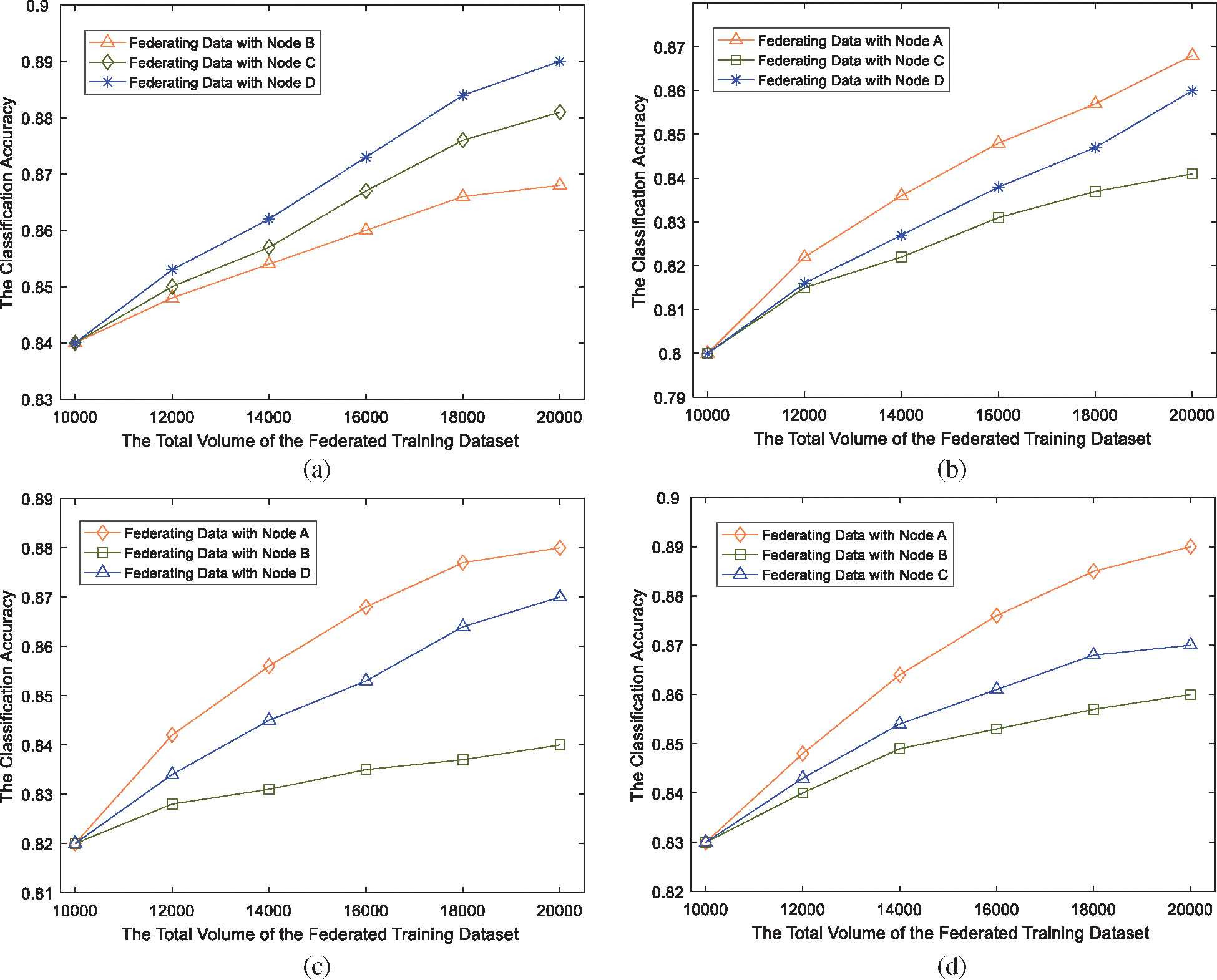
Figure 4: The classification accuracy of BIDTC when varying the data volume

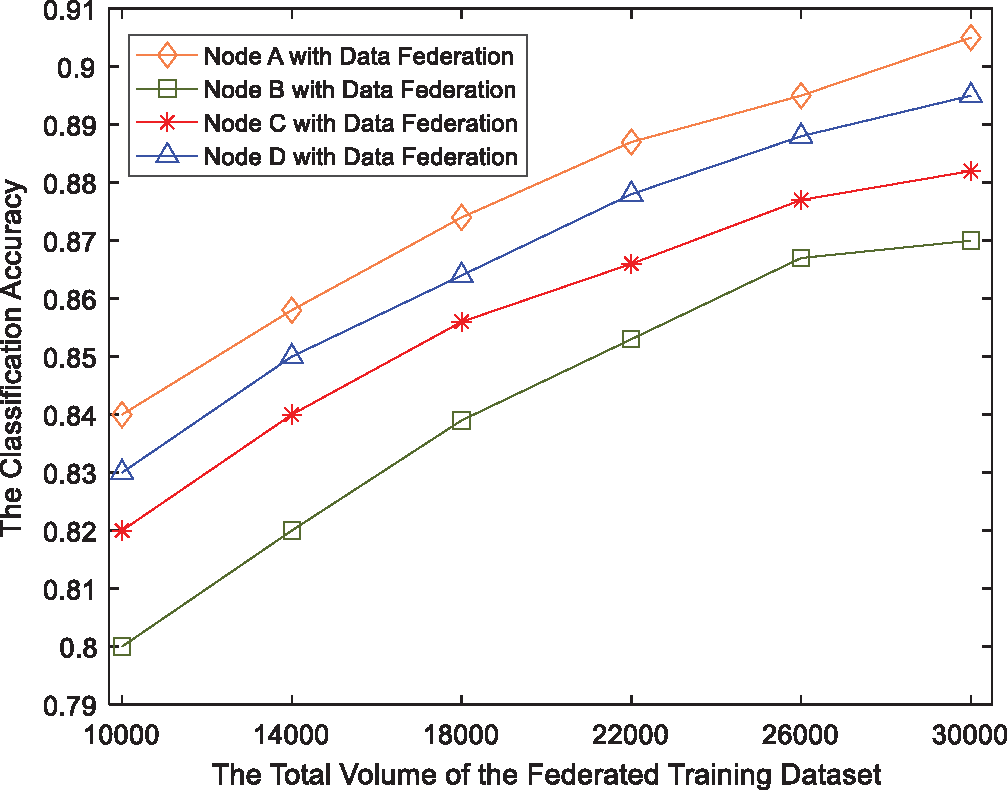
Figure 5: The trends of classification accuracy by BIDTC with multiple nodes

5.2.2 Classification Accuracy versus Data Quality

Eq. (9) is defined to measure the quality of the training dataset, where NS(i) is the total number of samples in the training dataset of Node i , and NSe(i) is the number of low-quality samples in the training dataset of Node i . The sample with the blurry picture or an incorrect class label in the training dataset can be marked as a low-quality sample.

Qi=1−NSe(i)NS(i) (9)

In this experiment, we uniformly select 10% of the original MNIST training dataset from each class and replace their class with random integer numbers in the range of 0~9. As a result, we obtain 6000 low-quality training samples, denoted by LQ . For each network node, when the volume of training data reaches a threshold Θ, we add some low-quality training samples into the corresponding nodes. For example, when the volume of the federated training data in Node A reaches 20000, we gradually add 0%~20% of low-quality training samples from LQ into its training dataset. Fig. 6 shows the experiment results when setting Θ as 104, 2*104, and 3*104. We can see that Fig. 6a has the maximum initial accuracy of 0.79 when the data volume amounts to 30000. Fig. 6b has the minimum initial accuracy of 0.66 when the data volume amounts to 10000. This is due to the fact that the initial data quality of the training dataset in Node A is highest while the one in Node B is the lowest. Again, we can see that for a given node, the classification accuracy improves significantly when increasing the training dataset volume. In addition, the better training data quality will result in higher classification accuracy from BIDTC.

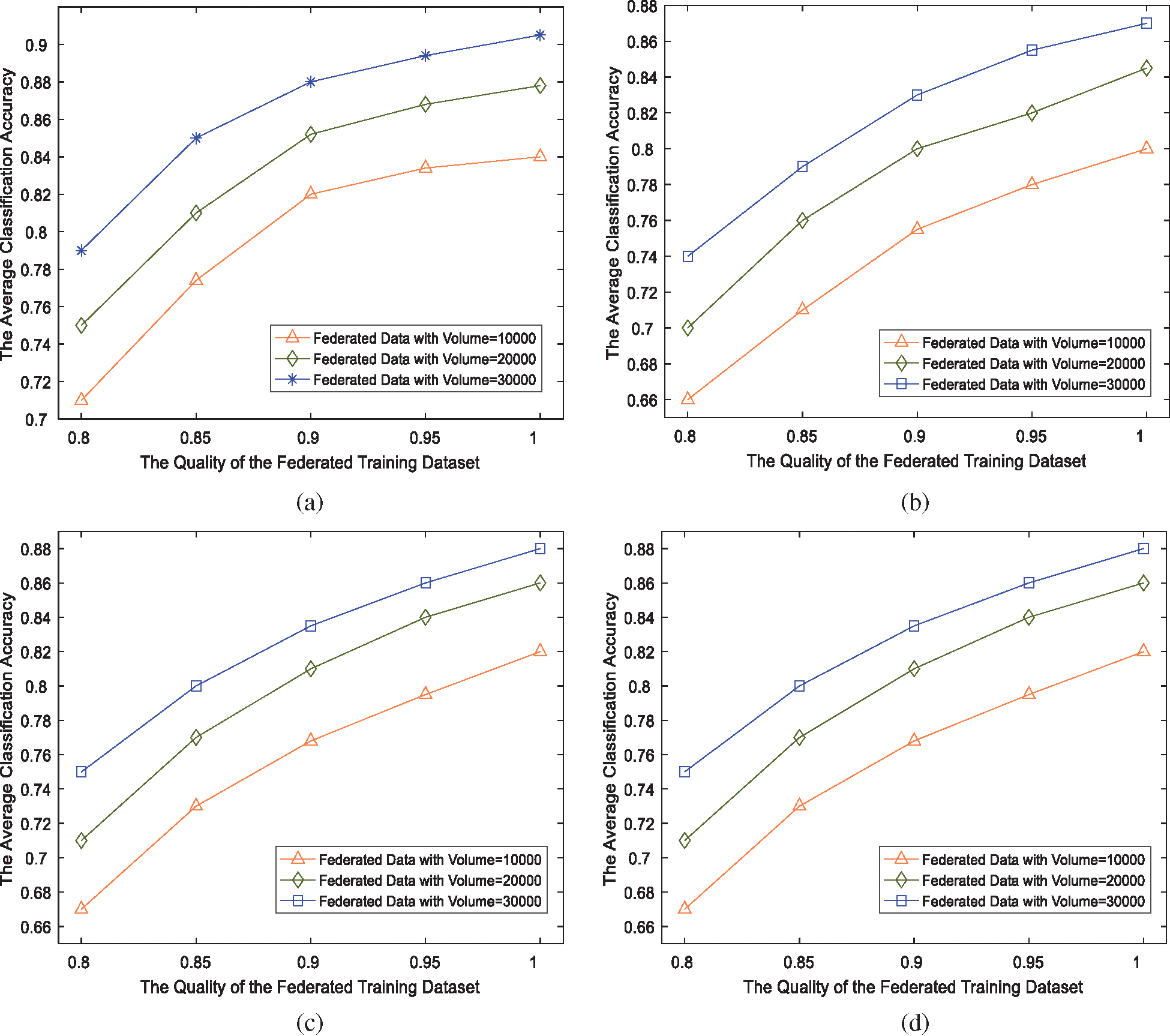
Figure 6: The classification accuracy versus training data quality

5.2.3 Comparing BIDTC with Traditional Classification Algorithms

In this experiment, we compare the proposed BIDTC algorithm with the existing algorithms, including the original ID3 algorithm (OIDA), the Neural Networks algorithm (NNA) [43], and the Random Forest algorithm (RFA) [44]. Without loss of generality, we generate a dataset based on the MNIST and argument it with low-quality samples from LQ such that the average quality level is 0.9. The volume of the initial training dataset is 10000 in each node, while the volume of the testing dataset is 2000. Tab. 2 shows the running time and accuracy of all algorithms in the same distributed network environment.

From Tab. 2, we can see that the running time of both the OIDA and the BIDTC is smaller than that of NNA and RFA, at the cost of slight accuracy loss. Here we define the average classification efficiency for K nodes in Eq. (10), where the CE is the average value of classification efficiency; the ACi is the classification accuracy of the node i and the CTi is the corresponding classification running time of node i .

CE=100×∑i=1KACiCTiK (10)

Fig. 7 shows how the classification efficiency CE varies when increasing the volume of the training datasets from 104 to 3*104. From Fig. 7, we can see that the average classification efficiency of the BIDTC is significantly higher than the other three algorithms. This is because the proposed BIDTC can take advantage of the three techniques: blockchain-based ID3 decision tree, enhanced homomorphic encryption, and stimulation smart contract to effectively conduct classification in the distributed environment.

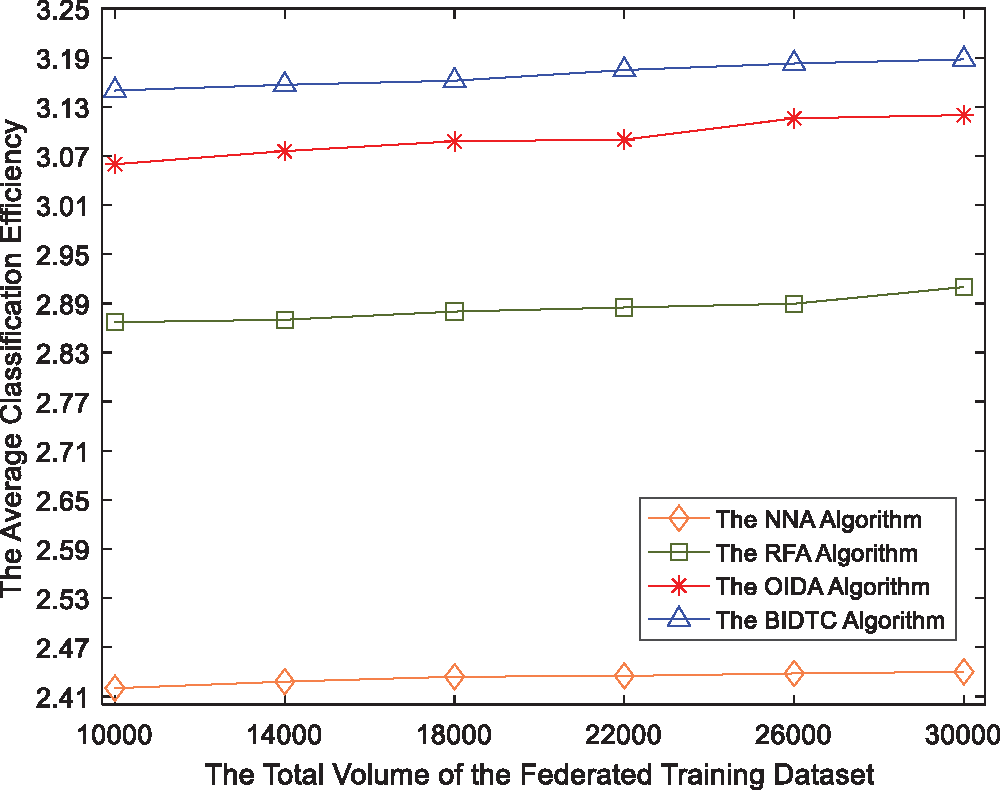
Figure 7: The classification efficiency from different algorithms

6  Conclusion and Future Direction

In this work, we have proposed a Blockchain-based improved ID3 Decision Tree Classification (BIDTC) algorithm for the distributed environment. The proposed BIDTC takes advantage of three techniques: blockchain-based ID3 decision tree, enhanced homomorphic encryption, and stimulation smart contract to conduct classification while effectively considering the data privacy and the value of the user data. The proposed BIDTC employs the proposed blockchain-based data sharing architecture to enlarge the volume of the training datasets, which is coupled with a smart contract-based stimulation scheme to enhance the quality of the training data. Our extensive experiments have shown that our algorithm significantly outperformed the existing techniques in terms of classification efficiency. In the future, we will explore how to improve the performances of the proposed algorithm for online data with high dimensions.

Acknowledgement: The authors would like to thank the anonymous reviewers of the manuscript for their valuable feedback and suggestions.

Funding Statement: This work was in part supported by the National Natural Science Foundation of China under Grant 11471110, the Scientific Research Fund of Hunan Provincial Education Department of China under Grant 20C1143, Hunan Province’s Strategic and Emerging Industrial Projects under Grant 2018GK4035, Hunan Provincial Science and Technology Project Foundation under Grant 2018TP-1018 and Hunan Province’s Changsha Zhuzhou Xiangtan National Independent Innovation Demonstration Zone projects under Grant 2017XK2058.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Sandryhaila and J. M. Moura, “Big data analysis with signal processing on graphs: Representation and processing of massive data sets with irregular structure,” IEEE Signal Processing Magazine, vol. 31, no. 5, pp. 80–90, 2014. [Google Scholar]

 2.  V. Cherkassky and F. M. Mulier, “Learning from data: Concepts, theory, and methods," in John Wiley & Sons, 2nd ed., New Jersey, USA, pp. 15–18, 2007. [Online]. Available: https://media.wiley.com [Google Scholar]

 3.  C. C. Aggarwal, “Data ming,” IBM Watson Research Center, New York, USA: York-town Heights, pp. 285–292, 2015. [Online]. Available at: https://link.springer.com. [Google Scholar]

 4.  A. Jain, R. Duin and J. Mao, “Statistical pattern recognition: A review,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 22, no. 1, pp. 4–37, 2000. [Google Scholar]

 5.  C. Aggarwal, Data classification: Algorithms and applications. CRC Press, 2014. [Google Scholar]

 6.  H. H. Ang, V. Gopalkrishnan, I. Žliobaitė, M. Pechenizkiy and S. C. Hoi, “Predictive handling of asynchronous concept drifts in distributed environments,” IEEE Transactions on Knowledge and Data Engineering, vol. 25, no. 10, pp. 2343–2355, 2013. [Google Scholar]

 7.  M. U. Khan, A. Nanopoulos and L. Schmidt-Thieme, “P2P RVM for distributed classification,” Data Science, Learning by Latent Structures, and Knowledge Discovery. Berlin Heidelberg: Springer, 2015. [Google Scholar]

 8.  Z. Xu, Y. Zhai and Y. Liu, “Distributed semi-supervised multi-label classification with quantized communication,” in Proc. of the 12th Int’l Conf. on Machine Learning and Computing, Shenzhen, China, pp. 57–62, 2020. [Google Scholar]

 9.  L. Vu, H. V. Thuy, Q. U. Nguyen, T. N. Ngoc and E. Dutkiewicz, “Time series analysis for encrypted traffic classification: A deep learning approach,” in Proc. of the 18th Int’l Sym. on Communications and Information Technologies (ISCITBangkok, pp. 121–126, 2018. [Google Scholar]

10. S. Rezaei and X. Liu, “Deep learning for encrypted traffic classification: An overview,” IEEE Communications Magazine, vol. 57, no. 5, pp. 76–81, 2019. [Google Scholar]

11. W. Zheng, C. Gou, L. Yan and S. Mo, “Learning to classify: A flow-based relation network for encrypted traffic classification,” in Proc. of the Web Conf. 2020, Taipei, China, pp. 13–22, 2020. [Google Scholar]

12. Q. Hu, X. Che, L. Zhang, D. Zhang and M. Guo, “Rank entropy-based decision trees for monotonic classification,” IEEE Transactions on Knowledge and Data Engineering, vol. 24, no. 11, pp. 2052–2064, 2012. [Google Scholar]

13. S. Patil and U. Kulkarni, “Accuracy prediction for distributed decision tree using machine learning approach,” in Proc. of the 2019 3rd Int’l Conf. on Trends in Electronics and Informatics (ICOEITirunelveli, India, pp. 1365–1371, 2019. [Google Scholar]

14. F. Es-Sabery and A. Hair, “An improved ID3 classification algorithm based on correlation function and weighted attribute*,” in Proc. of the 2019 Int’l Conf. on Intelligent Systems and Advanced Computing Sciences (ISACSTaza, Morocco, pp. 1–8, 2019. [Google Scholar]

15. R. Choudhary and M. Kapoor, “Optimal tree led approach for effective decision making to mitigate mortality rates in a varied demographic dataset,” in Proc. of the 3rd Int’l Conf. on Internet of Things: Smart Innovation and Usages (IoT-SIUBhimtal, pp. 1–5, 2018. [Google Scholar]

16. Y. Zheng, “Decision tree algorithm for precision marketing via network channel,” Computer Systems Science and Engineering, vol. 35, no. 4, pp. 293–298, 2020. [Google Scholar]

17. K. V. Uma and A. Alias, “C5.0 decision tree model using tsallis entropy and association function for general and medical dataset,” Intelligent Automation & Soft Computing, vol. 26, no. 1, pp. 61–70, 2020. [Google Scholar]

18. Z. Jia, Q. Han, Y. Li, Y. Yang and X. Xing, “Prediction of web services reliability based on decision tree classification method,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1221–1235, 2020. [Google Scholar]

19. H. Xiao and M. Wei, “An early warning method for sea typhoon detection based on remote sensing imagery,” Journal of Coastal Research, vol. 82, no. sp1, pp. 200–205, 2018. [Google Scholar]

20. S. Yang, J. Z. Guo and J. W. Jin, “An improved Id3 algorithm for medical data classification,” Computers & Electrical Engineering, vol. 65, no. 4, pp. 474–487, 2018. [Google Scholar]

21. S. Kraidech and K. Jearanaitanakij, “Reducing the depth of ID3 algorithm by combining values from neighboring important attributes,” in Proc. of the 22nd Int’l Computer Science and Engineering Conf. (ICSECChiang Mai, Thailand, pp. 1–5, 2018. [Google Scholar]

22. R. Bost, R. A. Popa, S. Tu and S. Goldwasser, “Machine learning classification over encrypted data,” Cryptology ePrint Archive, Report 2014/331, 2014, http://eprint.iacr.org. [Google Scholar]

23. X. Liu, R. Lu, J. Ma, L. Chen and B. Qin, “Privacy-preserving patient-centric clinical decision support system on Naive Bayesian classification,” IEEE Journal of Biomedical and Health Informatics, vol. 20, no. 2, pp. 655–668, 2016. DOI 10.1109/JBHI.2015.2407157. [Google Scholar] [CrossRef]

24. J. Bajard, P. Martins, L. Sousa and V. Zucca, “Improving the efficiency of SVM classification with FHE,” IEEE Transactions on Information Forensics and Security, vol. 15, pp. 1709–1722, 2020. DOI 10.1109/TIFS.2019.2946097. [Google Scholar] [CrossRef]

25. M. Vedara and P. Ezhumalai, “Enhanced privacy preservation of cloud data by using ElGamal Elliptic Curve (EGEC) homomorphic encryption scheme,” KSII Transaction on Internet and Information Systems, vol. 14, no. 11, pp. 4522–4536, 2020. [Google Scholar]

26. W. Ren, X. Tong, J. Du, N. Wang and A. K. Bashir, “Privacy-preserving using homomorphic encryption in Mobile IoT systems,” Computer Communications, vol. 165, no. 1, pp. 105–111, 2021. DOI 10.1016/j.comcom.2020.10.022. [Google Scholar] [CrossRef]

27. A. Alabdulatif, I. Khalil and X. Yi, “Towards secure big data analytic for cloud-enabled applications with fully homomorphic encryption,” Journal of Parallel and Distributed Computing, vol. 137, no. 3, pp. 192–204, 2020. DOI 10.1016/j.jpdc.2019.10.008. [Google Scholar] [CrossRef]

28. N. P. Smart and F. Vercauteren, “Fully homomorphic SIMD operations,” Designs Codes Cryptography, vol. 71, no. 1, pp. 57–81, 2014. DOI 10.1007/s10623-012-9720-4. [Google Scholar] [CrossRef]

29. X. Sun, P. Zhang, J. K. Liu, J. Yu and W. Xie, “Private machine learning classification based on fully homomorphic encryption,” IEEE Transactions on Emerging Topics in Computing, vol. 8, no. 2, pp. 352–364, 2020. [Google Scholar]

30. Y. Yuan and F. Wang, “Blockchain and cryptocurrencies: Model, techniques, and applications,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 48, no. 9, pp. 1421–1428, 2018. DOI 10.1109/TSMC.2018.2854904. [Google Scholar] [CrossRef]

31. Y. Yu, Y. Li, J. Tian and J. Liu, “Blockchain-based solutions to security and privacy issues in the Internet of Things,” IEEE Wireless Communications, vol. 25, no. 6, pp. 12–18, 2018. DOI 10.1109/MWC.2017.1800116. [Google Scholar] [CrossRef]

32. S. Wang, J. Wang, X. Wang, T. Qiu, Y. Yuan et al., “Blockchain-powered parallel healthcare systems based on the ACP approach,” IEEE Transactions on Computational Social Systems, vol. 5, no. 4, pp. 942–950, 2018. [Google Scholar]

33. P. Cui, J. Dixon, U. Guin and D. Dimase, “A blockchain-based framework for supply chain provenance,” IEEE Access, vol. 7, pp. 157113–157125, 2019. [Google Scholar]

34. B. Bordel, R. Alcarria, D. Martin and A. Sanchez-Picot, “Trust provision in the internet of things using transversal blockchain networks,” Intelligent Automation & Soft Computing, vol. 25, no. 1, pp. 155–170, 2019. [Google Scholar]

35. B. L. Nguyen, E. L. Lydia, M. Elhoseny, I. V. Pustokhina, D. A. Pustokhin et al., “Privacy preserving blockchain technique to achieve secure and reliable sharing of IoT data,” Computers, Materials & Continua, vol. 65, no. 1, pp. 87–107, 2020. [Google Scholar]

36. J. Wang, W. Chen, L. Wang, R. S. Sherratt and A. Tolba, “Data secure storage mechanism of sensor networks based on blockchain,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2365–2384, 2020. [Google Scholar]

37. Y. Qian, Y. Jiang, L. Hu, M. S. Hossain, M. Alrashoud et al., “Blockchain-based privacy-aware content caching in cognitive Internet of vehicles,” IEEE Network, vol. 34, no. 2, pp. 46–51, 2020. [Google Scholar]

38. L. Zhu, H. Yu, S. Zhan, W. Qiu and Q. Li, “Research on high-performance consortium blockchain technology,” Journal of Software, vol. 30, no. 6, pp. 1577–1593, (in Chinese2019, http://www.jos.org.cn/1000-9825/5737.htm. [Google Scholar]

39. W. He, “Research on key technologies of privacy-preserving machine learning based on homomorphic encryption,” M.S. thesis, Dept. of Comp. Science & Eng., Univ. of Electronic Science and Technology of China, Chengdu, China, 2019. [Google Scholar]

40. X. Huang, D. Ye, R. Yu and L. Shu, “Securing parked vehicle assisted fog computing with blockchain and optimal smart contract design,” IEEE/ CAA Journal of Automatica Sinica, vol. 7, no. 2, pp. 426–441, 2020. [Google Scholar]

41. Z. Zheng, S. Xie, H. N. Dai, W. Chen and M. Imran, “An overview on smart contracts: Challenges, advances and platforms,” Future Generation Computer Systems, vol. 105, no. 5, pp. 475–491, 2020. [Google Scholar]

42. Y. LeCun and C. Cortes, MNIST Handwritten Digit Database. 2010. [Online]. Available at: http://yann.lecun.com/exdb/mnist. [Google Scholar]

43. M. M. A. Ghosh and A. Y. Maghari, “A comparative study on hand-writing digit recognition using neural networks,” in Proc. of the 2017 Int’l Conf. on Promising Electronic Technologies (ICPETDeir El-Balah, pp. 77–81, 2017. [Google Scholar]

44. A. More and D. Rana, “Review of random forest classification techniques to resolve data imbalance,” in Proc. of the 2017 Int’l Conf. on Intelligent Systems and Information Management (ICISIMAurangabad, pp. 72–78, 2017. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.