DOI:10.32604/iasc.2021.015009
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.015009 | |
| Article |
Evaluating and Ranking Mobile Learning Factors Using a Multi-criterion Decision-making (MCDM) Approach
1College of Computer Science, King Khalid University, Abha, 61413, Saudi Arabia
2Department of Computer Science, Bahria University Lahore Campus, Punjab, 54600, Pakistan
3College of Engineering, King Khalid University, Abha, 61413, Saudi Arabia
4Department of Software Engineering, University of Gujrat, Punjab, 50700, Pakistan
5College of Science & Arts Rejal Almah, King Khalid University, Abha, 62529, Saudi Arabia
*Corresponding Author: Ansar Siddique. Email: dr.ansarsiddique@uog.edu.pk
Received: 02 November 2020; Accepted: 28 February 2021
Abstract: The escalating growth in digital technology is setting the stage for changes in university education, as E-learning brings students and faculties outside the contained classroom environment. While mobile learning is considered an emerging technology, there is comprehensive literature on mobile learning and its applications. However, there has been relatively little research on mobile learning recognition and readiness compared to mobile learning studies and implementations. The advent of mobile learning (M-learning) provides additional flexibility in terms of time and location. M-learning lacks an established place in university education. The influence of its critical success factors (CSFs) on the university education system must be analyzed and understood. In the present study, decision-makers establish four dimensions which are further classified into 13 CSFs to evaluate and rank them. It is imperative to judge the most important CSFs and rank them according to their importance. To this end, multi-criteria decision-making (MCDM), like the fuzzy analytic hierarchy process (FAHP), is an important tool to establish the influence of each CSF. It identifies the four dimensions of M-learning by evaluation in a crisp and fuzzy environment. Global and local weights have been employed for ranking in a decision-making process to enable universities to choose the best adoption factor for mobile learning. The result establishes the influence of CSFs in M-learning success, in decreasing order, as the technological dimension (TD), individual/user dimension (ID), pedagogical dimension (PD), and social dimension (SD). A greater understanding of the mobile learning implementation process can allow researchers and decision-makers to collaborate to incorporate effective mobile learning strategies.
Keywords: Analytic hierarchy process; critical success actors; e-learning; fuzzy analytic hierarchy process; multi-criteria decision-making; m-learning; university education
With the sheer competition in the educational field across the globe, universities must use innovative techniques to outperform rivals and survive. It might not be enough to initiate mobile learning (M-learning) with the prevailing infrastructure (hardware and software) for the best results. Universities may also integrate their stakeholders in such a way that M-learning becomes successful. As the prime beneficiaries, students play a significant role in the success of E-learning. Hence, universities may concentrate on student involvement in successful M-learning by incorporating advanced technologies [1].
M-learning facilitates personalized learning, and it is on the rise. Many mobile services offer applications that tap into university systems [2]. With growing digital technology, M-learning finds a place in the learning management system (LMS). The growing use of smartphones in M-learning enables a mobile-learning management system (M-LMS) [2]. The M-LMS may be accessed through smartphones, which are commonly used by faculties and students. It provides a flexible teaching-learning environment free from many constraints of time, location, and system architecture, but the system’s strengths and weaknesses require analysis and improvement, and there is a need to study the critical success factors (CSFs) [3]. M-learning offers more flexibility and mobility than E-learning, with options regarding the learning location, time, and content, and offers a novel pedagogical approach. The technology acceptance model (TAM) [4] has confirmed the intention to use technology in teaching and learning, but the in-depth study is needed to determine the factors that might affect the acceptability of technology [5].
Factors such as computer auto-efficiency, environmental support, technical sophistication, and individual motivational factors play an important role [6]. Students using LMS based on E-learning or M-learning can easily provide continual assessments. However, more variables must be included, such as learning content quality [6,7] and trust [6]. Several studies indicate that while M-learning is slowly being adopted, its use is far from complete and adequate in universities, and it hardly keeps pace with mobile phone usage. Intense efforts are needed to understand this gap, and the present study of CSFs will help to fill it. The rise of E-learning will facilitate the adoption of M-learning. The present research aims to bridge the prevailing gaps to build a framework to identify and evaluate the CSFs of M-learning. The analysis will determine the influence of each factor. The literature offers many studies on multi-criteria decision-making with group decision-making (MCDM-GDM). The AHP may be incorporated to analyze and rank the CSFs of M-learning in a crisp and fuzzy environment. Based on the above discussion, the following objectives are set:
1. To provide a systematic literature review of M-learning CSFs.
2. To provide an MCMD-based model to analyze and rank CSFs of M-learning in a crisp and fuzzy environment.
The remainder of this paper is organized as follows. Section 2 provides a literature review of M-learning CSFs, the M-learning framework, and the MCDM approach. The research methodology is documented in Section 3. The application of AHP and Fuzzy AHP (FAHP) to evaluate and classify the CSFs of M-learning is discussed in Section 4. Section 5 provides results and discussion on the CSFs of M-learning. Section 6 identifies the limitations of our study, incorporates conclusions, and discusses future research directions.
Various studies have researched the use of mobile technology in education. M-learning is a mobile-based teaching and learning process delivered through wireless communication services. The users of the modern educational system strive to utilize mobile technology in teaching and learning, but M-learning must establish its place. M-learning uses mobile technology to access E-learning, which enables access through devices such as laptops, desktops, tablets, smartphones, and electronic readers. Numerous models examine the user’s intention and attitude toward the adoption of new technology, such as TAM [4], the theory of planned behavior (TPB) [8], innovation diffusion theory (IDT) [9], the unified theory of acceptance and use of technology (UTAUT) [10], and the mobile learning usage model [11]. The theory of reasoned action (TRA) [12] has become the fundamental model for analyzing the success factors of human behavior toward prospective technology acceptance [13]. CSFs must be determined in planning so that they can be addressed critically during execution. Adequate monitoring and calculating the best possible quality standards will help to enhance the overall performance of a system [14,15]. Mobile technology is witnessing a rising trend. Smartphones have various operating systems, such as Android or the iPhone operating system (iOS), and offer different programming languages. A study indicates a close association between IT expertise and a learner’s intention to accept M-learning. Mobile devices provide educators, learners, and organizations with many advantages [16], along with challenges when students do not see mobile devices as useful learning tools [17]. In developing mobile learning systems, extensive educational improvements are needed to ensure a greater understanding of the CSFs that affect the acceptability of a learning device [18]. Several CSFs are identified for this research study. These constitute the issues that any university must address for effective online teaching. These factors enable higher education institutions from Saudi Arabia to effectively implement an M-Learning strategy. The introduction of M-Learning will help to enhance the teaching-learning and research processes. In addition, these factors can be used to measure the success or failure of M-learning in higher-education institutions.
3 Framework for Mobile Learning Factors
Many researchers have investigated CSFs in the use of M-learning. A literature review, identified 18 CSFs, which were reduced to 13 for the present study. The decision-makers (DMs) formed four groups, called dimensions, and assigned the 13 CSFs to these groups. Fig. 1 shows the dimensions and the CSFs they contain. Tab. 1 shows the CSFs with the corresponding citations.
Pedagogy is the method of teaching and practice. It includes theoretical concepts of teaching style. CSFs such as trust, interactivity, and the quality of learning content have been grouped under the pedagogical dimension.
- Trust: A student’s willingness to trust the M-learning system is related to experience and usage. Studies show the impact of the trust and commitment of students as a critical factor for using the system [1,6].
- Interactivity: M-learning contributes to the achievement of the classical design in E-learning. M-learning combine social and environment-related issues and attempts to involve the students [19]. Studies show the impact of the interactivity of students and faculty as a critical factor in M-learning [6,20].
- Learning content quality: Studies show that content quality affects M-learning. An indirect effect is shown in the quality of supervision and relationships [21,22].
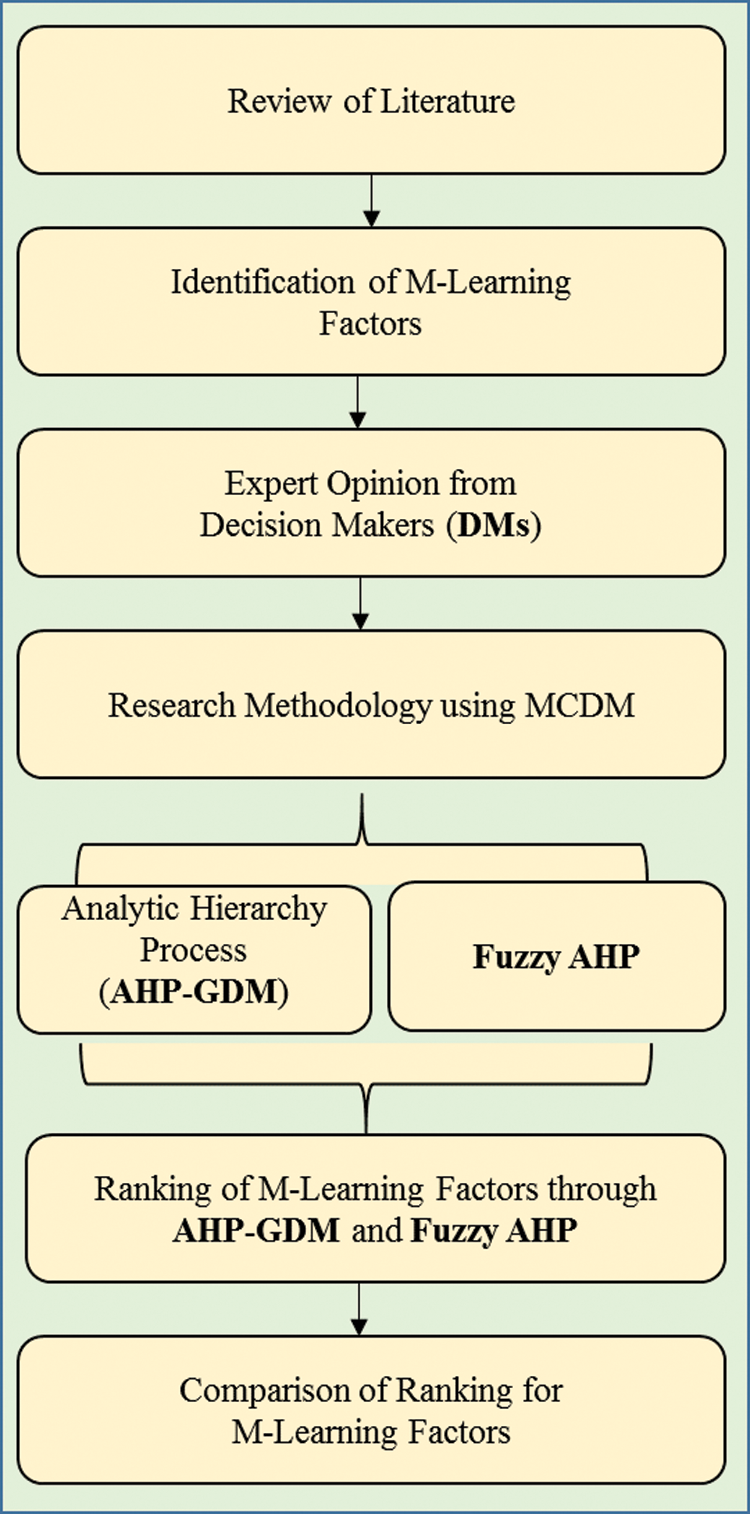
Figure 1: Research framework to evaluate and rank mobile learning factors
Technological factors influence and facilitate M-learning. The CSFs of facilitating conditions, user interface, and mobile device constraints have been grouped under the technological dimension. We discuss them further.
- Facilitating conditions: It is obvious that facilitating conditions help students to switch to M-learning [23–25].
- User interface: The user interface has a direct influence on M-learning. Several universities have adopted M-learning because of comfortable, user-friendly technology [6,21,25].
- Mobile device limitations: Studies show that M-learning usage is influenced by mobile device limitations, and this has a critical impact on student’s choice. Changes in digital technology require frequent device updates [6,26,27].
The social dimension of using M-learning is influenced by the surrounding people and their habits. CSFs like society influence, usefulness, and government and university support were grouped under this dimension.
- Society influence: social influence has a prime role in M-learning, and universities seek strategic competitive advantages in this area [28–30].
- Usefulness: This is a major factor in M-learning, as it dictates system usage. Usefulness criteria have a significant effect on M-learning outcomes [6,28,31,32].
- Government and university support: It is useful in the success of M-learning that will affect its usage policy and practices to influence its popularity.
- Personal innovation and enjoyment: Studies have investigated the influence of innovation and enjoyment on M-learning [30,33].
M-learning is also influenced by characteristics of the individual, such as attitude and lifestyle. The CSFs including attitude, self-efficacy, and behavioral intention were grouped under the individual/user dimension.
- Attitude: This is a crucial criterion, as it leads students and faculty toward the adoption of M-learning. Attitudes change among the faculty and students, and they affect the implementation and use of M-learning [25,34,35].
- Self-efficacy: This is an individual’s capacity to adopt a specific act and perform it in a specific manner to accomplish a defined goal. It empowers the individual to control one’s behaviors, motivation, and social environment. Thus it leads a person to become a goal achiever and motivates teaching, learning, and technology acceptance [35–37].
- Behavioral intention to adopt: To accept M-learning or M-LMS depends on one’s behavioral intention. Hence it is significant to study this criterion [24,38–40].
Table 1: M-learning dimensions and CSFs
AHP methodology is used to solve multi-faceted and multi-criteria problems, while FAHP is used to remove vagueness and bias from decision-making. Fuzzy-based methodology uses fuzzy set theory and the extension principle in decision-making.
4.1 A. MCDM-based AHP-GDM Methodology
Saaty (1988) developed AHP to solve a hierarchical problem using decision-making. It is used to solve simple or complex decision problems. AHP uses a series of pairwise comparisons to make a decision, and is applied to different types of research problems [44]. In a pairwise comparison, feedback from DMs is used, based on their expert knowledge and Saaty’s nine-point scale, as shown in Tab. 2. In decision-making, a single DM may lead to a biased decision; hence, a GDM is proposed and used. Using a group of DMs to solve a decision problem may provide an amicable, unbiased, accurate decision.
Table 2: Saaty’s nine-point scale [45]
The MCM-based AHP-GDM steps are described.
5.1 Step 1:
The comparison matrix D, also known as a decision matrix, is framed using CSFs of M-learning. The pairwise comparison of CSFs can be carried out. Element
5.2 Step 2:
Pairwise judgments by each DM involved in the GDM process can be used to build the matrix D. The cumulative geometric means (GM) approach may be used to synthesize the feedback of the DMs to obtain a priority vector (PV).
5.3 Step 3:
The decision matrix D may be used for the eigenvalue (
where
5.4 Step 4:
A DM must be consistent when determining the decision matrix. The DM plays a vital role in accepting the pairwise comparison judgment. The decision matrix is checked for consistency. The consistency index (C.I.) can be calculated for each decision matrix D as
where n is the matrix size.
5.5 Step 5:
The random index (R.I.) is important in calculating the consistency, and is calculated as
R.I. for a given pairwise matrix is also available in the form of a ready reckoner table in the literature.
5.6 Step 6:
The consistency ratio (C.R.) plays a role in checking the acceptance of rejections of the pairwise matrix. A C.R. value less than 0.01 is acceptable for use in the AHP process. The DM may derive another pairwise judgment by revisiting the matrix if the C.R. can be obtained using values that fail to meet the required condition. The C.R. can be calculated as
Fuzzy set theory and fuzzy numbers can be used to design pairwise comparison and increase the accuracy of decision-making. The intersection of two fuzzy sets is decided using the extension principle. The AHP relies on the knowledge and expertise of a DM. While due care should be taken to select a decision-making team, DMs may show bias. Vagueness or bias can be reduced using a fuzzy number [46]. Next, the general fuzzy set theory with extension principles is presented.
(i) Fuzzy Set Theory
The robustness of decision-making helps to produce an accurate evaluation. Fuzziness enhances the accuracy of a decision; therefore, a fuzzy environment may be preferred.
Various types of fuzzy numbers may be employed in decision-making. Triangular fuzzy numbers (l1, m1, n1), as shown in Fig. 2, are employed in this study, but trapezoidal numbers (l1, m1, n1, o1) can also be used [47].
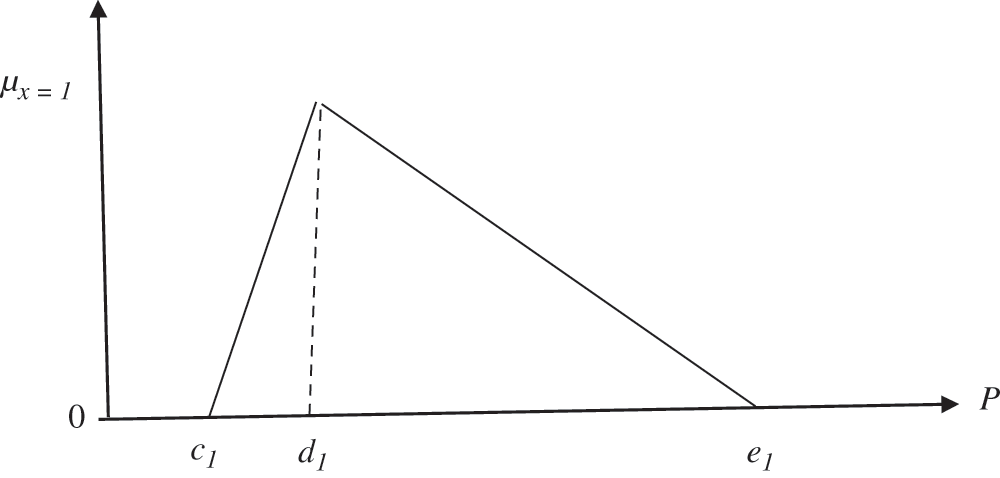
Figure 2: Triangular fuzzy number (P)
Fuzzy set theory allows different kinds of arithmetic operations [48]. Let fuzzy numbers A1 and A2 be triangular fuzzy numbers
(ii) Application under fuzzy environment
The extent analysis principle is used in the comparison of two TFNs [49]. The two sets P = {
where
Step 1: Framing a hierarchical structure to meet the goal
M-learning has dimensions and CSFs. The hierarchy of M-learning can be set using the feedback from DMs. The framing of the hierarchy helps in ranking. Hierarchy representation consists of three levels. The top-level has a goal, followed by dimension and CSFs of M-learning.
Step 2: Framing pairwise comparison of M-learning dimension and CSFs
DMs can analyze and compare the dimensions of M-learning, considering the goal. The TFN helps in framing a relationship by pairwise comparison.
Step 3: Fuzzy synthetic extent analysis to determine the value
Applying summation of TFNs, m extent analysis values are determined as
and
The inverse of each vector is calculated as
Step 4: Determining the possible degree of supremacy for two TFNs, i.e.,
and can be shown as
Generally, DMs provide the relevant feedback to frame group decision-making. For instance, k DMs are invited to provide feedback, and the subsequent pairwise comparisons yield n elements. A set of k matrices,
The two TFNs
Figure 3: Intersection of TFNs [41]
Step 5: Determining the possibility degree for a given convex fuzzy number such that it is greater than k
The fuzzy number
Considering
the weight vector is obtained as
Step 6: Determining the normalized weight vectors
The normalized weight vector is obtained as
where C is a crisp number.
Step 7: Determining the overall score of each CSF’s dimension and its factors for prioritization
The overall priority weights of each dimension and CSFs of M-learning can be determined by multiplying the local weight and the global weight. The obtained weights of M-learning dimensions and CSFs are arranged in descending order to select the most preferred CSF. For example, the weights 0.5, 0.1, 0.4 can be arranged as 0.5, 0.4, 0.1, where 0.5 is preferred over 0.4 and 0.1
5 MCDM-based Methodologies in M-learning
MCDM uses the AHP and FAHP methodologies to evaluate and prioritize the dimensions and CSFs of M-learning based on pairwise comparisons. The AHP-GDM approach using AHP with GDM is used to derive the weights of the dimensions and CSFs of M-learning. AHP is simple to use, and it is easy to formulate the pairwise matrix for subsequent comparisons, while FAHP may help reduce the vagueness of decision-making. Since the pairwise comparison in AHP and FAHP plays a significant role in decision-making, it is important to take due care in the identification and framing of the team. DMs were selected based on their experience and knowledge of the subject. An expert group with a minimum of six years of teaching experience in E-learning and M-learning formed the team of DMs. One of the three DMs was from the computer science discipline, and was familiar with hardware and software. The other two DMs were from the field of engineering and science, and were well versed with E-learning and M-learning. Brainstorming sessions provided DMs with initial knowledge of M-learning dimension and CSFs, and they practiced pairwise comparisons for dimensions and CSFs. DMs were engaged in the AHP methodology to make pairwise judgments. The pairwise judgments and subsequent weights were calculated, and are shown in Tabs. 3–6.
The hierarchy structure is shown in Fig. 4. The dimension and CSFs of M-learning were obtained through the following steps:
1. Setting the problem objective;
2. Preparation of hierarchical structure including the M-learning goal, dimensions, and CSFs;
3. The preparation of the pairwise matrix;
4. Synthesis of dimension and CSF matrix obtained by step 3;
5. Consistency check of DMs for accepting the decision matrix;
6. Deciding the rank.
The steps are described as follows.
Step 1 – Goal
The M-learning dimensions and CSFs are evaluated and prioritized.
Step 2 – Hierarchical Structure
The hierarchical structure is formed using dimensions and factors related to M-learning. Fig. 4 shows the first-level goal of ranking the factors of M-learning. In level 2, the pedagogical dimension (PD), technological dimension (TD), social dimension (SD), and individual/user dimension (ID) are shown. In the third level, factors under each dimension are identified. PD consists of learning content quality (PLQ), interactivity (PIN), and trust (PTR). TD includes facilitating conditions (TFC), user interface (TUI), and mobile device limitations (TML). SD consists of social influence (SSI), usefulness (SU), government and university support (SGU), and personal innovation and enjoyment (SPI). ID includes attitude (IA), self-efficacy (ISE), and behavioral intention to adopt M-learning (IBI).
Figure 4: M-learning hierarchical structure
Step 3 – Pairwise Comparison Matrices
There is a pairwise comparison matrix for each dimension and CSF of M-learning. It provides the relative contribution of each dimension or CSF. The feedback from DMs is essential in a pairwise comparison. A single opinion is sufficient to form a final decision, but sometimes it may be vague or biased. DMs may work together to remedy this issue. In the present case, three DMs gave their expert opinions using Saaty’s scale [45]. The pairwise comparison matrices are shown in Tabs. 3–5. These are further synthesized using the geometric mean method to obtain the final value of the pairwise comparison matrix. The obtained matrix is free from bias.
Table 3: AHP pairwise comparison matrix of M-learning dimensions (DM1)
Table 4: AHP pairwise comparison matrix of M-learning dimensions (DM2)
Table 5: AHP pairwise comparison matrix of M-learning dimensions (DM3)
Step 4 – Synthesis of Pairwise Comparison
The results were analyzed and tabulated as an output matrix after conducting a pairwise comparison of different dimensions of M-learning (Tabs. 3–5). This relates to the potential influence of one factor on another. In more precise decision-making, group decision-making plays a significant part. A geometric mean method (GMM) is used in GDM. This is preferred over the arithmetic mean method (AMM) for the non-reciprocity of the pairwise matrix. The matrix of pairwise comparisons obtained by DMs is formulated and presented in Tab. 6.
Table 6: AHP synthesized pairwise matrix of M-learning dimensions (DM1–DM3)
Step 5 – Checking Consistency
The decision consistency of DM is essential in a pairwise comparison, hence it must be checked for the acceptance and rejection of each pairwise comparison table. The consistency level (CI) and random index (RI) provide consistency checking. The consistency level of each pairwise comparison is verified.
Step 6 – Ranking
CSFs and dimensions are ranked based on their global weights, which indicate the relative contribution of each CSF in the success of M-learning. For each component, the AHP pairwise matrix offers local weights. The global weight may be obtained by multiplying the main dimension weight with the respective sub-criteria weight (24).
The global weights in decreasing order give the rankings of the CSFs of M-learning, so as to obtain the CSFs with the maximum influence. AHP provides the overall ranking of CSFs [15]. Tab. 7 shows M-learning composite weights. Fig. 5 shows the weights of M-learning dimensions. Fig. 6 provides the required M-learning ranking.
Table 7: AHP composite ranking of M-learning (dimension and CSFs)
Figure 5: M-learning dimension ranking
Figure 6: M-learning factor ranking
Similarly, FAHP is used to measure the dimensional weights and factor weights of M-learning to obtain the ranking. The TFN-based scale provides the M-learning weights of dimensions and CSFs, as shown in Tab. 8. To find local weights and global weights, the methodology mentioned in Section 3 is used. Tab. 9 shows a pairwise comparison of M-learning dimensions using FAHP. Tab. 10 shows the weight of each M-learning factor. The rankings obtained using AHP and FAHP are compared in Tab. 11.
Table 8: TFN scale for pairwise comparison using FAHP [50]
Table 9: FAHP pairwise comparison of M-learning dimensions
Table 10: FAHP composite rank of M-learning (dimensions and CSFs)
Table 11: AHP and FAHP composite weight comparison (dimensions and CSFs)
CSFs play a significant role in M-learning. A comprehensive method based on AHP and FAHP will prove crucial in evaluating and ranking the CSFs of M-learning. MCDM methods can easily and accurately measure the influence of each CSF, whose prioritization will help enable smooth and successful implementations in the LMS. Faculties will find it easy to continuously assess students, and to monitor and manage their courses. Since M-learning may require costly infrastructure (software and hardware), CSFs will help in the effective control of resources.
The results obtained through AHP and FAHP can be compared to obtain the true ranking. The influence of CSFs found through AHP are, in descending order, TD, 0.5541 > ID, 0.2519 > PD, 0.1267 > SD, 0.0673. Similarly, the priority and ranking obtained by FAHP are TD, 0.5522 > ID, 0.2602 > PD, 0.1237 > SD, 0.0639. It is concluded that the technological dimension plays a significant role in M-learning success. Universities must take necessary actions to update infrastructure and provide the latest technology while implementing.
7 Limitations and Scope for Future Work
M-learning is emerging quickly [51–53], and its dimensions and CSFs can influence its successful implementation. The present study has established the priority and ranking of dimensions and CSFs, which may be generalized with differing degrees of acceptance in other countries. The present study employed the MCDM approach and used AHP and FAHP with a limited number of DMs. Future research may use a large DM group size in AHP and FAHP methodologies. Other MCDM may also be used to find the weight, rank, synthesis of a pairwise matrix of the M-learning dimension, and CSF.
Today’s students are familiar with electronic devices, and mobility plays a vital role in M-learning. It promotes the learner's freedom from various constraints like learning place, learning content, and learning choice. M-learning technology includes smartphones, which are flexible, portable, easily available, and user-friendly, and hence may prove highly acceptable to students. Universities may also adopt prevailing mobile services for educational purposes. Faculties may modify course designs and prepare mobile modules for easy and effective learning. M-learning flexibility may also motivate students to engage in effective teaching-learning. Students from different social, cultural, and economic backgrounds use mobile devices for communication, learning, and entertainment, which can facilitate the implementation of M-learning systems. Learning through mobile devices may provide flexibility and speed up teaching, learning, and knowledge sharing. The acceptance of M-learning largely depends upon the CSFs, which university administrations must take action to control for successful implementation. MCDM techniques can potentially handle complex and conflicting criteria. This poses challenges in day-to-day decision-making, and to optimize these criteria takes effort and time. MCDM provides a simple but powerful methodology for high quality decision-making. MCDM method such as AHP and FAHP can prove simple and fruitful for evaluating and prioritizing the CSFs of M-learning for effective teaching-learning.
Acknowledgement: We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the General Research Project under grant number R.G.P.1/138/40.
Conflict of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Hamidi and A. Chavoshi, “Analysis of the essential factors for the adoption of mobile learning in higher education: A case study of students of the university of technology,” Telematics and Informatics, vol. 35, no. 4, pp. 1053–1070, 2018.
2. A. I. Saroia and S. Gao, “Investigating university students’ intention to use mobile learning management systems in sweden,” Innovations in Education and Teaching International, vol. 56, no. 5, pp. 569–580, 2019.
3. Nguyen L., Barton S. M. and Nguyen L. T., “iPads in higher education-Hype and hope,” British Journal of Educational Technology, vol. 46, no. 1, pp. 190–203, 2015.
4. F. D. Davis, “Perceived usefulness, perceived ease of use, and user acceptance of information technology,” MIS Quarterly, vol. 13, no. 3, pp. 319–340, 1989.
5. P. Legris, J. Ingham and P. Collerette, “Why do people use information technology? a critical review of the technology acceptance model,” Information & Management, vol. 40, no. 3, pp. 191–204, 2003.
6. A. Chavoshi and H. Hamidi, “Social, individual, technological and pedagogical factors influencing mobile learning acceptance in higher education: A case from Iran,” Telematics and Informatics, vol. 38, no. 5, pp. 133–165, 2019.
7. O. Viberg, A. Andersson and M. Wiklund, “Designing for sustainable mobile learning re-evaluating the concepts ‘formal’ and ‘informal,” Interactive Learning, vol. 29, no. 1, pp. 130–141, 2018.
8. I. Ajzen, “The theory of planned behavior,” Organizational Behavior and Human Decision Processes, vol. 50, no. 2, pp. 179–211, 1991.
9. E. M. Rogers, Diffusion of innovations. Simon and Schuster, New York: Free Press, New York, USA, 2010.
10. V. Venkatesh, M. G. Morris, G. B. Davis and F. D. Davis, “User acceptance of information technology: Toward a unified view,” MIS Quarterly, vol. 27, no. 3, pp. 425–478, 2003.
11. Q. N. Naveed, M. M. Alam and N. Tairan, “Structural equation modeling for mobile learning acceptance by university students: An empirical study,” Sustainability, vol. 12, no. 20, pp. 8618, 2020.
12. R. B. Douglass, “Belief, attitude, intention, and behavior: An introduction to theory and research,” JSTOR, New York, USA, Addision-Weseley, Reading, MA, vol. 10, pp. 130–132, 1977.
13. N. Marangunić and A. Granić, “Technology acceptance model: A literature review from 1986 to 2013,” Universal Access in the Information Society, vol. 14, no. 1, pp. 81–95, 2015.
14. Q. N. Naveed, A. Muhammad, S. Sanober, M. R. N. Qureshi and A. Shah, “A mixed method study for investigating critical success factors (CSFs) of e-learning in Saudi Arabian universities,” International Journal of Advanced Computer Science and Applications, vol. 8, no. 5, pp. 171–178, 2017.
15. Q. N. Naveed, M. N. Qureshi, A. Shaikh, A. O. Alsayed, S. Sanober et al., “Evaluating and ranking cloud-based e-learning critical success factors (CSFs) using combinatorial approach,” IEEE Access, vol. 7, pp. 157145– 157157, 2019.
16. H. Al Zahrani and K. Laxman, “A critical meta-analysis of mobile learning research in higher education,” Journal of Technology Studies, vol. 42, no. 1, pp. 2–17, 2016.
17. Y. L. Ting, “The pitfalls of mobile devices in learning: A different view and implications for pedagogical design,” Journal of Educational Computing Research, vol. 46, no. 2, pp. 119–134, 2012.
18. S. S. Liaw and H. M. Huang, “A case of study of investigating users’ acceptance toward mobile learning,” in Recent Progress in Data Engineering and Internet Technology. Springer, Berlin, Heidelberg, pp. 299–305, 2012.
19. C. Y. Chang, C. L. Lai and G. J. Hwang, “Trends and research issues of mobile learning studies in nursing education: A review of academic publications from 1971 to 2016,” Computers & Education, vol. 116, no. 3, pp. 28–48, 2018.
20. C. Gan, H. Li and Y. Liu, “Understanding mobile learning adoption in higher education: An empirical investigation in the context of the mobile library,” Electronic Library, vol. 35, no. 5, pp. 846–860, 2017.
21. M. Sarrab, M. Elbasir and S. Alnaeli, “Towards a quality model of technical aspects for mobile learning services: An empirical investigation,” Computers in Human Behavior, vol. 55, no. 1, pp. 100–112, 2016.
22. K. C. Li, L. Y. K. Lee, S. L. Wong, I. S. Y. Yau and B. T. M. Wong, “Mobile learning in nursing education: Catering for students and teachers’ needs,” Asian Association of Open Universities Journal, vol. 12, no. 2, pp. 171–183, 2017.
23. A. Althunibat, “Determining the factors influencing students’ intention to use m-learning in Jordan higher education,” Computers in Human Behavior, vol. 52, no. 6, pp. 65–71, 2015.
24. X. Hu, J. Ng, K. K. Y. Tsang and S. K. W. Chu, “Integrating Mobile learning to learning management system in community college,” Community College Journal of Research and Practice, vol. 44, no. 10–12, pp. 1–16, 2019.
25. M. Bakhsh, A. Mahmood and N. A. Sangi, “Examination of factors influencing students and faculty behavior towards m-learning acceptance: An empirical study,” International Journal of Information and Learning Technology, vol. 34, no. 3, pp. 166–188, 2017.
26. P. Harpur, “Mobile lecturers, mobile students: An exploratory study in a blended architectural technology context,” Journal of Enterprise Information Management, vol. 30, no. 5, pp. 748–778, 2017.
27. N. M. Sabah, “Exploring students’ awareness and perceptions: Influencing factors and individual differences driving m-learning adoption,” Computers & Education, vol. 65, pp. 522–533, 2016.
28. M. Sarrab, I. Al Shibli and N. Badursha, “An empirical study of factors driving the adoption of mobile learning in Omani higher education,” International Review of Research in Open and Distributed Learning, vol. 17, no. 4, pp. 331–349, 2016.
29. S. K. Sharma, M. Sarrab and H. Al-Shihi, “Development and validation of mobile learning acceptance measure,” Interactive Learning Environments, vol. 25, no. 7, pp. 847–858, 2017.
30. I. Milošević, D. Živković, D. Manasijević and D. Nikolić, “The effects of the intended behavior of students in the use of m-learning,” Computers & Education, vol. 51, pp. 207–215, 2015.
31. G. W. H. Tan, K. B. Ooi, L. Y. Leong and B. Lin, “Predicting the drivers of behavioral intention to use mobile learning: A hybrid SEM-neural networks approach,” Computers & Education, vol. 36, pp. 198–213, 2014.
32. M. Alrasheedi, L. F. Capretz and A. Raza, “Management’s perspective on critical success factors affecting mobile learning in higher education institutions-an empirical study,” Journal of Educational Computing Research, vol. 54, no. 2, pp. 253–274, 2016.
33. Y. S. Wang, M. C. Wu and H. Y. Wang, “Investigating the determinants and age and gender differences in the acceptance of mobile learning,” British Journal of Educational Technology, vol. 40, no. 1, pp. 92–118, 2009.
34. J. Abramson, M. Dawson and J. Stevens, “An examination of the prior use of e-learning within an extended technology acceptance model and the factors that influence the behavioral intention of users to use m-learning,” SAGE Open, vol. 5, no. 4, pp. 1–9, 2015.
35. L. Briz-Ponce, A. Pereira, L. Carvalho, J. A. Juanes-Méndez and F. J. Garcia-Peñalvo, “Learning with mobile technologies-students’ behavior,” Computers & Education, vol. 72, pp. 612–620, 2017.
36. H. Mohammadi, “Social and individual antecedents of m-learning adoption in Iran,” Computers & Education, vol. 49, pp. 191–207, 2015.
37. S. A. Raza, A. Umer, W. Qazi and M. Makhdoom, “The effects of attitudinal, normative, and control beliefs on m-learning adoption among the students of higher education in Pakistan,” Journal of Educational Computing Research, vol. 56, no. 4, pp. 563–588, 2018.
38. A. Badwelan and A. A. Bahaddad, “Cultural factors that influence m-learning for female university students: A Saudi Arabian case study,” International Journal of Computer Applications, vol. 166, no. 5, pp. 21–32, 2017.
39. M. H. Fagan, “Factors influencing student acceptance of mobile learning in higher education,” Computers in the Schools, vol. 36, no. 2, pp. 105–121, 2019.
40. H. Hamidi and M. Jahanshaheefard, “Essential factors for the application of education information system using mobile learning: A case study of students of the university of technology,” Telematics and Informatics, vol. 38, no. 2, pp. 207–224, 2019.
41. A. Badwelan, S. Drew and A. A. Bahaddad, “Towards acceptance m-learning approach in higher education in Saudi Arabia,” International Journal of Business and Management, vol. 11, no. 8, pp. 12, 2016.
42. Y. Liu, H. Li and C. Carlsson, “Factors driving the adoption of m-learning: An empirical study,” Computers & Education, vol. 55, no. 3, pp. 1211–1219, 2010.
43. G. W. H. Tan, K. B. Ooi, J. J. Sim and K. Phusavat, “Determinants of mobile learning adoption: An empirical analysis,” Journal of Computer Information Systems, vol. 52, no. 3, pp. 82–91, 2012.
44. M. Azam, M. N. Qureshi and F. Talib, “AHP model for Identifying best bealth care establishment,” International Journal of Productivity Management and Assessment Technologies, vol. 3, no. 2, pp. 34–66, 2015.
45. T. L. Saaty, “Decision making with the analytic hierarchy process,” International Journal of Services Sciences, vol. 1, no. 1, pp. 83–98, 2008.
46. Q. N. Naveed, M. R. N. Qureshi, A. O. Alsayed, A. Muhammad, S. Sanober et al., “Prioritizing barriers of e-learning for effective teaching-learning using fuzzy analytic hierarchy process (FAHP),” in 4th IEEE International Conference on Engineering Technologies and Applied Sciences (ICETASBahrain, pp. 1–8, 2017.
47. C. Kahraman, U. Cebeci and D. Ruan, “Multi-attribute comparison of catering service companies using fuzzy AHP: The case of Turkey,” International Journal of Production Economics, vol. 87, no. 2, pp. 171–184, 2004.
48. A. Kauffman and M. M. Gupta, Introduction to fuzzy arithmetic, theory and application. New York: Van Nostrand Reinhold, 1991.
49. D. Y. Chang, “Applications of the extent analysis method on fuzzy AHP,” European Journal of Operational Research, vol. 95, no. 3, pp. 649–655, 1996.
50. Q. N. Naveed, M. R. N. Qureshi, N. Tairan, A. H. Mohammad, A. Shaikh et al., “Evaluating critical success factors in implementing e-learning system using multi-criteria decision-making,” Plos One, vol. 15, no. 5, pp. e0231465, 2020.
51. A. Nisha Jebaseeli, “Opinion analysis model for classification of opinions for m-learning,” International Journal of Computer Applications, vol. 109, no. 16, pp. 51–54, 2015.
52. M. Lachgar and A. Abdali, “Modeling and generating native code for cross-platform mobile applications using DSL,” Intelligent Automation & Soft Computing, vol. 23, no. 3, pp. 445–458, 2016.
53. A. Balavivekanandhan and S. Arulchelvan, “A study on students acquisition of IT knowledge and its implication on m-learning,” Scientific World Journal, vol. 2015, no. 1, pp. 1–11, 2015.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |