Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.016865
Article

Efficient Three-Dimensional Video Cybersecurity Framework Based on Double Random Phase Encoding

Osama S. Faragallah1,*, Walid El-Shafai2, Ashraf Afifi1, Ibrahim Elashry3, Mohammed A. AlZain1, Jehad F. Al-Amri1, Ben Soh4, Heba M. El-Hoseny5, Hala S. El-Sayed6 and Fathi E.Abd El-Samie2

1Department of Information Technology, College of Computers and Information Technology, Taif University, P.O. Box 11099, Taif, 21944, Saudi Arabia
2Department of Electronics and Electrical Communications Engineering, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt
3Department of Electrical Engineering, Kafrelsheikh University, Kafrelsheikh, 61519, Egypt
4Department of Computer Science and Computer Engineering, La Trobe University, Bundoora, 3086, Australia
5Department of Electronics and Electrical Communication Engineering, Al-Obour High Institute for Engineering and Technology, 3036, Egypt
6Department of Electrical Engineering, Faculty of Engineering, Menoufia University, Shebin El-kom, 32511, Egypt
*Corresponding Author: Osama S. Faragallah. Email: o.salah@tu.edu.sa
Received: 14 January 2021; Accepted: 18 February 2021

Abstract: With the rapidly increasing rate of using online services and social media websites, cybercriminals have caused a great deterioration in the network security with enormous undesired consequences. Encryption techniques may be utilized to achieve data robustness and security in digital multimedia communication systems. From this perspective, this paper presents an optical ciphering framework using Double Random Phase Encoding (DRPE) for efficient and secure transmission of Three-Dimensional Videos (3DVs). Firstly, in the DRPE-based 3DV cybersecurity framework proposed in the paper, an optical emitter converts each frame of the transmitted 3DV into an optical signal. Then, the DRPE technique encrypts the obtained optical signal using two kinds of phase modulation in the time and frequency domains. Lastly, a Charge Coupled Device (CCD) digital camera converts, upon detection, the optical cipher frames to digital format. The proposed DRPE-based 3DV cybersecurity framework is examined and investigated through visual inspection and various security statistical metrics. Experiments and analysis show that the proposed DRPE-based 3DV cybersecurity framework is secure and effective to mitigate different multimedia attacks.

Keywords: Multimedia cybersecurity; DRPE; statistical security analysis

1  Introduction

Over the past few years, cybersecurity has become a vital issue in digital multimedia systems as the users are concerned with the security and protection of information transmission from exploitation attacks or unauthorized access. Recently, researchers have discussed three major areas in cybersecurity: application security, disaster recovery and information network security [1–3].

Application security is the process of protecting software applications from external threats by using procedural methods. Application security techniques are used to demonstrate security vulnerabilities at different stages of applications design, maintenance, and deployment to determine what security measures are appropriate. For example, intrusion detection/prevention can be utilized in resource program execution, while access control is needed in database or storage security to isolate non-application components from data elements. Other standard methods, such as logging, user/role authentication-authorization, parameter manipulation, input parameter verification, auditing, session management and exception management, are utilized in application security as explored in [4,5].

Disaster recovery represents another element of security planning with the potential of protecting an organization from the effects of significantly negative events. Moreover, disaster recovery involves establishing priorities, risk assessment and recovery strategies. Therefore, all establishments should have a specified plan for disaster recovery.

Information network security protects the usability, reliability, integrity, and safety of information in the network from unauthorized access to avoid identity theft. The network security structure may involve: (a) Firewall, to prevent unauthorized access, (b) Virtual Private Networks (VPNs), for allowing secure remote access, (c) Anti-virus and anti-spyware, (d) Intrusion prevention systems (IPS), to mitigate fast-spreading attacks, [6,7], (e) Identification, (f) User authentication, and (g) Cryptography [8–11].

With the rapid advances in multimedia processing techniques, a new field of research known as multimedia cybersecurity has emerged. Its goals include protection of image, audio, and video via encryption, watermarking and steganography.

Encryption schemes may be considered effective for data protection, by making the source data secret such that the data becomes unclear beyond the intentional transmitters and recipients. Data hiding schemes play a significant role in many security application fields [12–15]. Steganography and watermarking are the primary building blocks for developing efficient data hiding schemes. Multimedia encryption is a crucial procedure due to its numerous critical characteristics such as redundancy and high pixel correlation [16–18]. The traditional data encryption systems such as AES, IDEA, Triple-DES, and other symmetric encryption systems are not suitable for efficient multimedia encryption [19–21]. Therefore, to meet this challenge, more advanced encryption techniques have been suggested [22,23].

Encryption of video involves transforming multimedia data to make it unintelligible for anyone except the legitimate users. Video encryption can be performed either in spatial or transform domains [24]. In the spatial domain, traditional processing is applied on the video frame pixels. In transform-domain encryption, the values of pixels are transformed first and then operations are applied on the transformed coefficients.

A large number of opto-digital image encryption schemes have been introduced in the literature. These schemes possess good features such as high processing speed, parallelism, and large encryption flexibility. These schemes allow full phase-based encryption, full amplitude-based encryption, and polarization encoding-based encryption [25–28]. Due to phase non-linearities, full phase-based encryption is more robust compared to full amplitude-based encryption.

The DRPE is the most practical and efficient optical ciphering scheme, which encompass two secret random phase keys. One is employed in the spatial domain and the other in the Fourier Transform (FT) domain [29–31]. The DRPE setup consists of two cascaded lenses for applying the optical FT onto the input object [31–34].

The purpose of this paper is to introduce a DRPE-based 3DV cybersecurity framework. This framework is examined, tested, and analysed in terms of visual inspection, histogram and entropy analysis, differential and encryption quality analysis, encryption speed, PSNR, SSIM, FSIM, and edge detection. The paper is structured as follows. In Section 2, a brief introduction of the DRPE technique and its parameters is provided. Section 3 describes the suggested DRPE-based 3DV cybersecurity encryption/decryption framework. Section 4 presents the encryption analysis and the numerical outcomes. The paper conclusion is given in Section 5.

2  Double Random Phase Encoding (DRPE)

The role of optical image encryption has been studied by several researchers, beginning from the DRPE system presented by Réfrégier et al. [30]. The DRPE is mainly dependent on the spectral variations of images or video frames. Tab. 1 illustrates the random phase mask characteristics for encrypting a plain image or video frame into a noise-like sequence in both time and Fourier planes [31–33]. The architecture of the DRPE setup is based on two random phase masks: RPM1 and RPM2 in a 4f imaging system as illustrated in Fig. 1. The 4f setup is composed of two cascaded lenses separated by two focal lengths. The DRPE procedure is summarized as follows:

a)   The video frames are modulated via the RPM1 in the spatial plane providing the primary modulation of the video frame spectra.

b)   The primary modulated video frames are again modulated via the RPM2 in the Fourier plane providing another modulation to the video frame spectra.

c)   An Optical Fourier Transform (OFT) is employed via a second lens to get the encoded video frame in the 2-D space.

Table 1: Optical encryption methods

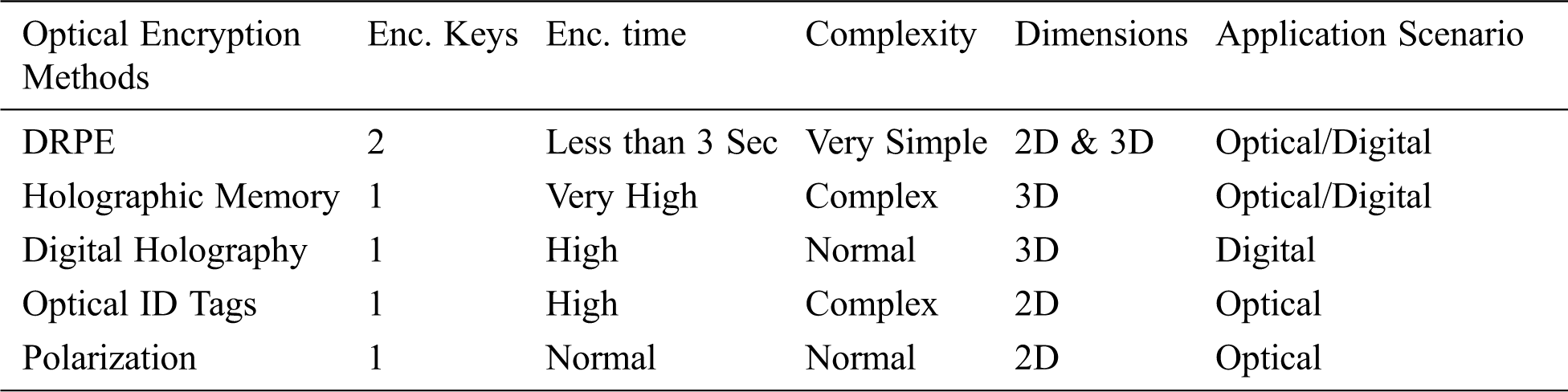
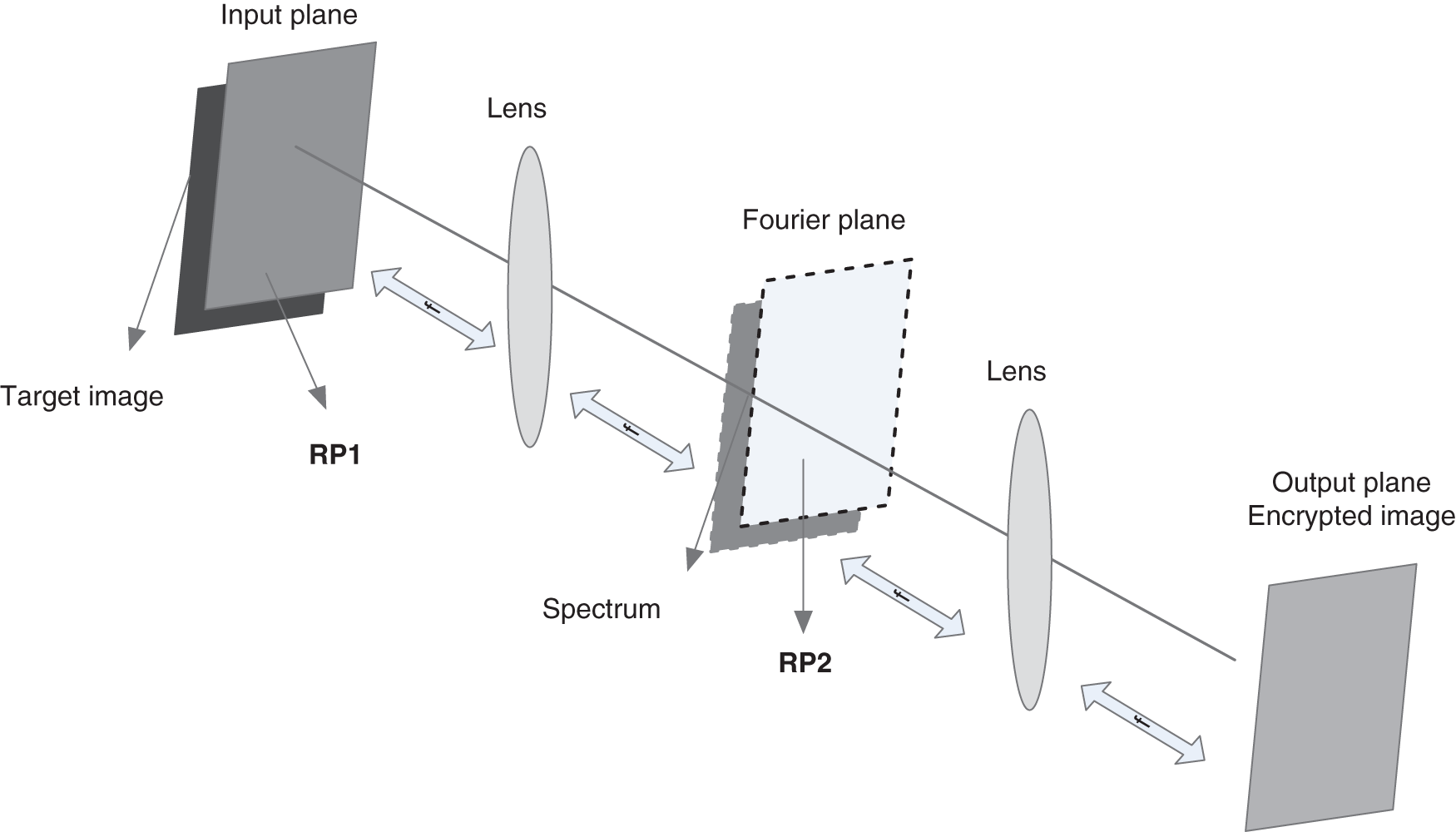
Figure 1: The block diagram of the DRPE encryption/decryption

The decryption operation depends on a complex conjugate Fourier phase key to decipher the video frames with the same Fourier RPM as in the encryption operation [33,34]. The mathematical formula of the fully phase-encrypted video frame is given as:

ψp(a,b)={exp⁡[iπf(a,b)]φn(a,b)}∗h(a,b)={exp⁡[iπf(a,b)]φn(a,b)}∗FT−1{φm(υ,η)} (1)

3  The Proposed Optical DRPE-Based 3DV Security Framework

In this section, the suggested optical DRPE-based 3DV encryption framework is explained in detail. As shown in Fig. 2, the 3DV data streams are firstly compressed with the H.264/MVC or the H.265/HEVC encoder to minimize the video size. Then, the encoded bit streams are encrypted using the proposed DRPE-based 3DV encryption technique and transmitted through the communication channel. Finally, the encoded bit streams are decrypted with the proposed DRPE-based 3DV decryption technique. Consequently, the decrypted bit streams are decoded by the 3D H.264/MVC or H.265/HEVC decoder.

Figure 2: The proposed 3DV cybersecurity communication system

In the presented encryption system, the diffusion process is performed by applying OFT using the DRPE technique on the MVC/HEVC frames, in which the two RPMs of the DRPE work as effective encryption keys. In the proposed 3DV cybersecurity framework, the DRPE is employed as a diffusion step to diffuse the 3DV frame pixels to complicate the relationship between the cipher 3DV frames and the plain 3DV frames.

The DRPE scheme employs a pair of RPMs. RPM1 affects the plain 3DV frame in the time domain. Then, RPM2 affects the result in the Fourier plane. Finally, an OFT is applied to reconfigure the cipher 3DV frame in the time domain. The DRPE encryption mechanism is mathematically expressed as [31]:

F(a,b)=FT−1{FT[I(a,b)exp⁡(i2πθ(a,b))]exp⁡(i2πω(u,v))} (2)

where I(a,b) and F(a,b) are the plain and cipher 3DV frames, respectively. The θ(a,b) and ω(u,v) denote key pair functions in the frequency/spatial domains.

The DRPE decryption process can be written as in [31], where exp⁡(i2πθ(a,b)) and exp⁡(−i2πω(u,v)) are the keys transferred along with the ciphered 3DV frame:

I(a,b)={FT−1[FT(F(a,b))exp⁡(−i2πω(u,v))}exp⁡(−i2πθ(a,b)) (3)

In the encryption process, the encoded 3DV frames are divided into separate frames. Then, an optical emitter (optical source) converts 3DV frames from electrical signals to optical signals to be encrypted by applying the DRPE technique. Finally, the 3DV frame is transformed back to digital format to allow processing through a computer. The encryption process of the proposed DRPE-based 3DV cybersecurity framework is shown in Fig. 3. It is listed as follows:

a)   Reading the encoded 3DV bit streams.

b)   Dividing the input compressed 3DV bit streams into separate plain 3DV frames.

c)   Multiplying each of the plain 3DV frames by RPM1, and then applying the Fourier Transform (FT) process to get the primary ciphered 3DV frame.

d)   Multiplying each of the resulting primary encrypted 3DV frames by RPM2, and then applying the inverse FT to get the final ciphered 3DV frame.

e)   Collecting all ciphered 3DV frames to produce the encrypted 3DV bit streams.

f)   Sending the ciphered 3DV bit streams to the receiver through a communication channel.

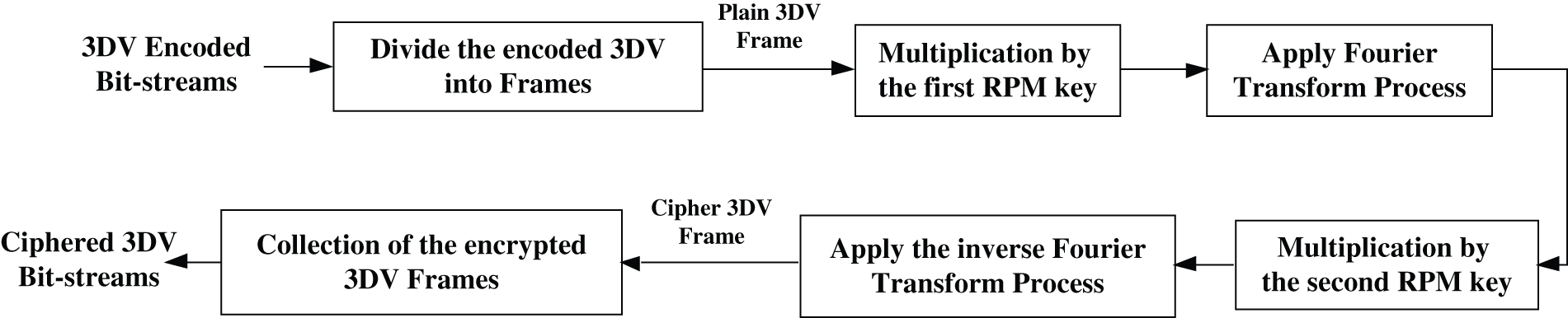
Figure 3: The proposed DRPE-based 3DV encryption mechanism

In the decryption process, the conjugates of RPMs are utilized to the decrypt optical signal to decipher the MVC/HEVC frames. Firstly, an optical detector converts the optical signal to the electrical signal. Then, the plain 3DV frames are collected to get the video bit-streams. Finally, the receiver module starts by receiving the ciphered 3DV bit-streams. The decryption process of the proposed DRPE-based 3DV cybersecurity framework is shown in Fig. 4 which is listed as follows:

a)   Receiving the ciphered 3DV bit streams.

b)   Dividing the input encrypted 3DV bit streams into separate ciphered 3DV frames.

c)   Multiplying each of the ciphered 3DV frames by the conjugate of RPM1, and then applying the FT process.

d)   Multiplying each of the resulting 3DV frames by the conjugate of RPM2, and then applying the inverse FT to get the optical plain 3DV frames.

e)   Employing the optical detector to change the optical 3DV frames to the electrical 3DV frames.

f)   Collecting all electrical plain 3DV frames to recover the encoded 3DV bit streams.

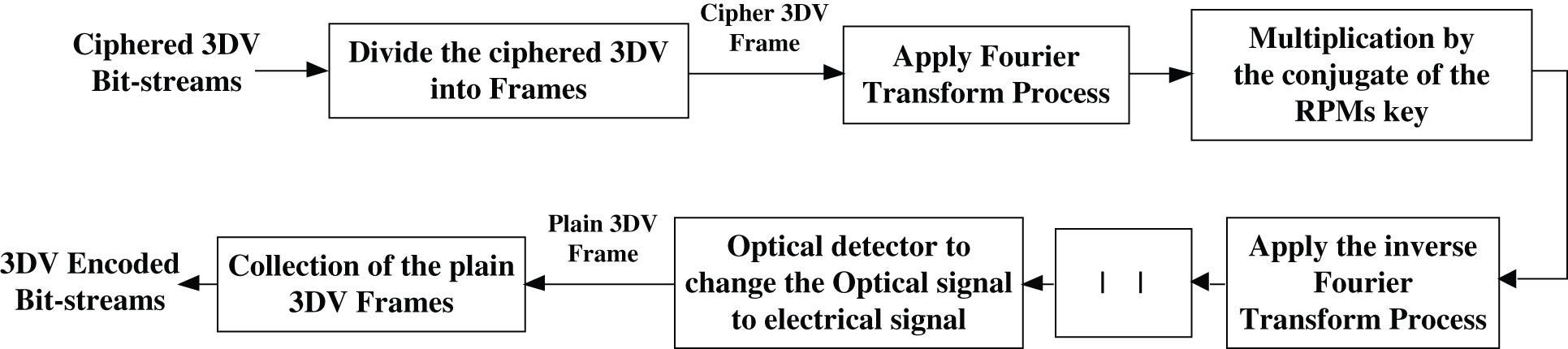
Figure 4: The proposed DRPE-based 3DV decryption mechanism

4  Performance Analysis and Results

In this section, the proposed technique is tested through visual inspection and security statistical metrics such as entropy, PSNR, SSIM, FSIM, histogram, ciphering quality, differential analysis metrics, edge strength, and computational processing time [23–25].

The performance of the proposed DRPE-based 3DV cybersecurity framework is examined and evaluated with various tests for standard 3DV sequences (Balloons, Objects, PoznanStreet, and Shark). The tested 3DV streams have various temporal and spatial characteristics. The PoznanStreet stream is a slow-moving video. The Objects and Balloons are intermediary-moving videos, and the Shark is a fast-moving video. For all 3DV sequences, the encoded data bit streams are acquired through applying the reference H.264/MVC and H.265/HEVC codecs at the encoder side. These reference 3DV codecs are utilized in the simulation work for the 3D video compression process. The employed compression conditions in the simulation tests are based on the Joint Video Team (JVT) standards.

Four different experiments have been carried out and analyzed on Balloons, Objects, PoznanStreet, and Shark frames shown in Fig. 5. The first experiment depends on frame # 50 from the Balloons sequence as a test plain 3DV frame. The second experiment depends on frame # 100 from the Objects sequence. The third experiment is carried out on frame # 150 from the PoznanStreet sequence. The fourth experiment is implemented on frame # 200 from the Shark sequence. Simulation experiments have been conducted using an Intel® Core™i7-4500U CPU @1.80GHz and 2.40 GHz with 8 GB RAM, utilizing Windows 10 64-bit operating system, and MATLAB 2017b.

Figure 5: Original plain 3DV frames of the tested 3D-MVC and 3D-HEVC sequences (a) Original Balloons frame 50 (b) Original Objects frame 100 (a) Original PoznanStreet frame 150 (b) Original Shark frame 200 (i) 3D-MVC sequences (ii) 3D-HEVC sequences

4.1 Visual Results

Visual assessment is one of the first, straightforward, and most astonishing tools in assessing the encryption quality and ciphering/deciphering efficiency. A ciphering algorithm is claimed to succeed in its operation if the distinguishing features of cipher video frames disappear. The results of the ciphered 3DV frames and their decrypted 3DV frames are shown in Fig. 6 for the tested 3DV sequences. From these results, all details of the ciphered 3DV frames disappear with the proposed technique. In addition, it is noticed that the decryption efficiency of the proposed technique is appreciated. Therefore, the proposed DRPE-based 3DV cybersecurity framework is appropriate for encrypting and hiding the main features of the 3DV frames. Also, it succeeds in decrypting the frames and recovering them from the original 3DV frames due to the advantages of the implemented optical DRPE technique.

Figure 6: Encrypted and decrypted 3DV frames of the tested 3D-MVC and 3D-HEVC sequences (a) Encrypted Balloons frame 50 (b) Decrypted Balloons frame 100 (c) Encrypted Objects frame 100 (d) Decrypted Objects frame 100 (i) 3D-MVC sequences (a) Encrypted PoznanStreet frame 150 (b) Decrypted PoznanStreet frame 150 (c) Encrypted Shark frame 200 (d) Decrypted Shark frame 200 (ii) 3D-HEVC sequences

4.2 Histograms Analysis

Histogram analysis of the video frames reflects the occurrence rate of each gray level in the frames. The histograms of the tested plain 3DV frames, their corresponding ciphered 3DV frames, and decrypted 3DV frames are presented in Fig. 7. It is noticed from the presented results that the ciphered 3DV frame histograms are uncorrelated with their corresponding decrypted 3DV frame histograms due to the diffusion induced by the DRPE. These results confirmed the validity of the proposed DRPE technique.

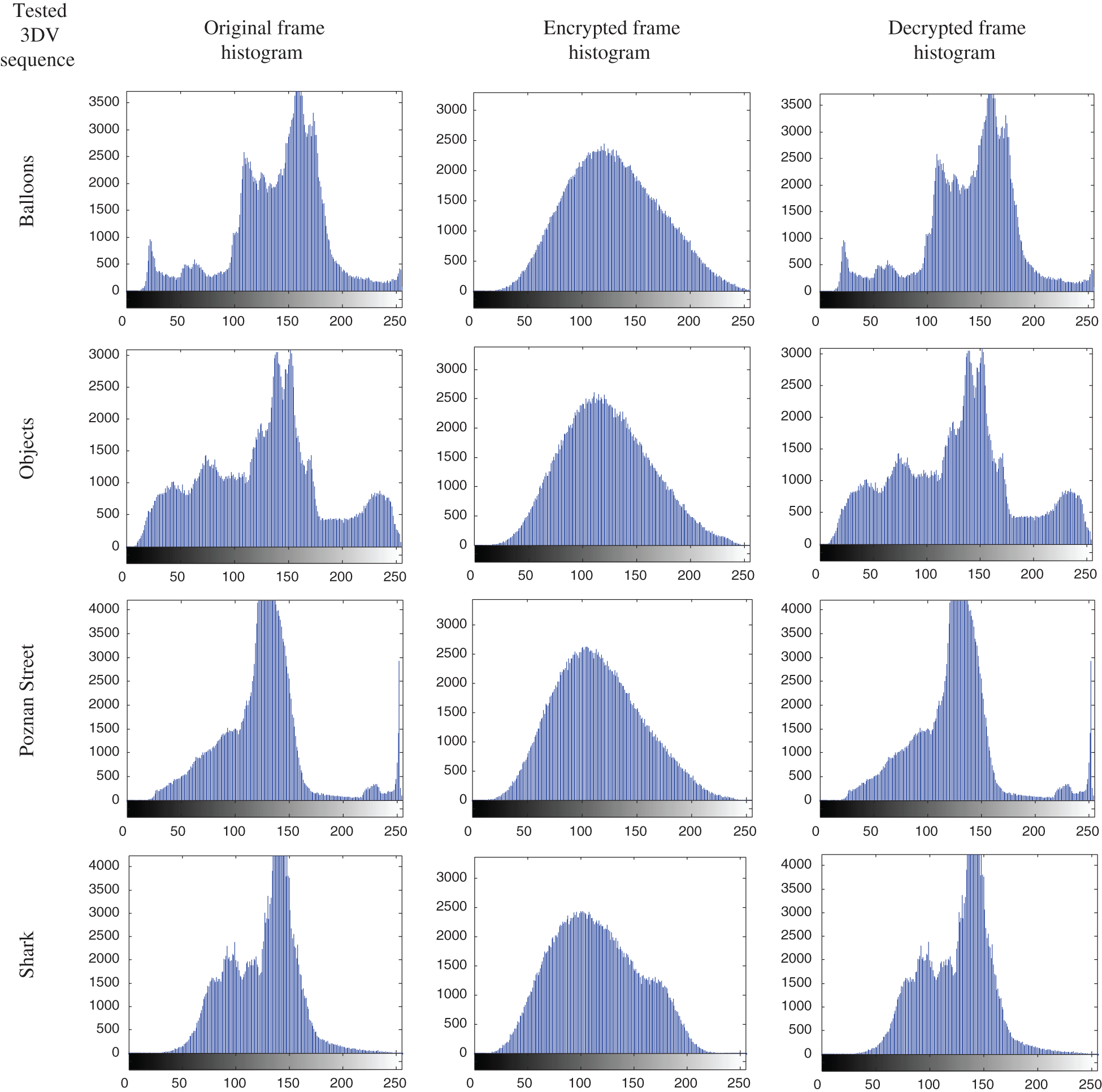
Figure 7: Histogram results of the original, encrypted, and decrypted 3DV frames of 3D-MVC and 3D-HEVC sequences

4.3 PSNR, SSIM and FSIM

In order to evaluate the quality of the enciphered 3DV frames, the PSNR, SSIM and FSIM values are estimated between the original plain 3DV frames and the encrypted 3DV frames. The performance of the encryption procedure is investigated with the PSNR value, since a lower PSNR value for enciphered 3DV frames indicates a better encryption performance of the proposed DRPE-based 3DV cybersecurity framework. The PSNR is calculated as follows [26]:

PSNR=10log(255)2∑i=0W−1∑j=0H−1[v1(i,j)−v2(i,j)]2 (4)

where v1(i,j) and v2(i,j) are pixel gray levels at the jth column and ith row of the W×H plain and encrypted 3DV frames, respectively. The computed results of PSNR for the four tested 3DV sequences are shown in Tab. 2 for the presented DRPE-based 3DV cybersecurity framework. For all of the tested cases, the PSNR values are low, which verifies and proves the efficiency of the presented encryption technique.

The SSIM is also estimated for investigating the encryption efficiency of the proposed DRPE-based 3DV cybersecurity framework. It is utilized for investigating the similarity between two 3DV frames. It is expressed as follows [26]:

SSIM(x,y|w)=(2w¯xw¯y+C1)(2σwxwy+C2)(w¯x2+w¯y2+C1)(σwx2+σwy2+C2) (5)

where w¯x is the mean of the region wx , w¯y is the mean of the region wy ; C1 and C2 are constant parameters; σwxwy is the covariance among the two regions, σwx2 is the variance of wx and σwy2 is the variance of wy . For better encryption quality, it is recommended to have lower values of SSIM of the encrypted 3DV frames. Tab. 2 presents the calculated SSIM outcomes for the four 3DV sequences. They are acceptable SSIM scores for the encrypted 3DV frames. These results confirm the efficiency of the proposed DRPE-based 3DV cybersecurity framework with different 3DV sequences, which have different spatio-temporal characteristics.

The FSIM is also utilized for investigating the encryption efficiency of the presented DRPE-based 3DV cybersecurity framework. It reflects the local similarity between the plain 3DV frame and the ciphered 3DV frame as follows [26]:

FSIM=∑x∈ΩSL(x).PCm(x)∑x∈ΩPCm(x) (6)

where SL(x) represents the similarity between the two 3DV frames, Ω and PCm(x) are the 3DV frame spatial domain and the phase congruency value. For effective encryption quality, a lower FSIM value is required for the encrypted 3DV frame. Tab. 2 shows the calculated FSIM results for the four 3DV sequences, which are low. These findings confirm the efficiency of the proposed DRPE-based 3DV cybersecurity framework with different 3DV sequences, which have different spatio-temporal characteristics.

4.4 Entropy

The entropy is utilized to assess the unpredictability of secret data of a ciphered MVC/HEVC frame cf as follows [33]:

E(cf)=−∑i=12N−1P(cfi)log2P(cfi) (7)

where P(cfi) represents the probability of cfi in the encrypted frame cf . N is the bits number of representing the cfi and log2 is employed to estimate the entropy value in terms of bits. The enciphered frame pixel values should cover the range from 0 to 255. The best expected entropy value is 8. In Tab. 2, the estimated entropy values are listed for each of the tested 3DV frames for the proposed DRPE-based 3DV cybersecurity framework. All entropy values of the enciphered frames are close to 8, which ensures the efficiency of the proposed framework. This implies that the information leak within the encryption may be neglected. Therefore, the presented 3DV encryption framework is robust against entropy attack.

Table 2: Quality metric results including PSNR, SSIM, FSIM, entropy, correlation coefficient, deviations, NPCR, UACI, and processing time values for the enciphered Balloons, Objects, PoznanStreet, and Shark MVC/HEVC sequence frames using the proposed DRPE-based 3DV cybersecurity framework

4.5 Encryption Quality

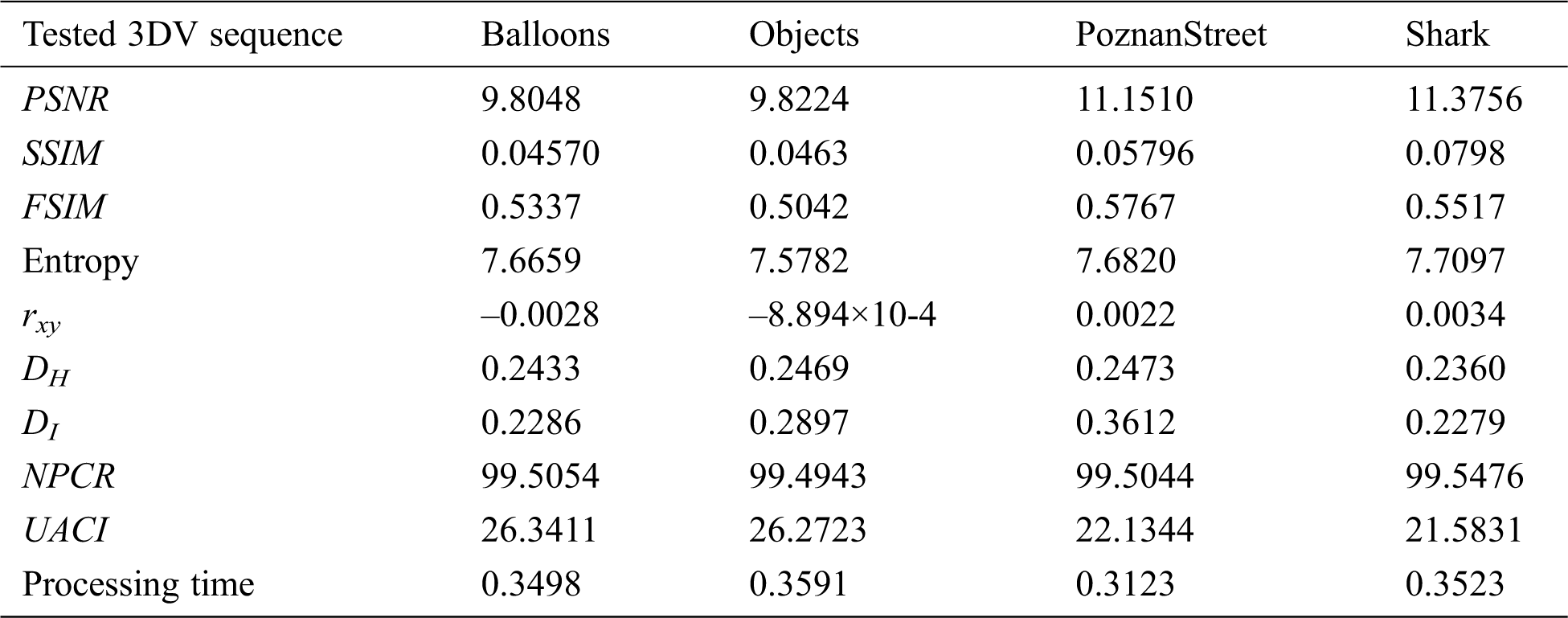
The encryption quality of the presented DRPE-based 3DV cybersecurity framework is examined with correlation coefficient between original and enciphered frames, and histogram deviation between 3DV frames and their corresponding encrypted frames, and the irregular deviation of encrypted 3DV frames from ideally encrypted ones.

The correlation coefficient rcp is computed between the 3DV frame and its corresponding encrypted frame. It can be computed by Eq. (8) [34]:

rcp=cov(c,p)D(c)D(p), (8)

where c and p are the 3DV plain frame and the corresponding 3DV enciphered frame, respectively. cov(c,p)=1L∑i=lL(c(i)−E(c))(p(i)−E(p)), D(c)=1L∑i=lL(c(i)−E(c))2, D(p)=1L∑i=lL(p(i)−E(p))2, and L is the pixel count in the 3DV frame.

The histogram deviation shows the quality of the proposed encryption technique through calculating the deviation between the original and encrypted 3DV frames using [26] as:

DH=(∑i=0255d(i))WxH, (9)

where d(i) represents the absolute difference between the histograms of the original and encrypted 3DV frames at intensity level i. The 3DV frame dimensions of both plain and encrypted frames are W×H.

The quality of the proposed encryption framework is verified through calculating the irregular deviation value DI as follows [26]:

DI=|∑i=0255hd(i)|WxH, (10)

hd(i)=|h(i)−M|, (11)

where h(i) and M are the enciphered 3DV frame histogram at intensity level i and the pre-assumed uniform histogram average for an ideally enciphered 3DV frame.

The correlation coefficient and the histogram deviation values between the original and encrypted 3DV frames, and also the irregular deviations of the plain 3DV frames for the tested 3DV sequences are presented in Tab. 2 for the proposed DRPE-based 3DV cybersecurity framework. The correlation coefficient values of the proposed encryption technique are close to zero, which means that there is a low correlation between the original and the encrypted 3DV frames. Furthermore, the obtained histogram deviation values are low and the resulting irregular deviation values are also low. Consequently, the plain 3DV frames and the ciphered 3DV frames are uncorrelated. All these findings ensure the great ciphering characteristics of the presented encryption technique.

4.6 Differential Analysis

The differential analysis includes variation of pixels or bits of the plain video frame. Consequently, one could find the changes between the original and the fake plain video frame. The performance of the presented 3DV ciphering framework with respect to such attack is examined through evaluating the Unified Averaged Changed Intensity (UACI) and the Number of Pixel Change Rate (NPCR) scores. In differential tests, the UACI and NPCR estimations are obtained for investigating the encryption system sensitivity to small changes in the plain 3DV frames. Assume two components CF1 and CF2 from two plain 3DV frames S1 and S2, respectively. The plain 3DV frames have 2-D matrices of size H×W with an assumption that if there is a pixel modification (i, j), then D(i, j) = 1. In this case, the UACI and NPCR are estimated for the enciphered 3DV frames CF1 and CF2 at position (i, j) as in [26,28]:

UACI=1W×H[∑i=1W∑j=1HCF1(i,j)−CF2(i,j)255]×100%, (12)

NPCR=∑i=1W∑j=1HD(i,j)W×H×100%, (13)

where W , and H are the enciphered MVC or HEVC frame width and height. In Tab. 2, the values of NPCR and UACI for the presented encryption framework are given for the tested 3DV frames. The obtained results show that the NPCR values are high and the UACI values are low, which means that the proposed encryption framework is secure and robust against differential attacks.

4.7 Encryption Time

The complexity of the proposed DRPE-based 3DV cybersecurity framework is determined by estimating the computational processing time of the encryption process. In Tab. 2, the average encryption time in seconds per frame for the proposed DRPE-based 3DV cybersecurity framework is illustrated. It is noticed that the proposed framework has low processing time for all tested 3DV sequences. So, it can be employed for real-time 3DV applications.

4.8 Edge Intensity

The proposed DRPE-based 3DV cybersecurity framework must mask the edge information in the 3DV encrypted frames and maintain this information after decryption in the presence of attacks. The visual distortion of the encrypted 3DV frames using the proposed encryption technique can be measured with the distortion presented in frame edges. The edge distortion may be estimated in terms of the edge differential ratio (EDR) that may be computed as [31]:

EDR=∑i,j=1N|PF(i,j)−CF¯(i,j)|∑i,j=1N|PF(i,j)+CF¯(i,j)| (14)

where PF(i,j) , and CF(i,j) are the detected maps of the plain and encrypted 3DV frames. PF¯(i,j) and CF¯(i,j) are the means of both maps, respectively. Fig. 8 illustrates the Laplacian of Gaussian edge detection for the plain, encrypted, and decrypted 3DV frames. Tab. 3 demonstrates that the EDR between the plain and corresponding encrypted 3DV frames is close to 1, which in turn confirms and verifies that the plain and enciphered 3DV frames are completely uncorrelated.

Figure 8: Laplacian of Gaussian edge detection of the plain, encrypted, and decrypted frames of the tested 3DV sequences

Table 3: The EDR for the encrypted 3DV frames of the tested 3DV sequences using the proposed DRPE-based 3DV encryption technique

5  Conclusion

The paper presented a DRPE-based 3DV cybersecurity framework that coverts a plain 3DV frame to an optical signal. Then, the optical signal is enciphered using the DRPE technique. Numerous tests using MATLAB have been executed on four distinctive 3DV sequences. The results of these tests and the security analysis prove that the proposed DRPE-based 3DV cybersecurity framework is secure and effective, with good immunity to different types of attacks. It is highly recommended for multimedia communication with security precautions.

Acknowledgement: The authors would like to thank the Deanship of Scientific Research, Taif University, Saudi Arabia, for funding the research project number 1-439-6083.

Funding Statement: This research was supported by the Deanship of Scientific Research, Taif University, Saudi Arabia, under research project number 1-439-6083.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Garae, R. K. Ko, J. Kho, S. Suwadi, M. A. Will et al. (2017). , “Visualizing the New Zealand cyber security challenge for attack behaviors,” in Trustcom/Big Data SE/ICESS, Sydney, NSW: IEEE, pp. 1123–1130. [Google Scholar]

 2.  A. Kott. (2014). “Towards fundamental science of cyber security,” in Network science and cybersecurity, New York, NY: Springer, pp. 1–13. [Google Scholar]

 3.  L. Pan, X. Zheng, H. X. Chen, T. Luan, H. Bootwala et al. (2017). , “Cyber security attacks to modern vehicular systems,” Journal of Information Security and Applications, vol. 36, no. 2, pp. 90–100. [Google Scholar]

 4.  A. Hahn, A. Ashok, S. Sridhar and M. Govindarasu. (2013). “Cyber-physical security testbeds: Architecture, application, and evaluation for smart grid,” IEEE Transactions on Smart Grid, vol. 4, no. 2, pp. 847–855. [Google Scholar]

 5.  Y. Yan, Y. Qian, H. Sharif and D. Tipper. (2012). “A survey on cyber security for smart grid communications,” IEEE Communications Surveys & tutorials, vol. 14, no. 4, pp. 998–1010. [Google Scholar]

 6.  H. Ogut, S. Raghunathan and N. Menon. (2011). “Cyber security risk management: public policy implications of correlated risk, imperfect ability to prove loss, and observability of self protection,” Risk Analysis: An International Journal, vol. 31, no. 3, pp. 497–512. [Google Scholar]

 7.  S. Subashini and V. Kavitha. (2011). “A survey on security issues in service delivery models of cloud computing,” Journal of Network and Computer Applications, vol. 34, no. 1, pp. 1–11. [Google Scholar]

 8.  D. S. A. Elminaam, H. M. Abdual-Kader and M. M. Hadhoud. (2010). “Evaluating the performance of symmetric encryption algorithms,” International Journal of Network Security, vol. 10, no. 3, pp. 216–222. [Google Scholar]

 9.  A. Rocha, W. Scheirer, T. Boult and S. Goldenstein. (2011). “Vision of the unseen: Current trends and challenges in digital image and video forensics,” ACM Computing Surveys (CSUR), vol. 43, no. 4, pp. 1–42. [Google Scholar]

10. T. R. Singh, K. M. Singh and S. Roy. (2013). “Video watermarking scheme based on visual cryptography and scene change detection,” AEU-International Journal of Electronics and Communications, vol. 67, no. 8, pp. 645–651. [Google Scholar]

11. P. Yadav, N. Mishra and S. Sharma. (2013). “A secure video steganography with encryption based on LSB technique,” in Computational Intelligence and Computing Research (ICCIC) IEEE Int. Conf. on, Enathi, India: IEEE, pp. 1–5. [Google Scholar]

12. L. Luo, Z. Chen, M. Chen, X. Zeng and Z. Xiong. (2010). “Reversible image watermarking using interpolation technique,” IEEE Transactions on Information Forensics and Security, vol. 5, no. 1, pp. 187–193. [Google Scholar]

13. W. L. Tai, C. M. Yeh and C. C. Chang. (2009). “Reversible data hiding based on histogram modification of pixel differences,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 19, no. 6, pp. 906–910. [Google Scholar]

14. T. Bianchi and A. Piva. (2013). “Secure watermarking for multimedia content protection: A review of its benefits and open issues,” IEEE Signal Processing Magazine, vol. 30, no. 2, pp. 87–96. [Google Scholar]

15. R. V. Solms and J. V. Niekerk. (2013). “From information security to cyber security,” Computers & security, vol. 38, no. 6, pp. 97–102. [Google Scholar]

16. D. Bouslimi, G. Coatrieux and C. Roux. (2012). “A joint encryption/watermarking algorithm for verifying the reliability of medical images: Application to echographic images,” Computer Methods and Programs in Biomedicine, vol. 106, no. 1, pp. 47–54. [Google Scholar]

17. X. Zhang. (2012). “Separable reversible data hiding in encrypted image,” IEEE Transactions on Information Forensics and Security, vol. 7, no. 2, pp. 826–832. [Google Scholar]

18. F. Y. Shih. (2017). Digital watermarking and steganography: fundamentals and techniques. Second Edition, CRC press, Boca Raton. [Google Scholar]

19. S. Li, G. Chen and X. Zheng. (2006). “Chaos-based encryption for digital image and video,” Multimedia Encryption and Authentication Techniques and Applications, First Edition, Auerbach Publications, pp. 129–163. [Google Scholar]

20. J. Fridrich. (2011). “Symmetric ciphers based on two-dimensional chaotic maps,” International Journal of Bifurcation and Chaos, vol. 08, no. 06, pp. 1259–1284. [Google Scholar]

21. R. Ye and H. Huang. (2010). “Application of the chaotic ergodicity of standard map in image encryption and watermarking,” International Journal of Image, Graphics and Signal Processing, vol. 2, no. 1, pp. 19–29. [Google Scholar]

22. R. Ye. (2011). “A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism,” Optics Communications, vol. 284, no. 22, pp. 5290–5298. [Google Scholar]

23. S. Ergün. (2015). “Security analysis of a chaos-based random number generator for applications in cryptography,” Communications and Information Technologies (ISCIT), Nara, Japan, pp. 319–322. [Google Scholar]

24. Y. Wang, K. W. Wong, X. Liao and G. Chen. (2011). “A new chaos-based fast image encryption algorithm,” Applied Soft Computing, vol. 11, no. 1, pp. 514–522. [Google Scholar]

25. D. Xiao, X. Liao and P. Wei. (2009). “Analysis and improvement of a chaos-based image encryption algorithm,” Chaos, Solitons & Fractals, vol. 40, no. 5, pp. 2191–2199. [Google Scholar]

26. E. A. Naeem, M. M. A. Elnaby, N. F. Soliman, A. M. Abbas, O. S. Faragallah et al. (2014). , “Efficient implementation of chaotic image encryption in transform domains,” Journal of Systems and Software, vol. 97, pp. 118–127. [Google Scholar]

27. L. Chen and D. Zhao. (2006). “Optical image encryption with Hartley transforms,” Optics Letters, vol. 31, no. 23, pp. 3438–3440. [Google Scholar]

28. B. Hennelly and J. T. Sheridan. (2003). “Optical image encryption by random shifting in fractional Fourier domains,” Optics Letters, vol. 28, no. 4, pp. 269–271. [Google Scholar]

29. S. Liu, L. Yu and B. Zhu. (2001). “Optical image encryption by cascaded fractional Fourier transforms with random phase filtering,” Optics Communications, vol. 187, no. 3, pp. 57–63. [Google Scholar]

30. P. Refregier and B. Javidi. (1995). “Optical image encryption based on input plane and Fourier plane random encoding,” Optics Letters, vol. 20, no. 7, pp. 767–769. [Google Scholar]

31. W. Qin and X. Peng. (2009). “Vulnerability to known-plaintext attack of optical encryption schemes based on two fractional Fourier transform order keys and double random phase keys,” Journal of Optics A: Pure and Applied Optics, vol. 11, no. 7, pp. 075402. [Google Scholar]

32. S. Liu, C. Guo and J. T. Sheridan. (2014). “A review of optical image encryption techniques,” Optics & Laser Technology, vol. 57, no. 6, pp. 327–342. [Google Scholar]

33. M. Cho and B. Javidi. (2013). “Three-dimensional photon counting double-random-phase encryption,” Optics Letters, vol. 38, no. 17, pp. 3198–3201. [Google Scholar]

34. Z. Liu, S. Li, W. Liu, Y. Wang and S. Liu. (2013). “Image encryption algorithm by using fractional Fourier transform and pixel scrambling operation based on double random phase encoding,” Optics and Lasers in Engineering, vol. 51, no. 1, pp. 8–14. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.