DOI:10.32604/iasc.2021.016822

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.016822 |  |
| Article |
Solid Waste Collection System Selection Based on Sine Trigonometric Spherical Hesitant Fuzzy Aggregation Information
1Deanship of Combined First Year, Umm Al-Qura University, Makkah, Saudi Arabia
2Department of Mathematics, Abdul Wali Khan University, Mardan, 23200, Pakistan
3Department of Mathematics and Statistics, Bacha Khan University, Charsadda, 24420, Pakistan
4Department of Mathematics, Deanship of Applied Sciences, Umm Al-Qura University, Makkah, Saudi Arabia
*Corresponding Author: Saleem Abdullah. Email: saleemabdullah@awkum.edu.pk
Received: 10 January 2021; Accepted: 12 February 2021
Abstract: Spherical fuzzy set (SFS) as one of several non-standard fuzzy sets, it introduces a number triplet (a,b,c) that satisfies the requirement
Keywords: Spherical fuzzy set; Hesitant fuzzy set; spherical hesitant fuzzy set; Sine trigonometric aggregation information; decision making
The smart city idea is focused on the incorporation of information and communication technologies (ICTs) into city services to accumulate information for the allocation of assets and services, along with enhancing value of life and susceptibility. Difficulties and inefficient solutions in today’s cities raise a need for the smart apps to solve existing challenges effectively. In this background, many academics, architects, urban planners, and even municipal representatives have been drawn to smart city applications. In addition, a wide variety of implementations are available for the smart city concept in areas such as town planning, waste disposal, resource management and municipal services [1–3].
In particular, the problem of solid waste collection system selection is a multi-criteria decision-making problem that should also take into account environmental, social, economic and technological aspects. Due to the labor strength of the job and the use of the large number of vehicles in these processes, sample and transport are commonly considered to be the most critical and expensive phases of the process [4]. As ever, certain issues such as quick disposal of wastes from half-full bins and thus excessive fuel use of collection and transport vehicles, higher pollution levels, inefficient usage of city assets and services are raised in the predefined scheduling [5]. In this respect, the brand-new visible light communication (VLC) technique makes it possible to communicate ultra-fastly among terminals through light bulbs and to become an essential competitor for conventional radio frequency (RF) communication like Wi-Fi [6]. Without providing some other [7] communication method, VLC can supply a room’s interior lighting and data exchange at the same time.
Multiple criteria group decision making (MCGDM) method [8–14] is a significant and arising subject to depict an approach for choosing the finest alternative with group of the decision makers (DMs) and conditions. Two serious tasks are there in this procedure. The first one is to depict the atmosphere where the values of various attributes can be scrutinized successfully, while the aggregation of the depicted data is the second task. Generally, the data which depict the substances are frequently taken in the form of the deterministic or crisp in nature. Though, with the rising complications of the frameworks step by step, hardly data can be accumulated, from the records, assets and specialists, in crisp form. Therefore, to present the data more openly, a notion of fuzzy sets
In this paper, we offered the pioneering view of T- spherical HeFS (T-SHFS) by using the concept of SFS and HeFS to check the incredibility and imprecise figures in DMPs to reform the supreme alternative in conferring to list of criteria. A DMPs AOs acts the supreme role to aggregate the data. Since, for every aggregation procedure the rules of the operation perform a key role. It is necessary to construct fresh laws for the operation and aggregation of T-SHFNs. Consequently, the aim of this paper is to suggest some new laws for the operation of T-SHFSs. Therefore, by using the above stated proofs, we offered the MCGDM algorithm to grip the assessment material for T-SHFSs.
This unit contains some basic definitions of FS, InFS, PytFS, SFS, HeFS and SHFS.
Definition 1. [18] Consider the ground set
where
Definition 2. [13] Consider the ground set
where
Definition 3: Consider the ground set
Where
Definition 4. [13] A T-spherical fuzzy set (T-SFS)
where
Definition 5. Suppose
(1)
(2)
(3)
Definition 6. Let
(1)
(2)
(3)
(4)
3 New Sine Trigonometric Operational Laws for T-SHFS
We express a number of new operational laws for T-SHFSs in this part.
Definition 7. Consider a non-empty set
It is obviously understood that the
the neutral function:
and the non-membership function:
Therefore
is a T-SHFS.
Definition 8. Let
then
4 Sine Trigonometric Aggregation Operators
On the basis of STOL of T-SHFNs, we describe the below weighted averaging and geometric aggregation operators. Let
Definition 9. Let
hence the mapping T-SpHeFWA is known as sine trigonometric T-SpHeF weighted averaging operator, where
Theorem 1. Consider the set
Proof: We prove the theorem using induction method. Since for each
(1) For
As from Definition 3.1, we can see that
Assume Eq. (1) holds for
Hence, Eq. (1) also valid for
Definition 10. A sine-trigonometric T-SHFN ordered weighted average (ST-T-SpHeFOWA) operator is a mapping ST-T-SpHeFOWA
where
Theorem 2. For a collection of
.
Definition 11. A sine-trigonometric T-SHFN hybrid average (ST-T-SpHeFHA) operator is a mapping ST-T-SpHeFHA
where
Theorem 3. For a collection of
.
Definition 12. Let
then the function ST-T-SpHeFWG is called sine trigonometric T-SpHeF weighted geometric operator, where
Theorem 4. Let
Definition 13. A sine trigonometric TSpHeF ordered weighted geometric (ST-TSpHeFOWG) operator is a mapping
where
Theorem 5. Let
Definition 14. A sine trigonometric T-SpHeF hybrid weighted geometric (ST-TSpHeFHG) operator is a mapping ST-TSpHeFHG
where
Theorem 6. Let
As similar to ST-TSHFWA operator, the ST-TSpHeFOWA, ST-TSpHeFHA, ST-TSpHeFWG, ST-TSpHeFOWG and ST-TSpHeFHG operators satisfy the properties such as boundedness, monotonicity.
Fundamental Properties of the Proposed AOs
In this subsection, we scrutinized some relations between the suggested AOs and study their various major properties as given below.
Theorem 7. For two T-SHFNs
Proof: Let
and
Since for any two non-negative real numbers
which further gives that
Similarly, we can obtain
And
Hence, by using Definition (i), we get
Theorem 8. Let
(1)
Proof: We will prove part (1) only. Part (2) can be obtained in a similar way. For this, let
and
For
Similarly, we can get
Therefore, from above Eqs, we get
Here, we have settled a structure for addressing improbability in decision making (DM) under TSpHeF material. Consider a DM problem with a set of m alternatives
where
Step-1: Construct the expert evaluation matrix
where
Step-2: Construct the normalized decision matrix
Step-3: Aggregate the individual decision matrices based on the T-sphrical hesitant fuzzy aggregation operators to construct the collective matrix. Exploit the established aggregation operators to achieve the TSHFN
Step-4: Compute the score of all the values
Step-5: Rank the alternatives
We analyze the results of the established MAGDM technique with a numerical example and compare the outcomes with the one of the existing MAGDM techniques, in this area. The aim of this research is to implement T-SpHeF data methodology in a smart city area to analyze and grade alternative waste collection systems.
Case Study; Municipal Waste Collection System Selection:
Descriptions of the Problem: For human health, aesthetics, and environmental consevation, municipal solid waste (SW) management is much more needed and essential facilities. It covers all the operations and steps necessary for waste management from selection to final disposal [1]. A critical stage of an effective waste management strategy is the identification of frequently contradictory natural, social and economic requirements and the list of alternatives. The waste disposal truck drives and stops at each building in this collection system to pick up the solid waste [2,3]. Four criteria are defined in this analysis;
Innovativeness and Aesthetics
Maintenance Efficiency
Sustainability
Setup Cost Advantage
Now following are the four alternatives concept and solution of above criteria. We suggest ideas for smart city solid waste collection (SWC) in this context, in which VLC are included. In addition, we use two new SWC ideas for smart cities in which Wi-Fi connectivity and cellular connectivity are used. Smart bins fitted with sensors, microprocessor, battery packs, compaction systems as well as solar power are taken into account in all alternatives. The bins are used both to collect waste and to collect waste data.
Wi-Fi-based SWC System
Cellular Communication-based SWC System
Li-Fi-based SWC System
Waste Management Collection and Transportation with Drones
Application of Proposed MAGDM Method
Suppose, three experts
Step-1: The expert evaluation information is in the form of
Table 1: Expert evaluation information (E)1

Step-2: The normalized expert evaluation information in enclosed in Tab. 2:
Table 2: Normalized expert evaluation information (N)1

Step-3: In this case study, we have only one expert so, we have no need to normalized
Step-4: In this step, we calculate the combined preference values of alternatives under criteria weight is
Case 1: Using WA
We apply ST-TSpHeFWA aggregation operator to the data provided in above matrix to find out the aggregated values. The combined preference values of each alternative using WA
Table 3: Overall preference value (ST-TSpHeFWA)

Case 2: Using ST-TSpHeFWG aggregation operator
We apply ST-TSpHeFWG aggregation operator to above matrix to find out the aggregated values. The combined preference values of each alternative using WGST–TSHF aggregation operator is enclosed in Tab. 4:
Table 4: Overall preference value (ST-TSpHeFWG)

Step-5: Score of collective overall preference values of each alternative is enclosed in Tab. 5:

Step-6: Rank the alternatives
Table 6: Ranking of the alternatives
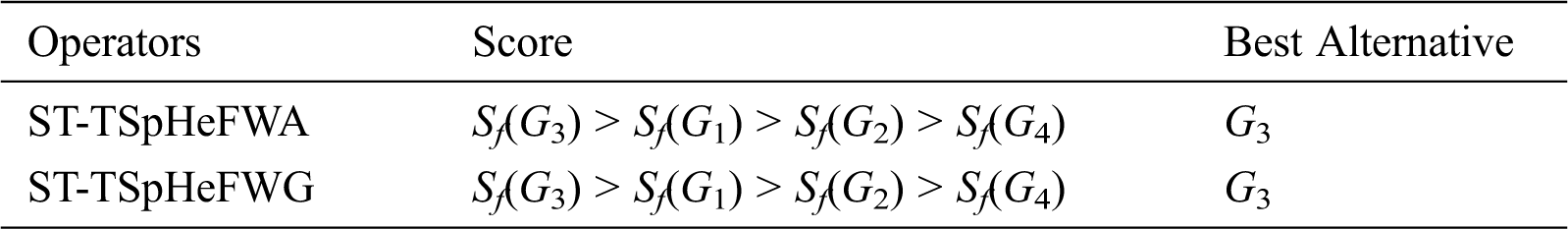
From the above computational process, we concluded that alternative Li-Fi-based solid waste collection system
7 Reliability and Validity Test
In fact, deciding the highest suitable alternative from the decision matrices provided by the group is extremely difficult. The approach to estimate the validity and reliability of decision-making approaches was started by Ashraf et al. [21]. The steps for testing are as follows.
Test Step-1.: If we substitute the normalized element for the worse element of the alternative by presenting the appropriate alternative with no modification and also with no altering the comparable position of each decision criterion, the appropriate and effective MAGDM technique is to do so.
Test Step-2.: Through an efficient and appropriate MAGDM procedure, transitive property must be met.
Test Step-3.: When an issue with MAGDM is turned into minor issues. A combined alternative rating should be equivalent to the original rating of un-decomposed problem to ranking the alternative, we apply identical approach on minor issues used in the problem of MAGDM.
To find the best result, the MAGDM problem was transformed into a smaller one and the same proposed decision-making approach were introduced. The suitable and efficient MAGDM strategy is that the outcome would be the same as the MAGDM problem if we apply the same technique to a small problem.
Validity Test the Proposed DM Methodology
In this area [21], using the validity and reliability test mentioned above, we check the appropriation and validation of our developed methodology. The normalized spherical hesitant fuzzy information is enclosed in the Tab. 2 (given Above):
Test Step-1: We substitute the normalized element for the worse element of the alternative by presenting the appropriate alternative with no modification and also with no altering the comparable position of each decision criterion, in this step. Tab. 7 enclosed the updated decision matrix
Table 7: Updated normalized T-Spherical hesitant fuzzy information

Now, we calculate the combined preference values of each alternative under criteria weight
Case-1: Using ST-TSpHeFWA aggregation operator:
The collective overall preference values of each alternative using ST-TSpHeFWA aggregation operator is enclosed in Tab. 8:
Table 8: Overall preference value (ST-TSpHeFWA)

Case-2: Using ST-TSpHeFWG aggregation operator
The combined preference values of each alternative using ST-TSpHeFWG aggregation operator is enclosed in Tab. 9:
Table 9: Overall preference value (ST-TSpHeFWG)

Now, Score of collective overall preference values of each alternative is enclosed in Tab. 10:

Rank the alternatives
Table 11: Ranking of the alternatives

We get again the same alternative
We are now testing the validity test Steps-2 & 3 to demonstrate that the proposed approach is reliable and relevant. To this end, we first transformed the MAGDM problem into three smaller sub-problems such as
In this analysis, using the T-spherical hesitant fuzzy set decision process, alternative municipal SWC systems based on various ICTs are analyzed and graded. Alternative SWC concepts are built on the above four alternatives, taking into account the current situation and needs of a study area. The case study is performed in an area where municipal authorities embrace the smart city strategy and there are ongoing smart city initiatives.
Attributes which are described above are taken into account when implementing the suggested T-spherical hesitant fuzzy set (T-SHFS) methodology. The outcomes of the study indicated that the more effective solutions for the survey are are Li-Fi and visible light communication-based collection systems. The findings of this research illustrate that in the smart city area, these devices can be chosen and applied, especially in the sense of SWC. The use of fuzzy sets has helped us to effectively transform the uncertainty and complexity of local decision-makers and scientific experts’ decisions. We developed certain robust sine-trigonometric (ST) operations laws (STOLs) for T-SHFSs and concluded new aggregation operators (AOs) to calculate T-SpHeF data which are ST weighted averaging and geometric operators.
In the future studies, the suggested T-SHFS methodology proposed here can be solve by applying TOPSIS method, q-ROFS based on real emergency and supply chain.
Acknowledgement: The authors would like to thank the Deanship of Scientific Research (DRS) at Umm Al-Qura University for supporting this work by Grant Code: 19-SCI-1-01-0041.
Funding Statement: The authors would like to thank the Deanship of Scientific Research (DRS) at Umm Al-Qura University for supporting this work by Grant Code: 19-SCI-1-01-0041.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Topaloglu, F. Yarkin and T. Kaya. (2018). “Solid waste collection system selection for smart cities based on a type-2 fuzzy multi-criteria decision technique,” Soft Computing, vol. 22, no. 15, pp. 4879–4890. [Google Scholar]
2. F. Mirzazadeh, F. Hadinejad and N. A. Roshan. (2018). “Investigating utility level of waste disposal methods using multicriteria decision-making techniques (case study: Mazandaran-Iran),” Journal of Material Cycles and Waste Management, vol. 20, no. 1, pp. 505–515. [Google Scholar]
3. I. A. Al-Khatib, H. A. Arafat, T. Basheer, H. Shawahneh, A. Salahat et al. (2007). , “Trends and problems of solid waste management in developing countries: A case study in seven Palestinian districts,” Waste Management, vol. 27, no. 12, pp. 1910–1919. [Google Scholar]
4. S. K. Amponsah and S. Salhi. (2004). “The investigation of a class of capacitated arc routing problems: The collection of garbage in developing countries,” Waste Management, vol. 24, no. 7, pp. 711–721. [Google Scholar]
5. J. M. Gutierrez, M. Jensen, M. Henius and T. Riaz. (2015). “Smart waste collection system based on location intelligence,” Procedia Computer Science, vol. 61, pp. 120–127. [Google Scholar]
6. A. Jovicic, J. Li and T. Richardson. (2013). “Visible light communication: opportunities, challenges and the path to market,” IEEE Communications Magazine, vol. 51, no. 12, pp. 26–32. [Google Scholar]
7. S. Rajagopal, R. D. Roberts and S. K. Lim. (2012). “IEEE 802.15.7 visible light communication: Modulation schemes and dimming support,” IEEE Communications Magazine, vol. 50, no. 3, pp. 72–82. [Google Scholar]
8. M. Lin, Z. Xu, Y. Zhai and Z. Yao. (2017). “Multi-attribute group decision-making under probabilistic uncertain linguistic environment,” Journal of the Operational Research Society, vol. 69, no. 2, pp. 157–170. [Google Scholar]
9. M. Lin, C. Huang, Z. Xu and R. Chen. (2020). “Evaluating IoT platforms using integrated probabilistic linguistic MCDM method,” IEEE Internet of Things Journal, vol. 7, no. 11, pp. 11195–11208. [Google Scholar]
10. M. Lin, H. Wang and Z. Xu. (2020). “TODIM-based multi-criteria decision-making method with hesitant fuzzy linguistic term sets,” Artificial Intelligence Review, vol. 53, no. 5, pp. 3647–3671. [Google Scholar]
11. M. Lin, W. Xu, Z. Lin and R. Chen. (2020). “Determine OWA operator weights using kernel density estimation,” Economic Research-Ekonomska Istraživanja, vol. 33, no. 1, pp. 1441–1464. [Google Scholar]
12. N. Jan, Z. Ali, T. Mahmood and K. Ullah. (2019). “Some generalized distance and similarity measures for picture hesitant fuzzy sets and their applications in building material recognition and multi-attribute decision making,” Punjab University Journal of Mathematics, vol. 51, no. 7, pp. 51–70. [Google Scholar]
13. Z. Ali, T. Mahmood and M. S. Yang. (2020). “TOPSIS method based on complex spherical fuzzy sets with Bonferroni mean operators,” Mathematics, vol. 8, no. 10, pp. 1739. [Google Scholar]
14. S. Ashraf, T. Mahmood, S. Abdullah and Q. Khan. (2019). “Different approaches to multi-criteria group decision making problems for picture fuzzy environment,” Bulletin of the Brazilian Mathematical Society, New Series, vol. 50, no. 2, pp. 373–397. [Google Scholar]
15. L. A. Zadeh. (1965). “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353. [Google Scholar]
16. K. T. Atanassov. (1986). “Intuitionistic fuzzy sets,” Fuzzy Sets and Systems, vol. 20, pp. 87–96. [Google Scholar]
17. R. R. Yager. (2013). “Pythagorean fuzzy subsets,” in 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPSEdmonton, AB, Canada: IEEE, pp. 57–61. [Google Scholar]
18. V. Torra. (2010). “Hesitant fuzzy sets,” International Journal of Intelligent Systems, vol. 25, no. 6, pp. 529–539. [Google Scholar]
19. R. R. Yager. (2014). “Pythagorean membership grades in multicriteria decision making,” IEEE Transactions on Fuzzy Systems, vol. 22, no. 4, pp. 958–965. [Google Scholar]
20. S. Ashraf, S. Abdullah and T. Mahmood. (2018). “GRA method based on spherical linguistic fuzzy Choquet integral environment and its application in multi-attribute decision-making problems,” Mathematical Sciences, vol. 12, no. 4, pp. 263–275. [Google Scholar]
21. S. Ashraf and S. Abdullah. (2019). “Spherical aggregation operators and their application in multiattribute group decision-making,” International Journal of Intelligent Systems, vol. 34, no. 3, pp. 493–523. [Google Scholar]
22. S. Ashraf, S. Abdullah, T. Mahmood, F. Ghani and T. Mahmood. (2019). “Spherical fuzzy sets and their applications in multi-attribute decision making problems,” Journal of Intelligent & Fuzzy Systems, vol. 36, no. 3, pp. 2829–2844. [Google Scholar]
23. Y. Jin, S. Ashraf and S. Abdullah. (2019). “Spherical fuzzy logarithmic aggregation operators based on entropy and their application in decision support systems,” Entropy, vol. 21, no. 7, pp. 628. [Google Scholar]
24. O. Barukab, S. Abdullah, S. Ashraf, M. Arif and S. A. Khan. (2019). “A new approach to fuzzy TOPSIS method based on entropy measure under spherical fuzzy information,” Entropy, vol. 21, no. 12, pp. 1231. [Google Scholar]
25. S. Ashraf and S. Abdullah. (2020). “Emergency decision support modeling for COVID-19 based on spherical fuzzy information,” International Journal of Intelligent Systems, vol. 35, no. 11, pp. 1601–1645. [Google Scholar]
26. S. Ashraf, S. Abdullah and A. O. Almagrabi. (2020). “A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19,” Soft Computing, vol. 54, no. 1–4, pp. 393. [Google Scholar]
27. R. Chinram, S. Ashraf, S. Abdullah and P. Petchkaew. (2020). “Decision support technique based on spherical fuzzy Yager aggregation operators and their application in wind power plant locations: A case study of Jhimpir, Pakistan,” Journal of Mathematics, vol. 2020, no. 6, pp. 21. [Google Scholar]
28. S. Ashraf, S. Abdullah and T. Mahmood. (2020). “Spherical fuzzy Dombi aggregation operators and their application in group decision making problems,” Journal of Ambient Intelligence and Humanized Computing, vol. 11, no. 7, pp. 2731–2749. [Google Scholar]
29. N. Chen, Z. Xu and M. Xia. (2013). “Interval-valued hesitant preference relations and their applications to group decision making,” Knowledge-Based Systems, vol. 37, pp. 528–540. [Google Scholar]
30. H. Jin, S. Ashraf, S. Abdullah, M. Qiyas, M. Bano et al. (2019). , “Linguistic spherical fuzzy aggregation operators and their applications in multi-attribute decision making problems,” Mathematics, vol. 7, no. 5, pp. 413. [Google Scholar]
31. M. Rafiq, S. Ashraf, S. Abdullah, T. Mahmood and S. Muhammad. (2019). “The cosine similarity measures of spherical fuzzy sets and their applications in decision making,” Journal of Intelligent & Fuzzy Systems, vol. 36, no. 8, pp. 1–15. [Google Scholar]
32. S. Ashraf, S. Abdullah and L. Abdullah. (2019). “Child development influence environmental factors determined using spherical fuzzy distance measures,” Mathematics, vol. 7, no. 8, pp. 661. [Google Scholar]
33. S. Ashraf, S. Abdullah, M. Aslam, M. Qiyas and M. A. Kutbi. (2019). “Spherical fuzzy sets and its representation of spherical fuzzy t-norms and t-conorms,” Journal of Intelligent & Fuzzy Systems, vol. 36, no. 6, pp. 6089–6102. [Google Scholar]
34. S. Zeng, A. Hussain, T. Mahmood, M. Irfan Ali, S. Ashraf et al. (2019). , “Covering-based spherical fuzzy rough set model hybrid with TOPSIS for multi-attribute decision-making,” Symmetry, vol. 11, no. 4, pp. 547. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |