DOI:10.32604/iasc.2020.012813

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.012813 |  |
| Article |
Reconstruction and Optimization of Complex Network Community Structure Under Deep Learning and Quantum Ant Colony Optimization Algorithm
1Digital Performance and Simulation Technology, School of Computer Science & Technology, Beijing Institute of Technology, Beijing, 100081, China
2Fujian Provincial Key Laboratory of Information Processing and Intelligent Control, Minjiang University, Fuzhou, 350117, China
3Department of Computer Science, University of California, Davis, CA, 95616, USA
*Corresponding Author: Fuquan Zhang. Email: zhangqing94@126.com
Received: 13 July 2020; Accepted: 16 August 2020
Abstract: Community structure is a key component in complex network systems. This paper aims to improve the effectiveness of community detection and community discovery in complex network systems by providing directions for the reconstruction and optimization of community structures to expand the application of intelligent optimization algorithms in community structures. First, deep learning algorithms and ant colony algorithms are used to elaborate the community detection and community discovery in complex networks. Next, we introduce the technology of transfer learning and propose an algorithm of deep self-encoder modeling based on transfer learning (DSEM-TL). The DSEM-TL algorithm’s indicators include normalized mutual information and modularity. Finally, an algorithm that combines the ant colony optimization (ACO) algorithm and the quantum update strategy, called QACO, is proposed. The proposed community structure reconstruction scheme is compared with other methods using the accuracy rate as the indicator. The results show that the DSEM-TL algorithm exhibits the optimal detection rate, better applicability, and higher effectiveness in real networks. Under the given the condition that the number of edges between communities Zout is >6, DSEM-TL shows better performance on the Girvan–Newman benchmark network than several other community discovery algorithms. Furthermore, under the given condition that the mixed parameter μ is >0.65, the DSEM-TL algorithm outperforms several other algorithms on the Lancichinetti–Fortunato–Radicchi benchmark network. When given μ < 0.4, the QACO algorithm can determine the proper division of the corresponding network. When the case is μ > 0.45, the division result corresponding to the QACO algorithm is closer to the real community division, which has a faster convergence speed and better convergence performances. Consequently, the proposed community structure reconstruction scheme has higher accuracy. The proposed two intelligent optimization algorithms have potential application in the reconstruction and optimization of community structure.
Keywords: Complex network; DSEM-TL algorithm; QACO algorithm; community detection; community discovery
As a branch of network science, the complex network can be regarded as a collection formed by some individuals, which shows the interconnection between individuals [1,2]. Most research on complex networks consists of structure, models, dynamics, structure mining prediction, and control [3]. In additional, network reconstruction belongs to the category of dynamics [4], which predict a network’s topological structure by mining the missing information in the network [5,6]. Various scholars have conducted research on community structure because of its critical role in complex networks [7–10]. Jia et al. [11] proposed a k nearest neighborhoods (k-NN) graph with increased node attributes to mitigate the sparsity and noise effects of the original network. K-NN enhances the community structure in complex networks and is expected to be widely applied in large-scale network analysis. Guendouz et al. [12] proposed a discrete improved firework algorithm (FWA) for community detection in complex networks based on the label propagation strategy. They believed that the new algorithm had sound effects. Zou et al. [13] proposed an optimized multi-objective discrete backtracking search algorithm (MODBSA/D) and decomposed it into community detection in complex networks. Afterward, they proved that the algorithm performs well in the community detection of complex networks. Li et al. [14] combined orthogonal triangulation decomposition with compressed sensing and proposed a method to solve the reconstruction problem of complex networks using input noise. This research method reconstructed sparse complex networks and was useful in the reconstruction of dense and complex networks. Ma et al. [15] proposed an approach based on statistical reasoning to solve the problem of reconstructing complex network structures in observed binary data. The application of the expectation-maximization (EM) algorithm provided a new supplement for the rapidly expanding reconstruction problems of complex network systems. Based on the issue of binary state dynamics in the reconstruction of complex network systems, Li et al. [16] developed a data-based linearization method, which provided a framework for the reconstruction of complex networks using binary state dynamics. Fu et al. [17] proposed a new node degree variance ratio method for distinguishing a leading community from a self-organizing community in a complex network system. This method achieved robustness on a real network. In summary, while research results about the reconstruction and optimization of community structures in complex network systems vary, the methods of integrating quantum mechanisms into them are rarely reported.
Therefore, to explore the reconstruction and optimization of the community structure in the complex network systems, the optimized deep learning algorithm and quantum ant colony optimization (QACO) algorithm are applied to community detection and community discovery. The algorithms aim to improve the effectiveness of community detection, discovery, and mining. Hopefully, the results can provide some references for the reconstruction and optimization of community structure.
2.1 Complex Network Community Detection and Discovery
Community detection is a critical characteristic of complex networks. The analysis and mining of community structures in complex networks are of great significance for discovering the inherent development rules of complex networks and the correlation of relevant indicators within these networks [18,19]. Nodes belonging to the same community have a higher degree of similarity in the representation of related features. Community discovery of complex networks is an effective way to classify these nodes in complex networks. In the study of complex networks, the exploration of community structure not only discovers the unknown laws or phenomena but also leads to an understanding of the relationship between the structures and corresponding functions. Complex networks, such as transportation systems, power grid systems, and the World Wide Web are in inextricably linked to the daily lives of people. However, finding and mining useful information inside the network is a challenge. We need to learn how to retrieve information from the massive amounts of big data in the study of complex networks.
In the real network structure, the community structure is widespread. From the perspective of network nodes, it can be divided into a collection of many nodes. If there is a close connection within the network node collection, and this connection between them also shows a relatively loose state, it will be determined that the corresponding complex network has a community structure. The accurate identification of community structure has developed into a crucial stage of obtaining sufficient information [20,21]. The topological structure of a complex network can be expressed as:

where:  represents the topology of the complex network,
represents the topology of the complex network, 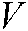 represents the set
represents the set 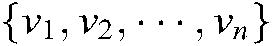 corresponding to the points including
corresponding to the points including 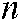 nodes, and
nodes, and 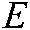 represents the set of edges corresponding to two random nodes in
represents the set of edges corresponding to two random nodes in 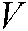 .
.
2.2 Community Discovery Optimization Algorithm Based on Deep Learning
Because deep learning algorithms have excellent performance in feature extraction, deep learning has been successfully applied in the fields of image classification and semantic recognition [22,23]. Fig. 1 below illustrates a hidden learning network structure composed of three hidden layers. The technologies of self-encoders, deep belief networks, and convolutional neural networks are widely utilized in deep learning. Self-encoders are built for deep structures through stacking and layerwise training. The encoder can also fine-tune the input signal in the entire network [24]. Therefore, combined with transfer learning, self-encoders are applied to community discovery for complex network community structures.

Figure 1: Structural composition of the deep learning network
The proposed deep self-encoder modeling based on transfer learning (DSEM-TL) consists of the data preprocessing module, the feature extraction module, and the optimization module. The data preprocessing module is primarily responsible for the preprocessing of the original adjacency matrix in the complex network. Based on the topology of the complex network, the community discovery problem is to divide complex network systems into nodes as different groups or communities. The problem can be expressed as:


where: 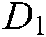 represents the converted adjacency matrix,
represents the converted adjacency matrix,  represents the function
represents the function 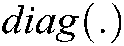 among
among 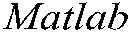 , which can realize the construction of the diagonal matrix, and
, which can realize the construction of the diagonal matrix, and 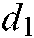 represents the degree of the network node. The realization of the entire matrix conversion process is completed by vector operation. Thus, we need to construct the matrix
represents the degree of the network node. The realization of the entire matrix conversion process is completed by vector operation. Thus, we need to construct the matrix 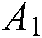 and
and 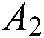 . The corresponding expression is
. The corresponding expression is


Then, based on the eigenvalue function, the maximum eigenvalue 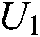 corresponding to
corresponding to 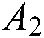 is calculated. The corresponding calculation is
is calculated. The corresponding calculation is

where: 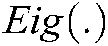 represents the
represents the 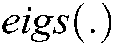 function in
function in  ,
, 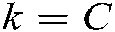 , and
, and  represents the size of the community in a complex network. Finally, the transformed similarity matrix can be obtained,
represents the size of the community in a complex network. Finally, the transformed similarity matrix can be obtained,

where: 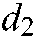 represents the row sum corresponding to the matrix
represents the row sum corresponding to the matrix 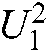 , and
, and 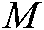 corresponds to the input matrix of the self-encoder.
corresponds to the input matrix of the self-encoder.
In the feature extraction module, transfer learning is introduced to build a target prediction model with excellent generalization performance. The algorithm is trained by a parameter-based migration method. Specifically, the overall loss function is defined
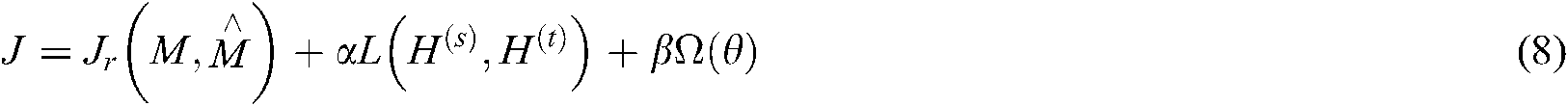
where: 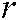 represents the source domain and the target domain,
represents the source domain and the target domain,  and
and 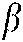 correspond to the adjustment of parameters in the overall loss function,
correspond to the adjustment of parameters in the overall loss function, 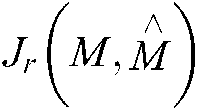 represents the reconstruction error between the source domain and the target domain in the objective function,
represents the reconstruction error between the source domain and the target domain in the objective function, 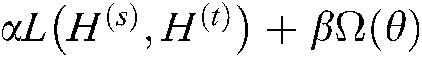 represents the
represents the  divergence that the embedding instance has between two different domains, and
divergence that the embedding instance has between two different domains, and 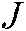 represents the overall loss function.
represents the overall loss function.
In the optimization module, through the application of the backpropagation algorithm based on the stochastic gradient descent method, the minimization problem in the overall loss function is solved. The update of the weight and the update of the offset term parameters are then realized by the following rules




where: 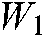 ,
, 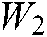 ,
, 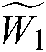 , and
, and 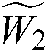 represent weights,
represent weights, 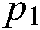 ,
, 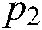 ,
, 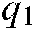 , and
, and 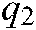 represent bias term parameters, and
represent bias term parameters, and 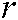 represents the learning rate. The implementation process of the DSEM-TL algorithm is shown in Fig. 2.
represents the learning rate. The implementation process of the DSEM-TL algorithm is shown in Fig. 2.

Figure 2: Implementation process of DSEM-TL algorithm
To test the effectiveness of the proposed DSEM-TL algorithm, the learning rate corresponding to the deep self-encoder is set to 0.01, and the number of training iterations is set to 100,000. Furthermore, by comparing and analyzing the widely used community discovery solutions in the Girvan–Newman (GN) and the Lancichinetti–Fortunato–Radicchi (LFR) benchmark network, we test the effectiveness of the DSEM-TL algorithm in structural reconstruction and optimization in the complex network community. The selected commonly used community discovery schemes the subspace pursuit (SP) algorithm [25], unified link and content (ULC) [26], fast Fourier transform (FFT) Accumulation Method (FAM) [27], fast unfolding algorithm (FUA) [28], and deep nonlinear reconstruction algorithm based on cross-entropy (DNR-CE) [29]. SP is a method for detecting community structure by spectral analysis using Laplace or modularity matrix. ULC is a heuristic search algorithm based on modularity optimization problem-solving. FAM is a greedy clustering algorithm. FUA is a community discovery method based on modularity. DNR-CE achieves community discovery based on the nonlinear reconstruction of deep neural networks. The evaluation datasets and phase information composition are shown in Tab. 1. The evaluation datasets, which can gauge the effectiveness of the algorithm in real networks, are Karate, which represents the karate club network; Friendship 6, which represents the campus relationship network; Polbooks, which represents the Books about US politics; Citeseer, which represents a citation network of computer science publications; Cora, which represents a dataset of citation types; and Football, which represents a network of U.S. football teams. These six datasets are all widely used network datasets in community discovery research. The normalized mutual information (NMI) and modularity (Q) are chosen as the evaluation indicators. In this field, modularity is expressed as “Q” [30,31].
Table 1: Information composition of network datasets based on community discovery

2.3 Quantum ACO Algorithm Based on Community Detection
The ant colony optimization (ACO) algorithm is an intelligent optimization heuristic algorithm. It has strong robustness and well-integrated with other algorithms. It has strong applicability in solving discrete optimization and complex network community detection problems, and is more applicable in the network structure for small-scale datasets [32,33]. Therefore, for large-scale datasets, the ACO algorithm is combined with the quantum update strategy to form the proposed QACO algorithm, which we then apply to the community detection of complex networks.
For the ACO algorithm, when the ants move from the starting node to a viable neighbor node, the generation of the solution can be expressed as
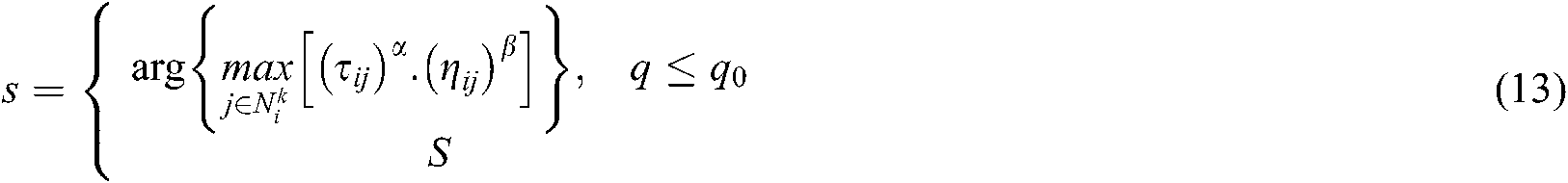
where: 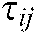 and
and 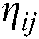 represent the corresponding pheromone and heuristic information between node
represent the corresponding pheromone and heuristic information between node 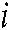 and node
and node 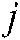 ,
,  and
and 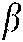 correspond to the parameters that regulate the ratio between
correspond to the parameters that regulate the ratio between 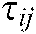 and
and 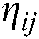 ,
, 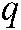 represents a uniformly distributed random number,
represents a uniformly distributed random number, 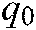 describes the preset parameters, and
describes the preset parameters, and 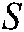 corresponds to a selection variable of the probability distribution. In the case of
corresponds to a selection variable of the probability distribution. In the case of  , the artificial ant selects the next node according to the transition probability
, the artificial ant selects the next node according to the transition probability 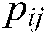 , where the transition probability
, where the transition probability 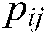 can be expressed as
can be expressed as

In Eq. (14), the meaning of each symbol is the same as in that of Eq. (13) above.
As for quantum computing, the state of qubits can be expressed as

where:  and
and 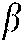 represent the probability amplitude in the corresponding state. Furthermore, in the QACO algorithm, the pheromone can be expressed as
represent the probability amplitude in the corresponding state. Furthermore, in the QACO algorithm, the pheromone can be expressed as

The update of pheromone can be expressed as

where 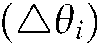 represents the rotation angle.
represents the rotation angle.
A specific number of ants are randomly assigned among the complex network nodes using the QACO algorithm. The ants move from one node to another according to the heuristic information and the strength of the pheromone. Then, small groups appear in the population. We will integrate the small groups into the community according to the maximization of modularity and community division to realize the determination of the community structure in the complex network. In this process, the rotation and mutation mechanism based on quantum computing enhance the global search capability and solution diversity of the algorithm. Once the optimal solution or the maximum number of iterations appears, the entire optimization process terminates accordingly. The specific implementation process of the QACO algorithm is shown in Fig. 3.

Figure 3: Specific implementation process of QACO algorithm
During the implementation of the QACO algorithm, the pheromone in the initialization phase can be expressed as

The heuristic information calculation between nodes can be expressed as

where: 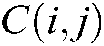 represents the Pearson correlation matrix. It can be defined as
represents the Pearson correlation matrix. It can be defined as

where: 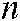 represents the number of nodes,
represents the number of nodes, 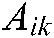 represents the
represents the 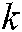 -th element corresponding to row
-th element corresponding to row 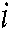 in the adjacency matrix
in the adjacency matrix 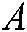 ,
, 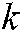 represents the average value corresponding to node
represents the average value corresponding to node 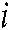 , and
, and 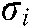 represents the value of standard deviation corresponding to the node
represents the value of standard deviation corresponding to the node 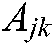 .
. 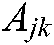 ,
, 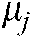 , and
, and 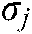 may be deduced by analogy.
may be deduced by analogy.
Furthermore, it is possible to update the pheromone intensity by using quantum rotation gates. The new pheromone intensity obtained at this time can be expressed as

where: 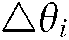 represents the quantum rotation angle corresponding to each qubit.
represents the quantum rotation angle corresponding to each qubit.
The extended GN benchmark network is used to verify the effectiveness of the QACO algorithm. At the same time, the QACO algorithm is compared with the interest factor-based ACO algorithm (IACO), the multi-objective discrete particle swarm optimization (MODPSO) community detection algorithm, the quantum distribution algorithm (QDM), the quantum genetic algorithm (QGA), and the locally optimized community detection algorithm (MABA) based on minimum spanning tree. In this way, we analyze the performance of the QACO algorithm in the detection of complex network community with NMI and Q selected as evaluation indicators.
All the nodes are treated as having integrity in the complex network community structure. We introduce the concept of game theory to excavate the implicit constraint conditions. The results are achieved through the DSEM-TL and QACO algorithms. The advantages of the deep self-encoder based on the DSEM-TL and QACO algorithms are organically integrated so that the accuracy of community detection in the community structure can be improved. To verify the effectiveness of applying the two optimized community detection algorithms in the reconstruction of the community structure, the DSEM-TL and QACO algorithms are integrated to complete the reconstructed community structure. In two typical game models Prisoner’s Dilemma and the Sprague-Grundy theorem both proposed algorithms are compared with the traditional node reconstruction (NR) and partition reconstruction (PR) method. For comparative analysis of complex networks, the random network (RN), small-world network (SWN), and scale-free network (SFN) are selected.
3.1 Performance of Deep Learning-Based Community Discovery Optimization Algorithm
Figs. 4a and 4b illustrate the comparison results of NMI values of DSEM-TL and the six commonly used discovery schemes of complex network community on the selected six real network datasets, as well as the comparison results of the modularity measures of DSEM-TL and the six discovery schemes of complex network community on the six real network datasets.

Figure 4: Performance comparison between DSEM-TL algorithm and other algorithms: (a) NMI; (b) modularity measures
Analysis of the NMI corresponding to different community discovery schemes in Fig. (a) shows that the detection rate corresponding to DSEM-TL is superior to that of the DNR-CE method, as well as several other complex network community discovery schemes. The analysis concludes that the DSEM-TL algorithm has better applicability and more effectiveness in real networks. Analysis of the modularity measures corresponding to different community discovery schemes in Fig. (b) shows that while the clustering effect of the DSEM-TL and DNR-CE algorithms is almost the same. Meanwhile, the DNR-CE algorithm shows a better clustering effect than several other algorithms.
The performance comparison of the six complex network community discovery solutions on the GN and LFR benchmark network is shown in Figs. 5a and 5b.
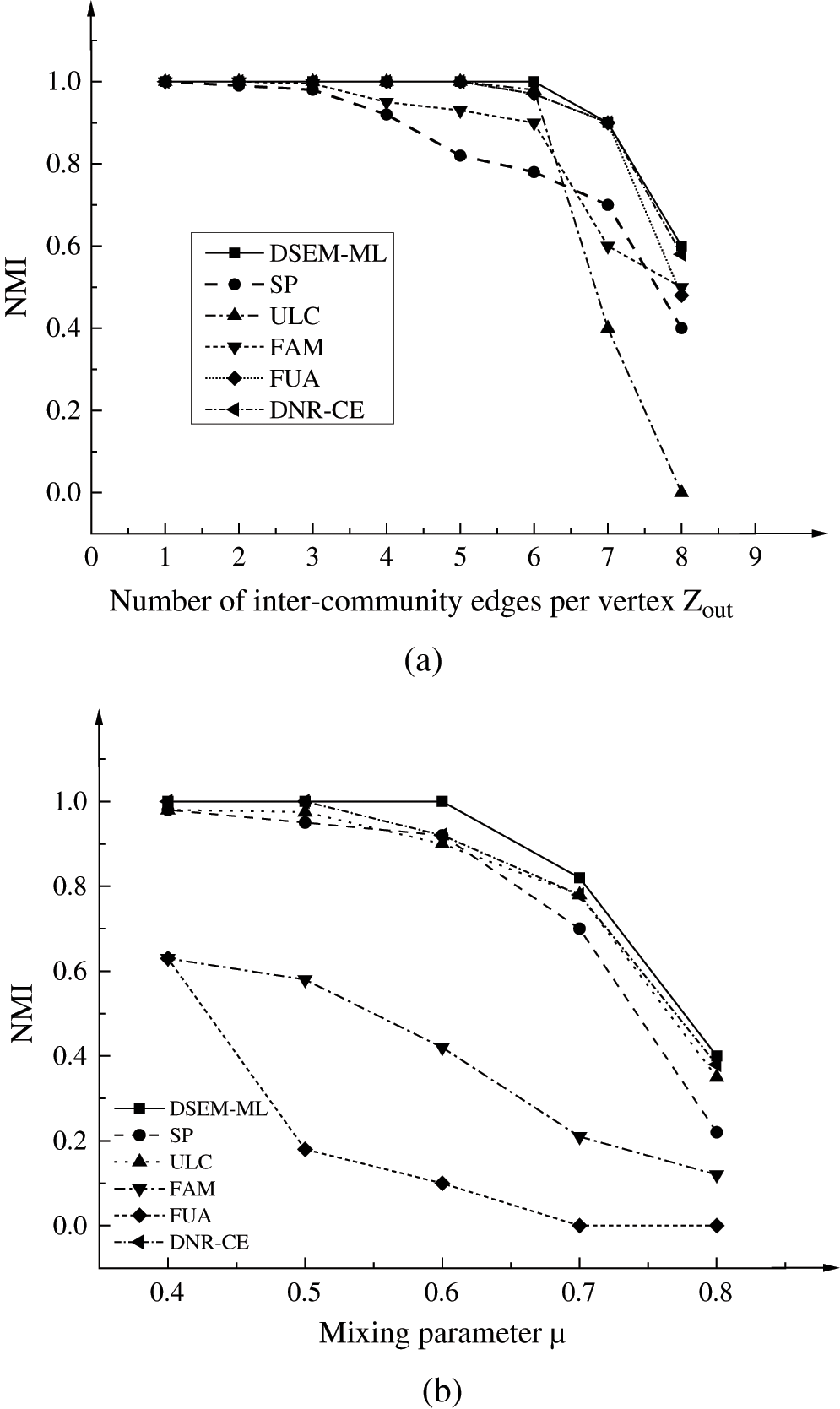
Figure 5: Performance comparison of six complex network community discovery solutions on two benchmark networks: (a) GN; (b) LRF
In the above figure, Zout represents the number of edges between each vertex community.
As shown in Fig. 5, when Zout is greater than 6, DSEM-ML shows better performance on the GN benchmark network than other community discovery methods. Similarly, when the mixed parameter μ is greater than 0.65, the performance of DSEM-TL is superior to several other algorithms on the LRF benchmark network. This further validates the effectiveness of the DSEM-ML algorithm in complex network community discovery and community detection.
The above analysis reveals that the proposed DSEM-TL algorithm has the best performance. The reason is that the new method used for matrix preprocessing in the model construction process of DSEM-TL actually highlights the local information of the vertex. n additional, the DSEM-TL algorithm employs transfer learning to obtain low-dimensional feature matrices. Therefore, DSEM-TL has useful community discovery and community detection performances in complex networks. Furthermore, the DSEM-TL algorithm model based on deep learning has applicability in the artificial benchmark network. Accordingly, it is predicted that this complex network community discovery and community detection method based on deep learning has vast application potential in the reconstruction and optimization of community structure.
3.2 Performance of Community Detection QACO Algorithm
The NMI comparison results of the QACO algorithm with IACO, MODPSO, QDM, QGA, and MABA algorithms are shown in Fig. 6a. The modularity measures comparison results of the QACO algorithm with these five algorithms, are shown in Fig. 6b.
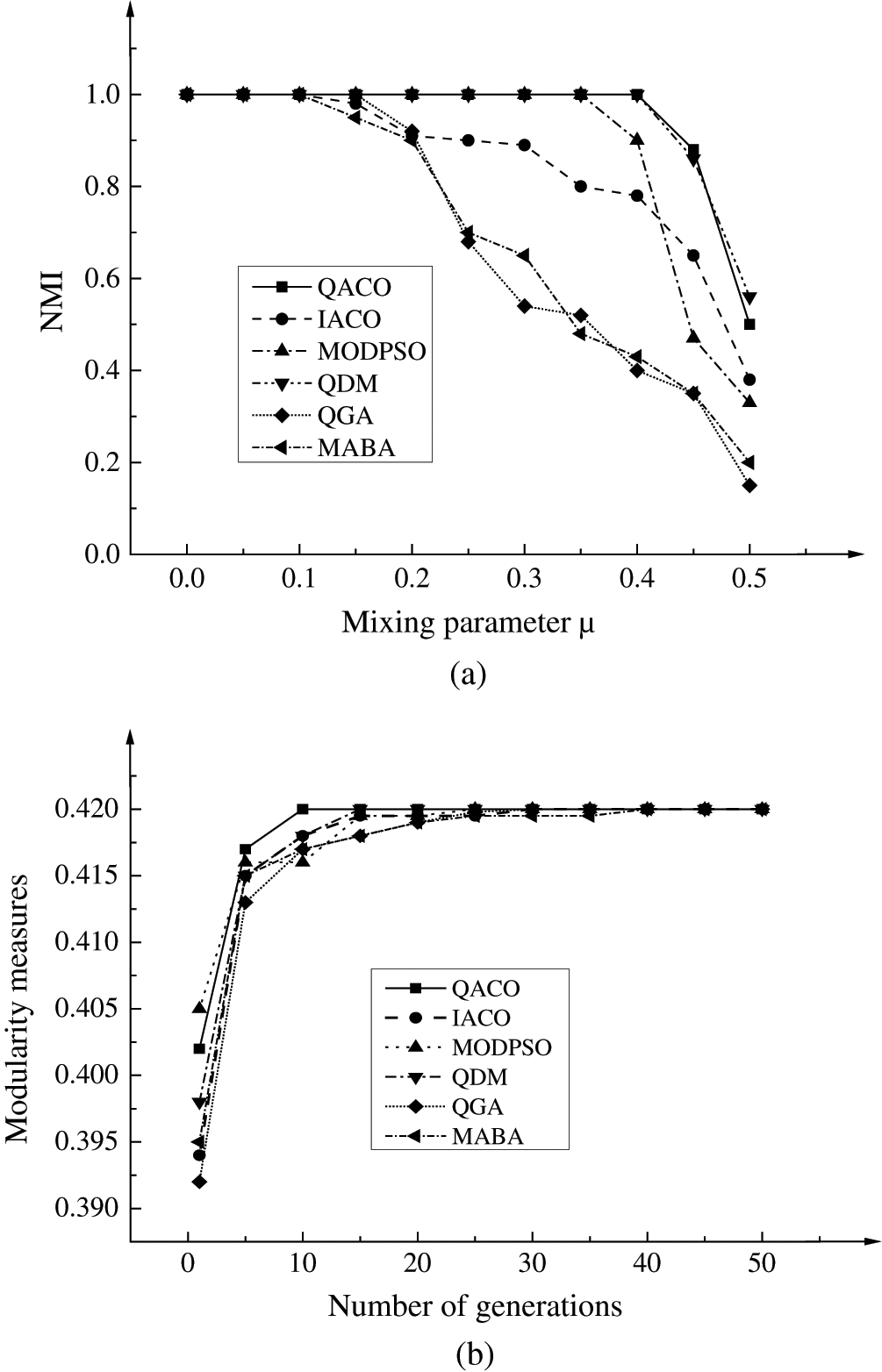
Figure 6: Performance comparison results of QACO and several algorithms: (a) NMI; (b) modularity measures
We compare the results of the NMI and modularity measures of several algorithms, as shown in Fig. 6. When the mixed parameter μ is smaller than 0.4, the QACO and QDM-PSO algorithms can determine the real division of the corresponding networks. At this point, the corresponding NMI value is 1. When the mixed parameter μ is not greater than 0.25, the situation is reversed. The other algorithms can determine the correct community structure of complex networks. When the mixed parameter μ is higher than 0.45, none of the algorithms can determine the real community division of the network. However, the division result corresponding to the QACO algorithm is more inclined to the actual community division. From the perspective of the changes in the modularity measures of each algorithm, the QACO algorithm has a faster convergence speed than the QGA algorithm, but the QDM-PSO and MODPSO algorithms have faster convergence speeds in the initial stage. Overall, the convergence of the QACO algorithm is better and faster.
The comparison between the proposed optimization scheme of complex network community structure and several community reconstruction methods is shown in Fig. 7.
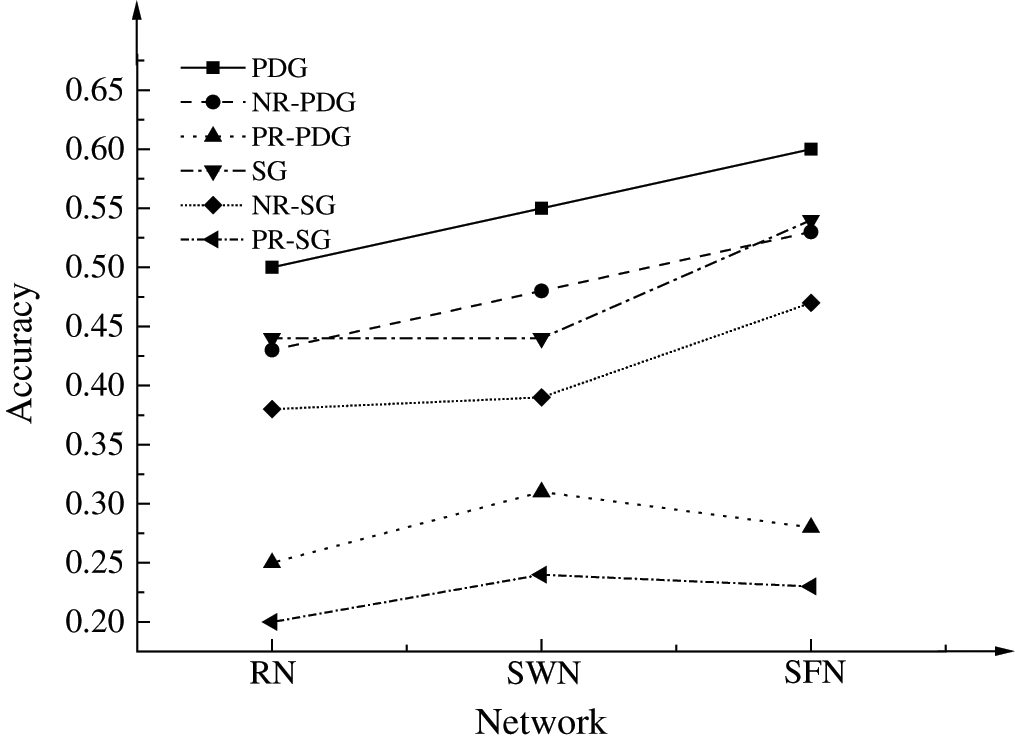
Figure 7: Comparison between the proposed optimization scheme of complex network community structure and several community reconstruction methods
As shown in Fig. 7, the complex network community reconstruction scheme incorporating two optimization algorithms has the highest accuracy rate. Therefore, the DSEM-TL method and the QACO algorithm have promoted the reconstruction and optimization of the complex network community structure.
The QACO algorithm can improve the accuracy of the GN benchmark network community division. The integration of quantum mechanisms gives the network a faster convergence speed, which leads to superior performance in complex network community testing. The introduction of quantum strategy has expanded the application of the ACO algorithm in solving community detection problems. The QACO algorithm is more applicable to the detection of complex network community structure than other algorithms, and therefore can play an active role in the reconstruction and optimization of complex network community structure. Notably, the proposed community structure reconstruction scheme has a high accuracy rate.
This article proposes the DSEM-TL algorithm model, which introduces transfer learning into deep self-encoders, and the QACO algorithm, which integrates the quantum strategy into the ACO algorithm. The results show that the two algorithms have significant advantages in the application of community discovery and community detection in complex network community structures. The combination of the two optimization algorithms shows the best accuracy in the reconstruction of the complex network community structure. However, the optimization of the complex network community structure still stays in the exploration stage. At this time, the coverage of the selected real network dataset is limited, and there has not been sufficient consideration of the characteristics of the complex network structure. Resolving these issues, which are due to several factors, is a focus of future research.
Acknowledgement: We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. H. Jiang, X. Y. Gao, H. Z. An, H. J. Li and B. Sun. (2017). “Reconstructing complex network for characterizing the time-varying causality evolution behavior of multivariate time series,” Scientific Reports, vol. 7, no. 1, pp. 10486. [Google Scholar]
2. T. Alhindi, Z. Zhang, P. Ruelens, H. Coenen, H. Degroote,. (2017). et al., “Protein interaction evolution from promiscuity to specificity with reduced flexibility in an increasingly complex network,” Scientific Reports, vol. 7, no. 1, pp. 44948, . DOI 10.1038/srep44948. [Google Scholar]
3. D. Tsiotas and S. Polyzos. (2018). “The complexity in the study of spatial networks: An epistemological approach,” Networks & Spatial Economics, vol. 18, no. 1, pp. 1–32, . DOI 10.1007/s11067-017-9354-1. [Google Scholar]
4. K. K. Huang, S. Li, P. L. Dai, Z. Wang and Z. F. Yu. (2020). “A stacked denoising autoencoder method for game dynamics network structure reconstruction,” Neural Networks, vol. 126, pp. 143–152, . DOI 10.1016/j.neunet.2020.03.008. [Google Scholar]
5. L. Bai, J. Y. Liang, H. Y. Du and Y. K. Guo. (2018). “A novel community detection algorithm based on simplification of complex networks,” Knowledge-Based Systems, vol. 143, pp. 58–64. [Google Scholar]
6. L. Q. Pang, Y. X. Zhang and S. F. Liu. (2017). “Monolayer-by-monolayer growth of platinum films on complex carbon fiber paper structure,” Applied Surface Science, vol. 407, pp. 386–390, . DOI 10.1016/j.apsusc.2017.02.144. [Google Scholar]
7. M. A. Riolo and M. E. J. Newman. (2020). “Consistency of community structure in complex networks,” Physical Review E, vol. 101, no. 5. [Google Scholar]
8. L. Q. Gan, X. Y. Wang, N. Yan and L. Wang. (2018). “Detecting community structure in complex networks based on node similarity,” Computer & Digital Engineering. [Google Scholar]
9. F. Ali, S. Osat and F. Radicchi. (2018). “Characterizing the analogy between hyperbolic embedding and community structure of complex networks,” Physical Review Letters, vol. 121, no. 9. [Google Scholar]
10. T. T. Dai, C. J. Shan and Y. S. Dong. (2017). “Community structure of complex networks based on continuous neural network,” IOP Conference Series: Materials Science and Engineering, vol. 231, no. 1, pp. 012154, . DOI 10.1088/1757-899X/231/1/012154. [Google Scholar]
11. C. Y. Jia, Y. F. Li, M. B. Carson, X. Y. Wang and J. Yu. (2017). “Node attribute-enhanced community detection in complex networks,” Scientific Reports, vol. 7, no. 1, pp. 2626. [Google Scholar]
12. M. Guendouz, A. Amine and R. M. Hamou. (2017). “A discrete modified fireworks algorithm for community detection in complex networks,” Applied Intelligence, vol. 46, no. 2, pp. 373–385, . DOI 10.1007/s10489-016-0840-9. [Google Scholar]
13. F. Zou, D. Chen, S. Li, R. Q. Lu and M. Y. Lin. (2017). “Community detection in complex networks: Multi-objective discrete backtracking search optimization algorithm with decomposition,” Applied Soft Computing, vol. 53, pp. 285–295, . DOI 10.1016/j.asoc.2017.01.005. [Google Scholar]
14. L. X. Li, D. F. Xu, H. P. Peng, J. Kurths and Y. X. Yang. (2017). “Reconstruction of complex network based on the noise via qr decomposition and compressed sensing,” Scientific Reports, vol. 7, no. 1, pp. 15036. [Google Scholar]
15. C. Ma, H. S. Chen, Y. C. Lai and H. F. Zhang. (2018). “Statistical inference approach to structural reconstruction of complex networks from binary time series,” Physical Review E, vol. 97, no. 2, pp. 022301, . DOI 10.1103/PhysRevE.97.022301. [Google Scholar]
16. J. W. Li, Z. S. Shen, W. X. Wang, C. Grebogi and Y. C. Lai. (2017). “Universal data-based method for reconstructing complex networks with binary-state dynamics,” Physical Review E, vol. 95, no. 3, pp. 032303. [Google Scholar]
17. J. C. Fu, W. X. Zhang and J. L. Wu. (2017). “Identification of leader and self-organizing communities in complex networks,” Scientific Reports, vol. 7, no. 1, pp. 704. [Google Scholar]
18. X. R. Liu, Y. Z. Du, M. Jiang, M. Jiang and X. X. Zeng. (2020). “Multiobjective particle swarm optimization based on network embedding for complex network community detection,” IEEE Transactions on Computational Social Systems, vol. 7, no. 2, pp. 437–449, . DOI 10.1109/TCSS.2020.2964027. [Google Scholar]
19. D. S. Lyu, B. Wang and W. Z. Zhang. (2020). “Large-scale complex network community detection combined with local search and genetic algorithm,” Applied Sciences, vol. 10, no. 9, pp. 3126, . DOI 10.3390/app10093126. [Google Scholar]
20. P. Kumar, S. Gupta and B. Bhasker. (2017). “An upper approximation-based community detection algorithm for complex networks,” Decision Support Systems, vol. 96, no. C, pp. 103–118, . DOI 10.1016/j.dss.2017.02.010. [Google Scholar]
21. Y. K. Xue and P. Bogdan. (2017). “Reliable multi-fractal characterization of weighted complex networks: Algorithms and implications,” Scientific Reports, vol. 7, no. 1, pp. 7487. [Google Scholar]
22. K. Crosby, T. Garbowski and S. Nickell. (2019). “Towards fast and direct memory read-out by multi-beam scanning electron microscopy and deep learning image classification,” Microscopy and Microanalysis, vol. 25, no. S2, pp. 192–193, . DOI 10.1017/S1431927619001697. [Google Scholar]
23. A. S. Toor and H. Wechsler. (2018). “Biometrics and forensics integration using deep multi-modal semantic alignment and joint embedding,” Pattern Recognition Letters, vol. 113, pp. 29–37, . DOI 10.1016/j.patrec.2017.02.012. [Google Scholar]
24. A. Siddiqua and G. L. Fan. (2019). Semantics-enhanced supervised deep autoencoder for depth image-based 3d model retrieval,” Pattern Recognition Letters, vol. 125, pp. 806–812, . DOI 10.1016/j.patrec.2019.08.004. [Google Scholar]
25. W. Dai and O. Milenkovic. (2009). “Subspace pursuit for compressive sensing signal reconstruction,” IEEE Transactions on Information Theory, vol. 55, no. 5, pp. 2230–2249, . DOI 10.1109/TIT.2009.2016006. [Google Scholar]
26. J. Y. Yang. (2018). “Research on community discovery technology based on user behavior analysis,” M.S. dissertation. Beijing University of Posts and Telecommunications, China. [Google Scholar]
27. S. Peng, L. X. Zhang, Z. Man and T. Yong. (2013). “Realization of cyclic spectrum based on time-smoothing FFT accumulation method,” Electronic Design Engineering. [Google Scholar]
28. V. D. Blondel, J. L. Guillaume, L. Renaud and L. Etienne. (2008). “Fast unfolding of communities in large networks,” Journal of Statistical Mechanics: Theory and Experiment, vol. 2008, no. 10, pp. 10008, . DOI 10.1088/1742-5468/2008/10/P10008. [Google Scholar]
29. Y. Xie, X. M. Wang, D. Jiang and R. B. Xu. (2019). “High-performance community detection in social networks using a deep transitive autoencoder,” Information Sciences, vol. 493, pp. 75–90, . DOI 10.1016/j.ins.2019.04.018. [Google Scholar]
30. M. Chen, M. Zhang, M. Li, M. W. Leng and Z. C. Yang,. (2019). et al., “Detecting communities by suspecting the maximum degree nodes,” International Journal of Modern Physics B, vol. 33, no. 13, pp. 281–297. [Google Scholar]
31. S. Vairachilai. (2018). “A comparative analysis of community detection algorithms on complex network based on modularity,” Journal of Computational and Theoretical Nanoscience, vol. 15, no. 9–10, pp. 2729–2735, . DOI 10.1166/jctn.2018.7531. [Google Scholar]
32. T. Selçuk and A. Alkan. (2019). “Detection of microaneurysms using ant colony algorithm in early diagnosis of diabetic retinopathy,” Medical Hypotheses, vol. 129, pp. 109242. [Google Scholar]
33. N. J. Cheung, X. M. Ding and H. B. Shen. (2017). “A nonhomogeneous cuckoo search algorithm based on quantum mechanism for real parameter optimization,” Cybernetics IEEE Transactions on, vol. 47, no. 2, pp. 391–402. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |