DOI:10.32604/iasc.2020.012805

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.012805 |  |
| Article |
Imperfect Premise Matching Controller Design for Interval Type-2 Fuzzy Systems under Network Environments
1Mechanical Engineering College, Beihua University, Jilin, 132013, China
2Mathematic College, Beihua University, Jilin, 132013, China
3School of Computing, University of Eastern Finland, Kuopio, 70211, Finland
*Corresponding Author: Dawei Wang, Email: wdw9211@126.com
Received: 13 July 2020; Accepted: 11 September 2020
Abstract: The interval type-2 fuzzy sets can describe nonlinear plants with uncertain parameters. It exists in nonlinearity. The parameter uncertainties extensively exist in the nonlinear practical Networked Control Systems (NCSs), and it is paramount to investigate the stabilization of the NCSs on account of the section type-2 fuzzy systems. Notice that most of the existing research work is only on account of the convention Parallel Distribution Compensation (PDC). For overcoming the weak point of the PDC and acquire certain guard stability conditions, the state tickling regulator under imperfect premise matching can be constructed to steady the NCSs using the section type-2 indistinct muster, where the fuzzy plant and fuzzy regulator may enjoy together not the same membership functions. By leading into the message of the up and down membership functions of both the fuzzy pattern and fuzzy regulator, we build a new composed term of the section type-2 network systems. The new results we obtained can provide a larger area of stability than the conventional membership unconcerned stability results. Moreover, a novel unmatching state feedback controller design method for the interval type-2 networked systems is explored in our work. The proposed approach can significantly improve the design flexibility of the fuzzy controllers, because their membership functions can be arbitrarily selected. Two numerical examples are further used to demonstrate the less-conservativeness and effectiveness of the novel technique.
Keywords: Network control systems; stability analysis; interval type-2 fuzzy systems; controller design; imperfect premise matching
As we know, the Takagi-Sugeno can efficacious express non-linear dynamics, and often is called a type-1 system. Unfortunately, the type-1 fuzzy sets have some difficulties in describing the nonlinear plants with uncertain parameters. In order to handle this drawback [1], Zadeh [2] introduced the type-2 fuzzy sets as an extension of the type-1 fuzzy sets. In view of the type-2 fuzzy sets, Mendel et al. [3] proposed the section Type-2 (IT2) fuzzy sets. During the past decades, the IT2 fuzzy model has been widely applied in practice [4,5]. For example, in Lam et al. [6], the stability area and the fuzzy regulator for the IT2 fuzzy model-based system were examined, in which the parameter non-determinacy are captured by both the up and down grades of fuzzy membership. Most of the controller design methods reported in the literature are inspired by the PDC scheme, and the fuzzy pattern and fuzzy regulator are provided with the identical membership functions. Nevertheless, Lam developed the concept of “imperfect premise matching” in Lam et al. [7], i.e., the membership functions of the fuzzy regulator probable be distinct from fuzzy model. The stabilization issue of the type-1 systems was investigated in Zhang et al. [8–11]. Li et al. [12,13] generalized these research results to the IT2 fuzzy model with the imperfect premise matching, thus improving the flexibility in highway design and cutting down the complexity of implementation. More work on the Interval type-2 fuzzy model stability conditions and controller design was presented in Wu et al. [14–16].
The Networked Control Systems (NCSs) have been got a lot of attention owing to their theory and reality purport [17]. Compared with the conventional point-point connections, the network systems reduce the heavy expenses of cables and facility maintenances. The network systems have found numerous applications in the fields of automobile, aerospace, industrial manufacturing, etc. [18–21]. Moreover, It is difficult if not impossible to guarantee the steadiness of the NCSs. what to analyze and devise the stability requirement for the T-S under NCSs has been a popular research topic [22,23]. Such as in Chi et al. [24], the networked 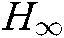 filtration with many output and many transducer nonsynchronous take sample for the T-S fuzzy systems was explored. By drawing into Laypunov-Krasovskii function to analysis the robust stability and the project of the state feedback for the NCSs in Rouamel et al. [25]. Actually, the above issues were received in view of the type-1 fuzzy set theory. NCSs also have parameter uncertainties, and considerable research work concerning the sector type-2 fuzzy pattern has been carried out [26,27]. However, the current efforts on the controller design are mainly inspired by the convention PDC idea. For the sake of overcoming the shortcomings of the PDC and receive a number of less conservative stability conditions, a novel devise way was put forward to manage the unmatching premise of the type-1 systems [28]. It is necessary to further investigate the controller design scheme under the imperfect premise matching for the Interval type-2 T-S fuzzy systems under NCSs.
filtration with many output and many transducer nonsynchronous take sample for the T-S fuzzy systems was explored. By drawing into Laypunov-Krasovskii function to analysis the robust stability and the project of the state feedback for the NCSs in Rouamel et al. [25]. Actually, the above issues were received in view of the type-1 fuzzy set theory. NCSs also have parameter uncertainties, and considerable research work concerning the sector type-2 fuzzy pattern has been carried out [26,27]. However, the current efforts on the controller design are mainly inspired by the convention PDC idea. For the sake of overcoming the shortcomings of the PDC and receive a number of less conservative stability conditions, a novel devise way was put forward to manage the unmatching premise of the type-1 systems [28]. It is necessary to further investigate the controller design scheme under the imperfect premise matching for the Interval type-2 T-S fuzzy systems under NCSs.
In this article, the innovations of the paper are as follows:
A less conservative stability conditions are obtained.
The unmatching regulator is designed for the nonlinear NCSs in view of the Interval typ-2 T-S, which makes the regulator design simpler and more flexible.
The proposed method can be generalized to other types of nonlinear control systems.
The rest of our article is arranged as follows. In Section 2, the controller design problem under consideration is represented in details. In Section 3, the synthesis of the state-feedback type-2 fuzzy controller under the imperfect premise matching is presented. In Section 4, for explaining the practicability and validity of the recommend technique, we give two numerical examples. Ultimately, In Section 5, we summarize this paper with some remarks and conclusions
Here the interval type-2 T-S fuzzy model can be described as follows:
The 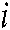 th rule can be represented as follows:
th rule can be represented as follows:
IF 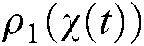 is
is  …
… 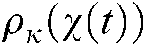 is
is 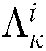 THEN
THEN

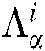 ,
, 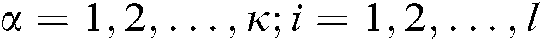 l is the number of the fuzzy rules.
l is the number of the fuzzy rules. 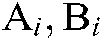 are the constant matrices.
are the constant matrices. 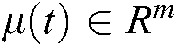 is the input vector,
is the input vector, 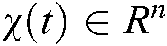 is the state vector.
is the state vector.
We have:
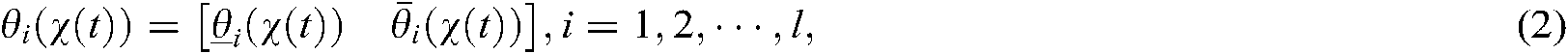
where
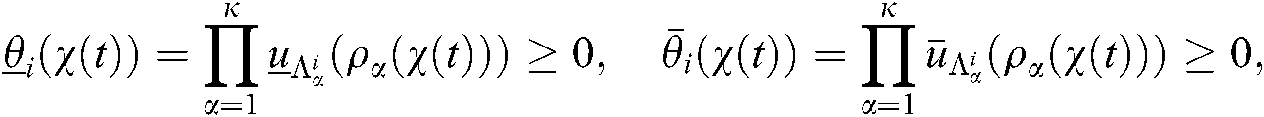
They content the character of 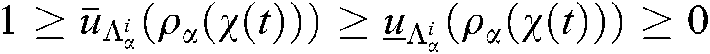 , and
, and 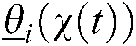 and
and 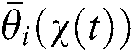 show the down and up grades of the membership. Then we have
show the down and up grades of the membership. Then we have

where
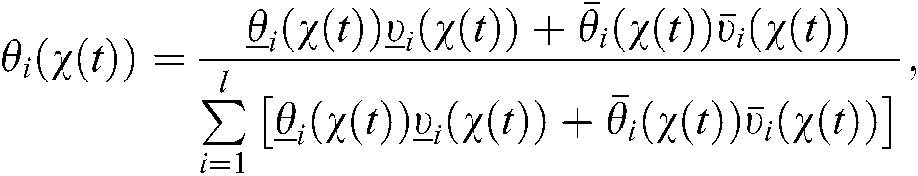
in which 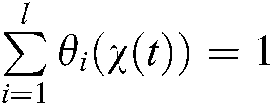 , and
, and 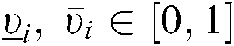 are the nonlinear functions with
are the nonlinear functions with 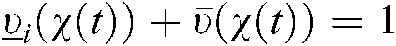 .
.
In this article, The system in Eq. (1) through IP based network control, system status can be used for feedback, as shown in Fig. 1 [29].
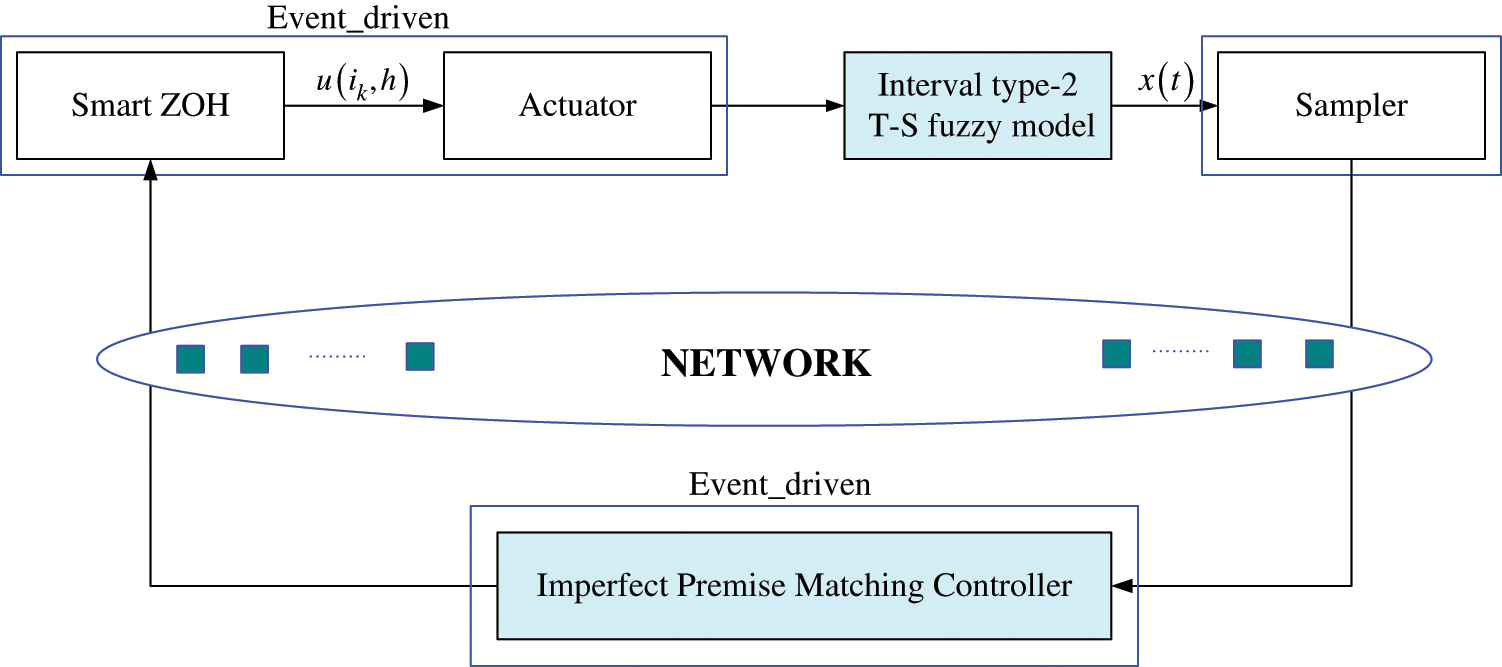
Figure 1: The interval type-2 networking system diagram
Distinct of the famous Parallel Distributed Compensation (PDC) plan means, we adopt a new unmatching fuzzy control law to make the interval type-2 fuzzy systems in Eq. (3) stable. For the NCSs, the transducer is clock-driven and 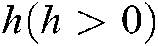 express the sampling period is constant. The regulator and actuator are eventdriven. Suppose that
express the sampling period is constant. The regulator and actuator are eventdriven. Suppose that 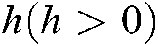 express the sampling cycle of the semaphore, and the
express the sampling cycle of the semaphore, and the 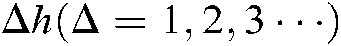 express the Δth acquisition time.
express the Δth acquisition time.
Under imperfect premise matching, we have the following fuzzy regulator:
Rule 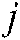 : IF
: IF 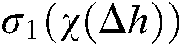 is
is 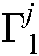 …
…  is
is  THEN
THEN
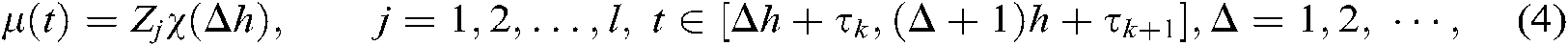
where  are the unknown tickling gains to be pending. On the other hand,
are the unknown tickling gains to be pending. On the other hand,
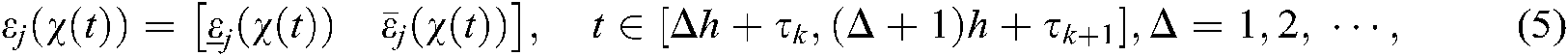
where
For  , we have
, we have

Here the  and
and  express the down and up membership functions. They satisfy the character
express the down and up membership functions. They satisfy the character 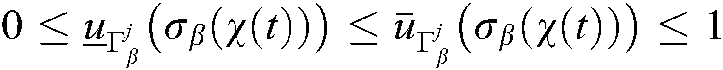 .
. 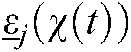 and
and 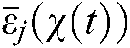 express the down and up grades of the membership functions. We have
express the down and up grades of the membership functions. We have

Owing to the network slowdown is invariably bounded, The input delay is:

where 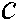 is the upper limit of the lag. Putting Eq. (8) into Eq. (6), the following regulator can be shown:
is the upper limit of the lag. Putting Eq. (8) into Eq. (6), the following regulator can be shown:
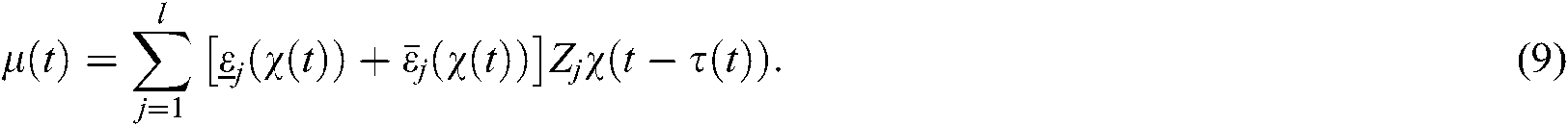
We have the following closed-loop networked system:
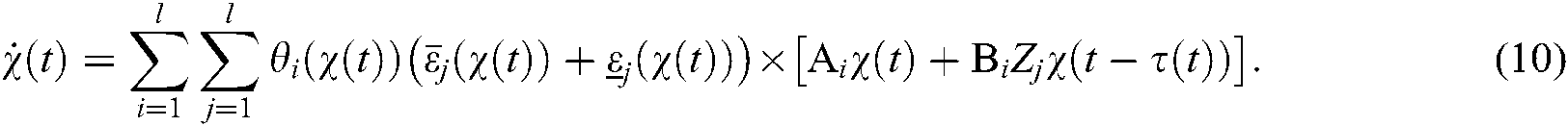
Lemma 1 [30] For 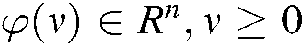 ,
, 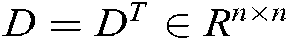 , supposing that there has
, supposing that there has 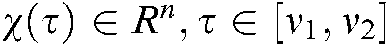 , for
, for 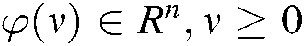 ,
, 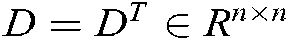 , we have:
, we have:
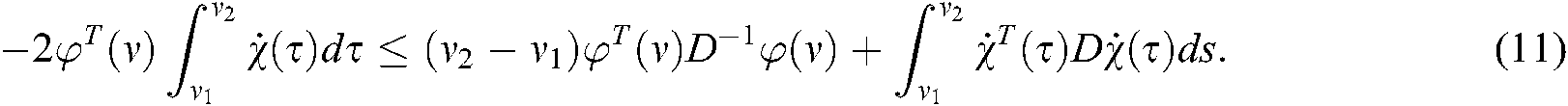
Lemma 2 [31] 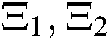 , and
, and  are constant matrices, and
are constant matrices, and 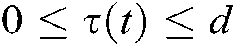 . We have
. We have

if and only if 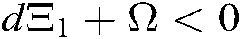 and
and 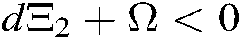 set up.
set up.
Lemma 3 [32] The 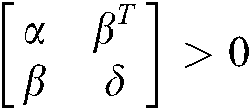 is equivalent to
is equivalent to  ,
, 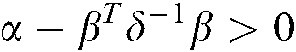 , where
, where 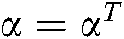 ,
, 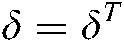 , and
, and 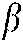 is a matrix .
is a matrix .
Theorem 1 When the membership functions satisfy 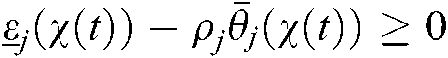 and
and 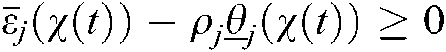 for all
for all 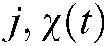 , where
, where 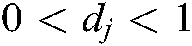 , and for given invariant
, and for given invariant  and matrix
and matrix 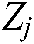 , and there exist matrices
, and there exist matrices 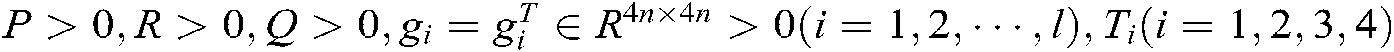 and
and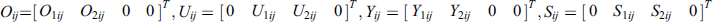 of such that the following LMIs hold:
of such that the following LMIs hold:




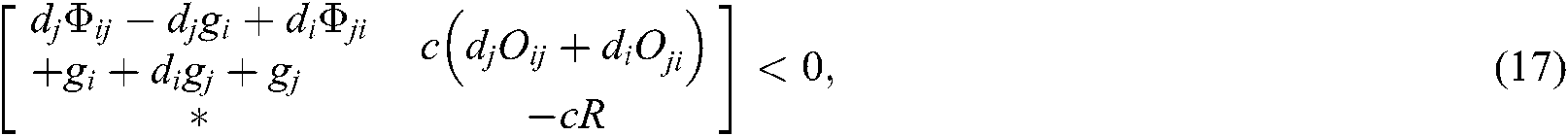
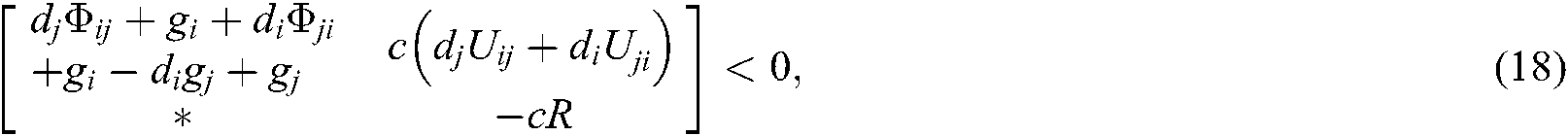





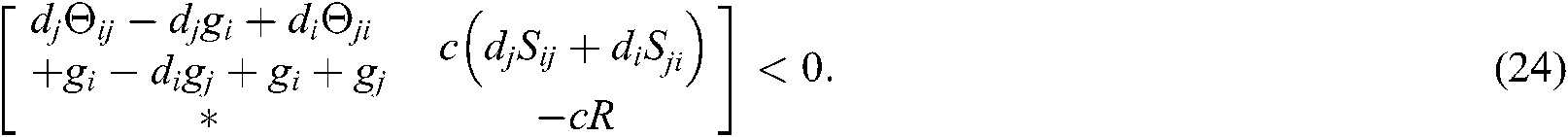
where
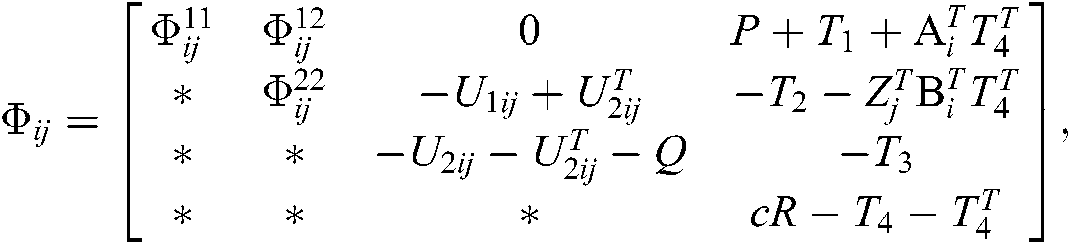
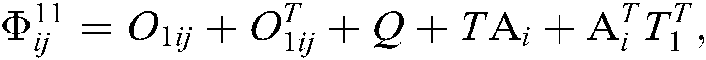
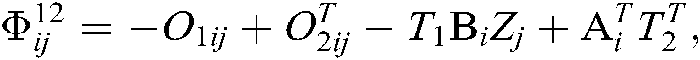
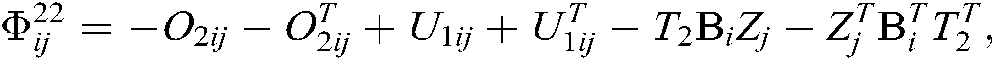

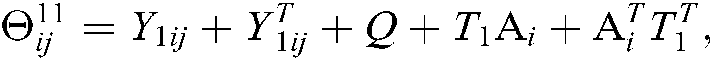
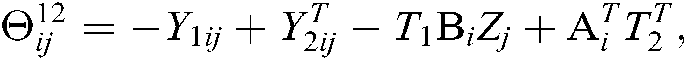
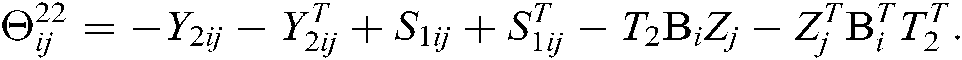
Here, “*” represents the transposition of symmetric position elements, then the fuzzy type-2 NCSs described by Eq. (10) is asymptotically stable.
Proof. Select the following Lyapunov function:

where
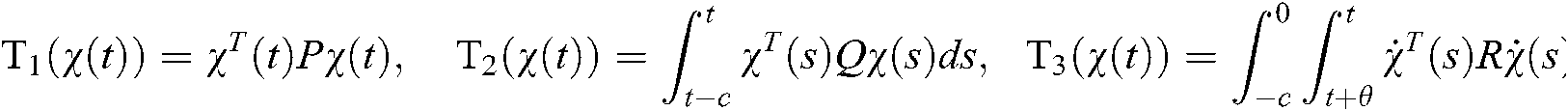
We take the derivative of 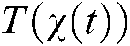 :
:

where
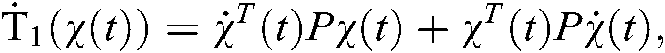
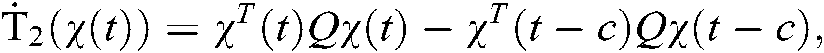
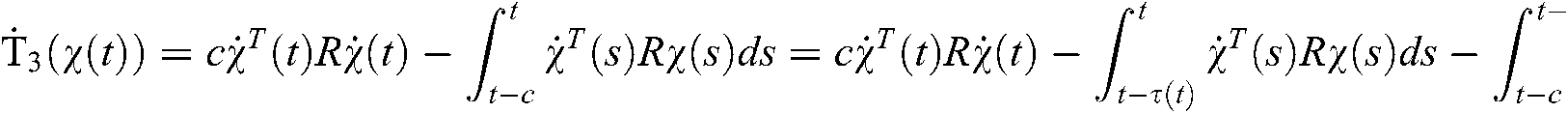
.
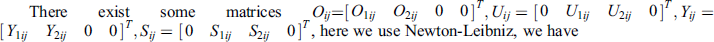
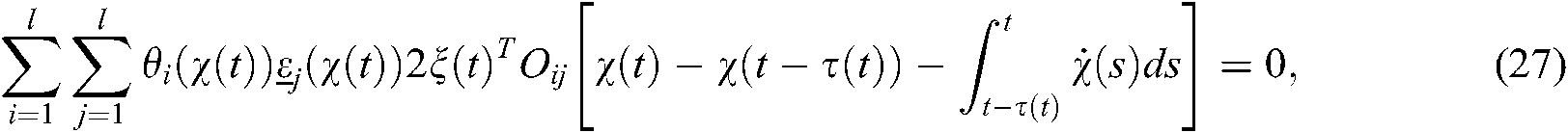
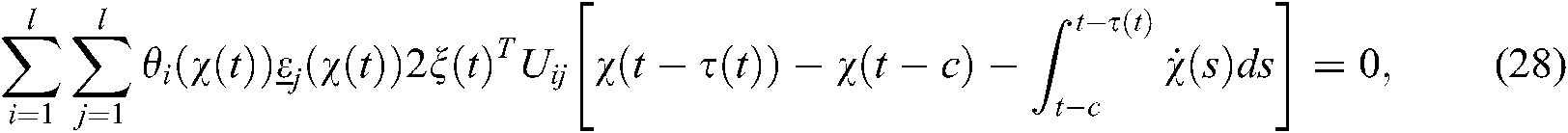
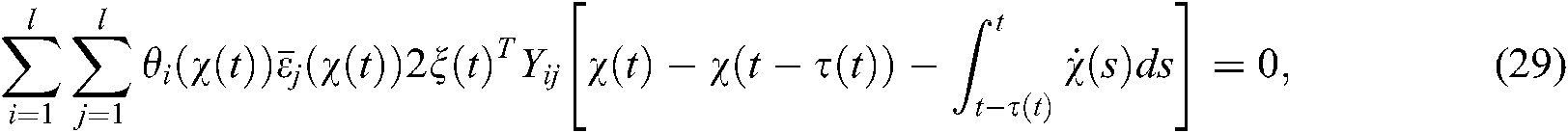
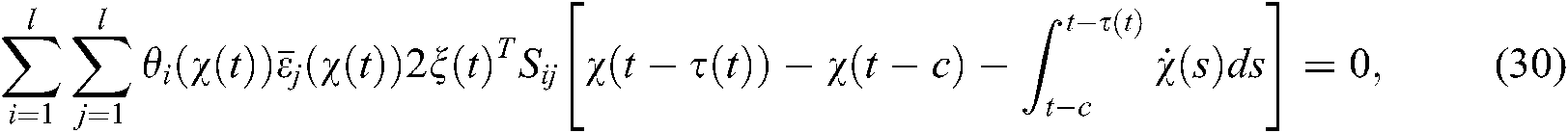
where
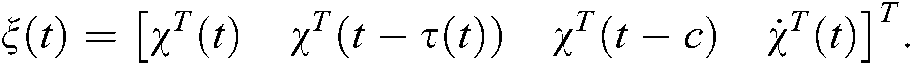
For any matrices 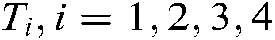 , we have :
, we have :
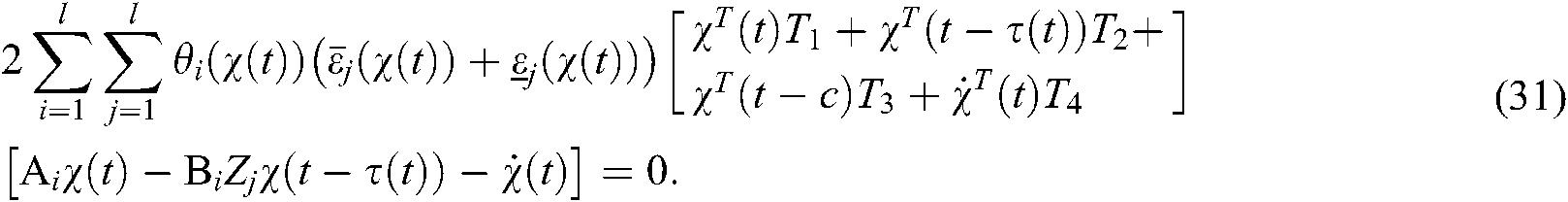
By Lemma 1, we get
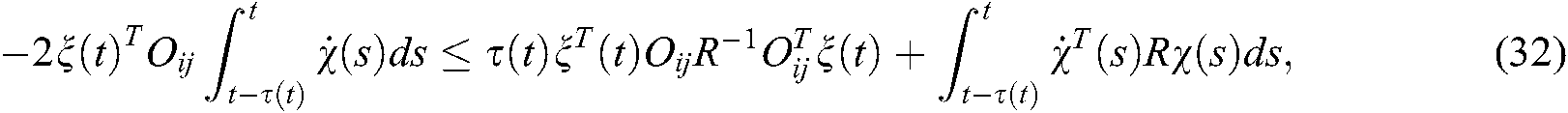
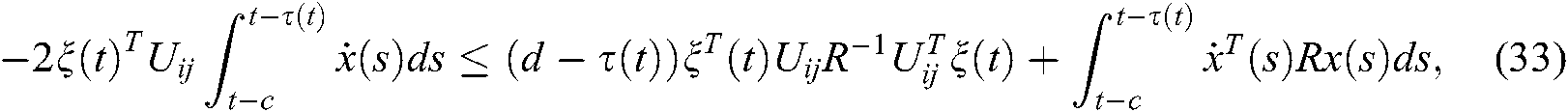
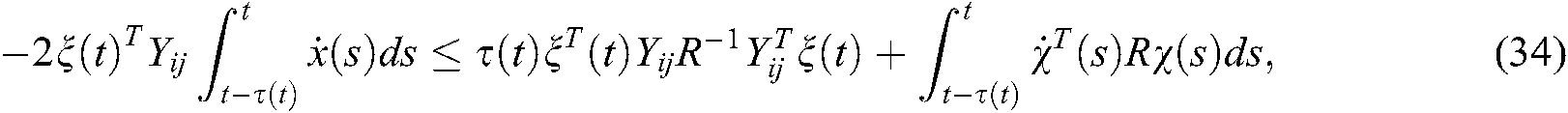

With the above equation, we have
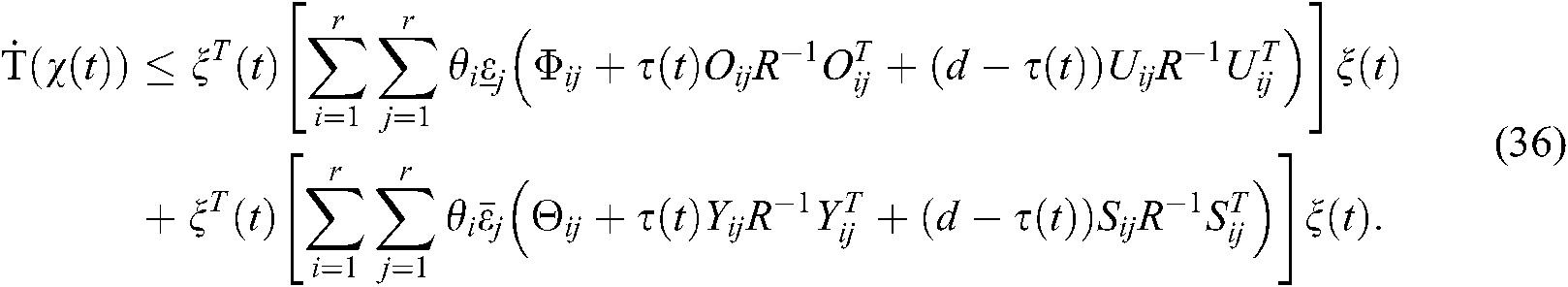
Let
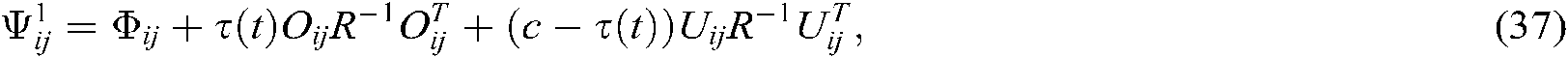
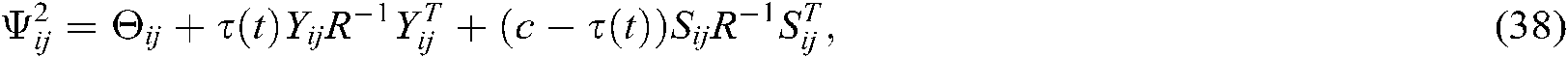
where
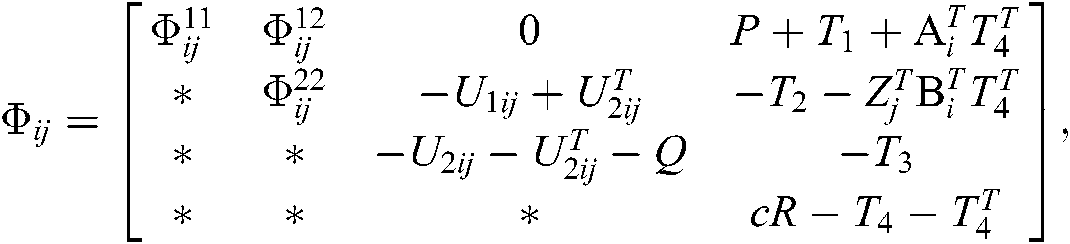
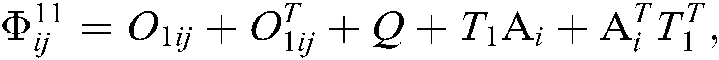
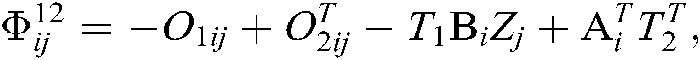
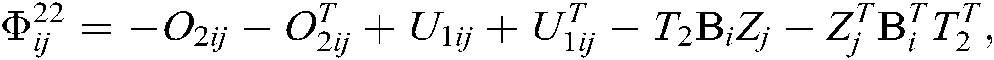
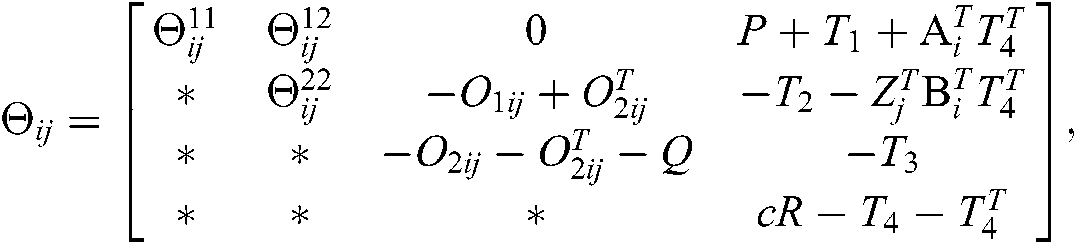
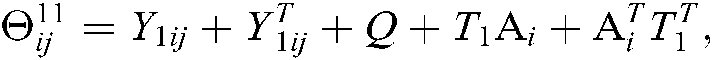
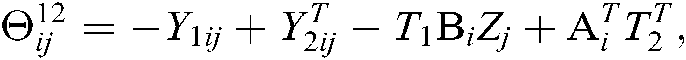
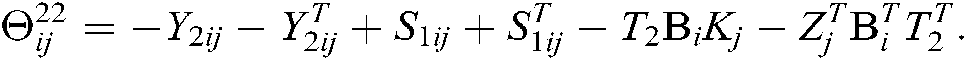
From Eq. (34), it is obvious that if


we have 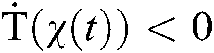 . Next, we will consider the following equation
. Next, we will consider the following equation
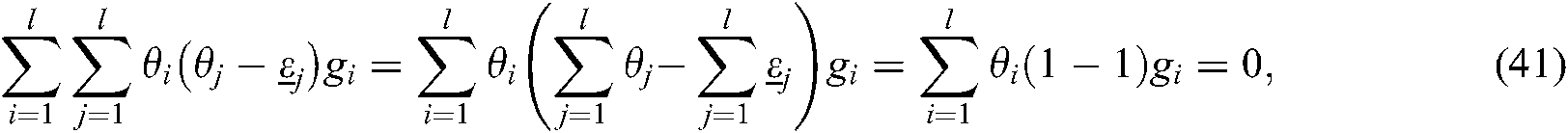

where 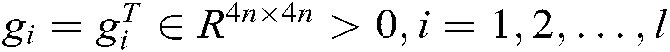 . For reducing the conservativeness, the above equations are added to Eqs. (39) and (40), we have
. For reducing the conservativeness, the above equations are added to Eqs. (39) and (40), we have
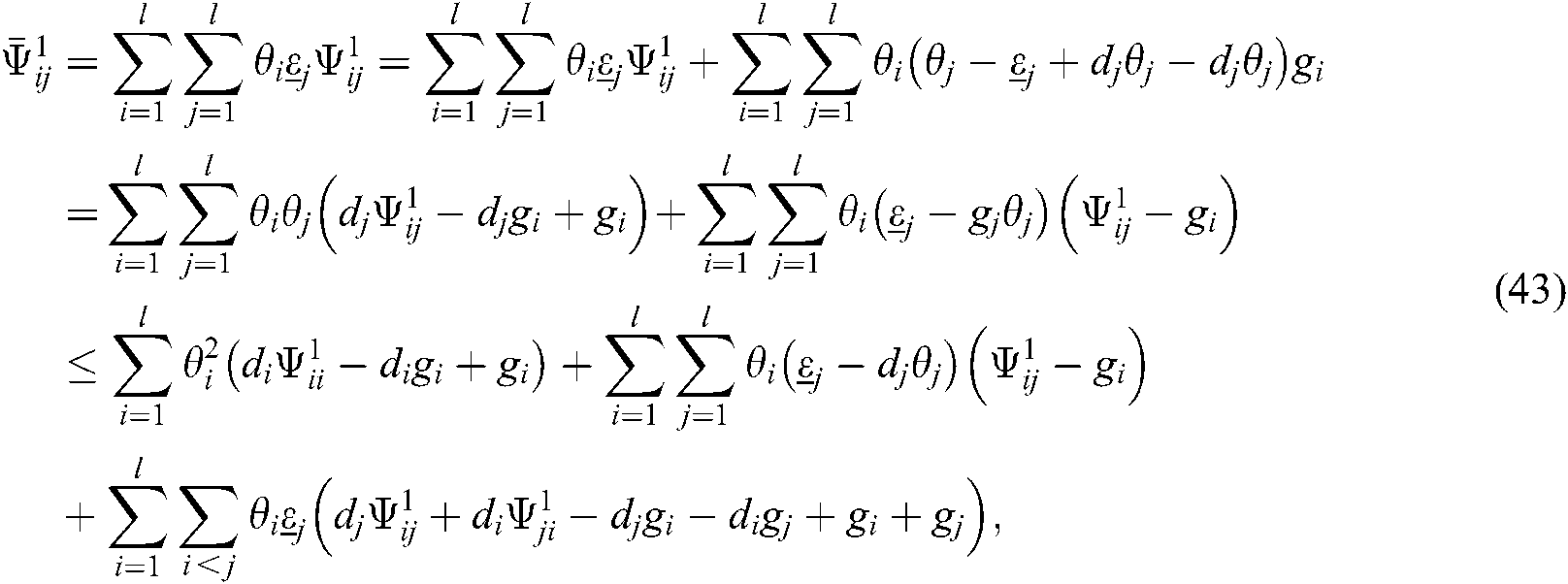
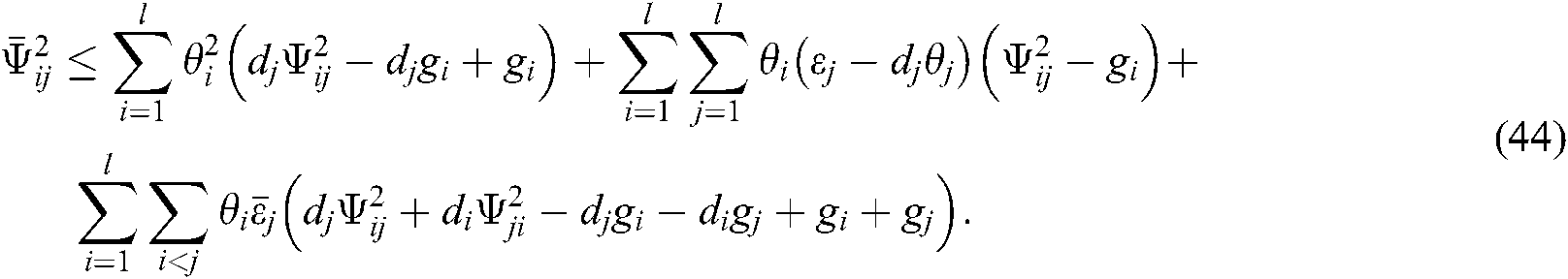
If 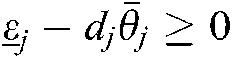 and
and 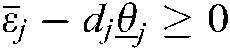 ,
, 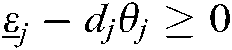 and
and 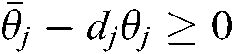 hold. With
hold. With 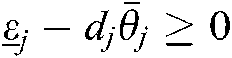 and
and 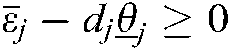 , let
, let


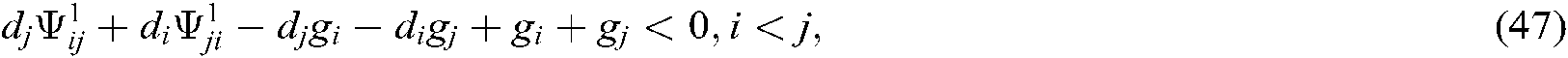


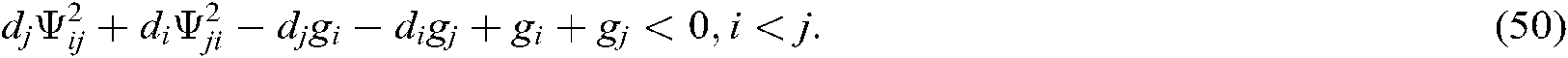
The Eqs. (45)–(50) are equivalent to the following inequalities on the basis of Eq. (37), Eq. (38) and Lemma 2:




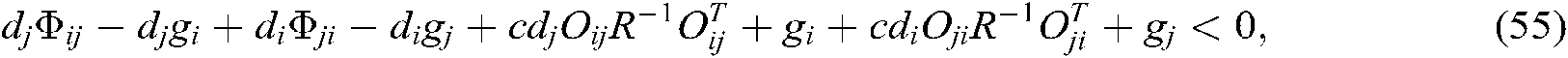
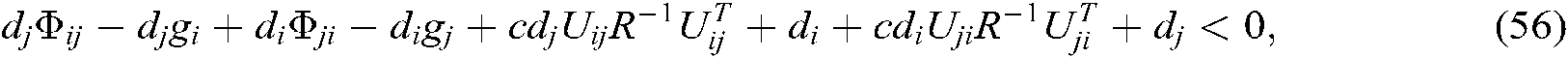




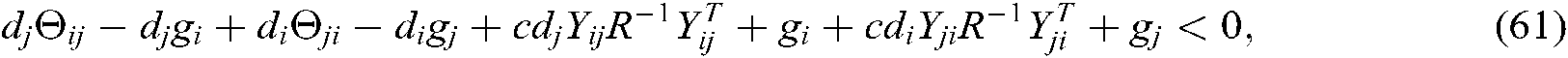
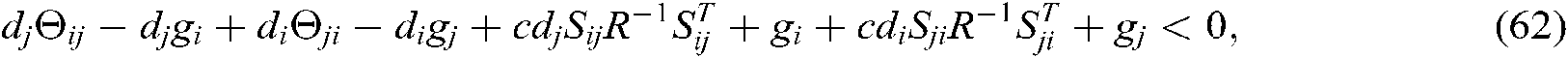
We can see from Shur complement, the above inequalities Eqs. (51)–(62) are equivalent to Eqs. (13)–(24). Since 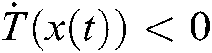 , the system described in Eq. (10) is asymptotically stable.
, the system described in Eq. (10) is asymptotically stable.
Remark 1 We consider the relationship between the membership and the fuzzy regulator in Theorem 1, which is more relaxed than the stability condition that does not consider the information of the membership (Corollary 1). When 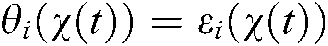 , Theorem 1 can be reduced to Corollary 1 below, i.e., the membership function independent stability condition.
, Theorem 1 can be reduced to Corollary 1 below, i.e., the membership function independent stability condition.
Corollary 1. The scalars 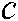 and the matrix
and the matrix 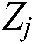 are given, the Eq. (10) is asymptotically stable, if there exist matrices
are given, the Eq. (10) is asymptotically stable, if there exist matrices  and
and 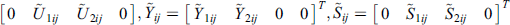 make the under non-equality set up:
make the under non-equality set up:
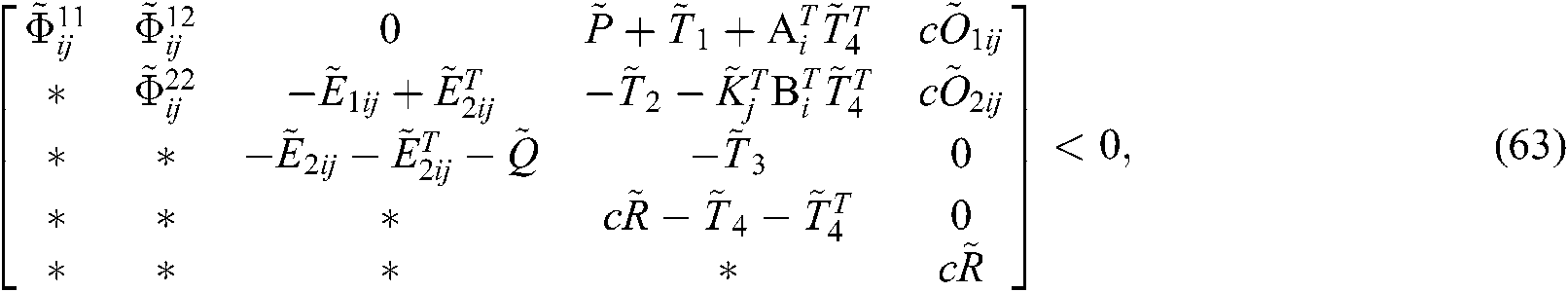
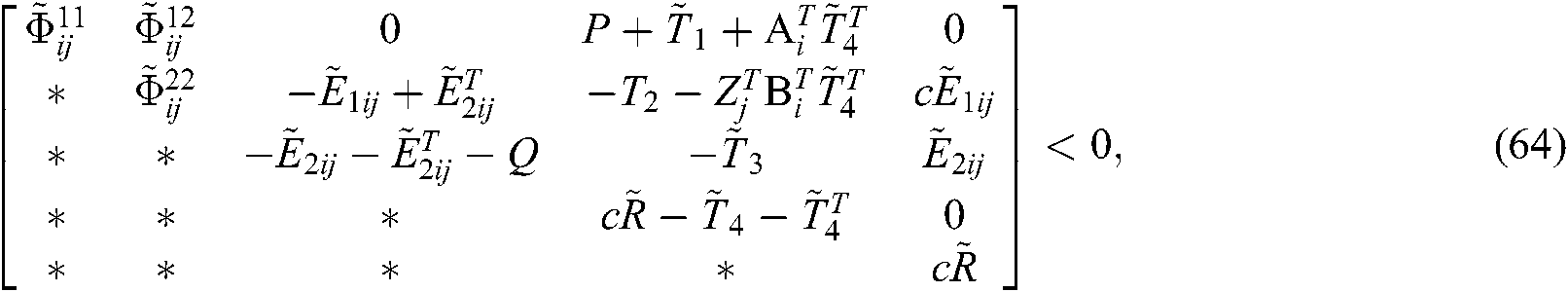


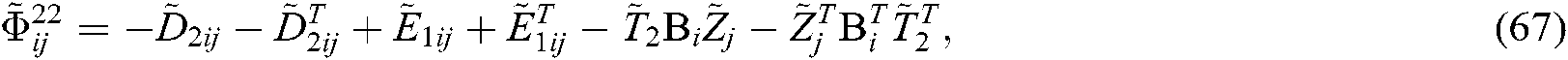
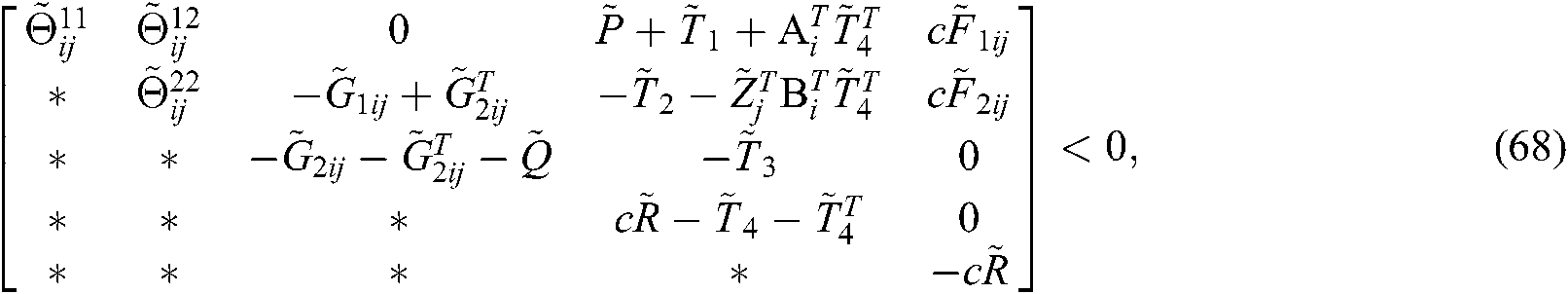
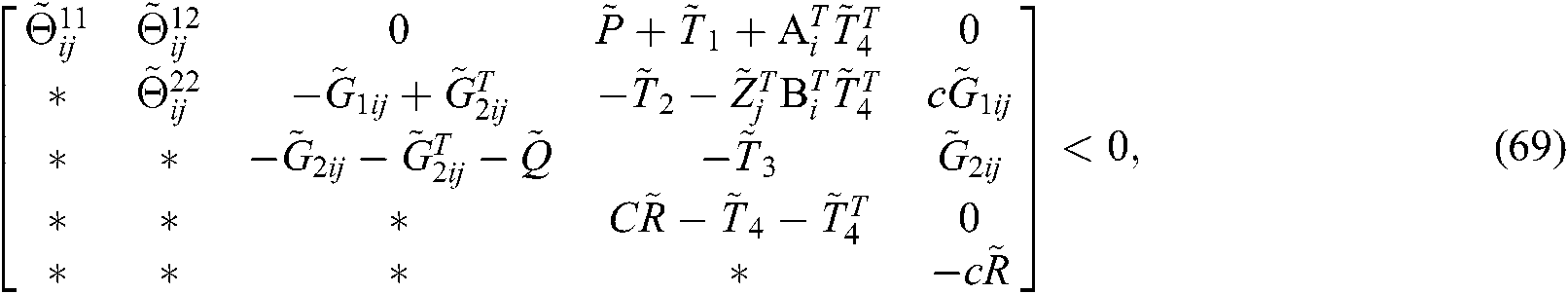


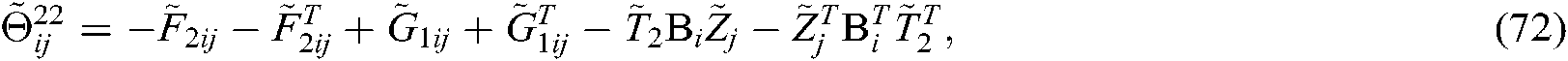
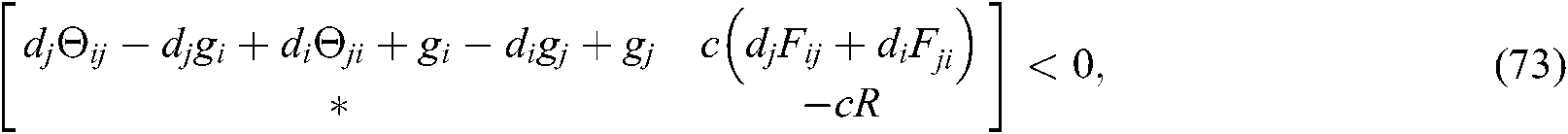
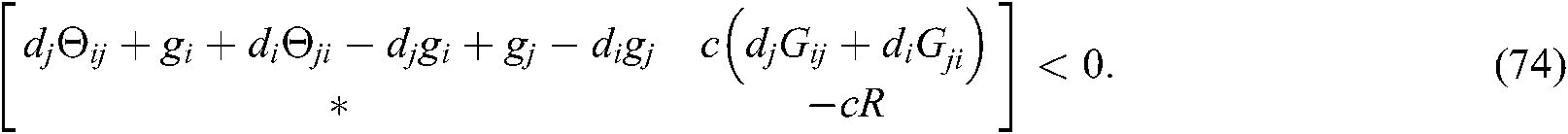
Based on Theorem 1, The following theorem 2 will give the controller design method.
Theorem 2. The scalars  are given, the Eq. (10) is asymptotically stable with feedback gains
are given, the Eq. (10) is asymptotically stable with feedback gains 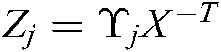 , if there satisfy satisfy
, if there satisfy satisfy 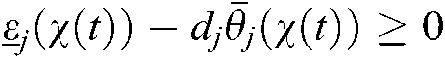 and
and  for all
for all 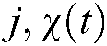 , where
, where 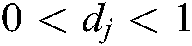 , and the following matrices
, and the following matrices 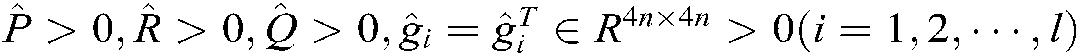 and
and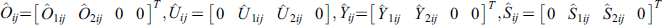 exist, and make the following LMIs set up:
exist, and make the following LMIs set up:




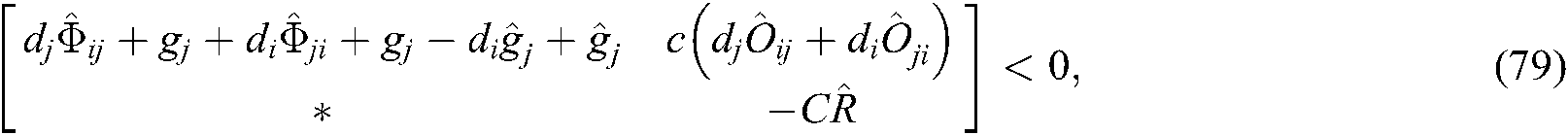
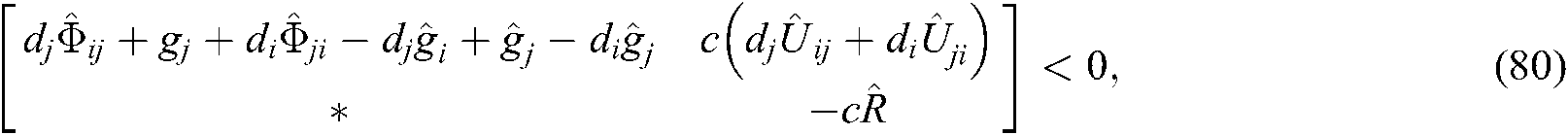




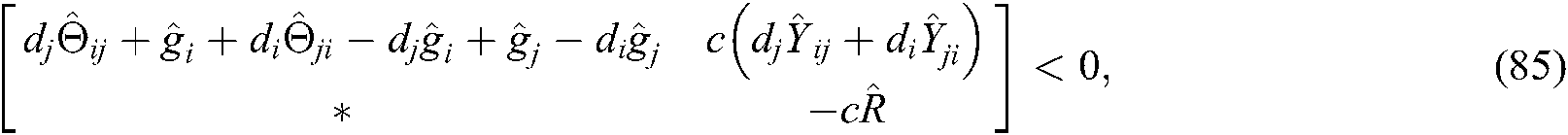
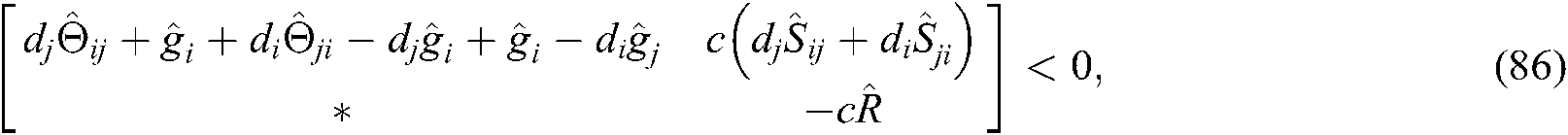
where
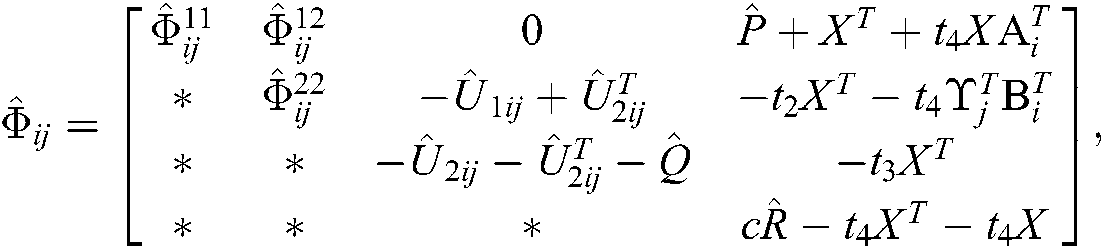

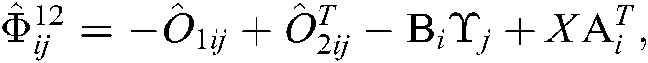
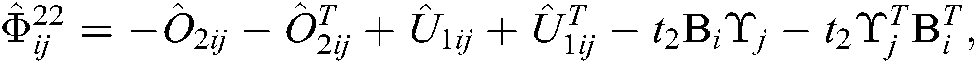
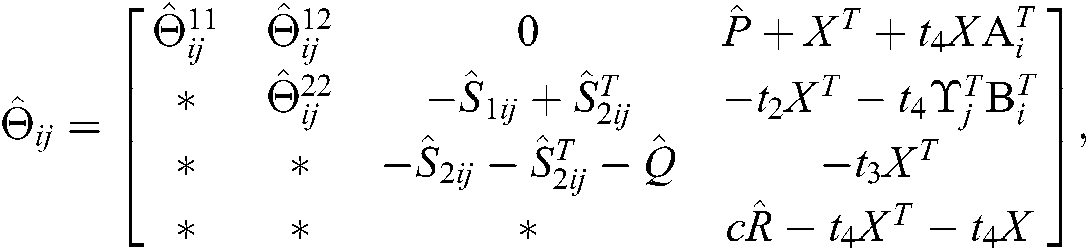
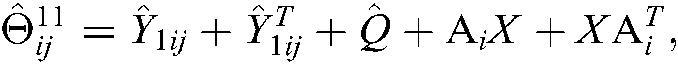
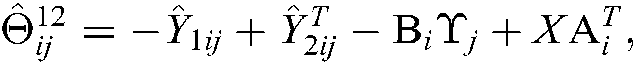
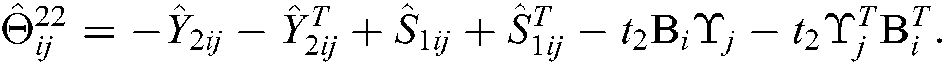
Proof. Pre- and post-multiply the diag 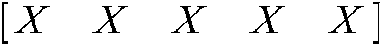 and its transpose to both sides of Eqs. (13)–(24). Let
and its transpose to both sides of Eqs. (13)–(24). Let 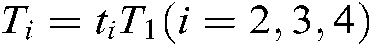 , and the new variables are as follows:
, and the new variables are as follows: 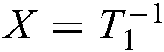 ,
,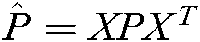 ,
,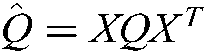 ,
, 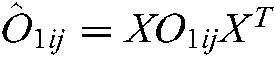 ,
, 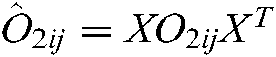 ,
, 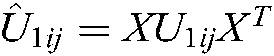 ,
, 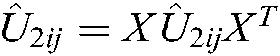 ,
, 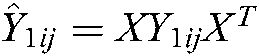 ,
, 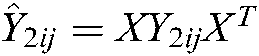 ,
, 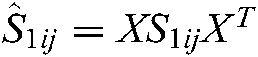 ,
, 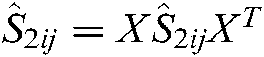 . With
. With 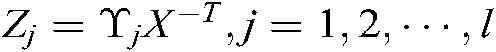 , the inequalities Eqs. (75)–(86) can be obtained.
, the inequalities Eqs. (75)–(86) can be obtained.
Example 1 [33]. In order to compare the results of Theorem 1 and Corollary 1, stability regions are shown in Figs. 2(a) and 2(b).
Rule 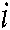 :
: 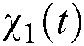 is
is 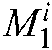 ,
,
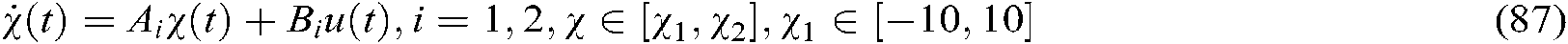
where

We choose the following function as the membership functions of Eq. (87)
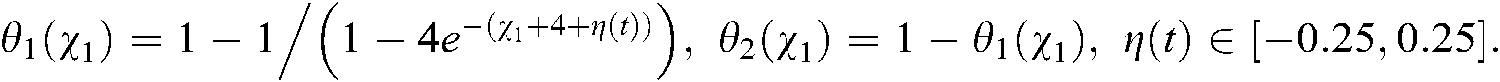
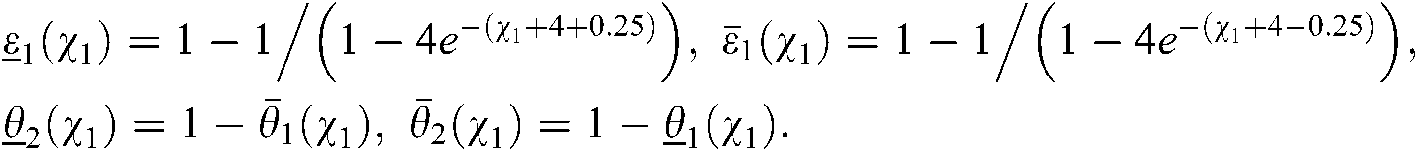
Distinct of the above membership, the down and up membership functions of controller are
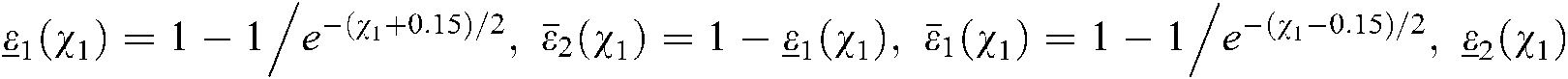
Here, we select 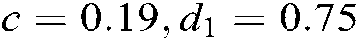 , and
, and 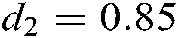 , and the feedback gains of
, and the feedback gains of 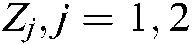 take the value when the characteristic root is
take the value when the characteristic root is 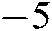 , and we obtain the stability area which is shown in Figs. 2(a) and 2(b) based on Theorem 1 and Corollary 1. we can see larger stability area can be obtained from Theorem 1 than that from Corollary 1(based on the PDC method), which means that the stability condition under the incomplete premise matching is less conservative.
, and we obtain the stability area which is shown in Figs. 2(a) and 2(b) based on Theorem 1 and Corollary 1. we can see larger stability area can be obtained from Theorem 1 than that from Corollary 1(based on the PDC method), which means that the stability condition under the incomplete premise matching is less conservative.
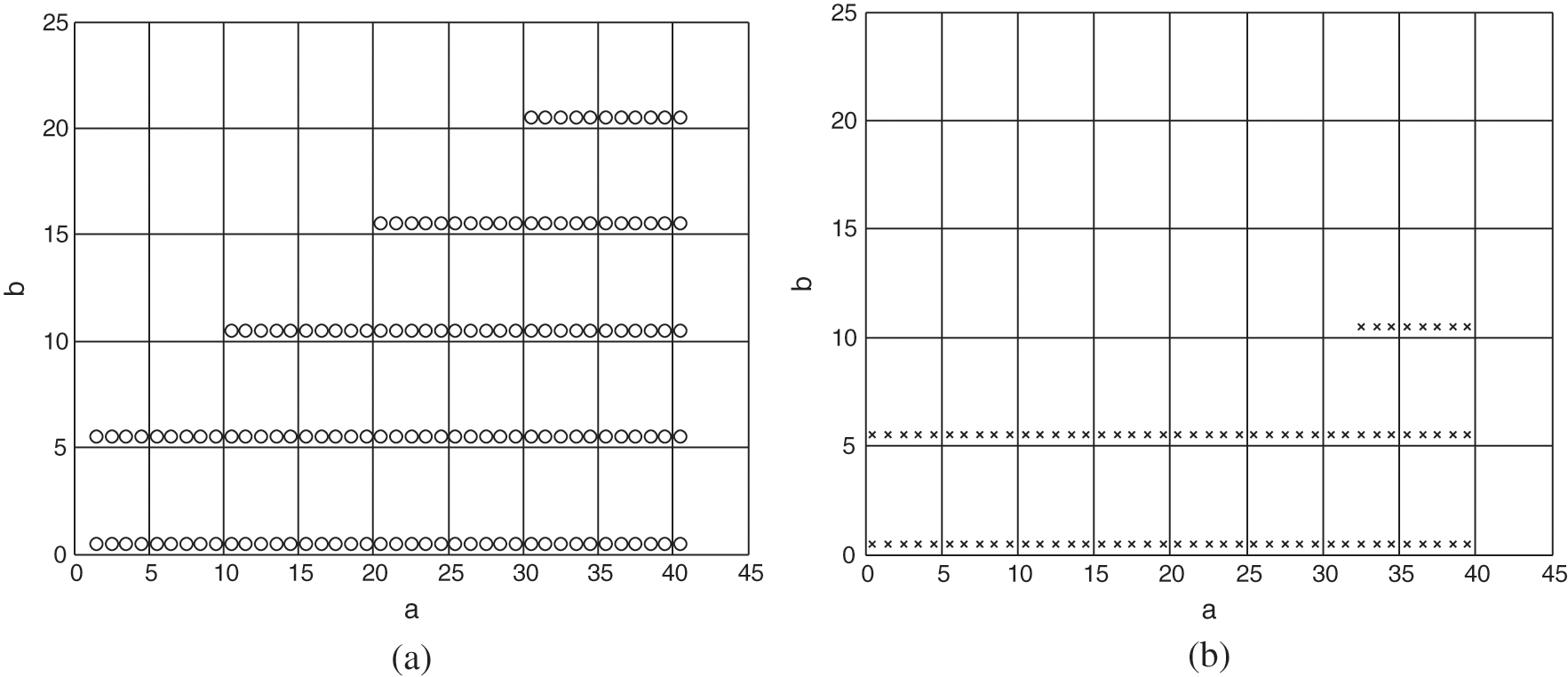
Figure 2: (a) Stable area of Theorem 1 with 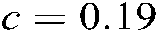 ,
, 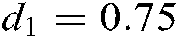 ,
, 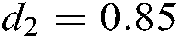 (denoted by “o”); (b) Stable area of Corollary 1 with
(denoted by “o”); (b) Stable area of Corollary 1 with 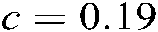 (denoted by “×”)
(denoted by “×”)
Example 2 Consider the following mechanical system [27]

Let 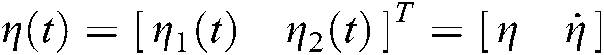 ,
, 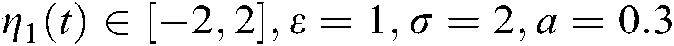 , and
, and 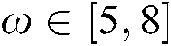 .
.  ,
, 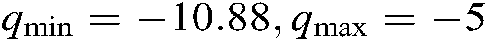 . The mass-spring-damper system in Eq. (88) is described as:
. The mass-spring-damper system in Eq. (88) is described as:

where

In this example, the lower and upper bounds of the membership functions of the plant in Eq. (89) can be selected as the same as those in Example 1. However, according to Theorem 2, the membership functions of the controller cannot be chosen as 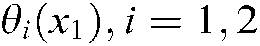 . For simplification, they are set to be
. For simplification, they are set to be 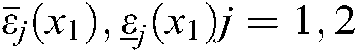 , which satisfy
, which satisfy 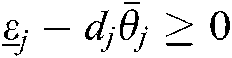 and
and 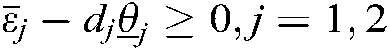 . Using Theorem 2 with
. Using Theorem 2 with 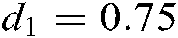 and
and 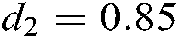 , we can obtain the maximum value of delay
, we can obtain the maximum value of delay 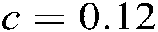 , and the controller gains are:
, and the controller gains are:
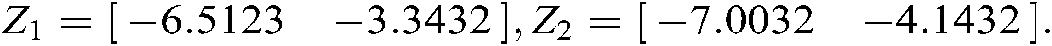
With the controller gains and membership functions 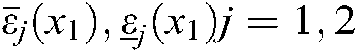 , the controller in Eq. (6) is applied to control the mass-spring-damper mechanical system in Eq. (89). The system responses and control inputs are shown in Figs. 3 and 4, respectively under the initial condition of
, the controller in Eq. (6) is applied to control the mass-spring-damper mechanical system in Eq. (89). The system responses and control inputs are shown in Figs. 3 and 4, respectively under the initial condition of 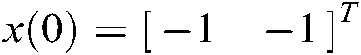 , which demonstrate that the proposed controller design method is indeed effective and efficient.
, which demonstrate that the proposed controller design method is indeed effective and efficient.
Remark 2 Compared with conventional controller design techniques proposed in Lam et al. [6,14–16,26,27] where the fuzzy regulator is bear on the up and down membership functions of the interval type-2 model, the membership functions of our networked fuzzy controller are much simpler, thus significantly enhancing the controller design flexibility.
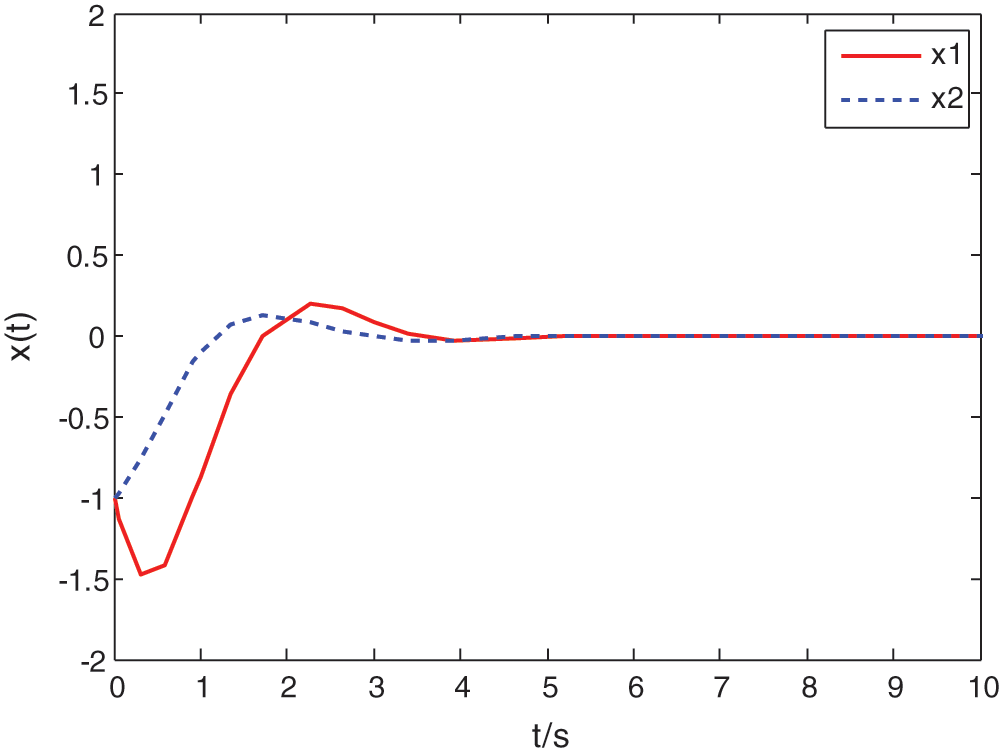
Figure 3: Answers of the control system in Eq. (10) with 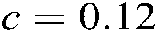
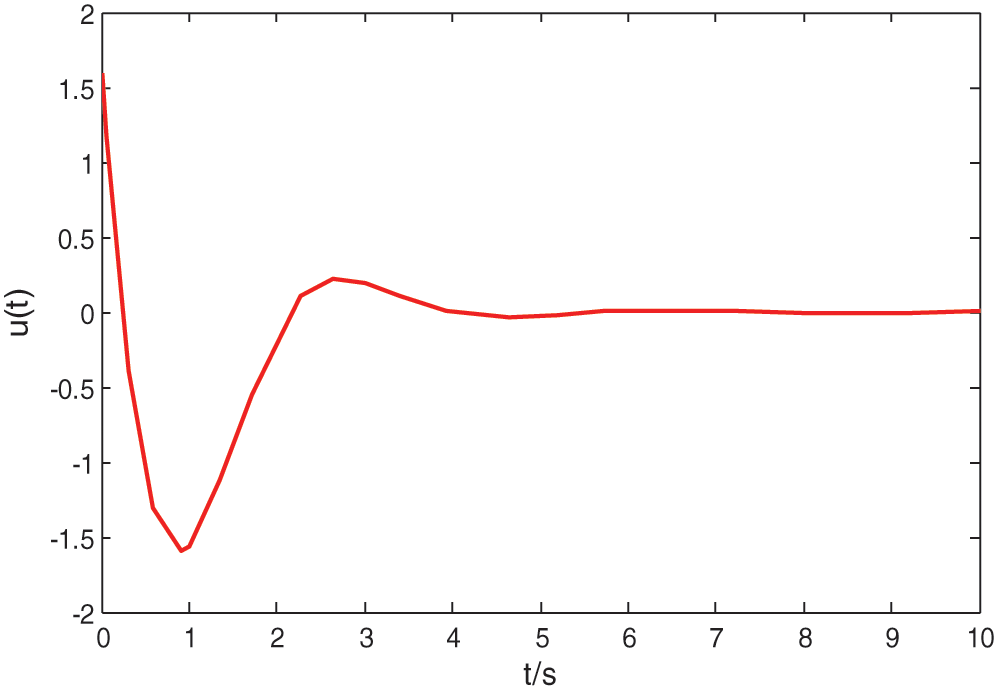
Figure 4: System control input
In this article, we investigate the stability and synthesis for the interval type-2 fuzzy systems. A less conservative stability criterion is got. The stability condition can offer larger stability regions than those obtained from the traditional PDC scheme. Furthermore, a new design technique under the imperfect premise matching is developed in order to stabilize the control systems. Distinct of the PDC controller design method, some simple and certain functions as the membership functions of the fuzzy controller can be selected. Two numerical examples are used to demonstrate the less conservativeness of the above methods. They can significantly improve the design flexibility as well as reduce the implementation complexity of the fuzzy controller.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. T. Takagi and M. Sugeno. (1985). “Fuzzy identification of systems and its applications to modeling and control,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 15, no. 1, pp. 116–132. [Google Scholar]
2. L. A. Zadeh. (1974). “The concept of a linguistic variable and its application to approximate reasoning, ” in Learning Systems and Intelligent Robots. New York: Plenum Press, pp. 1–10. [Google Scholar]
3. J. M. Mendel and R. B. John. (2002). “Type-2 fuzzy sets made simple,” IEEE Transactions on Fuzzy Systems, vol. 10, no. 2, pp. 117–127. [Google Scholar]
4. S. Coupland and R. John. (2007). “Geometric type-1 and type-2 fuzzy logic systems,” IEEE Transactions on Fuzzy Systems, vol. 15, no. 1, pp. 3–15. [Google Scholar]
5. M. Benbrahim, N. Essounbouli, A. Hamzaoui and A. Betta. (2013). “Adaptive type-2 fuzzy sliding mode controller for SISO nonlinear systems subject to actuator faults,” International Journal of Automation and Computing, vol. 10, no. 4, pp. 335–342. [Google Scholar]
6. H. K. Lam and S. Lakmal. (2008). “Stability analysis of interval type-2 fuzzy-model-based control systems,” IEEE Transactions on Systems, Man, and Cybernetics, Part B, vol. 28, no. 3, pp. 617–628. [Google Scholar]
7. H. K. Lam and M. Narimani. (2009). “Stability analysis and performance design for fuzzy-model-based control system under imperfect premise matching,” IEEE Transactions on Fuzzy Systems, vol. 17, no. 4, pp. 949–961. [Google Scholar]
8. Z. J. Zhang, X. L. Huang, X. J. Ban and X. Z. Gao. (2012). “New delay-dependent robust stability and stabilization for uncertain T-S fuzzy time-delay systems under imperfect premise matching,” Journal of Central South University, vol. 19, no. 12, pp. 3415–3423. [Google Scholar]
9. Z. J. Zhang, X. Z. Gao, K. Zenger and X. L. Huang. (2013). “Delay-dependent stability analysis of uncertain fuzzy systems with state and input delays under imperfect premise matching,” Mathematical Problems in Engineering, vol. 2013., pp. 1–13, 2013. [Google Scholar]
10. Z. J. Zhang, X. L. Huang, X. J. Ban and X. Z. Gao. (2011). “Stability analysis and design for discrete fuzzy systems with time-delay under imperfect premise matching,” Journal of Information & Computational Science, vol. 13, no. 1, pp. 2611–2622. [Google Scholar]
11. Z. J. Zhang, X. L. Huang, X. J. Ban and X. Z. Gao. (2012). “Stability analysis and controller design of T-S fuzzy systems with time-delay under imperfect premise matching,” Journal of Beijing Institute of Technology, vol. 21, no. 3, pp. 387–393. [Google Scholar]
12. Y. Li, H. K. Lam and L. Zhang. (2015). “Interval type-2 fuzzy-model-based control design for time-delay systems under imperfect premise matching,” in Proc. of 2015 IEEE Int. Conf. on Fuzzy Systems, Istanbul, pp. 1–6. [Google Scholar]
13. T. Zhao and J. Xiao. (2015). “A new interval type-2 fuzzy controller for stabilization of interval type-2 T-S fuzzy system,” Journal of the Franklin Institute, vol. 352, no. 4, pp. 1627–1648. [Google Scholar]
14. D. Wu, J. M. Mendel and S. Coupland. (2011). “Enhanced interval approach for encoding words into interval type-2 fuzzy sets and its convergence analysis,” IEEE Transactions on Fuzzy Systems, vol. 20, no. 3, pp. 499–513. [Google Scholar]
15. H. Li, C. Wu and L. Wu. (2015). “Filtering of interval type-2 fuzzy systems with intermittent measurements,” IEEE Transactions on Cybernetics, vol. 46, no. 3, pp. 668–678. [Google Scholar]
16. Z. Du, Y. Kao and J. H. Park. (2020). “New results for sampled-data control of interval type-2 fuzzy nonlinear systems,” Journal of the Franklin Institute, vol. 357, no. 1, pp. 121–141. [Google Scholar]
17. C. Peng, Y. C. Tian and D. Yue. (2010). “Output feedback control of discrete-time systems in networked environments,” IEEE Transactions on Systems, Man, and Cybernetics, Part A, vol. 41, no. 1, pp. 185–190. [Google Scholar]
18. F. Rossi, R. D. Lglesias and M. Alizadeh. (2019). “On the interaction between autonomous mobility-on-demand systems and the power network: Models and coordination algorithms,” IEEE Transactions on Control of Network Systems, vol. 7, no. 1, pp. 384–397. [Google Scholar]
19. R. Akhtyamov, I.Cruz, H. Matevosyan, D. Knoll, U. Pica et al. (2016). , “An implementation of software defined radios for federated aerospace networks: Informing satellite implementations using an inter-balloon communications experiment,” Acta Astronautica, vol. 123, pp. 470–478. [Google Scholar]
20. Y. Wu, H. R. Karimi and R. Lu. (2018). “Sampled-data control of network systems in industrial manufacturing,” IEEE Transactions on Industrial Electronics, vol. 65, no. 11, pp. 9016–9024. [Google Scholar]
21. H. Feng and J. Li. (2015). “Distributed adaptive synchronization of complex dynamical network with unknown time-varying weights,” International Journal of Automation and Computing, vol. 12, no. 3, pp. 323–329. [Google Scholar]
22. C. Hua, L. Zhang and X. Guan. (2018). Decentralized fuzzy networked control system design with sector input. Singapore: Springer, 129–155. [Google Scholar]
23. A. Sakr, A. M. El-Nagar, M. El-Bardini and M. Sharaf. (2018). “Model predictive control based on modified smith predictor for networked control systems,” Journal of Electronic Engineering Research, vol. 27, no. 2, pp. 237–258. [Google Scholar]
24. X. Chi, X. Jia and F. Cheng. (2019). “Networked H∞ filtering for Takagi-Sugeno fuzzy systems under multi-output multi-rate sampling,” Journal of the Franklin Institute, vol. 356, no. 6, pp. 3661–3691. [Google Scholar]
25. M. Rouamel, S. Gherbi and F. Bourahala. (2020). “Robust stability and stabilization of networked control systems with stochastic time-varying network-induced delays,” Transactions of the Institute of Measurement and Control, vol. 42, no. 10, pp. 1782–1796. [Google Scholar]
26. Z. Du, Y. Kao and H. R. Karimi. (2019). “Interval type-2 fuzzy sampled-data H∞ control for nonlinear unreliable networked control systems,” IEEE Transactions on Fuzzy Systems, vol. 21, no. 5, pp. 1480–1496. [Google Scholar]
27. Q. Zhou, D. Liu, Y. B. Gao and H. K. Lam. (2015). “Interval type-2 fuzzy control for nonlinear discrete-time systems with time-varying delays,” Neurocomputing, vol. 157, pp. 22–32. [Google Scholar]
28. S. D. Ma, C. Peng, J. Zhang and X. P. Xie. (2017). “Imperfect premise matching controller design for T-S fuzzy systems under network environments,” Applied Soft Computing, vol. 52, pp. 805–811. [Google Scholar]
29. C. Peng, D. Yue and Q. L. Han. (2015). “Delay distribution-dependent control for networked Takagi-Sugeno fuzzy systems,” in Communication and control for networked complex systems. Berlin, Heidelberg: Springer, pp. 1–58. [Google Scholar]
30. L. Sheng and X. Ma. (2014). “Stability analysis and controller design of interval type-2 fuzzy systems with time delay,” International Journal of Systems Science, vol. 45, no. 5, pp. 977–993. [Google Scholar]
31. E. Tian, D. Yue and Y. Zhang. (2009). “Delay-dependent robust H∞ control for T-S fuzzy system with interval time-varying delay,” Fuzzy Sets and Systems, vol. 160, no. 12, pp. 1708–1719. [Google Scholar]
32. G. Cheng and B. K. Su. (2008). “Delay-dependent robust robust H∞ control of convex polyhedral uncertain fuzzy systems,” Journal of Systems Engineering and Electronics, vol. 19, no. 6, pp. 1191–1198. [Google Scholar]
33. Z. Zhang, D. Wang and X. Z. Gao. (2020). “Stability analysis for interval type-2 fuzzy systems based on network environments under imperfect premise matching,” in The 39th Chinese Control Conf., China. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |