DOI:10.32604/iasc.2020.013086
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.013086 | |
| Article |
Soft Computing Based Evolutionary Multi-Label Classification
1Department of Computer Science, COMSATS University Islamabad, Islamabad, 4550, Pakistan
2Department of Computer Science & IT, The Islamia University of Bahawalpur, Bahawalpur, 63100, Pakistan
*Corresponding Author: Rubina Adnan. Email: rubina_adnan@comsats.edu.pk
Received: 25 July 2020; Accepted: 28 August 2020
Abstract: Machine Learning (ML) has revolutionized intelligent systems that range from self-driving automobiles, search engines, business/market analysis, fraud detection, network intrusion investigation, and medical diagnosis. Classification lies at the core of Machine Learning and Multi-label Classification (MLC) is the closest to real-life problems related to heuristics. It is a type of classification problem where multiple labels or classes can be assigned to more than one instance simultaneously. The level of complexity in MLC is increased by factors such as data imbalance, high dimensionality, label correlations, and noise. Conventional MLC techniques such as ensembles-based approaches, Multi-label Stacking, Random k-label sets, and Hierarchy of Multi-label Classifiers struggle to handle these issues and suffer from the increased complexity introduced by these factors. The application of Soft Computing (SC) techniques in intelligent systems has provided a new paradigm for complex real-life problems. These techniques are more tolerant of the inherent imprecision and ambiguity in human thinking. Based on SC techniques such as evolutionary computing and genetic algorithms, intelligent classification systems can be developed that can recognize complex patterns even in noisy datasets otherwise invisible to conventional systems. This study uses an evolutionary approach to handle the MLC noise issue by proposing the Evolutionary Ensemble of Credal C4.5 (EECC). It uses the Credal C4.5 classifier which is based on imprecise probability theory for handling noisy datasets. It can perform effectively in diverse areas of multi-label classification. Experiments on different datasets show that EECC outperforms other techniques in the presence of noise and is noise-robust. Statistical tests show the significance of EECC as compared to other techniques.
Keywords: Multi-label classification; genetic algorithm; ensemble; noisy datasets; Credal C4.5
Machine Learning has played a pivotal role in automating the classification process. The introduction of Multi-Label Classification (MLC) paved the way for automated categorization of text documents and other data into pre-defined categories. Initially, it could assign no more than one category to an instance, formally known as Single Label Classification (SLC). As text classification remained the dominant area for label classification, single-label classification could not deal with its multi-dimensional nature [1]. Assigning more than one labels to an instance is a complex problem but moving from SLC to MLC seemed to be a natural solution for demanding applications like document classification, medical diagnosis, bioinformatics [2,3], news analysis, movies/music categorization, web resources classification and computer vision [4,5].
Multilabel Classification (MLC) in data mining is defined as a predictive task having a wide range of real-world applications. There are numerous scenarios where more than one category or label may be associated with an instance of a dataset. Let L = {λ1, λ1, λn} be the set of n different binary labels (with n > 2) and D the set of y instances with each instance having x features. Thus we can define multi-label classification as learning a mapping that exists between di ∈ D and a set of labels li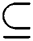 
L. We can deduce that the labels in set li are the ones having relevance to instance di and the rest having no relevance.
There are two high-level approaches to deal with problems of multilabel classification. The first and least difficult of the two; transformation, change a multi-classification problem into a lot of particular parallel grouping problems while the second; adaptation, utilizes complex algorithms or algorithm ensembles. Different studies have been conducted and categorized as transformation, adaptation, and ensemble-based approaches. Each approach is focused on solving an issue of multi-label classification. However, the most challenging issues faced thus far have been label imbalance, label relationships, high dimensionality, and noise.
Label imbalance in a dataset can be caused by an uneven number of instances per label [6]. The most frequent labels take over the infrequent ones in the dataset resulting in a bias of prediction. If a classifier can’t handle label imbalance it will most probably produce biased results. Proposed techniques to handle label imbalance include random under-sampling and random over-sampling [6] and are based on LP transformations. In an under-sampling loss of information may occur as essential labels may be removed. Over-sampling attempts to balance the minority class instances in the dataset [7]. Another sampling technique Synthetic Minority Oversampling Technique (SMOTE) generates synthetic minority class instances by interpolating the minority class instances [8].
Label relationships or dependencies help in finding relevant categories [9]. Labels are inherently related to or dependent on each other. A news article written on politics may also belong to finance or governance. The likelihood of a song being labeled as “Pop” becomes stronger if it has been labeled as “Hip Hop” or “RB” [10,11]. Capturing meaningful relationships among members of a social network generates new trends increasing the predictive performance of the classifier [12]. Understandably label relationships are important and ignoring or harnessing their power can directly affect the prediction power of a classifier.
The challenge of high-dimensionality is related to output space in multi-label classification [13]. The output space increases exponentially as the number of labels increases and with that, the possible number of combinations also increases.
Since data may come from various sources, there is a possibility of pollution or noise. Anything that is polluting the actual data is noise. Encryption is also a source of noise [14]. When we query a search engine for information extraction, there is a possibility of the query to be noisy and produce irrelevant results [15–17]. Noise can be of two types; feature noise and label or class noise [18]. The presence of incorrect labels is also referred to as label noise. Label noise is known for decreasing the prediction performance of the classifier. If label noise can be reduced, only relevant labels participate in classification, and performance is improved.
In this study, we propose an evolutionary ensemble-based approach that adopts the transformation method, Label Power-set (LP), combined with Credal C4.5 as a base classifier that uses the idea of imprecise probabilities to solve the problem of noise. We focus on finding its deficiencies, discuss them in detail, and suggest improvements based on empirical analysis of results. Finally, we propose an improved algorithm that handles label imbalance, label relationships, and noise by conducting trials on existing and new multi-label data. The key contributions of our study are as follows:
• Propose an Evolutionary Ensemble of Credal C4.5 (EECC) for multi-label classification that handles noise in datasets to capture meaningful dependencies among labels.
• Propose a linear fitness function that helps to achieve better label combinations.
• Handling class imbalance by considering majority and minority labels.
The rest of the paper is organized as follows: Section 2 presents the literature review whereas. The proposed approach is described in Section 3 and Section 4 discusses the proposed EECC algorithm. Section 5 presents the experimental results of the proposed EECC approach, and Section 6 discusses the results. Finally, Section 7 concludes the study.
This section elaborates methods proposed for multi-label classification problems. On a higher level these can be divided into two approaches.
These methods, transform the multi-label problem into multiple single-label problems, include Support Vector Machines (SVM), Neural Networks (NN), and Naïve Bayes (NB). Binary Relevance (BR) has been widely used in MLC where a learning task is broken down into multiple binary problems. It produces one binary dataset for each label. However, it assumes that the labels are independent and completely ignores potential correlations among labels [19] while suffering from label imbalance.
Label Combination (LC) or Label Powerset (LP) makes a new class out of each possible combination of labels, thus treating it as a single label multi-class problem. Building these multiple instances increases the worst-case computational complexity as the number of labels increase, with a tendency to over-fit model on the test data. It works well on the training data but is unable to show generalized effectiveness [5].
Pruned Set (PS) transformation focuses on class imbalance [2]. In this technique, by considering only the important and most frequent combinations of label sets, the inherent complexity of LP is further reduced. However, it does not guarantee to keep all the important information and thus increases the probability of overfitting.
Classifier Chains (CC) [9] produce a chain of binary datasets that are merged with the feature space. Each classifier receives input in the form of label predictions from the previous classifier forming a chain. However, the selection and ordering of the chain directly impact the performance of the classifier as it is propagated along the chain.
Problem Adaptation methods are based on a particular single label classification algorithms, already being used in machine learning. These are adapted, extended, and customized to suit Multi-label classification, enabling them to directly handle multi-label data.
The most popular method, improved in various ways in several research works is MLkNN. It is based on the k-Nearest Neighbors (kNN) method, traditionally used for single-label data. To predict an unseen instance, it first finds k-nearest neighbors of that instance. Finally the maximum A Posteriori principle is used to predict the label set for the new instance [20]. It is prone to introducing class-imbalance problems and ignoring the relationships between labels, affecting its overall performance and accuracy [21].
The Ada-Boost algorithm is used to construct a strong classifier as a linear combination of simple weak classifiers. Ada-Boost.MH targets Hamming Loss (HL) and Ada-Boost.MR targets the RL by ordering of labels and keeping the correct ones at the top of ranking [22]. In addition to that the Ada-Boost. MH was combined with other algorithms for creating decision trees and hence produce human-readable models [23]. Problems may occur in the form of overfitting as the number of iterations continues to increase [22].
Decision Trees have been at the center of some traditional methods for classification of binary or multi-class data. A popular algorithm C4.5 based on Decision Tree and an extension of its predecessor, the ID3 algorithm, applies heuristics to prune decision trees after construction [24]. When used in Multi-Class classification it predicts exactly one class for an instance and not a set of classes. A new algorithm Multi-label C4.5 has been adapted to be used for Multi-label classification. Here each leaf of a decision tree can have multiple labels and the entropy definition is also modified to handle multiple labels.
Multi-label Decision Tree (ML-DT) is a first-order approach that assumes label independence for calculating multi-label entropy. The use of the Decision Tree Model adds efficiency gains to ML-DT giving it an advantage on its predecessors. ML-DT can be further improved by including a pruning strategy or ensemble learning technique [25,26].
Predictive Clustering Technique (PCT) is also based on Decision Trees. The Rank SVM method, an adaptation of SVM, proposed by Joachims [27] in 2002. Reference [28] shows improved performance over BR.
Support Vector Machines (SVMs) [29,30] are popular and thought to be a successful methodology for classification problems. SVMs most often optimize accuracy on a given dataset. When training data is unbalanced, accuracy is often a poor metric to use.
A higher order of algorithms makes the MLC task delve deep into correlations among labels by considering the influence of each label on all other labels. This results in a higher order of correlations among labels or random subsets of labels. The increased complexity also costs in terms of computational power [31,32].
There also exists a third kind of methodology for multi-label classification problems, called ensembles. It is based on the notion that the collective knowledge of a group of people is better than a single expert. An ensemble of weak classifiers offers a diverse approach to the classification problem. The more diverse the individual classifiers are the better the results, as each classifier can have different biases.
Label Powerset/LC can model label correlations but introduces over-fitting on training data as by design it can only model label sets found in the training data [3,33]. The ensembles are designed to collect information from more than one generalizer or learners reducing the biases of different learners.
RAndom k-labELsets (RAkEL) is an ensemble of LP, it breaks down an initial set of labels into smaller, random k subsets. Where the parameter k determines the size of the subsets. These subsets are called label-sets [3]. It then employs LP to train a corresponding classifier. RAkEL gives an advantage over LP by avoiding the computation-intensive operations as the label-sets are simpler. The correlations among the labels are also preserved to some extent and the class imbalance is largely addressed for a high number of labels. It can predict unseen label-sets but makes label combinations randomly, ignoring any meaningful relationships, which might affect the overall accuracy of classification.
2.3.1 Evolutionary Approach in Building Ensembles
Different evolutionary approaches have been proposed for the automatic generation of ensembles of diverse and competitive multi-label classifiers [11]. It takes into consideration some key challenges of multi-label classification, like taking into account simple and complex relationships among the labels, imbalance of data, and complexity of the output space. In these evolutionary approaches, C4.5 is used which does not handle noise efficiently.
In previous studies mostly noise-related problems are handled as binary classification problems and a limited number of works have been done related to multi-label classification. As real-world dataset contains abnormalities such as missing values, redundant labels, and outliers, these types of errors are known as label noise [34] and cause problems during classification, producing an over-fitting model. Different noise handling techniques have been proposed to solve these issues [35] and can be categorized into two classes: Algorithms level approaches and Noise Robust Methods
2.3.3 Algorithm Level Approaches
Algorithm level approaches are applied as a pre-processing stage. They does not require any previous technique to be applied [36].
These methods learn without noise modeling or data cleaning even when some amount of noise labeling is present. These methods use ensembles to handle noise, thus increasing the robustness of base classifiers [37]. Boosting methods such as Ada-boost degrade performance when some level of noise is present in the dataset.
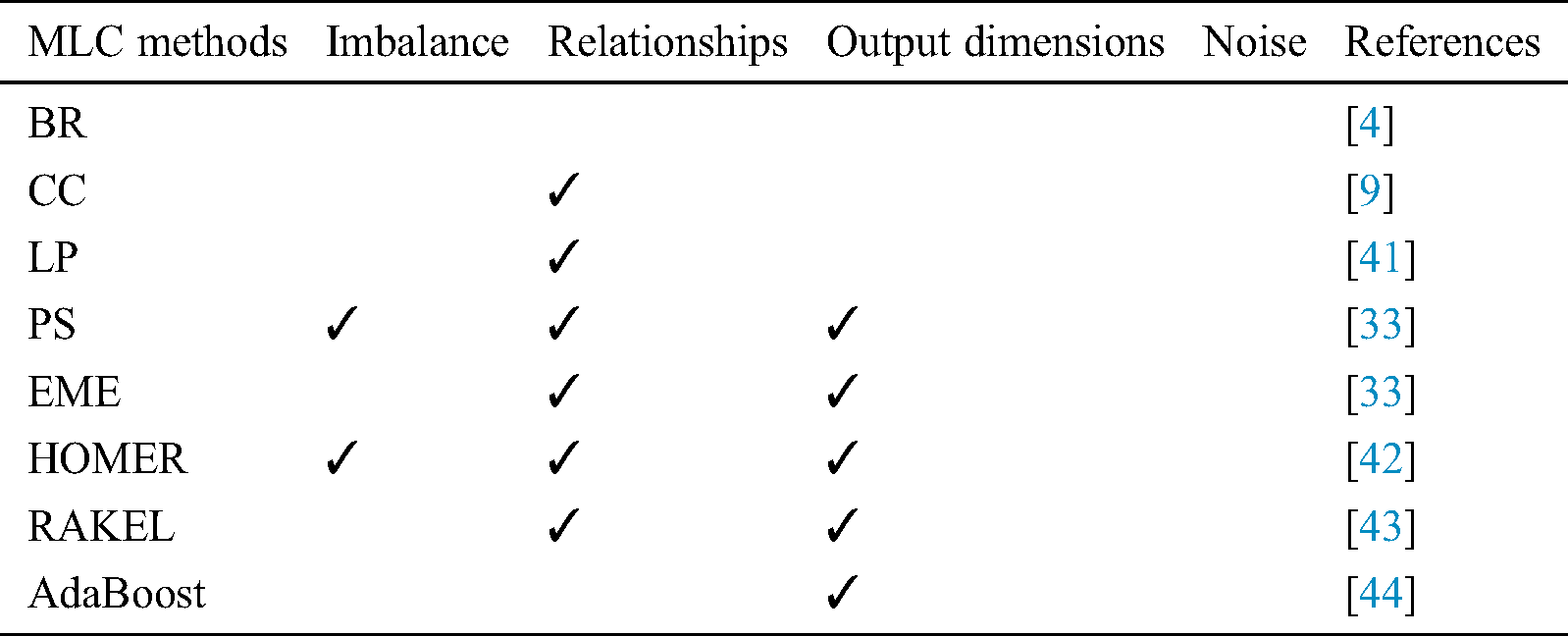
In reference [38] the authors proposed to modify the C4.5 [39] with the Credal Decision Tree (CDT) method. They called the new algorithm Credal C4.5. It uses the information gain ratio as splitting criteria. This process is based on the precise probabilities therefore it considers the training data to be reliable. However, this situation can be unstable when we are classifying noisy data [39,40]. The comparison of different algorithms that use decision trees as a base classifier has been provided in Tab. 1.
Table 1: Comparison of multi-label classification techniques in terms of classification problems
The proposed approach of EECC consists of four steps. In the first steps, k-label combinations of Multi-Label CC4.5 (MLCC4.5) are generated randomly, where each set of labels consists of 3 labels. We have chosen 3 as an optimal size as increasing it any further will increase the complexity. We have used Label Powerset (LP) as a base classifier. The idea is to use each classifier to model the label relationships from the entire output space. As the chosen label space, using the evolutionary technique is smaller, the imbalance ratio is lower. In the second step, the crossover operation is applied to the generated label sets. In the third step, we apply mutation operations to the offspring generated from crossover operation, and in the fourth step, we calculate the fitness of the individual. For each instance, the MLCC4.5 is trained on label sets using LP and then on the given predictions for the label sets. The outputs of all the classifiers are used for the final prediction of EECC. Before the final prediction, the evolutionary selection criteria are adopted which includes the crossover and mutation operations. The final prediction is computed based on majority voting.
3.1 Individuals Representation
The population of each individual is already discussed at the beginning of Section 3. Each individual of multi-label classifier and labels is encoded into a binary representation or an array with values 1 or 0. In each individual, 1 represents the presence of the λl label. All the labels with a value of 1 mean they have been used to train the MLCC4.5. This representation is depicted in step 1 of Fig. 1.
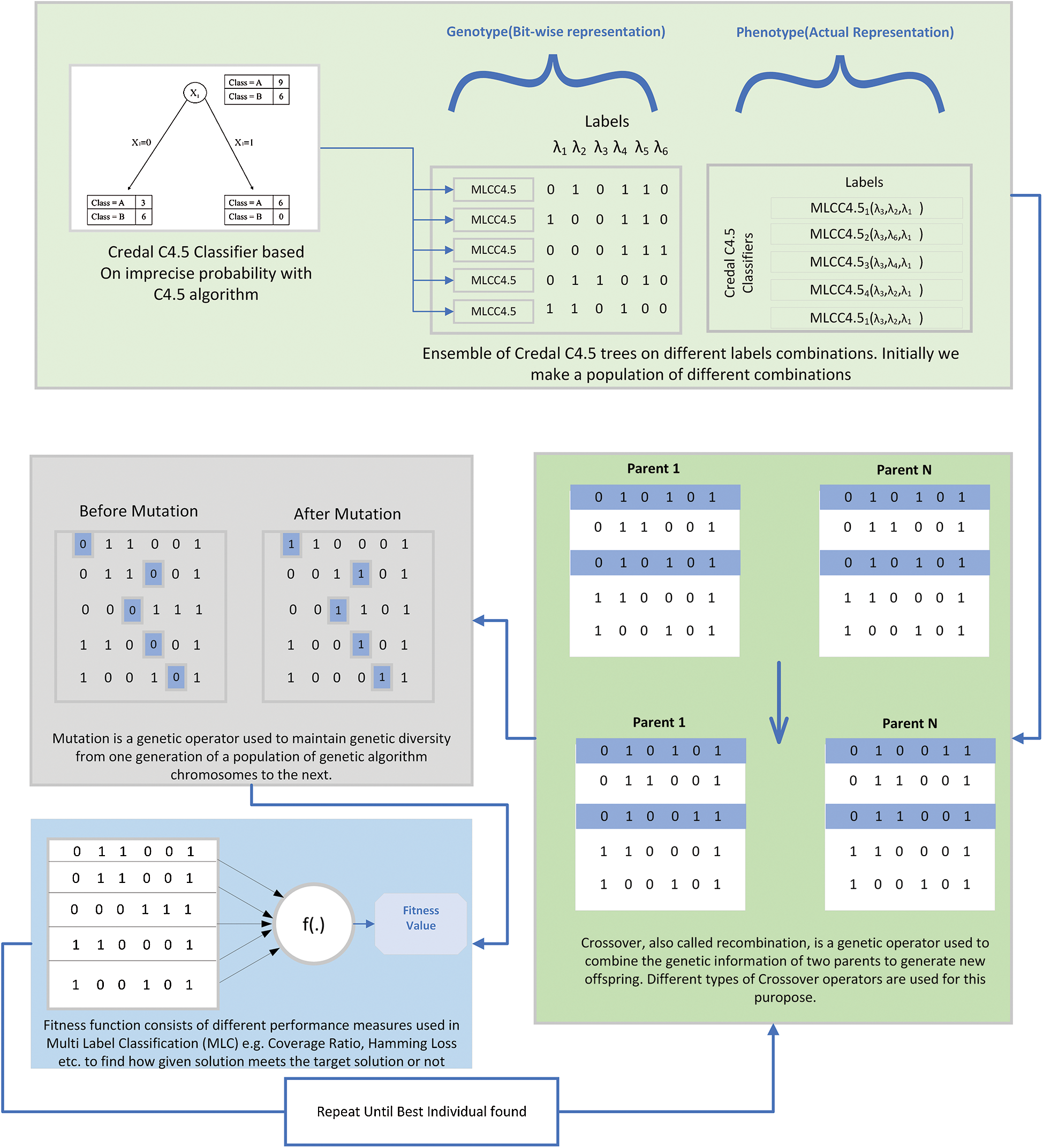
Figure 1: System diagram of the proposed methodology
3.2 Individuals Initialization
The individuals need to be created at the beginning of the evolution process based on the frequency of labels. Frequency represents the importance and complexity of label relationships. However, if this assumption ignores minority labels it will reduce the performance. Thus initial population not only contains frequently occurring labels but also contains infrequently occurring labels to ensure the presence of both labels in the population.
The crossover operator swaps two individuals ind_1 and ind_2 to create a new individual. The idea behind a crossover operator is to create new individuals while preserving previous individuals’ information. This is illustrated by Step 2 in Fig. 1. We have used a uniform crossover operator where a random variable is generated from some probability distribution. The individual falling before that position is picked from one ensemble and the other is picked from another ensemble and is swapped. In this way, the new individual inherits the characteristics of both the parents.
The mutation operator swaps the bit values of the individual. For any individual it generates a random number for any bit from that individual and swaps a 0 to 1 and 1 to 0. Fig. 1 shows the mutation operation applied after the individual generated using the crossover operation.
The fitness function proposed in this study is based on the fitness function proposed in [45]. It takes into account two important measures; the performance of the classifier and the number of times each label falls in the ensemble. This helps it in choosing the individuals with the highest performance that also considers all the labels the same number of times regardless of their overall frequency in the dataset. The choice of evaluation measures in MLC is significant to gauge the prediction results correctly. We must choose a measure that also evaluates the label relationships in an ensemble. Example-based F Measure (ExF), defined in Eq. (1) calculates the FMeasure for MLC. It indicates the percentage of samples that are correctly identified. Using this measure helps to identify the individuals that give higher performance. Coverage Ratio is used to find the number of times each label appears in the ensemble, it is defined in Eq. (2). In the following equations ↓ and ↑ indicate if the measures are minimized or maximized respectively. Our fitness function is a combination of these two measures as shown in Eq. (3).
4 Evolutionary Credal C4.5 Ensemble (EECC4.5)
The algorithm of the proposed EECC is shown in Algorithm 1. The multi-label dataset, population size, individual numbers, and the number of generations are input parameters. The algorithm generates predictions of a multi-label dataset in terms of different evaluation metrics. It initializes the population as discussed in Section 3. After initializing the population, it applies crossover and mutation on the population to generate new individuals, and tshen based on fitness value, the new generation evolves.
Algorithm 1: Proposed Evolutionary multi-label classification ensemble
For our experiments, we used hardware configuration of 8 GB RAM, SSD storage, and Intel Core i7, 7th generation processor. Credal C4.5 is implemented in Python programming language. For the implementation of the Parallel genetic algorithm, we will use the DEAP (Distributed Evolutionary Algorithms in Python) library. For comparison of our technique with other transformation methods, we used MeKa (An extension of WeKa library for Multi-label Classification) [5].
We have used a mutation probability of 0.33 [46] with uniform crossover operation and the number of generations depends on the complexity of datasets. For datasets that contain a large number of labels, we have used 300 generations and for small datasets, 30 generations are used.
In the case of standard multi-class classification, we would use evaluation measures like Accuracy, Precision, and Recall, etc., but in the case of multilabel classification, these measures are not sufficient. For assessment of multilabel classification various performance measures have been suggested which are discussed below:
This measure finds how many times the labels are misclassified, returns the mean values across the test set. It compares the ground-truth labels with the predicted-labels.
where p is the number of labels and Yi is the predicted labels and Xi is the actual labels.
This measure means the number of more labels on average should include covering all relevant labels. It is defined as:
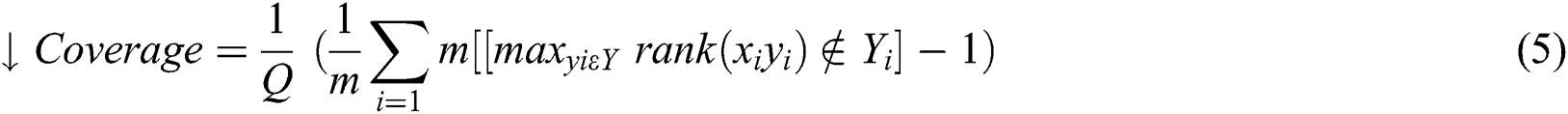
Subset Accuracy (SA) is a strict measure to check the correct predictions. It is also known as the Exact Match Ratio (EMR). It is represented as:
where p is the number of classes and Yi is the predicted labels and Xi is the actual labels.
This method takes the average of all the precision scores of the predicted and represented as:
P1 and P2 represent the precision of a single class whereas, precision is represented as:
where TP stands for True Positives and FP for False Positives.
This method takes the average of all the Recall scores of the predicted and represented as:
Here R1 and R2 represent the recall score of different classes where recall is represented as:
where TP stands for True Positives and FN for False Negatives.
We have performed experiments on various datasets using a 10-fold cross-validation technique. The characteristics of datasets are shown in Tab. 2. It shows the name, number of samples, features, and labels of the dataset. The type of the dataset, its domain, and the Imbalance Ratio is provided to show the imbalance ratio between the labels.
Table 2: List of datasets used to perform experiments with their details
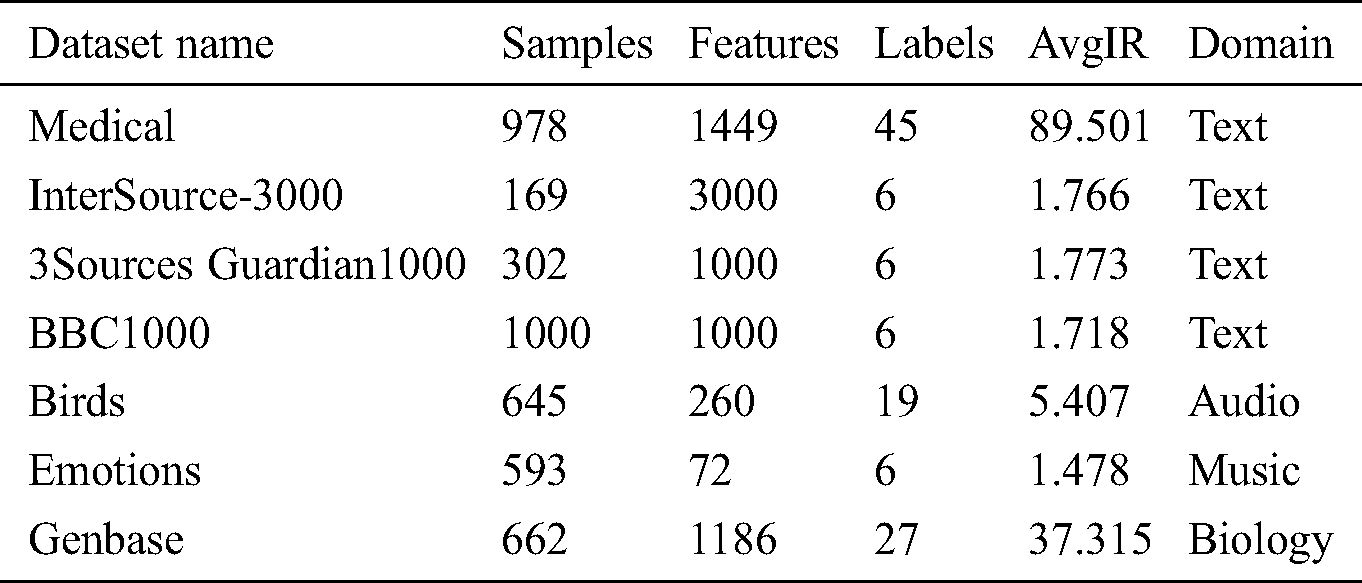
We have performed experiments on different datasets and compared the approach with baseline architecture. This comparison of different datasets with before and after the addition of noise is shown here. We have also performed a comparison of different performance measures, before and after the addition of 10% noise in labels.
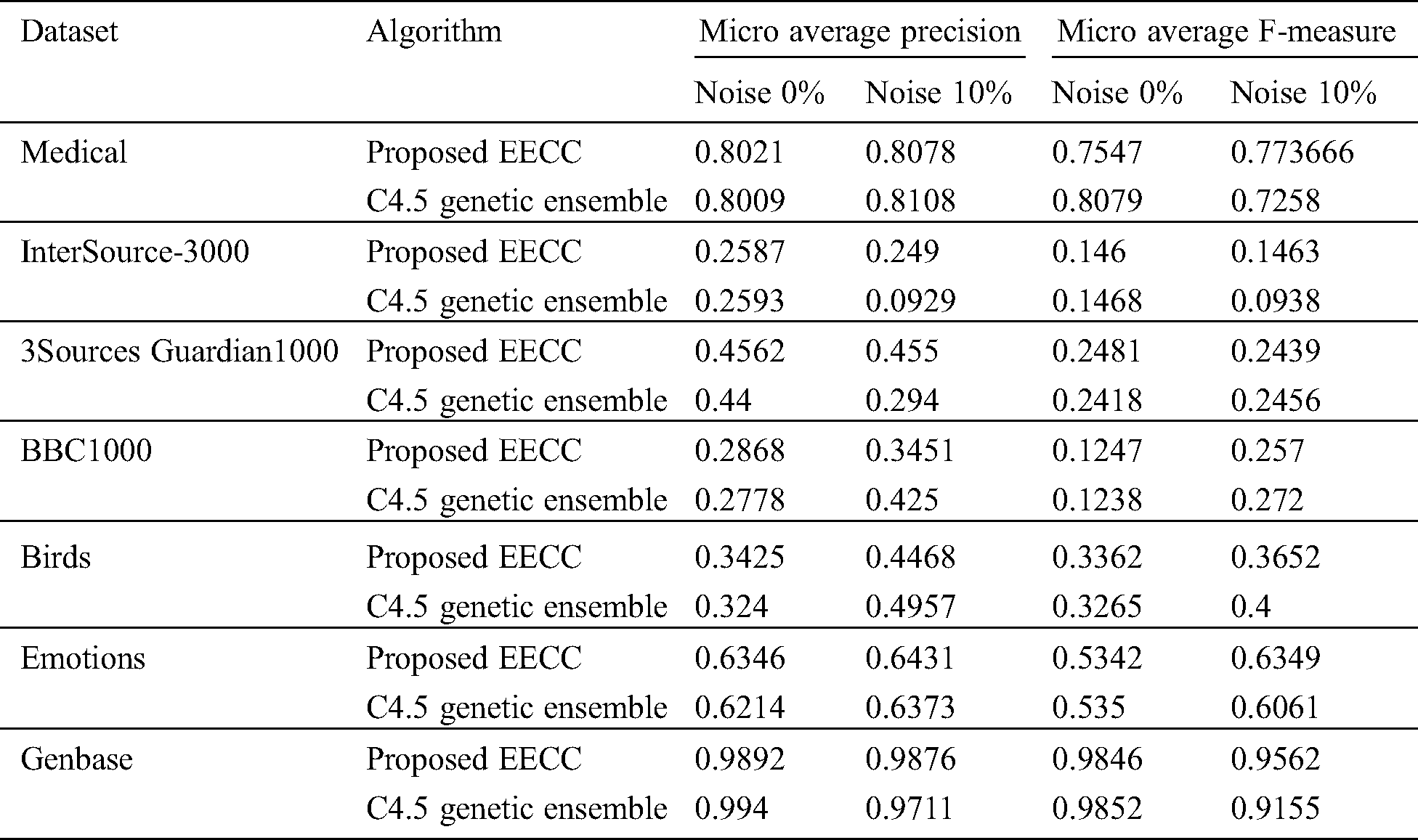
The effect on Example-based F-Measure, before and after the addition of 10% noise is shown in Tab. 3. The EECC does not show a significant change in the ExF score compared to the C4.5 ensemble, before the addition of noise.
Table 3: Results comparison of example-based F-measure score of our proposed EECC with C4.5 ensemble with before and after the addition of noise
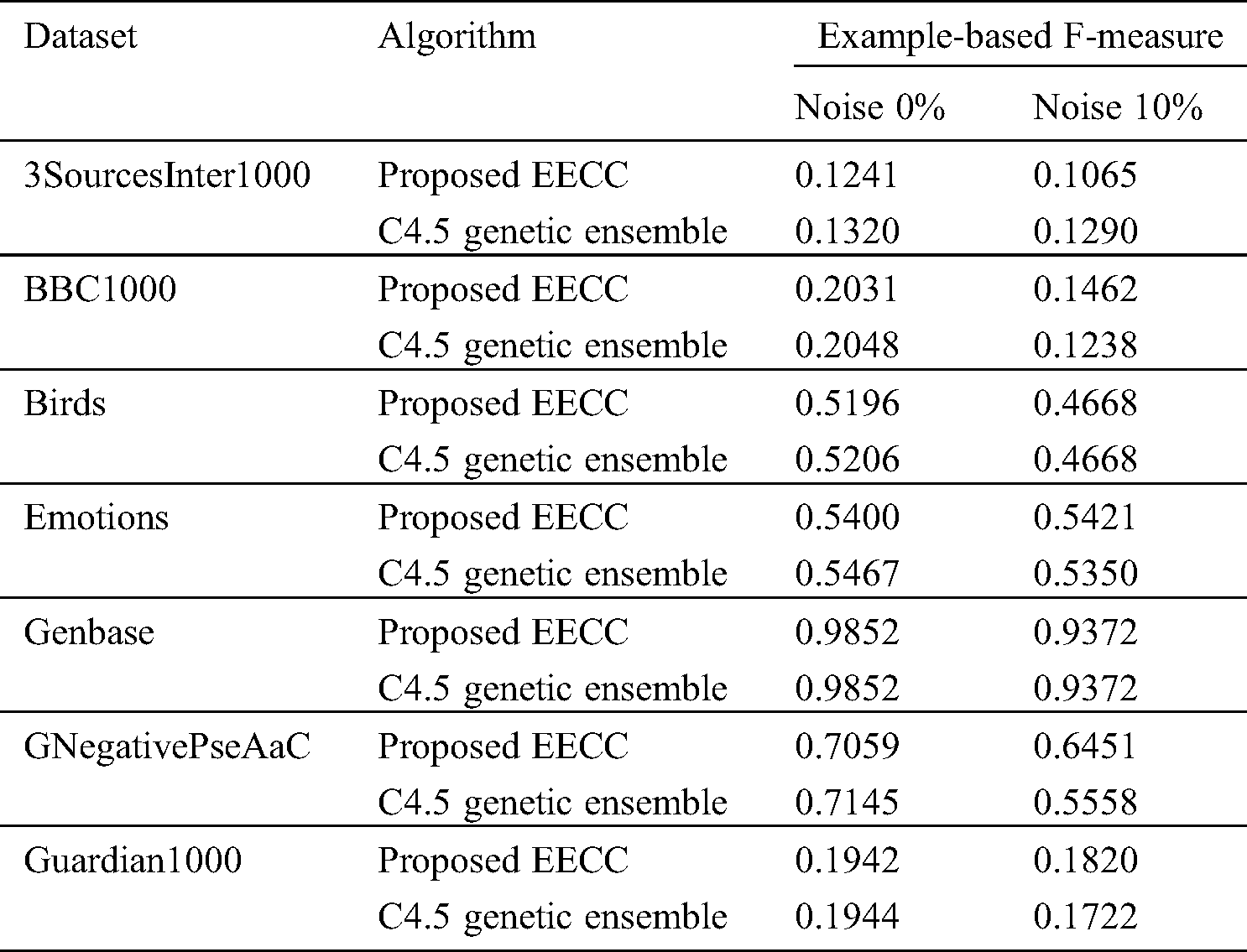
However after the addition of noise in labels the ExF score of C4.5 Genetic Ensemble decreases and that of EECC increases.
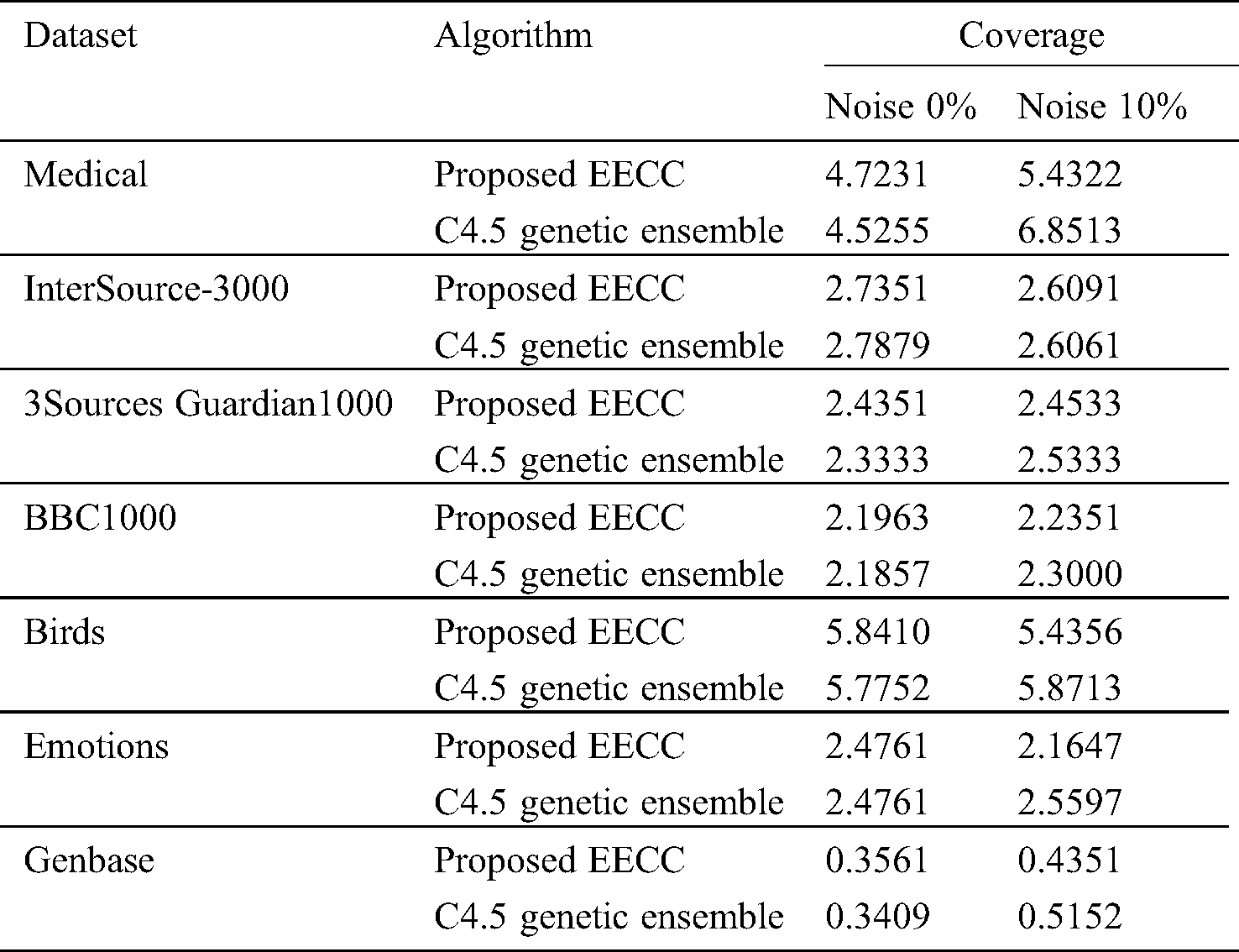
The effect on Coverage Ratio, before and after the addition of 10% noise is shown in Tab. 4. The EECC does not show a significant change in coverage score compared to C4.5 Genetic Ensemble, before the addition of noise. However after the addition of noise in labels the Coverage score of C4.5 Genetic Ensemble increases and that of EECC decreases showing that it is noise-robust and prunes the redundant labels efficiently. In terms of Coverage Ratio, for the datasets, Medical, 3Sources Guardian1000, BBC1000, Birds, Emotions, and Genbase, EECC has performed better in presence of label noise.
Table 4: Results comparison of proposed EECC with C4.5 genetic ensemble of coverage on different noise levels on multiple datasets
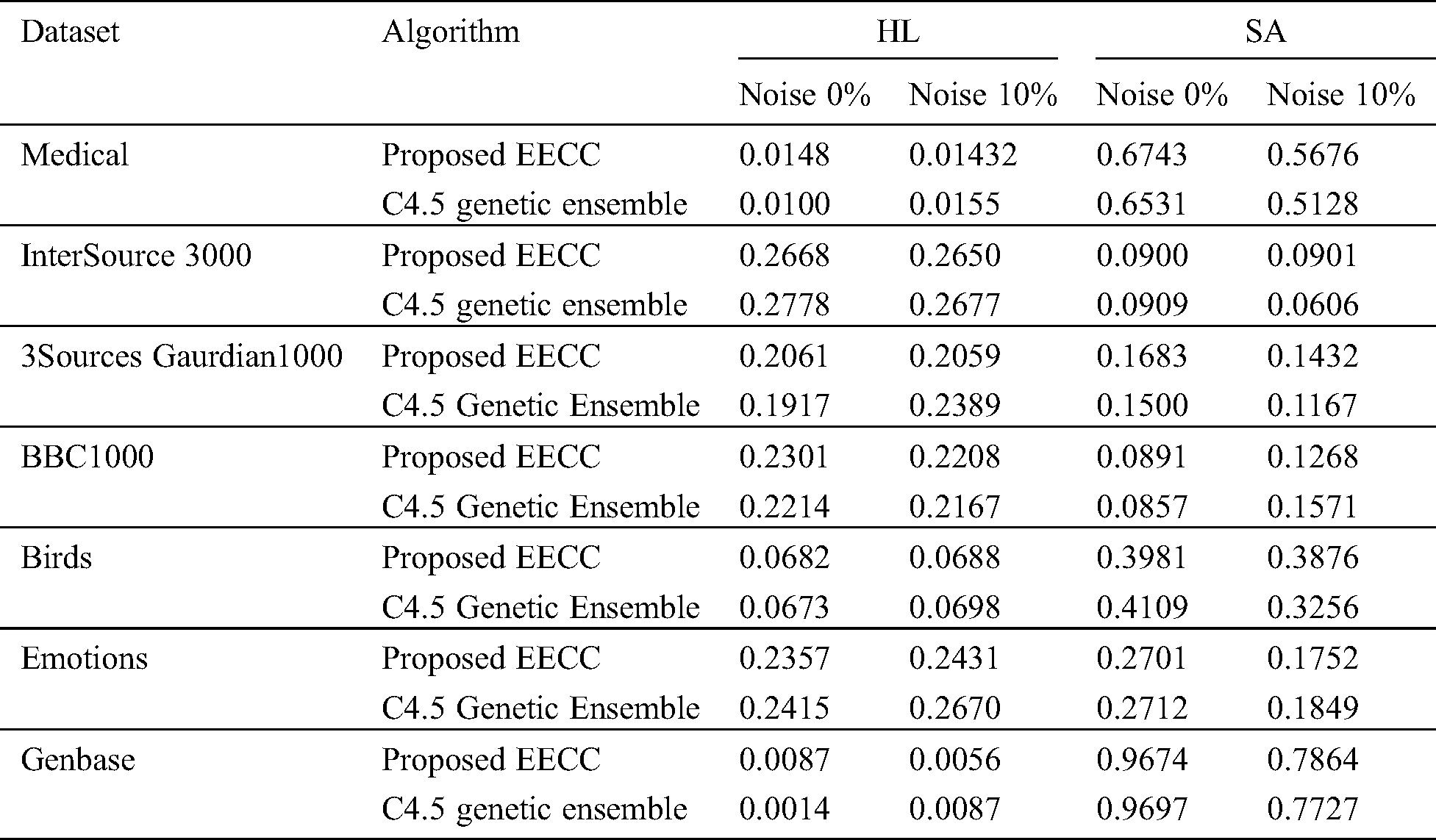
The Subset Accuracy (SA) is an important measure in multi-label classification which is a strict measure to check the exact matching of labels. The comparison of our proposed approach with the C4.5 ensemble shows that after the addition of noise our proposed approach shows a slight improvement in SA for the Birds, Emotions, Genbase dataset. It means that by handling noise, meaningful label relationships are taken into account. HL in Medical, Birds, and Emotions dataset is slightly improved as shown in Tab. 5.
Table 5: Results comparison of HL and SA of proposed EECC with C4.5 genetic ensemble in terms of 10% addition of noise
Similarly, the results of Micro Average F-Measure (MAF) and Micro Average Precision (MAP) is also given in Tab. 6. The results show that before the addition of noise, the performance of the C4.5 Genetic Ensemble is better as compared to EECC but after the addition of noise the performance decreases but EECC performance remains better. We have set s = 1 value of EECC for all these experiments. The value of s has a different effect on noise handling but mostly in literature s = 1 is suggested. The result of different values of s on the sample dataset is given in Fig. 2.
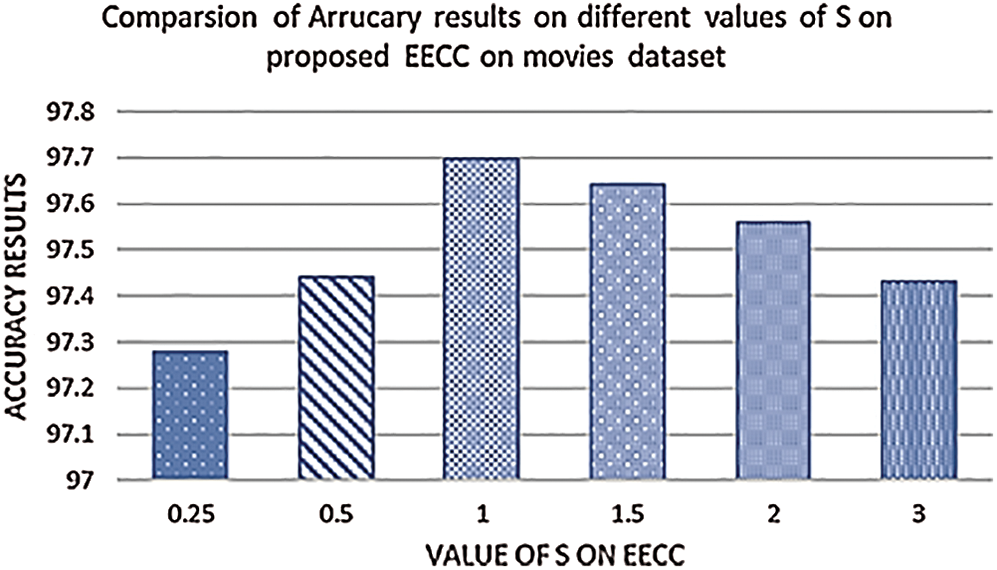
Figure 2: Comparison of performance evaluation of different values of s
Table 6: Results comparison of MAS and micro- average F-measure of the proposed approach with C4.5 genetic ensemble in terms of 10% addition of noise
For the assessment of our proposed technique, we have conducted experiments using different performance measures such as Coverage, One Error, IS Error, MAS, MAP, and MAR. After the addition of noise, the proposed EECC shows a slight improvement in performance in terms of these measures. We have also observed from the results that for the datasets having a large number of labels the improvement in performance is less as compared to datasets having a small number of labels. This shows that complexity increases as the dataset size increases. We have also conducted experiments using different transformation and adaptation methods with Credal C4.5 as a base classifier and compared results with C4.5. The results show that in presence of noise, the Credal C4.5 performs better as compared to C4.5. However, our study is related to evolutionary techniques. In the existing literature, the value of s is also discussed. The standard value of s in Credal C4.5 is set to be 1 as suggested by the literature [47]. It is a hyper-parameter belonging to Imprecise Dirichlet Model (IDM), discussed above. This measure is used for the regularization of convergence speed of lower and upper probability as sample size increases. In [47] the authors didn’t recommend the value of s but recommend the value s = 1. We have performed experiments by setting different values of s on EECC for Movies dataset. The Visualized results on different values of s are shown in Fig. 3. The results show that when s = 1 it gives 97.7% Accuracy and then s = 1.5 and so on. The comparison of proposed EECC with C4.5 Ensemble fitness values on 300 generations, before and after the addition of 10% noise for BBC1000 dataset. The blue line represents the fitness values before the addition of noise, orange shows the fitness values of C4.5 classifier after addition of noise and grey one represents the fitness value after the addition of noise. This figure shows that after the addition of noise the fitness values of the C4.5 classifier drastically reduces but the fitness values of EECC have a small loss as compared to C4.5. We have also compared our proposed approach EECC with other state-of-art multi-label classification techniques, before and after the addition of noise and compiled the results in a graph shown in Fig. 3.
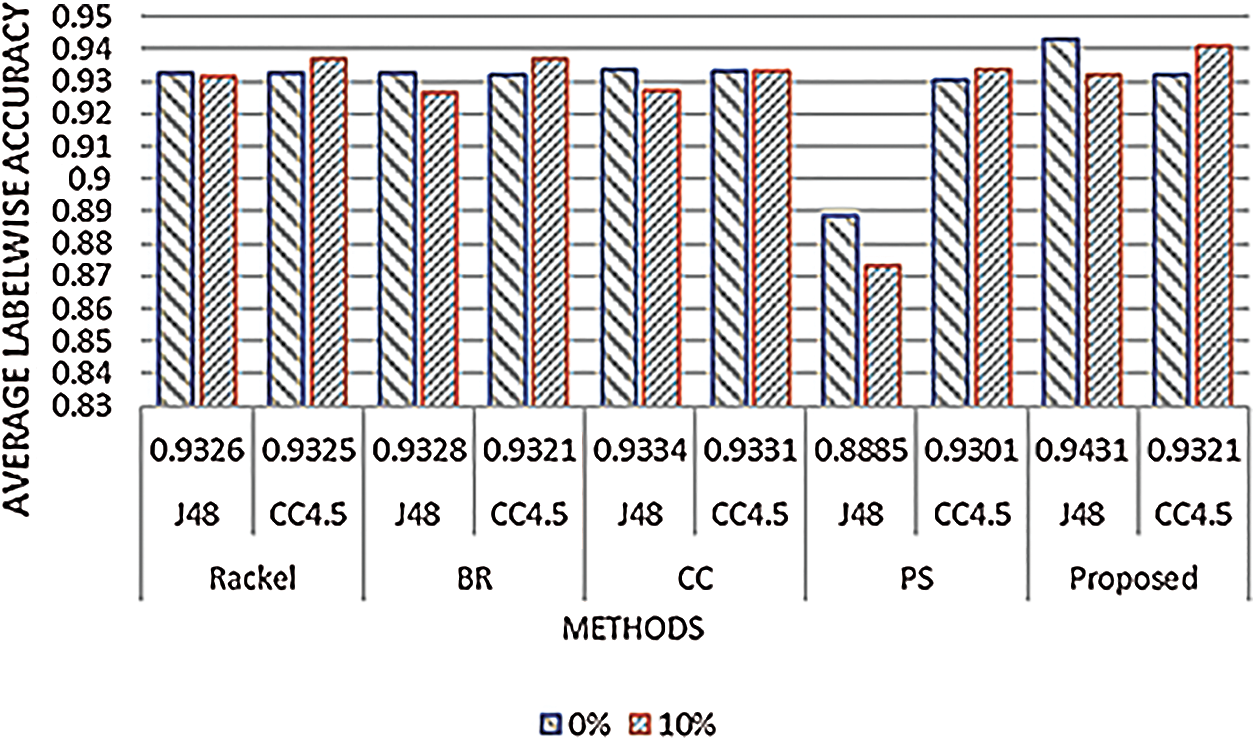
Figure 3: Comparison of various state-of-art multi-label classification techniques, before and after the addition of noise, with EECC
For the validation of our results, we have used different tests such as Fredman Rank Test, Average Accuracy, and Neymani Test. The details about these tests are as under.
The average results show that after the addition of noise, the average accuracy value of Credal C4.5 is greater than C4.5. This difference is notable when 10% of the noise is added.
It is a non-parametric test used to measure the repeated analysis by variance. The results of before and after the addition of 10% noise of Friedman’s rank test on accuracy results on all datasets are shown in Tab. 7. According to the results, the C4.5 ensemble rank is lower than EECC. This shows that EECC shows good classification results when noise is added as compared to C4.5 is given in Tab. 8. Different studies have been conducted for handling noise in multi-label classification. These studies include building ensemble of Credal C4.5 classifiers using the bagging technique but this technique combines the average of each model, whereas our approach trains classifier on different combinations of labels and then combines them by using different labels transformation techniques. In prior studies, transformation techniques are also found to be effective in solving noise-related problems.
Table 7: Comparison of average accuracy scores
Table 8: Result of Friedman rank test with α = 0.1 on before and after the addition of noise on the accuracy results on different datasets
In this paper, we proposed the EECC (Evolutionary Ensemble of Credal C4.5 Classifiers) for multi-label classification, which handles noisy, imbalanced datasets without reducing the performance. We have used an evolutionary approach to build the ensembles automatically, for label combinations. In our approach, the best label combinations are obtained by evolution as compared to RAkEL or CC which make random combinations of labels without considering any criteria. For the assessment of our proposed technique, we have conducted experiments on standard publicly available multi-label datasets and evaluated key performance measures.
We have compared our approach with existing evolutionary ensembles techniques that do not take uniform label noise into account. Each of these techniques was observed and compared before and after the addition of noise, to our proposed approach. Our proposed ensemble outperforms other techniques in terms of Coverage, Subset Accuracy, and Hamming Loss for the majority of the datasets. In the future, we plan to use multi-objective fitness functions to provide the best trade-offs between competing objectives in multi-label classification.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. Alazaidah and F. Kabir. (2016). “Trending challenges in multi label classification,” International Journal of Advanced Computer Science and Applications, vol. 7, no. 10, pp. 127–131. [Google Scholar]
2. J. Read. (2008). “A pruned problem transformation method for multi-label classification,” in Proc. 2008 New Zealand Computer Science Research Student Conf., vol. 143150, pp. 143–150. [Google Scholar]
3. G. Tsoumakas and I. Vlahavas. (2007). “Random k-labelsets: An ensemble method for multilabel classification,” in Proc. European Conf. on Machine Learning, Warsaw, Poland, pp. 406–417. [Google Scholar]
4. M. L. Zhang, Y. K. Li, X. Y. Liu and X. Geng. (2018). “Binary relevance for multi-label learning: An overview,” Frontiers of Computer Science, vol. 12, no. 2, pp. 191–202. [Google Scholar]
5. J. Read, P. Reutemann, B. Pfahringer and G. Holmes. (2016). “MEKA: A multi-label/multi-target extension to WEKA,” Journal of Machine Learning Research, vol. 17, pp. 1–5. [Google Scholar]
6. F. Charte, A. J. Rivera, M. J. del Jesus and F. Herrera. (2015). “Addressing imbalance in multilabel classification: Measures and random resampling algorithms,” Neurocomputing, vol. 163, pp. 3–16. [Google Scholar]
7. N. Japkowicz. (2000). “Learning from imbalanced data sets: A comparison of various strategies,” AAAI Workshop on Learning from Imbalanced Data Sets, vol. 68, pp. 10–15. [Google Scholar]
8. N. V. Chawla, K. W. Bowyer, L. O. Hall and W. P. Kegelmeyer. (2002). “SMOTE: Synthetic minority over-sampling technique,” Journal of Artificial Intelligence Research, vol. 16, pp. 321–357. [Google Scholar]
9. J. Read, B. Pfahringer, G. Holmes and E. Frank. (2011). “Classifier chains for multi-label classification,” Machine Learning, vol. 85, no. 3, pp. 254–269. [Google Scholar]
10. M. L. Zhang and K. Zhang. (2010). “Multi-label learning by exploiting label dependency,” in Proc. the 16th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Washington DC, USA, pp. 999–1008. [Google Scholar]
11. J. Huang, G. Li, S. Wang, Z. Xue and Q. Huang. (2017). “Multi-label classification by exploiting local positive and negative pairwise label correlation,” Neurocomputing, vol. 257, pp. 164–174. [Google Scholar]
12. A. Alabdullatif, B. Shahzad and E. Alwagait. (2016). “Classification of Arabic twitter users: A study based on user behaviour and interests,” Mobile Information Systems, vol. 2016, no. 15, pp. 1–11. [Google Scholar]
13. G. Tsoumakas, I. Katakis and I. Vlahavas. (2008). “Effective and efficient multilabel classification in domains with large number of labels,” in Proc. ECML/PKDD 2008 Workshop on Mining Multidimensional Data, vol. 21, pp. 53–59. [Google Scholar]
14. M. Samiullah, W. Aslam, H. Nazir, M. I. Lali and B. Shahzad et al.. (2020). , “An image encryption scheme based on DNA computing and multiple chaotic systems,” IEEE Access, vol. 8, pp. 25650–25663. [Google Scholar]
15. M. S. Nawaz, R. U. Mustafa and M. I. U. Lali. (2018). “Role of online data from search engine and social media in healthcare informatics,” in Applying Big Data Analytics in Bioinformatics and Medicine. Hershey, PA, USA: IGI Global, pp. 272–293. [Google Scholar]
16. B. Shahzad, K. M. Awan, A. M. Abdullatif, I. U. Lali, M. S. Nawaz et al.. (2019). , “Quantification of productivity of the brands on social media with respect to their responsiveness,” IEEE Access, vol. 7, pp. 9531–9539.
17. K. Saleem, A. Derhab, J. Al-Muhtadi, B. Shahzad and M. A. Orgun. (2015). “Secure transfer of environmental data to enhance human decision accuracy,” Computers in Human Behavior, vol. 51, pp. 632–639. [Google Scholar]
18. M. L. Zhang and Z. H. Zhou. (2013). “A review on multi-label learning algorithms,” IEEE Transactions on Knowledge and Data Engineering, vol. 26, no. 8, pp. 1819–1837. [Google Scholar]
19. H. Yu, Y. Kim and S. Hwang. (2009). “RV-SVM: An efficient method for learning ranking SVM,” in Pacific-Asia Conf. on Knowledge Discovery and Data Mining, Bangkok, Thailand, pp. 426–438. [Google Scholar]
20. M. L. Zhang and Z. H. Zhou. (2007). “ML-KNN: A lazy learning approach to multi-label learning,” Pattern Recognition, vol. 40, no. 7, pp. 2038–2048. [Google Scholar]
21. S. Vembu and T. Gärtner. (2010). “Label ranking algorithms: A survey,” in Preference Learning, Berlin, Heidelberg: Springer, pp. 45–64. [Google Scholar]
22. F. De Comité, R. Gilleron and M. Tommasi. (2003). “Learning multi-label alternating decision trees from texts and data,” in Int. Workshop on Machine Learning and Data Mining in Pattern Recognition, Leipzig, Germany, pp. 35–49. [Google Scholar]
23. R. E. Schapire and Y. Singer. (2000). “BoosTexter: A boosting-based system for text categorization,” Machine Learning, vol. 39, no. 2–3, pp. 135–168. [Google Scholar]
24. A. Clare and R. D. King. (2001). “Knowledge discovery in multi-label phenotype data,” in European Conf. on Principles of Data Mining and Knowledge Discovery, Freiburg, Germany, pp. 42–53. [Google Scholar]
25. D. Kocev, C. Vens, J. Struyf and S. Džeroski. (2007). “Ensembles of multi-objective decision trees,” in European Conf. on Machine Learning, Warsaw, Poland, pp. 624–631. [Google Scholar]
26. X. Zhang, Q. Yuan, S. Zhao, W. Fan and W. Zheng et al.. (2010). , “Multi-label classification without the multi-label cost,” in Proc. 2010 SIAM Int. Conf. on Data Mining, Columbus, Ohio, pp. 778–789. [Google Scholar]
27. T. Joachims. (2002). “Optimizing search engines using click through data,” in Proc. the Eighth ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Edmonton, Alberta, Canada, pp. 133–142. [Google Scholar]
28. Y. Yang and S. Gopal. (2012). “Multilabel classification with meta-level features in a learning-to-rank framework,” Machine Learning, vol. 88, no. 1–2, pp. 47–68. [Google Scholar]
29. C. Cortes and V. Vapnik. (1995). “Support-vector networks,” Machine Learning, vol. 20, no. 3, pp. 273–297. [Google Scholar]
30. N. Cristianini and J. Shawe-Taylor. (2000). An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge: Cambridge University Press. [Google Scholar]
31. R. E. Schapire and Y. Singer. (1999). “Improved boosting algorithms using confidence-rated predictions,” Machine Learning, vol. 37, no. 3, pp. 297–336. [Google Scholar]
32. A. Elisseeff and J. Weston. (2002). “A kernel method for multi-labelled classification,” in Advances in Neural Information Processing Systems, Vancouver, British Columbia, Canada, pp. 681–687. [Google Scholar]
33. J. Read, B. Pfahringer and G. Holmes. (2008). “Multi-label classification using ensembles of pruned sets,” in 2008 Eighth IEEE Int. Conf. on Data Mining, Pisa, Italy, pp. 995–1000. [Google Scholar]
34. R. C. Prati, J. Luengo and F. Herrera. (2019). “Emerging topics and challenges of learning from noisy data in nonstandard classification: A survey beyond binary class noise,” Knowledge and Information Systems, vol. 60, no. 1, pp. 63–97. [Google Scholar]
35. J. Calvo-Zaragoza, J. J. Valero-Mas and J. R. Rico-Juan. (2015). “Improving kNN multi-label classification in prototype selection scenarios using class proposals,” Pattern Recognition, vol. 48, no. 5, pp. 1608–1622. [Google Scholar]
36. A. Cappozzo, F. Greselin and T. B. Murphy. (2019). “A robust approach to model-based classification based on trimming and constraints,” Advances in Data Analysis and Classification, vol. 14, no. 2, pp. 1–28. [Google Scholar]
37. P. S. Rao. (2018). “Study and analysis of noise effect on big data analytics,” International Journal of Management, Technology and Engineering, vol. 8, no. 12, pp. 5841–5850. [Google Scholar]
38. C. J. Mantas and J. Abellán. (2014). “Credal-C4.5: Decision tree based on imprecise probabilities to classify noisy data,” Expert Systems with Applications, vol. 41, no. 10, pp. 4625–4637. [Google Scholar]
39. J. Quinlan. (1993). C4. 5: Programs for Machine Learning. Morgan Kaufmann, San Francisco, CA, USA. [Google Scholar]
40. J. R. Quinlan. (1986). “Induction of decision trees,” Machine Learning, vol. 1, no. 1, pp. 81–10. [Google Scholar]
41. G. Tsoumakas, I. Katakis and I. Vlahavas. (2010). “Random k-labelsets for multilabel classification,” IEEE Transactions on Knowledge Data Engineering, vol. 23, no. 7, pp. 1079–1089.
42. C. Vens, J. Struyf, L. Schietgat, S. Džeroski and H. Blockeel. (2008). “Decision trees for hierarchical multi-label classification,” Machine Learning, vol. 73, no. 2, pp. 185.
43. M. J. Er, R. Venkatesan and N. Wang. (2016). “A high speed multi-label classifier based on extreme learning machines,” in Proc. ELM-2015, Springer, Cham, Hangzhou, China, vol. 2, pp. 437–454.
44. Z. Fu, L. Wang and D. Zhang. (2014). “An improved multi-label classification ensemble learning algorithm,” in Chinese Conf. on Pattern Recognition, Changsha, China, pp. 243–252.
45. J. M. Moyano, E. L. Gibaja, K. J. Cios and S. Ventura. (2019). “An evolutionary approach to build ensembles of multi-label classifiers,” Information Fusion, vol. 50, pp. 168–180. [Google Scholar]
46. R. N. Greenwell, J. E. Angus and M. Finck. (1995). “Optimal mutation probability for genetic algorithms,” Mathematical and Computer Modelling, vol. 21, no. 8, pp. 1–11. [Google Scholar]
47. P. Walley. (1996). “Inferences from multinomial data: Learning about a bag of marbles,” Journal of the Royal Statistical Society: Series B (Methodological), vol. 58, no. 1, pp. 3–34. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |