DOI:10.32604/iasc.2020.012663
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.012663 | |
| Article |
A Genetic Algorithm Optimization for Multi-Objective Multicast Routing
1Faculty of Computers and Information, Department of Computer Science, Sohag University, Sohag, 82524, Egypt
2Department of Computer Science and Artificial Intelligence, College of Computer Science and Engineering, University of Jeddah, Jeddah, 21959, Saudi Arabia
3Faculty of Science, Department of Mathematics and Computer Science, Aswan University, Aswan, 81528, Egypt
*Corresponding Author: M. R. Hassan. Email: mr.hassan@sci.aswu.edu.eg
Received: 08 July 2020; Accepted: 12 August 2020
Abstract: Many applications require to send information from a source node to multiple destinations nodes. To support these applications, the paper presents a multi-objective based genetic algorithm, which is used in the construction of the multicast tree for data transmission in a computer network. The proposed algorithm simultaneously optimizes total weights (cost, delay, and hop) of the multicast tree. Experimental results prove that the proposed algorithm outperforms a recently published Multi-objective Multicast Algorithm specially designed for solving the multicast routing problem. Also, the proposed approach has been applied to ten-node and twenty-node network to illustrate its efficiency. In addition, the execution time is reported for each studied case and the obtained results are compared with the results obtained by the previously based ant colony algorithm presented recently to solve the same problem. Finality, summing up the three objectives (cost, delay, and hop) to be one objective called the weight of the tree to speed up the searching process by using the proposed algorithm to find the best solutions.
Keywords: Multimedia communication; multicast routing; genetic algorithm; cost; delay; hop
Nomenclature
| G: | A network graph. |
| N: | The number of vertices in G. |
| E: | The number of edges in G. |
| eij: | A link between node i and node j in G. |
| D(e): | The delay of a link e. |
| C(e): | The cost of a link e. |
| H(e): | The hop of link e. |
The multicast routing problem is a well-known problem in combinatorial optimization. It is defined as finding the route between two nodes in the weighted graph where that path is the shortest, and shortest means the path with a minimum summation of weights, where an edge between any two nodes always has a certain weight. The problem is to find accordingly the shorter path between a source and a destination in computer networks.
Gen et al. [1] considered the problem of searching the shortest paths with two conflicting objectives of minimizing cost and maximizing flow, as a bicriteria network design problem. They proposed a multi-objective hybrid genetic algorithm (GA) to solve it.
Granat et al. [2], presented an interactive method to analyze the multicriteria shortest path problem by the reference point approach. The multi-objective problem was converted into a parametric single-objective problem. The algorithm succeeded to find the Pareto-optimal shortest path according to the specified preferences.
There are many applications such as multimedia conferencing, distant learning, and video on demand to encourage the network service provider to adapt their network to support additional multicast traffic. The multicast routing problem is the problem of searching a multicast tree that spans all vertices in a communication network [3]. Searching low-cost multicast tree or low delay multicast tree are discussed in [3–5].
To serve the penalty number of users and satisfy quality-of-service (QoS) in real-time applications, this problem is taken into consideration as NP-Complete [6]. Many optimization algorithms based on GA have been proposed to solve the QoS multicast routing (QMR) problem (with different types of QoS constraints) [6–10].
Authors in [11–13] discussed and solved the QoS with multiple constraints like bandwidth, delay, and packet loss rate. An ant colony based heuristic presented by Chu et al. [14] to search minimum cost multicast tree within the case of considering QoS metrics, like bandwidth, delay, delay jitter, and packet loss rate. While, Huang et al. [15], discussed low-cost multicast tree problem subject to delay constraints and ASDLMA (Ant system for delay-constrained low-cost multicast routing algorithm) was constructed to solve it.
It is known that GA is one of the heuristic algorithms that can solve many problems, network design problems [16], real road network problems [17], and unicast routing [18]. Also, GAs used to solve the multicast routing problem [19,20]. In addition, there is a constrained QoS problem [21–27] and [4].
In the case of considering more than one constraint like the cost of the tree, hop count, bandwidth utilization, the problem is considered as a Multi-Objective Problem (MOP) [28].
Ant colony optimization (ACO) is a meta-heuristic approach that has been applied to QoS multicast routing problems [29,30].
Younes et al. [29] presented an AC based algorithm to search a multicast tree with low-cost, minimum delay, and a minimum number of hops. The problem is treated as a multi-objective multicast tree problem.
In this paper, an algorithm based on GA is proposed to solve the multi-objective multicast tree problem. The experimental results prove that the solutions found by the proposed GA are better than those obtained by using AC presented by Younes et al. [30].
The rest of the paper is organized as follows: Section 2 presents the problem description and formulation. Sections 3 describe GA components. The entire GA algorithm is given in Section 4. Studied cases are presented in Section 5. Section 6 gives the conclusion.
2 Problem Description and Formulation
Let G = (N, E) is a weighted directed graph with N vertices and E edges represents a network with |N| nodes and |E| links. The multicast tree from the source node n0 to the set of destination nodes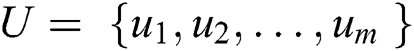 
denotes a set of destination nodes. Let 
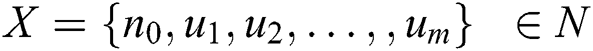be a set of from source to destination nodes of the multicast tree. Multicast tree T = (NT , ET ), where 
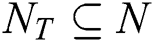and 
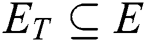, there exists the path PT (n0 , d) from source node n0 to each destination node 
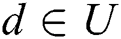in T. Three non-negative real value functions are associated with each link e (
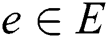): C(e), D(e), and H(e). The link cost function, C(e), may be either monetary cost or any measure of resource utilization. The link delay functions, D(e), define the criteria. The link hop is the number of hops, H(e) = 1.
The cost of the path PT is defined as the sum of the cost of all links in that path and can be given by
The total cost of the tree T is defined as the sum of the cost of all links in that tree and can be given by
The total delay of the path PT(n0,d) is simply the sum of the delay of all links along with PT(n0,d):
The delay of multicast tree T is the maximum value of delay in the path from source node n0 to each destination node d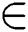
U.
The hop of the path PT is defined as the sum of the hop of all links in that path and can be given by
The hop of multicast tree is defined as the sum of the hop of all links in that tree and can be given by:
The vector SW(PT) of the path PT consists of the vector sum of the vectors corresponding to arcs.
The objective of the presented problem is to find a multicast routing tree (T) such that minimizes the cost C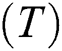
, the delay 
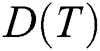, and the hop 
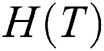. The problem can be formulated as follows:
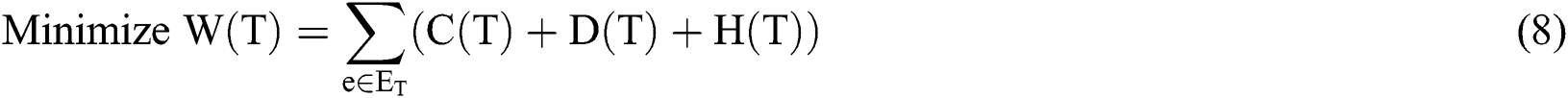
where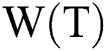 
is the weight of a multicast routing tree (T). The cost C
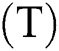, the delay 
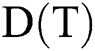, and the hop 
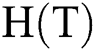are defined as follows:
If the given network has N nodes, then the candidate path is represented by a chromosome x of N fields, each field represents a node in the network. At least two fields have none zero values to consider the candidate path to be a real path (we called here the reality condition).
The generated chromosome in the initial population must contain at least two none zero elements to be a real candidate path. The following steps show how to generate pop_size chromosomes of the initial population:
1. A chromosome x is generated randomly.
2. Check the reality condition for x.
3. Repeat steps 1 and 2 to generate pop_size chromosomes.
The objective function (The fitness) is the weight of a multicast routing tree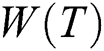 
if the candidate path satisfies the following conditions:
• The reality condition.
• The candidate path is connected. i.e., each node within that path connects at least one another.
In our GA, we adopt the single cut point crossover to obtain a new offspring from two parents that are randomly selected based on Pc (Pc =0.90).
The uniform mutation is used here based on Pm (Pm = 0.02). The mutated bit is selected randomly to change its value.
The following steps show how the presented GA solves the multi-objective multicast routing tree problem of a given network.
The presented GA is implemented using Borland C++ Ver. 5.5, where pop_size, max_gen, Pm, and Pc equals to 25, 50, 0.95 and 0.02 respectively. Two networks with 10 and 20 nodes are studied to show the efficiency of the proposed GA. Also, the results are compared with the AC algorithm presented in Younes et al. [30].
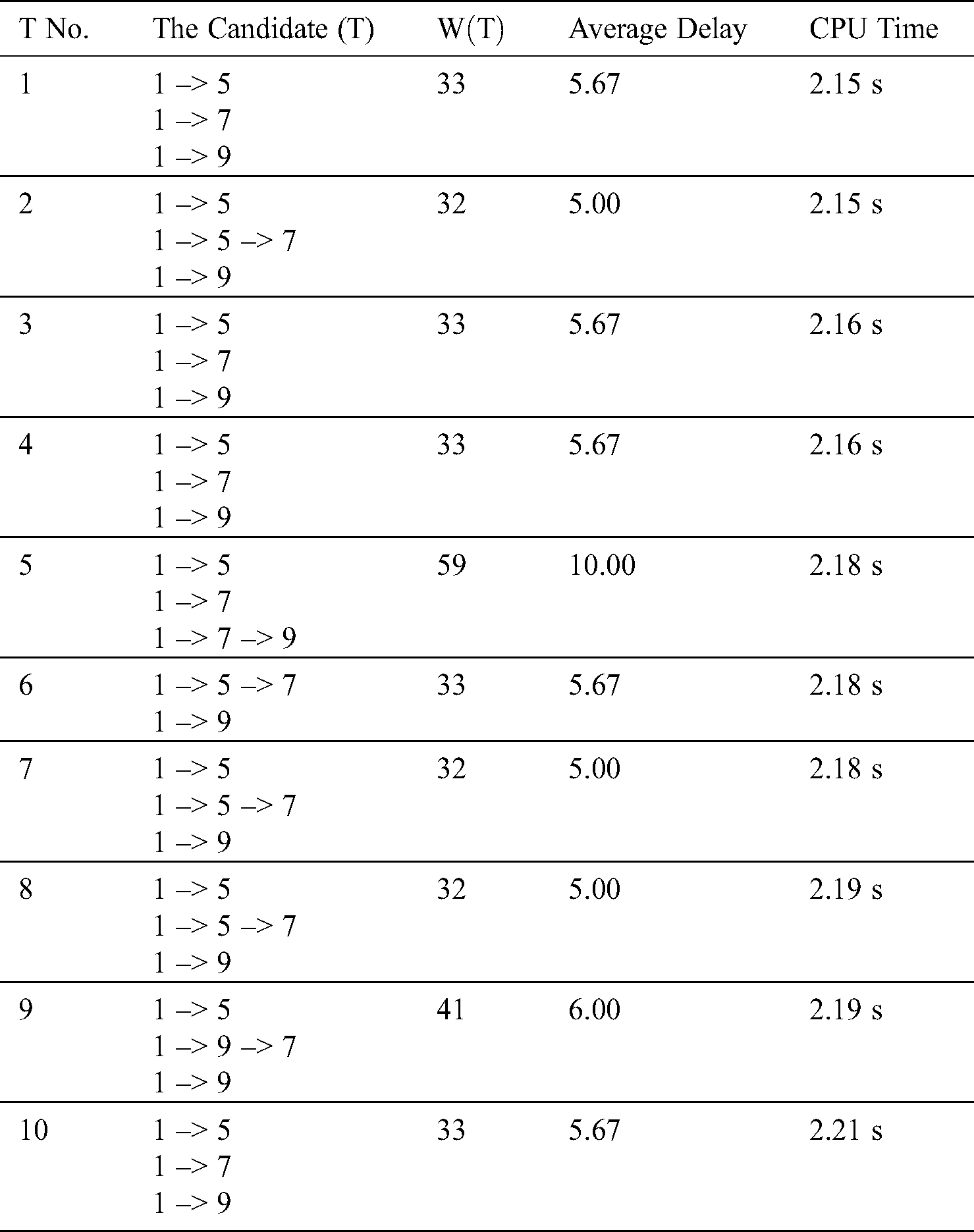
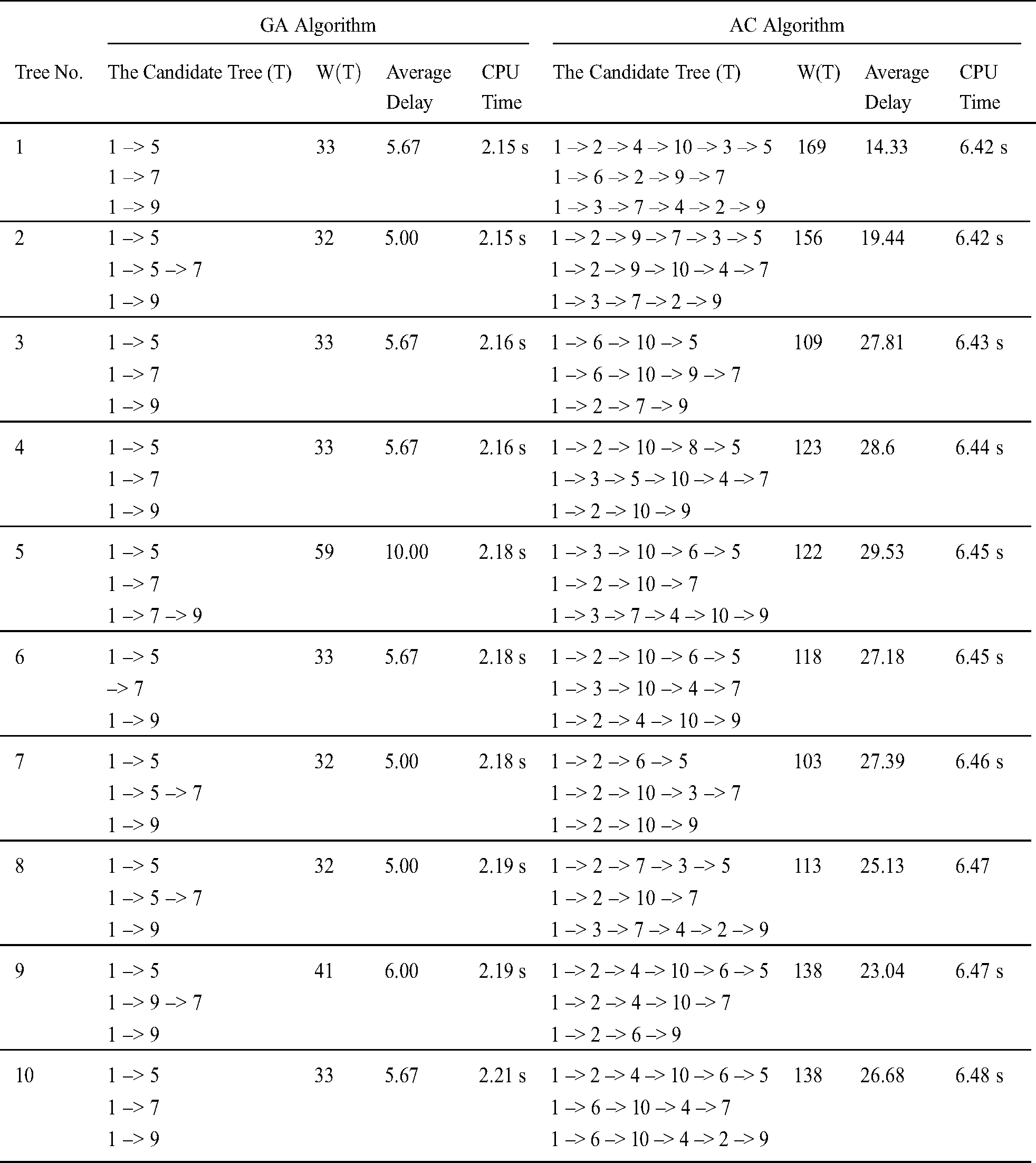
We applied our GA to the network with 10 nodes. Note that the connection matrix and the links’ weight are obtained from Younes et al. [30]. Assuming that n0 = 1 and U = {5, 7, 9}, Tab. 1 shows the value of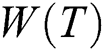 
for each candidate T. In addition, the execution time (in seconds) required obtaining each T. The minimum value for 
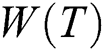is 32 for tree no. 2. The cost, delay, and hop of that tree equals 21, 7, and 4 respectively.
Table 1: The value of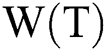 
for each T
The weight, average delay, and execution time for each tree is shown in Figs. 1–3 respectively.
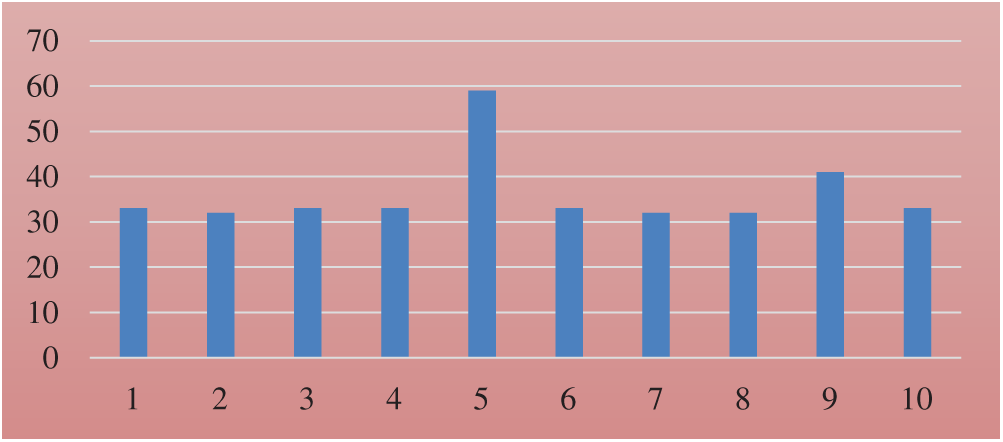
Figure 1: Weight for each tree
Figure 2: Average delay for each tree
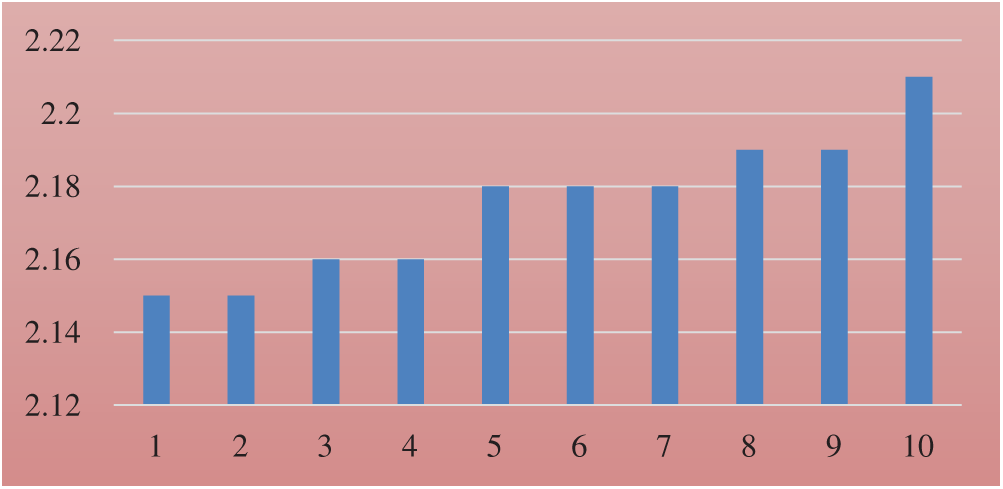
Figure 3: Execution Time for each tree
Here, we compare the results of the proposed GA with that obtained by the AC algorithm, Younes et al. [30] as shown in Tab. 2.
Table 2: Comparison between the proposed GA and AC presented by Younes et al. [30]
Comparing the results obtained by the proposed GA to those obtained by AC algorithm Younes et al. [30], it is observed that the value minimum 
found by the proposed GA is less than that obtained by Younes et al. [30]. Therefore, the proposed GA obtains better optimal solutions. The weight, average delay, and execution time for the best tree found by the proposed genetic algorithm in comparison with Younes, et al. [30] are shown in Fig. 4.
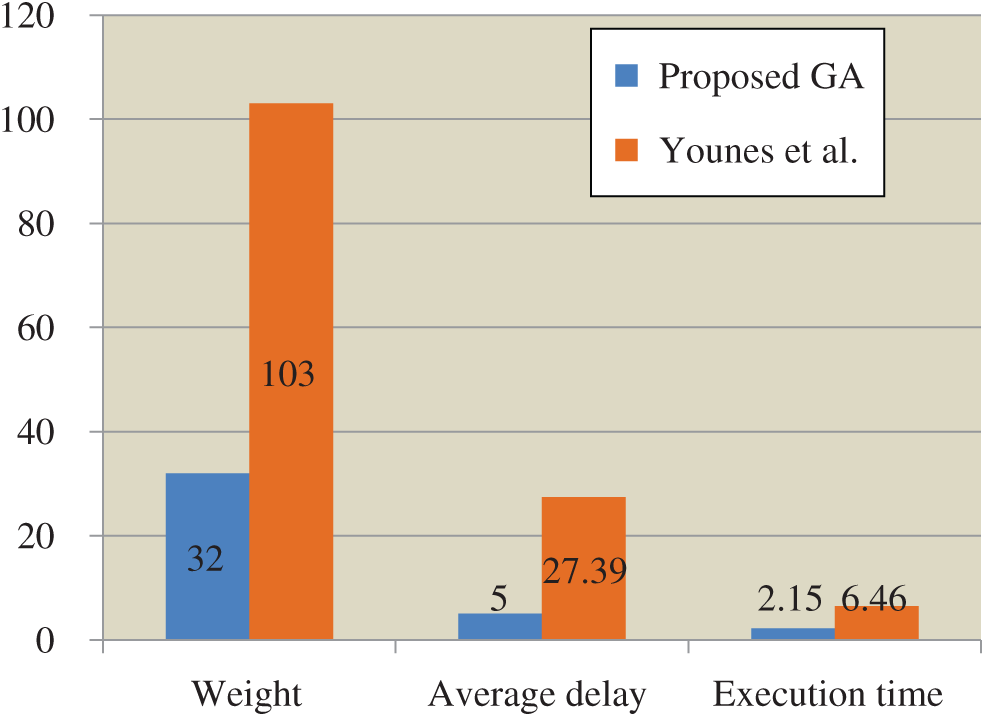
Figure 4: Comparison between the proposed GA and Younes et al. [30]
The proposed GA is applied to the twenty-node network, this network along with its information is generated randomly. Also, the connection, cost, hop, and delay matrices are given in Tabs. A1–A4 respectively. Given that n0 = 1 and U = {5, 7, 9, 12, 15, 20}, Tab. 3 shows the value of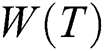 
, Average delay, and the execution time (in seconds) for each candidate T. The minimum value for 
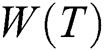is 185 for tree no. 6. The cost, delay, and hop of that tree equals 123, 42, and 20 respectively. The weight, average delay, and execution time for each tree are shown in Figs. 5–7 respectively.
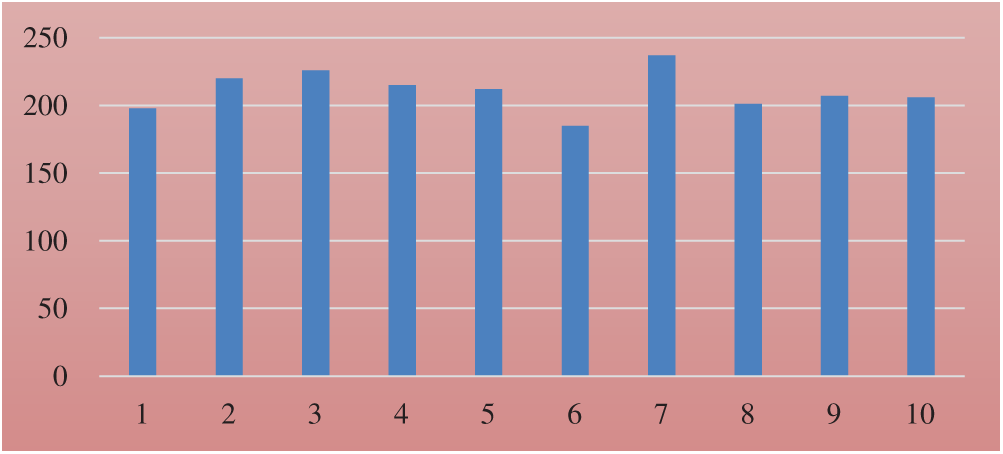
Figure 5: Weight for each tree
Figure 6: Average delay for each tree
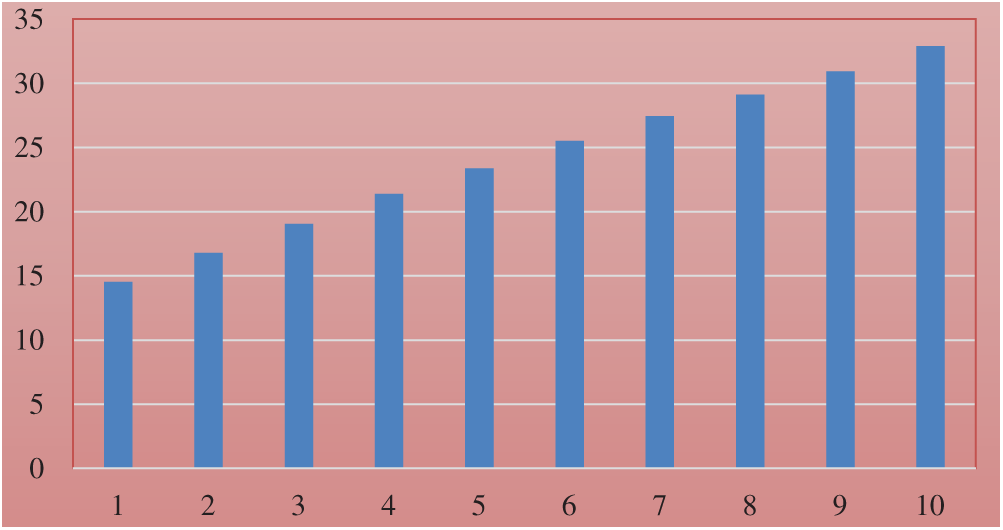
Figure 7: Execution Time for each tree
A multi-objective multicast routing problem subject to cost, hop, and delay is presented and formulated as a minimization problem. Furthermore, an approach based on GA is proposed to solve the presented problem. The experimental results illustrated that the proposed GA is efficient in solving this problem and searching the minimum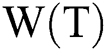 
in a few seconds. In addition, the results obtained by the proposed GA are better than those obtained by AC algorithm presented by Hamed et al. [30].
Acknowledgement: We would like to thank all the parties involved in this research work.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Gen and L. Lin, “Multiobjective hybrid genetic algorithm for bicriteria network design problem,” in The 8th Asia Pacific Sym. on Intelligent and Evolutionary Systems, Cairns, Australia, pp. 73–82, 2004. [Google Scholar]
2. J. Granat and F. Guerriero. (2003). “The interactive analysis of the multicriteria shortest path problem by the reference point method,” European Journal of Operational Research, vol. 151, no. 1, pp. 103–111. [Google Scholar]
3. L. H. Sahasrabuddhe and B. Mukherjee. (2000). “Multicast routing algorithms and protocols: A tutorial,” IEEE Network, vol. 14, no. 1, pp. 90–102. [Google Scholar]
4. B. Wang and J. C. Hou. (2000). “Multicast routing and its QoS extension: problems, algorithms, and protocols,” IEEE Network, vol. 14, no. 1, pp. 22–36. [Google Scholar]
5. H. F. Salama, D. S. Reeves and Y. Viniotis. (1997). “Evaluation of multicast routing algorithms for real-time communication on high-speed networks,” IEEE Journal on Selected Areas in Communications, vol. 15, no. 3, pp. 332–345. [Google Scholar]
6. Z. Wang and B. Shi. (2001). “Solution to QoS multicast routing problem based on heuristic genetic algorithm,” Journal of Computer, vol. 24, no. 1, pp. 55–61. [Google Scholar]
7. A. Younes. (2010). “A genetic algorithm for finding the k shortest paths in a network,” Egyptian Informatics Journal, vol. 10, no. 2, pp. 75–79.
8. Z. Y. Wang, B. X. Wang and E. Zhao. (2001). “Bandwidth-delay-constrained least-cost multicast routing based on heuristic genetic algorithm,” Computer Communications, vol. 24, no. 7–8, pp. 685–692.
9. X. Zhou, C. Chen and G. Zhu. (2000). “A genetic algorithm for multicasting routing problem,” Int. Conf. on Communication Technology, vol. 2, pp. 1248–1253.
10. Z. Wang and J. Crowcroft. (1996). “Quality of service for supporting multimedia applications,” IEEE Journal on Selected Areas in Communications, vol. 14, no. 7, pp. 1228–1234. [Google Scholar]
11. L. Guo and I. Matta. (1999). “QDMR: An efficient QoS dependent multicast routing algorithm,” in Proc. of the Fifth IEEE Real-Time Technology and Applications Sym., Vancouver, BC, Canada, pp. 213–222. [Google Scholar]
12. N. Chen, L. Liand and D. Wushi. (2006). “Multicast routing algorithm of multiple QoS based on widest-bandwidth,” Journal of Systems Engineering and Electronics, vol. 17, no. 3, pp. 642–647.
13. C. Chu, J. Gu, X. Hou and Q. Gu. (2002). “A heuristic ant algorithm for solving QoS multicast routing problem,” Proceedings of the Evolutionary Computation, vol. 2, pp. 1630–1635. [Google Scholar]
14. L. Huang, H. Han and H. Jian. (2007). “Multicast routing based on the ant system,” Applied Mathematical Sciences, vol. 1, no. 57, pp. 2827–2838. [Google Scholar]
15. C. W. Ahn and R. S. Ramakrishna. (2002). “A genetic algorithm for shortest path routing problem and the sizing of population,” IEEE Transaction on Evolutionary Computation, vol. 6, no. 6, pp. 566–579. [Google Scholar]
16. H. Chen and S. Baolin. (2005). “Multicast routing optimization algorithm with bandwidth and delay constraints based on GA,” Journal of Communication and Computer, vol. 2, no. 5, pp. 63–67. [Google Scholar]
17. G. H. Peng, K. T. Dong and J. S. Su. (2013). “A random road network model and its effects on topological characteristics of mobile delay-tolerant networks,” IEEE Transactions on Mobile Computing, vol. 13, no. 12, pp. 2706–2718. [Google Scholar]
18. L. Atzori and A. Raccis. (2004). “Network capacity assignment for multicast services using genetic algorithms,” IEEE Communications Letters, vol. 8, no. 6, pp. 403–405. [Google Scholar]
19. R. H. Hwang, W. Y. Do and S. C. Yang. (2000). “Multicast routing based on genetic algorithms,” Journal of Information Science and Engineering, vol. 16, pp. 885–901. [Google Scholar]
20. R. Bhattacharya, P. Venkateswaran, S. K. Sanyal and R. Nandi. (2005). “Genetic algorithm based efficient outing scheme for multicast networks,” in IEEE Int. Conf. on Personal Wireless Communications, New Delhi, India, pp. 500–504. [Google Scholar]
21. L. Chen, Z. Yang and Z. Xu. (2004). “A degree-delay-constrained genetic algorithm for multicast routing tree,” in The Fourth Int. Conf. on Computer and Information Technology, IEEE Computer Society, USA, pp. 1033–1038. [Google Scholar]
22. M. Hamdan and M. E. El-Hawary. (2004). “Multicast routing with delay and delay variation constraints using genetic algorithm,” Canadian Conference on Electrical and Computer Engineering, vol. 4, pp. 2363–2366.
23. L. S. Randaccio and L. Atzori. (2006). “A genetic algorithms based approach for group multicast routing,” Journal of Networks, vol. 1, no. 4, pp. 1–9.
24. M. Mahseur, Y. Meraihi, A. Boukra and A. Ramdane-Cherif. (2017). “QoS multicast routing based on a hybrid quantum evolutionary algorithm with firefly algorithm,” in 5th Int. Conf. on Electrical Engineering-Boumerdes, Boumerdes, pp. 1–6.
25. X. X. Zhang, C. X. Shi, H. Y. Chen, J. Yang, P. Wang et al. (2018). , “A hybrid scatter search algorithm for QoSmulticast routing problem,” in The 30th Chinese Control and Decision Conf., Shenyang, pp. 4875–4878.
26. X. Li, Y. Tian, G. Ledwich, Y. Mishra and C. Zhou. (2019). “Minimizing multicast routing delay in multiple multicast trees with shared links for smart grid,” IEEE Transactions on Smart Grid, vol. 10, no. 5, pp. 5427–5435.
27. A. Van Veldhuizen, “Multiobjective Evolutionary Algorithms: Classifications, Analyses, and New Innovations,” PhD thesis, Department of Electrical and Computer Engineering. Graduate School of Engineering. Air Force Institute of Technology, Wright-Patterson AFB, OH, 1999. [Google Scholar]
28. M. Dorigo and G. Di Caro. (1999). “The ant colony optimization meta-heuristic,” in New Ideas in Optimization, D. Corne, M. Dorigo, F. Glover (eds.London, UK: McGraw Hill, pp. 11–32. [Google Scholar]
29. D. N. Kumar and M. J. Reddy. (2006). “Ant colony optimization for multi-purpose reservoir operation,” Water Resources Management, vol. 20, no. 6, pp. 879–898. [Google Scholar]
30. A. Y. Hamed, M. H. Alkinani and M. R. Hassan. (2020). “Ant colony optimization for multi-objective multicast routing,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1159–1173. [Google Scholar]
Table 3: Candidate route tree from source node 1 to the destination nodes
Table A1: Connection matrix of twenty-node network
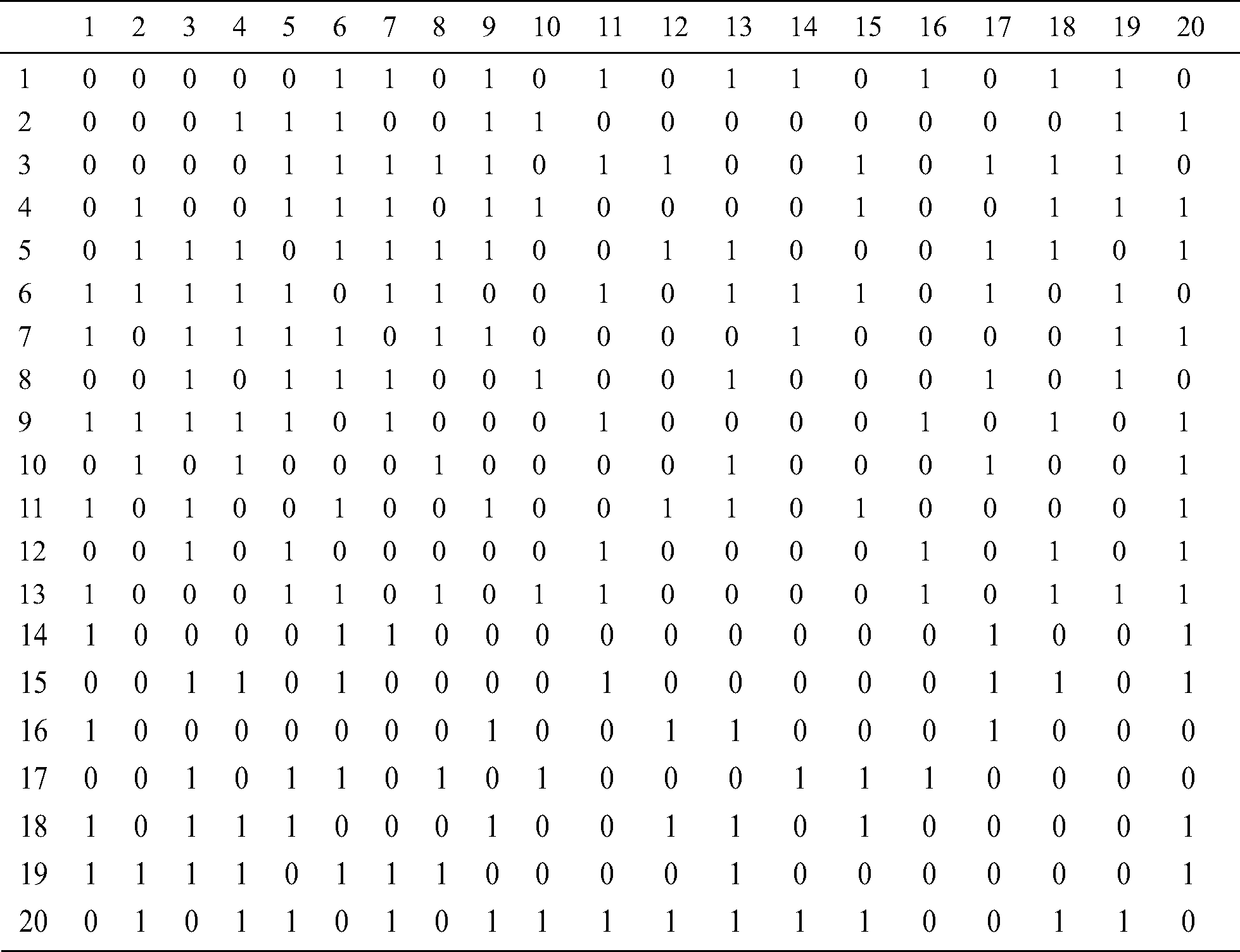
Table A2: Cost matrix of twenty-node network
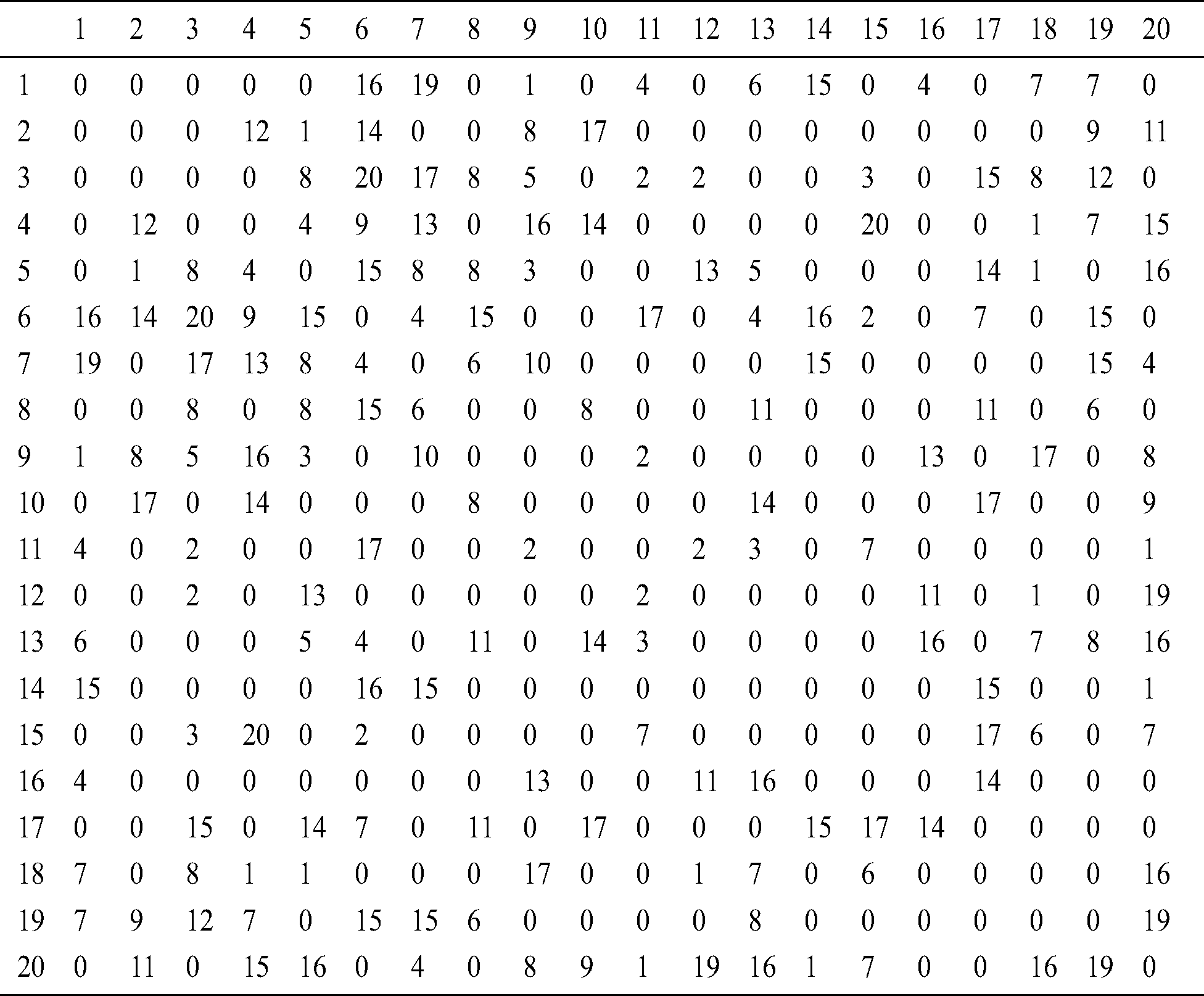
Table A3: Hop matrix of twenty-node network
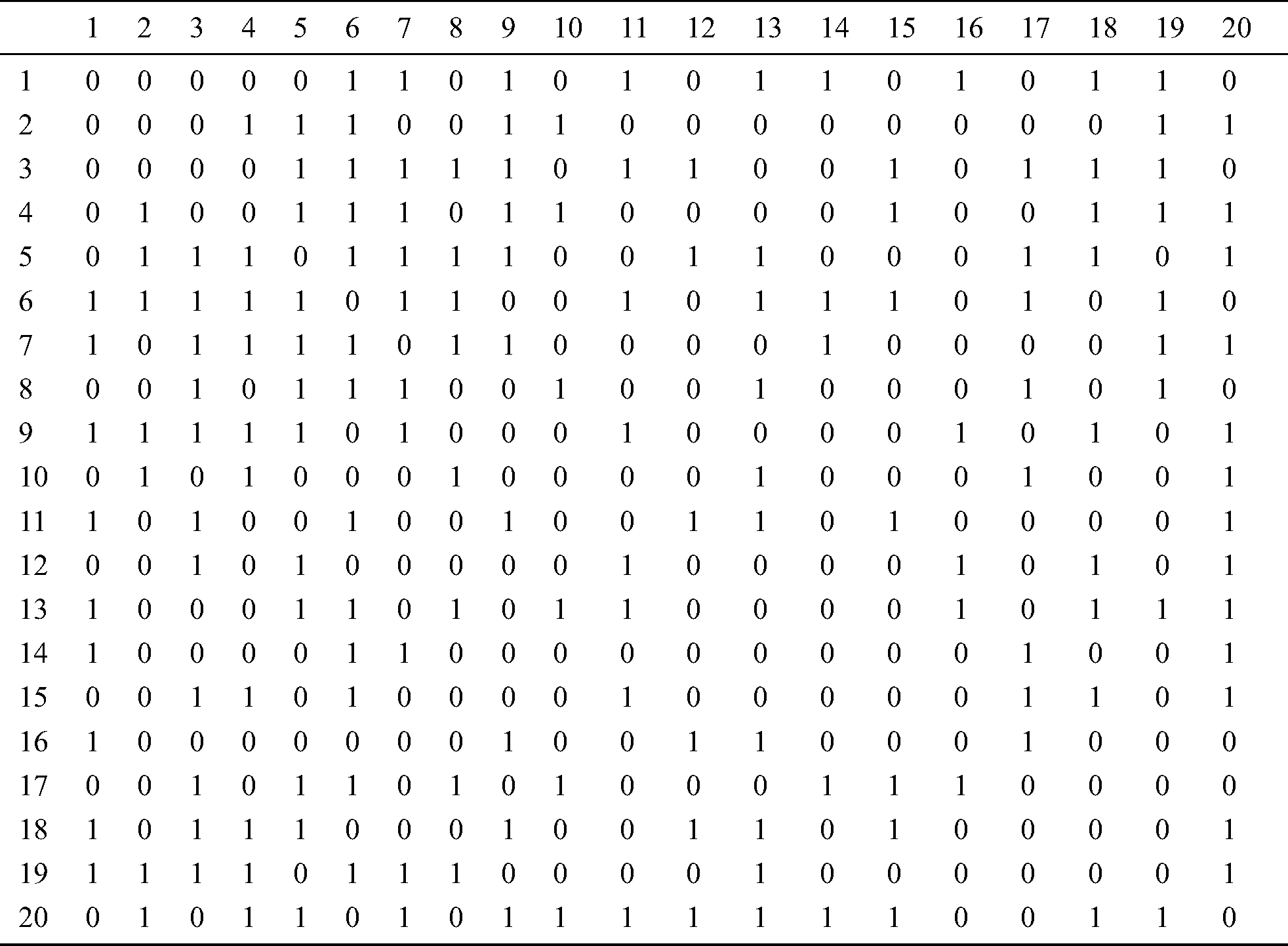
Table A4: Delay matrix of twenty-node network
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |
