DOI:10.32604/iasc.2020.012144
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.012144 | |
| Article |
HGG-CNN: The Generation of the Optimal Robotic Grasp Pose Based on Vision
1Shanghai Maritime University, Shanghai, China
2HZ University of Applied Sciences, Vlissingen, Zeeland, Netherlands
*Corresponding Author: Shiyin Qiu. Email: 201710234028@stu.shmtu.edu.cn
Received: 16 June 2020; Accepted: 23 August 2020
Abstract: Robotic grasping is an important issue in the field of robot control. In order to solve the problem of optimal grasping pose of the robotic arm, based on the Generative Grasping Convolutional Neural Network (GG-CNN), a new convolutional neural network called Hybrid Generative Grasping Convolutional Neural Network (HGG-CNN) is proposed by combining three small network structures called Inception Block, Dense Block and SELayer. This new type of convolutional neural network structure can improve the accuracy rate of grasping pose based on the GG-CNN network, thereby improving the success rate of grasping. In addition, the HGG-CNN convolutional neural network structure can also overcome the problem that the original GG-CNN network structure has in yielding a recognition rate of less than 70% for complex artificial irregular objects. After experimental tests, the HGG-CNN convolutional neural network can improve the average grasping pose accuracy of the original GG-CNN network from 83.83% to 92.48%. For irregular objects with complex man-made shapes such as spoons, the recognition rate of grasping pose can also be increased from 21.38% to 55.33%.
Keywords: Convolutional neural network; optimal grasping pose generation; robotic grasping
In recent years, manipulator has played an important role in many aspects of human life, such as cooperative control, autonomous obstacle avoidance, and assisted grasping. As the basic ability of a manipulator is to work cooperatively with human beings, grasping is the fundamental guarantee for completing various subsequent complex autonomous tasks. Among them, grasping unknown and irregular objects with various shapes and positions is an important part of the current research in the field of manipulator control, and the rapid and stable generation of objects’ grasping pose with visual information is the main focus. At present, there are many methods to quickly and stably generate the optimal grasping pose of the manipulator at home and abroad. However, these methods still have many problems that can be optimized [1–6].
Recently, a revolution of deep learning in the field of computer vision has been witnessed. Deep learning directly learns the internal connection and depth information of the image from the image element level data and has achieved unprecedented performance in many scene-comprehension tasks, especially in object detection, object segmentation and classification. For decades, thanks to the development of parallel computing devices and large data sets, and to the performance of online resource accessibility and its advantages in modeling, the deep learning model represented by Convolutional Neural Network (CNN) has achieved rapid development and has been successfully applied in many computer vision (CV, computer-vision) cases, such as face recognition, pedestrian re-recognition, scene text detection, and targets tracking and automatic driving, etc. [7].
Based on vision and deep learning, the generation of robotic grasping pose is combined with both, pattern recognition and image processing technology. By analyzing and processing the image acquired by the acquisition equipment, the position extraction and azimuth estimation of the target are completed. This overcomes the defects of traditional manual feature extraction methods, such as high artificial feature requirements, sensitive factors such as the shape, size and angle of the target object, weak generalization ability, and the inability of a stable application in varied scenes. Therefore, the deep learning-based optimal grasping pose generation method of manipulator not only has important academic research value, but also has a very broad market application prospect.
At present, researchers have come up with many methods to detect the grasping pose of objects. For the traditional algorithm, Pas et al. [2] successively proposed two detection methods based on geometric constraints, whose main idea is to define some geometric conditions on the object to support the subsequent calculation of the optimal grasping pose (please add the reference number). Peng et al. [4] used the manipulator and the grasping object to perform geometric level fitting and studied the grasping pose on the voxelized 3D-object. These models are stable, but because such methods focus on using models, they often cannot be generalized to new grasping objects; and in some cases, modeling is difficult and cannot be transferred well to the real world.
In addition, the new intelligent control algorithm is gaining popularity in the recognition of the optimal grasping pose of the manipulator. In recent years, deep learning methods based on convolution networks, such as region convolution neural networks (RCNN) [8], have also indirectly promoted the research on robotic grasping. Wu et al. [5–9] introduced a pose interpretation neural network based entirely on synthetic pose data, and designed a grabbing pose estimation method by using the mixed hierarchy feature. Kumra et al. [10] used RGB-D image training convolutional network to predict the optimal grasping pose in image plane. Guo et al. [11–15] designed an end-to-end network to predict the possible fetching points of the target object and used a reference rectangle to represent the fetching position in the image.
With the increase of computing resources, the way robots learn to grasp from human experience or data sets has become an emerging research direction. Jiang et al. [16] established Cornell’s crawling data set [17,18], using sparse coding and support vector machine to obtain the object’s grasping frame. Since 2015, deep learning methods have shown an explosive growth in the field of grasping pose detection. Grabbing methods based on two-level and three-level [19–21] cascade detection networks, AlexNet convolution network and residual network have been gradually applied to grasping pose detection. Mahler et al. [22] used the robust GWS (Grasp Wrench Space) method to analyze the grasping quality of 1500 3D-model parallel grippers, and trained GQ-CNN (Grasp Quality Convolutional Neural Network) for the quality evaluation of grasping poses. Zhong et al. [23] used multi-mode feature deep learning to construct a stacked deep network to achieve optimal judgment of robotic grasping pose. Du et al. [24] optimized the grasping detection time by narrowing the grasping search area and reducing the rotation times of the search window. In addition, Morrison et al. [25] proposed to generate a grasping convolution neural network (GG-CNN), which can obtain the grasping pose on a pixel level [17–19].
Although these methods are simple and efficient, there have still some problems such as the accuracy of pose generation needs to be improved, the generalization ability is not strong, and so on. This paper mainly proposes a vision-based optimal grasping pose generation algorithm HGG-CNN obtained by improving GG-CNN, which optimizes the recognition rate of GG-CNN algorithm, improves the generalization ability of optimal grasping pose of the manipulator, and enables the manipulator to be applied to a wide range of fields in the industry [20–22].
3 Description of the Generation Process of Grasping Pose
Similar to other literature work [26–30], this paper is a generation process of grabbing poses of unknown objects perpendicular to the plane under the given scene depth image.
Similarly, in this paper, a grasping pose perpendicular to the plane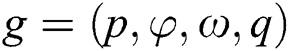 
is defined by its Cartesian coordinates 
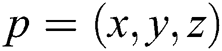, the angle of rotation 
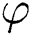around the 
-axis, and the width of the gripper 
required to successfully grasp the object. Among them, the extra parameter—the width of the gripper 
can make the grasping pose have better prediction performance than the general grasping pose defined only by the two parameters of position and rotation [24,25].
The input image required by the algorithm for calculation is a grab set 
consisting of 2.5 D depth images with the width of W and the height of H. By performing deep learning on the grab set, the final grasping pose is output.
In Eq. (1), 
is the pixel coordinate of the center point defined by the grasping pose 
in the input image, 
is the rotation angle of the camera reference system relative to the input image reference system defined by the grasping pose 
, 
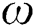is calculation of the width of the gripper for the deep learning algorithm through a given convolutional neural network, such as GG-CNN [1].
Through the transformation in the following formula, the grasping pose 
defined in the camera coordinate system can be converted into the grasping pose 
defined in the world coordinate system.
In Eq. (2), 
defines the transformation from the image coordinate system to the world (robot) coordinate system, and 
defines the transformation of the grasping pose 
from the two-dimensional to the three-dimensional in the camera coordinate system. Both of these transformations are based on the inherent parameters of the camera that captured the image and calibration parameters between the known robot coordinate system and camera coordinate system.
The algorithm defines a set of grabbing poses in the camera coordinate system as grabbing pose map [26–33].
In Eq. (3), 
, 
and 
all belong to 
, and they both contain the value 
, 
and 
at every central pixel 
.
In addition, the algorithm does not calculate the grabbing pose after sampling, but directly performs deep learning operations on each picture separately to calculate the corresponding grabbing pose 
. In order to achieve this function, GG-CNN defines a function 
for mapping the output captured image in the camera coordinate system from the input depth image. From Eq. (2), the best visible grasping pose 
in the camera coordinate system is calculated.
4.1 GG-CNN Convolutional Neural Network
The deep learning network in this paper is improved on the basis of GG-CNN convolutional neural network [1]. GG-CNN convolutional neural network [1] uses a relatively small neural network to solve the problem of grasp sampling by directly generating grasping poses for every pixel in the image.
Similar to other deep learning networks, GG-CNN convolutional neural network [1] proposes to use neural networks to fit complex functions 
, where 
represents neural network with weight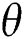 
.
In the GG-CNN convolutional neural network [1], 
. The network uses the L2 loss function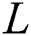 
to learn from the training set 
and corresponding output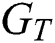 
by Eq. (4).
The algorithm is executed at the Cartesian point 
and estimates various parameters of the set of grasping poses corresponding to every pixel 
to generate a grasping pose image 
. Each grabbing pose image 
consists of a group pictures of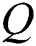 
, 
and 
. Among them, 
is an image describing the quality of the grasping pose generated at any point 
. The value range of every pixel in the figure is in the interval [0, 1], and the closer the value is to 1, the better the quality of the grasping pose and the more likely it is to succeed in grasping; 
is an image describing the angle of the grasping pose at each point. Since the grasping pose is symmetrical about the arc 
, the range of the angle belongs to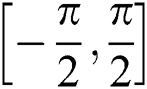 
, 
is an image describing the width of the gripper used to grasp at each point. Taking into account the invariance of the depth, the value range of the width is 
pixels, and the depth camera parameters and measured depth can be used later to convert it into measurement data that can be used realistically.
The network structure of GG-CNN convolutional neural network [1] is a fully convolutional topology structure, the schematic diagram is shown in Fig. 1 below.
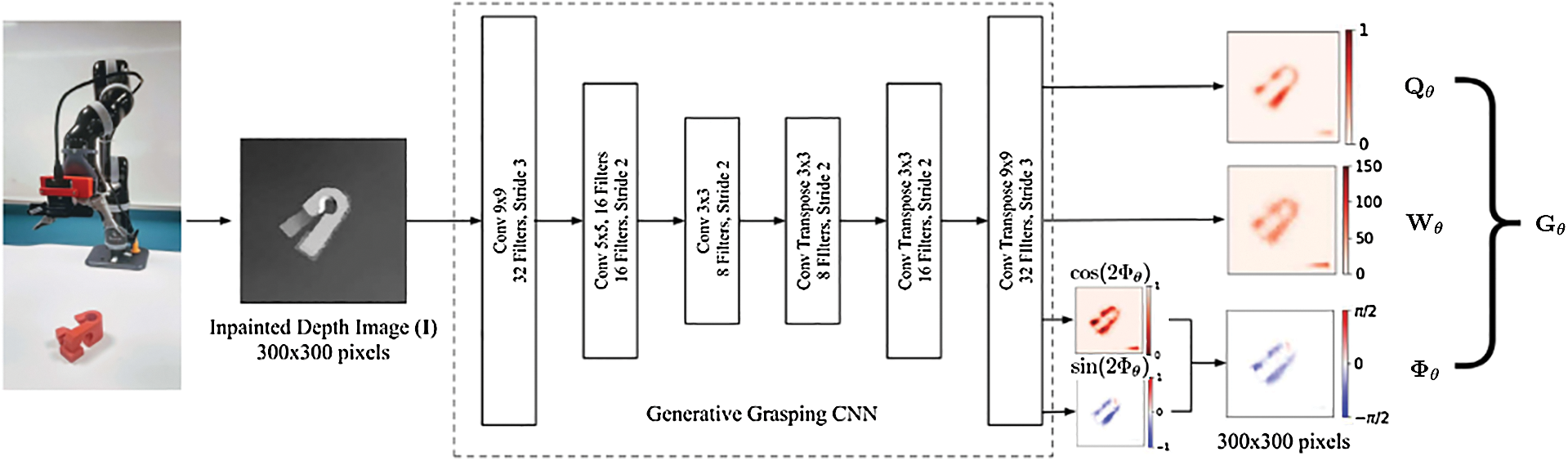
Figure 1: GG-CNN network topology structure
The use of GG-CNN convolutional neural network [1] can directly estimate the grasping pose 
from the input depth image 
, and it performs well in computer vision tasks such as image segmentation and contour detection that require transmission between image domains. The GG-CNN convolutional neural network [1] calculated the function 
, in which, 
, 
, 
and 
all represent the 
image. The two images output by the network represent the unit vector component of 
, where 
.
GG-CNN convolutional neural network [1] contains 62420 parameters, which makes it much smaller than CNNs used to grasp candidate classifications in other works with hundreds of thousands or millions of parameters, and the calculation speed is also fast much more.
In order to increase the accuracy of the grapping pose of the convolutional neural network, this paper introduces the Inception Block network structure to increase the width of the network. Inception Block is a sparse network structure, but can produce dense data, which can not only increase the performance of the neural network, but also ensure the efficiency of the use of computing resources. This structure stacks the convolutions (1 × 1, 3 × 3, 5 × 5) and pooling operations (3 × 3) commonly used in CNN (the same size after convolution and pooling, and the channels are added together), which increases the width of the network on one hand, and increases the adaptability of the network to scale on the other hand. The schematic diagram of its network structure is shown in Fig. 2 below.
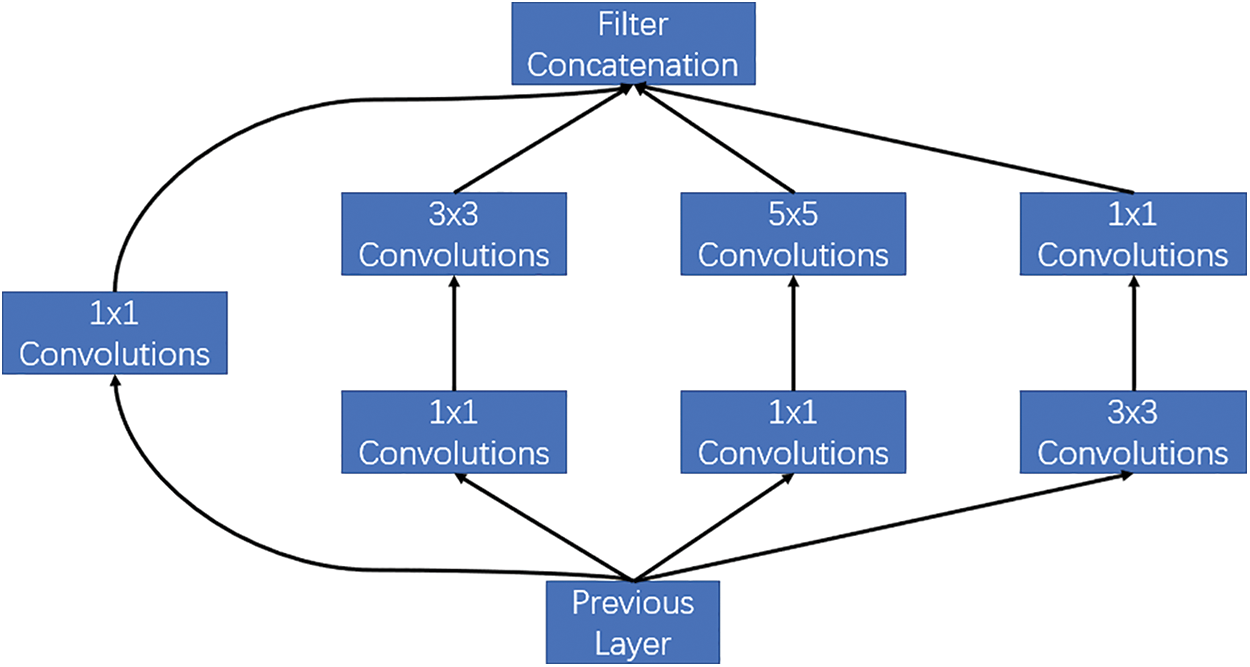
Figure 2: Inception block network structure
The network in the convolution layer of the Inception Block network can extract every detail information of the input, and the 
filter can also cover most of the input of the receiving layer. It can also perform a pooling operation to reduce the size of the space and reduce overfitting. Above these layers, a ReLU activation operation is performed after each convolutional layer to increase the nonlinear characteristics of the network. The main purpose of the 
convolutional layer is to reduce the dimension, which is also used to modify the linear activation (ReLU). For the data of upper layer of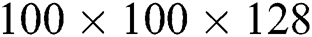 
, after adding the convolutional layer 
to perform dimensionality reduction, the amount of convolution parameters can be reduced by about 4 times.
In order to alleviate the problem of gradient disappearance and explosion, and ensure the maximum information flow in the network, this paper introduces the Dense Block network structure [15], so that each layer is connected to all layers before it is changed. Dense Block is composed of 
Dense Layer, and between every layer is Dense Connectivity. Each layer of Dense Layer is completed in four steps: normalization, activation, convolution, and Dropout. The schematic diagram of its network structure is shown in Fig. 3 below.
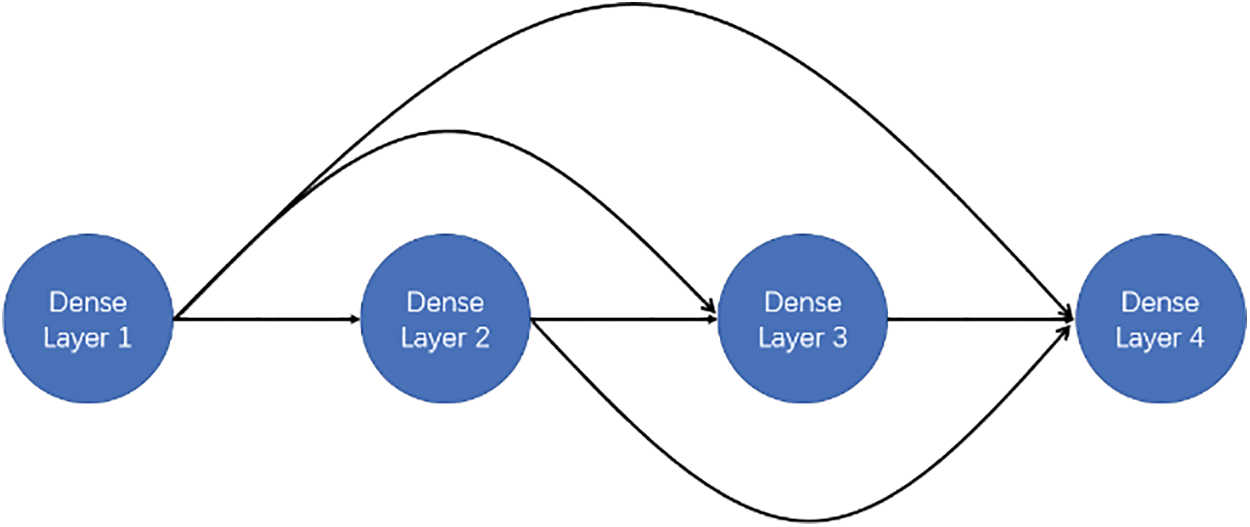
Figure 3: Dense block network structure
Among them, the output 
of the 
Dense Layer can be calculated by the following Eq. (5)
In the formula,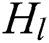 
is the calculation function of the layer. The input is the stitching 
to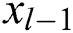 
, that is, the stitching of the original output 
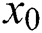of the model and the output of each layer in the channel dimension.
In order to solve the loss caused by the different importance of the channels in the feature map during the convolution pooling process, this paper introduces the SELayer network structure [12], so that the difference in the importance of different channels in the feature map can be reflected, and the problem can be treated specifically. The schematic diagram of its network structure is shown in Fig. 4 below.
Figure 4: SELayer network structure
In the figure, firstly, the input feature map is globally pooled. By the operation of global pooling, the width and height of the feature map can be reduced to 1, and then the first fully connected layer reduces the channel dimension, the second fully-connected layer raises the dimension of the channel again. The advantage is that it adds more nonlinear processing and fits the complex correlation between the channels. Then it connects another sigmod layer, and finally performs the full multiplication operation with the feature map. The reason why full multiplication is not matrix multiplication is because it can get feature maps of different channels with different importance.
The HGG-CNN convolutional network structure is obtained by the integration of Inception Block [34], Dense Block [15], and SELayer [12]. Similar to the structure of the GG-CNN convolutional network, the HGG-CNN convolutional neural network also calculates the function 
, where 
, 
, 
and 
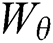all represent the 
image. The two images output by the network represent the unit vector component of 
, where 
. The schematic diagram of HGG-CNN convolutional network structure is shown in Fig. 5 below.
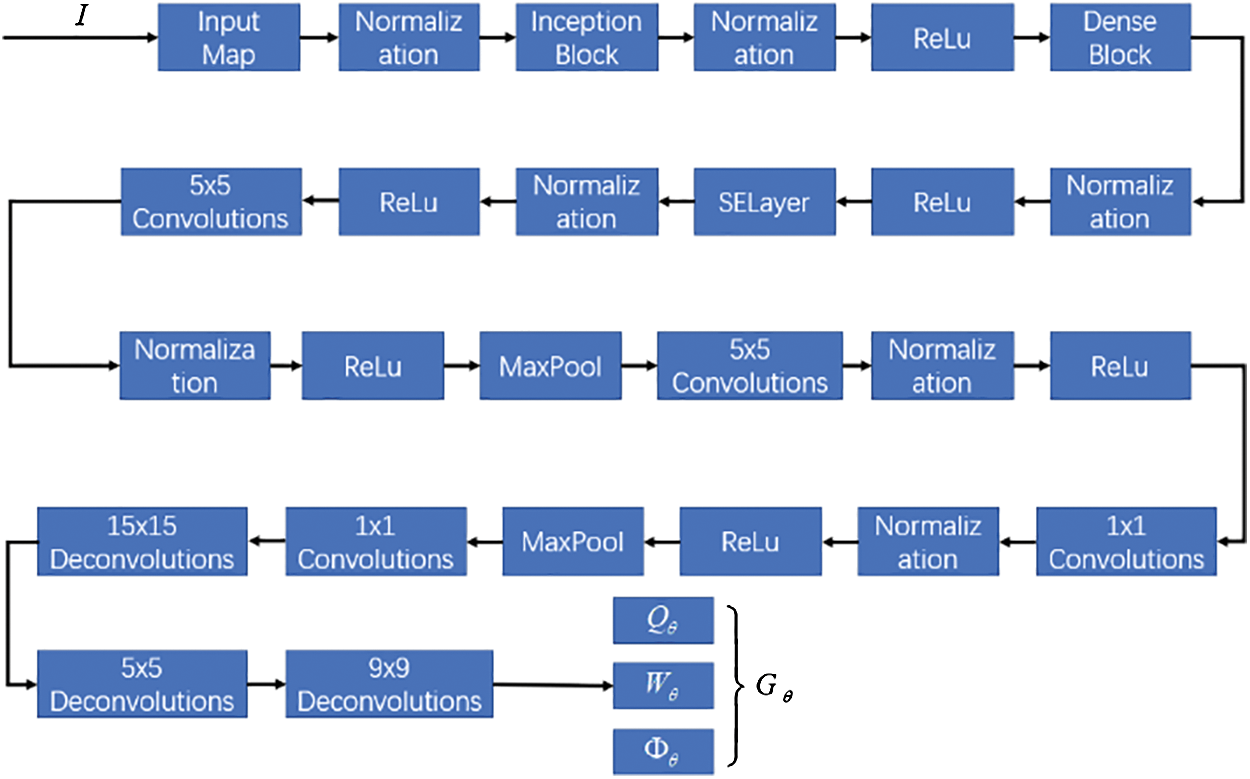
Figure 5: HGG-CNN network structure
In the figure, the input image 
is normalized first and then enters the sub-module of Inception Block, which will improve the accuracy of HGG-CNN’s pose recognition; the output of the Inception sub-module enters the sub-module of Dense Block after a normalization operation, this module can avoid the problem of gradient disappearance and gradient explosion; then it enters the sub-module of SElayer after another normalization. This module will give different weights to different channels. Finally, after one normalization operation, four deconvolution operations are performed, and finally four output images are calculated by the same method of GG-CNN. The HGG-CNN convolutional neural network contains a total of 8,806,986 parameters.
5 Experiment Preparation (Device)
The convolutional network structures before and after improvements, such as GG-CNN, HGG-CNN, etc., are calculated on a computer running Windows 10 1809 Professional Edition. The computer is equipped with an Intel Core i7-9750H processor at 4.5 GHz and an NVIDIA GeForce GTX 1660Ti graphics card. The code is mainly written in Python.
In order to train our network, we grab a dataset from Cornell [27] to create a new dataset. The Cornell grasping dataset contains 885 RGB-D images of real objects, 5110 human-marked forward and 2909 reverse-grasping. Compared with some recent synthetic data sets [28,31], this is a relatively small grasping data set, but the data in the Cornell grasping set is more suitable for representing the pixel grasp contained in each image provided as multiple crawl marks. For example, document [28] adds random trimming, scaling and rotation to the image based on the Cornell grasping data set, creating a set of 8840 depth images and related grasping pose images 
, containing 51100 effective grasping example.
The Cornell grasping dataset uses a pixel coordinate system aligned to the jaw position and rotation angle to map pixel coordinates to rectangles [32]. In order to convert this rectangular mapping method to the image-based mapping representation G in this paper, we use the central third of each grab rectangle as the image marker, which corresponds to the position of the center of the grabber. We use this image tag to update our training image. We only consider forward grasping to train our network and assume that any other location is not an effective grasping pose. There are four parameters in the output of the data set: grasping quality 
, rotation angle 
, jaw width 
and depth input.
: This article takes each true forward grasping pose from the Cornell grasping dataset as a binary marker and sets the value of the corresponding position 
to 1. All other pixel positions are set to 0.
: This article calculates the rotation angle range of each grasping pose rectangle within the angle range 
and sets the corresponding area 
. If the original rotation angle of the grasping pose is used, this article will encode the rotation angle as a partial vector on the two unit circles [33], record the value in the range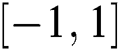 
and delete any data that does not continuously occur in the angle 
, making subnets easier to learn. Because the mapping of the grasping pose is symmetrical in the angle 
, this paper uses two component 
and 
,which will output the only data 
that is symmetrical in the angle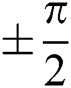 
.
: Similarly, we calculate the pixel width of each grasping pose rectangle, the maximum value of the width data is 150, which is the width of the gripper, and set the corresponding part 
. During training, we scale the value 
by 
to make it within the range 
. The width of the physical gripper can be further calculated by camera parameters and measured depth.
Depth: The Cornell grasping dataset is captured with a real camera. It already contains real sensor noise, so no noise is needed. Depth images use OpenCV [34] to delete invalid values. In this paper, the average value of each depth image is subtracted, and its value is concentrated near 0 to provide depth invariance.
In this paper, 80% of the data set is used as the training data set, which is used to train the network, while retaining 20% of the data set as the evaluation data set. In this paper, gradient descent is used in training, and the batch size parameter is 1000; Adam optimizer is used to train the test data set for 150 rounds.
In order to compare the accuracy of grasping pose recognition for different convolutional network structures, this paper evaluates each detected true positive grasping pose in the 20% evaluation data set containing 1710 enhanced images and calculates the corresponding IOU to compare the relative performance between different networks.
In order to evaluate the performance of the HGG-CNN convolutional network structure and the GG-CNN convolutional network structure, we conducted 150 rounds of deep learning training to train each network. The trained network includes the original GG-CNN convolutional neural network [1] structure, the Inception GG-CNN network structure that separately introduces into the Inception Block network structure, the Dense GG-CNN network structure that separately introduces into the Dense Block network structure, and the HGG-CNN without SE network structure that introduces Inception Block and Dense Block network structure but without introducing SELayer network structure, and HGG-CNN with SE convolution network structure with three network structures of Inception Block, Dense Block and SELayer at the same time. In the experiment, these network structures were trained for a total of 150 rounds. In order to compare the experimental results with other experimental results, our goal is to reproduce similar experiments as much as possible. We use the training grasping set defined in the previous article to train the deep learning network for repeatable experiments.
The timing values of the pose generation accuracy IOU and the loss function Loss during the training process of each convolutional network structure are shown in Figs. 6 and 7:
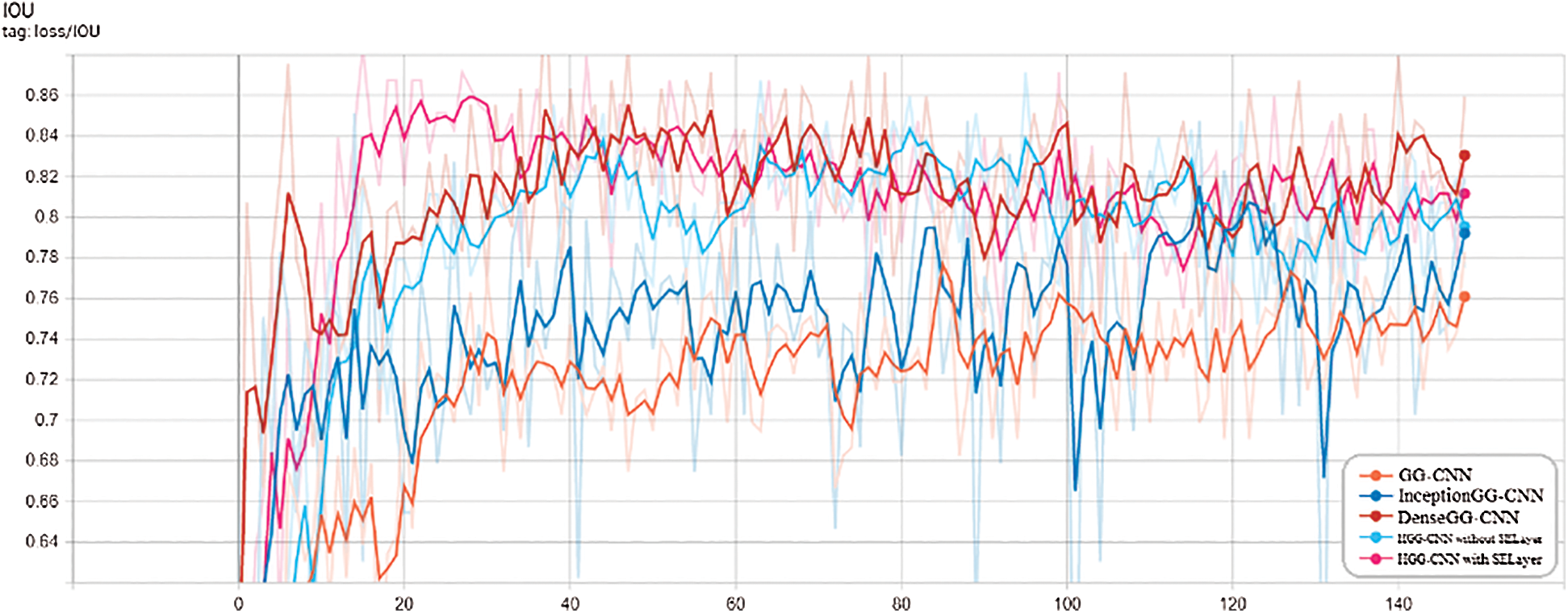
Figure 6: IOU timing diagram of the pose accuracy of each convolution network structure
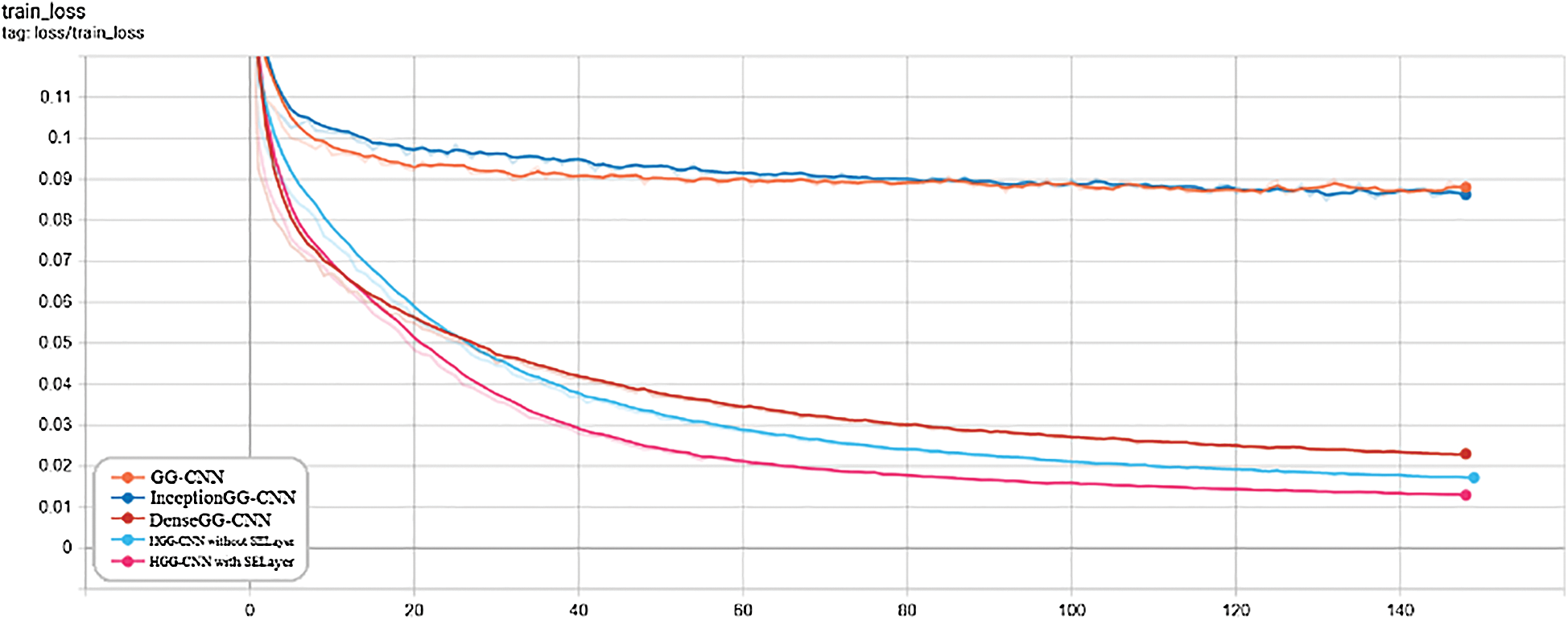
Figure 7: Loss timing diagram of the loss function of each convolutional network structure
As can be seen from the figure, the recognition accuracy of the improved network structure Inception GG-CNN, Dense GG-CNN, HGG-CNN without SE and HGG-CNN with SE are higher than the original GG-CNN model, among them, the HGG-CNN convolutional network model is significantly better than other network structures, and the accuracy of pose generation IOU is expected to increase by about 10%. In addition, the loss of HGG-CNN convolutional network structure Loss is also significantly reduced compared to the original GG-CNN convolutional network structure, which is expected to be around 0.07.
In order to accurately evaluate the improvement of the pose generation accuracy of the HGG-CNN convolutional network structure compared to the original GG-CNN convolutional network structure, this paper uses the trained model to generate a grasping pose for the test data set and calculate its pose generating accuracy rate IOU, the experimental data of the test set pose generation accuracy rate is shown in Tab. 1 below.
Table 1: Accuracy results of test set pose generation
It can be seen from Tab. 1 that the original GG-CNN convolutional network structure has a higher accuracy rate compared to the generation of grasping poses for simple natural objects with simple geometric shapes such as shells and bottles, and the IOU values are all greater than 80%; but for complex artificial irregular objects such as toothbrushes, light bulbs, spoons, etc., the accuracy rate of the grasping pose generation is low, and the IOU value is below 70%. Among them, the accuracy rate of the grasping pose generation of the spoon is the worst. The value is only 21.38%. In the improved four convolutional network structures, they all can play the effect of optimizing the intersection and IOU, but the optimization effect of the HGG-CNN convolutional network structure is higher than the other three, whether simple natural objects or complex man-made objects can be accurately identified, and the accuracy of pose generation is more than 75%. Both of them have the highest accuracy rate of the bottle's grasping pose. The HGG-CNN’s accuracy rate of the bottle’s grasping pose is 81.54%. In addition, the new HGG-CNN convolutional network structure improves the accuracy of grasping pose generation from the original GG-CNN convolutional network structure from 83.83% to 92.48%, with an increase of 10.32%.
In order to reflect the improvement of the accuracy of the HGG-CNN convolutional network structure compared to the GG-CNN convolutional network structure, the article selects two objects, a toothbrush and a spoon, and uses two network structures to generate the grab pose respectively. The generated color RGB image of the captured pose, the depth image of the depth, the captured pose quality image 
and the captured angle image 
are shown in Fig. 8 below.
Figure 8: Comparison of GG-CNN and HGG-CNN generation
In the figure above, the left side is the grasping scheme of toothbrush and spoon generated by the GG-CNN convolutional network structure, and the right side is the grasping scheme of toothbrush and spoon generated by the HGG-CNN convolutional network structure. For toothbrushes, the IOU of the HGG-CNN network structure generation grasping scheme is 15.16% higher than that of the GG-CNN network structure generation grasping scheme, and for the spoon, it is increased by 34.95%.
This paper improves on the basis of the GG-CNN convolutional neural network [1] and proposes a new convolutional neural network that generates a grasping pose—HGG-CNN, which is similar to GG-CNN and directly generates grab gestures from depth images on a pixel-level basis instead of sampling and classifying individual grab candidates as in other deep learning techniques. Experiments show that when the parameter of Batch size is 1000, the Adam optimizer is used, and the training round is 150 times. HGG-CNN can improve the average pose recognition accuracy rate IOU from 83.83% to 92.48%, an increase of 10.32%. after 150 rounds of training. It can be seen that the new HGG-CNN convolutional neural network organically combines the advantages of the three sub-networks of Inception Block, Dense Block and SElayer, and improves the problem that the original GG-CNN network has low recognition accuracy during the generation of the grasping pose of the manipulator and effectively improves the accuracy of grasping pose recognition.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Jain and C. C. Kemp. (2010). “EL-E: An assistive mobile manipulator that autonomously fetches objects from flat surfaces,” Autonomous Robots, vol. 28, no. 1, pp. 45–64. [Google Scholar]
2. A. T. Pas, M. Gualtieri, K. Saenko and R. Platt. (2017). “Grasp pose detection in point clouds,” International Journal of Robotics Research, vol. 36, no. 13–14, pp. 1455–1473. [Google Scholar]
3. M. Sun, S. S. Kumar, G. Bradski and S. Savarese. (2013). “Object detection, shape recovery, and 3D modelling by depth-encoded hough voting,” Computer Vision and Image Understanding, vol. 117, no. 9, pp. 1190–1202.
4. P. Peng, Z. Fu and L. Liu. (2018). “Grasp planning via hand-object geometric fitting,” Visual Computer, vol. 34, no. 2, pp. 257–270. [Google Scholar]
5. J. Wu, B. Zhou, R. Russell, V. Kee, S. Wagner et al.. (2018). “Real-time object pose estimation with pose interpreter networks,” in IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, Madrid, Spain, pp. 6798–6805. [Google Scholar]
6. R. Girshick, J. Donahue, T. Darrell and J. Malik. (2014). “Rich feature hierarchies for accurate object detection and semantic segmentation,” in The IEEE Int. Conf. on Computer Vision, Columbus, OH, pp. 580–587. [Google Scholar]
7. R. Girshick. (2015). “R fast-CNN,” in The IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 1440–1448. [Google Scholar]
8. Ren S., He K., Girshick R. and Sun J. (2015). “Faster R-CNN: Towards real-time object detection with region proposal networks,” IEEE Transactions on Pattern Analysis & Machine Intelligence, vol. 39, no. 6, pp. 1137–1149. [Google Scholar]
9. G. Wu, W. Chen, H. Cheng, W. Zuo, D. Zhang et al.. (2019). “Multi-object grasping detection with hierarchical feature fusion,” IEEE Access, vol. 7, pp. 43884–43894. [Google Scholar]
10. S. Kumra and C. Kanan. (2017). “Robotic grasp detection using deep convolutional neural networks,” in IEEE/RSJ Int. Conf. on Intelligent Robots & Systems, Vancouver, BC, Canada, pp. 769–776. [Google Scholar]
11. D. Guo, F. Sun, T. Kong and H. Liu. (2017). “Deep vision networks for real-time robotic capture detection,” International Journal of Advanced Robotic Systems, vol. 14, no. 1, pp. 1–8. [Google Scholar]
12. X. Zhong, O. Gong, W. Huang, L. Li and H. Xia. (2019). “Squeeze-and-excitation wide residual networks in image classification,” in 2019 IEEE Int. Conf. on Image Processing, Taipei, Taiwan, pp. 395–399. [Google Scholar]
13. D. Chen and Q. Q. Lin. (2019). “Research on 3D object optimal grasping method-based on cascaded faster-RCNN,” Chinese Journal of Scientific Instrument, vol. 40, no. 4, pp. 229–237.
14. D. Morrison, P. Corke and J. Leitner. (2018). “Closing the loop for robotic grasping: A real-time, generative grasp synthesis approach,” in Robotics: Science and Systems, Pittsburgh, PA, USA, pp. 1–10.
15. H. Gao, Z. Liu and K. Q. Weinberger. (2017). “Densely connected convolutional networks,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 2261–2269. [Google Scholar]
16. Y. Jiang, S. Moseson and A. Saxena. (2011). “Efficient grasping the from RGB-D images: Learning using a new rectangle representation,” in IEEE Int. Conf. on Robotics and Automation, Piscataway, USA: IEEE, pp. 3304–3311. [Google Scholar]
17. A. Krizhevsky, I. Sutskever and G. E. Hinton. (2012). “ImageNet classification with deep convolutional neural networks,” in Neural Information Processing Systems Foundation, La Jolla, CA, USA, pp. 1097–1105. [Google Scholar]
18. I. Lenz, H. Lee and A. Saxena. (2015). “Deep learning for detecting robot-IC grasps,” International Journal of Robotics Research, vol. 34, no. 4–5, pp. 705–724. [Google Scholar]
19. Q. C. Yu, W. W. Shang and C. Zhang. (2018). “Object grabbing detection based on three-level convolutional neural network,” Robot, vol. 40, no. 5, pp. 762–768. [Google Scholar]
20. J. Redmon and A. Angelova. (2015). “Real-time grasp detection using convolutional neural networks,” in IEEE Int. Conf. on Robotics and Automation, Piscataway, USA: IEEE, pp. 1316–1322. [Google Scholar]
21. S. Kumra and C. Kanan. (2017). “Robotic grasp detection using deep convolutional neural networks,” in IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, Piscataway, USA: IEEE, pp. 7, 69–776. [Google Scholar]
22. J. Mahler, J. Liang, S. Niyaz, M. Laskey, R. Doan et al.. (2019). “Dex-Net 2.0: deep learning to plan robust grasps with synthetic point clouds and Analyt-IC grasp metrics,” [DB/OL], arXiv: 1703. 09312. [Google Scholar]
23. X. G. Zhong, M. Xu, X. Y. Zhong and X. F. Peng. (2016). “Multimodal features deep learning for robotic potential recognition,” Acta Auto-Matica Sinica, vol. 42, no. 7, pp. 1022–1029. [Google Scholar]
24. X. D. Du, Y. H. Cai, T. Lu, S. Wang and Z. Yan. (2017). “A robotic grasping method-based on deep learning,” Robot, vol. 39, no. 6, pp. 820–828, 837. [Google Scholar]
25. D. Morrison, P. Corke and J. Leitner. (2019). “Closing the loop for Robot-IC grasping: A real-time, generative grasp short approach,” [DB/OL], arXiv: 1804.05172. [Google Scholar]
26. J. Edward, L. Stefan and J. D. Andrew. (2016). “Deep learning a grasp function for grasping under gripper pose uncertainty,” in Proc. of the IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, Deajeon, Korea, pp. 4461–4468. [Google Scholar]
27. I. Lenz, H. Lee and A. Saxena. (2015). “Deep learning for detecting robotic grasps,” International Journal of Robotics Research, vol. 34, no. 4–5, pp. 705–724. [Google Scholar]
28. J. Mahler, J. Liang, S. Niyaz, M. Laskey, R. Doan et al.. (2017). “Dex-Net 2.0: Deep learning to plan robust grasps with synthetic point clouds and analytic grasp metrics,” in Robotics: Science and Systems, , arXiv: 1703.09312. [Google Scholar]
29. L. Pinto and A. Gupta. (2016). “Supersizing self-supervision: learning to grasp from 50k tries and 700 robot hours,” in Proc. of the IEEE Int. Conf. on Robotics and Automation, Stockholm, Sweden, pp. 3406–3413.
30. U. Viereck, A. Pas, K. Saenko and R. Platt. (2017). “Learning a visuomotor controller for real world robotic grasping using simulated depth images,” in Proc. of the Conf. on Robot Learning, Mountain View, CA, USA, pp. 291–300. [Google Scholar]
31. J. Mahler, F. T. Pokorny, B. Hou, M. Roderick, M. Laskey et al.. (2016). “Dex-Net 1.0: a cloud-based network of 3D objects for robust grasp planning using a multi-armed bandit model with correlated rewards,” in Proc. of the IEEE Int. Conf. on Robotics and Automation, Stockholm, Sweden, pp. 1957–1964. [Google Scholar]
32. Y. Jiang, S. Moseson and A. Saxena. (2011). “Efficient grasping from RGBD images: learning using a new rectangle representation,” in Proc. of the IEEE Int. Conf. on Robotics and Automation, Shanghai, China, pp. 3304–3311. [Google Scholar]
33. K. Hara, R. Vemulapalli and R. Chellappa. (2017). “Designing deep convolutional neural networks for continuous object orientation estimation,” arXiv: 1702.01499. [Google Scholar]
34. S. Christian, W. Liu, Y. Q. Jia, P. Sermanet, S. Reed et al.. (2015). “Going deeper with convolutions,” in 2015 IEEE Conf. on Computer Vision and Pattern Recognition, Santiago, Chile, pp. 1–9. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |