DOI:10.32604/iasc.2020.011721
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.011721 | |
| Article |
Multiple Faces Tracking Using Feature Fusion and Neural Network in Video
1College of Mathematics and Econometrics, Hunan University, Changsha, 410082, China
2College of Mathematics and Statistics, Hengyang Normal University, Hengyang, 421002, China
3School of Computer Engineering and Applied Mathematics, Changsha University, Changsha, 410003, China
4College of Computer Science and Electronic Engineering, Hunan University, Changsha, 410082, China
5Key Laboratory of Digital Signal and Image Processing of Guangdong, Shantou, 515063, China
*Corresponding Author: Boxia Hu. Email: huboxia@hynu.edu.cn
Received: 26 May 2020; Accepted: 07 August 2020
Abstract: Face tracking is one of the most challenging research topics in computer vision. This paper proposes a framework to track multiple faces in video sequences automatically and presents an improved method based on feature fusion and neural network for multiple faces tracking in a video. The proposed method mainly includes three steps. At first, it is face detection, where an existing method is used to detect the faces in the first frame. Second, faces tracking with feature fusion. Given a video that has multiple faces, at first, all faces in the first frame are detected correctly by using an existing method. Then the wavelet packet transform coefficients and color features from the detected faces are extracted. Furthermore, we design a backpropagation (BP) neural network for tracking the occasional faces. At last, a particle filter is used to track the faces. The main contributions are. Firstly, to improve face tracking accuracy, the Wavelet Packet Transform coefficients combined with traditional color features are utilized in the proposed method. It efficiently describes faces due to their discrimination and simplicity. Secondly, to solve the problem in occasional face tracking, and improved tracking method for robust occlusion tracking based on the BP neural network (PFT_WPT_BP) is proposed. Experimental results have been shown that our PFT_WPT_BP method can handle the occlusion effectively and achieve better performance over other methods.
Keywords: Face tracking; feature fusion; neural network; occlusion
The problem of face tracking can be considered as finding an effective and robust way. It is based on using the geometric dependence of facial features to combine the independent face detectors of various facial features, and then get an accurate estimation of the position of each image’s facial features in the video sequence [1]. Particle filter realizes recursive Bayesian filtering by the Nonparametric Monte Carlo simulation method [2]. It can be applied to any nonlinear system which can be described by the state-space model, and its accuracy can approach the optimal estimation. The Particle filter is simple and easy to implement and provides an effective method for the analysis of nonlinear dynamic systems [3,4]. It has attracted extensive attention in the fields of target tracking, signal processing, and automatic control Bui Quang et al. [5]. It approximates the posterior distribution through a set of weighted assumptions which are called particles. During the tracker based on particle filter, there is a likelihood function that generates a weight for each particle and the particles are distributed according to a tracking model. Then, the particles are properly placed, weighted, and propagated. After calculating the posterior distribution of the particles, the most likely position of a face can be estimate sequentially [6,7]. In many cases including some complex backgrounds, particle filter achieves good performance and is used in more and more applications [8]. Though particle filter has a good performance in target tracking, there still exist some problems in face tracking. The common particle filter methods cannot handle an occlusion especially a full occlusion [9,10]. Some tracking results with and without occlusions for particle filter are shown in Fig. 1. The tracking performance becomes poor when a face occlusion occurs. The main reason is faces are similar and the re-sampling would propagate the wrong random samples since the likelihood of those occluded faces and lead to meaningless tracking. Therefore, dealing with occlusions is a crucial part of multiple faces tracking.
Figure 1: Examples of multiple faces tracking with and without occlusion
This paper presents an occlusion robust tracking (PFT_WPT_BP) method for multiple faces tracking. The three main contributions of this paper are summarized as follows:
– After detecting faces, wavelet packet decomposition is used to generate some frequency coefficients of images. We separately use its higher and lower frequency coefficients of the reconstructed signal to improve the faces tracking performance.
– We define a neural network for tracking the faces with occlusion. When faces tracking fails due to face-occlusion, the neural network is used to predict the next step of the occlusion face/faces.
– A method based on particle filter and multiple feature fusion for faces tracking in the video is proposed. The proposed method has good performance and is robust in multiple faces tracking.
The particle filter algorithm is derived from the idea of Monte Carlo [11], which refers to the probability of an event by its frequency. Therefore, in the process of filtering, where probability such as P(x) is needed, variable x is sampled, and P(x) is approximately represented by a large number of samples and their corresponding weights. Thus, with this idea, particle filter can deal with any form of probability in the process of filtering, unlike Kalman filter [12], which can only deal with the probability of linear Gaussian distribution. This is one of the advantages of a particle filter.
Some researchers use a histogram method of tracking face [13]. Nevertheless, this method has a significant limitation, and many factors can affect the similarity of the two images, such as light, posture, face vertical or left-right angle deviation, and so on. As a result, the face tracking result sometimes is poor, and it is hard to use in practical application. Reference [14] proposed a new face-tracking method which is based on the Meanshift algorithm. In these methods, the face position of the current frame is updated according to the histogram of the target in the previous frame and the image obtained in the current frame. These methods are suitable for single target tracking, and the effect is charming. However, when the non-target and target objects are occluded, it often leads to the temporary disappearance of the target [15]. When the target reappears, it is often unable to track the target accurately. Therefore, the robustness of the algorithm is reduced. Because color histograms are robust to partial occlusion, invariant to rotation and scaling, and efficient in computation, they have many advantages in tracking nonrigid objects. Reference [16] proposed a color-based particle filter for face tracking. In this method, Bhattacharyya distance is used to compare the histogram of the target with the histogram of the sample position during the particle filter tracking. When the noise of the dynamic system is minimal, or the variance of observation noise is microscopic, the performance of the particle filter is terrible. In these cases, the particle set quickly collapses to a point in state space. Reference [17] proposed a Kernel-based Particle Filter for face tracking. The standard particle filter usually cannot produce the set of particles that capture the “irregular” motion, which leads to the gradual drift of the estimated value and the loss of the target. There are two difficulties in tracking different numbers of nonrigid objects: First, the observation model and target distribution can be highly nonlinear and non-Gaussian. Secondly, the existence of a large number of different objects will produce overlapping and fuzzy complex interactions [18,19]. A practical method is to combine the hybrid particle filter with AdaBoost. The critical problem of the hybrid particle filter is the selection of scheme distribution and the processing of objects leaving and entering the scene. Reference [20] proposed a three-dimensional pose tracking method that mixes particle filter and AdaBoost. The hybrid particle filter is very suitable for multi-target tracking because it assigns a hybrid component to each player. The proposed distribution can be built by using a hybrid model that contains information from each participant’s dynamic model and test assumptions generated by AdaBoost.
3 The Framework of Our Multiple Faces Tracking Approach
Given a face model, a state equation is defined as
where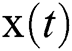 
is the state at time t, 
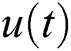is the control quantity, 
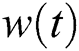and 
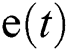are the state noise and observation noise respectively. The former equation describes the state transition, and the latter is the observation equation. The framework of our multiple faces tracking approach is shown in Fig. 2.
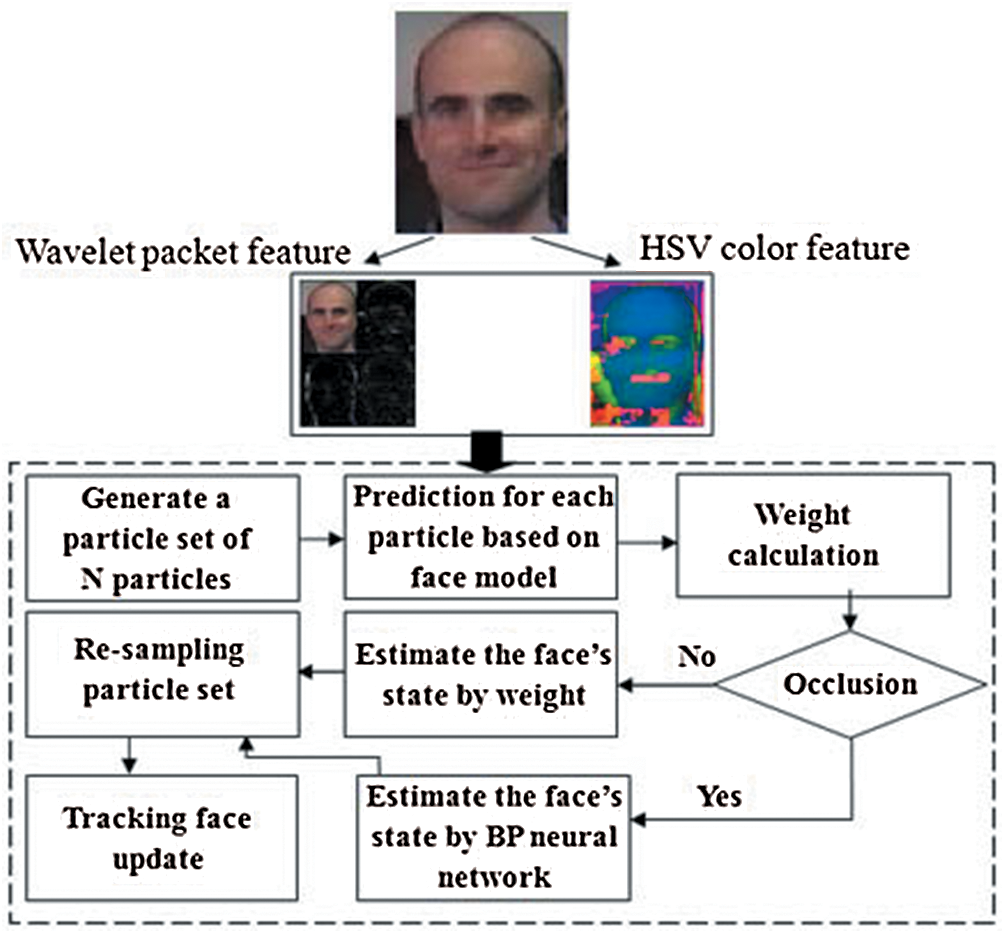
Figure 2: The framework of multiple faces tracking algorithm using feature fusion
For such faces tracking problems, particle filter filters out the real state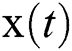 
from observation 
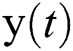, and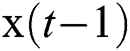 
, u(t) by following steps.
Prediction stage: Particle filter firstly generates a large number of samples according to the probability distribution of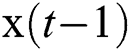 
, which are called particles. Then the distribution of these samples in the state space is the probability distribution of 
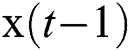. Well, then according to the state transfer equation and the control quantity, we can get a prediction particle for each particle.
Correction stage: After the observation value y arrives, all particles are evaluated by using the observation equation, i.e., conditional probability p(y|xi). To be frank, this conditional probability represents the probability of obtaining the observation y when assuming the real state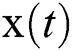 
takes the ith particle xi. Let this conditional probability be the weight of the i-th particle. In this way, if all particles are evaluated, the more likely they are to get the particles observing y, the higher the weight of course.
Resampling algorithm: Remove the particles with low-weight and copies the particles with high weight. What we get is, of course, the real state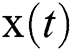 
we need, and these resampled particles represent the probability distribution of the real state. In the next round of filtering, the resampled particle set is input into the state transition equation, and the predicted particles can be obtained directly.
Since we know nothing about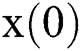 
at first, we can think that 
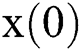is evenly distributed in the whole state space. So the initial samples are distributed in the whole state space. Then all the samples are input into the state transition equation to get the predicted particles. Then we evaluate the weights of all the predicted particles. Of course, only some of the particles in the whole state space can get high weights. Finally, resampling is carried out to remove the low weight, and the next round of filtering is reduced to the high weight particles.
In our method, the state of a face at time t is denoted as st and its history is S = {s1; s2;…; st}. The basic idea of the particle filter algorithm is to compute the posterior state-density at time t using process density and observation density. Aiming to improve the sampling of the particle filter, we propose an improved algorithm based on combining with Wavelet Packet Transform and HSV color feature.
4 Face Tracking Model with Wavelet Packet Transform and Color Feature Fusion
4.1 Face Feature Extraction Base on the Wavelet Packet Transform
The theory of Wavelet Packet Transform and feature extraction are introduced in this part. Wavelet packet analysis is an extension of wavelet analysis and will decompose not only the approximate but also the detail of the signal [21]. Wavelet packet decomposition provides the finer analysis as follows:
where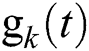 
and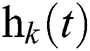 
are a pair of complementary conjugate filters [22], t is a parameter in the time-domain, k = 1,2,3…N. The result of the Wavelet Packet Transform is shown as a full decomposition tree, as depicted in Fig. 3. A low (L) and high (H) pass filter is repeatedly applied to the signal S, followed by decimation by Eq. (2), to produce a complete subband tree decomposition to some desired depth.
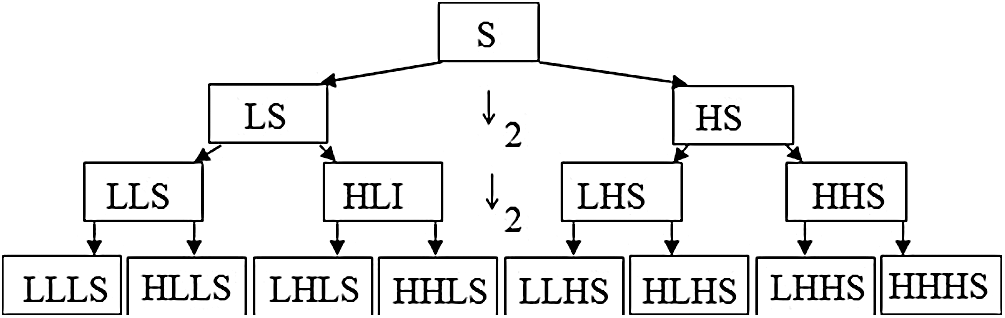
Figure 3: The wavelet packet decomposition tree
More face features are generated by wavelet packet decomposition and are used in face tracking. An example of face image decomposition is shown in Fig. 4.
Figure 4: Four wavelet packet coefficient features
In our work, the face model is defined as parameters set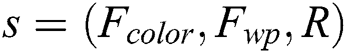 
, where R is a rectangle represented by 
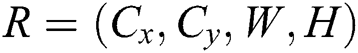, and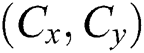 
is the center position, and W, H are the width and height of the rectangle. We consider the face as a discrete-time 2-dimensional motion with constant velocity. The state at time step k is denoted by 
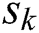, our face dynamics model are modeled as
where P is the transition matrix, Q is the system noise matrix and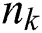 
is a Gaussian noise vector. This dynamic model is used in the sampling step of particle filters. With an assumption that the object moves with constant velocity, we can describe the motion in the following equations.
where xk, yk represent the center of the target region at time step k. From this, the state vector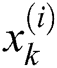 
of the i-th particle at time step k, the system matrices P and Q, and noise vectors 
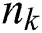are defined as Eqs. (5)–(7), respectively.
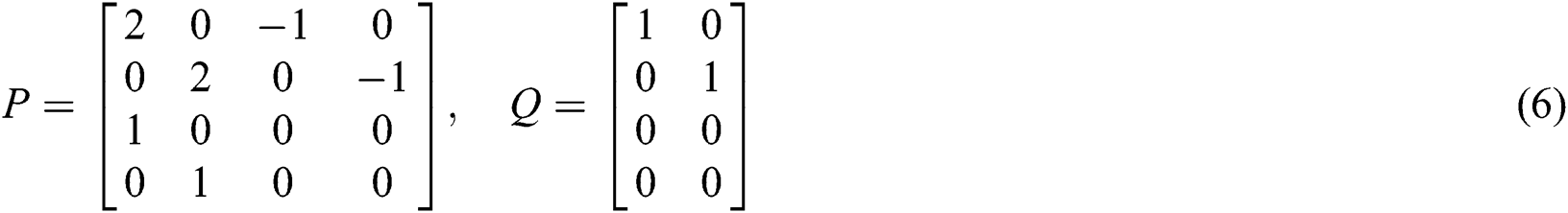
The observation process is performed to measure and weigh all the newly generated samples. The visual observation is a process of visual information fusion including two sub-processes: The computation sample weights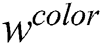 
, 
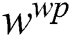based on color histogram features and wavelet packet features, respectively. To consider timing issue, one- to four-level wavelet packet decomposition is used.
For the kth sample, we obtaine the weight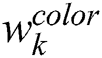 
through a Bhattacharyya similarity function [16] as shown in Eq. (8), calculating the similarity between sample histogram features 
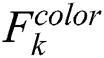and the reference histogram features template 
.
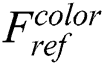where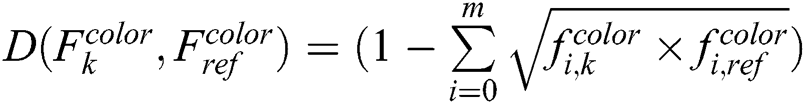 
and m is the number of segments of the segmented color space. Here, we use color space with 6 × 6 × 6 bins.
To compute the sample weight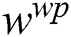 
based on the wavelet packet feature, the Euclidean distance between the sample feature vector 
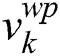and the reference feature vector 
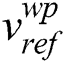is employed in our system. The expression of 
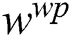is as follows:
where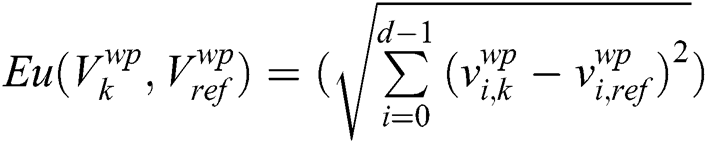 
, d is the number of feature dimensions.
With two different visual cues, we obtain the final weight for the kth sample as:
where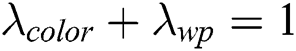 
, 
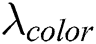and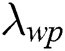 
are the coefficient values the weights of color histogram features and wavelet packet features, respectively. We can determine their values from experiences.
4.3 Multi-Face Tracking Algorithm Based on Particle Filter
Our multi-face tracking system consists of two parts: Automatic face detection and particle filter tracking. In the tracking system, the boosted face detector which is introduced above achieves automatic initializations when the system starts or when a tracking failure occurs. The face detection results are used to update the reference face model. The updating criterion is confidence values that are less than a threshold valued for M successive frames.
The proposed tracking algorithm includes four steps, as shown below.
1. Initialization:
i) Automatic face detection and n faces are detected.
ii) Initialize the K particles.
2. Particle filter tracking: Probability density propagation from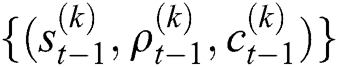 
to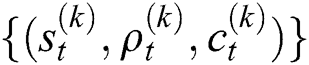 
, where 
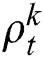is the weights for the k th sample at time t, and 
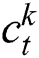indicates the cumulative weights for the 
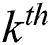sample at time t.
For k = 1:K
For j = 1:n
(1) Sample selection, generate a sample set as follows
i) Generate a random number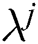 
∈ [0,1], uniformly distributed;
ii) Find, by binary subdivision, the smallest p for which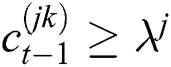 
;
iii) Set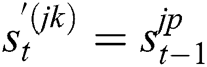 
.
(2) Prediction, obtain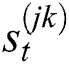 
with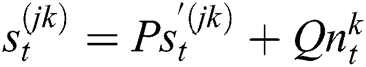 
.
(3) Weight measurement
i) Calculate the color histogram feature according to Eq. (8).
ii) Calculate the wavelet packet decomposition feature according to Eq. (9).
iii) Calculate the sample weight according to Eq. (10).
End
End
3. For each face, normalize the sample set so that weight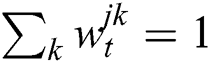 
, and update them 
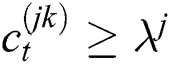as follows:
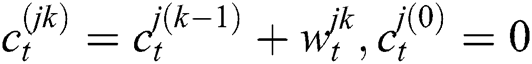
4. Estimate state parameters of the pointing gesture at time-step t:
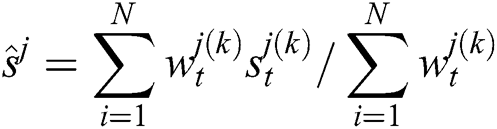
5. If updating criteria are satisfied, go to Step 1; otherwise, go to Step 2.
5 Multiple Faces Tracking in Occlusions
An occlusion usually exists in multiple faces tracking and, it could cause a failure in the tracking of multiple faces because two objects are of high similarity. In our study, an occlusion tracking method combined with a neural network algorithm is proposed.
Take two faces as an example, if no faces are occluded, there are very few relationships between the particles in different faces. The two faces can be tracked by using a traditional particle filter. When a facial occlusion occurs, the particles in different faces will be occluded, as shown in Fig. 5. The overlapped area will affect the tracking result, even causes tracking failure.
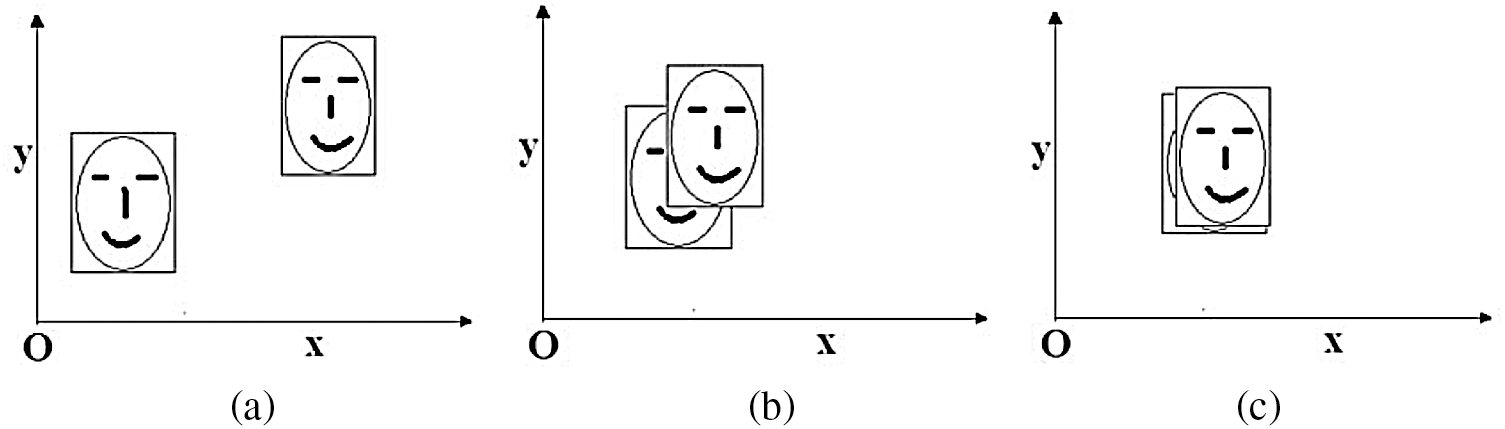
Figure 5: Illustration of face occlusion ((a) no occlusion, (b) a part occlusion, (c) complete occlusion)
(1) Occlusion detection
During initializing, the face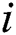 
is marked as a rectangular region 
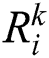, which is shown as in Fig. 1, where k is the frame, 
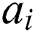is the area of 
.
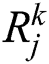The overlapped area between two faces in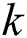 
th frame is defined as
If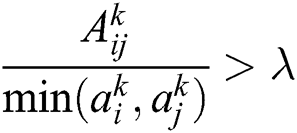 
, face-occlusion occurs, otherwise, there is no face-occlusion, where 
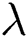is the threshold value.
(2) The spatial position of overlapped area judgment
After the face-occlusion detecting, the spatial position of these faces must be judged. We can define the likelihood between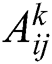 
and the detected face 
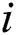area based on their color histogram.
If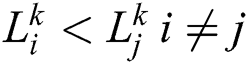 
, face 
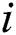is occluded in 
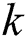th frame, otherwise face 
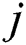is occluded in 
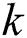th frame.
(3) Face tracking update
Define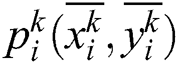 
as the center position of the rectangular region 
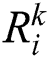, where k = 1, 2, 3…N. If face 
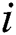is occluded in 
th frame, where m>24.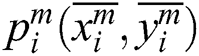 
is the center position of the rectangular region 
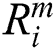. The BP neural network training processing can be shown as in Fig. 6.
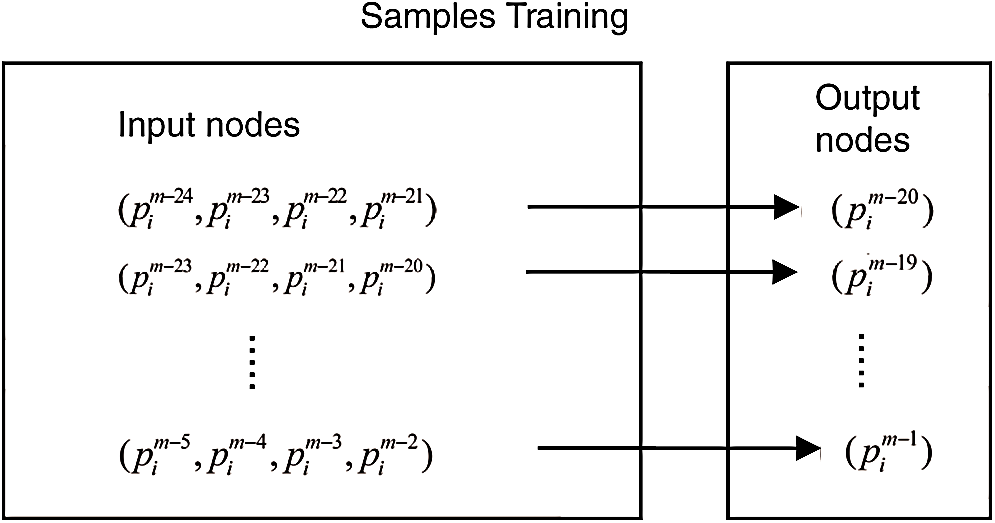
Figure 6: BP neural network training
Define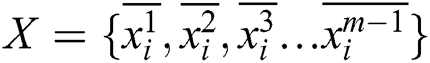 
, and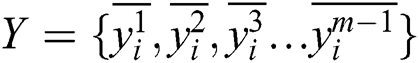 
, during the three-layer BP neural network, X, Y are chosen as samples to train BP neural network. For example, input cells are 
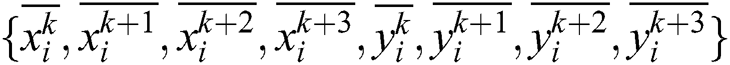, output cells are 
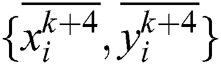, where 0 < k < m−4. The tracker position (
, 
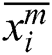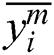) in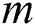 
th frame can be estimated by BP neural network.
Choosing input nodes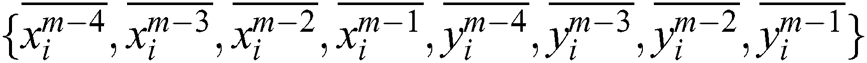 
, BP neural network can get output 
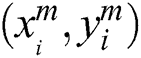, and the position of the target face is updated with 
.
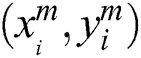We experimented using video data sets downloaded from [20]. The experiments were implemented on a Intel(R) Xeon(R) E31220 3.1 GHz CPU and 8192 MB RAM. The resolution of each frame was 720 × 480 pixels per image. During our research, we do not focus on face detection, since many existing methods can be used to detect faces [21,22]. Comparing with other methods, the method [22] performed well and provided excellent results achieving a higher detection rate, and it was used in our face detection.
We have carried out some experiments to track one face with our proposed method PFT_WPT_BP, and the particle filter number was 200. The color square showed the region of the tracked face. Fig. 7 showed the experimental results of one face tracking (even numbers in frame 1 to 13) based on different methods with Kalman Filter [12], Particle Filtering [10] and PFT_WPT_BP, where f is a label of the frame in the video. And Fig. 8 showed the tracking results of one face tracking in frame 19 to 31. We can find that satisfactory experimental results were achieved in three methods.
Figure 7: One face tracking base on different methods (line 1 is based on Kalman Filter [12], line 2 is based on particle filtering [10], line 3 is based on PFT_WPT_BP)
Figure 8: One face tracking base on different methods (line 1 is based on Kalman Filter, line 2 is based on particle filtering, line 3 is based on PFT_WPT_BP)
6.2 Multiple Faces Tracking Results
We have carried out some experiments to track multiple faces too, and the particle filter number was 200. The colored square shows the region of the tracked face. Fig. 9 shows theexperimental results of three faces tracked (frame 1 to 13) which provided satisfactory results.
Figure 9: Multiple faces tracking in no-occlusion based on PFT_WPT_BP
With face-occlusion (frame 20 to 37), we experimented using different tracking methods. The face of the first person (blue cloth) occluded the face of the second person (black cloth) in frame 20 to 33. And Fig. 10 showsfaces tracking with occlusion based on different methods. We found that the faces tracking failed for occluded faces based on Kalman Filter and Particle Filtering methods as indicated in Fig. 10 (line 1 and 2). But our method could achieve acceptable results in Fig. 10 (line 3).
Figure 10: Multiple faces tracking in occlusion based on different methods (line 1 is based on Kalman Filter, line 2 is based on particle filtering, line 3 is based on PFT_WPT_BP)
After several frames, the third person’s face (white cloth) occluded the second person’s face (black cloth) at the beginning of the frame. We detected the faces again, and found that the faces tracking failed in face-occlusion after frame 70. The results based on Kalman Filter and particle filtering is shown in Fig. 11 (lines 1 and 2). The occluded face was successfully tracked based on our method as shown in Fig. 11 (line 3). The system successfully recovered the faces from occlusion. After the occlusion, each face was normally re-sampled and the face appearances were updated again.
Figure 11: Multiple faces tracking in occlusion based on different methods (line 1 is based on Kalman Filter, line 2 is based on particle filtering, line 3 is based on PFT_WPT_BP)
This paper presents an occlusion robust tracking method for multiple faces. Experimental results have been shown that our PFT_WPT_BP method can handle the occlusion effectively and achieve better performance than several previous methods. BP neural network is used to predict the occasional faces. We assume that the occasional face would not miss a long time. If a face is missing for a long time, it is difficult to track it, and we can find the face by face detection. The faces tracking in a more complex environment will be researched in our future work.
Funding Statement: The Project Supported by Scientific Research Fund of Hunan Provincial Education Department (16C0223), the Project of “Double First-Class” Applied Characteristic Discipline in Hunan Province (Xiangjiaotong [2018] 469), the Project of Hunan Provincial Key Laboratory (2016TP1020).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Goenetxea, L. Unzueta, F. Dornaika and O. Otaegui. (2020). “Efficient deformable 3D face model tracking with limited hardware resources,” Multimedia Tools & Applications, vol. 79, no. 6, pp. 12373–12400. [Google Scholar]
2. M. Tian, Y. Bo and Z. Chen. (2019). “Multi-target tracking method based on improved firefly algorithm optimized particle filter,” Neurocomputing, vol. 359, no. 24, pp. 438–448. [Google Scholar]
3. G. S. Walia, A. Kumar, A. Sexena, K. Sharma and K. Singh. (2019). “Robust object tracking with crow search optimized multi-cue particle filter,” Pattern Analysis & Applications, vol. 3, no. 1, pp. 434–457. [Google Scholar]
4. K. Yang, J. Wang, Z. Shen, Z. Pan and W. Yu. (2019). “Application of particle filter algorithm based on gaussian clustering in dynamic target tracking,” Pattern Recognition and Image Analysis, vol. 29, no. 3, pp. 559–564. [Google Scholar]
5. P. B. Quang, C. Musso and F. L. Gland. (2016). “Particle filtering and the laplace method for target tracking,” IEEE Transactions on Aerospace and Electronic Systems, vol. 52, no. 1, pp. 350–366. [Google Scholar]
6. T. T. Yang, H. L. Feng, C. M. Yang, G. Guo and T. S. Li. (2018). “Online and offline scheduling schemes to maximize the weighted delivered video packets towards maritime CPSs,” Computer Systems Science and Engineering, vol. 33, no. 2, pp. 157–164. [Google Scholar]
7. Y. T. Chen, J. Wang, S. J. Liu, X. Chen, J. Xiong. (2019). et al., “Multiscale fast correlation filtering tracking algorithm based on a feature fusion model,” Concurrency and Computation: Practice and Experience, vol. 31, no. 10, pp. e5533. [Google Scholar]
8. X. Zhang, W. Lu, F. Li, X. Peng and R. Zhang. (2019). “Deep feature fusion model for sentence semantic matching,” Computers, Materials & Continua, vol. 61, no. 2, pp. 601–616. [Google Scholar]
9. Y. T. Chen, W. H. Xu, J. W. Zuo and K. Yang. (2019). “The fire recognition algorithm using dynamic feature fusion and IV-SVM classifier,” Cluster Computing, vol. 22, no. 3, pp. 7665–7675. [Google Scholar]
10. T. Wang, W. Wang, H. Liu and T. Li. (2019). “Research on a face real-time tracking algorithm based on particle filter multi-feature fusion,” Sensors, vol. 19, no. 5, pp. 1245. [Google Scholar]
11. Q. Wang, M. Kolb, G. O. Roberts and D. Steinsaltz. (2019). “Theoretical properties of quasi-stationary Monte Carlo methods,” Annals of Applied Probability, vol. 29, no. 1, pp. 434–457. [Google Scholar]
12. P. R. Gunjal, B. R. Gunjal, H. A. Shinde, S. M. Vanam and S. S. Aher. (2018). “Moving object tracking using kalman filter,” in International Conf. on Advances in Communication and Computing Technology, Sangamner, India, pp. 544–547. [Google Scholar]
13. W. Singh and R. Kapoor. (2018). “Online object tracking via novel adaptive multicue based particle filter framework for video surveillance,” International Journal of Artificial Intelligence Tools, vol. 27, no. 6, 1850023. [Google Scholar]
14. M. Long, F. Peng and H. Y. Li. (2018). “Separable reversible data hiding and encryption for HEVC video,” Journal of Real-Time Image Processing, vol. 14, no. 1, pp. 171–182. [Google Scholar]
15. S. Sonkusare, D. Ahmedt-Aristizabal, M. J. Aburn, V. T. Nguyen, T. Pang. (2019). et al., “Detecting changes in facial temperature induced by a sudden auditory stimulus based on deep learning-assisted face tracking,” Scientific Reports, vol. 9, no. 1, pp. 4729. [Google Scholar]
16. R. D. Kumar, B. N. Subudhi, V. Thangaraj and S. Chaudhury. (2019). “Walsh-Hadamard kernel based features in particle filter framework for underwater object tracking,” IEEE Transactions on Industrial Informatics, vol. 16, no. 9, pp. 5712–5722. [Google Scholar]
17. B. Eren, E. Egrioglu and U. Yolcu. (2020). “A hybrid algorithm based on artificial bat and backpropagation algorithms for multiplicative neuron model artificial neural networks,” Journal of Ambient Intelligence and Humanized Computing, vol. 2, no. 6, pp. 1593–1603. [Google Scholar]
18. K. Picos, V. H. Diaz-Ramirez, A. S. Montemayor, J. J. Pantrigo and V. Kober. (2018). “Three-dimensional pose tracking by image correlation and particle filtering,” Optical Engineering, vol. 57, no. 7, 073108. [Google Scholar]
19. Y. Song, G. B. Yang, H. T. Xie, D. Y. Zhang and X. M. Sun. (2017). “Residual domain dictionary learning for compressed sensing video recovery,” Multimedia Tools and Applications, vol. 76, no. 7, pp. 10083–10096. [Google Scholar]
20. J. Wang and Y. Yagi. (2008). “Integrating color and shape-texture features for adaptive real-time object tracking,” IEEE Transactions on Image Processing, vol. 17, no. 2, pp. 235–240. [Google Scholar]
21. H. H. Zhao, P. L. Rosin and Y. K. Lai. (2019). “Block compressive sensing for solder joint images with wavelet packet thresholdin,” IEEE Transactions on Components Packaging & Manufacturing Technology, vol. 9, no. 6, pp. 1190–1199. [Google Scholar]
22. J. Chen, D. Jiang and Y. Zhang. (2019). “A common spatial pattern and wavelet packet decomposition combined method for EEG-based emotion recognition,” Journal of Advanced Computational Intelligence and Intelligent Informatics, vol. 23, no. 2, pp. 274–281. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |