 Open Access
Open Access
ARTICLE
Multi-Objective Optimization of Swirling Impinging Air Jets with Genetic Algorithm and Weighted Sum Method
1 Future Urban and Energy Lab for Sustainability (FUEL-S), Faculty of Sustainable Design Engineering (FSDE), University of Prince Edward Island, Charlottetown, PE C1A4P3, Canada
2 Department of Mechanical Engineering, Khulna University of Engineering & Technology (KUET), Khulna, 9203, Bangladesh
3 School of Engineering, Newcastle University, Newcastle Upon Tyne, NE17RU, UK
4 Dyson Institute of Engineering and Technology, Tetbury Hill, Malmesbury, SN160RP, UK
5 Department of Mechanical and System Engineering, Okayama University, Okayama, 7008530, Japan
6 Faculty of Sustainable Design Engineering (FSDE), University of Prince Edward Island, Charlottetown, PE C1A4P3, Canada
* Corresponding Author: Muhammad Ikhlaq. Email:
Frontiers in Heat and Mass Transfer 2025, 23(1), 71-94. https://doi.org/10.32604/fhmt.2024.059734
Received 15 October 2024; Accepted 09 December 2024; Issue published 26 February 2025
Abstract
Impinging jet arrays are extensively used in numerous industrial operations, including the cooling of electronics, turbine blades, and other high-heat flux systems because of their superior heat transfer capabilities. Optimizing the design and operating parameters of such systems is essential to enhance cooling efficiency and achieve uniform pressure distribution, which can lead to improved system performance and energy savings. This paper presents two multi-objective optimization methodologies for a turbulent air jet impingement cooling system. The governing equations are resolved employing the commercial computational fluid dynamics (CFD) software ANSYS Fluent v17. The study focuses on four controlling parameters: Reynolds number (Re), swirl number (S), jet-to-jet separation distance (Z/D), and impingement height (H/D). The effects of these parameters on heat transfer and impingement pressure distribution are investigated. Non-dominated Sorting Genetic Algorithm (NSGA-II) and Weighted Sum Method (WSM) are employed to optimize the controlling parameters for maximum cooling performance. The aim is to identify optimal design parameters and system configurations that enhance heat transfer efficiency while achieving a uniform impingement pressure distribution. These findings have practical implications for applications requiring efficient cooling. The optimized design achieved a 12.28% increase in convective heat transfer efficiency with a local Nusselt number of 113.05 compared to 100.69 in the reference design. Enhanced convective cooling and heat flux were observed in the optimized configuration, particularly in areas of direct jet impingement. Additionally, the optimized design maintained lower wall temperatures, demonstrating more effective thermal dissipation.Graphic Abstract
Keywords
Nomenclature
| Cp | Pressure Coefficient (non-dimensional) (2(p − p∞)/ρUb2) |
| D | Nozzle diameter (40 mm) |
| Cf | Skin Friction Coefficient (non-dimensional) |
| H | Nozzle to impinging plate spacing (mm) |
| Z | Distance separating adjacent jets (mm) |
| k | Fluid’s thermal conductivity (W/(m.K)) |
| Nu | Nusselt number (non-dimensional) (hD/k) |
| Re | Reynolds number (non-dimensional) (UbD/ν) |
| S | Swirl number (non-dimensional) (Wb/Ub) |
| ¯Nu | Area averaged Nusselt number |
| ¯Cp | Area averaged wall pressure coefficient |
| Abbreviation | |
| ANN | Artificial Neural Network |
| CFD | Computational Fluid Dynamics |
| GA | Genetic Algorithm |
| MRA | Multivariate Regression Analysis |
| NSGA-II | Non-dominated Sorting Genetic Algorithm |
| PRESTO | PREssure STaggering Option |
| RBNN | Radial Basis Neural Network |
| RSM | Response Surface Methodology |
| WSM | Weighted Sum Method |
| ANN | Artificial Neural Network |
Jet impingements have a significant impact on various industrial approaches, providing numerous benefits that make them incredibly valuable. One notable advantage is its capability to enhance heat transfer and cooling rate. By directing a forceful fluid jet onto a solid surface, impinging jets increase the surface area and encourage turbulent flow, leading to enhanced heat transfer rates. Additionally, it can be precisely controlled for targeted cooling or heating in specific areas, which is crucial in processes demanding high precision and efficiency. Through adjustments of parameters like jet velocity, temperature, and nozzle spacing, customization can be achieved for specific industrial requirements, further enhancing operational flexibility.
The ability to achieve rapid, uniform cooling and precise thermal control finds application in aerospace, electronics, power generation, and several manufacturing processes [1–5]. In the past several generations, a variety of theoretical, experimental and computational researches have been carried out to investigate turbulent impinging jets, which were aimed to understand and analyze the mysterious characteristics and behaviors of turbulent flow in jet impingements [6–10]. Numerous studies have extensively examined and documented the flow dynamics and heat and mass transfer properties of both single and multiple impinging jet configurations. Martin provided a comprehensive survey on the heating and cooling of large surface area products using slot nozzle arrays, along with empirical equations for estimating heat and mass transfer coefficients [11]. Baughn et al. focused on the heat transfer characteristics of a single turbulent air jet impinging on a flat surface [12]. They addressed the lack of data on jet characteristics and mixed thermal boundary conditions by providing new experimental results. Hrycak examined heat transfer from round jets striking flat plates, considering various distances, Reynolds numbers, and nozzle diameters while the study primarily concentrated on the experimental data at the stagnation point [13]. Lytle et al. examined the local heat transfer properties of air jet impingement at minimal nozzle-to-plate spacing [14]. They found that decreased spacing resulted in enhanced heat transfer because of accelerated fluid flow and increased turbulence coupled with the stagnation point minimum, and the outer and inner heat transfer peaks. Viskanta studied the heat transfer properties of single and multiple isothermal turbulent air and flame jets impinging on surfaces with a focus on applications in materials processing, considering circular and slot two-dimensional jets along with the impact of crossflow [15]. Key points include similarities in stagnation point heat transfer despite jet differences and the identification of areas needing additional research. Additionally, Huber et al. examined the influence of spent air exits located between air jets on the local heat transfer coefficient in a confined square array [16]. Their findings revealed that incorporating spent air exits enhanced the convective heat transfer coefficient and altered the optimal jet separation distance.
In a study conducted by Aldabbagh Sezai, they numerically examined the flow field and thermal characteristics of laminar multiple impinging square jets [17]. Their findings indicated that the jet-to-plate distance had a profound effect on these characteristics. However, the jet-to-jet spacing did not affect the value of the local peak Nusselt number at the stagnation zone. Andreini et al. conducted a study to assess the heat transfer coefficient and thermal performance of an engine-like active control clearance (ACC) system, investigating the impact of under-cowl flow field on jet impingements using experimental tests and numerical calculations [18]. Caliskan et al. tested how the shape of jets (elliptic and rectangular) affects the fluid flow and thermal characteristics [19]. Through a integration of experiments and numerical simulations, they observed that the elliptic jets outperformed circular jets, demonstrating higher Nusselt numbers and superior heat transfer performance. Gharraei et al. conducted a numerical investigation into laminar flow and heat transfer characteristics of power-law non-Newtonian fluids from multiple impinging square jets [20]. Their findings revealed that increasing the index of power-law resulted in increased impingement velocity and enhanced wall Nusselt number while reducing the jet-to-surface spacing eliminated circumferential entrainment vortices and increased wall Nusselt number. Draksler et al. employed Large Eddy Simulation (LES) to investigate the behaviors of flow dynamics and thermal dissipation of multiple impinging jets [21]. By comparing the LES results with experimental data, they examined the transient flow field and identified the frameworks that contribute to enhanced heat transfer, namely convective cooling and intense quasi-periodic heat dissipation arising from large-scale vortical structures. Kilic et al. carried out a numerical investigation of heat enhancement and fluid flow behavior using nanofluids in three impinging jets, exploring various volume fractions, heat fluxes, and nanofluid types [22]. Increasing the volume ratio led to a 10.4% average increase in Nusselt number while heat flux had no significant effect. Besides the Cu-water nanofluid resulted in improved Nusselt numbers compared to other nanofluids.
The optimization of impinging jets is a significant area of study focused on improving their performance in specific applications. It includes single-objective optimization, adjusting parameters like velocity and geometry, and multi-objective optimization to balance conflicting objectives. Through these optimization efforts, researchers achieve improved efficiency, enhanced heat transfer, and better mixing. Brignoni and Garimella optimized impact of air jets on a pin-fin heat sink, testing different nozzle configurations [23]. Results showed modest effects on heat transfer with enhancement factors ranging from 2.8 to 9.7, aiding in configuration optimization. Brevet et al. researched impinging jet heat transfer using the heated-thin-foil technique [24]. The study identified an optimal impingement distance and design rules for minimizing cooling air usage. Chiang used response surface methodology (RSM) to study thermal performance of a parallel-plain fin (PPF) heat sink combined with an axial-flow cooling fan [25]. The optimal design parameters found were a 60 mm fin height, 1.07 mm fin thickness, a passage width of 3.32 mm between fins, and a gap of 2.03 mm between the cooling fan and the fin tip. Heo et al. conducted optimization and a parametric approach using RBNN model (Radial Basis Neural Network) of a single nozzle impinging jet with cross flow resulting in a 7.89% increase in the Nusselt number by optimizing the inclination angle of the jet nozzle [26]. Badra et al. utilized computational fluid dynamics (CFD) for simulating and optimizing single and multiple circular jets while the optimization focused on the jets impingement on a moving plate, considering the parameters Z/D and H/D [27]. Husain et al. conducted an optimization study on a silicon-based micro-jet impingement heat sink for electronic cooling, utilizing 3D numerical analysis, surrogate modeling, and a multi-objective evolutionary algorithm [28]. This process yielded a global Pareto-optimal front for overall thermal resistance and pumping power, highlighting a correlation between these two parameters. Chauhan et al. applied the preference selection index (PSI) method to optimize the design of solar thermal collectors with impinging air jets [29]. Their research identified an optimal configuration with a streamwise pitch ratio of 0.435, a spanwise pitch ratio of 0.869, a jet diameter ratio of 0.065, and a Reynolds number of 16,000. Furthermore, Chauhan et al. implemented Taguchi-based DOE approach and achieved optimal design combination with a performance improvement around 37%–48.3%, within Reynolds number of 4000–16,000 [30].
In recent years, genetic algorithm (GA) has become increasingly popular among researchers as an effective optimization technique for impinging jet systems [31–34]. Eghtesad et al. utilized artificial neural network (ANN) and GA to optimize twin turbulent sweeping impinging jets for achieving uniform cooling across a flat surface [35]. The research successfully obtained a evenly distributed Nusselt number on the target plate with an accuracy exceeding 98%. Mahmoudabadbozchelou et al. applied ANN with GA to optimize heat transfer phenomena in jet impingement with nanofluids [36]. The study focused on nanoparticle chemistry, size, and volume ratio in water to attain uniform cooling on a heated plate. Results demonstrated that increasing nanoparticle size and concentration enhanced heat transfer and improved Nusselt distribution. Singh et al. examined thermal effects in slot jet impinging on a concave plane with protrusions [37]. They used numerical simulations and ANN to determine optimal protrusion locations for maximum heat transfer. Multiple protrusions in the best configuration resulted in an 8% enhancement in heat transfer relative to a smooth surface.
While GA is commonly used for multi-objective optimization problems, some researchers prefer alternative methods like the Weighted Sum Method (WSM). GAs have a stochastic nature, leading to different solutions in different runs due to randomness. This variability makes reproducing results and comparing runs challenging. In contrast, the WSM involves assigning weights to objectives and aggregating them into a single objective function. It offers a deterministic approach, producing a single solution without the need for multiple runs. While there are numerous implementations of GA documented in literature for jet impingement problems, it appears that the usage of the WSM for this specific domain is not commonly found among researchers. As such, the current research has employed both NSGA-II (Non-dominated Sorting Genetic Algorithm) and Weighted Sum Method (WSM) to effectively perform multi-objective optimization on two different nozzle arrangements of turbulent swirling air jets impinging on a flat surface. Before implementing the optimizations, numerical analyses were carried out to examine the flow and heat transfer behavior of the multi-jet impingement system. The jet impingement system comprises aerodynamic swirl nozzles with multiple arrangements and spacing, which are operated under various geometric and flow conditions.
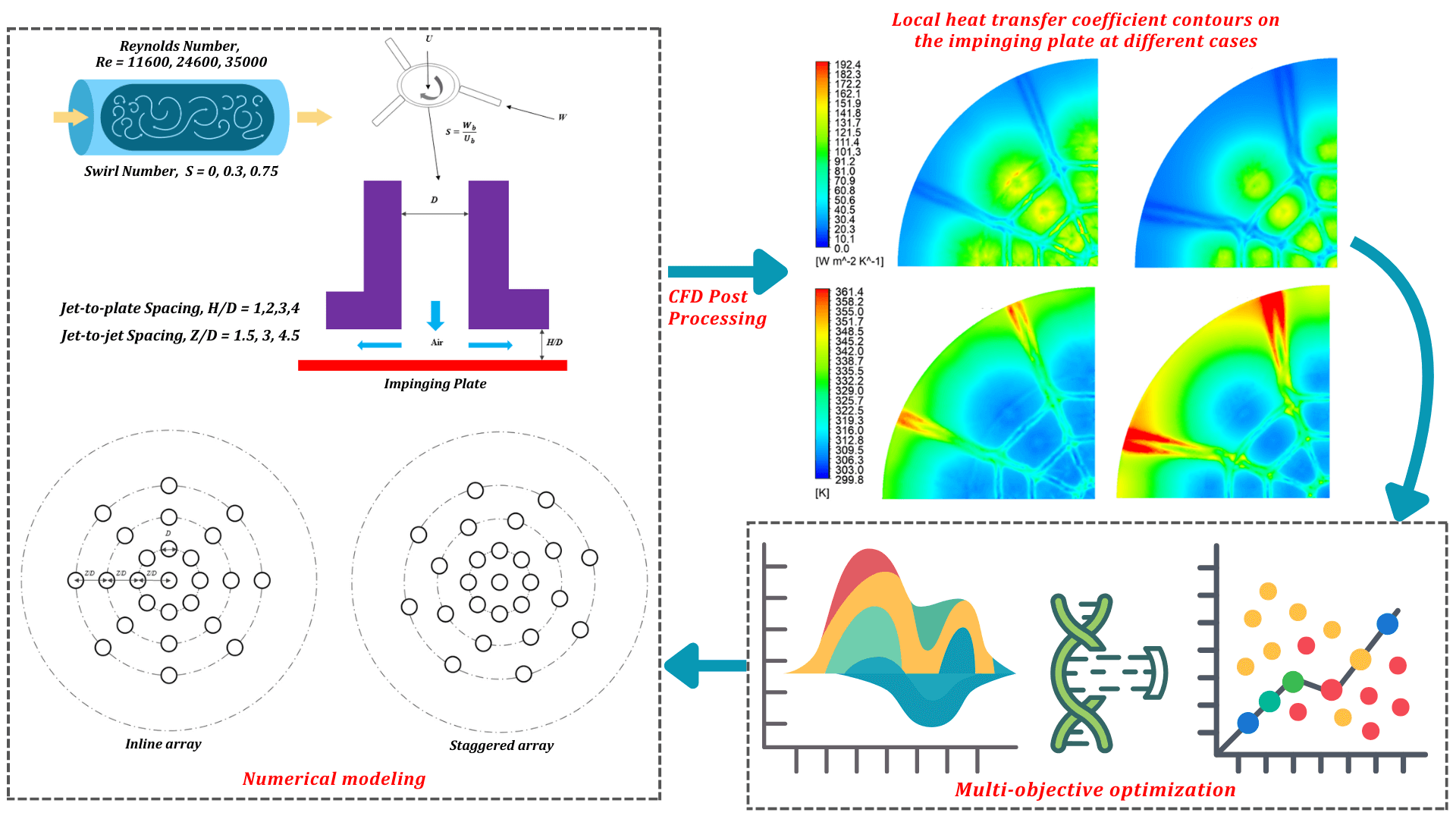
This study examines a physical system involving 25 turbulent swirling air jets interacting with a planar surface as presented in Fig. 1. The jets are emitted from a swirl nozzle that allows for a smooth transition between no swirl and high swirl flow. All jets are organized in two different configurations: inline and staggered, forming three circles around a central nozzle. Each circular nozzle has a diameter (D) of 40 mm. Multiple parameters such as impingement distances from nozzle to plate (H/D = 1, 2, 3, 4), Reynolds numbers of the flow (Re = 11,600, 24,600, 35,000), multiple swirl numbers (S = 0, 0.3, 0.75) and the gaps in between adjacent nozzles (Z/D = 1.5, 3, 4.5) are varied to analyze the flow field and thermal characteristics.
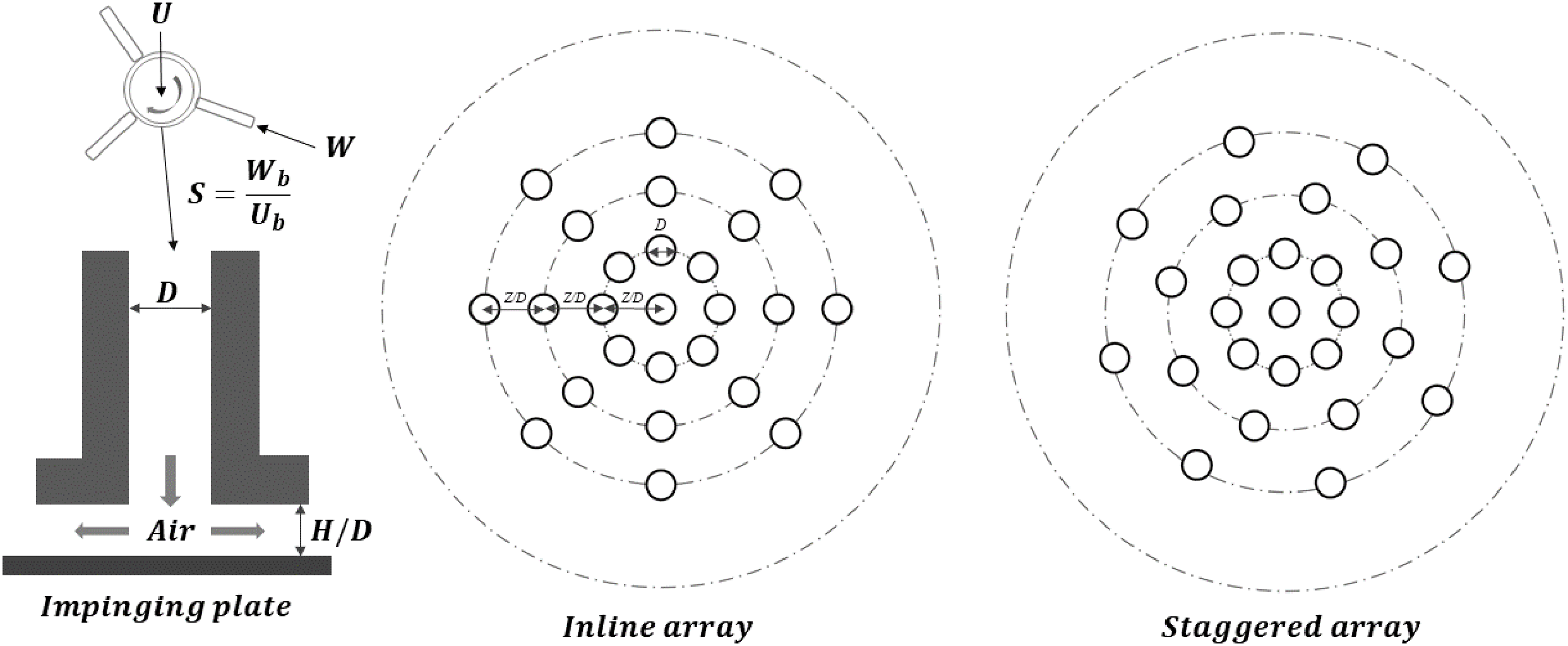
Figure 1: Physical arrangement of the jet impingement cooling system along with different design variables for the multi-objective optimization approaches
To optimize computational efficiency, only a quarter of the system is considered due to its symmetrical nature. The equations defining mass, momentum, and energy conservation in the context of fluid flow and convective heat transfer can be expressed as follows:
∂ρ∂t+∂(ρui)∂xi=0(1)
∂(ρui)∂t+∂(ρuiuj)∂xj=−∂p∂xj+∂∂xj[μ(∂ui∂xj+∂uj∂xi−23δij∂uk∂xk)]+∂(−ρ―u′iu′j)∂xj(2)
∂(ρE)∂t+∇.[→v(ρE+p)]=∇.[keff∇T−∑jhjJj+(ˉˉτeff)]+Sh(3)
These governing equations are solved using the commercial software package ANSYS Fluent v17. Velocity inlet boundary conditions, obtained from the literature [38], are applied at the nozzle exit plane. The mean velocity and turbulence data for both non-swirling and swirling cases, as reported by Ahmed et al. [39], are shown in Fig. A1 for reference. The mean and turbulence profiles, defined by k and ω, are implemented in Fluent through a User Defined Function (UDF), with local cylindrical coordinates assigned at the nozzle face for easier application. No-slip boundary conditions and a steady wall heat flux of 1000 W/m2 are applied at the impinging plate, while atmospheric pressure (101.3325 kPa) is maintained at the inlet and outlet boundaries. A pressure inlet condition is imposed on the upper part of the computational domain, excluding the nozzle areas, while a pressure outlet condition is set for the outlet boundary. Symmetry and periodic boundary conditions are applied to the sides of the domain for the non-swirling and swirling cases, respectively. The pressure-velocity coupling is handled using the coupled solver. Gradient discretization follows the Green-Gauss node-based method, while pressure discretization employs the PREssure STaggering Option (PRESTO) scheme. Convective terms are discretized using second-order schemes, and diffusion terms are resolved with a second-order accurate method. The computational domain is meshed with an unstructured tetrahedral grid, featuring 15 inflation layers with a growth rate of 1.2 near the impingement surface to capture flow and thermal behavior effectively. A coarser mesh is used at the outer and upper edges of the domain to accommodate relatively uniform flow conditions. A grid independence study was conducted with node counts of 391, 488, 611, 818, and 1168 k. As shown in Fig. 2, the average Nusselt number and skin friction coefficient at the center of the surface exhibit deviations of less than 1% for node counts exceeding 600 k. Consequently, a mesh with 818 k nodes was chosen to balance numerical accuracy and computational efficiency. The mesh design ensures y+ values remain below one across the solution domain for both inline and staggered nozzle arrangements, enabling accurate resolution of near-wall characteristics. Further details can be found in the referenced studies [40,41] and are not repeated here for brevity.
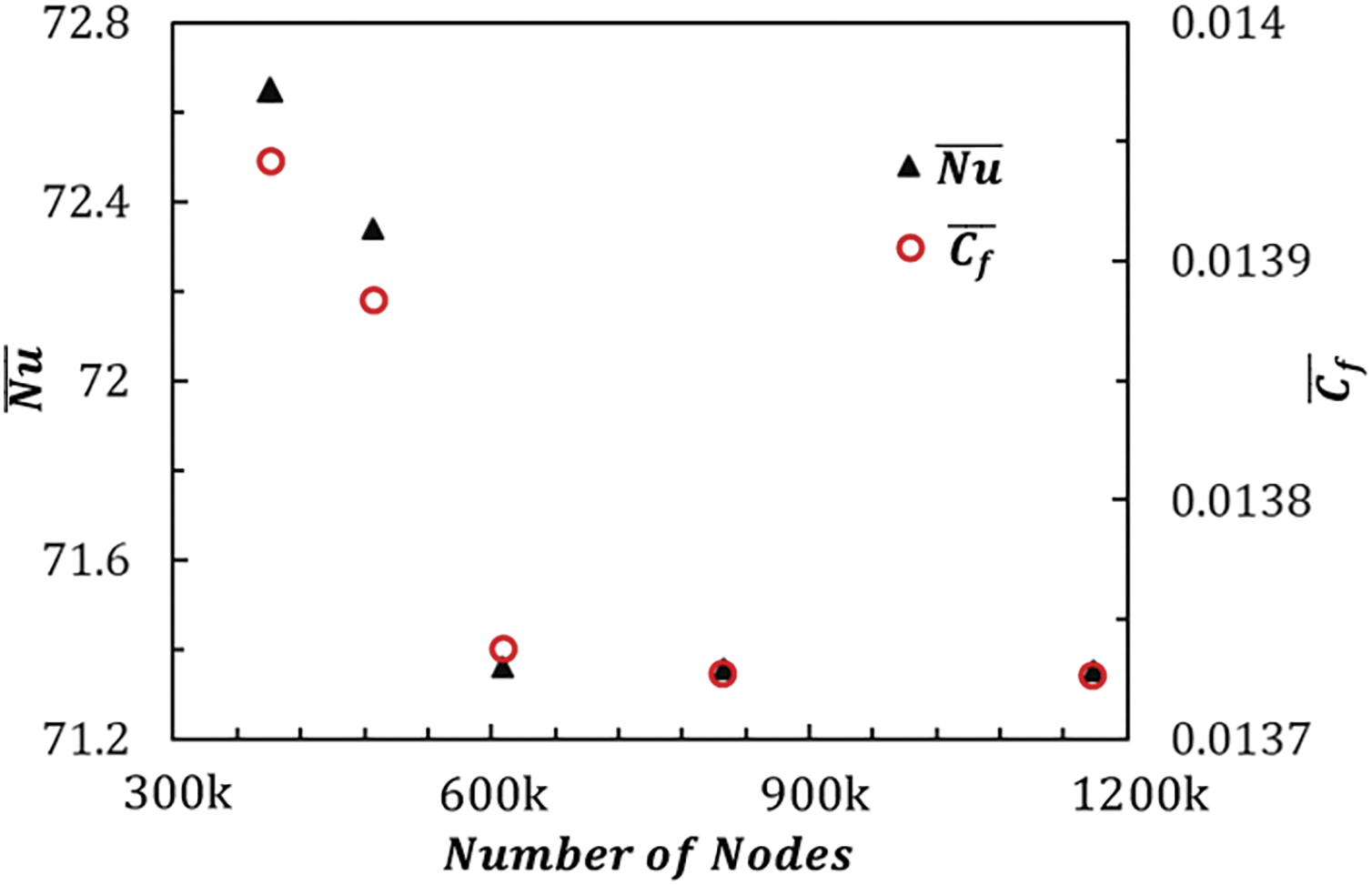
Figure 2: Effect of number of nodes on mean Nusselt number and skin friction coefficient
Accurate prediction of flow parameters in turbulent jet impingement relies on selection of appropriate turbulence model. To ensure reliability, several model validations were performed. Fig. 3 represents numerical predictions for both axial velocity profiles and skin friction coefficient, comparing multiple turbulence modeling with experimental data. In Fig. 3a, the radial variation of normalized axial velocity (u/Ub, while Ub = 9.32 m/s) at x/D = 0.025 is shown for non-swirling (S = 0) jet at a Reynolds number of 24,600, using the SST k–ω, transition SST, and realizable k–ε models against experimental data derived from previous studies [38,42–44]. The predicted outcomes from numerical models align well with the experimental measurements, with minor discrepancies in the velocity profiles, likely due to variations in nozzle diameters, inlet boundary conditions, and impingement distances. Among the tested three turbulence models, SST k–ω shows the closest agreement with experimental results.
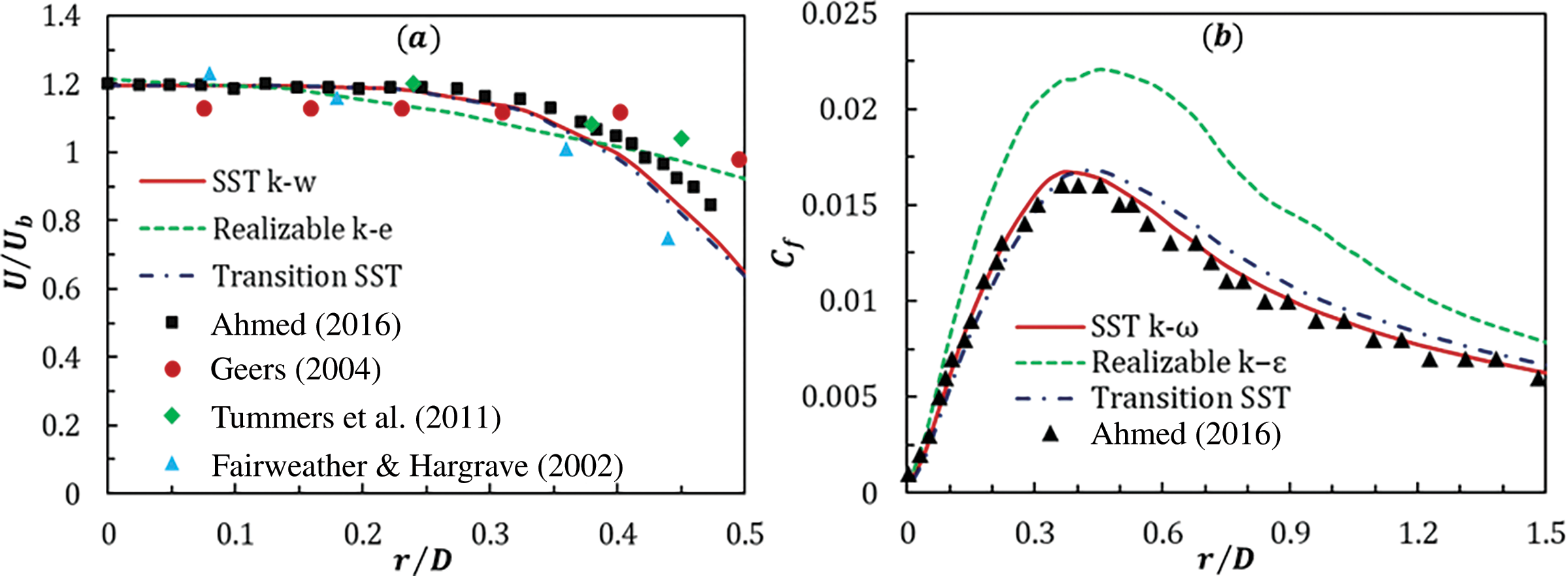
Figure 3: (a) Comparisons of u/Ub profiles at x/D = 0.025 for a single nozzle non-swirl (S = 0) jet at Re = 24,600, using various turbulence models; (b) radial distribution of skin friction coefficient (Cf) for a single nozzle medium swirl (S = 0.3) jet at Re = 35,000 and H = 1D, comparing multiple turbulence models with corresponding experimental data [38, 42–44]
In Fig. 3b, the coefficient of skin friction (Cf) along the radial line of the impinging plate in the horizontal direction is presented for a single nozzle medium swirl (S = 0.3) jet at Re = 35,000 and H = 1D. The SST k−ω model closely matches the past experimental data, while Transition SST accurately estimates the Cf near the impinging zone but overestimates it in downstream locations. In contrast, the Realizable k−ε model consistently overpredicts the skin friction coefficient across the entire domain. Therefore, the SST k–ω model was chosen for the study for its superior accuracy in matching experimental results. The SST k−ω is a hybrid turbulence model formed by Menter [45] that combines aspects of k−ω and k−ε models depending on the proximity to the closest wall.
Original k−ω model equations:
∂(ρk)∂t+∂(ρujk)∂xj=τij∂ui∂xj−β∗ρωk+∂∂xj[(μ+σk1μt)∂k∂xj](4)
∂(ρω)∂t+∂(ρujω)∂xj=γ1νtτij∂ui∂xj−β1ρω2+∂∂xj[(μ+σω1μt)∂ω∂xj](5)
Transformed k−ε model equations:
∂(ρk)∂t+∂(ρujk)∂xj=τij∂ui∂xj−β∗ρωk+∂∂xj[(μ+σk2μt)∂k∂xj](6)
∂(ρω)∂t+∂(ρujω)∂xj=γ2νtτij∂ui∂xj−β2ρω2+∂∂xj[(μ+σω2μt)∂ω∂xj]+2ρσω2ω∂k∂xj∂ω∂xj(7)
The governing and turbulence transport equations (Eqs. (1)–(7)) are solved until the convergence criteria are met. Convergence is considered achieved when the residuals of all variables decrease by a least of 10−5.
Fig. 4 illustrates the coupled effects of swirl, impingement distances, jet-to-jet separations and Reynolds number on area averaged Nusselt number ¯Nu variations for both nozzle arrangements at the impingement plate. It is obvious that, ¯Nu increases proportionately as of Re for all cases. As the Reynolds number increases, the flow sustains a transition from laminar to turbulent, resulting in enhanced fluid mixing and improved heat transfer. This increased momentum and turbulence promote more efficient convective heat transfer near the heated surface, which subsequently increase the average Nusselt number. Overall, for non-swirl and medium swirl flows, maximum heat transfer is achieved for Z/D = 3, which could be because of the balanced combination of fluid mixing and effective impingement and they allow for optimal heat transfer closer to the impinging surface. However, for the maximum impinging distance and medium swirl flow at Z/D = 4.5, longer residence time and enhanced fluid mixing contribute to achieving maximum heat transfer despite the increased distance between jets. For the maximum swirl number, heat transfer generally decreases except the lowest impingement distance. This decline in heat transfer can be attributed to excessive flow disruption and reduced impingement effectiveness resulting from the intense swirling motion. However, at the lowest impingement distance, enhanced fluid mixing and turbulence associated with the high swirl may still lead to improved heat transfer despite the overall decrease observed at other distances. Among all studied cases, the maximum magnitudes of ¯Nu is obtained at H/D = 1 and Z/D = 3 for Re = 35,000 while nozzles are arranged in staggered array.

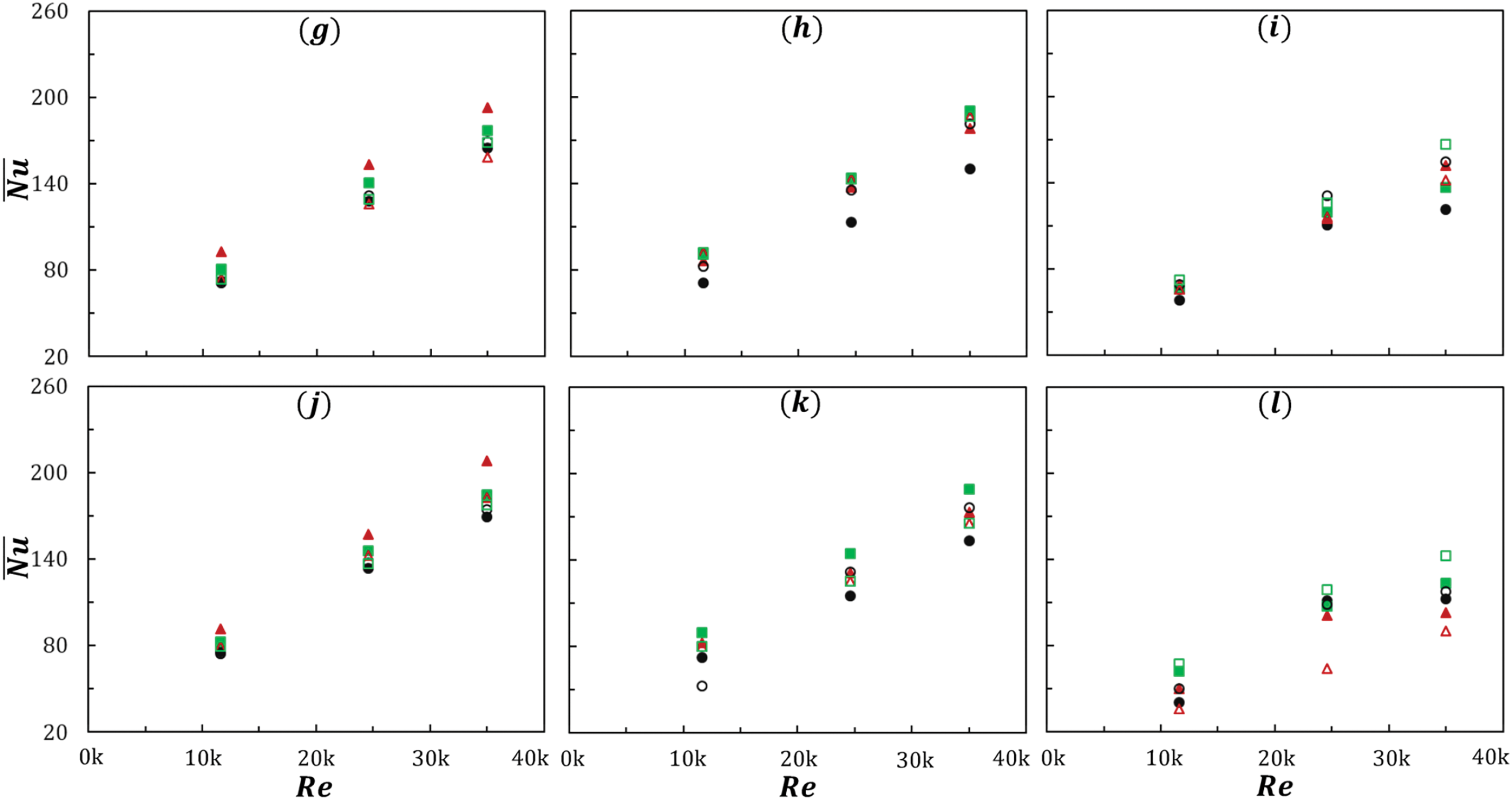
Figure 4: Area averaged Nusselt number ¯(Nu) against Re for different jet-to-jet separations at: (a–c) H/D = 1; (d–f) H/D = 2; (g–i) H/D = 3; and (j, k, l) H/D = 4 at: (a, d, g, j) S = 0; (b, e, h, k) S = 0.3; and (c, f, i, l) S = 0.75
3.2 Impinging Pressure Analysis
Fig. 5 demonstrates the influence of swirl, impingement distances, jet-to-jet separations and Reynolds number on area averaged wall pressure coefficient (¯Cp) variations for both nozzle arrangements. It is obvious that there is a general trend of reducing ¯Cp with the increase of Re. As the Reynolds number expands, the flow develops into more turbulent and energetic, resulting in increased fluid momentum. This higher momentum leads to more efficient mixing and reduced pressure gradients along the wall. Overall, the lowest jet-to-jet separation provides higher ¯Cp and the maximum one is obtained at H/D = 1 while Re = 11,600 and jets are organized at inline array. The lower Z/D leads to more intense interactions and collisions between the jets that cause increased momentum transfer and pressure buildup on the wall surface. Moreover, ¯Cp increases significantly for the influence of swirl intensity rather than non-swirl as the swirling motion enhances fluid mixing, leading to better momentum transfer near the wall and increased pressure fluctuations. In addition, the presence of a swirl generates vortical structures and secondary flow patterns, intensifying the pressure gradients along the wall. However, the variations in impinging distance do not have a pivotal role on the pressure circulation along the wall.
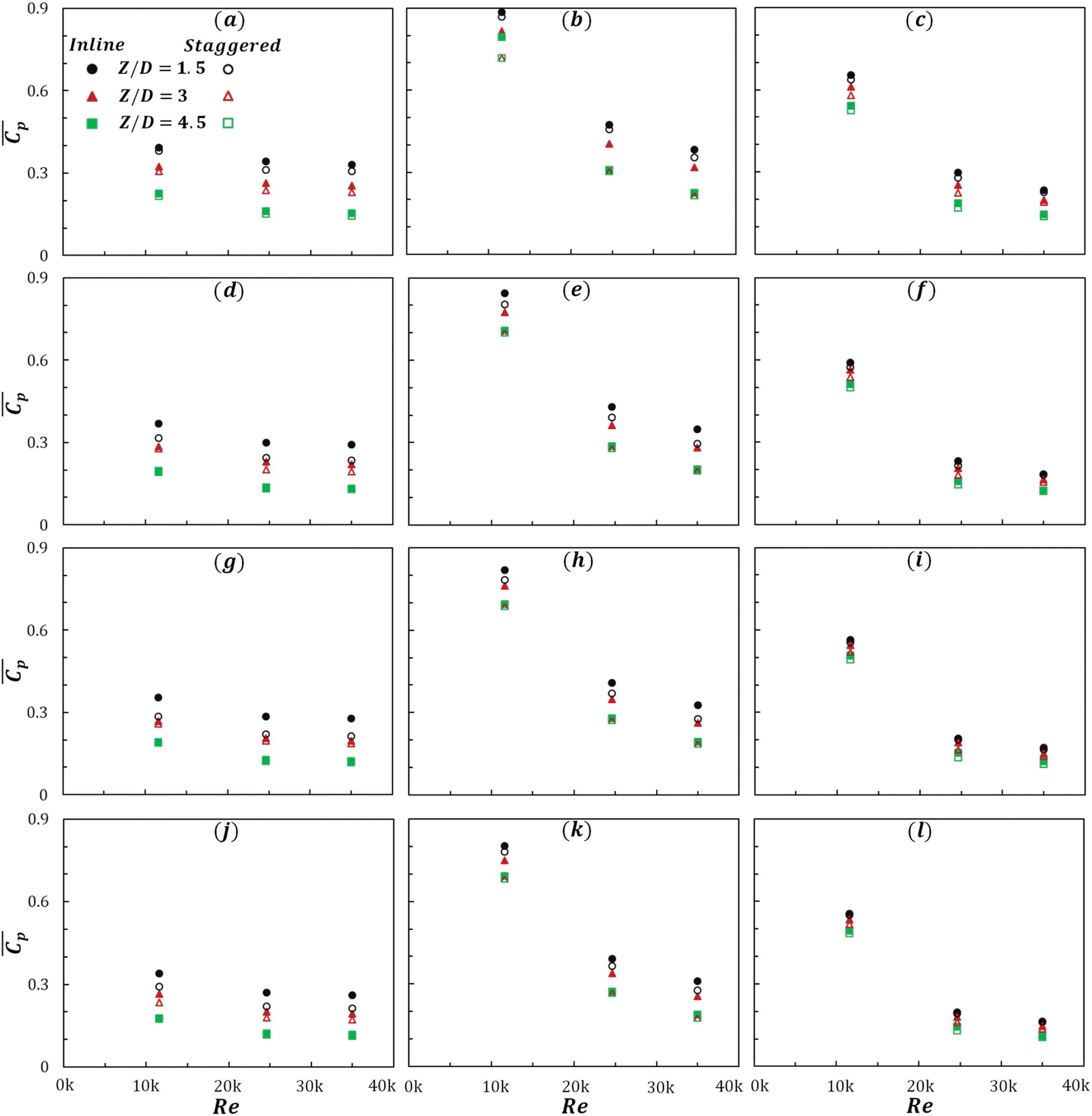
Figure 5: Area averaged pressure coefficient (¯Cp) against Re for different jet-to-jet separations at: (a–c) H/D = 1; (d–f) H/D = 2; (g–i) H/D = 3; and (j, k, l) H/D = 4 at: (a, d, g, j) S = 0; (b, e, h, k) S = 0.3; and (c, f, i, l) S = 0.75
Multiple impinging jet configurations are more intricate than single-jet geometries because of the interactions occurring between the jets. In this study, four key design variables are examined: Reynolds number (Re), Swirl number (S), the perpendicular height between the jet exit plane and impinging surface (H/D) and the spacing between the jets (Z/D) while all geometrical parameters are normalized by the jet diameter. The upper and lower bounds considered for the design variables are given in Table 1.
Since the aim of this study is to maximize the cooling efficiency, the optimization of the design variables needs to perform in such a way that enhance heat transfer distribution on the impinging plate. Therefore, to acquire the optimal designs for multiple turbulent air jet impingement system, ¯Nu and ¯Cp are chosen as the objective functions so that cooling is maximized at maximum ¯Nu and ¯Cp generations. The objective of maximizing the average Nusselt number is to achieve higher heat transfer rates on the impinging plate, resulting in better cooling performance and improved thermal management. Similarly, maximizing the average pressure coefficient aims to optimize the pressure distribution, enhancing fluid flow and heat transfer properties. This helps to control flow patterns, pressure gradients and boundary layer behavior, ultimately leading to improved cooling efficiency. To define the objective functions, multivariate regression analysis is used to derive surrogate models based on data generated from CFD simulations [40,41]. The simulations produced values for both heat transfer (Nusselt number, ¯Nu) and pressure distribution (pressure coefficient, ¯CP) across varied parameters, including Reynolds number (Re), swirl number (S), jet-to-jet spacing (Z/D), and impingement height (H/D). IBM SPSS software was employed to derive both linear and nonlinear regression models that captured the relationship between these parameters and the performance metrics. The regression analysis began with a linear model to establish baseline trends, followed by the inclusion of nonlinear terms to better capture complex interactions. The resulting models for ¯Nu and ¯CP were then evaluated based on statistical metrics; the coefficient of determination (R²) to ensure accuracy and predictive reliability. Both linear and nonlinear correlations can be expressed as follows:
¯Nu=0.004(Re)−10.058(HD)+4.167(ZD)−1.068(S)+48.407(8)
¯Cp=−1.409×10−5(Re)−0.02(HD)−0.037(ZD)+0.06(S)+0.803(9)
¯Nu=0.145(Re)0.683(HD)−0.264(ZD)0.118(S)−0.051(10)
¯Cp=12840.5(Re)−1.066(HD)−0.097(ZD)−0.176(S)−0.424(11)
Fig. 6 presents Pearson’s correlation coefficient map for the selected variables. Pearson correlation coefficient is one of the most effective methods to show the dependency of one variable on the base of a number ranging from −1 to +1 [46]. Fig. 6a and b shows Pearson’s correlation coefficients for in-line arrangement and staggered arrangement of nozzles, respectively. The Nusselt number has a high dependency on the Reynolds number, which is quite understandable as the Reynolds number provides more mass flux provided the geometric and fluid properties are fixed. The impinging distance has a negative impact on the average Nusselt number as the impingement distance increases the overall mixing of surrounding air increases and also the imparting momentum on the target surface also decreases. Swirl intensity has a negative impact on heat transfer for in-line arrangements while for staggered arrangement it shows positive influence.
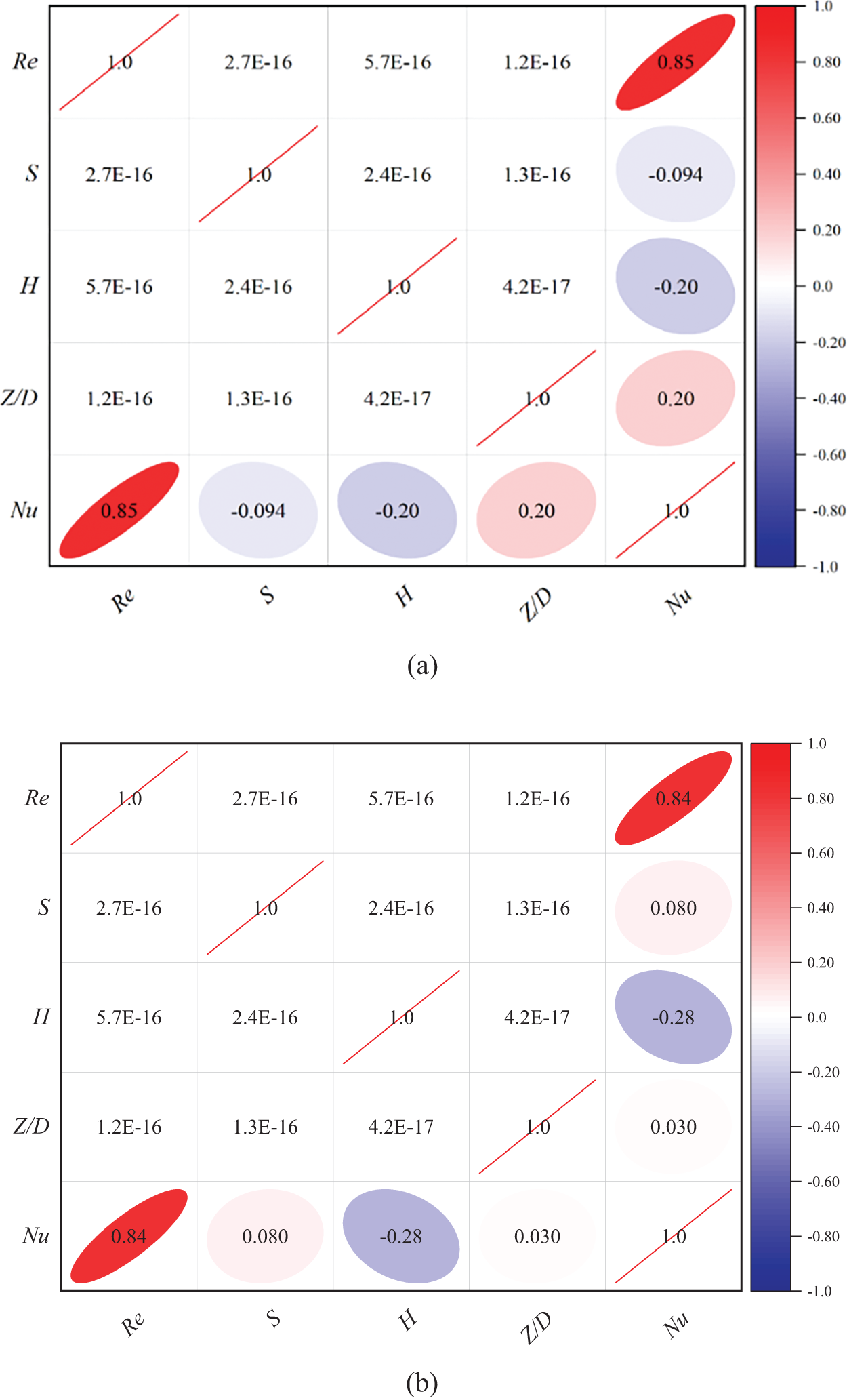
Figure 6: The Pearson’s correlation coefficients for input dimensionless groups and average Nusselt number for (a) in-line arrangement of nozzles and (b) staggered arrangement of nozzles
The nozzle spacing shows significant impact for in-line nozzle arrangement compared to the staggered nozzle arrangement. Figs. 7 and 8 portray the comparison between the numerical value and the correlated data with ±10% error bands. It appears that for Eqs. (10) and (11), the majority of the values fall within these error bands. The R2 values for Eqs. (8)–(11) are 0.786, 0.535, 0.848 and 0.975 respectively that demonstrate that the generated surrogate models hold adequately significance at 78%, 53%, 84% and 97% confidence limits, respectively. As such, Eqs. (10) and (11) are chosen for current optimization approaches. NSGA-II (Non-dominated Sorting Genetic Algorithm) and Weighted Sum Method (WSM) are used to optimize objective functions and find the optimal configuration for the impingement cooling system.
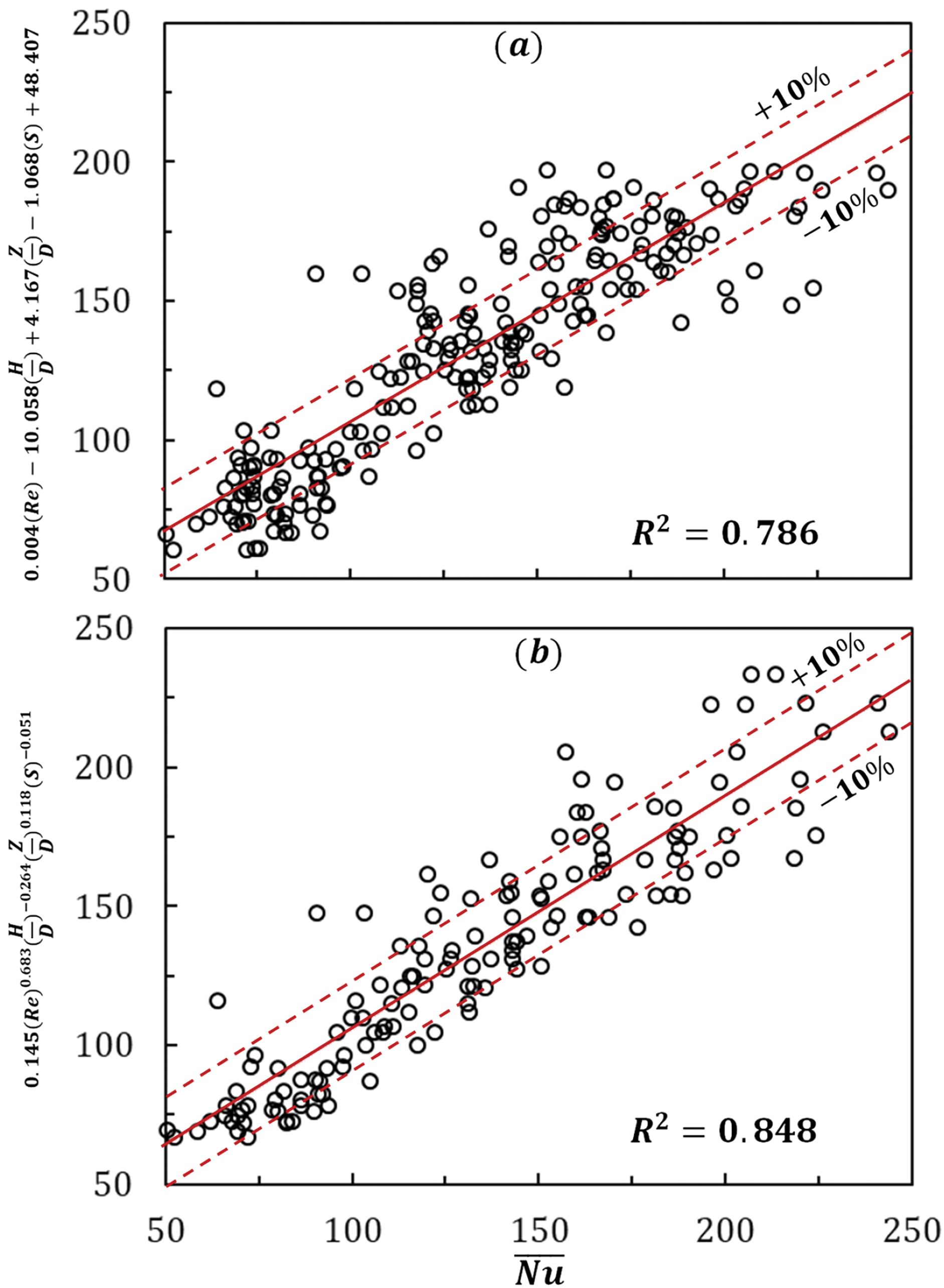
Figure 7: Comparisons between the numerical data and the value from the correlation for the area average Nusselt number (¯Nu) with ±10% error bands: (a) Eq. (8) and (b) Eq. (10)
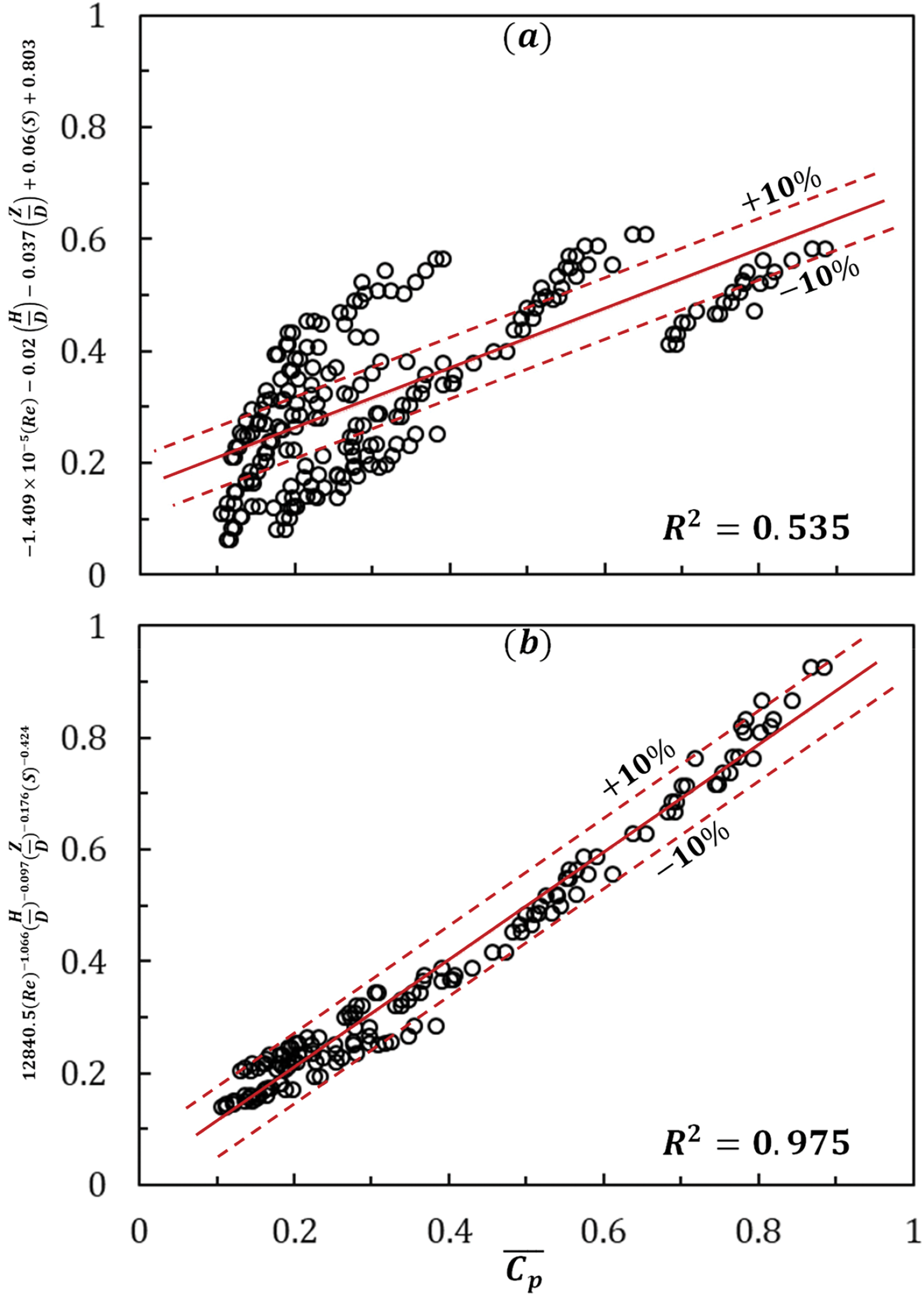
Figure 8: Comparisons between the numerical data and the value from the correlation for the area average Pressure coefficient (¯Cp) with ±10% error bands: (a) Eq. (9) and (b) Eq. (11)
NSGA-II is a variant of the multi-objective genetic algorithm, designed to improve its performance. It was introduced by Deb et al. [47,48] and incorporates elitism, making it an elitist non-dominated sorting genetic algorithm. It discovers non-dominated solutions for multiple conflicting objectives using genetic operators. It sorts solutions into fronts based on dominance, maintains diversity with crowding distance and evolves the best solutions iteratively. The result is a diverse and Pareto-optimal set, providing decision-makers with various trade-off options. Fig. 9 illustrates the basic flow chart of the NSGA-II. The Gamultiobj [49,50] function of the Global Optimization Toolbox in MATLAB is employed in current study while the multi-objective optimization problem is formulated as below:
Maximize:¯Nu=f(Re,HD,ZD,S)
Maximize:¯Cp=f(Re,HD,ZD,S)
Subjected to:
11600≤Re≤35000
1≤H/D≤4
1.5≤ZD≤4.5
0≤S≤0.75
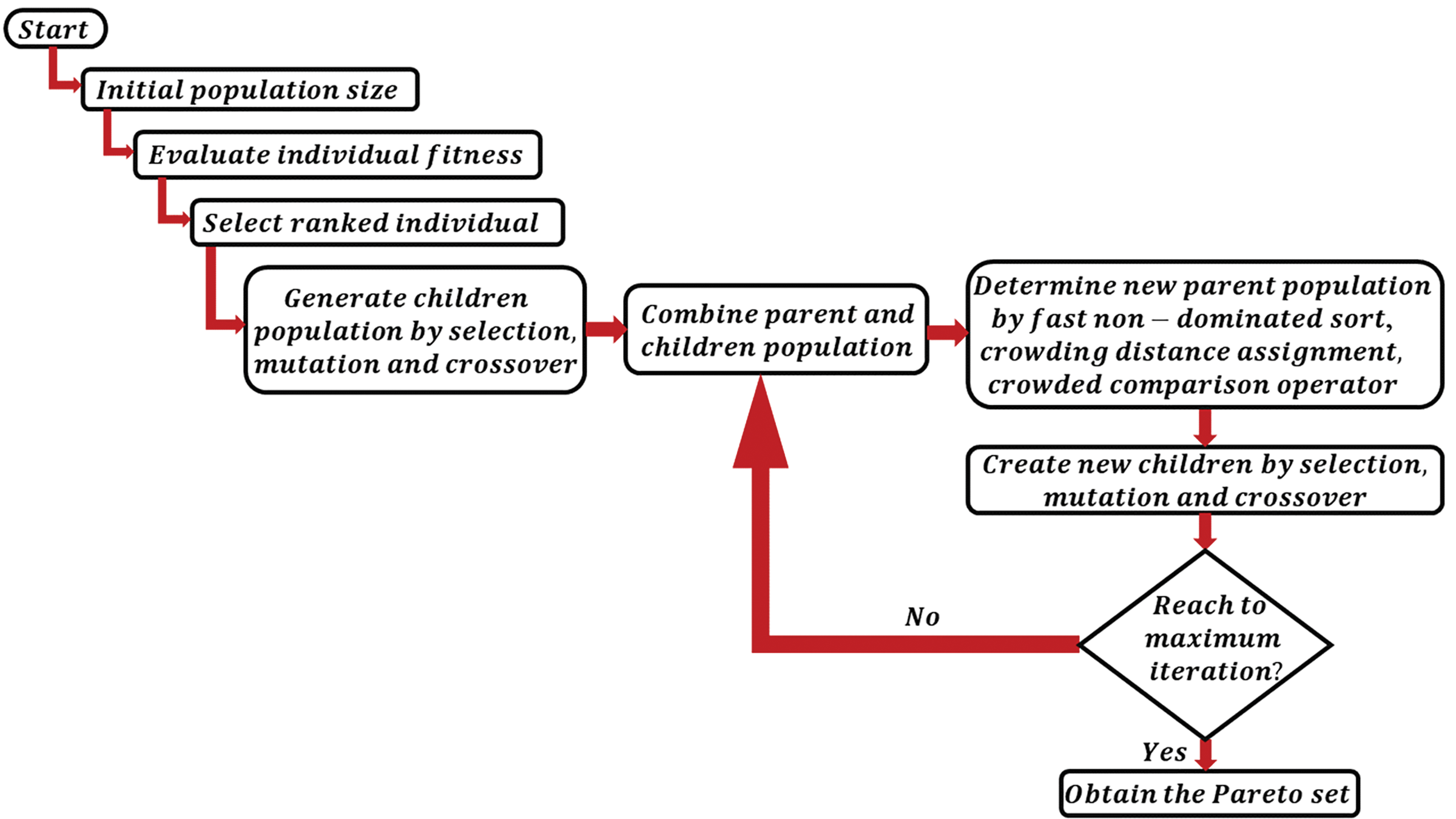
Figure 9: Flow chart of NSGA-II (Non-dominated Sorting Genetic Algorithm)
The NSGA-II process begins by initializing a population of solutions where each individual represents a unique configuration of design parameters, including Reynolds number (Re/D), swirl number (S), jet-to-jet spacing (Z/D), and impingement height (H/D). The fitness of each individual is evaluated through CFD simulations to determine two objective functions—heat transfer (measured by the average Nusselt number) and pressure distribution (measured by the pressure coefficient)—which are essential for assessing the cooling performance of the impingement system. Next, individuals are ranked based on non-domination levels, with non-dominated solutions forming the top Pareto front, representing the best trade-offs between the objectives. Selection, crossover, and mutation operations are then applied to create a new population of offspring, introducing diversity and exploring new regions of the solution space. The parent and offspring populations are combined, and the best solutions are selected through non-dominated sorting and crowding distance calculations, which prioritize solutions that maintain diversity by favoring individuals in less crowded areas of the Pareto front. This iterative process continues, with each generation combining, ranking, and selecting the best individuals until a maximum number of generations or convergence criteria are met, signifying that no significant improvements are observed across generations. The final output is a Pareto-optimal set of solutions, offering a range of optimal configurations that represent trade-offs between maximizing heat transfer and achieving a uniform pressure distribution, thereby allowing decision-makers to select the most suitable design for specific cooling requirements. This approach aligns with the general methodology of applying NSGA-II to multi-objective optimization problems, as demonstrated by Singh et al. [51] in their study on cooling tower performance optimization.
Table 2 displays the Pareto-optimal solutions obtained from the optimization process while Fig. 10 illustrates the Pareto front in the criterion space.
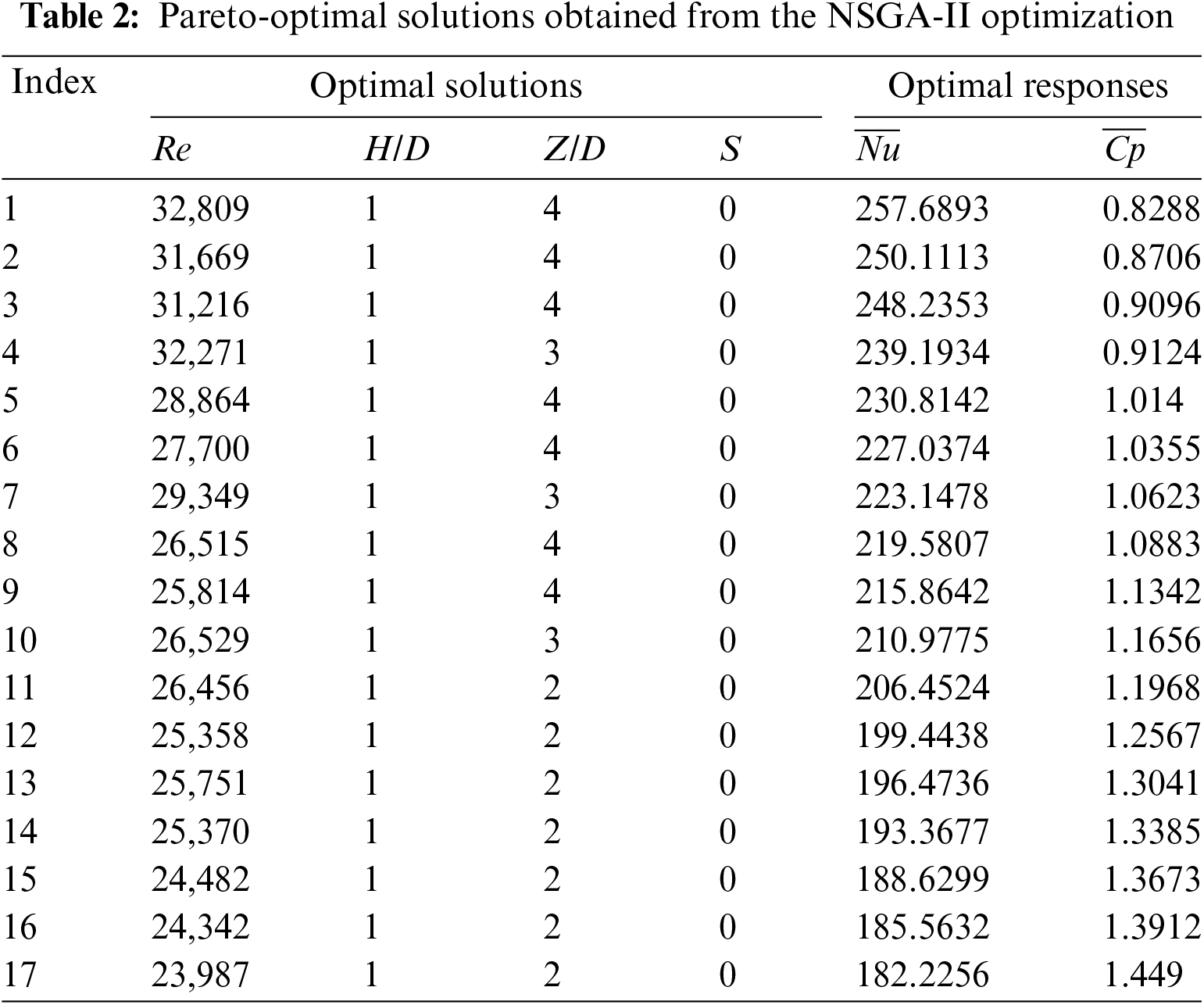
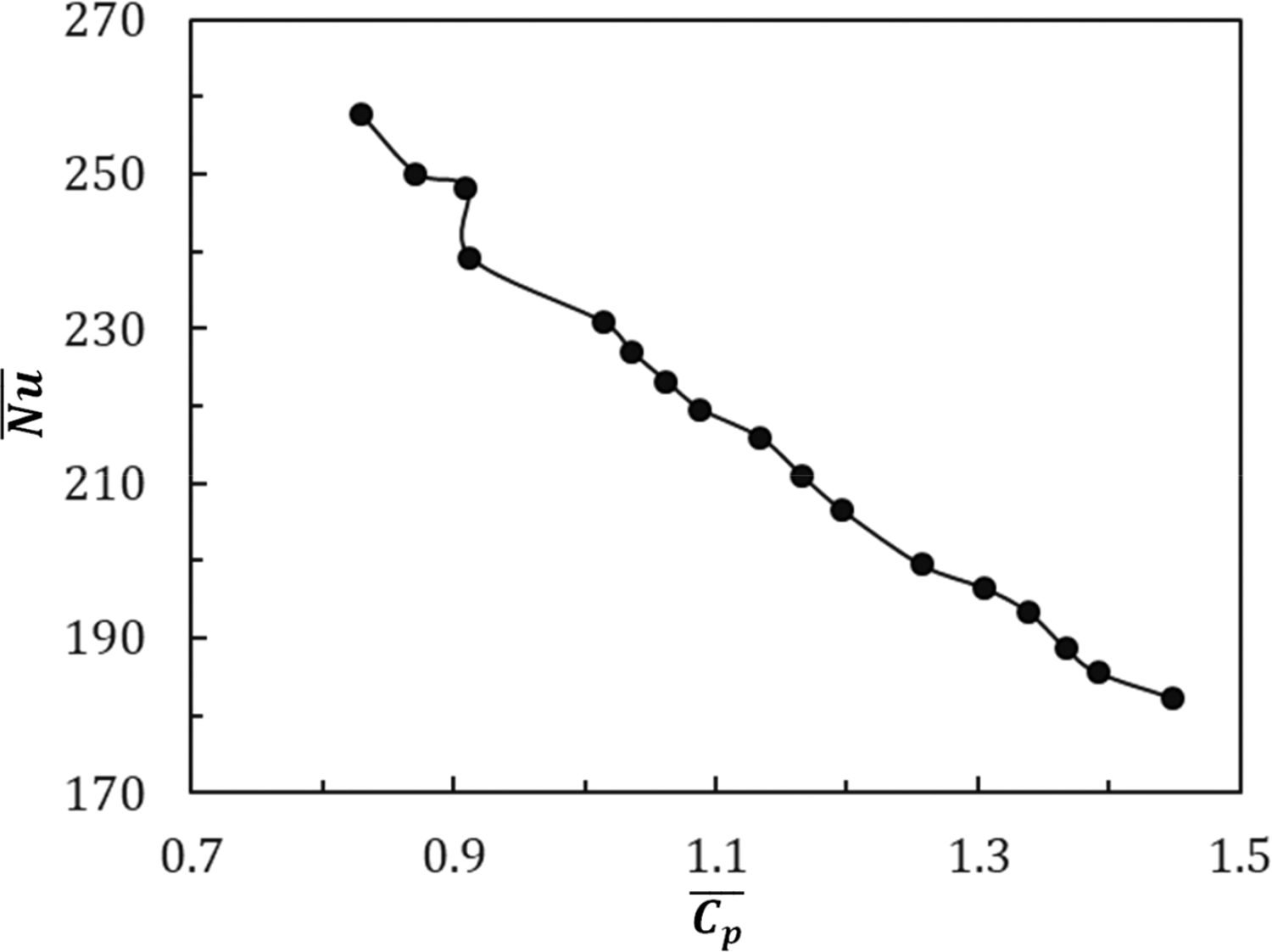
Figure 10: The Pareto front resulting from the NSGA-II optimization
The Weighted Sum Method provides a structured approach to consider multiple objectives and their importance in decision-making. It combines objective functions by multiplying them with weighting factors (Wi). These weights reflect the relative importance of the objectives. By assigning appropriate weights certain objectives can be emphasized. The objective functions weighted accordingly, are combined into a single function. The goal is to minimize this composite function, representing the overall performance or desirability of the alternatives. The optimization problem can be formulated as following:
Minimize:∑Ii=1WiFi(X)(12)
Subjected to:lb≤X≤ub
Wi>0
∑Ii=1Wi=1
Fnormi=(Fi−Fmini)/(Fmaxi−Fmini)(13)
W = Weighing factor; F = Objective function; X = Design variables; lb = Lower bound; ub = Upper bound.
The fmincon [52] function in MATLAB is utilized along with Eq. (12) to find the Pareto optimal solutions. The fmincon function is a versatile tool for constrained nonlinear optimization problems. It minimizes an objective function subject to diverse constraints, including linear equality or inequality, bounds, and nonlinear constraints. At its core, fmincon employs several algorithms like interior-point, sqp (Sequential Quadratic Programming), and trust-region-reflective, which are appropriate for distinct problem structures. Choice of algorithm impacts convergence, performance, and feasibility in acquiring a global or local minimum, especially in complex or high-dimensional topography. The fmincon enables adequate command over the solution path and constraint satisfaction through setting prospects such as initial guess (x0), bounds (lb and ub), and linear or nonlinear constraints. Implementation of fmincon brings noteworthy drifts in optimization as it allows for the structured incorporation of real-world limitations, enabling solutions that are both optimal and feasible within practical constraints. The weighting factor values are methodically changed, such as starting from 0 and increasing by 0.1 up to 1. The objective functions are normalized through Eq. (13) as ¯Nu and ¯Cp differ highly in magnitude. Table 3 exhibits the Pareto-optimal solutions and Fig. 11 illustrates the Pareto front in the criterion space.
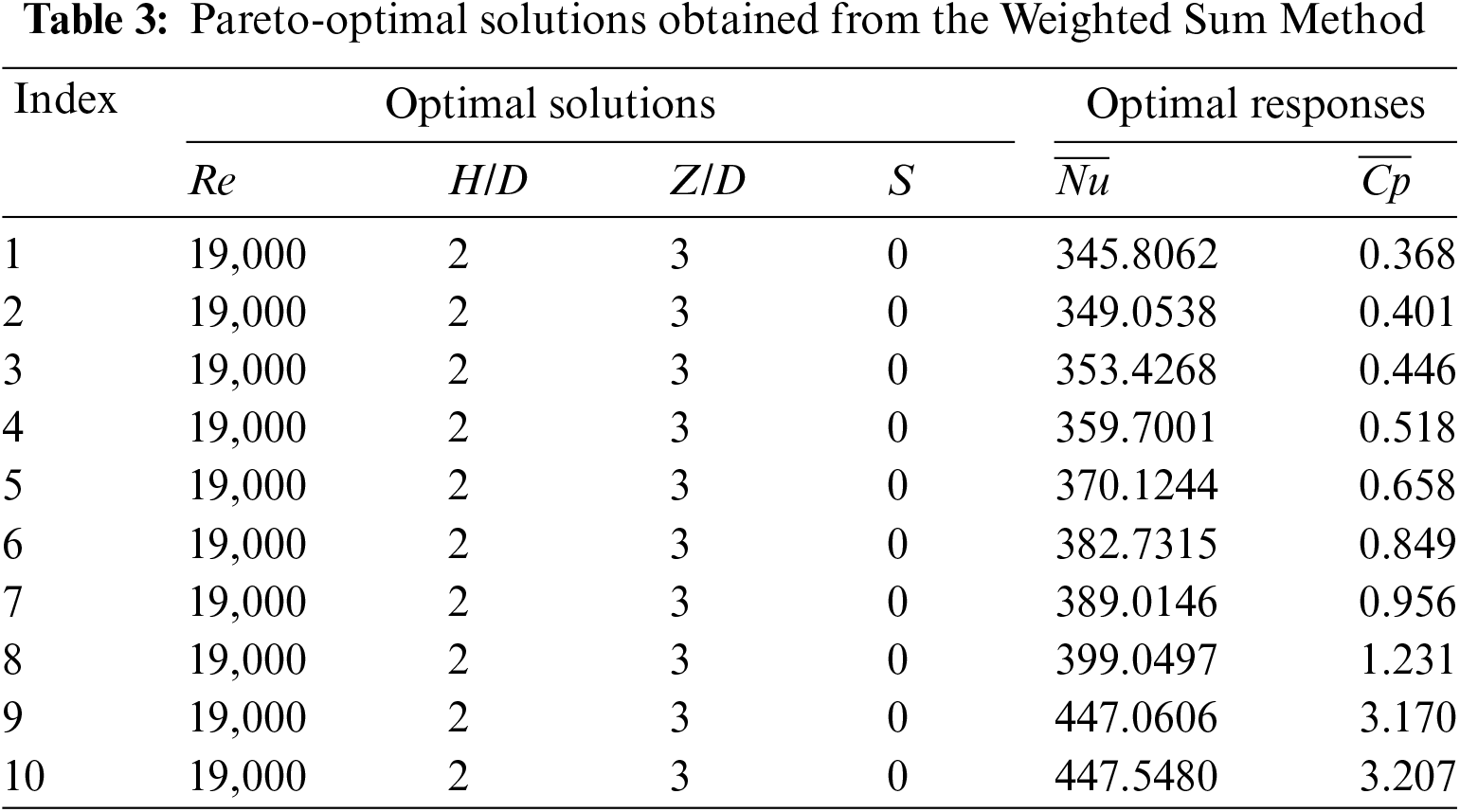

Figure 11: The Pareto front resulting from the Weighted Sum Method
As such, current study strategically utilized NSGA-II and Weighted Sum Method (WSM) addressing complex trade-offs between heat transfer (Nusselt number) and pressure distribution (Cp). With ability to generate a comprehensive Pareto front, NSGA-II provides a broad spectrum of Pareto-optimal solutions. It further enables nuanced exploration of trade-offs without the need for predefined weights—ideal for navigating complex, non-convex solution spaces. This ensures a thorough examination of optimal configurations under various operational conditions. In contrast, WSM offers a deterministic framework by combining multiple objectives into a single weighted function, producing consistent, reproducible solutions that align with specific performance priorities. Together, NSGA-II’s robust exploration of multi-objective solutions and WSM’s targeted, weight-driven optimization enables a well-rounded approach for maximizing cooling efficiency in this system, enhancing both the analytical depth and operational relevance of the study.
5 Thermal Performance Comparison between Optimized and Reference Designs
Fig. 12 illustrates a comparative analysis of the local heat transfer coefficient and wall temperature contours on the impinging plate between optimized and reference designs. Fig. 12a and c depict the optimized design (Index 4; Table 2), while (b) and (d) correspond to the reference design. In the optimized configuration, the contour indicates regions with elevated convective heat transfer, especially in zones directly impacted by jet impingement which reflects an enhancement in thermal boundary layer disruption and heat flux compared to the other case, which exhibits a more uniform and diminished heat transfer profile. The wall temperature contours further substantiate these findings; the optimized design exhibits a more pronounced thermal gradient, with localized cooling regions where lower wall temperatures are achieved. This contrasts with the reference design as it shows elevated wall temperatures, indicating suboptimal convective heat transfer and less effective thermal dissipation. These results underscore the superior thermal management efficacy of the optimized design, attributable to intensified convective cooling and enhanced thermophysical interactions within the impinging flow field. In addition, the local Nusselt number on the impinging plate is calculated for both cases over circumferential areas with a radius of 10D, with values of 100.69 and 113.05 for the reference and optimized cases, respectively demonstrating a 12.28% increase in convective heat transfer efficiency for the optimized design. Further details on the results of the reference designs are available in [40,41] and are not elaborated here for brevity.
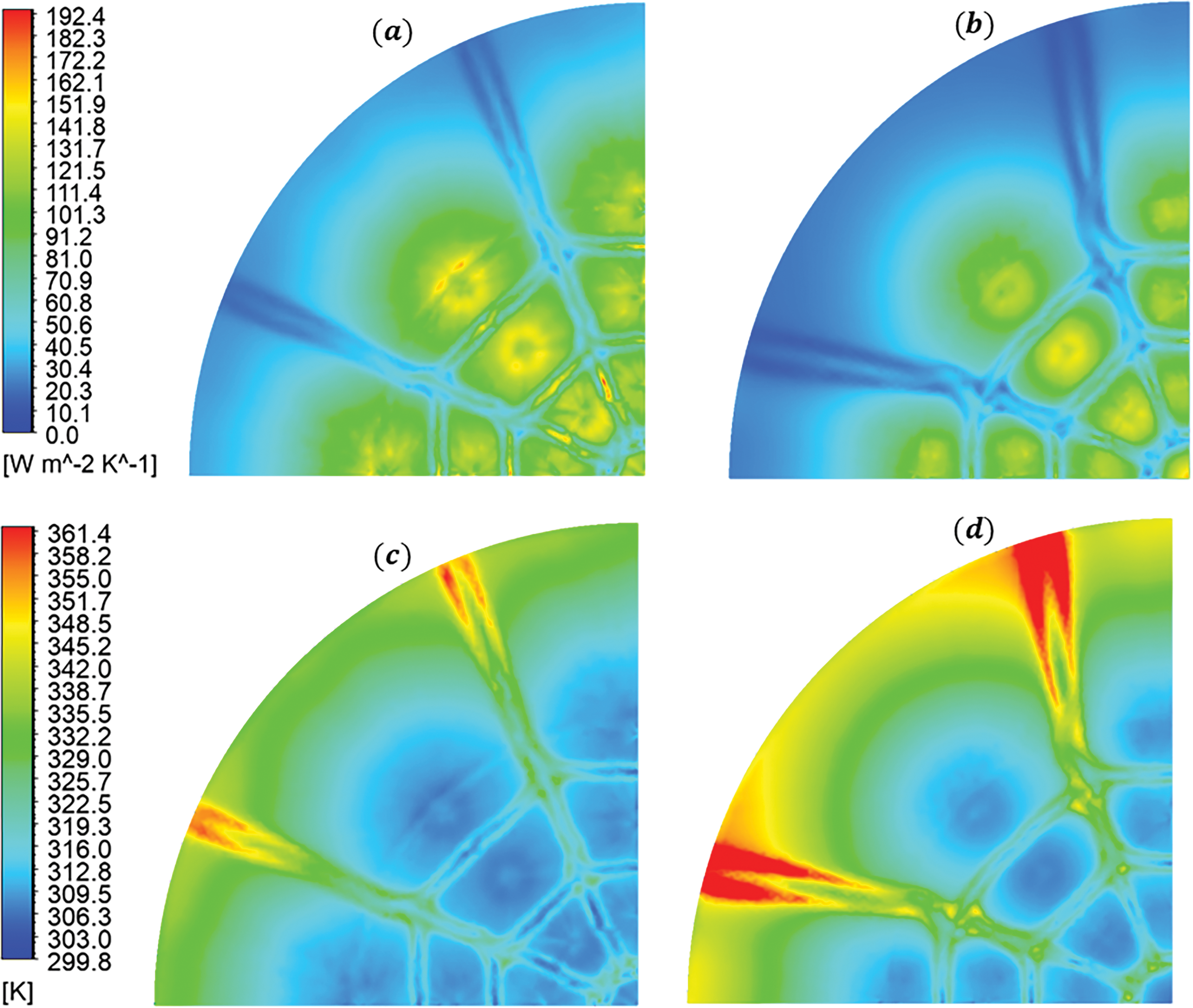
Figure 12: Local heat transfer coefficient contours on the impinging plate at different cases: (a) Inline, Z/D = 3, H/D = 1, Re = 32,271 and S = 0; (b) Inline, Z/D = 3, H/D = 4, Re = 24,600 and S = 0; Wall temperature contours on the impinging plate at different cases: (c) Inline, Z/D = 3, H/D = 1, Re = 32,271 and S = 0; (d) Inline, Z/D = 3, H/D = 4, Re = 24,600 and S = 0
Comparative studies on optimization techniques for impinging jet configurations, such as the work by Singh et al. [37], demonstrate that surrogate modeling using Artificial Neural Networks (ANN) offers a robust approach for optimizing complex thermal systems. They developed an ANN-based surrogate model to systematically investigate various geometric parameters and determine optimal locations for semi-circular protrusions on a concave surface, achieving an 8% enhance in heat transfer compared to a smooth baseline configuration. Further, Jahromi et al. [53] developed three high-accuracy surrogate models using backpropagation artificial neural networks (ANN) to estimate air compression power, average Nusselt number, and heat transfer uniformity. The NSGA-II algorithm was then utilized for optimization, with results indicating that up to a 5% increase in heat transfer uniformity is achievable. Nagesha [54] applied eight machine learning algorithms, including Multiple Linear Regression and Decision Tree Classifier, to analyze heat transfer performance in turbulent jet impingement. The study tried to accurately predict the impact of different roughness configurations on cooling, achieving up to a 66.5% improvement in predictive accuracy over traditional regression models. Findings indicate that while certain roughness configurations initially enhance heat transfer, larger surface areas can reduce effectiveness due to increased natural convection interference.
A computational study has been performed to observe the fluid flow and heat transfer of a heated impingement surface with two different arrays of turbulent air jets. The effects of Reynolds number (Re), swirl number (S), jet-to-plate height (H/D) and jet-to-jet height (Z/D) on Nu distribution and impingement pressure are analyzed. Heat transfer increases with increasing Re and maximum heat transfer is observed at Z/D = 3 for non-swirl and medium swirl flows. Longer residence time and enhanced fluid mixing contribute to maximum heat transfer at the maximum impingement distance and medium swirl flow with Z/D = 4.5. The maximum magnitudes of Nu are obtained at H/D = 1 and Z/D = 3 for Re = 35,000 in staggered array configuration. Swirl intensity affects Cp significantly, while variations in impinging distance have minimal impact on pressure distribution. The study considers four design variables (Re, S, H/D, Z/D) and uses NSGA-II and Weighted Sum Method for optimization, focusing on maximizing heat transfer (Nu) and pressure coefficient (Cp) for enhanced cooling performance. Multivariate regression analysis is employed to derive surrogate models for defining objective functions and the optimization aims to find the optimal configuration of the impingement cooling system. In the end, the study successfully determines the Pareto optimal solutions for the two distinct multi-objective optimization methods.
Acknowledgement: The authors would like to express their gratitude to the reviewers for their insightful and constructive comments, which have significantly contributed to enhancing the quality of this article according to the journal’s standards. Authors also want to acknowledgement technical support by Faculty of Sustainable Design Engineering, UPEI, PEI, Canada.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Sudipta Debnath, Zahir Uddin Ahmed; data collection: Sudipta Debnath, Md. Tanvir Khan; analysis and interpretation of results: Sudipta Debnath, Zahir Uddin Ahmed; draft manuscript preparation: Sudipta Debnath, Zahir Uddin Ahmed, Muhammad Ikhlaq, Md. Tanvir Khan, Avneet Kaur, Kuljeet Sing Grewal. Sudipta Debnath, Zahir Uddin Ahmed, Muhammad Ikhlaq, Md. Tanvir Khan contributed to addressing reviewer comments and the preparation of the revised manuscript. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available on a request from corresponding author.
Ethics Approval: This study did not involve human or animal subjects and, as such, ethical approval was not required.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Jiang C, Han T, Gao Z, Lee CH. A review of impinging jets during rocket launching. Prog Aerosp Sci. 2019;109(1):100547. doi:10.1016/j.paerosci.2019.05.007. [Google Scholar] [CrossRef]
2. Jones-Jackson S, Rodriguez R, Emadi A. Jet impingement cooling in power electronics for electrified automotive transportation: current status and future trends. IEEE Trans Power Electron. 2021;36(9):10420–10435. doi:10.1109/TPEL.2021.3059558. [Google Scholar] [CrossRef]
3. Wu R, Fan Y, Hong T, Zou H, Hu R, Luo X. An immersed jet array impingement cooling device with distributed returns for direct body liquid cooling of high power electronics. Appl Therm Eng. 2019;162(4):114259. doi:10.1016/j.applthermaleng.2019.114259. [Google Scholar] [CrossRef]
4. Ewe WE, Fudholi A, Sopian K, Solomin E, Yazdi MH, Asim N, et al. Jet impingement cooling applications in solar energy technologies: systematic literature review. Thermal Sci Eng Progress. 2022;34(12):101445. doi:10.1016/j.tsep.2022.101445. [Google Scholar] [CrossRef]
5. Al-Hadhrami LM, Shaahid S, Al-Mubarak AA. Jet impingement cooling in gas turbines for improving thermal efficiency and power density. Adv Gas Turbine Technol. 2011;191:210. [Google Scholar]
6. Hackenhaar W, Mazzaferro JA, Montevecchi F, Campatelli G. An experimental-numerical study of active cooling in wire arc additive manufacturing. J Manuf Process. 2020;52:58–65. doi:10.1016/j.jmapro.2020.01.051. [Google Scholar] [CrossRef]
7. Perry KP. Heat transfer by convection from a hot gas jet to a plane surface. Proc Inst Mech Eng. 1954;168(1):775–84. doi:10.1243/PIME_PROC_1954_168_071_02. [Google Scholar] [CrossRef]
8. Gardon R, Akfirat JC. The role of turbulence in determining the heat-transfer characteristics of impinging jets. Int J Heat Mass Transf. 1965;8(10):1261–72. doi:10.1016/0017-9310(65)90054-2. [Google Scholar] [CrossRef]
9. Hollworth BR, Berry RD. Heat transfer from arrays of impinging jets with large jet-to-jet spacing. J Heat Transfer. 1978;100(2):352–7. doi:10.1115/1.3450808. [Google Scholar] [CrossRef]
10. Koopman RN. Local and average transfer coefficients for multiple impinging jets (Ph.D. Thesis). University of Minnesota: Minneapolis, MN, USA; 1975. [Google Scholar]
11. Martin H. Heat and mass transfer between impinging gas jets and solid surfaces. In: Advances in heat transfer. Elsevier; 1977. vol. 13, p. 1–60. [Google Scholar]
12. Baughn JW, Shimizu S. Heat transfer measurements from a surface with uniform heat flux and an impinging jet. J Heat Transf. 1989;111(4):1096–8. doi:10.1115/1.3250776. [Google Scholar] [CrossRef]
13. Hrycak P. Heat transfer from round impinging jets to a flat plate. Int J Heat Mass Transf. 1983;26(12):1857–65. doi:10.1016/S0017-9310(83)80156-2. [Google Scholar] [CrossRef]
14. Lytle D, Webb BW. Air jet impingement heat transfer at low nozzle-plate spacings. Int J Heat Mass Transf. 1994;37(12):1687–97. doi:10.1016/0017-9310(94)90059-0. [Google Scholar] [CrossRef]
15. Viskanta R. Heat transfer to impinging isothermal gas and flame jets. Exp Therm Fluid Sci. 1993;6(2):111–34. doi:10.1016/0894-1777(93)90022-B. [Google Scholar] [CrossRef]
16. Huber AM, Viskanta R. Convective heat transfer to a confined impinging array of air jets with spent air exits. J Heat Transfer. 1994;116(3):570–6. doi:10.1115/1.2910908. [Google Scholar] [CrossRef]
17. Aldabbagh LBY, Sezai I. Numerical simulation of three-dimensional laminar multiple impinging square jets. Int J Heat Fluid Flow. 2002;23(4):509–18. doi:10.1016/S0142-727X(02)00141-8. [Google Scholar] [CrossRef]
18. Andreini A, Da Soghe R, Facchini B, Maiuolo F, Tarchi L, Coutandin D. Experimental and numerical analysis of multiple impingement jet arrays for an active clearance control system. J Turbomach. 2013;135(3):031016. doi:10.1115/1.4007481. [Google Scholar] [CrossRef]
19. Caliskan S, Baskaya S, Calisir T. Experimental and numerical investigation of geometry effects on multiple impinging air jets. Int J Heat Mass Transf. 2014;75(4):685–703. doi:10.1016/j.ijheatmasstransfer.2014.04.005. [Google Scholar] [CrossRef]
20. Gharraei R, Vejdani A, Baheri S. Numerical investigation on the fluid flow and heat transfer of non-Newtonian multiple impinging jets. Int J Therm Sci. 2016;104(A2):257–65. doi:10.1016/j.ijthermalsci.2016.01.012. [Google Scholar] [CrossRef]
21. Draksler M, Končar B, Cizelj L, Ničeno B. Large Eddy Simulation of multiple impinging jets in hexagonal configuration-Flow dynamics and heat transfer characteristics. Int J Heat Mass Transf. 2017;109(12):16–27. doi:10.1016/j.ijheatmasstransfer.2017.01.080. [Google Scholar] [CrossRef]
22. Kilic M, Ali HM. Numerical investigation of combined effect of nanofluids and multiple impinging jets on heat transfer. Therm Sci. 2019;23(5):3165–73. doi:10.2298/TSCI171204094K. [Google Scholar] [CrossRef]
23. Brignoni LA, Garimella SV. Experimental optimization of confined air jet impingement on a pin fin heat sink. IEEE Trans Compon Packag Technol. 1999;22(3):399–404. doi:10.1109/6144.796542. [Google Scholar] [CrossRef]
24. Brevet P, Dejeu C, Dorignac E, Jolly M, Vullierme JJ. Heat transfer to a row of impinging jets in consideration of optimization. Int J Heat Mass Transf. 2002;45(20):4191–4200. doi:10.1016/S0017-9310(02)00128-X. [Google Scholar] [CrossRef]
25. Chiang KT. Modeling and optimization of designing parameters for a parallel-plain fin heat sink with confined impinging jet using the response surface methodology. Appl Therm Eng. 2007;27(14–15):2473–82. doi:10.1016/j.applthermaleng.2007.02.004. [Google Scholar] [CrossRef]
26. Heo MW, Lee KD, Kim KY. Optimization of an inclined elliptic impinging jet with cross flow for enhancing heat transfer. Heat Mass Transf. 2011;47(6):731–42. doi:10.1007/s00231-011-0763-2. [Google Scholar] [CrossRef]
27. Badra J, Masri AR, Behnia M. Enhanced transient heat transfer from arrays of jets impinging on a moving plate. Heat Transf Eng. 2013;34(4):361–71. doi:10.1080/01457632.2013.717046. [Google Scholar] [CrossRef]
28. Husain A, Kim SM, Kim KY. Performance analysis and design optimization of micro-jet impingement heat sink. Heat Mass Transf. 2013;49(11):1613–24. doi:10.1007/s00231-013-1202-3. [Google Scholar] [CrossRef]
29. Chauhan R, Singh T, Thakur NS, Patnaik A. Optimization of parameters in solar thermal collector provided with impinging air jets based upon preference selection index method. Renew Energy. 2016;99:118–26. doi:10.1016/j.renene.2016.06.046. [Google Scholar] [CrossRef]
30. Chauhan R, Singh T, Kumar N, Patnaik A, Thakur NS. Experimental investigation and optimization of impinging jet solar thermal collector by Taguchi method. Appl Therm Eng. 2017;116:100–9. doi:10.1016/j.applthermaleng.2017.01.025. [Google Scholar] [CrossRef]
31. Lam PAK, Prakash KA. A numerical investigation and design optimization of impingement cooling system with an array of air jets. Int J Heat Mass Transf. 2017;108:880–900. doi:10.1016/j.ijheatmasstransfer.2016.12.017. [Google Scholar] [CrossRef]
32. Lam PA, Prakash KA. Multi-objective optimization of turbulent jet impingement cooling system: A thermal and thermodynamic study. IOP Conf Ser: Mater Sci Eng. 2021;1132:012017. doi:10.1088/1757-899X/1132/1/012017. [Google Scholar] [CrossRef]
33. Singh A, Prasad BVSSS. Optimization of protrusions for an impinging jet on a curved surface. In: Recent advances in mechanical engineering. Singapore: Springer; 2021. p. 117–26. doi:10.1007/978-981-15-7711-6_12. [Google Scholar] [CrossRef]
34. Yildizeli A, Cadirci S. Multi-objective optimization of multiple impinging jet system through genetic algorithm. Int J Heat Mass Transf. 2020;158(1):119978. doi:10.1016/j.ijheatmasstransfer.2020.119978. [Google Scholar] [CrossRef]
35. Eghtesad A, Mahmoudabadbozchelou M, Afshin H. Heat transfer optimization of twin turbulent sweeping impinging jets. Int J Therm Sci. 2019;146:106064. doi:10.1016/j.ijthermalsci.2019.106064. [Google Scholar] [CrossRef]
36. Mahmoudabadbozchelou M, Eghtesad A, Jamali S, Afshin H. Entropy analysis and thermal optimization of nanofluid impinging jet using artificial neural network and genetic algorithm. Int Commun Heat Mass Transf. 2020;119:104978. doi:10.1016/j.icheatmasstransfer.2020.104978. [Google Scholar] [CrossRef]
37. Singh A, Chakravarthy B, Prasad BVSSS. Numerical simulations and optimization of impinging jet configuration. Int J Numer Methods Heat Fluid Flow. 2021;31(1):1–25. doi:10.1108/HFF-01-2020-0053. [Google Scholar] [CrossRef]
38. Ahmed ZU. An experimental and numerical study of surface interactions in turbulent swirling jets (Ph.D. Thesis). School of Engineering, Edith Cowan University: Mount Lawley, WA, Australia; 2016. [Google Scholar]
39. Ahmed ZU, Al-Abdeli YM, Guzzomi FG. Impingement pressure characteristics of swirling and non-swirling turbulent jets. Exp Therm Fluid Sci. 2015;68:722–32. doi:10.1016/j.expthermflusci.2015.07.017. [Google Scholar] [CrossRef]
40. Debnath S, Ahmed ZU, Ikhlaq M, Khan T. Thermal characteristics of arrays of swirling impinging jets: effect of Reynolds number, impingement distance, and jet-to-jet separation. Heat Transf. 2023;52(1):585–608. doi:10.1002/htj.22708. [Google Scholar] [CrossRef]
41. Debnath S, Khan MT, Ahmed ZU. Substrate characteristics of multiple arrays of turbulent swirling impinging jets. J Flow Vis Image Process. 2023;30(4):67–96. doi:10.1615/JFlowVisImageProc.2023045132. [Google Scholar] [CrossRef]
42. Geers LFG. Multiple impinging jet arrays: An experimental study on flow and heat transfer (Doctoral Dissertation). Delft University of Technology: Delft, The Netherlands; 2004. [Google Scholar]
43. Tummers MJ, Jacobse J, Voorbrood SGJ. Turbulent flow in the near field of a round impinging jet. Int J Heat Mass Transf. 2011;54(23–24):4939–48. doi:10.1016/j.ijheatmasstransfer.2011.07.007. [Google Scholar] [CrossRef]
44. Fairweather M, Hargrave G. Experimental investigation of an axisymmetric, impinging turbulent jet. 1. Velocity field. Exp Fluids. 2002;33(3):464–71. doi:10.1007/s00348-002-0479-7. [Google Scholar] [CrossRef]
45. Menter FR. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994;32(8):1598–1605. doi:10.2514/3.12149. [Google Scholar] [CrossRef]
46. Cohen I, Huang Y, Chen J, Benesty J, Benesty J, Chen J, et al. Pearson correlation coefficient. In: Noise reduction in speech processing. Springer, Berlin, Heidelberg; 2021. doi:10.1007/978-3-642-00296-0_5. [Google Scholar] [CrossRef]
47. Deb K, Agrawal S, Pratap A, Meyarivan T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In: Parallel problem solving from nature PPSN VI. Paris, France: Springer Berlin Heidelberg; 2000. p. 849–58. doi:10.1007/3-540-45356-3_83 [Google Scholar] [CrossRef]
48. Deb K, Pratap A, Agarwal S, Meyarivan TAMT. A fast and elitist multiobjective genetic algorithm: nSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–97. doi:10.1109/4235.996017. [Google Scholar] [CrossRef]
49. Fun. Find Pareto front of multiple fitness functions using genetic algorithm—MATLAB. Available from: https://www.mathworks.com/help/gads/gamultiobj.html. [Accessed 2024]. [Google Scholar]
50. GAMULTIOBJ. MathWorks. Available from: https://www.mathworks.com/help/gads/gamultiobj-algorithm.html. [Accessed 2024]. [Google Scholar]
51. Singh K, Das R. An experimental and multi-objective optimization study of a forced draft cooling tower with different fills. Energy Convers Manag. 2016;111:417–30. doi:10.1016/j.enconman.2015.12.080. [Google Scholar] [CrossRef]
52. Fun. Find minimum of constrained nonlinear multivariable function—MATLAB. Available from: https://www.mathworks.com/help/optim/ug/fmincon.html. [Accessed 2024]. [Google Scholar]
53. Jahromi HB, Kowsary F. A comprehensive parametric study and multi-objective optimization of turbulent jet array impingement for uniform cooling of gas turbine blades with minimized compression power. Int J Therm Sci. 2024;201:109035. doi:10.1016/j.ijthermalsci.2024.109035. [Google Scholar] [CrossRef]
54. Nagesha K. Machine learning algorithms to study the relative roles of jet convection and natural convection in the presence of surface roughness elements on enhancement of jet impingement heat transfer. Int J Therm Sci. 2024;198(3):108847. doi:10.1016/j.ijthermalsci.2023.108847. [Google Scholar] [CrossRef]
Appendix A
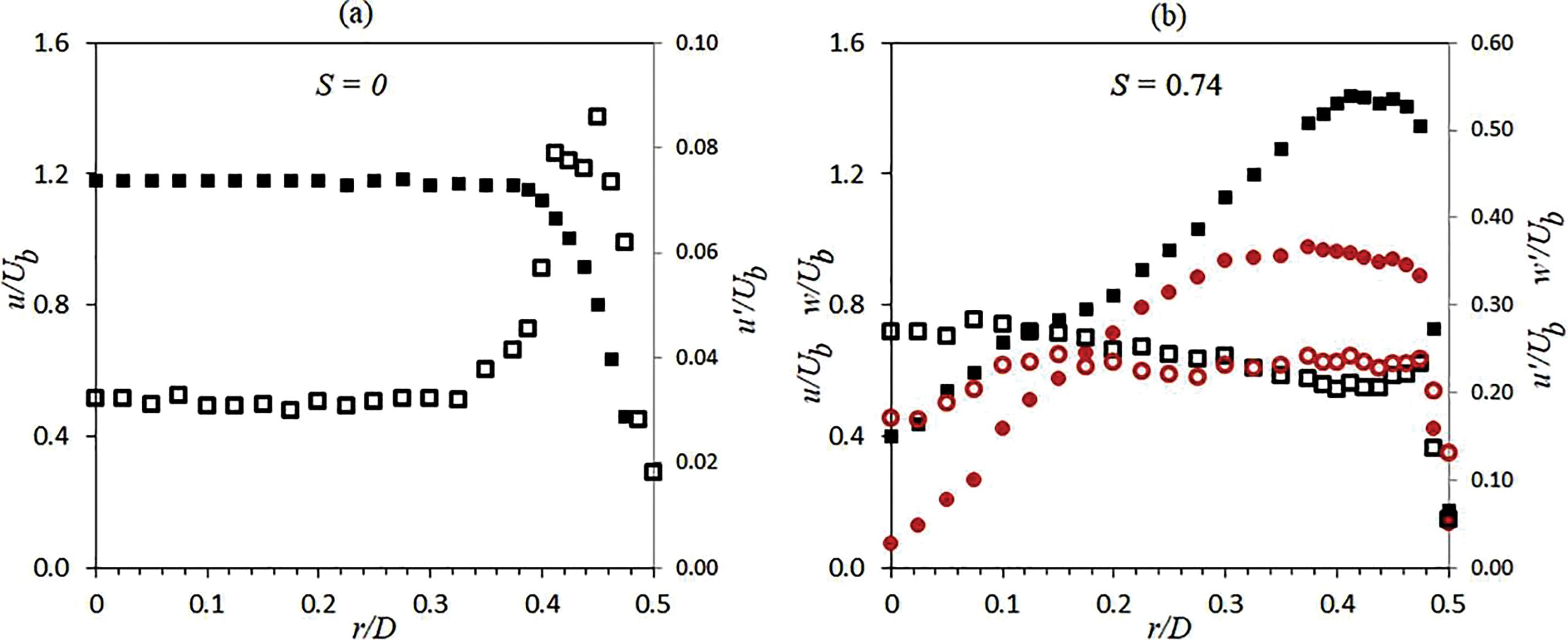
Figure A1: Normalized mean and turbulence profiles for axial and tangential velocity components served as velocity inlet conditions for (a) S = 0 and (b) S = 0.74. Filled square and circular markers denote the mean axial and tangential velocities, respectively, whereas hollow markers indicate the associated turbulence values for each
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
