First and Second Law Analysis of a LiBr-Water Absorption Cycle with Recovering Condensation Heat for Generation

Nomenclature

1  Introduction

The worldwide energy demand in the industrial sector and households has been growing rapidly during the last few years [1,2]. In majority of these society sectors use refrigeration and air conditioning systems based on vapor compression technology to keep their comfort conditions, however, they consume around 30% of the electricity produced [3]. To save electricity, absorption refrigeration systems are becoming a viable alternative because they can use waste heat from thermal systems or solar energy [4] and they can use refrigerants with low or null global warming potential, which could be considered an ecological refrigeration technology [5,6].

The most common absorption refrigeration technology uses LiBr-Water and NH3-Water as working fluids, where LiBr-Water mixture is employed for air conditions applications [7], while NH3-Water mixture is commonly used for refrigeration applications [8]. Nevertheless, LiBr/H2O mixture exhibits higher energy performance than NH3/H2O [9,10]. Furthermore, the challenge with the absorption systems is to improve their energy performance so that they can be competitive in comparison with the traditional vapor compression chillers. For this reason, various authors have published works where energy analysis has been applied to absorption refrigeration systems.

Ayou et al. [11] made an energy study in a LiBr-Water reversible absorption refrigeration system for cooling, ventilation and household hot water modes. The proposed configuration is to improve the operation time and the primary energy in a LiBr-Water single effect ARS driven by an evacuated solar tube collector. Their results revealed that the generator temperature is a critical factor in the system performance, then, a generator temperature of 110°C is required to obtain the highest COP of 0.74 without solution crystallization risk. Ahmad et al. [12] made a detailed energy analysis for a single effect LiBr-Water ARS under different climate conditions and the results were compared with the LiCl-Water mixture. The optimum COP for the LiBr-Water system ranged between 0.74 to 0.90 and for the LiCl-Water cycle was 0.809 to 0.926 at the minimum generator temperature of 54.56°C and 26.25°C, respectively.

Jeong et al. [13] investigated a hybrid cooling/heating absorption heat pump using LiBr/Water as a refrigerant mixture. The COP for the hybrid heat pump was found superior to the conventional single effect ARS. Wang et al. [14] evaluated thermodynamically a novel combined cooling and power ARS, where an ejector was incorporated at the lower turbine back pressure. This configuration showed an increase of 13% in the electricity produced and 45% in the thermal performance, in comparison with a similar system without an ejector. Razmi et al. [15] analyzed a hybrid absorption/recompression cycle, where the generator and compressor were compacted, avoiding the use of the condenser and improving the COP considerably. Furthermore, Babaei et al. [16] presented a thermodynamic simulation to predict the COP and exergy efficiency in an innovative absorption-recompression chiller where Fe, Al2O3 and SiO2 nanoparticles were dissolved in LiBr-Water mixture. They concluded that Fe-LiBr-Water mixture can improve 14.6% and 18% of the energy performance and electricity consumption in the compressor when compared with the other two. Peng et al. [17] evaluated a hybrid absorption chiller, employing low grade-heat to reduce the work in the compressor. The proposed novel system resulted in a reduction of 9.3% and 10.45% in the compressor energy consumption in comparison with the two-stage compression chiller and the cascade absorption-compression chiller. To reduce the thermal load in the condenser, Wang et al. [18] incorporated two compressors between the generator and the condenser and this configuration was named absorption-compression refrigeration hybrid cycle (RCHG-ARS). They compared the energetic efficiency of the alternative cycle with those of the basic ARS under different working conditions. Their results evidenced that the thermal load in the generator can be reduced between 70%–80% and the COP enhanced by 97.1%, in comparison with the ARS.

Other studies evaluate the exergetic efficiency and quantify the irreversibilities in absorption refrigeration cycles from the second thermodynamics point of view. In this sense, Pacheco-Cedeño et al. [19] applied an exergetic study to the configuration proposed by Wang et al. [18]. According to their analysis, the RCHG-ARS presented 0.20% higher exergetic performance than ARS at the lowest generator pressure (PGE = 5.94 bar), although the lowest relative exergy destroyed was found at high generation and condensing temperatures (100°C and 40°C) and an evaporating temperature of −5°C. Ochoa et al. [20] presented an exergy study in a LiBr-Water single effect ARS by varying the ambient temperature from 10°C to 50°C. Derived from their study, the authors found that the solution heat exchanger presented the highest exergy destroyed and the maximum exergetic efficiency was found in the generator. Blanco-Marigorta et al. [21] studied the key aspects of the exergy analysis for each of the components in different LiBr-Water absorption refrigeration cycles under different ambient temperatures. Their results revealed that the exergy destruction in the system can present some differences according to the methodology applied. Banu et al. [22] developed a detailed exergy analysis approach in a LiBr-Water absorption chiller to evaluate the irreversibilities of each cycle. Likewise, Mohtaram et al. [23] conducted an exergy analysis in an ARS using LiBr-Water as working fluid. According to their simulation results, the absorber showed 35.87% of the total exergy destruction in the system, due to the low efficiency of this component, then it is recommended to pay attention to the outlet exergy of this component.

According to the literature, analyzing absorption refrigeration cycles from the first and second laws of thermodynamics is necessary to determine the best energy and exergy performance, as well as the irreversibilities presented in the system. So, this work aims to analyze an alternative ARS, where part of the thermal load in the condenser is recovered via the solution heat exchanger and supplied into the generator (HR-ARS), in which LiBr/Water is used as a refrigerant mixture. The results obtained are contrasted with those of traditional ARS under the same operating conditions. Furthermore, some parameters such as generator, condenser/absorber and evaporator temperatures as well as the efficiency of the solution heat exchanger on the coefficient of performance and exergetic efficiency are examined and compared with the conventional ARS.

Finally, those parameters also were investigated on the entropy generation in the system, because these are very important to identify and minimize the thermodynamic losses, which can enhance the performance of the system.

2  Thermodynamic Analysis of the Systems

2.1 Operating Principle

Fig. 1a,b shows the representation of traditional and alternative absorption refrigeration systems. The systems consist of the eight basic components: generator (GE), condenser (CO), evaporator (E), absorber (AB), solution pump (SP), solution throttling valve (SEV), solution heat exchanger (SHX) and refrigerant throttling valve (REV). It is important to point out that the operating principle of the conventional ARS cycle is very similar to the alternative HR-ARS cycle. First, in the evaporator the refrigerant exits as saturated vapor (10) and then enters the AB mixing with the poor concentration coming from the GE (6), producing a high concentration (1), which is sent back to the GE via the SP, raising its pressure (2). After, the strong solution is preheated through SHX (3), using the heat of the weak solution stream coming from the GE (4) got a lower temperature in the poor concentration (5) and sent back to the AB through the SEV.

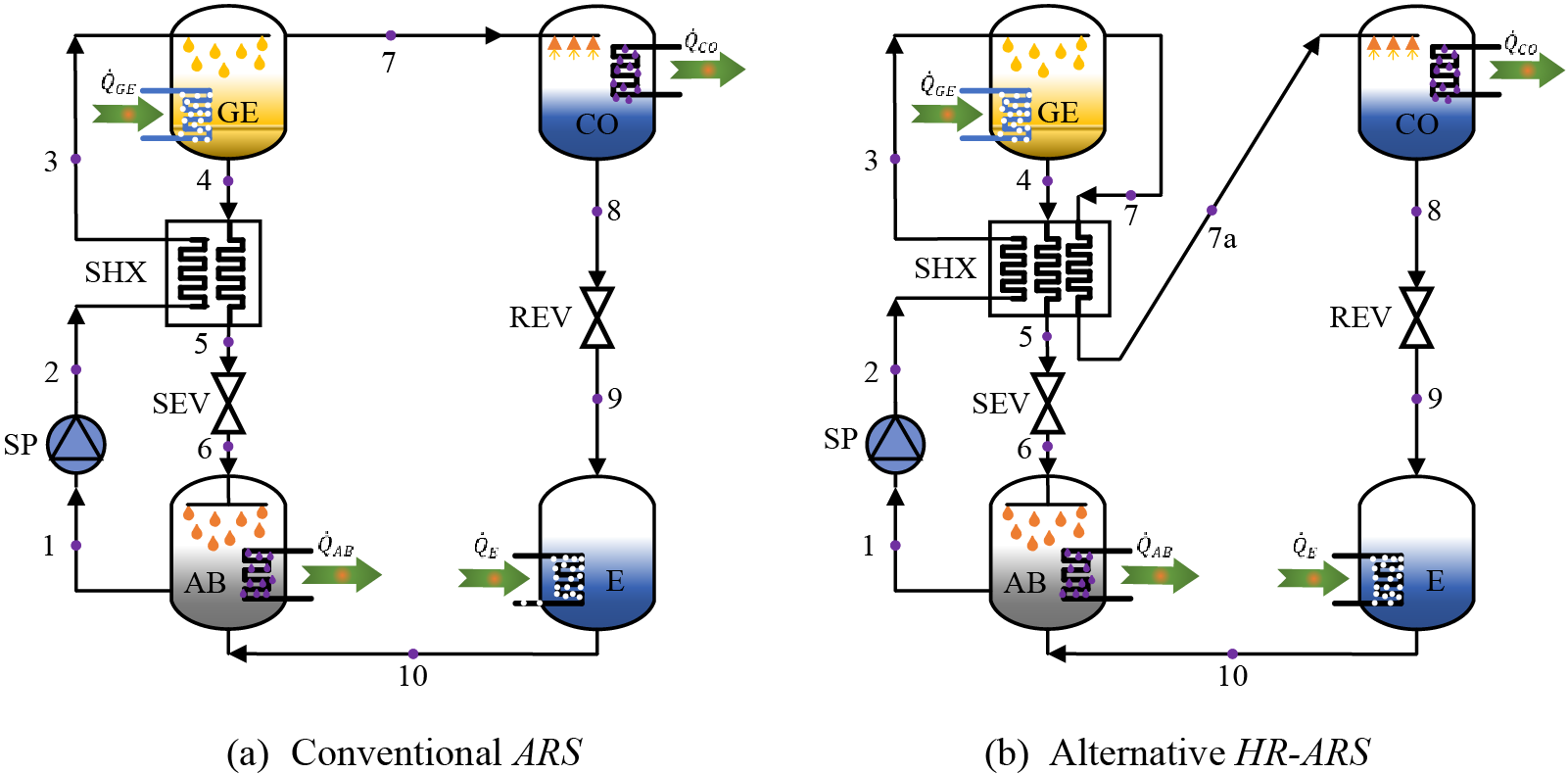
Figure 1: Schematic of conventional ARS and alternative HR-ARS

In the GE, the strong solution is heated until it boils applying external heat and refrigerant vapor is produced (7). Subsequently, it flows into the CO until saturated liquid (8). Furthermore, the refrigerant liquid goes directly to the REV, reducing its pressure and temperature, becoming a two-phase mixture (9). Then, the refrigerant enters the E where it is boiled by the heat absorbed from the refrigerated space until it becomes saturated vapor (10) and then, the cycle is repeated. The difference between the HR-ARS cycle concerning the conventional ARS system is that both, the refrigerant produced in the generator (7) as well as the weak solution (4) give up heat to the strong solution (3) in the SHX causes that the generator thermal load decrease and the performance of the HR-ARS can be improved.

2.2 First Law Analysis and Assumptions

For the simulation of the HR-ARS and the conventional ARS cycle, mass and energy conservation analysis are applied in each component of the system. The simulation was made under steady-state conditions and the effects of potential and kinetic energies are negligible. The main equations of each component of both cycles are described as follows:

Mass balance

∑m˙i=∑m˙e(1)

Mass concentration balance

∑m˙ixi=∑m˙exe(2)

Energy balance

∑Q˙−∑W˙=∑m˙ehe−∑m˙ihi(3)

For the simulation of the systems, is necessary to adopt the following assumptions:

1.    Steady-state conditions.

2.    The potential and kinetic energy effects are insignificant.

3.    The pressure drop through the components is considered to be negligible, except in the expansion valves.

4.    The heat losses in the system components are negligible.

5.    The poor concentration and the refrigerant at the outlet of the generator and evaporator are as saturated vapor, while strong concentration and the refrigerant leaving the absorber and condenser are as saturated liquid.

6.    The refrigerant vapor entering the condenser is considered as superheated vapor.

7.    Refrigerant and strong solution have the same temperature at the outlet and inlet of the solution heat exchanger.

8.    The temperature and pressure of the dead state are considered as 25°C and 1.013 bar, respectively.

The energy balance in each of the components of the ARS and HR-ARS systems is given by the equations presented in Table 1.

A parameter used to measure the energy efficiency in an absorption chiller is called the coefficient of performance (COP), which is defined as the ratio of cooling production (Q˙E) concerning the total energy supplied (Q˙GE+W˙SP). In the HR-ARS and ARS systems, the coefficient of performance can be calculated using the following equation [24,25]:

COP=Q˙EQ˙GE+W˙SP(4)

To improve the COP of HR-ARS and ARS systems, a solution heat exchanger is used between the generator and absorber. Then, the efficiency of the solution heat exchanger is evaluated by the following expression [26,27]:

ηSHX=T4−T5T4−T2(5)

3  Second Law Analysis

The second law of thermodynamics consists of evaluating the exergy performance in a system, whose reduction is associated with losses in the components system. According to Asensio-Delgado et al. [28], exergy can be defined as the maximum useful power that can be produced by a system or flow. Besides, Jiménez-García et al. [29] used Eq. (6) to calculate the irreversibility in an absorption chiller:

I=∑E˙i−∑E˙e+[∑(Q˙(1−T0T))i−∑(Q˙(1−T0T))e]±∑W˙(6)

where, I is the internal irreversibility of the system, Q˙(1−T0T) and W˙ are the exergy loss associated with heat transfer rate and the mechanical power transferred to or from the control volume, respectively, while E˙ is the exergy loss of each stream, which is calculated by the following equation:

E˙=m˙[(h−h0)−T0(s−s0)](7)

Applying Eq. (6) in the HR-ARS and ARS systems, the irreversibility for each component is shown in Table 2. Furthermore, the total irreversibility in the system is calculated by the following expression:

ITotal=IE+IAB+ICO+IGE+ISP+IREV+ISEV+ISHX(8)

The exergy efficiency is the reason the exergy produced respect the exergy input, which can be obtained by the following expression [30]:

ηex=Q˙E(1−T0Tr)Q˙GE(1−T0TGE)+W˙SP(9)

The exergetic performance also can be defined as the ratio of the exergy rate produced and the exergy of the fuel [31,32], which can be calculated according to the following equation:

ηex=E˙PE˙F=1−ITotalEF(10)

4  Model Verification

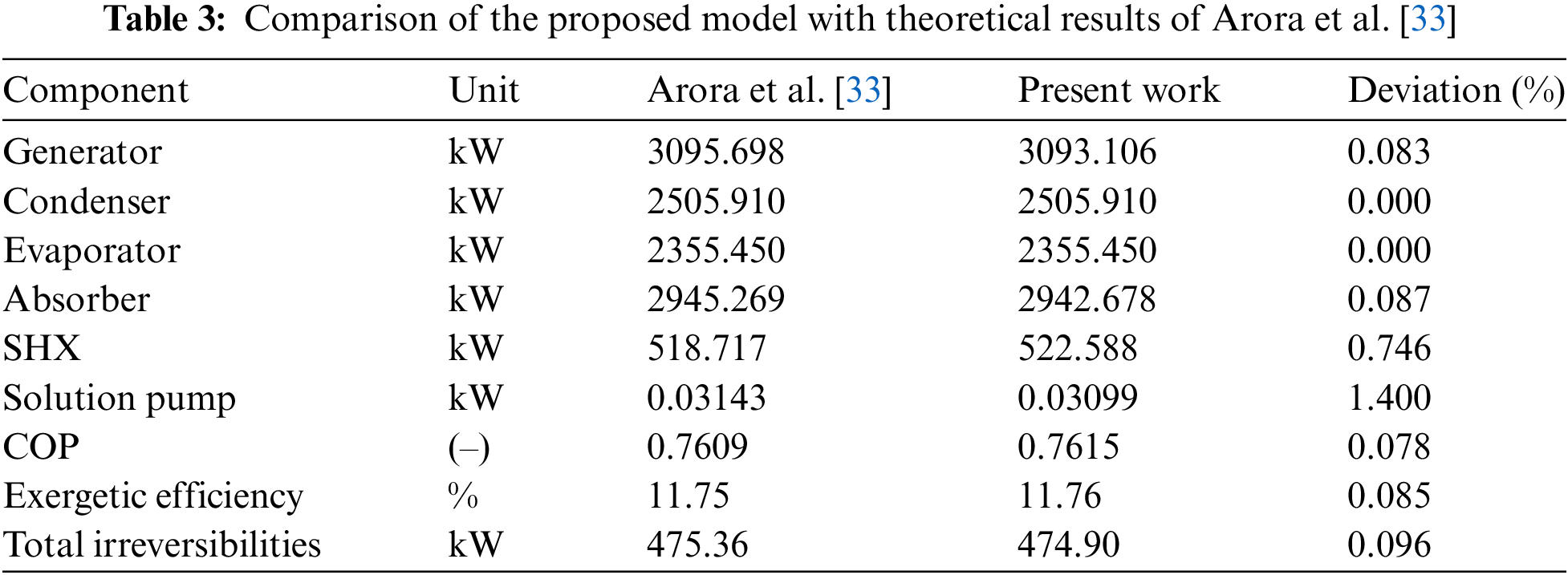
To verify the current model, energy and exergy results for the ARS cycle have been compared with those results obtained by Arora et al. [33] under the same operating conditions (TGE = 87.8°C, TCO = TAB = 37.8°C, TE = 7.2°C, ηIHX=70% and refrigerant mass flow rate = 1 kg/s). Table 3 shows that the maximum relative deviation between both models was 1.40%, then, according to the comparison, the accuracy of the model was verified.

5  Model Validation

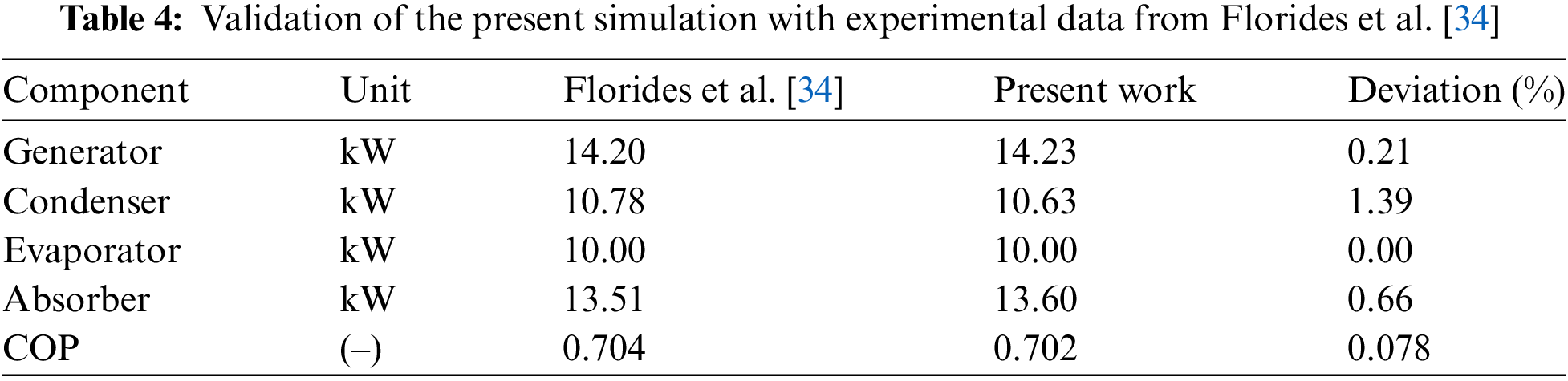
The validation of the present simulation was compared with experimental data presented by Florides et al. [34], considering the following operating conditions: TGE = 90°C, TCO = 44.3°C, TAB = 34.9°C, TE = 6°C, solution heat exchanger effectiveness (ηSHX=0.522) and cooling capacity of 10 kW and the results are showed in Table 4. It can be seen that the deviations are less than 1.4% ratifying the exactitude of our model.

Simulation and Operating Conditions

The simulation has been developed using the computational software EES [35] to carry out the energy and exergy analysis of HR-ARS and ARS cycles. The choice of this software is justified because it contains the thermodynamic and transport properties of LiBr-H2O. To investigate the energetic and exergetic efficiencies of the alternative HR-ARS cycle and compare it with the basic ARS system, the input operating conditions shown in Table 5 were used.

6  Results and Discussion

The influence of the main working conditions on the energy and exergy performance in the alternative HR-ARS and conventional ARS is studied. Moreover, the comparison between the exergy destruction in the alternative HR-ARS and the conventional ARS is also examined.

6.1 Variation of TGE and TCO on COP

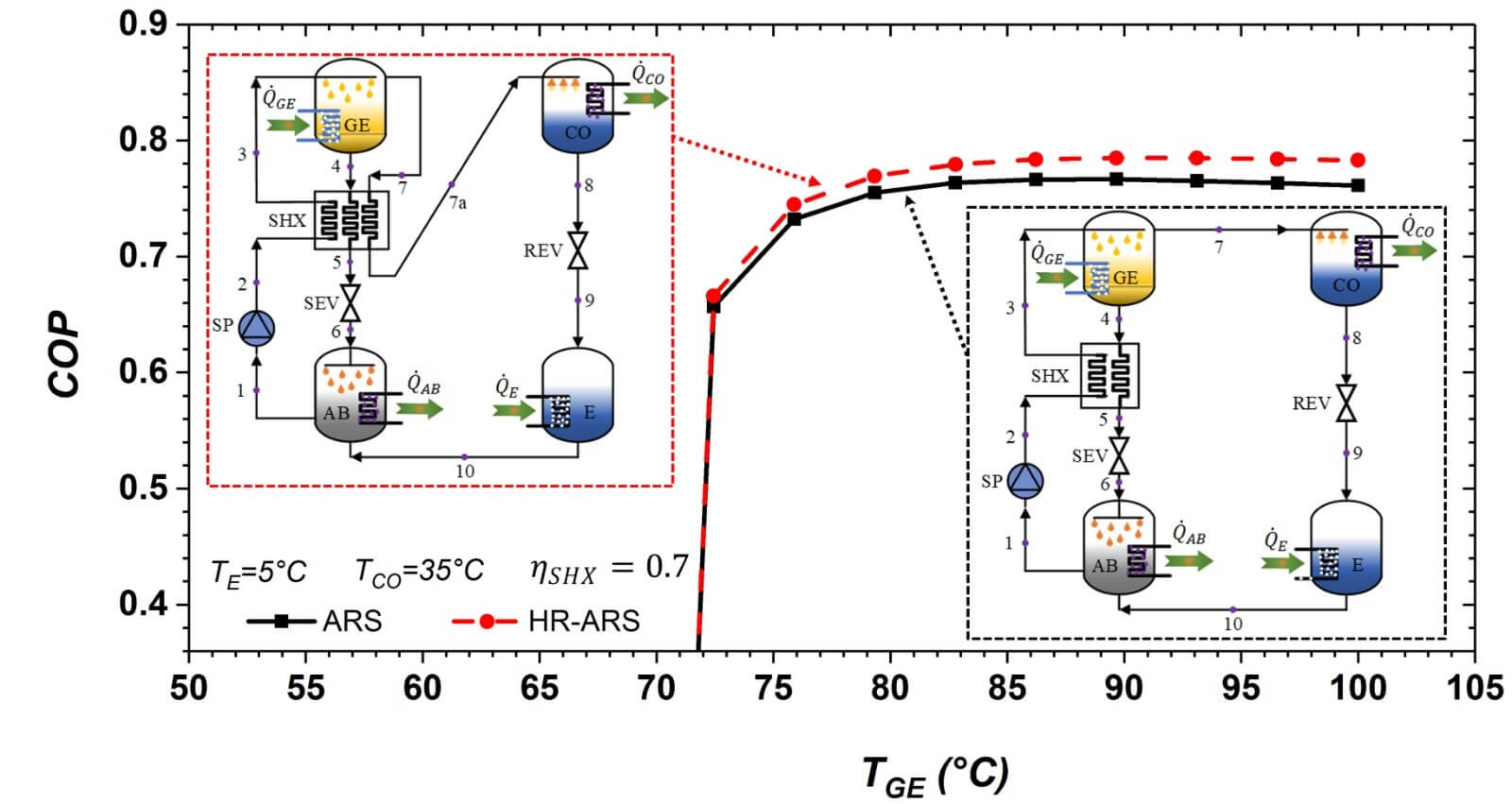
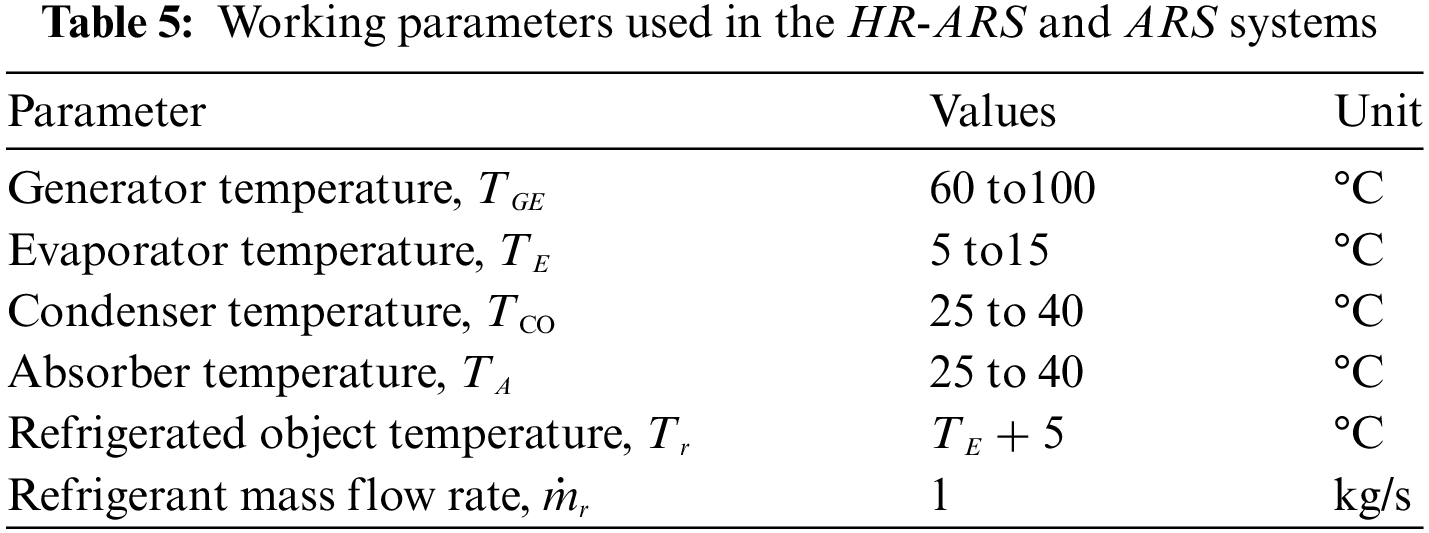
Fig. 2 displays the variations of COP with TGE and TCO = TA (30°C, 35°C and 40°C). For the analysis, TE and ηSHX are kept fixed as 5°C and 0.7, respectively. From the results, it is observed an increase of the COP in the ARS and HR-ARS as the in the generator temperature increases. Initially it increases until an optimal value and then it decreases slowly, these behaviors are in concordance with the results obtained by Ahmad et al. [12]. It is due to that, to increase TGE causes that the concentration circulation ratio decreases and subsequently, the energy supplied in the generator also decreases. The reason for this effect is showed in Fig. 2. It also can be found that the HR-ARS system presents a higher COP than the conventional ARS system over the entire range of generator temperatures. Furthermore, to reduce TCO from 40°C to 30°C, reduces TGE to approximately 22°C, while the COP for the ARS and HR-ARS can be improved by around 5.77% and 6.33%, respectively. Comparatively, the COP for the HR-ARS system is 2.57% higher than the ARS system at TCO = 40°C. However, when the condenser temperature is reduced at TCO = 35°C and 30°C, the COPs for the HR-ARS system results be 2.86% and 3.11% higher than the ones obtained by the ARS system. Also, it is obtained that the maximum COP = 0.8173 in the HR-ARS is found at TCO = 30°C, but at TCO = 35°C and 40°C these values are of 0.785 and 0.756, respectively. In contrast, in the ARS system, the maximum COPs at the considered condenser temperatures are 0.801, 0.766 and 0.737, respectively. The former is because, if TCO decreases, PGE also decreases, so that the heat supplied in the generator is reduced and then, the COP of the systems will be improved.

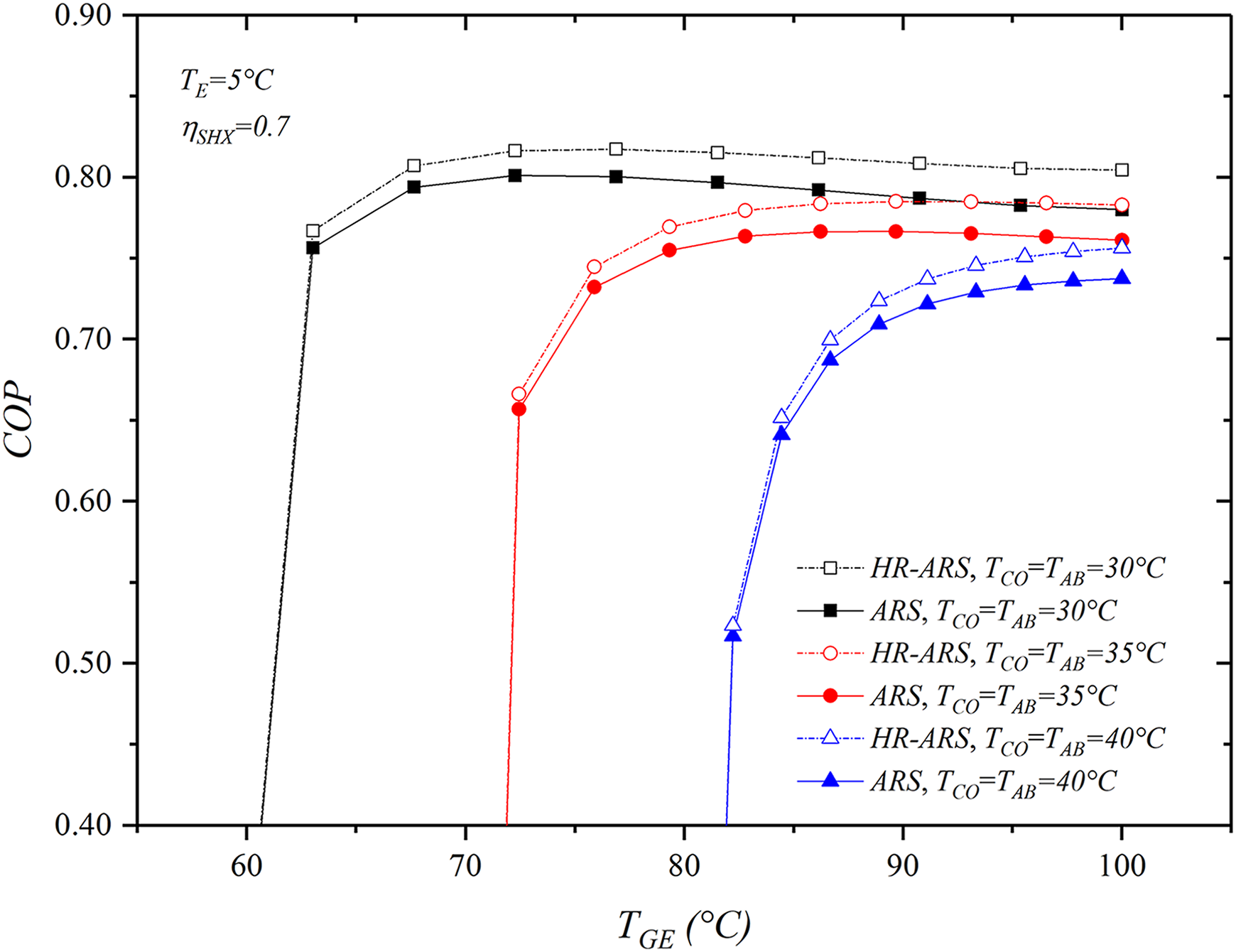
Figure 2: Variations of COP with TGE for the HR-ARS and conventional ARS at different condenser temperatures

6.2 Variation of TGE on QGE and QCO

Fig. 3 shows the influence of TGE on the QGE and QCO in the alternative HR-ARS and ARS systems. It can be seen that the load in the generator is reduced between 26% to 28% in both systems as TGE increases and for high TGE, the thermal load in the generator becomes almost constant, while the condensation heat increases between 1.2% to 3.3% as the generation temperature also is increased. Lamine et al. [36] have found that the generator load is reduced with increasing the generator temperature, although condenser heat increases slightly. Reductions of 21% in the generator’s heat load have also been found by Marashli et al. [37] in a basic LiBr/Water absorption chiller varying the generator temperature from 95°C to 105°C. For all ranges of generator temperatures, the thermal load in the generator and condenser results be lower in the HR-ARS system than in the conventional ARS. It is due to that in the HR-ARS system, part of the heat in the condenser is recovered via the solution heat exchanger, then the temperature and enthalpy at the inlet in the generator (Point 3) increase and the temperature at the inlet in the condenser (Point 7a) is reduced, so lower energy in the generator and condenser is required. Under the operating conditions of TE = 5°C, TCO = TAB = 30°C and ηSHX = 0.7, the heat supplied in the HR-ARS system is around 1.51%–3.76% lower than the one required in the ARS system. On the other hand, at TGE = 60°C, the condensation heat for the HR-ARS system is 1.51% less than the conventional ARS, but when the generation temperature is increased at TGE = 100°C, it can be reduced up to 3.76%. It leads to a reduction in the heat exchanger area and the manufacturing cost of the condenser and generator are minor than the basic ARS.

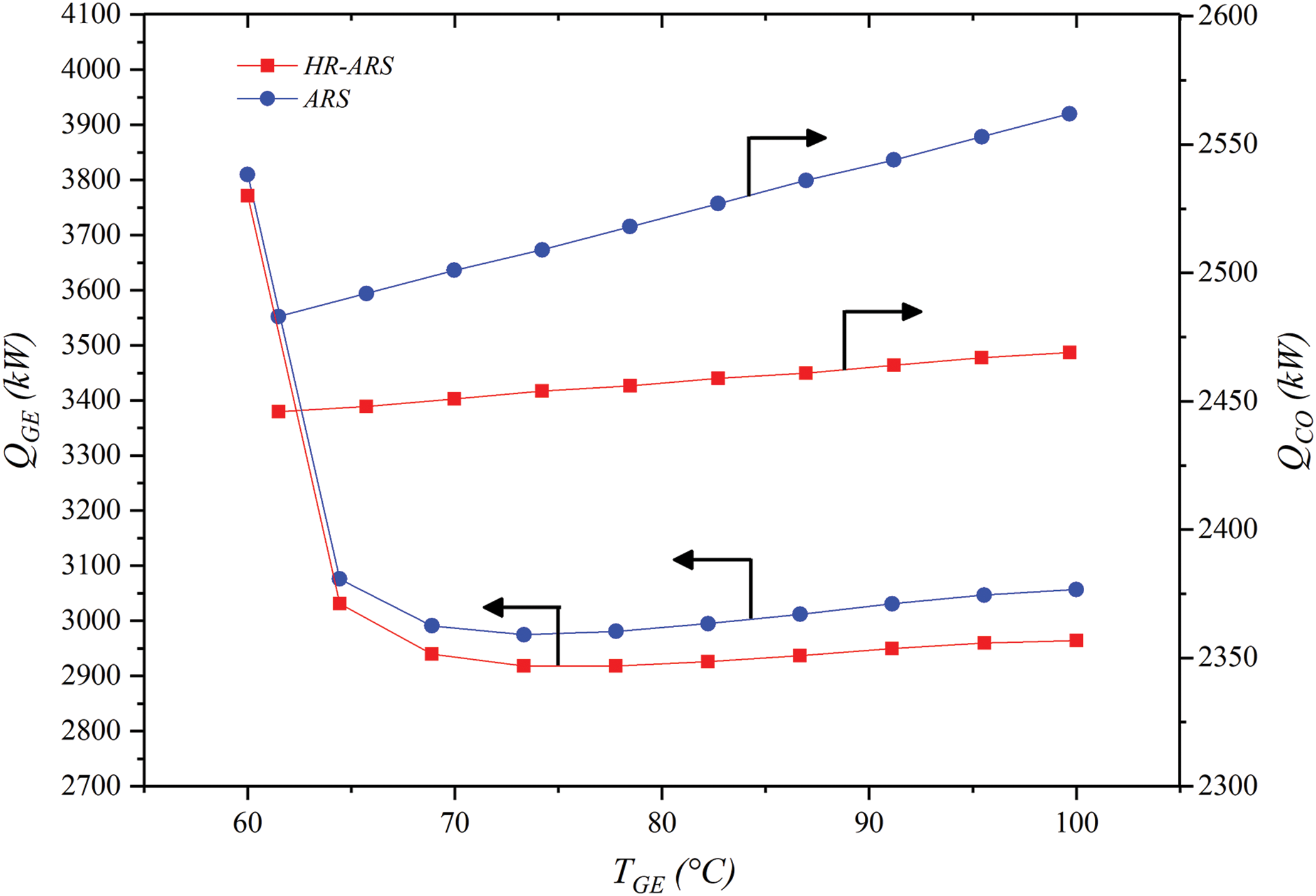
Figure 3: Effect of TGE on QGE and QCO for the HR-ARS and ARS

Fig. 4 illustrates the variations of the COP for the HR-ARS and ARS cycles with respect to the condenser temperature (T8). For the study, both the condenser and absorber were considered to be at the same temperature (TCO = TAB). The COP was analyzed under three different generator temperatures (TGE = 80°C, 90°C and 100°C) and kept as constant TE = 5°C and solution heat exchanger effectiveness = 0.7 in order to cover a greater range of operating conditions. It was found that raising TCO reduces the coefficient of performance in both systems and these behaviors have also been found by Kaynakli et al. [38]. When TGE = 80°C, the reductions are around 23%, but at generator temperatures of TGE = 90°C and 100°C, the reductions are around 11% and 9%, respectively. The reason is because, when the condenser and absorber temperature increase, the generation pressure also becomes higher and the strong solution concentration at the generator inlet is reduced, then, the thermal load of the generator rises and the COP of the systems gets worse.

Figure 4: Influence of TCO = TAB on COP for the HR-ARS and conventional ARS

The highest energy performance is obtained at low condenser and generator temperatures. For example, at TCO = 25°C and TGE = 80°C, the COP for the HR-ARS and ARS systems is 0.8386 and 0.8179, respectively. When TGE rises at TGE = 90°C, the highest COPs for the HR-ARS and ARS are 0.8286 and 0.8048, but at TGE = 100°C, energy performances are 0.8026 and 0.8301, respectively. In comparison, the COP for HR-ARS is between 2.53%–3.42% higher than that for ARS. The results also show that at generator temperatures of 100°C and 90°C, both systems can work without problem in all range of condenser temperatures, although, at TGE = 80°C, these only can operate in a condenser and absorber temperature range of 25°C–38.3°C.

Finally, the highest energy performances are found at TGE = 80°C and TCO < 33°C, while for a TGE = 100°C, is recommended to work both systems at TCO > 36.66°C to reach the highest energy performances.

The influence of TE on COP in the alternative and conventional ARS systems is shown in Fig. 5. In these calculations, TCO = TAB = 30°C, TGE = 80°C, 90°C and 100°C, ηSHX=0.7 were assumed. As it is expected, increasing TE has a positive effect on the COP and this is slightly higher as TGE decreases [39]. This is clarified by the fact that less refrigerant capacity is produced from the evaporator as TE decreases, then if TE is increased better COP is obtained and it is higher than one with a lower TE. On the other hand, at higher generator temperatures, more refrigerant mass rate is produced, improving the COP in both systems.

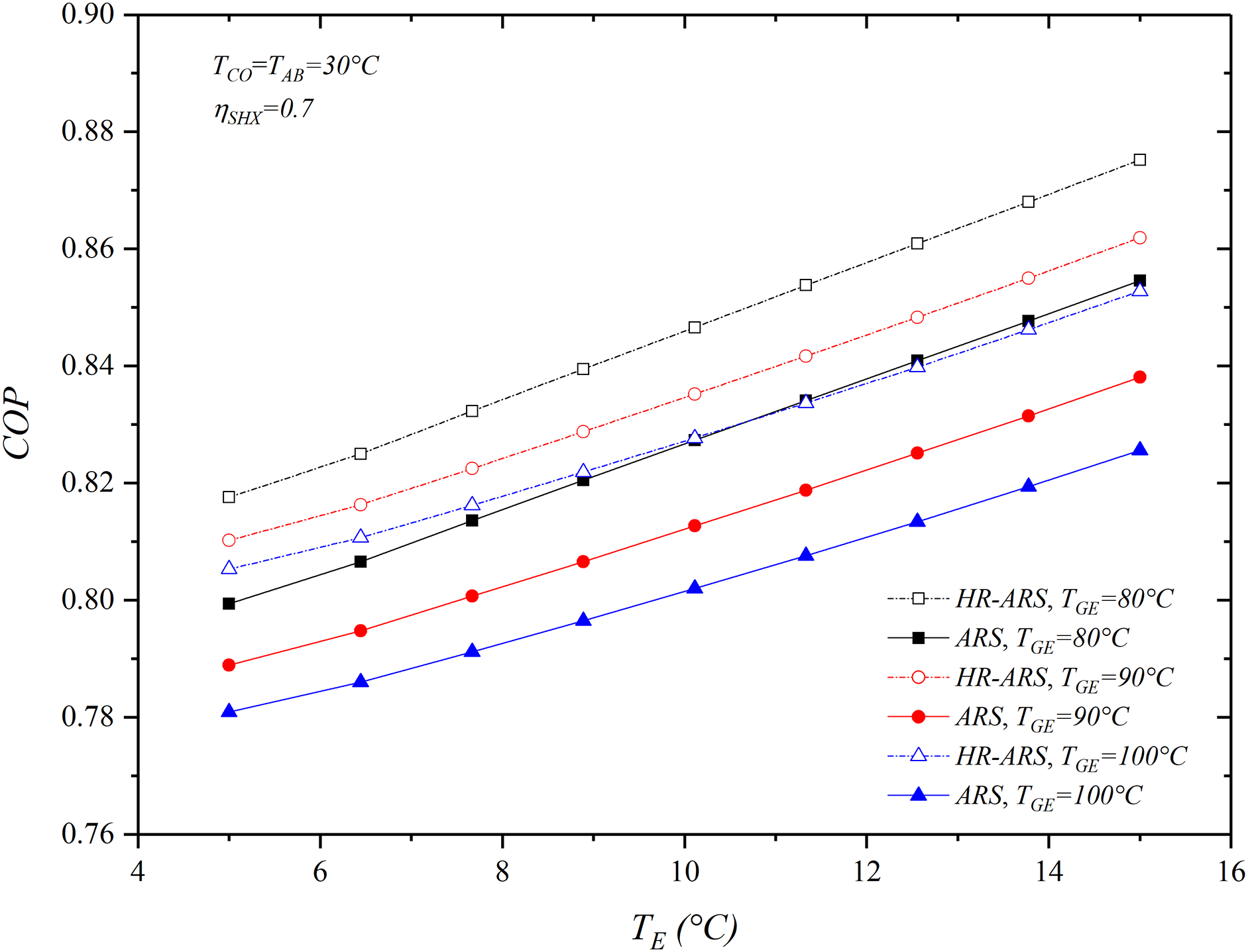
Figure 5: Effect of TE on COP for the HR-ARS and ARS

The best coefficient of performance is obtained at the lowest generator temperature (TGE = 80°C) and the highest evaporator temperatures (TE = 15°C), while the lowest one corresponds at high generator temperatures (TGE = 100°C). For a TGE = 80°C and TE ranging from 5°C to 15°C, the COP in the HR-ARS increases by 8.06% and for the ARS, the increase is 7.89%. When the generator temperature is raised at TGE = 90°C, the COP increases by 7.20% and 7.03%, respectively. However, at TGE = 100°C, the COP augmentation is 6.40% and 6.60%, respectively. It was found that the COP for the HR-ARS cycle is around 3% superior to that found with the ARS at the three different generator temperatures here analyzed.

Fig. 6 depicts the effect of ηSHX on the COP at different generator temperatures (TGE = 80°C, 90°C and 100°C) for the proposed HR-ARS system as well as for the conventional ARS, considering as constant the evaporation and condensing temperatures of 5°C and 30°C, respectively. It can be seen that the COP for both cycles increases as ηSHX effectiveness increases and these trends are like for the generator temperatures here studied, which is in concordance with those results obtained by References [27,38]. The reason for this change is that as the ηSHX effectiveness increases, the generator temperature entering the generator also increases, reducing the thermal load in the generator, which results be lower for the HR-ARS system than that required for the ARS system.

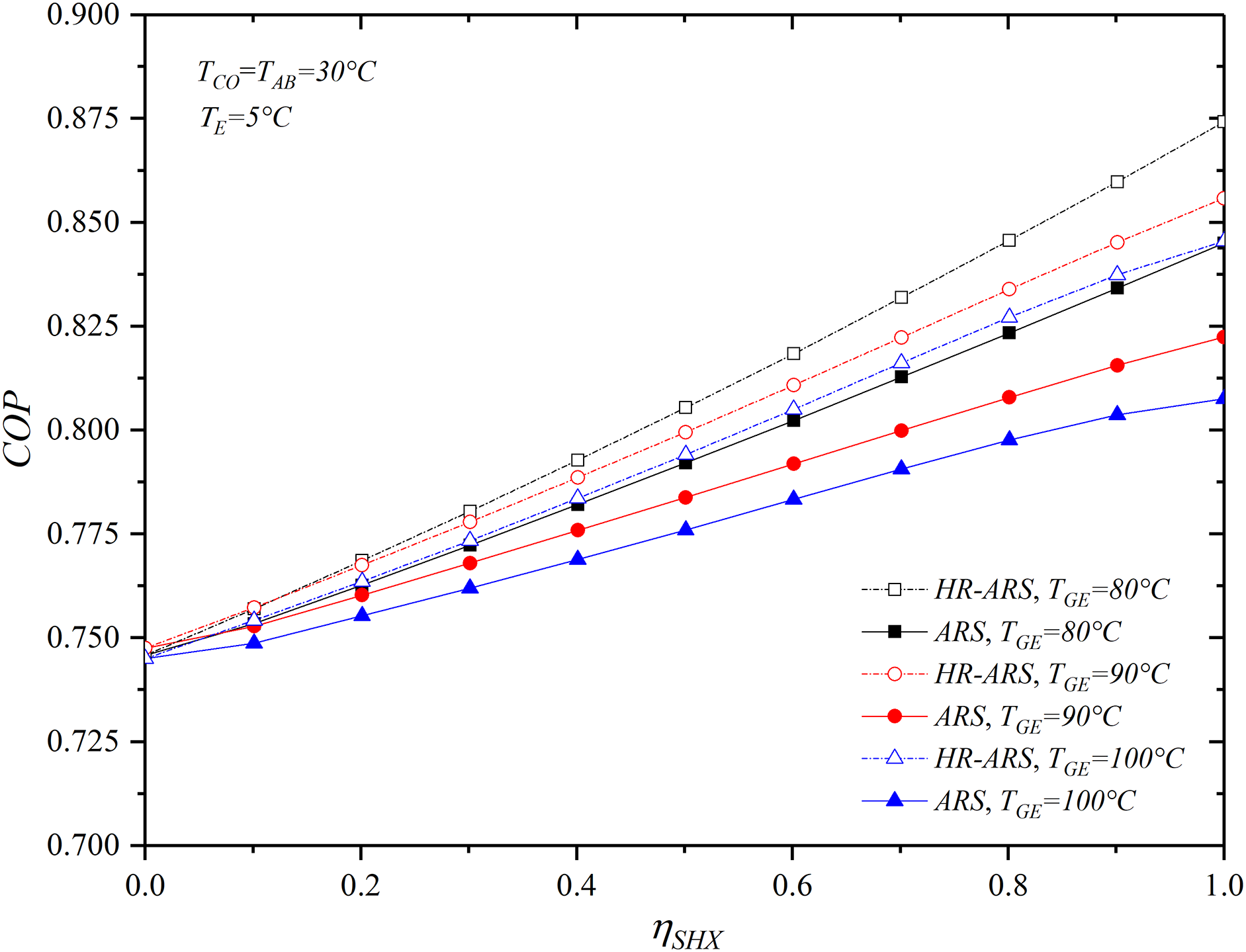
Figure 6: Effect of ηSHX on the COP for different TGE values

The results also show that for all ηSHX effectiveness and TGE range, an increase between 8.40%–19.25% on the COP is found for the ARS cycle. When the HR-ARS cycle is used, these increases vary between 13.48%–22.62%, which means that the HR-ARS is better in 3.37% to 5.08% than the conventional ARS system. It also is appreciated that the COP is lower as TGE rises. It is because, if the generator temperature gets higher, the concentration difference between the weak and strong solution also increases, then improves the COP for both systems. For example, at a ηSHX=1 and TGE = 80°C, the COP for the HR-ARS cycle is 0.874 and at TGE = 100°C is 0.845, while for the ARS system, the COPs obtained are 0.845 and 0.807, respectively. In comparison, the HR-ARS has between 3.43%–4.70% higher COP than the conventional ARS system at the mentioned generator temperatures.

Fig. 7 illustrates the influence of TGE on the exergetic performance of the HR-ARS and ARS systems at different condenser temperatures and fixed values of evaporation temperature and solution heat exchanger effectiveness at 5°C and 0.7, respectively. The results show that the exergy efficiency is higher as the generator temperature rises, as well as the condenser temperature decreases, then, it reaches an optimum value and after is reduced. These observations also have been found by Kaushik et al. [40] in a conventional absorption cycle for TGE varying from 55°C–105°C and TCO values of 30°C, 35°C and 40°C. The before is because a high generator temperature produces more vapor refrigerant, however, it implies a higher heat input to the system and then, the irreversibilities in the generator also increase. However, reducing the condenser temperature increases the refrigerant effect and reduces the irreversibility in the cycle, improving the energy and exergy performance.

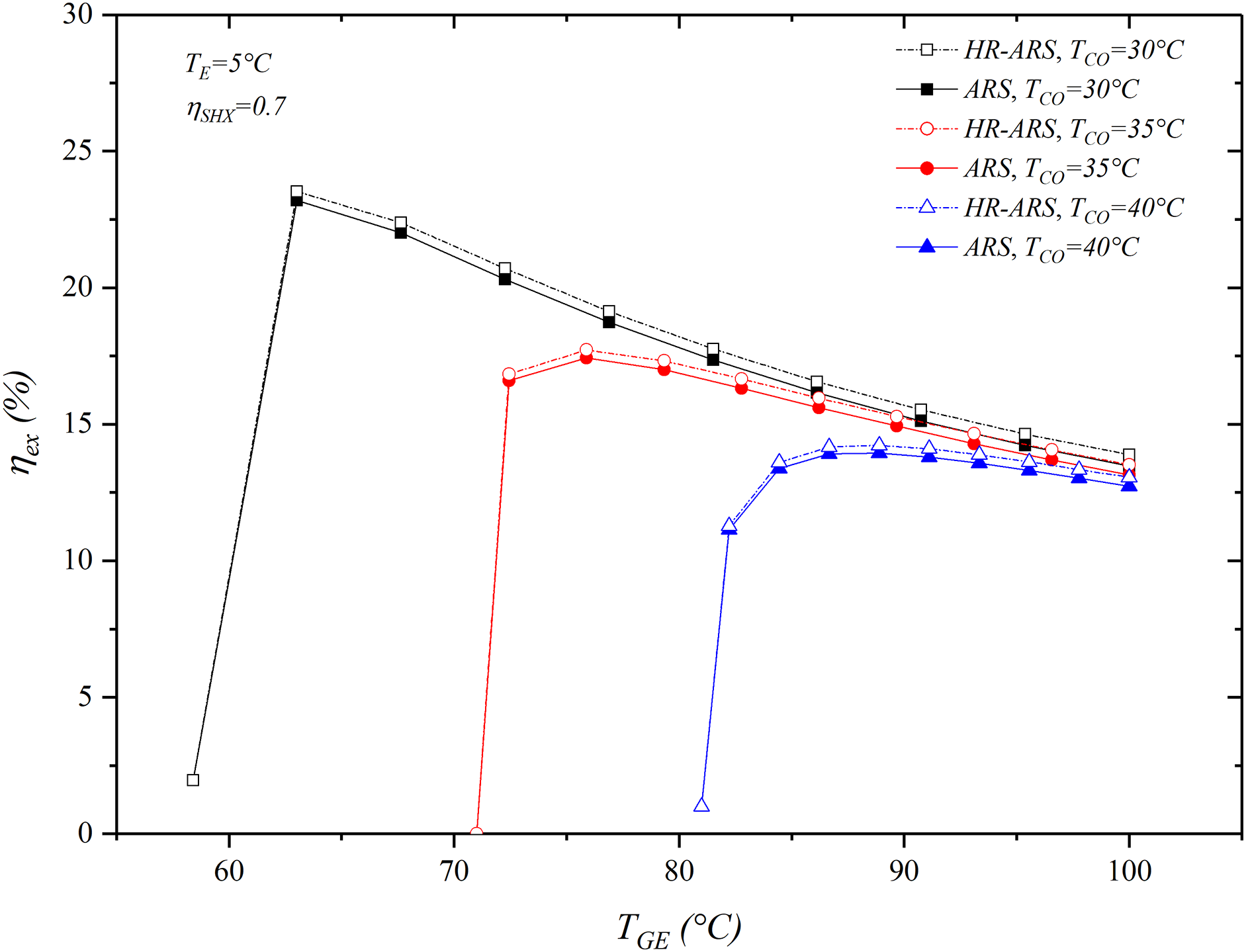
Figure 7: Effect of TGE on ηex for the HR-ARS and conventional ARS at different condenser temperatures

From the figure, it is found that at TCO = 30°C, the maximum exergy efficiency of 23.53% and 23.22% are obtained with the HR-ARS and ARS systems at the corresponding generator temperature of 63.02°C. When the condenser temperature rises to 35°C, the optimum exergy efficiency obtained for both systems are 17.72% and 17.43%, respectively, which are found at a generator temperature of 67.64°C. However, at TCO = 40°C, its maximum exergy efficiency is 14.23% and 13.95%, respectively, at TGE = 76.88°C. The results also show that at TGE = 100°C, the exergetic efficiencies for the considerate condenser temperatures are very similar.

The influence of TE and TGE on exergy performance for HR-ARS and ARS was studied and compared, taking as constant TCO = TAB = 30°C and a solution heat exchanger effectiveness = 0.7, and its behavior is shown in Fig. 8. When TE increases, the exergy efficiency is reduced between 17%–20%, and this increases between 2.3%–6.3% as the generator temperature decreases. As is presented in the figure, the highest exergetic efficiency for the HR-ARS (ηex=29.49%) and ARS (ηex=28.84%) are obtained at low evaporator and generator temperatures (TE = 5°C and TGE = 80°C), while that at the same TE and TGE = 100°C, the lowest exergetic efficiency for the HR-ARS and ARS are ηex=22.57% and ηex=21.89%, respectively. It means that at the mentioned evaporator and generator temperatures, the exergetic performance for the HR-ARS is around 0.7% superior that the traditional ARS. It also is found that, when the evaporator temperature is increased until TE = 15°C, the exergetic efficiency for the HR-ARS system is very similar for the three generator temperatures under study, showing only a difference of 0.22% with respect to the values found for the conventional ARS system.

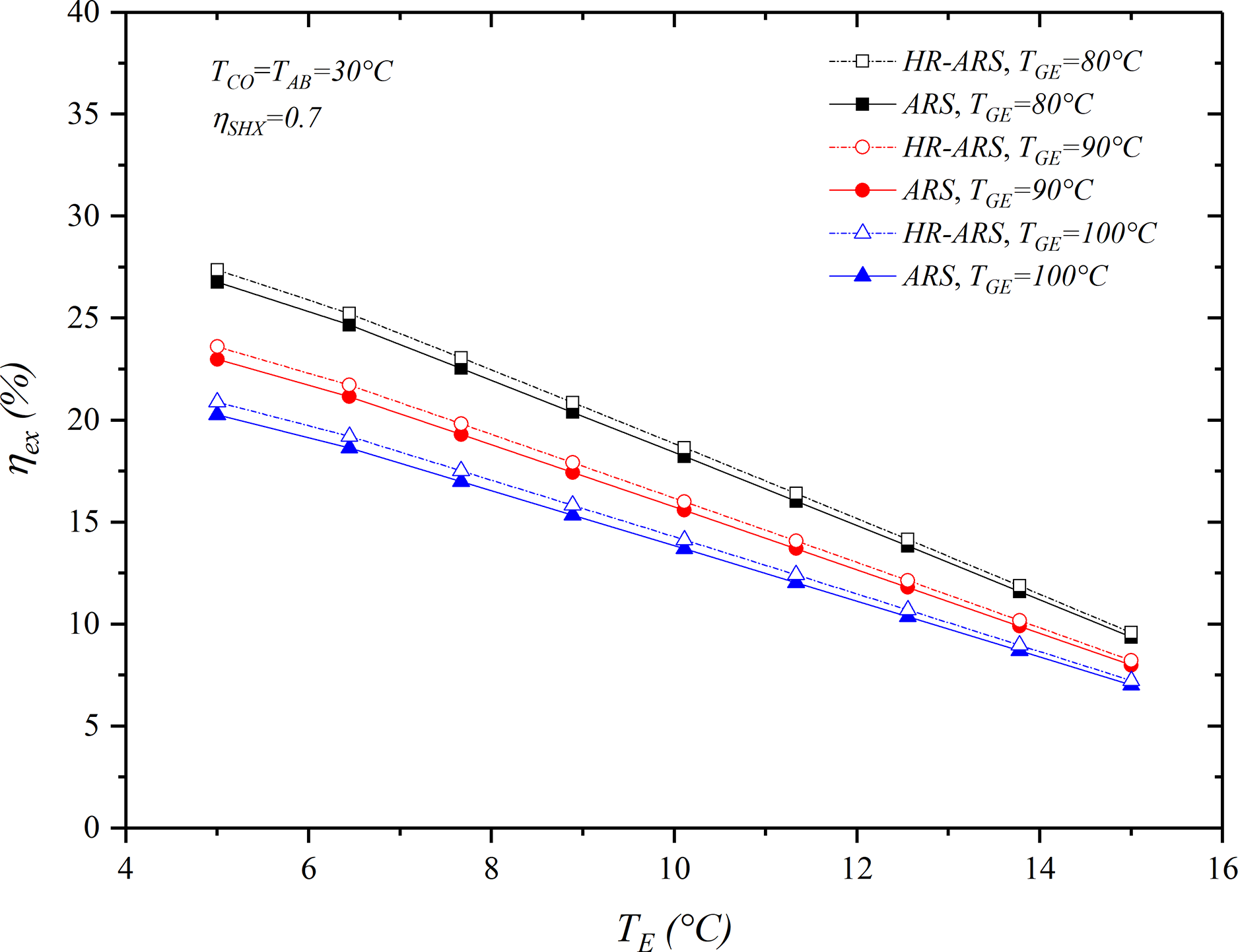
Figure 8: Effect of TE on ηex for the HR-ARS and conventional ARS at different generator temperatures

Fig. 9 shows the influence of TCO = TAB on the exergetic efficiency of both systems. A reduction in the exergy efficiency is found as TCO = TAB increases, and this is more significant as the generator temperature decreases at 80°C. It was found that when TGE = 90°C and 100°C are considered, the systems can operate in the entire temperature range in the condenser, while at the generator temperature of 80°C, both systems work adequately at condenser temperatures between 25°C to 38.33°C. Furthermore, when the systems work with the lowest TGE and TCO, the highest exergetic efficiencies can be obtained, while the lowest ones are found at high generator temperatures.

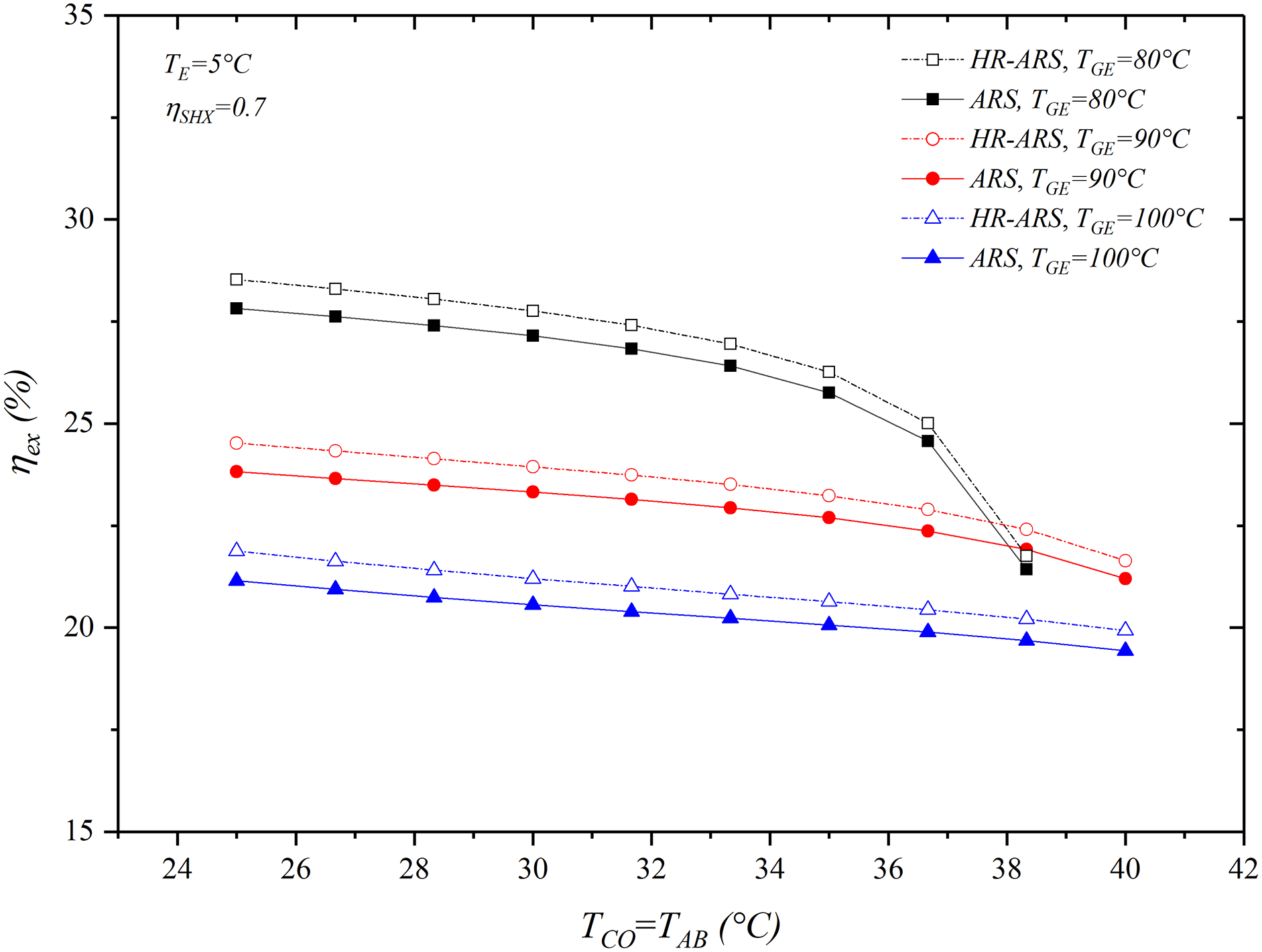
Figure 9: Influence of TCO = TAB on ηex for the HR-ARS and conventional ARS

The results also show that the highest exergetic efficiency of 28.53% is obtained with the HR-ARS system operates at TCO = 25°C and TGE = 80°C, but it is reduced by 4.02% and 6.63% when the TGE decreases from 90°C and 100°C, respectively. At condensation and generator temperatures of 40°C and 100°C, respectively, the exergy efficiency is 19.93% for the HR-ARS system and 19.43% for the ARS. However, by reducing the generator temperature to 90°C, the exergy efficiency increases by 8.58% with the HR-ARS and 9.10% with the ARS system. It also found that the HR-ARS presents between 2.55% to 3.33% higher exergy performance when TCO varies from 25°C to 40°C, in comparison with those results found with the ARS system.

The variations of the exergetic efficiency with ηSHX and TGE in both systems are shown in Fig. 10. The exergetic efficiency increases as ηSHX increases and decreases as TGE is reduced. The best exergy efficiency values are obtained in both systems at the maximum solution heat exchanger effectiveness. Furthermore, when ηSHX varies from 0 to 1, the exergy efficiency for the HR-ARS system increases between 14.88% to 20.07%, while for the conventional ARS refrigeration system, the increases are in the order of 9.79% to 16.05%. The results also show that at the maximum charge of the solution heat exchanger, the exergy efficiency of the HR-ARS cycle is between 3.43%–4.70% higher than the ARS system. When both systems work without a solution heat exchanger, the exergy efficiency at TGE = 80°C is 16.04%, while when TGE is increased to 90°C and 100°C, the exergy efficiencies are 14.10% and 12.56%, respectively. This represents that at the generator temperature of 80°C, the exergy efficiency is 1.94% and 3.48% higher than that at generator temperatures of 90°C and 100°C, respectively.

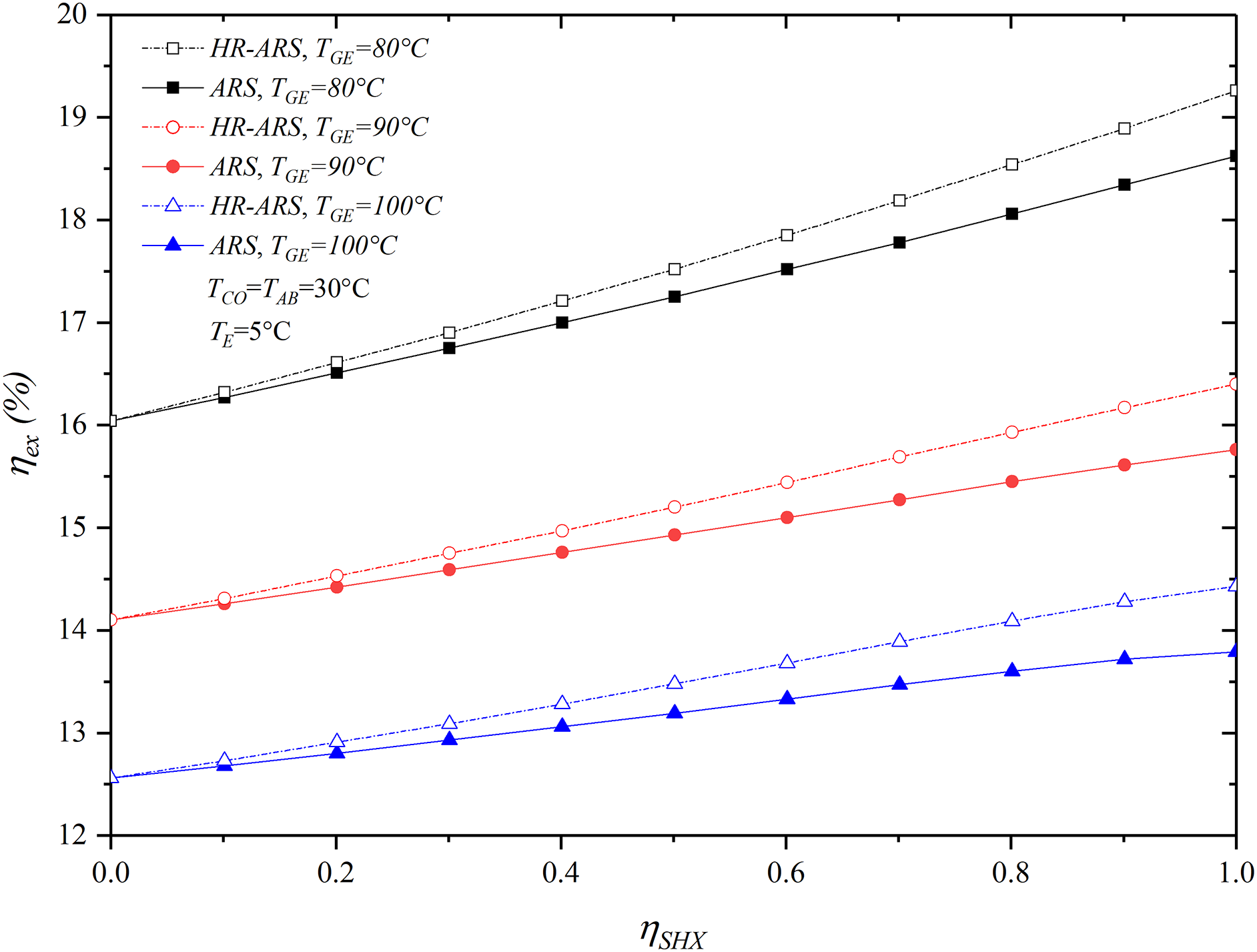
Figure 10: Effect of ηSHX on ηex for the HR-ARS and conventional ARS

Fig. 11 illustrates the impact of TGE on the exergy destruction in the different components of the HR-ARS and ARS cycles. As the generator temperature increases, the absorber, generator and condenser increase their exergy destruction rate, while the opposite situation occurs with the evaporator, refrigerant throttling valve and solution heat exchanger. It was found that the evaporator, generator and absorber are the main components to contribute to the total exergy destroyed. At low generator temperatures, the evaporator has the highest exergy destruction with around 49%, followed by the absorber with 17% and the generator with 12%, while at high generator temperatures (TGE = 100°C), the largest contributors to the irreversibilities of the system are the absorber (38%), generator (36%) and evaporator (20%). The condenser and refrigeration expansion valve do not contribute significantly to the total exergy destruction.

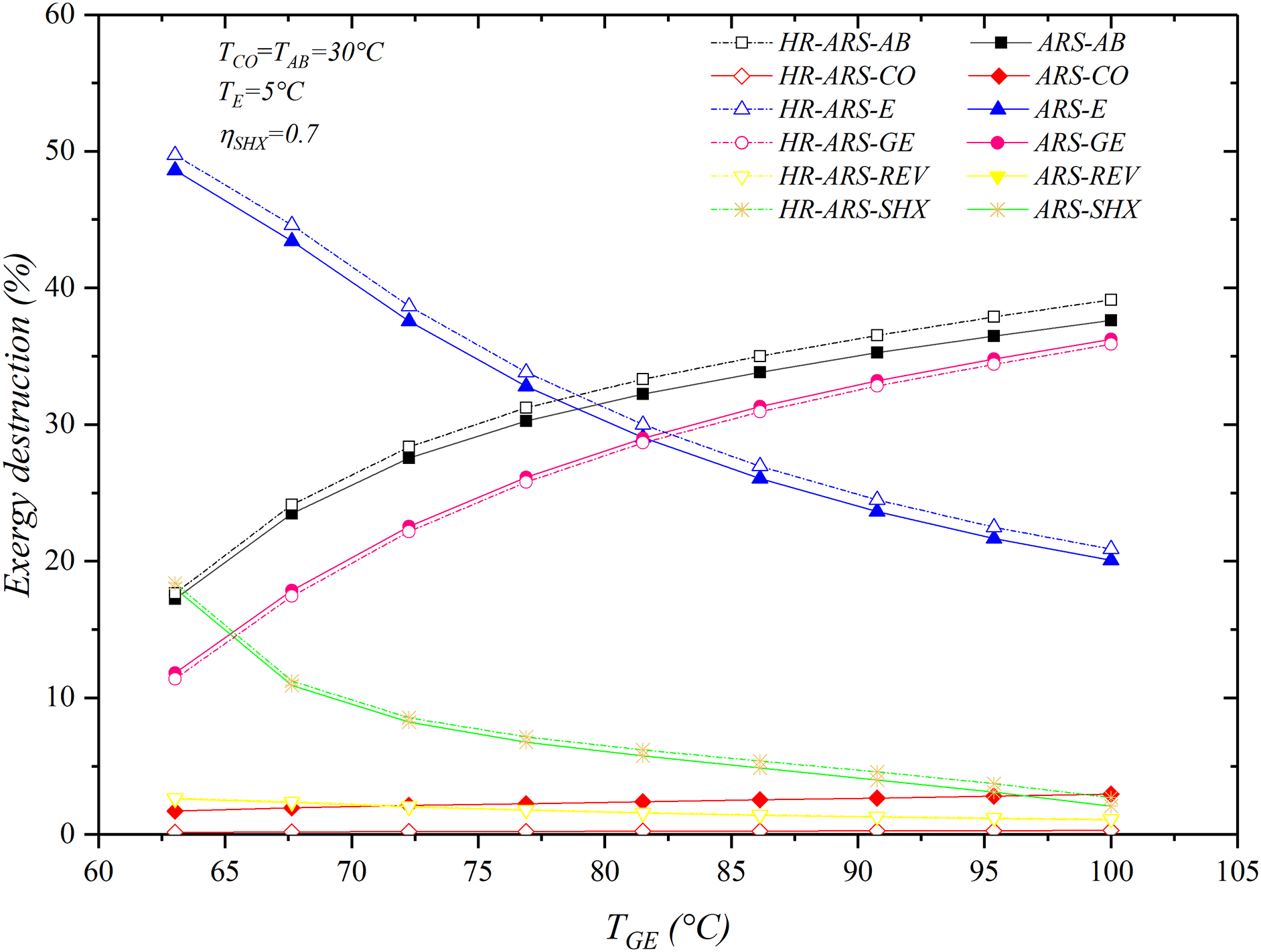
Figure 11: Effect of TGE on exergy destruction for the HR-ARS and conventional ARS

The irreversibilities in the evaporator are due to the difference of temperature between the surroundings and the fluid, but the irreversibilities in the absorber are caused by the difference of temperature between the component and the environment, which can be reduced by increasing its surface area, while the exergy destruction in the generator is outstanding to the difference of temperatures between the heat source and the working mixture. It can be also seen that, for all range of generator temperatures, the exergy destroyed in the absorber and generator increase in 21.49% and 24.51%, respectively, while in the evaporator and solution heat exchanger it is reduced 28.87% and 15.95%, respectively. From the figure, it is seen that the irreversibilities for the HR-ARS system are slightly superior to the ARS system in the most of the components, except for the condenser and generator, which are reduced in 0.47% and 2.65%, respectively.

Finally, in order to improve the second law efficiency, more emphasis could be made in the evaporator, absorber and generator in the overall design.

Fig. 12 shows the behavior of the destroyed exergy concerning the condensation temperature. The results show a reduction in the exergy destroyed in the absorber and generator as TCO increases, while the opposite situation occurs with the evaporator, solution heat exchanger and refrigerant throttling valve as the temperature condensation increases, except in the condenser, where no significant variations are shown. It can be observed that the exergy destroyed in the absorber and generator are very similar at low condenser temperatures (TCO = 25°C) and these components are responsible to contribute in almost 80% of the overall exergy destroyed, similar percentages have also been found by Cai et al. [41]. It can also be observed that the exergy destroyed in the solution heat exchanger resulted higher for the other components at TCO > 37°C, while the exergy destruction is slightly reduced in the evaporator, refrigerant valve and condenser.

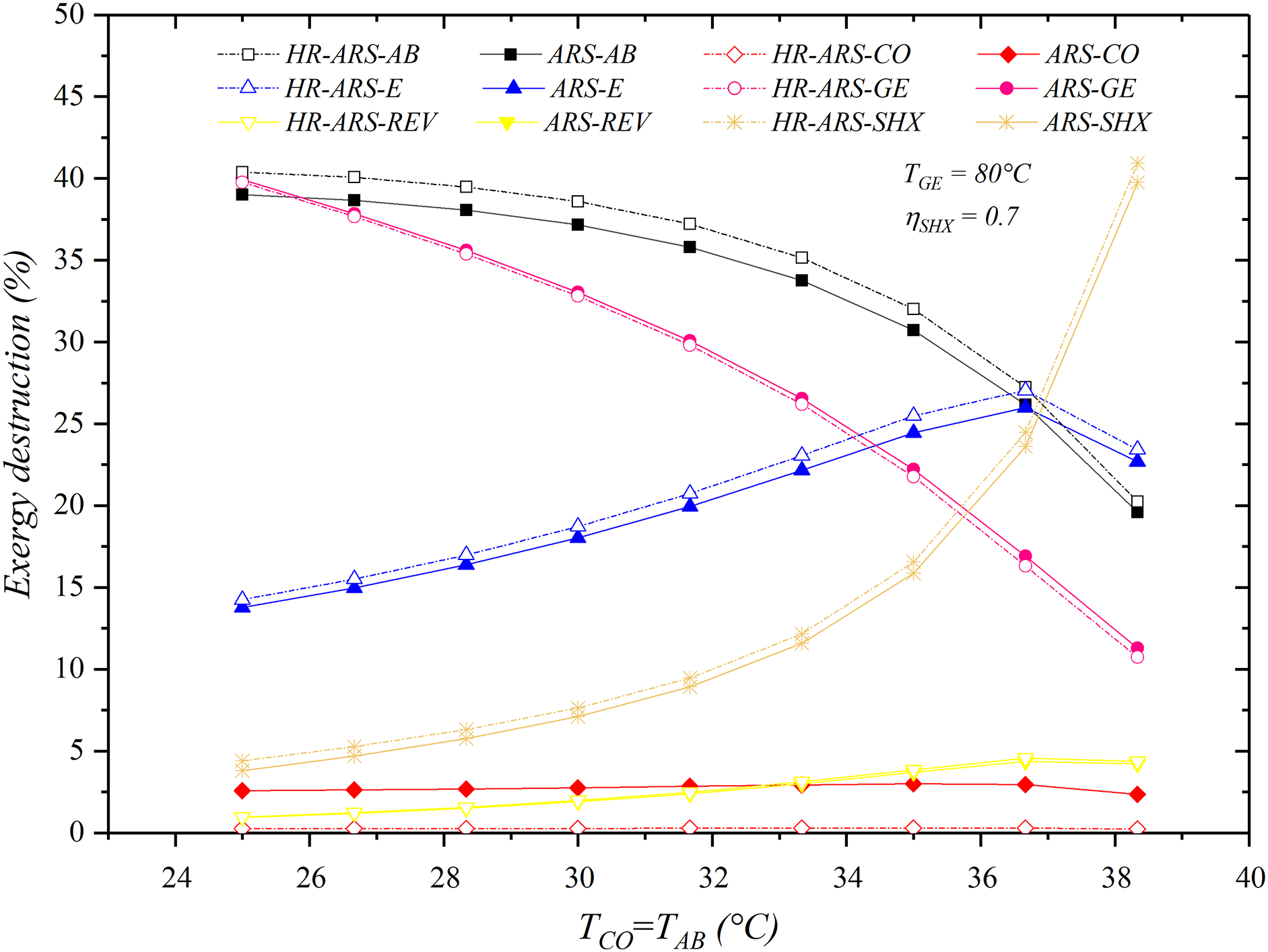
Figure 12: Effect of TCO = TAB on exergy destroyed for the HR-ARS and ARS

For the entire temperature range in the condenser, the exergy destroyed for the absorber and generator is reduced by 19.4% and 28.64%, while for the case of the evaporator, solution heat exchanger and refrigerant valve, the exergy destruction increases by 8.9%, 35.95% and 3.30%, respectively. For high condenser temperatures (TCO = 40°C), the largest exergy destroyed is obtained in the solution heat exchanger, followed by the evaporator, absorber and generator. It was found that in both systems, the largest exergy destroyed corresponds to the solution heat exchanger at TCO > 36.66°C.

Fig. 13 shows the influence of the evaporation temperature on the exergy destroyed for the HR-ARS and ARS systems. If TE is increased, the exergy destroyed in the generator also increases, although the opposite occurs with the other components in both systems. The results also show that the evaporation temperature does not present significant effects on the exergy destroyed in the throttling valve and condenser.

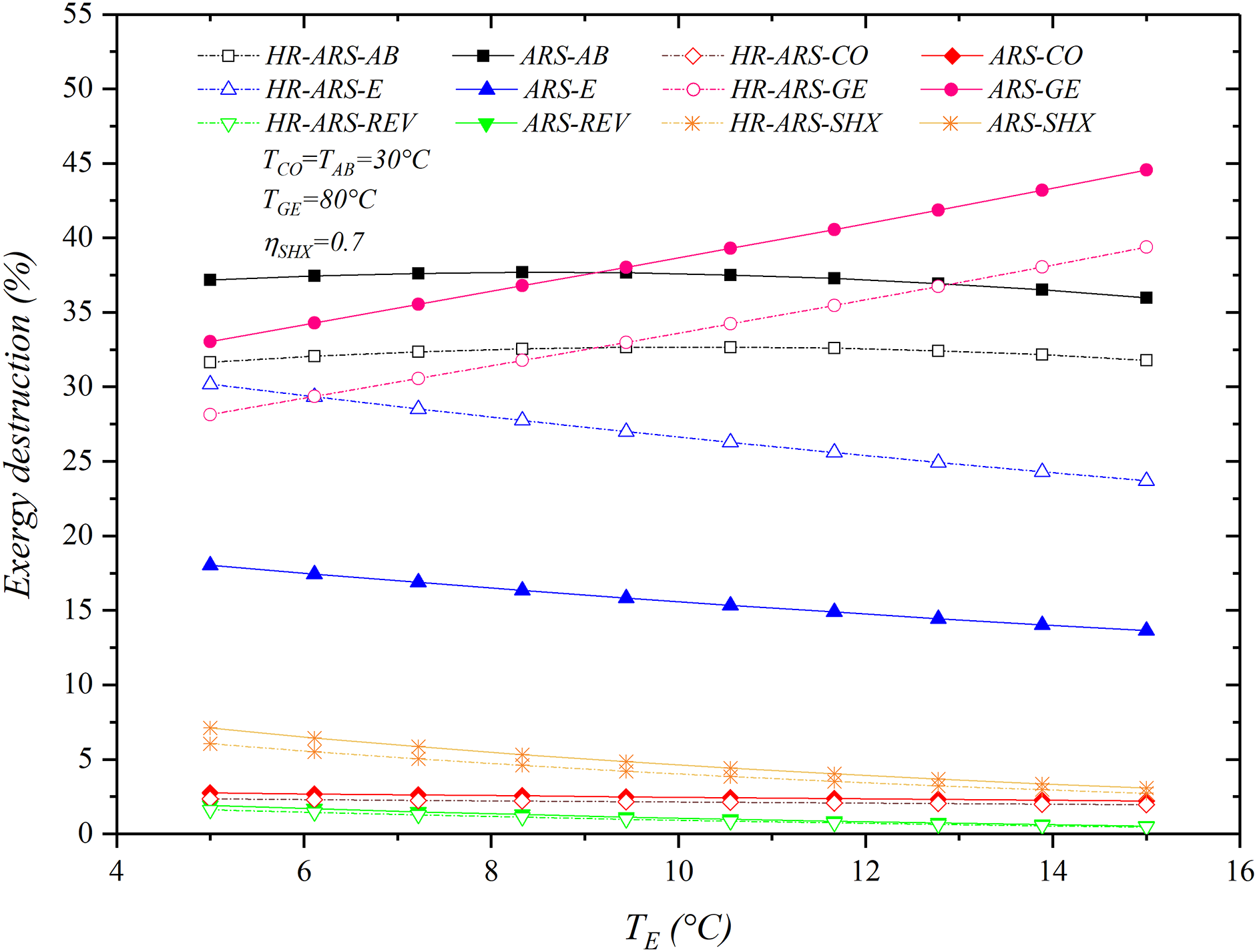
Figure 13: Effect of TE on exergy destruction for the HR-ARS and conventional ARS

The results reveal that of the overall exergy destroyed, 88% is mainly outstanding to the absorber, generator and evaporator in both systems, which is obtained at TE = 5°C. For a TE = 15°C, these components contribute to 94% of the total exergy destroyed. The absorber presents the largest amount of exergy destroyed at low evaporation temperatures, followed by the generator and absorber, while at high evaporation temperatures, the generator is the main component contributor to the exergy destruction. For evaporator temperatures ranging from 5°C to 15°C, the exergy destroyed in the generator increases by 12%, while for the absorber, evaporator, solution exchanger, condenser and refrigeration expansion valve, the exergy destroyed is reduced by approximately 1.19%, 4.39%, 4.04%, 0.54% and 1.38%, respectively. Comparatively, the exergy destroyed is lower for almost all of the components for the HR-ARS in all ranges of evaporator temperatures than the ones for the ARS system, except for the evaporator, which increases.

The contribution of the exergy destroyed for different solution heat exchanger effectiveness in each component for both systems is shown in Fig. 14. As depicted, the main contributor to the exergy destruction in the HR-ARS and ARS systems is the absorber. The other two components with significant exergy losses are the generator and condenser. It is also observed that as the ηSHX increases, the exergy destruction in the generator, SHX and condenser is reduced, while in the other components, there are no significant variations in the exergy destruction. When ηSHX=0.7, the overall exergy destroyed for the HR-ARS is 3.24% smaller than the one found for the ARS system. Moreover, at ηSHX=0.8,0.9and1, the reductions in the total exergy destruction for the HR-ARS are 3.79%, 4.39% and 5.01%, all of these in comparison with the ARS system. This is due to an increase in the ηSHX, which increases the strong concentration temperature at the inlet of the generator reduces the inlet temperature in the condenser and the exergy in the Streams 3 and 11 as well as the heat supplied in the generator and condenser, reducing with this the irreversibilities in these components. Furthermore, the exergy loss in the solution heat exchanger is reduced because the difference in temperature between the poor and strong concentrations also is reduced.

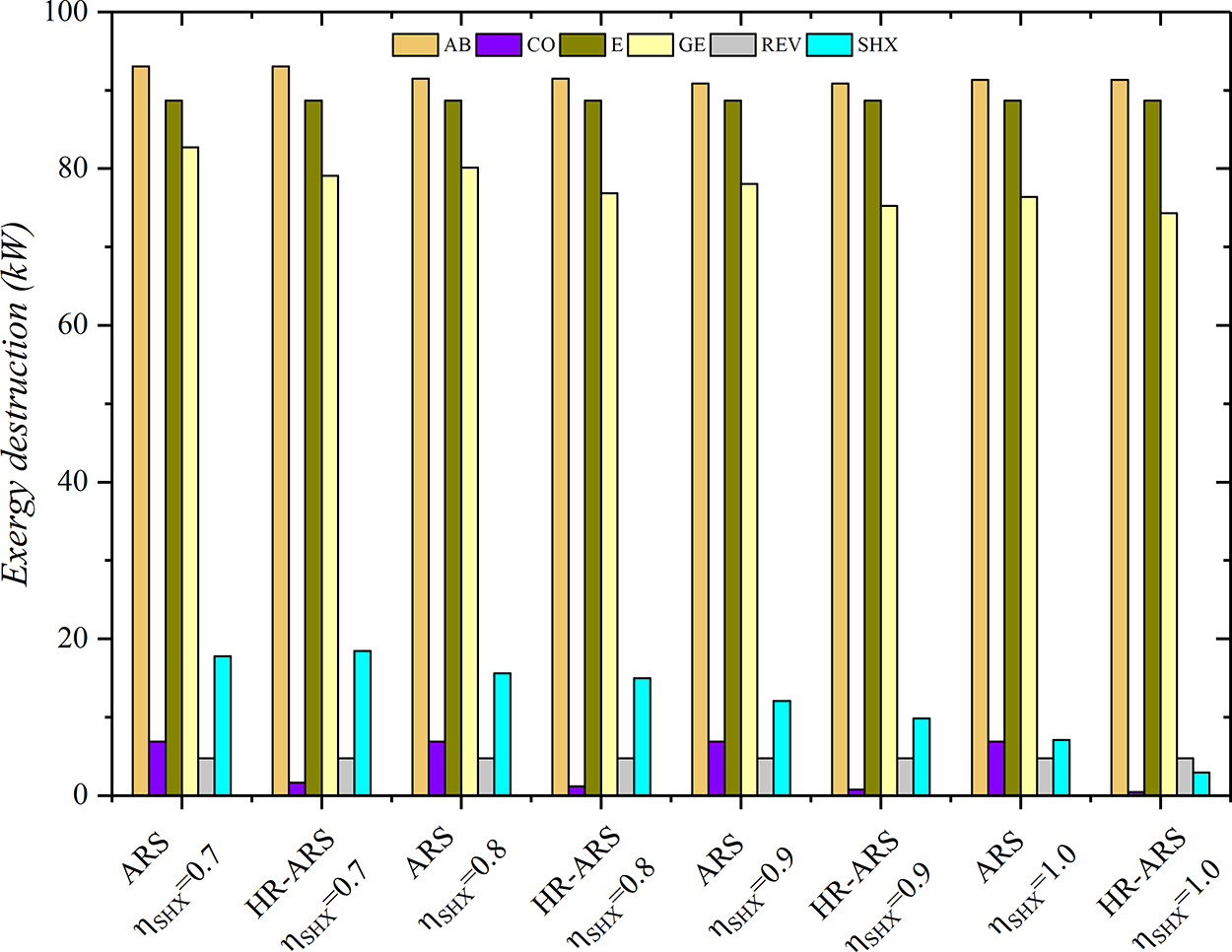
Figure 14: Contribution of exergy destruction for HR-ARS and ARS at different ηSHX

7  Conclusions

In this work, an alternative ARS configuration in which part of the thermal load in the condenser is recovered via the solution heat exchanger and supplied to the system (HR-ARS) was energy and exergy investigated. The influence of the main working parameter as well as the efficiency of the solution heat exchanger on the coefficient of performance, exergy performance and exergy destroyed for the HR-ARS system were analyzed and compared with the traditional ARS system at the same working conditions. The main conclusions of the simulation are described as follows:

1.    The COP increases as TGE and TE increase, but it reduces as TCO increases. The highest COP = 0.8173 is found with the HR-ARS at TGE = 80°C and TCO = 30°C. Comparatively, the COP for the HR-ARS is 2.57% higher than the ARS system at TGE = 80°C and TCO = 40°C. However, it can be improved by 2.86% when TCO = 35°C and 3.11% when TCO = 30°C.

2.    For all ranges of generator temperatures, the thermal load in the generator and condenser in the HR-ARS are between 1.51%–3.76% and 1.2%–3.3% lower than the ones required in the ARS system. It leads to a reduction in the heat exchangers area, so the manufacturing cost of the alternative HR-ARS can be smaller than the ARS system.

3.    The COP and exergy efficiency increase as ηSHX increases. The highest energy and exergy efficiency are obtained at ηSHX = 1. For ηSHX varying from 0 to 1, the exergy performance for the HR-ARS increases between 14.88% to 20.07%, while for the conventional ARS refrigeration system these increases are in the order of 9.79% to 16.05%. Which means that the HR-ARS system has 3.43%–4.70% higher exergy efficiency than the ARS system. On the other hand, for all ranges of solution heat exchanger effectiveness, the HR-ARS system showed 3.79%–5.01% lower exergy destroyed than ARS.

4.    The exergy performance increases as the generator temperature rises, as well as when the condenser and evaporator temperature decrease. The largest values of exergy are obtained at the lowest generator, condenser and evaporator temperatures. The maximum exergy efficiency of 23.53% and 23.22% are found when the HR-ARS and ARS systems operate at TCO = 63.02°C and TCO = 30°C, but it is slightly lower as TCO increases from 30°C to 40°C. It implies that the exergy performance with HR-ARS system is around 0.3% higher than the ARS. Furthermore, when TE increases from 5°C to 15°C, the exergy efficiency is reduced between 17%–20%, and this increases between 2.3%–6.3% as the generator temperature decreases. For all ranges of evaporating temperatures, the exergy efficiency for the HR-ARS is between 0.22% to 0.7% higher than the traditional ARS.

5.    The values of exergy destruction in the generator, absorber and evaporator increase as the generator temperature increases, while that opposite situation occurs with the other components of the system. On the other hand, when TE rises, the exergy destroyed in the generator also rises. The results also showed a reduction in the exergy destroyed in the absorber and generator, while the exergy destruction in the evaporator, solution heat exchanger and refrigerant throttling valve rises if TCO increases, except in the condenser, where no significant variations are shown. Furthermore, the exergy destruction for the HR-ARS resulted 3.24% lower than the ARS system at ηSHX=0.7. However, when ηSHX= 0.8, 0.9 and 1 are used, HR-ARS showed 3.79%, 4.39% and 5.01% lower irreversibilities than the ARS.

6.    Finally, the results revealed that the HR-ARS system can be a suitable alternative in the field of absorption refrigeration because lower energy is required, it has higher energy and exergy performance as well as lower exergy destruction than the ARS system.

Acknowledgement: The authors thank the Autonomous University of Hidalgo State for the support provided for the realization of this research paper.

Funding Statement: The authors not received funding for the realization of this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: J. L. Rodríguez-Muñoz, J. S. Pacheco-Cedeño, I. J. González-Hernández; data collection: J. F. Ituna-Yudonago, J. J. Ramírez-Minguela; analysis and interpretation of results: J. L. Rodríguez-Muñoz, I. J. González-Hernández, J. S. Pacheco-Cedeño; draft manuscript preparation: J. L. Rodríguez-Muñoz, J. F. Ituna-Yudonago, J. J. Ramírez-Minguela. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data will be made available on request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Al-Sayyab AKS, Mota-Babiloni A, Navarro-Esbrí J. Renewable and waste heat applications for heating, cooling, and power generation based on advanced configurations. Energy Convers Manag. 2023;291:117253. doi:10.1016/j.enconman.2023.117253. [Google Scholar] [CrossRef]

2. Gürel AE, Yıldız G, Ergün A, Ceylan I. Exergetic, economic and environmental analysis of temperature controlled solar air heater system. Clean Eng Technol. 2021;6(2):100369. doi:10.1016/j.clet.2021.100369. [Google Scholar] [CrossRef]

3. Belman-Flores JM, Barroso-Maldonado JM, Rodríguez-Muñoz AP, Camacho-Vázquez G. Enhancements in domestic refrigeration, approaching a sustainable refrigerator–a review. Renew Sustain Energ Rev. 2015;51(6):955–68. doi:10.1016/j.rser.2015.07.003. [Google Scholar] [CrossRef]

4. Meraj M, Azhar M, Khan MZ, Salik Anjum MS, Sahil Faiz Ahmad M, Ab Rasheed MF, et al. Thermal modelling of PVT-CPC integrated vapour absorption refrigeration system. Mater Today: Proc. 2021;38(1–2):391–6. doi:10.1016/j.matpr.2020.07.547. [Google Scholar] [CrossRef]

5. Braccio S, Phan HT, Wirtz M, Tauyeron N, Pierres N. Simulation of an ammonia-water absorption cycle using exchanger effectiveness. Appl Therm Eng. 2022;213:118712. doi:10.1016/j.applthermaleng.2022.118712. [Google Scholar] [CrossRef]

6. Kumar A, Rakshit D. A critical review on waste heat recovery utilization with special focus on Organic Rankine Cycle applications. Clean Eng Technol. 2021;5(6):100292. doi:10.1016/j.clet.2021.100292. [Google Scholar] [CrossRef]

7. Misenheimer CT, Terry SD. The development of a dynamic single effect, lithium bromide absorption chiller model with enhanced generator fidelity. Energy Convers Manage. 2017;150(193):574–87. doi:10.1016/j.enconman.2017.08.005. [Google Scholar] [CrossRef]

8. Kallitsis K, Koulocheris V, Pappa G, Voutsas E. Evaluation of water + imidazolium ionic liquids as working pairs in absorption refrigeration cycles. Appl Therm Eng. 2023;233(1):121201. doi:10.1016/j.applthermaleng.2023.121201. [Google Scholar] [CrossRef]

9. Aman J, Henshaw P, Ting DS-K. Bubble-pump driven LiBr-H2O and LiCl-H2O absorption air-conditioning systems. Thermal Sci Eng Progress. 2018;6(1998):316–22. doi:10.1016/j.tsep.2017.10.022. [Google Scholar] [CrossRef]

10. Kumbhar A, Gulhane N, Pandure S. Theoretical analysis of hybrid chiller. Energy Proc. 2017;109:487–96. doi:10.1016/j.egypro.2017.03.082. [Google Scholar] [CrossRef]

11. Ayou DS, Wardhana MFV, Coronas A. Performance analysis of a reversible water/LiBr absorption heat pump connected to district heating network in warm and cold climates. Energy. 2023;268:126679. doi:10.1016/j.energy.2023.126679. [Google Scholar] [CrossRef]

12. Ahmad T, Azhar M, Sinha MK, Meraj M, Mahbubul IM, Ahmad A. Energy analysis of lithium bromide-water and lithium chloride-water based single effect vapour absorption refrigeration system: a comparison study. Cleaner Eng Technol. 2022;7:100432. doi:10.1016/j.clet.2022.100432. [Google Scholar] [CrossRef]

13. Jeong J, Jung HS, Lee JW, Kang YT. Hybrid cooling and heating absorption heat pump cycle with thermal energy storage. Energy. 2023;283(1):129027. doi:10.1016/j.energy.2023.129027. [Google Scholar] [CrossRef]

14. Wang J, Liu Z, Wang H, Lui H. A new combined cooling and power system based on ammonia-water absorption refrigeration cycle: thermodynamic comparison and analysis. Energy Convers Manag. 2022;270(13):116262. doi:10.1016/j.enconman.2022.116262. [Google Scholar] [CrossRef]

15. Razmi A, Soltani M, Kashkooli FM, Garousi Farshi L. Energy and exergy analysis of an environment friendly hybrid absorption/recompression refrigeration system. Energy Convers Manag. 2018;164:59–69. doi:10.1016/j.enconman.2018.02.084. [Google Scholar] [CrossRef]

16. Babaei SM, Razmi AR, Soltani M, Nathwani J. Quantifying the effect of nanoparticles addition to a hybrid absorption/recompression refrigeration cycle. J. Cleaner Prod. 2020;260(48):121084. doi:10.1016/j.jclepro.2020.121084. [Google Scholar] [CrossRef]

17. Peng Z, Li Z, Zeng J, Yu J, Lv S. Thermo-economic analysis of absorption compression hybrid cooling systems with parallel subcooling and recooling for small scale low-grade heat source and low temperature application. Int J Refrig. 2022;138:220–32. doi:10.1016/j.ijrefrig.2022.03.003. [Google Scholar] [CrossRef]

18. Wang J, Wang B, Wu W, Li X, Shi W. Performance analysis of an absorption-compression hybrid refrigeration system recovering condensation heat for generation. Appl Therm Eng. 2016;108:54–65. doi:10.1016/j.applthermaleng.2016.07.100. [Google Scholar] [CrossRef]

19. Pacheco-Cedeño JS, Rodríguez-Muñoz JL, Ramírez-Minguela JJ, Pérez-García V. Comparison of an absorption-compression hybrid refrigeration system and the conventional absorption refrigeration system: exergy analysis. Int J Refrig. 2023;155(2):81–92. doi:10.1016/j.ijrefrig.2023.08.003. [Google Scholar] [CrossRef]

20. Ochoa GV, Forero JD, Quinones LO. Exergetic analysis of a LiBr-H2O singe effect absorption refrigeration system. Int J ChemTech Res. 2018;11:363–8. doi:10.20902/IJCTR.2018.110743. [Google Scholar] [CrossRef]

21. Blanco-Marigorta AM, Marcos JD. Key issues on the exergetic analysis of H2O/LiBr absorption cooling systems. Case Stud Therm Eng. 2021;28:101568. doi:10.1016/j.csite.2021.101568. [Google Scholar] [CrossRef]

22. Banu PA, Premkumar TM, Sivamani S, Vijayabalan PA. Detailed second law (exergetic) analysis approach of H2O-LiBr vapour absorption cooling system. IOP Conf Ser: Mater Sci Eng. 2020;998:01062. doi:10.1088/1757-899X/998/1/012062. [Google Scholar] [CrossRef]

23. Mohtaram S, Chen W, Lin J. A study of an absorption refrigeration cycle by exergy analysis approach. IOP Conf Ser: Earth Environ Sci. 2018;182:012021. doi:10.1088/1755-1315/182/1/012021. [Google Scholar] [CrossRef]

24. FathiAlmas Y, Ghadamian H, Aminy M, Moghdasi M, Amirian H, Hoeinadesh S, et al. Thermo-economic analysis, energy modeling and reconstructing of components of a single solar-absorption lithium bromide chiller for energy performance enhancement. Energy Build. 2023;285:112894. doi:10.1016/j.enbuild.2023.112894. [Google Scholar] [CrossRef]

25. Abid M, Khan MS, Ratlamwala TA, Amber KP. Thermo-environmental investigation of solar parabolic dish-assisted multi-generation plant using different working fluids. Int J Energy Res. 2020;44(15):1–19. doi:10.1002/er.5340. [Google Scholar] [CrossRef]

26. Herold K. Absorption chillers and heat pumps. Boca Raton: CRC Press; 2016. [Google Scholar]

27. Li Na, Luo C, Su QA. Working pair of CaCl2-LiBr-LiNO3/H2O and its application in a single-stage solar driven absorption refrigeration cycle. Int J Refrig. 2018;86(2):1–13. doi:10.1016/j.ijrefrig.2017.11.004. [Google Scholar] [CrossRef]

28. Asensio-Delgado JM, Asensio-Delgado S, Zarca G, Urtiaga A. Analysis of hybrid compression absorption refrigeration using low-GWP HFC or HFO/ionic liquid working pairs. Int J Refrig. 2022;134:232–41. doi:10.1016/j.ijrefrig.2021.11.013. [Google Scholar] [CrossRef]

29. Jiménez-García JC, Rivera W. Exergy analysis of an experimental ammonia/water absorption cooling system. Case Stud Therm Eng. 2023;49:103167. doi:10.1016/j.csite.2023.103167. [Google Scholar] [CrossRef]

30. Tenkeng M, Wouagfack PAN, Techinda R. Exergy analysis of a double-effect solar absorption refrigeration system in Ngaoundere. World J Eng Technol. 2019;7(1):158–74. doi:10.4236/wjet.2019.71011. [Google Scholar] [CrossRef]

31. Mohtaram S, Omidi M, Lin J, Sun H, Chen W. Exergy analysis of a multi mixture working fluid absorption refrigeration cycle. Case Stud Therm Eng. 2019;15(4):100540. doi:10.1016/j.csite.2019.100540. [Google Scholar] [CrossRef]

32. Zhang Ke, Ma H, Li Q, Wang D, Song Q, Wang X, et al. Thermodynamic analysis and optimization of variable effect absorption refrigeration system using multi-island genetic algorithm. Energy Rep. 2022;8:5443–54. doi:10.1016/j.egyr.2022.04.004. [Google Scholar] [CrossRef]

33. Arora A, Kaushik SC. Theoretical analysis of LiBr/H2O absorption refrigeration systems. Int Energy Res. 2009;33(15):1321–40. doi:10.1002/er.1542. [Google Scholar] [CrossRef]

34. Florides GA, Kalogirou SA, Tassou SA, Wrobel LC. Design and construction of a LiBr-water absorption machine. Energy Convers Manag. 2003;44(15):2483–508. doi:10.1016/S0196-8904(03)00006-2. [Google Scholar] [CrossRef]

35. Klein SA. Engineering equation solver (EESversion 10.2. Madison, USA: F-Chart Software; 2020. Available from: www.fchart.com/. [Accessed 2024]. [Google Scholar]

36. Lamine CM, Said Z. Energy analysis of single effect absorption chiller (LiBr/H2O) in an industrial manufacturing of detergent. Energy Proc. 2014;50:105–12. doi:10.1016/j.egypro.2014.06.013. [Google Scholar] [CrossRef]

37. Marashli A, Alfanatseh E, Shalby M, Gomaa M. Modelling single-effect of Lithium Bromide-Water driven by an evacuated solar tube collector in Ma'an city (Jordan) case study. Case Stud Therm Eng. 2022;37(2):102239. doi:10.1016/j.csite.2022.102239. [Google Scholar] [CrossRef]

38. Kaynakli O, Kilic M. Theoretical study on the effect of operating conditions on performance of absorption refrigeration system. Energy Convers Manag. 2007;48(2):599–607. doi:10.1016/j.enconman.2006.06.005. [Google Scholar] [CrossRef]

39. Ghatos S, Janan MT, Mehdari A. Thermodynamic model of a single stage H2O-LiBr absorption cooling. E3S Web Conf. 2021;234:00091. doi:10.1051/e3sconf/202123400091. [Google Scholar] [CrossRef]

40. Kaushik SC, Arora A. Energy and exergy analysis of single effect and series flow double effect water-lithium bromide absorption refrigeration systems. Int J Refrig. 2009;32(6):1247–58. doi:10.1016/j.ijrefrig.2009.01.017. [Google Scholar] [CrossRef]

41. Cai D, He G, Tian Q, Tang W. Exergy analysis of a novel air-cooled non-adiabatic absorption refrigeration cycle with NH3–NaSCN and NH3–LiNO3 refrigerant solutions. Energy Convers Manag. 2014;88:66–78. doi:10.1016/j.enconman.2014.08.025. [Google Scholar] [CrossRef]