Contact Melting in an Elliptical Tube under the Second Kind of Thermal Boundary Condition

Nomenclature

1  Introduction

Contact melting occurs when solid phase change materials (PCM) and heat sources come into direct contact and exert pressure on each other, provided that the temperature of the heat source is higher than the melting point of the PCM [1]. The research indicates that under identical operating conditions, contact melting exhibits a melting rate that is 1–7 times greater than that of non-contact or constrained melting [2]. Contact melting has wide applications in various engineering and natural contexts, including melting ice and snow, storing heat energy, welding, geological exploration, and nuclear safety [3]. It is considered a highly efficient melting method and has garnered the interest of numerous scholars [4].

In recent years, the utilization of phase change materials (PCM) for latent heat thermal energy storage (LHTES) has garnered significant attention, particularly in solar-powered energy systems. For solar energy systems requiring substantial heat transfer, implementing a latent thermal energy storage system (LTES) utilizing phase change materials presents a practical and economical approach [5]. Phase change materials achieve energy storage by absorbing heat and melting. Therefore, the melting efficiency determines the effective performance of the latent heat energy storage system. The experimental results indicate that contact melting significantly enhances heat transfer during the melting process and increases melting efficiency [6]. Contact melting is intricately linked to both geometric and thermal boundary conditions. The geometric conditions encompass the shape of the heat source and the configuration of the solid material. In contrast, the thermal conditions concerning how the heat source warms the PCM and the temperature distribution across the source’s surface. Over the past four decades, numerous investigations into contact melting have been conducted [7–10]. In particular, the research on contact melting driven by temperature difference, called ΔT-driven melting, is extensive and in-depth. For example, in 1980, Nicholas and Bayazitoglu first conducted numerical analysis and experimental research on contact melting of free solids in horizontal circular tubes and obtained the flow and temperature fields in the melt liquid area and the solid shape change [11]. Subsequently, Bareiss et al. [12], Riviere et al. [13], Webb et al. [14] further carried out theoretical and experimental studies on contact melting in horizontal circular tubes and determined the flow and temperature field distribution in the melt liquid film as well as the change rule of solid volume. Hirata et al. [15] and Lacroix [16] respectively analyzed the contact melting in the rectangular cavity and established a three-dimensional analysis model. Wilchinsky et al. [17] used the analytical methods of Bareiss et al. [12] to discuss contact melting in plastic containers. Aljaghtham et al. [6] conducted a study to explore how slip velocity and temperature affect the contact melting process of an electrically conductive PCM when exposed to a magnetic field. A comprehensive analytical solution has been devised for thin film flow and energy transport, incorporating unsteady phase change heat transfer under Navier slip conditions. This solution also accounts for interactions with electromagnetic fields, which are defined by Maxwell’s equations. Fu et al. utilized pressure-enhanced close-contact melting as a means to maintain elevated energy and power densities [9]. A decrease in the performance of thermal energy storage systems based on phase change materials was observed as the melt front progressed further away from the heat source. The research above adopted the analysis model under the condition of an isothermal heat source, which belongs to the first kind of thermal boundary condition. It can be seen from the analysis results that melting speed, liquid film thickness distribution, and other parameters are expressed as a function of temperature difference or Stefan number, so this analysis model is called the temperature difference contact melting model. In recent years, the application of phase change materials (PCM) for latent heat thermal energy storage (LHTES) has garnered significant interest. Experimental results have shown that contact melting notably improves heat transfer efficiency during the melting process [18]. However, in the energy storage system, the constant heat flux boundary condition is easier to control and implement compared to the constant temperature boundary condition. The PCM in the heat storage element absorbs heat and melts, the heat flux on the surface of the component is steady, and the surface temperature is not uniform [19], which belongs to the melting under the second kind of thermal boundary condition and is different from that under the first kind of thermal boundary condition. Studies on contact melting within a container subjected to a constant heat flux are relatively scarce. Elliptical cross-sections demonstrate excellent performance in structural mechanics, particularly when subjected to axial compressive loads [20]. Compared to circular cross-sections, elliptical cross-sections exhibit superior mechanical properties and stability [21]. This advantage endows elliptical cross-sections with potential application prospects in energy storage structure designs that demand high strength and stability [2]. Furthermore, due to their high thermal conductivity and significant engineering applications, several researchers have examined the contact melting processes occurring both around and within heat sources with elliptical geometries. In the present work, the contact melting process of phase change material in a horizontal elliptical tube under the second kind of boundary condition is analyzed.

2  Melting Model and Equations

The physical model of the problem under consideration is shown in Fig. 1, where the elliptical tube section satisfies the equation x2a2+y2b2=1 and θ is the angle between the tangent of the ellipse and the horizontal line. We mainly analyzed the contact melting of PCM which the density of solid phase is greater that of liquid phase, namely ρs>ρl. At the initial moment, the solid PCM in the elliptical tube is uniformly at the melting point temperature and heated by the inner tube wall under the constant heat flux q′′. The solid PCM close to the tube wall will melt to form a thin liquid film, and the thickness is δ(ϕ). The height of melted liquid gathered at the upper of the tube is written as H(τ), and the falling speed of solid PCM is H˙(H˙=dH/dτ).ϕA is the boundary angle of the contact melting zone. When ϕ<ϕA, the solid takes place the contact melting. As previously mentioned, Bareiss et al. [12] studied contact melting within a horizontal cylindrical tube and determined that natural convection contributed to only approximately 10%–15% of the total melting. Therefore, it is assumed that natural convection can be disregarded. As summarized, during the solid contact melting process, it is assumed that [1,22] (a) the contact melting mainly occurs at the bottom of solid PCM, and the non-contact melting is slow at the top of solid PCM and can be ignored. (b) During the melting process, the solid PCM descends in a vertical and axisymmetric manner, as observed in earlier experiments conducted by Riviere et al. [13], as well as Bahrami et al. [23]. This indicates that there is no slip at the capsule wall or melting front, and the shape of the solid PCM’s upper surface remains constant. (c) The thickness δ of the molten liquid film at the bottom of the solid is far less than the minimum heat source radius (a, b), i.e., δ≪min (a,b), the pressure gradient to the direction s is ignored because of the thin liquid film. (d) The inertia force in the liquid film is negligible compared with the pressure. (e) According to relevant experimental phenomena, parameters such as liquid film thickness during contact melting are independent of the melting process [23–25]. The solid melting rate is slow, and the solid melting is approximately a steady state process at a certain moment, which satisfies the force equilibrium. (f) The thermal properties of phase change materials are constant.

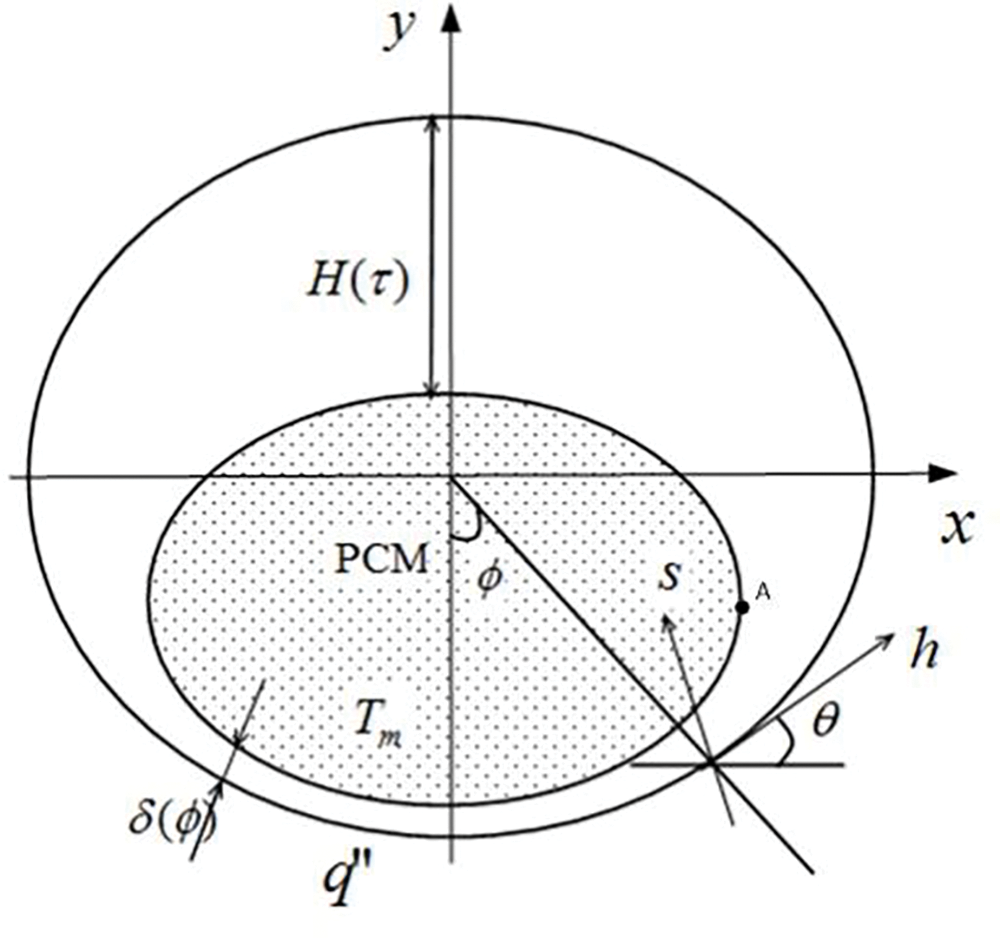
Figure 1: Physical model and coordinates of constant heat flux melting in elliptical tubes

According to the above assumptions, the governing equations of the flow in the molten liquid film, namely the continuity, momentum and energy equations are simplified as follows:

∂u∂h+∂v∂s=0(1)

µ∂2u∂s2=dpdh(2)

u∂T∂h+v∂T∂s=α∂2T∂s2(3)

By analyzing the temperature distribution in the liquid film, it is found that the tangential (along direction h) temperature gradient is much smaller than the vertical temperature gradient (along direction s), namely ∂T/∂h≪∂T/∂s. And the change of liquid film pressure p along direction s is negligible, v is approximately as −H˙cosϕ. Thus, energy Eq. (3) can be further simplified as:

−H˙cosϕ∂T∂s=α∂2T∂s2(4)

The temperature boundary condition of liquid film layer is:

s=0,∂T∂s=−q′′λ;s=δ,T=Tm(5)

Using the boundary condition Eq. (5), the differential Eq. (4) was solved to obtain the liquid film temperature distribution as follows:

T=Tm+q′′αλH˙cosϕ[exp⁡(−H˙scosϕα)−exp⁡(−H˙δcosϕα)](6)

The energy balance equation at the solid-liquid contact melting interface is:

−λ∂T∂s|s=δ=ρsLmH˙cosϕ(7)

Substituting the derivative of Eq. (6) with respect to s into Eq. (7), the liquid film thickness distribution can be obtained as follows:

δ=αln⁡(ρsH˙Lmcosθq′′)H˙cosθ(8)

The boundary conditions of liquid flow velocity are:

s=0:u=0;s=δ:u=0(9)

Using the boundary condition Eq. (9), the momentum Eq. (2) is twice integrated along s to obtain u as follows:

u=−12μdpdh(s2−δs)(10)

The mass conservation equation of melting process is:

∫0δρl uds=∫0ϕρsH˙cosθdh(11)

Substituting Eq. (10) into Eq. (11), the tangential pressure in the molten liquid film can be written as:

dpdh=−12μρsH˙ρl δ3∫0ϕcosθdh(12)

The force balance equation of solid in the melting process is:

2∫0ϕApcosθdh=(ρs−ρl)gVs(13)

According to Fig. 1, the following geometric relationship exists:

dh=bfJ(ϕ)dϕ(14)

where, fJ(ϕ)=1+J4 tan2ϕ1+J2 tan2ϕ1cos2ϕ+J2 sin2ϕ, and J = b/a, which is so-called the ellipse compression coefficient.

The relation between the angles ϕ and θ is:

tanθ=J2tanϕ(15)

The relation between the boundary angle ϕA and the liquid height H∗ is:

cos⁡ϕA=H(τ)2[H(τ)2]2+a2{1−[H(τ)2b]2}=JH∗1+(J2−1)(H∗)2(16)

The residual solid volume Vs during the melting can be expressed as:

Vs=2ab[arccos⁡(H2b)−(H2b)1−(H2b)2](17)

Substituting Eqs.(14) and (17) into Eqs. (12) and (13) results in:

dpdϕ=−12µb2ρsH˙fJ(ϕ)ρlδ3∫0ϕcos⁡θfJ(ϕ)dϕ(18)

∫0ϕApcosθfJ(ϕ)dϕ=g(ρs−ρl)a[arccos⁡(H2b)−(H2b)1−(H2b)2](19)

Introduce the following dimensionless parameters:

δ∗=δb,H∗=H2b,H˙∗=H˙bα,p∗=pρsgb,Pr=υα,Ar=gb3υ2

Substituting the dimensionless quantities above into Eqs. (8), (18) and (19) yields:

δ∗=−ln⁡(ρsH˙Lmcosθq′′)H˙∗cosθ(20)

dp∗dϕ=−12H˙∗fJ(ϕ)PrArδ∗3∫0ϕcosθfJ(ϕ)dϕ(21)

∫0ϕAp∗cosθfJ(ϕ)dϕ=(1−ρm∗)J[arccos⁡(H∗)−H∗1−H∗2](22)

Eqs. (20)–(22) are dimensionless equations of constant heat flux contact melting of phase change material in an elliptical tube heat source, where the independent variable is the height H∗ of molten liquid, and the unknown parameters to obtain are the solid falling speed H˙∗, liquid film pressure p∗, liquid film thickness δ∗, and angle θ. The boundary conditions are that p∗=0 when ϕ=ϕA. Through numerical solution, the variations of melting parameters H∗˙, p∗ and δ∗ with H∗ can be obtained under different operating conditions, further the change rule of solid complete melting time Fof and melting rate V∗. First, an initial value is temporarily assigned, and the liquid film thickness distribution δ∗ obtained from Eq. (20) is substituted into Eq. (21), and the difference method is adopted to solve the problem. Second, the precision is set to 10−4, combined with boundary conditions, the pressure distribution p∗ in the liquid film is obtained. Third, the pressure distribution was substituted into the left side of Eq. (22) for integration, then H˙∗ was adjusted by comparing the size of result values on both sides of the Eq. (22). Fourth, the iterative calculation was carried out until Eq. (22) was satisfied within the precision range, and the corresponding relationship between the falling speed H˙∗ of solid and the height H∗ of liquid was obtained.

3  Analysis and Discussion

When the compression coefficient J is equal to 1, θ=ϕ and fJ(ϕ)=1. Then, Eqs. (20–22) are transformed into, respectively:

δ∗=−ln⁡(ρsH˙Lmcosθq′′)H˙∗cosθ(23)

dp∗dϕ=−12H˙∗sinϕPr⋅Arδ3(24)

∫0∅Ap∗cosϕdϕ=(1−ρm∗)[arccos⁡(H∗)−H∗1−H∗2](25)

Eqs. (23)–(25) are the analytical results of the solid contact melting process in the horizontal circular tube [26].

In this paper, n-octadecane is chosen as the PCM material for calculation and discussion. The thermophysical properties of PCM are Tm = 28°C, ρs=814 kg/m3, ρl=778 kg/m3, µ=3.9×10−3 kg/(m⋅s), λl=0.152 w/(m⋅k), Lm = 242 kJ/kg. The Ellipse size is b = 0.25 m, a = 0.5 m where J = 0.5.

Fig. 2 shows the change curve of solid PCM’s falling speed H˙∗ with melting height H∗ during contact melting in an elliptical tube heat source, where J=0.5. The height of the residual solid PCM is 1−H˙∗. As can be seen from Fig. 2, the velocity of the solid falling decreases gradually, as the height of the solid decreases. This is due to the fact that as melting proceeds, the liquid film thickness gradually increases. According to the heat flow density relationship q″=λ(Tw−Tm)/δ, the melting rate will gradually slow down as the liquid film thickness increases and the wall temperature of the heat source required for melting increases, making melting more difficult. The effect of heat flow density q″ on the melting velocity is obvious. q″ increases, the velocity H˙∗ increases significantly and the change in melting velocity becomes apparent during the melting process.

Figure 2: Variation of H˙∗ with H∗ for J = 0.5

The relationship between dimensionless the solid melting rate V∗ and the liquid height H∗ can be expressed as:

V∗=1−Vsπab=1−2π[arccos⁡H∗−H∗1−H∗2](26)

The dimensionless melting time Fo and falling speed H˙∗ satisfy the relationship:

Fo=ατR2=∫0H∗(H˙∗)−1dH∗(27)

The variation curve of the solid melting rate V∗ with the Fourier number Fo for different heat flux q″ is given in Fig. 3, where J= 0.5. When Fo increases, the melting rate V∗ increases monotonically with the increase of heat flux q″. When V∗=1, the PCM melts completely and it is clear that the heat flow density q″ increases and the time required for complete melting is reduced. Analyzing the trend of the curve, when q′′ increases from 5 to 10 KW/m2, the number of Fo at the end moment of melting decreases from 0.016 to 0.01, a decrease in Fo of about 0.006. While when q′′ increases from 10 to 15 KW/m2, the decrease in the number of Fo at the end moment of melting is 0.002. Therefore, when the heat flux is small, its change has a significant effect on the time required for the solid to melt completely.

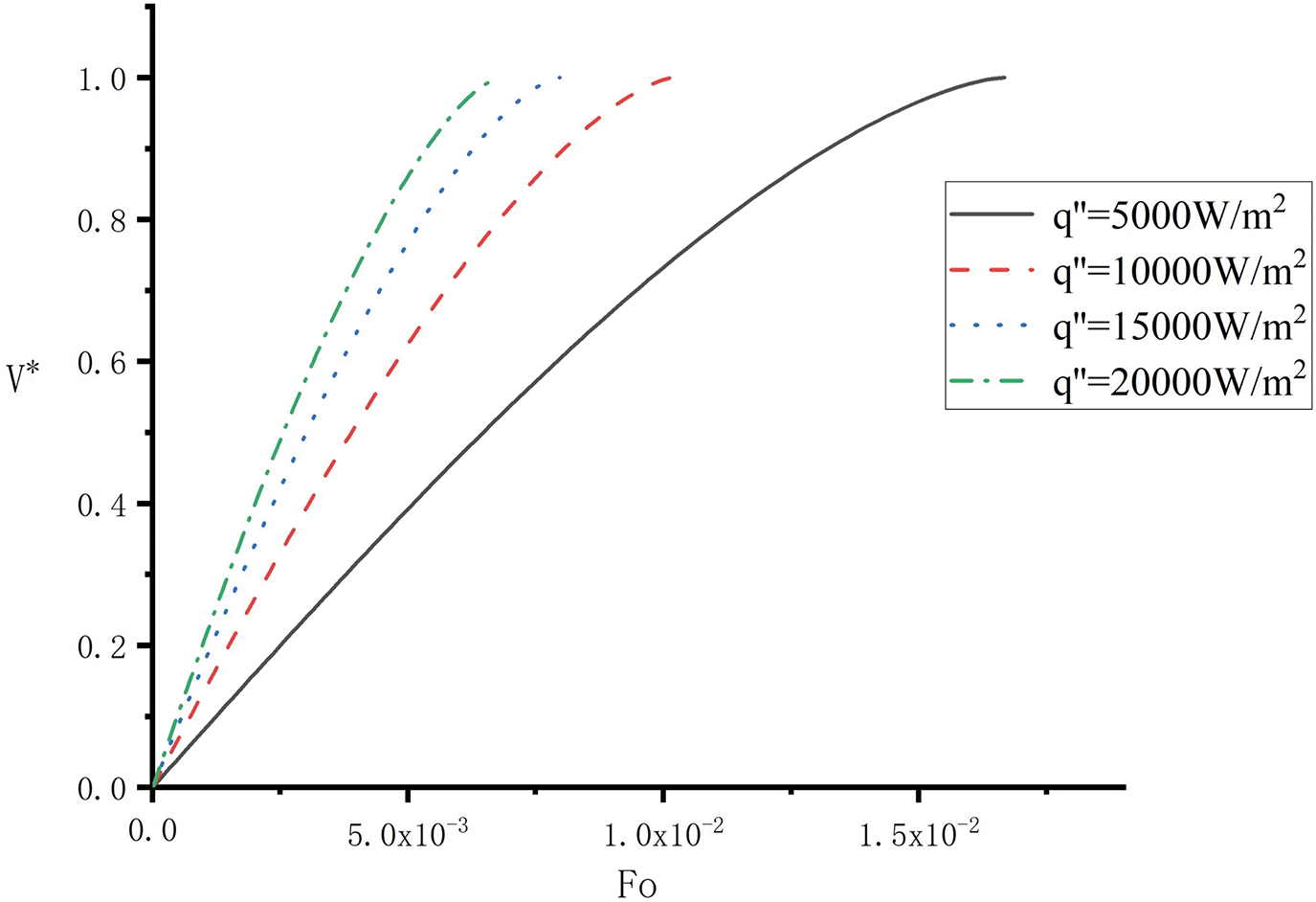
Figure 3: Variation of V∗ with Fo for J = 0.5

The variation of the liquid film thickness δ0∗ with Fo at ϕ=0 is given in Fig. 4. As can be seen in Fig. 4, the liquid film thickness gradually increases as the melting progresses. The film thickness changes relatively slowly at the start of melting and then gradually increases as the melting progresses. This is because as melting proceeds, the volume of the solid gradually decreases, gravity and buoyancy gradually decrease and the liquid film begins to expand under the action of the liquid film pressure, resulting in an increase in the thickness of the liquid film. In addition, by comparing the different heat flux, it can be seen that the higher the heat flux the higher the film thickness, which is due to the fact that the higher the heat flux, the faster the solid melting rate and therefore the greater the film thickness.

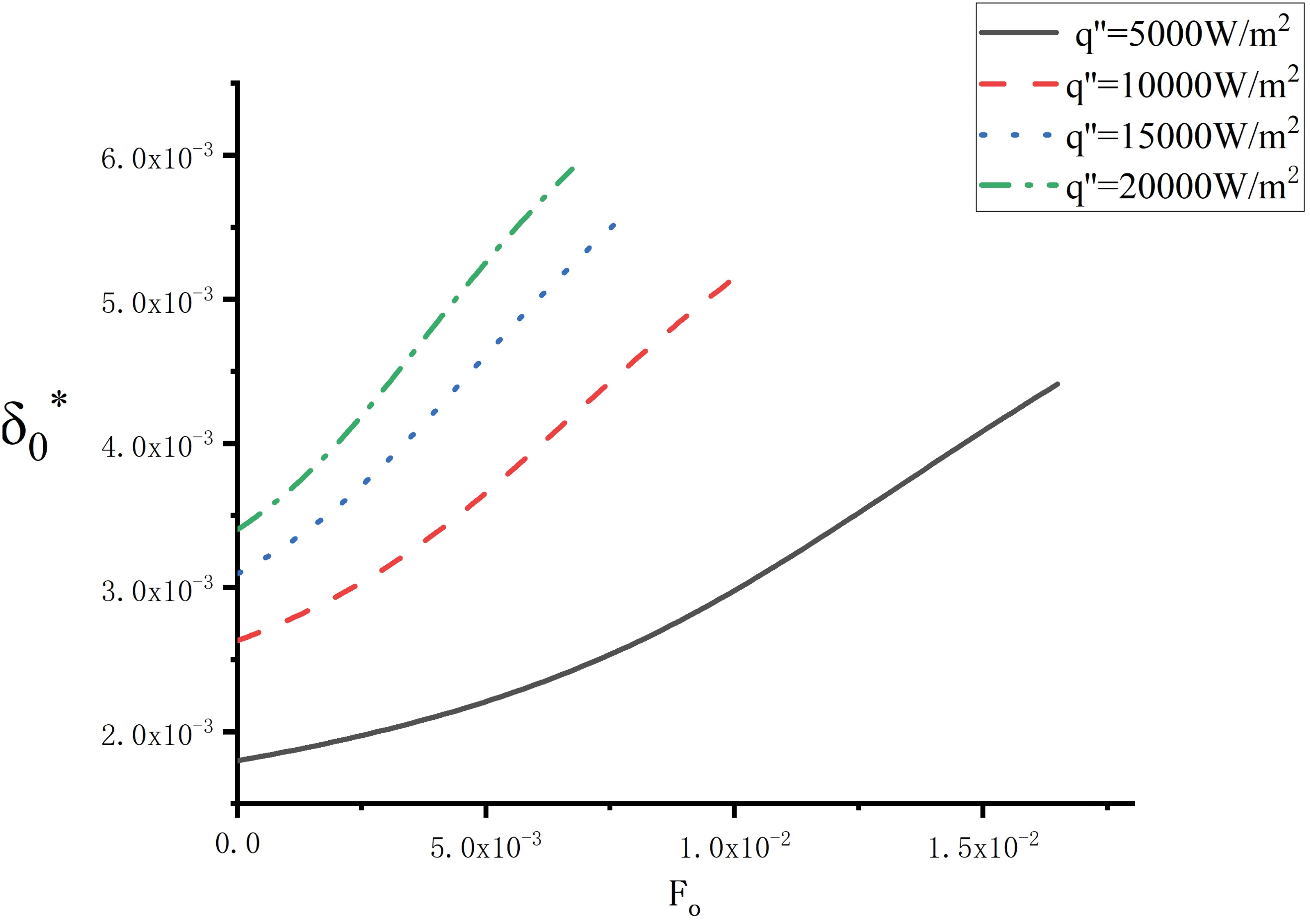
Figure 4: Variation of δ0∗ with Fo for J = 0.5

To evaluate the effect of the elliptical shape on the melting, Fig. 5 shows the variation of the falling velocity H∗˙ with the melting height H* for the melting of solids in elliptical tubes with different compression ratios. The Figure shows that the higher the J, the higher the falling velocity. In the early stages of melting, the higher the J value the slower the falling velocity decreases, but at the end of melting the higher the J, the faster the falling velocity decreases. The reason for the slow decrease in speed in the early stages is that the higher the value of J, the smaller the length of the ellipse a, and the greater the pressure on the wall at ϕ = 0, so the liquid film thickness δ∗ stays at a lower level in the early stages of melting, as shown in Fig. 6. At this time the heat transfer thermal resistance is small and the change in solid volume has less effect on the liquid film thickness, so the larger the J value at the beginning of melting, the slower the melting rate decreases. As the J value increases, the contact area between the gravity direction and the heating wall decreases, leading to higher pressure and a thinner liquid film. At this stage, the solid’s gravity significantly affects the liquid film. During melting, the solid mass diminishes, the liquid content rises, gravity weakens, and buoyancy strengthens. Once the critical threshold is reached, the influence of gravity becomes significantly weaker than that of the liquid film pressure, causing the liquid film to rapidly rise. This effect intensifies with a higher J value, as illustrated in Fig. 6. The rapid expansion of the liquid film results in a swift increase in heat transfer resistance, leading to a faster decrease in melting rate for higher J values, as demonstrated in Fig. 5.

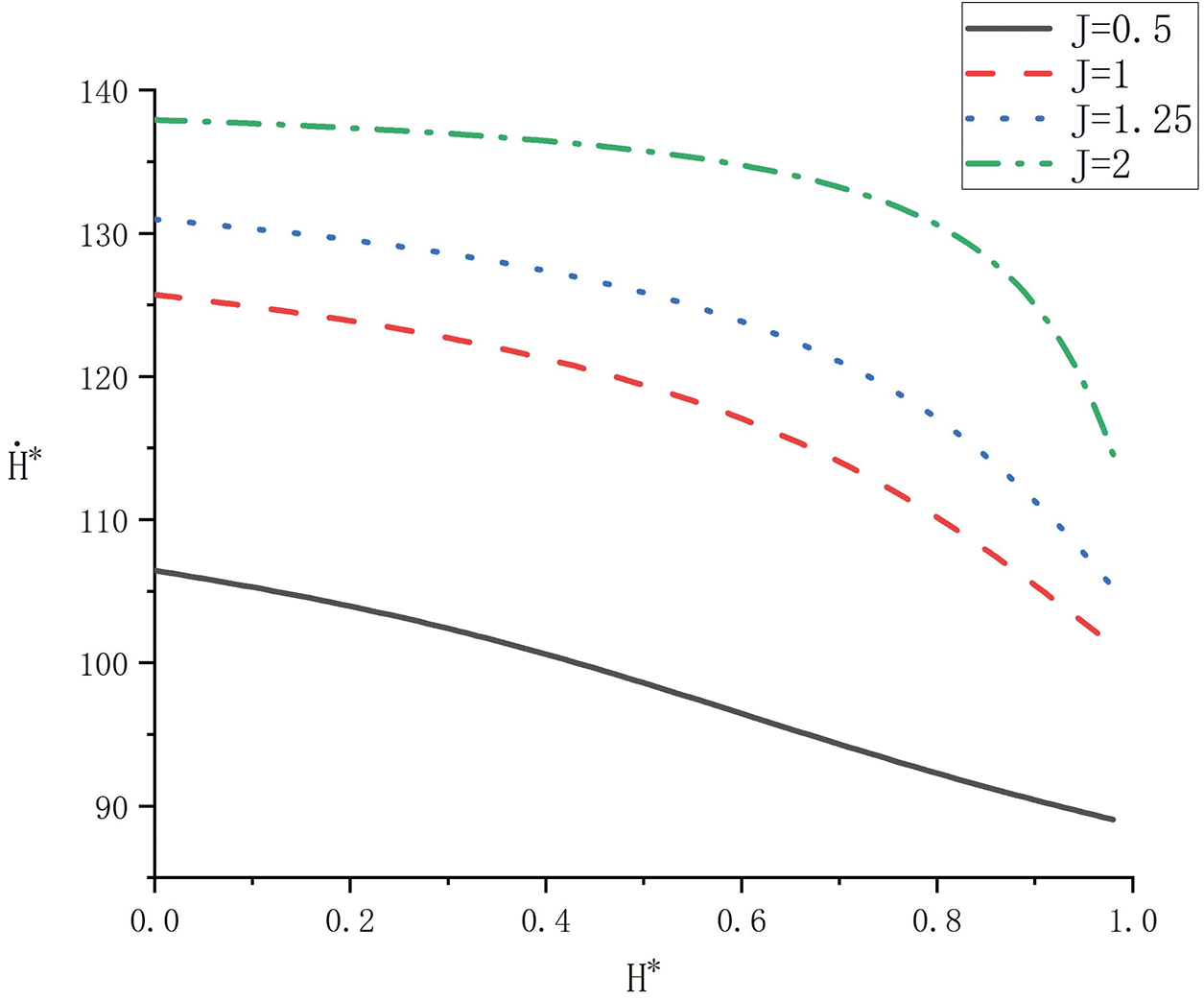
Figure 5: Variation of H˙∗ with H∗ for q″=10 KW/m2

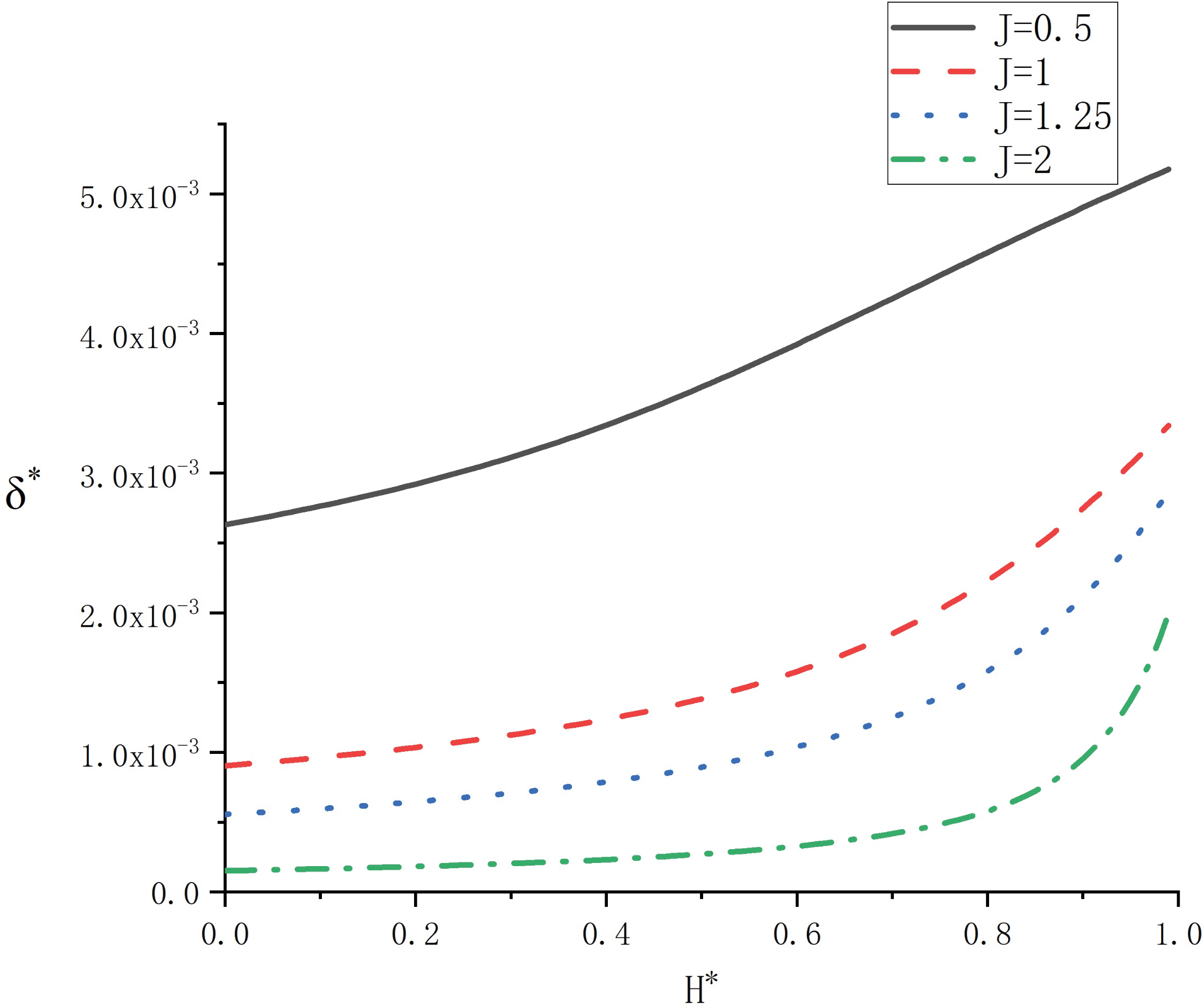
Figure 6: Variation of δ∗ with H∗ for q″=10 KW/m2

The influence of heat source shape on melting rate was analyzed for the same solid volume at q″=10000 W/m2, the results were shown in Fig. 7. It is obvious that increasing the compression coefficient J shortens the time for complete melting of the solid. This is because the greater the J, the greater the ratio of solid PCM height to width, which corresponds to a smaller liquid film thickness, so the heat transfer thermal resistance is lower and the melting efficiency is higher. So for the same volume, the heat source melting efficiency of all elliptical tubes for J > 1 is higher than that of circular tubes (J = 1).

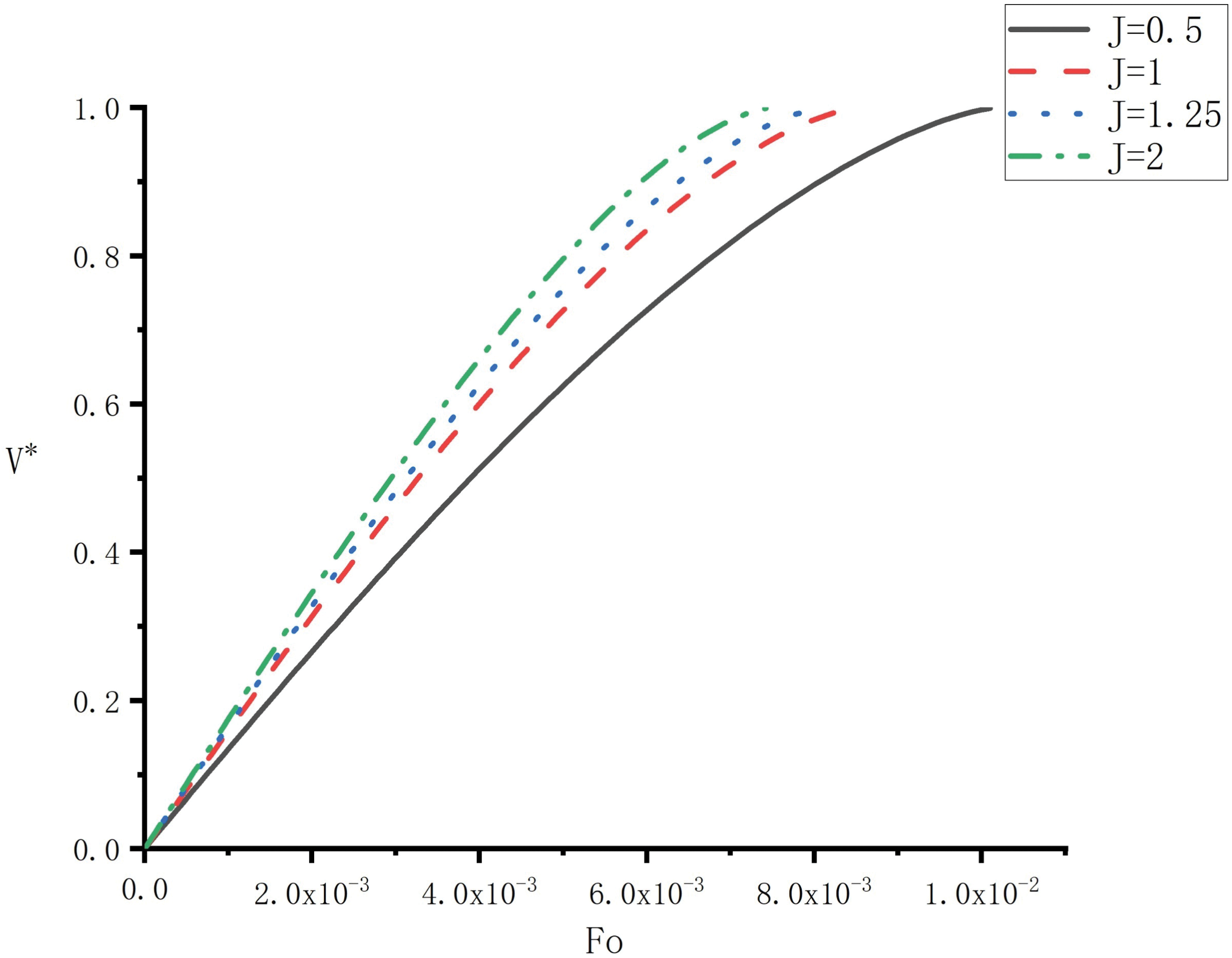
Figure 7: Influence of heat source shape on melting rate

Fig. 8 illustrates the impact of J on the dimensionless parameters of the temperature Tw∗ of the heat wall, expressed as Tw∗=Tw/Tm, at q″=10,000 W/m2. It can be clearly seen from the figure that as the J value increases, the temperature of the heating wall decreases. This is because at the same heat flux, thinner liquid films require smaller temperature differences. In addition, due to the small J value, the thickness of the liquid film will increase rapidly at the end of melting, and the heating wall temperature will increase rapidly at this time.

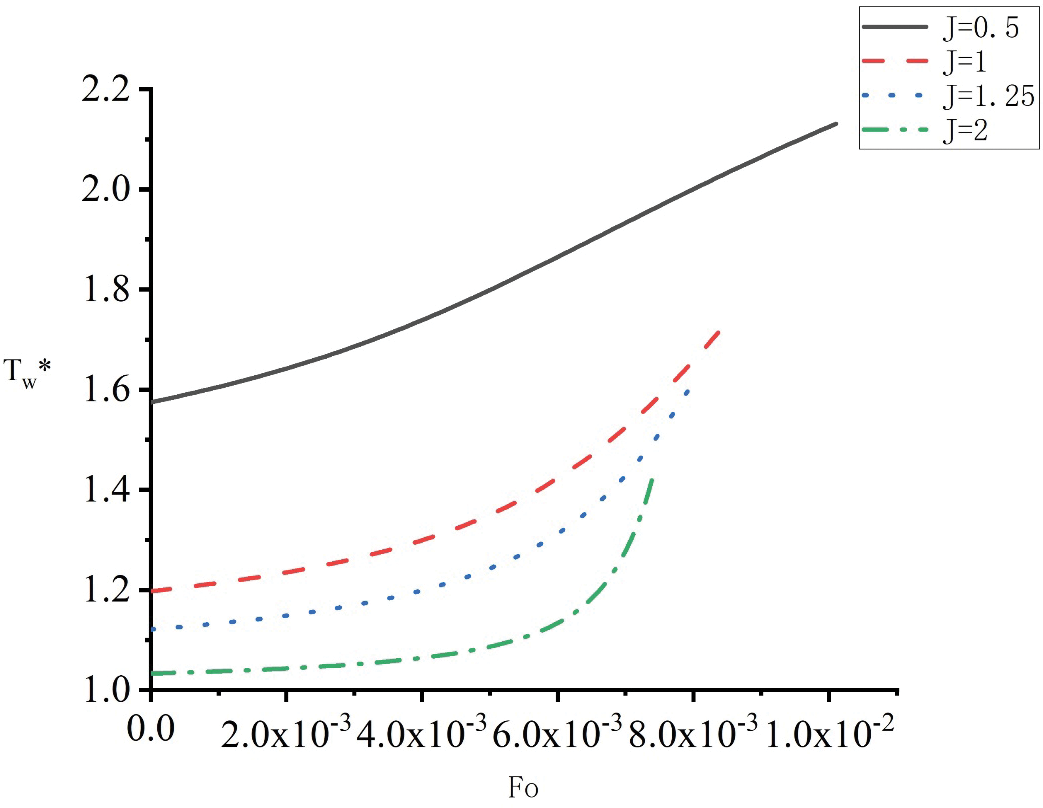
Figure 8: Influence of heat source shape on heat wall temperature

Fig. 9 compares the variation of the complete melting times Fof with heat flux for four typical elliptical tubes with compression coefficient of 0.5, 1, 1.25 and 2, respectively. As can be seen from the graph, the heat flow density increases with a corresponding decrease in the complete melting times Fof. At q″<2500 W/m2, the change in J value has a small effect on the complete melting time. At q″>2500 W/m2, the larger the J value, the smaller the complete melting time. Although the J value affects the thickness of the liquid film and subsequently affects heat transfer, the overall heat flux is still low, resulting in lower heat transfer in the liquid film and slower melting rate of PCM solids. Therefore, compared with high heat flux conditions, the influence of J value on melting time is significantly small and can be almost ignored.

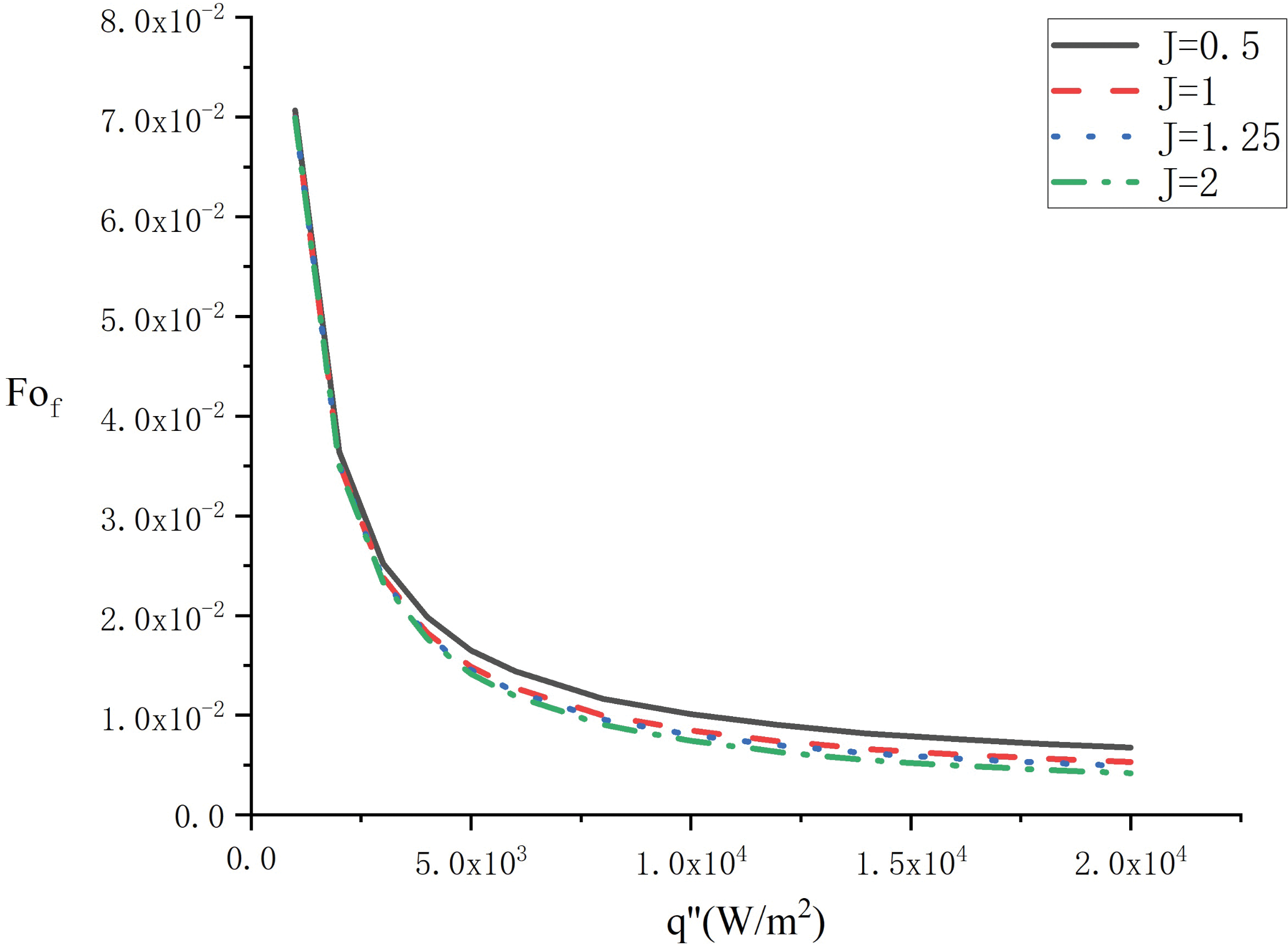
Figure 9: Variation of the elapsed time with heat flux

It is shown from Fig. 10 that the completed melting time for constant heat flux melting is longer than that for constant temperature melting which calculated by Reference [21] under the condition of the same heat flux, so the heat transfer efficiency of constant heat flux melting is lower than that of constant temperature melting. Under conditions of low heat flux, the melting efficiency of constant temperature melting is significantly higher than that of constant heat flux. Nevertheless, under conditions of high heat flux, the disparity in melting time between constant temperature and constant heat flux conditions is minimal. Consequently, an energy storage heating method that is more easily attainable can be chosen depending on the specific energy storage conditions.

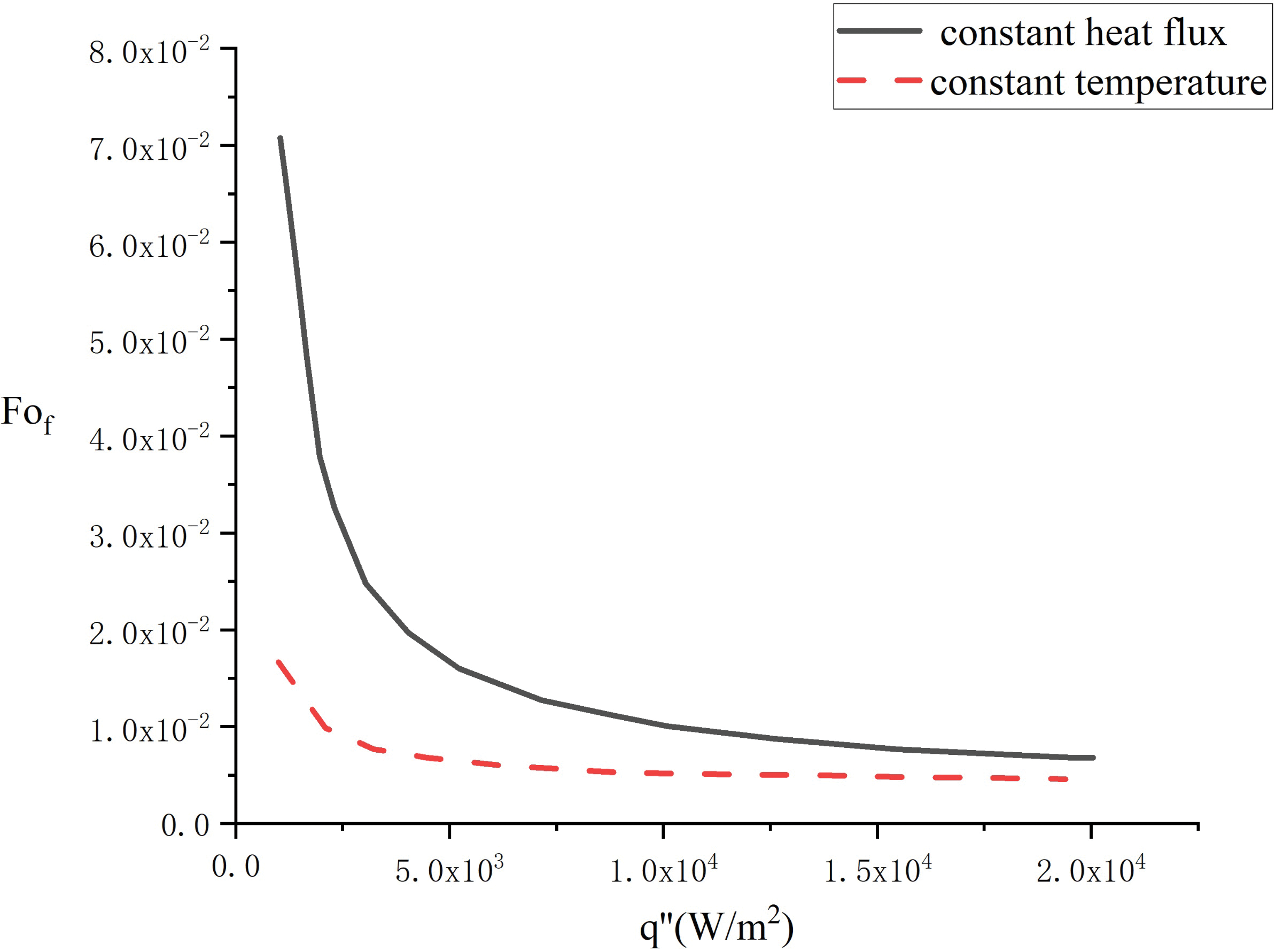
Figure 10: Comparison of the elapsed time of first and second thermal boundary conditions

4  Conclusions

The contact melting of solid PCM in a horizontal elliptical tube with constant heat flux is analyzed. The control equations of melting are established by the Nusselt theory. Through theoretical derivation, the dimensionless equations describing the contact melting process are obtained and solved using the numerical method. This paper chooses n-octadecane as the PCM material for calculation and discussion. The variations of melting parameters such as falling speed, melting rate, solid height, and liquid film distribution under different heat fluxes from heat sources were derived and discussed. The results are applicable to phase change heat transfer problems under the second kind of thermal boundary condition. The following conclusions were drawn:

(1) During the contact melting of solid PCM in elliptical tubes, the thickness of contact melting liquid film increases gradually with the decrease of solid height, which reduces the melting speed.

(2) The increase in heat flux reduces the time required for complete melting of the PCM. And under low heat flux conditions, increasing the heat flux will more effective in improving the melting efficiency.

(3) At the same heat flux, the higher the ellipse compression coefficient J, the higher the falling speed H˙∗ and the shorter the melting time. However, the influence of the J value on melting is relatively minor when the heat flux is small. In the early stages of melting, the greater the J value, the slower the falling speed of the PCM solid as melting proceeds. However, at the end of melting, the falling speed of PCM solids with larger J values decreases rapidly as melting proceeds. This is related to the trend of liquid film thickness during melting.

(4) Under conditions of low heat flux, the melting efficiency of constant temperature melting is significantly higher than that of constant heat flux. However, under high heat flux conditions, the difference in melting time between constant temperature and constant heat flux conditions is relatively small, so a more easily achievable energy storage heating method can be selected based on the energy storage conditions.

Acknowledgement: The authors deeply grateful to supervisor and peers for their invaluable guidance and support.

Funding Statement: This research was financially supported by the National Natural Science Foundation of China (Project number 12175311).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Wenzhen Chen; data collection: Junjie Ma; analysis and interpretation of results: Wenzhen Chen, Junjie Ma, Jianli Hao; draft manuscript preparation: Wenzhen Chen, Junjie Ma. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Junjie Ma, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Bejan A. Contact melting heat transfer and lubrication. Adv Heat Transfer. 1994;24:1–28. doi:10.1016/S0065-2717(08)70231-4. [Google Scholar] [CrossRef]

2. Chen WZ. Analysis of contact melting. Beijing: Chinese Atomic Energy Press; 2022 (In Chinese). [Google Scholar]

3. Chen WZ, Ma JJ, Xiao HG. Study on contact melting process of vertical cylindrical materials in a circular container. Prog Nucl Energy. 2023;166:104974. doi:10.1016/j.pnucene.2023.104974. [Google Scholar] [CrossRef]

4. Hu N, Lia ZR, Xua ZW, Fan LW. Rapid charging for latent heat thermal energy storage: a state-of-the-art review of close-contact melting. Renew Sustain Energy Rev. 2022;155:111918. doi:10.1016/j.rser.2021.111918. [Google Scholar] [CrossRef]

5. Abolfazl N, Marcello I, Giuseppe L, Nicola B. Thermal enhancement techniques for a lobed-double pipe PCM thermal storage system. Appl Therm Eng. 2023;233:121139. doi:10.1016/j.applthermaleng.2023.121139. [Google Scholar] [CrossRef]

6. Aljaghtham M, Premnath K, Alsulami R. Investigation of time-dependent microscale close contact melting. Int J Heat Mass Transfer. 2021;166:120742. doi:10.1016/j.ijheatmasstransfer.2020.120742. [Google Scholar] [CrossRef]

7. Myers TG, Mitchell SL, Muchatibaya G. Unsteady contact melting of a rectangular cross-section material on a flat plate. Phys Fluids. 2008;20(10):103101. doi:10.1063/1.2990751. [Google Scholar] [CrossRef]

8. Cregan V, Williams J, Myers TG. Contact melting of a rectangular block with temperature-dependent properties. Int J Therm Sci. 2020;150(2):106218. doi:10.1016/j.ijthermalsci.2019.106218. [Google Scholar] [CrossRef]

9. Fu W, Yan X, Gurumukhi Y, Garimella VS, King WP, Miljkovic N. High power and energy density dynamic phase change materials using pressure-enhanced close contact melting. Nat Energy. 2022;7(3):270–80. doi:10.1038/s41560-022-00986-y. [Google Scholar] [CrossRef]

10. Ma JJ, Chen WZ, Xiao HG. Study of contact melting of plate bundles by molten material in severe reactor accidents. Nucl Eng Technol. 2023;55(11):4266–73. doi:10.1016/j.net.2023.08.003. [Google Scholar] [CrossRef]

11. Nicholas D, Bayazitoglu Y. Heat transfer and melting front within a horizontal cylinder. J Sol Energy Eng. 1980;102(3):229–32. doi:10.1115/1.3266160. [Google Scholar] [CrossRef]

12. Bareiss M, Beer H. An analytical solution of the heat transfer process during melting of an unfixed solid phase change material inside a horizontal tube. Int J Heat Mass Transfer. 1984;27(5):739–46. doi:10.1016/0017-9310(84)90143-1. [Google Scholar] [CrossRef]

13. Riviere P, Beer H. Experimental investigation of melting of unfixed ice in an isothermal horizontal cylinder. Int Commun Heat Mass Transfer. 1987;14(2):155–65. doi:10.1016/S0735-1933(87)81006-0. [Google Scholar] [CrossRef]

14. Webb BW, Moallemi MK, Viskanta R. Experiments of melting unfixed ice in a horizontal cylindrical capsule. ASME J Heat Transfer. 1987;109(2):454–9. doi:10.1115/1.3248103. [Google Scholar] [CrossRef]

15. Hirata T, Makino Y, Kaneko Y. Analysis of close-contact melting for octadecane and ice inside isothermally heated horizontal rectangular capsule. Int J Heat Mass Transfer. 1995;34(12):3097–106. doi:10.1016/0017-9310(91)90079-T. [Google Scholar] [CrossRef]

16. Lacroix M. Contact melting of a phase change material inside a heated parallelepedic capsule. Energy Convers Manage. 2001;42(1):35–47. doi:10.1016/S0196-8904(00)00047-9. [Google Scholar] [CrossRef]

17. Wilchinsky AV, Fomin SA, Hashida T. Contact melting inside an elastic capsule. Int J Heat Mass Transfer. 2002;45(20):4097–106. doi:10.1016/S0017-9310(02)00121-7. [Google Scholar] [CrossRef]

18. Shockner T, Ziskind G. Combined close-contact and convective melting in a vertical cylindrical enclosure. Int J Heat Mass Transfer. 2021;177(3):121492. doi:10.1016/j.ijheatmasstransfer.2021.121492. [Google Scholar] [CrossRef]

19. Schüller K, Kowalski J. Spatially varying heat flux driven close contact melting–a Lagrangian approach. Int J Heat Mass Transfer. 2017;115(3):1276–87. doi:10.1016/j.ijheatmasstransfer.2017.08.092. [Google Scholar] [CrossRef]

20. Ruiz-Teran AM, Gardner L. Elastic buckling of elliptical tubes. Thin-Walled Struct. 2008;46(11):1304–18. doi:10.1016/j.tws.2008.01.036. [Google Scholar] [CrossRef]

21. Chen WZ, Yang QS, Dai MQ, Cheng SM. Analytical solution of the heat transfer process during contact melting of phase change material inside a horizontal elliptical tube. Int J Energy Res. 1998;22(2):131–40. doi:10.1002/(ISSN)1099-114X. [Google Scholar] [CrossRef]

22. Schilichting H. Boundary layer theory. New York: McGrawHill Book Company; 1979. [Google Scholar]

23. Bahrami PT, Wang TG. Analysis of gravity and conduction-driven melting in a sphere. ASME J Heat Mass Transfer. 1987;109(3):806–9. doi:10.1115/1.3248166. [Google Scholar] [CrossRef]

24. Moallemi MK, Webb BW, Viskanta R. An experimental and analytical study of close contact melting. ASME J Heat Transfer. 1986;108(4):894–9. doi:10.1115/1.3247030. [Google Scholar] [CrossRef]

25. Moallemi MK, Viskanta R. Analysis of close contact melting heat transfer. Int J Heat Mass Transfer. 1986;29(6):855–67. doi:10.1016/0017-9310(86)90181-X. [Google Scholar] [CrossRef]

26. Zhao YS, Liang WH, Chen WZ. Contact melting of unfixed solid phase change material inside a cylindrical tube with constant heat flux. Chin J Comput Phys. 2011;28(4):529–34 (In Chinese). [Google Scholar]