Chemical Reaction on Williamson Nanofluid’s Radiative MHD Dissipative Stagnation Point Flow over an Exponentially Inclined Stretching Surface with Multi-Slip Effects

Nomenclature

1  Introduction

When a fluid interacts with a solid surface, it divides and circulates around the surface, creating a “stagnation point.” This phenomenon displays unique characteristics, including heat transfer, mass deposition rate, and fluid pressure, which distinguish it from ordinary conventional flow situations encountered in the stagnation zone. Chiam [1] and Khashi’ie et al. [2] were pioneers in the identification and analysis of stagnation point flow behavior, concentrating their research on flow over stretching and shrinking sheets. As technology has gotten better, shapes like discs, cylinders, and wedges are being used more and more in the study of stagnation point flow in a wide range of situations [3–5].

Nanofluid technology has emerged as a significant area of research in recent years. The fundamental concept of nanofluids involves suspending nanoparticles in a base fluid to significantly increase its thermal conductivity, a concept first proposed by Choi et al. [6], thereby improving heat transfer in various energy systems. Common nanoparticles consist of components like titania, alumina, copper, copper oxide, and gold, with water and certain organic solvents typically serving as the base fluids. Lin et al. [7] conducted an experimental investigation on the application of nanofluids in pulsing heat pipes, utilizing silver nanoparticles. Their results showed that adding silver nanofluid greatly improved heat transfer performance. This shows that silver nanoparticles are good for improving heat transfer efficiency in these systems. Kuznetsov et al. [8] utilized Buongiorno’s [9] established nanofluid model to investigate the nature of Brownian motion and thermophoresis on natural convective nanofluid flow across a vertical surface, while also integrating critical boundary conditions. Many researchers have since examined nanofluid flows, accounted for Brownian motion and thermophoretic forces in boundary layer dynamics. This study incorporates the significance of these effects within the solutal boundary layer of nanoparticles into its analysis. Wong et al. [10] indicated that nanotechnology is essential in numerous contemporary scientific and technological developments, encompassing applications in heat absorption, energy processing, and nuclear reactors.

Because non-Newtonian fluids are so complicated, the Navier-Stokes equations are not enough to explain flow problems involving them. Non-Newtonian fluids, including Eyring-Powell fluid, Williamson fluid, Casson fluid, Prandtl fluid, Reiner-Philippoff fluid, micropolar fluid, Carreau fluid, Prandtl-Eyring fluid, and power law fluid, have attracted considerable attention from researchers due to their extensive applications in diverse industrial domains. Among these, the Williamson fluid is especially significant. Sectors such as food processing, adhesive and paint manufacturing, nuclear power plant cooling systems, and polymer production extensively utilize this fluid. In 1929, Williamson [11] created a scientific model for materials exhibiting variable flow properties under pressure. This model offered an innovative method for comprehending fluid dynamics through equations instead of conventional analytical techniques. It represented a notable progression in the examination of materials that modify their viscosity in response to stress. Taj et al. [12] studied the flow characteristics of a Williamson fluid that can’t be squished and has viscous dissipation over a rough, non-linear stretching surface, taking into account how heat and mass move together. Recent research has concentrated on the flow characteristics of Williamson fluid and its various applications [13–17].

A variety of technical and industrial processes could greatly benefit from research on the fluid flow over an exponentially stretched sheet. In the fabrication of plastic sheets from a die, stretching sheet flows are involved in processes such as rubber extrusion, wire drawing, hot rolling, and the creation of plastic sheets. It is also possible for these flow problems to occur during the production of polymer sheets, melt spinners, synthetic films, and synthetic fibers. As a consequence of this, specialists in fluid mechanics have been concentrating more and more on the study of fluid flow during the past few years. Although earlier researchers have conducted significant studies, they have not effectively addressed certain critical difficulties. Crane [18] was the first to investigate the boundary layer flow and heat transfer of an electrically conducting viscous fluid across a stretching sheet. With the purpose of scientifically and quantitatively resolving the difficulties of this phenomenon, Magyari et al. [19] carried out an in-depth investigation of the exchange of thermal heat and mass in the dynamic boundary layer flow. This flow is characterized by an exponentially elongating continuous surface. Bidin et al. [20] gave an analytical answer for boundary layer transport over an inclined exponentially stretched sheet in the context of thermal slip conditions. Numerous academics [21–22] have noticed the multitude of applications of this methodology in the manufacturing sector. These researchers are particularly interested in examining the dynamics under slip situations because of the extensive applications of this methodology.

Magnetohydrodynamics (MHD), a branch of fluid mechanics that focuses on electromagnetic processes and fluids that transmit electricity, has led to significant industrial improvements. The extensive implementation of MHD across a variety of sectors has led to the development of a wide variety of applications. Radiation significantly natures many physical processes. Radiation facilitates the transfer of heat energy through fluid particles. The effect that radiation has on fluid flow plays a crucial role in engineering and numerous industrial advancements. These developments include high-temperature applications such as fuel pumps, paper plates, frozen metal shards, and various electrical chips. As a consequence of this, scientists are obligated to investigate the radiation process that is generated by considerable temperature differences. Researchers have explored a variety of flow parameters to study radiation processes. When it comes to research on mass and heat transfer, chemical reactions play a key role across a wide range of scientific and technical domains. The extensive use of chemical reactions in industry explains this. There are a variety of applications that need chemical reactions, including but not limited to the creation of chemical processing equipment, the synthesis of polymers, cooling towers, pollution control, fog generation and dispersion, temperature regulation, and fiber insulation.

Ishak [23] did a study on radiation affects the flow of a magnetohydrodynamic (MHD) boundary layer over a sheet that is stretching exponentially. Nayak et al. [24] did a lot of research on the effects of a changing magnetic field, a field density distribution that isn’t uniform, and thermal energy on the flow of fluids caused by a sheet that is stretching exponentially. Megahed [25] used a nonlinearly exponentially stretched sheet to study viscous dissipation and thermal radiation in the flow of Williamson fluid. Ahmed et al. [26] performed a numerical analysis of magnetohydrodynamic Williamson nanofluid flow over an exponentially stretched surface. Khan et al. [27] studied the boundary layer flow of Williamson fluid with the help of the homotopy analysis method (HAM). Nadeem et al. [28] came up with a mathematical theory to explain how Williamson fluid flows over a two-dimensional surface that has sheets that stretch in both linear and exponential ways.

Hayat et al. [29] developed a methodology to characterize the uniform magnetohydrodynamic flow of Williamson fluid across a permeable surface. Akbar et al. [30] looked into the changes in temperature and chemical reactions that affect the basic ideas of Williamson fluid, specifically how blood flows in a small vein that ends in a point. Ibrahim et al. [31] conducted an analysis of the stagnation point in magnetohydrodynamics (MHD), taking into account the effects of thermal radiation. Ibrahim et al. [32] examined the slip flow characteristics of a nanofluid on an inclined plane. Nadeem et al. [33] looked into how thermal energy affects the boundary layer flow of a nanofluid in magnetohydrodynamics. They looked at slip and convective boundary conditions.

Khan et al. [34] investigated the radiative stagnation point flow of a time-dependent Casson fluid over a permeable stretching/shrinking surface, incorporating mass suction, a magnetic field, and a non-uniform heat source and sink. Raza et al. [35] examined the impact of chemical reactions on the dynamics of mono and hybrid nanofluids in the presence of a magnetic field and activation energy. Koriko et al. [36] examined the gravity-driven flow of a thixotropic fluid with nanoparticles and gyrotactic microorganisms along a vertical surface in the presence of chemical reactions. Zhang et al. [37] investigated the characteristics of convection and Joule heating in the magnetohydrodynamic two-dimensional stagnation point flow of a nanofluid over a permeable curved stretching or shrinking surface with mass suction. Rajendar et al. provided additional insights into the MHD stagnation point flow of Williamson nanofluid over an exponentially stretching sheet with variable parameters [38].

Extensive research and evaluation indicate that advanced investigations are required to comprehend the impact of multi-slip effects under suction and injection on Magnetohydrodynamic (MHD) Williamson nanofluid flow over an exponentially inclined stretching sheet. This study focuses on non-Fourier and non-Fick laws to identify essential components in heat and mass transfer processes. This research is expected to address gaps identified in prior studies. The analysis includes the effects of thermophoresis, Brownian motion, chemical reactions, viscous dissipation, and radiation, contributing to the resolution of another significant challenge. The issue was addressed numerically through the HAM method, accompanied by graphical data and a brief discussion. Additionally, particular cases are analyzed to verify our conclusions.

2  Mathematical Formulation

Study a 2D flow at stagnation point of Williamson nanofluid in the direction of a elongating sheet, which is inclined at an angle Ω, retained at a perpetual temperature Tw and concentration C∞. The ambient temperature and concentration are T∞ and C∞, respectively. The flow is subjected to a constant transverse magnetic field of strength B(x)=B0ex2L which is assumed to be applied in the positive y-direction, normal to the surface where B0 is a constant magnetic field. The induced magnetic field is considered negligible relative to the applied magnetic field and is therefore disregarded. Additionally, it is assumed that the base fluid and the suspended nanoparticles are in thermal equilibrium. We take the coordinate structure such that x-axis is along the elongating sheet with the velocity U=Uw=bexL, also the ambient fluid velocity is U∞=aexL,a>0,b>0. The schematic flow diagram and the coordinate system of the problem are both displayed in Fig. 1. Presumptuous that there is no pressure gradient and the properties of Brownian motion are measured. Here we considered heat radiation, injection, suction, viscous dissipation, multi slip effects and chemical changes.

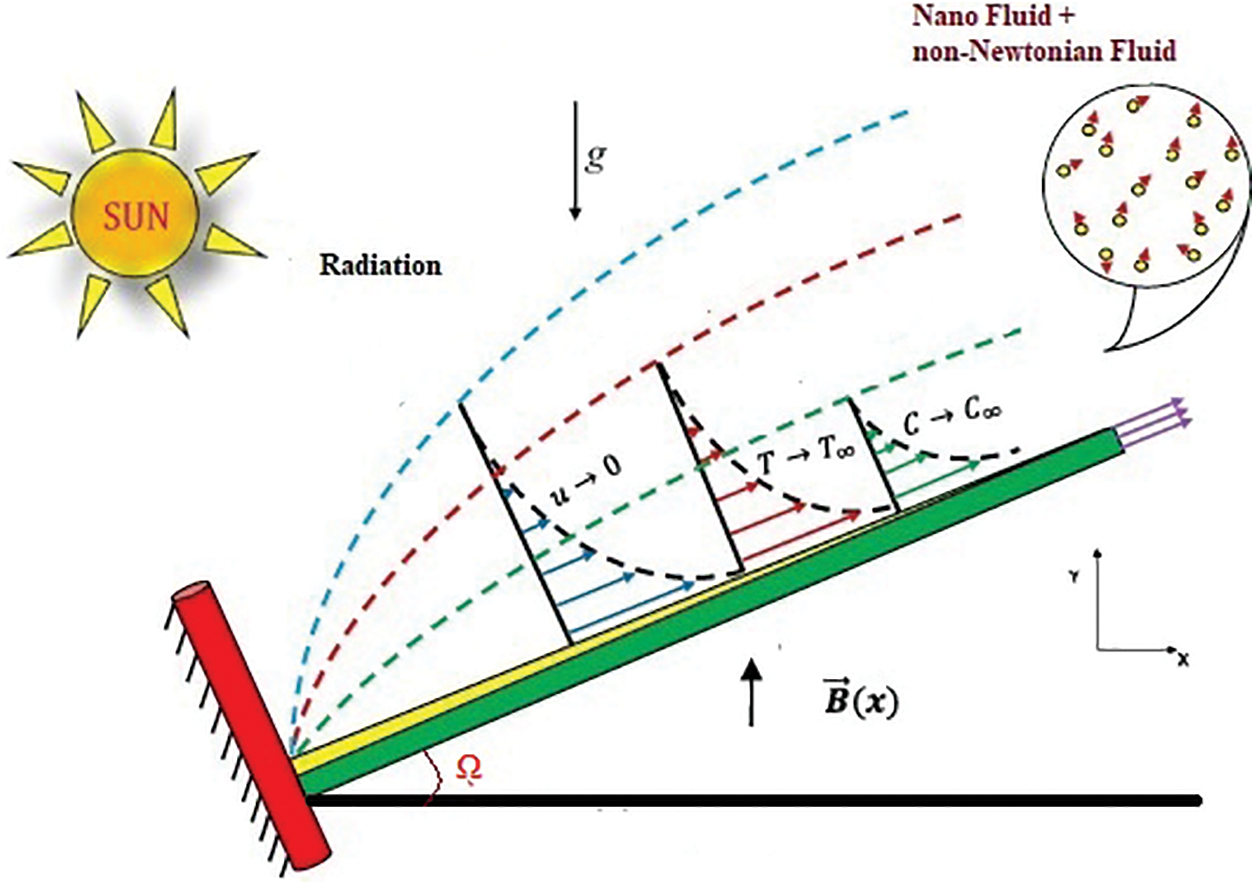
Figure 1: Geometry of flow problem

The Nadeem et al. [28] study incorporates the Williamson fluid classical. In the current fluid classical, the Cauchy stress tensor, represented by the symbol S, is demarcated as follows:

S=−pI+τ1S=−pI+(μ∞+μ0−μ∞1−Γα)A1

Here, τ1 is stress tensor of Williamson’s fluid model, μ0 is variable of no viscosity shear rate and μ∞ is variable viscosity at inestimable shear rate, Γ(positive values only) is referred to as perpetual time, A1 is the first Rivlin-Erickson tensor and α is demarcated as

α=12 π,

where π = trace(A12)

α=(∂u∂x)2+12+(∂u∂y+∂v∂x)2+(∂v∂y)2

Here, we reflected the situation for which μ∞= 0 and Γα < 1.

Then, we achieved τ1=(μ0A11−Γα).

The corresponding partial differential equations (PDEs) leading from the above MHD, Williamson nanofluid flow model, are written as follows [38]:

∂u∂x+∂v∂y=0,(1)

u∂u∂x+v∂u∂y=υ∂2u∂y2+2υΓ∂u∂y∂2u∂y2+g[βT(T−T∞)+βC(C−C∞)]cos⁡Ω+U∞dU∞dx+σfB02ρf(U∞−u),(2)

u∂T∂x+v∂T∂y=α∂2T∂y2+τ[DB∂C∂y∂T∂y+DTT∞(∂T∂y)2]+μ(cp)f(∂u∂y)2−1(ρcp)f∂qr∂y,(3)

u∂C∂x+v∂C∂y=DB∂2C∂y2+DTT∞∂2T∂y2−Kr(C−C∞).(4)

The following boundary conditions (B.Cs) apply to these complex PDEs:

u=Uw(x)+δ1∗(∂u∂y),v=Vw,T=Tw(x)+δ2∗(∂T∂y),C=Cw(x)+δ3∗(∂C∂y)aty=0,u→U∞,T→T∞+T0ex/(2L),C→C∞+C0ex/(2L),as y→∞,(5)

where α=k(ρcp)f, υ=μρf, τ=(ρcp)p(ρcp)f, Vw(x)=V0ex/(2L).

The Roseland estimate, the radiative thermal flux is

qr=−σ∗4κ∗3∂T4∂y.(6)

Here, σ∗ represents the Stefan-Boltzmann constant and κ∗ is the mean absorption coefficient. Assuming an adequately large internal temperature gradient in the flow, T4 can be approximated as a linear function of temperature. By performing a Taylor series T4 expansion around T∞, a reference temperature and abandoning higher-order terms, we obtain

T4≅T4T∞3−3T∞4(7)

Consuming Eqs. (6) and (7), the Eq. (3) adapts into

u∂Tw∂x+v∂Tw∂y=(α+16σ∗T∞33κ∗(ρc)f)∂2Tw∂y2+τ[DB∂Cw∂y∂Tw∂y+DTT∞(∂Tw∂y)2]+μcf(∂u∂y)2.(8)

To make the mathematical analysis more straightforward, the similarity transformation that is presented below is utilized [38]:

ζ=(a2νL)1/2ex/2Ly,u=aex/L f′(ζ),v=−νa2Lex/2L(f(ζ)+ζf′(ζ)),T=Tw=T∞+T0ex/(2L) θ(ζ),C=Cw=C∞+C0ex/(2L) θ(ζ).}.(9)

Here, ζ is the similarity variable.

The controlling PDE’s are turned into an ODE’s by employing transformations (9) and can be written as

f′′′+λf′′f′′′+ff′′−2f′2+2A2+M(A−f′)+(Grθ+Gcϕ)cos⁡Ω=0,(10)

(1+43R)θ′′+Prfθ′−Prf′θ+PrNbϕ′θ′+PrNtθ′2+PrEc(f′′)2=0,(11)

ϕ′′+Sc(fϕ′−f′ϕ−γϕ)+NtNbθ′′=0.(12)

Dimensionless boundary conditions are

f(0)=S,f′(0)=1+δ1f′′(0),θ(0)=(1+δ2θ′(0)),ϕ(0)=(1+δ3ϕ′(0)).f′(∞)→A,θ(∞)→0,ϕ(∞)→0,(13)

The expressions of embedded physical parameters

λ=Γa3e3x/LυL, M=2LσfB02ρfa, Grx=2LgβT(Tw−T∞)x2a2, Gr=GrxRex2, Gcx=g2LβC(Cw−C∞)x2a2, Gc=GcxRex2, A=ba, Pr=υα, Nb=τDB(Cw−C∞)ν, Nt=τDT(Tw−T∞)υT∞, R=4σ∗T∞3k∗k, Sc=υDB, γ=2LKra, δ1=δ1∗a2Lυ, δ2=δ2∗a2υL, δ3=δ3∗a2Lυ, S=V0/(aυ2L) , Ec=U2cf(Tw−T∞).

As a sequel to the above elucidation, the related local quantities of interest are local Sherwood number Shx, skin friction factor Cfx, local Nusselt number Nux, and, whose reduced forms are given by

Cfx=1ρUw2(μ(∂u∂y+Γ2(∂u∂y)2))y=0,Nux=−2L(Tw−T∞)ex2L(∂T∂y)y=0,Shx=−2L(Cw−C∞)ex2L(∂C∂y)y=0.

By applying similarity transformations to Eq. (9), the resulting dimensionless forms are derived as follows:

2RexCfx=(f′′(0)+λ2(f′′(0))2),NuxRex=−(1+43R)θ′(0),ShxRex=−ϕ′(0),

where Rex=axex/Lv.

2.1 HAM

In order to reflect the homotopic illuminations of Eqs. (10) to (13), we have enumerated the key deductions and linear operators as surveys.

f0(ζ)=S+Aζ+(1−A1+δ1)(1−e−ζ),θ0(ζ)=e−ζ1+δ2,ϕ0(ζ)=e−ζ1+δ3,

Lf(f)=f′′′−f′,Lθ(θ)=θ′′−θ,Lϕ(ϕ)=ϕ′′−ϕ,

with

Lf(D1+D2eζ+D3e−ζ)=0,Lθ(D4eζ+D5e−ζ)=0,Lϕ(D6eζ+D7e−ζ)=0.

Here, Di(i=1to7) will be the random coefficients.

We will hypothesis the zeroth-order distortion calculations

−(p−1)Lf(f(ζ;p)−f0(ζ))=pℏfNf[f(ζ;p),θ(ζ;p),ϕ(ζ;p)],(14)

−(p−1)Lθ(θ(ζ;p)−θ0(ζ))=pℏθNθ[f(ζ;p),θ(ζ;p),ϕ(ζ;p)](15)

−(p−1)Lϕ(ϕ(ζ;p)−ϕ0(ζ))=pℏϕNϕ[f(ζ;p),θ(ζ;p),ϕ(ζ;p)],(16)

considering the boundary settings

f(0;p)=S,f′(0;p)=[1+δ1f′′(0)],f′(∞;p)=0,θ(0;p)=[1+δ2θ′(0)],θ(∞;p)=0,ϕ(0;p)=[1+δ3ϕ′(0)],ϕ(∞;p)=0.(17)

Here,

Nf[f(ζ;p),θ(ζ;p),ϕ(ζ;p)]=∂3f(ζ;p)∂ζ3+f(ζ;p)∂2f(ζ;p)∂ζ2+λ∂2f(ζ;p)∂ζ2∂3f(ζ;p)∂ζ3−2(∂f(ζ;p)∂ζ)2+2A2+M(A−∂f(ζ;p)∂ζ)+(Grθ(ζ;p)+Gcϕ(ζ;p))cos⁡Ω,(18)

Nθ[f(ζ;p),θ(ζ;p),ϕ(ζ;p)]=1Pr(1+43R)∂2θ(ζ;p)∂ζ2+f(ζ;p)∂θ(ζ;p)∂ζ+Nb∂θ(ζ;p)∂ζ∂ϕ(ζ;p)∂ζ+Nt(∂θ(ζ;p)∂ζ)2+Ec(∂2f(ζ;p)∂ζ2)2,(19)

Nϕ[f(ζ;p),θ(ζ;p),ϕ(ζ;p)]=∂2ϕ(ζ;p)∂ζ2+Scf(ζ;p)∂ϕ(ζ;p)∂ζ+NtNb∂2θ(ζ;p)∂ζ2−Scγϕ(ζ;p),(20)

anywhere p∈[0,1] is the indulging constraint, ℏf,ℏθ and ℏϕ are non-vanishing assisting limitations and Nf,Nθ and Nϕ are non-linear operatives.

The nth order alteration estimates surveys will be

Lf(fn(ζ)−χnfn−1(ζ))=ℏfRnf(ζ),(21)

Lθ(θn(ζ)−χnθn−1(ζ))=ℏθRnθ(ζ),(22)

Lϕ(ϕn(ζ)−χnϕn−1(ζ))=ℏϕRnϕ(ζ),(23)

with the subsequent boundary environs

fn(0)=0,fn′(0)=δ1fn′′(0),fn′(∞)→0,θn(0)=δ2θn′(0),θn(∞)→0,ϕn(0)=δ3ϕn′(0),ϕn(∞)→0.(24)

Here,

Rnf(ζ)=fn−1′′′+λ∑i=0n−1fn−1−i′′ fi′′′+2∑i=0n−1fn−1−ifi′′−∑i=0n−1fn−1−i′fi′+(1−χn)(2A2+M)−Mfn−1′+(Grθm−1+Gcϕm−1)cos⁡Ω(25)

Rnθ(ζ)=1Pr(1+4R3)θn−1′′+∑i=0n−1fn−1−iθi′+Nb∑i=0n−1θn−1−i′ϕi′+Nt∑i=0n−1θn−1−i′θi′+Ec∑i=0n−1fn−i−1′′fi′′,(26)

Rnϕ(ζ)=ϕn−1′′+Sc(∑i=0n−1fn−1−iϕi′−γϕn−1)+NtNbθn−1′′,(27)

χn={0,n≤1,1,n>1.

If we let fn(ζ),θn(ζ)andϕn(ζ) as the unusual solutions of nth order distortion computations, then the common elucidation is assumed by

fn(ζ)=fn∗(ζ)+D1+D2eζ+D3e−ζ,θn(ζ)=θn∗(ζ)+D4eζ+D5e−ζ,ϕn(ζ)=ϕn∗(ζ)+D6eζ+D7e−ζ,(28)

Here, the integral constants Di(i=1to7) are found out through the assistance of boundary situations.

By exhausting MATHEMATICA the above given linear homogeneous equations are solved for n=1,2,…

2.2 Convergence of HAM

To get the suitable standards for the non-zero ancillary constraints, ℏ-curves are described in Fig. 2. As per this figure, the surmisable intermission of ancillary constraint is [−1.0,0.0]. The elucidations are convergent for whole constituency of ζ when ℏf=ℏθ=ℏϕ=−0.60. Convergence of the technique is specified in Table 1.

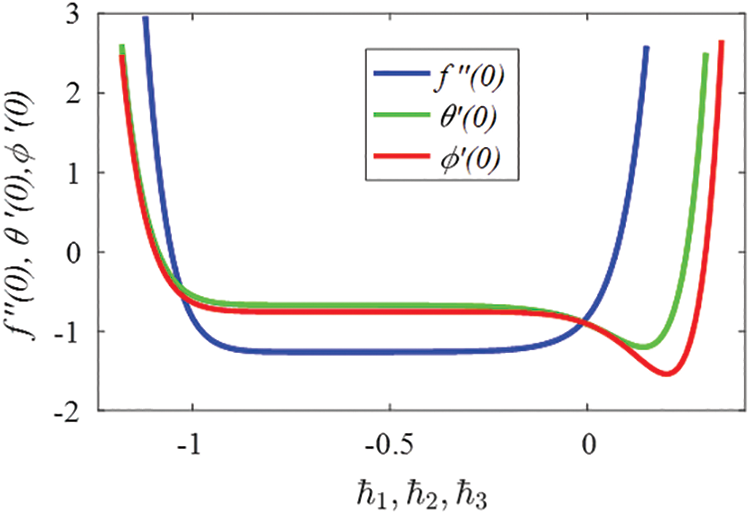
Figure 2: ℏ-curves for f′′(0),θ′(0)andφ′(0) at 15th order guesstimates

3  Results and Discussions

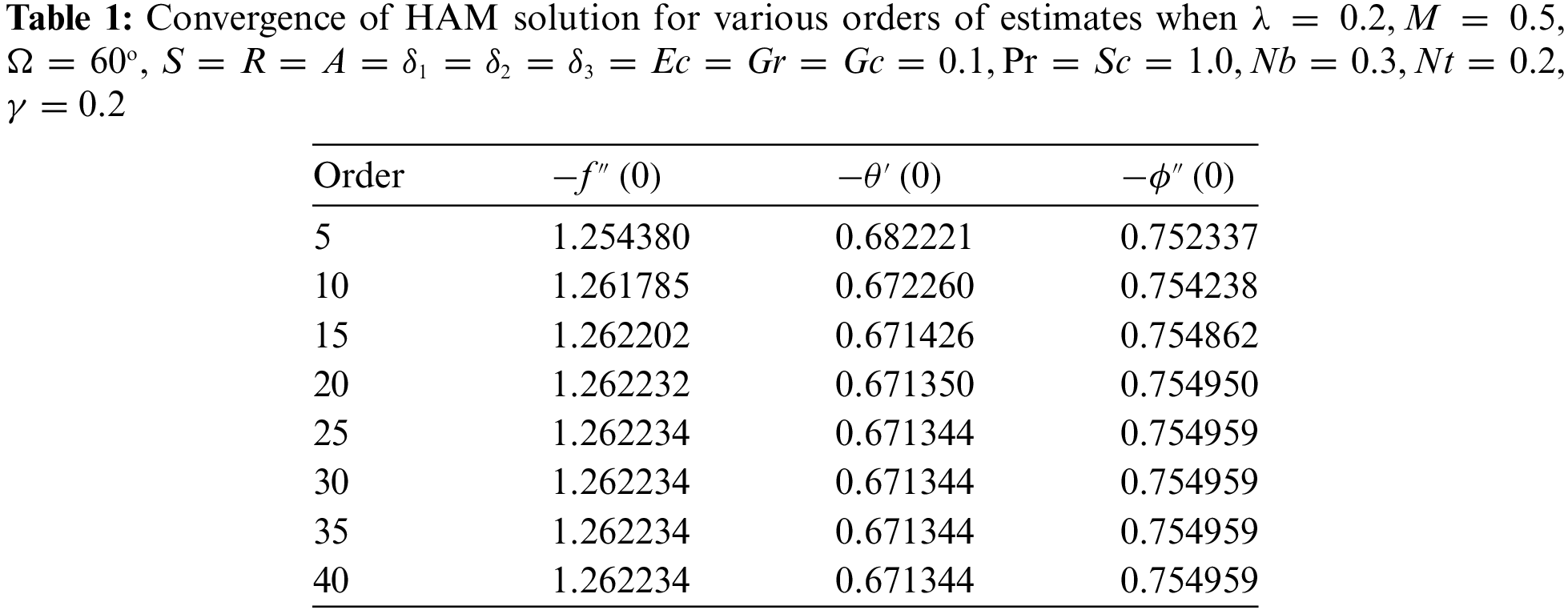
The purpose of this study is to evaluate the effects that fluid motion, electromagnetic fields, heat conduction, and dynamic conductivity have on the boundaries of velocity, temperature, and concentration. The governing equations were solved with the help of HAM, and the results were displayed in a graphic format in order to illustrate how the system behaves. Throughout the study, various physical parameters were analyzed, including the Williamson parameter λ, magnetic parameter M, stretching velocity ratio A, reaction rate parameter γ, and slip conditions δ1,δ2,δ3, along with thermophoresis index Nt, Brownian motion coefficient Nb, Prandtl number pr, and Schmidt number Sc on velocity distribution, temperature, and mass flow. A detailed flow diagram illustrates mass distribution under various conditions. We explored a diverse array of statistical methodologies, such as λ=0.2,M=0.5,Ω=60o,S=R=A=δ1=δ2=δ3=Ec=Gr=Gc=0.1,Pr=Sc=1.0,Nb=0.3,Nt=0.2,γ=0.2. With the exception of the tables and graphs that are relevant to verifying the variations in parameters, the values of these variables remain consistent for the entirety of the article, unless otherwise noted.

Table 2 represents the comparison of −θ′(0) value with published papers and present results. The present results obtained numerical results are compared with published research [20,23], and [38] for −θ′(0). This comparison is made for several reduced examples. It may be observed that our findings and the studies that have been published are in good agreement.

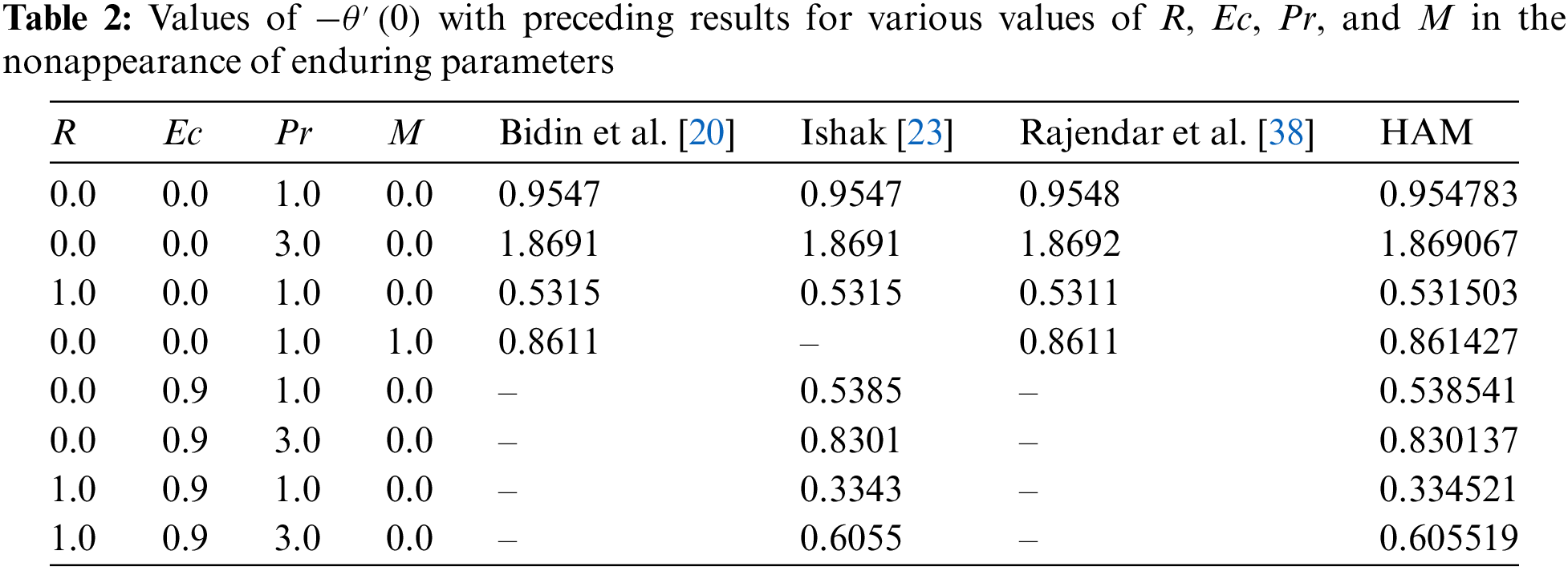
Comparison table for local Nusselt number skin friction when (We = γ = M = Sc = Kp = 0; Pr = 0.72); Nt = 0.1; and Nb = 0.2; against a few values of λ.

Fig. 3 illustrates the Williamson nanofluid parameter λ affects the flow distribution. A rise in this parameter results in a reduction in velocity magnitude. This behavior corresponds with the physical interpretation of the Williamson fluid parameter λ, which is directly proportional to relaxation time and inversely proportional to shear rate. As a result, a greater Williamson parameter λ is associated with an extended relaxation time, leading to a decrease in fluid velocity because of heightened frictional resistance. On the other hand, as the velocity diminishes, both the temperature and nanoparticle volume fraction profiles show an increasing trend, as demonstrated in Figs. 4 and 5.

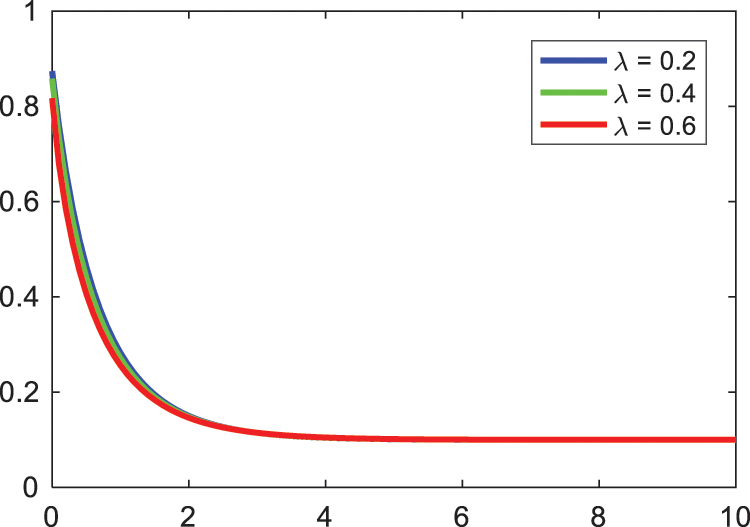
Figure 3: Nature of Williamson parameter on f′(ζ)

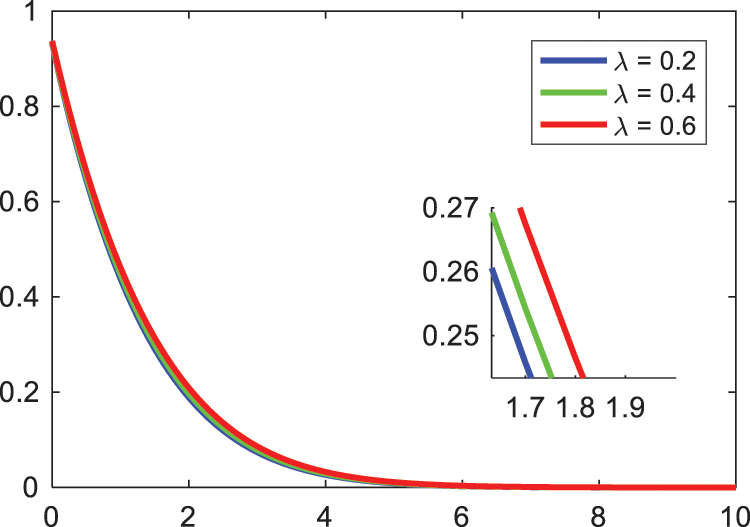
Figure 4: Nature of Williamson parameter on θ(ζ)

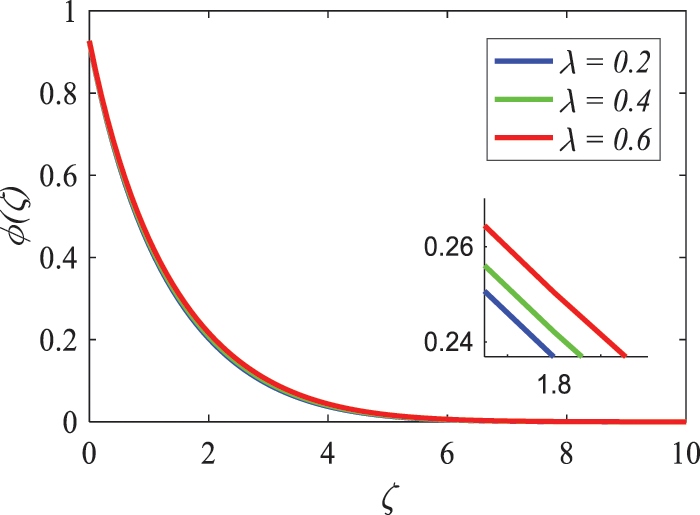
Figure 5: Nature of Williamson parameter on ϕ(ζ)

Fig. 6 depicts the effect that a strong magnetic field, denoted by M, has on a sheet that is stretched in an inclined position. As the magnetic field grows, it is found that the velocity component decreases. This is because the magnetic parameter M induces opposite Lorentz forces, which cause the velocity component to drop. A large reduction in the thickness of the momentum boundary layer also occurs when the value of M is increased. It can be seen in Fig. 6 that the magnetic field has a significant impact on the overall reduction of the fluid flow. As shown in Figs. 7 and 8, respectively, the contours of temperature and concentration are provided for a variety of values of the magnetic parameter M. There is a correlation between elevated temperature profiles and an increase in M, and Fig. 8 demonstrates that the concentration rises as M rises.

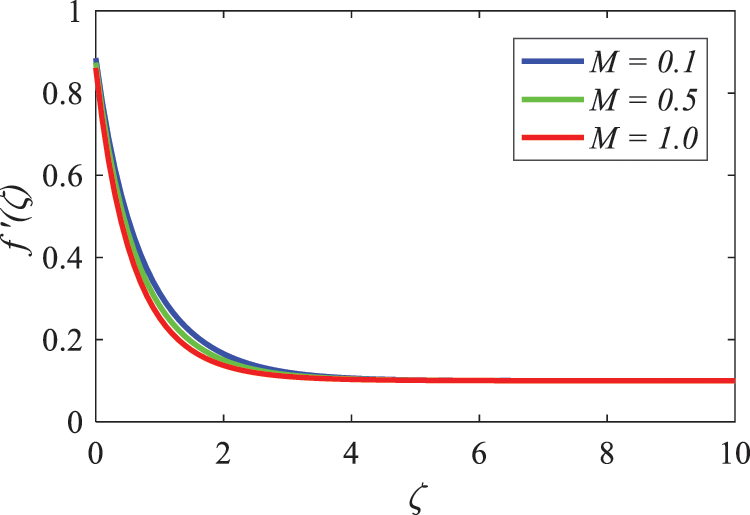
Figure 6: Nature of magnetic field parameter on f′(ζ)

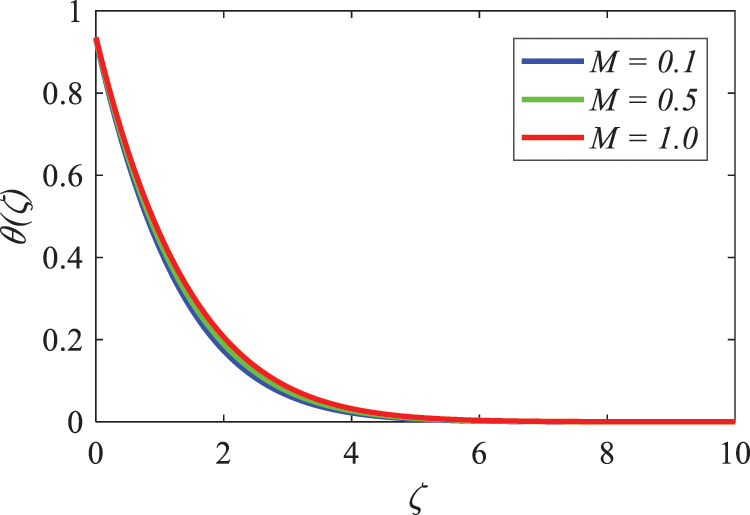
Figure 7: Nature of magnetic field parameter on θ(ζ)

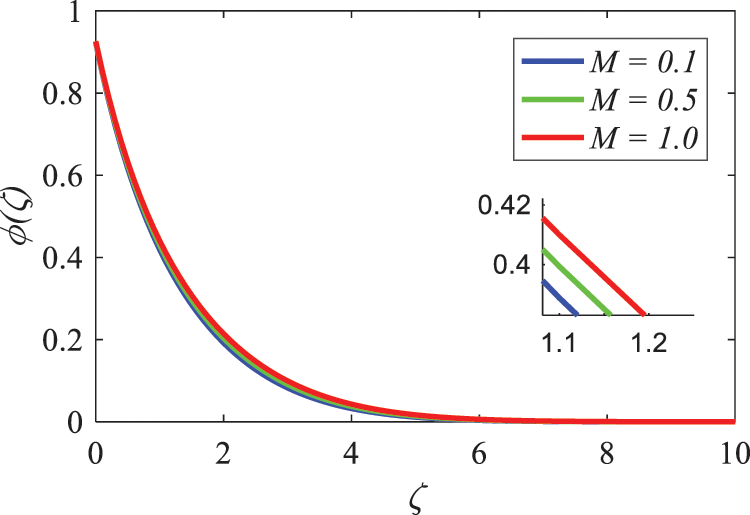
Figure 8: Nature of magnetic field parameter on ϕ(ζ)

In Fig. 9, we see a nonlinear velocity profile that is influenced by several values of the velocity ratio parameter A. When the boundary layer is further away from the wall, the fluid velocity is higher, whereas it is lower when it is closer to the wall. The velocity of the wall is much higher than the velocity of the free stream when the value of A is taken into consideration. However, the fluid may undergo local acceleration at specific distances, which might potentially cause the velocity to dip below the free-stream value. This occurs as the fluid gradually slows down as it approaches the wall with a high inertia. Because of this, the fluid that moves more slowly is forced forward by the uninterrupted flow. At a value of A = 0, the free-stream velocity is extremely close to zero, and there is no free-flow drag. It is the imposed flow rate that defines the local velocity beyond the boundary layer for all values of A > 0.

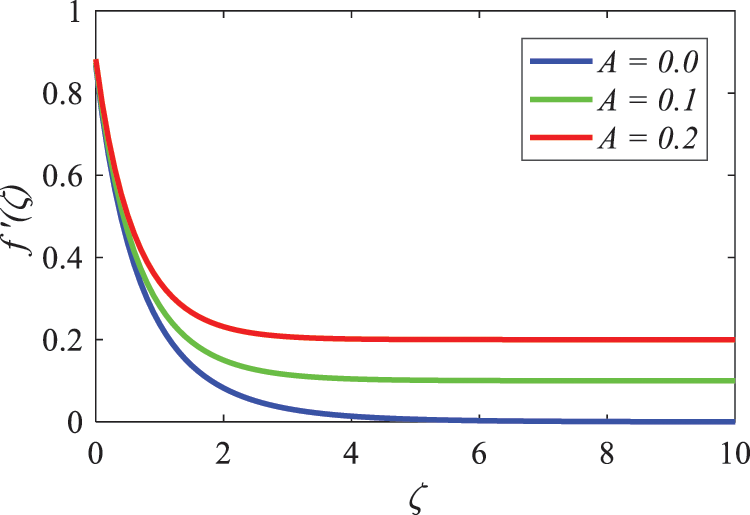
Figure 9: Nature of velocity ratio parameter on f′(ζ)

Fig. 10 depicts the temperature distribution as a function of the velocity ratio parameter A. The thickness of the thermal boundary layer reduces in proportion to the velocity ratio parameter A increasing value. In addition, a temperature profile that is lowering may be seen when the surface temperature gets closer to its maximum value, which is increasing with the value of A. Fig. 11 is a representation of the relationship that exists between concentration and the velocity ratio parameter represented by A. A decrease in the thickness of the concentration boundary layer occurs whenever the value of A is increased.

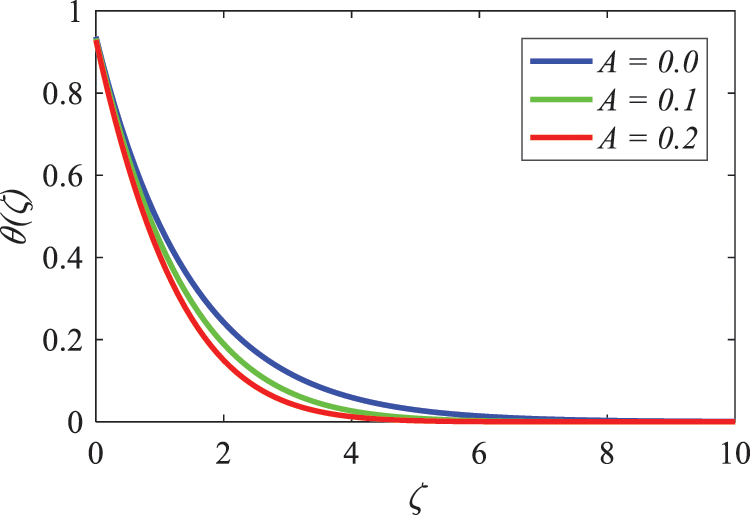
Figure 10: Nature of velocity ratio parameter on θ(ζ)

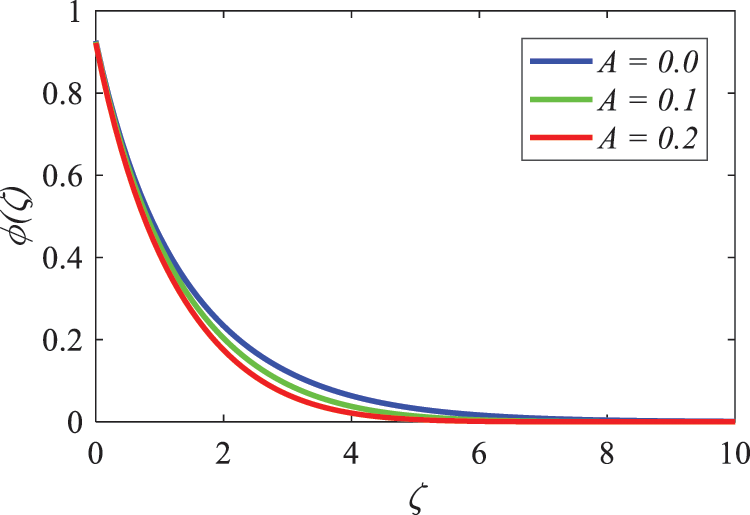
Figure 11: Nature of velocity ratio parameter on ϕ(ζ)

It is seen in Fig. 12 that the velocity reduces as the inclination angle Ω increases. The existence of Lorentz forces close to the solid surface is responsible for the changes in flow pattern that have occurred, which in turn have led to a decrease in the velocity of the fluid. A representation of the impact that the suction parameter S has on velocity profiles may be found in Fig. 13. An increase in S results in an increase in the velocity gradient. The boundary layer is reduced in thickness as a result of the removal of fluid via suction. The presence of a thinner boundary layer leads to a steeper velocity gradient, which indicates a quicker transition of velocity from the wall to the free stream. This, in turn, often results in a reduction in the velocity profile as a whole.

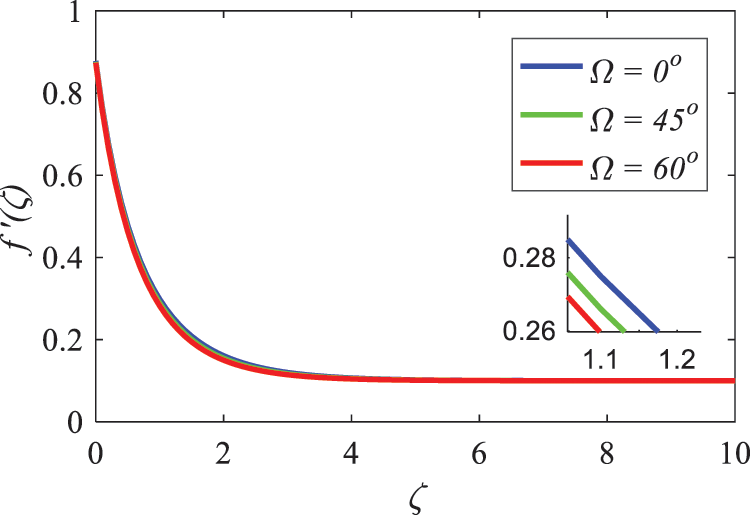
Figure 12: Nature of Inclination angle on f′(ζ)

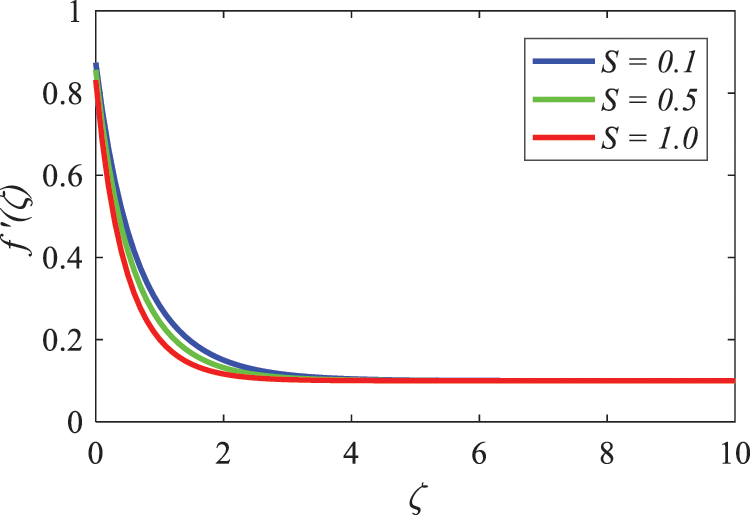
Figure 13: Nature of suction on f′(ζ)

The influence of the local Grashof number (Gr) on velocity profiles is seen in Fig. 14, which demonstrates that velocity increases as Gr increases. A greater Grashof number suggests a stronger free convection flow, which ultimately results in higher fluid velocities. Additionally, as can be seen in Fig. 15, the velocity profiles also increase when the values of the modified Grashof number (Gc) increase.

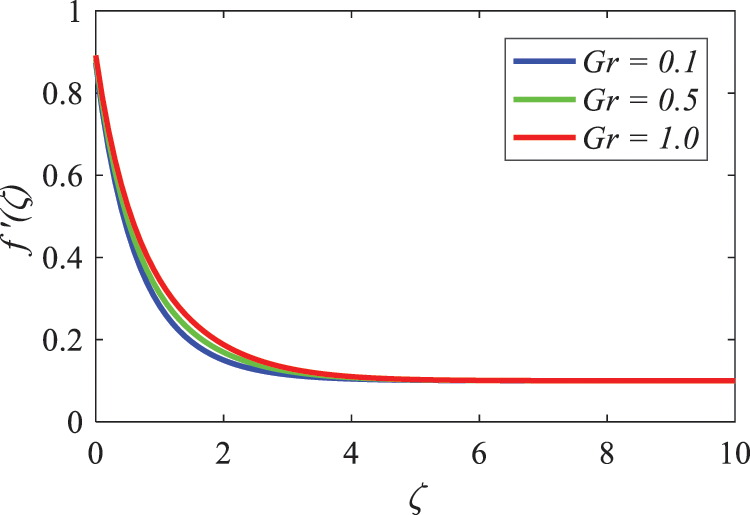
Figure 14: Nature of Grashof number parameter on f′(ζ)

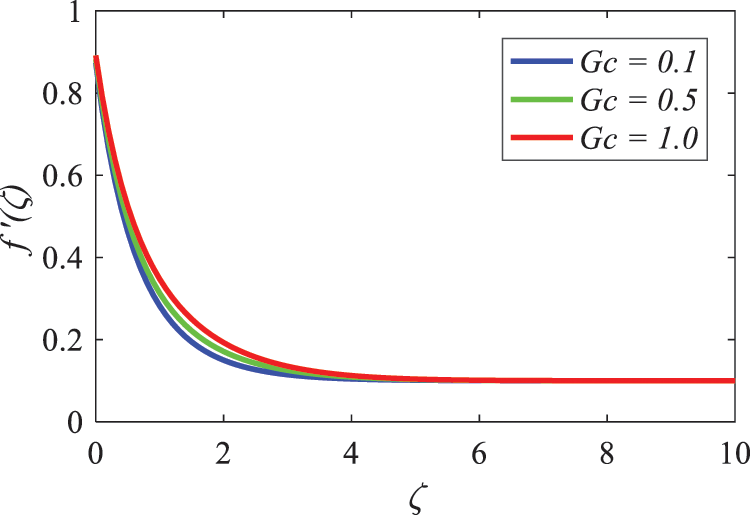
Figure 15: Nature of modified Grashof number parameter on f′(ζ)

Fig. 16 depicts the consequence of the flow slip parameter δ1 on the flow distribution. After a thorough examination, it is clear that the upsurge in the flow slip parameter δ1, which stands for the swiftness profile, decreases. Increasing the slip parameter clearly results in a diminishing swiftness, as seen in the Fig. 16. Upon first introduction, the velocity distribution starts to decrease along the edge in boundary. Fig. 17 shows impact of the temperature profile is affected by the thermal jump parameter δ2. As the thermal jump parameter increases over the boundary film region, the fluid temperature drops, as seen in this depiction. The amount of fluid transmitted to the updraft boundary slip increases as the impact increases. These indications to a decline in the thickness of the thermal boundary layer and an increase in the rate of heat transmission.

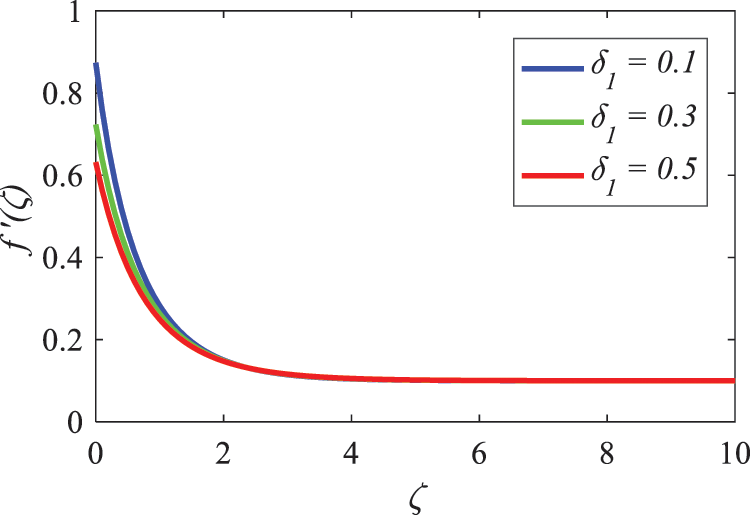
Figure 16: Nature of velocity slip factor on f′(ζ)

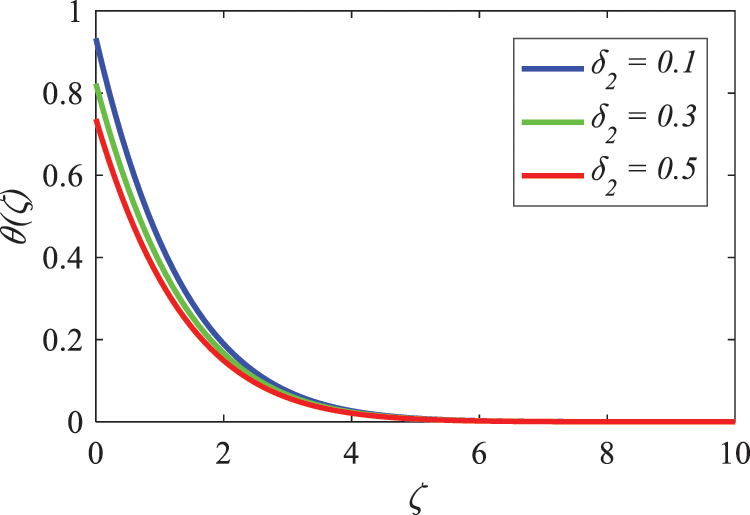
Figure 17: Nature of thermal slip factor θ(ζ)

Concentration changes as a function of the concentration slip parameter δ3 is sown in Fig. 18. As the concentration slip parameter increases, the concentration profile progressively decreases, as is readily visible. When the slip parameter is larger, the boundary resistance to particle flow tends to decrease. As a result, particles may be quickly moved away from the boundary, subsequent in a thinner boundary layer and a lower overall concentration close the boundary.

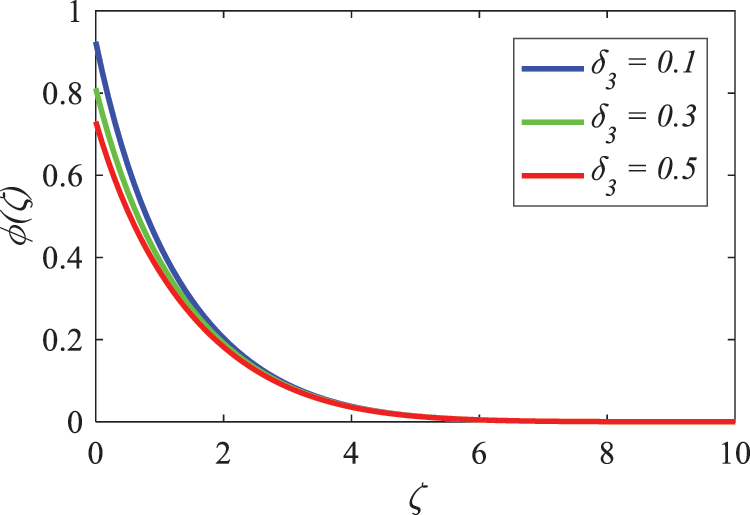
Figure 18: Nature of concentration slip factor on ϕ(ζ)

An increase in the radiation parameter R leads to an increase in the dimensionless temperature, as seen in Fig. 19, which illustrates this relationship. Increasing the amount of thermal radiation causes an increase in the rate at which heat is absorbed by the particles that make up the fluid. In consequence of this, a greater amount of thermal energy is maintained, which ultimately results in an increase in the local temperature distribution, also known as the temperature profile, across the fluid. This impact is especially significant in systems that involve high temperatures, as it is in these systems that radiative heat transfer becomes the predominant mode of energy transmission.

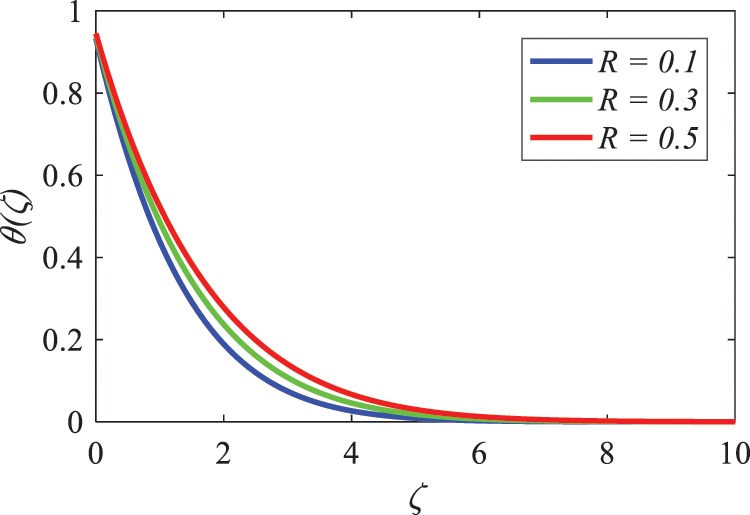
Figure 19: Nature of radiation parameter on θ(ζ)

In accordance with the results reported in Fig. 20, the temperature drops as the Prandtl number (Pr) grows. It may be deduced from the fact that the temperature field decays more slowly with higher Pr values that a larger Prandtl number results in a reduction in thermal diffusivity. When the Prandtl number is larger, it indicates that the momentum diffusivity can be considered higher than the thermal diffusivity. It is observed that the thickness of the boundary layer that is caused by updrafts diminishes as the Prandtl number increases. In general, the Prandtl number establishes a connection between the momentum diffusivity and the thermal diffusivity of a fluid. This connection demonstrates that the plate concentration rises as the Pr value increases.

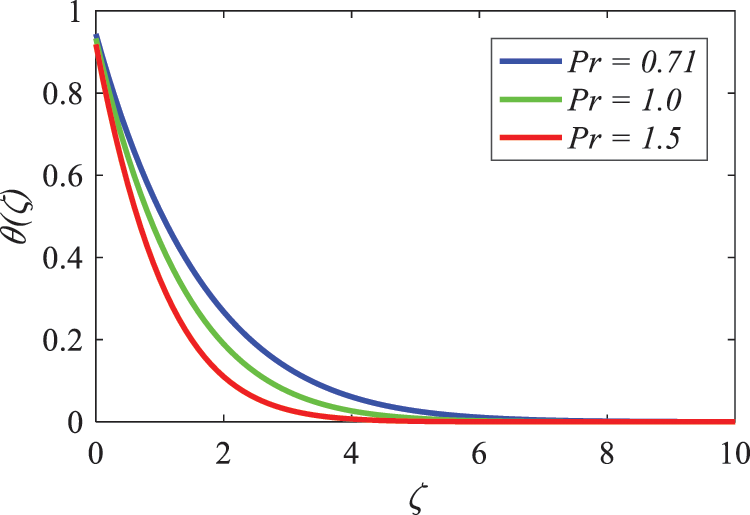
Figure 20: Nature of Prandtl factor on θ(ζ)

Fig. 21 provides a visual representation of the impact that the Eckert number (Ec) has on the temperature distribution of heat energy. When there is a significant increase in Ec, it is common knowledge that the temperature has a tendency to rise. When there is a substantial amount of internal friction inside the fluid, heat is generated as a result of the strong interaction and competition among the particles of the fluid. This is the process that causes viscous dissipation. The fluid’s overall thermal energy is increased as a result of this added heat, which contributes to the overall rise.

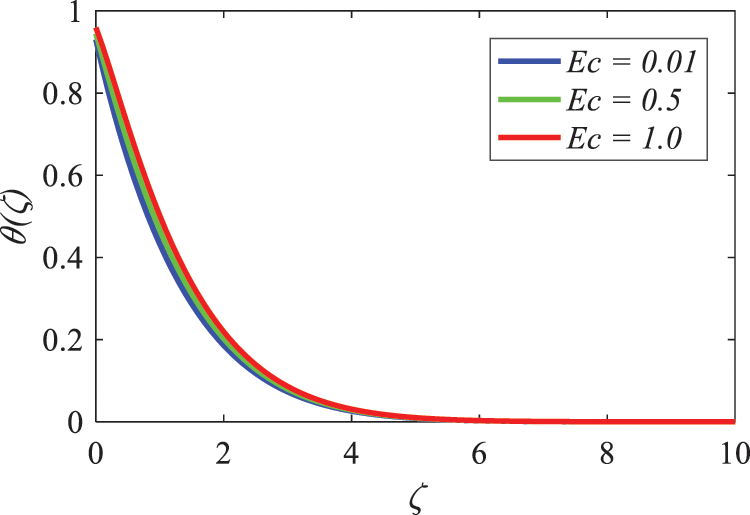
Figure 21: Nature of Eckert number on θ(ζ)

The influence of the Brownian motion Nb parameter on the temperature profile is illustrated in Fig. 22, which has been provided for your reference. Based on the information that is currently available, it is possible to draw the conclusion that the distance between the boundaries of the thermal boundary layers grows as the Brownian motion parameter Nb in the system increases. The association between the concentration distribution and the Brownian motion parameter (Nb) is illustrated in Fig. 23, which may be found here. Based on the findings, it can be observed that the thickness of the concentration boundary layer reduces as the value of Nb increases. It is also possible to gain valuable insights from the graphical representation, which demonstrates that the thickness of the thermal barrier layer does not change significantly even when the values of Nb increase.

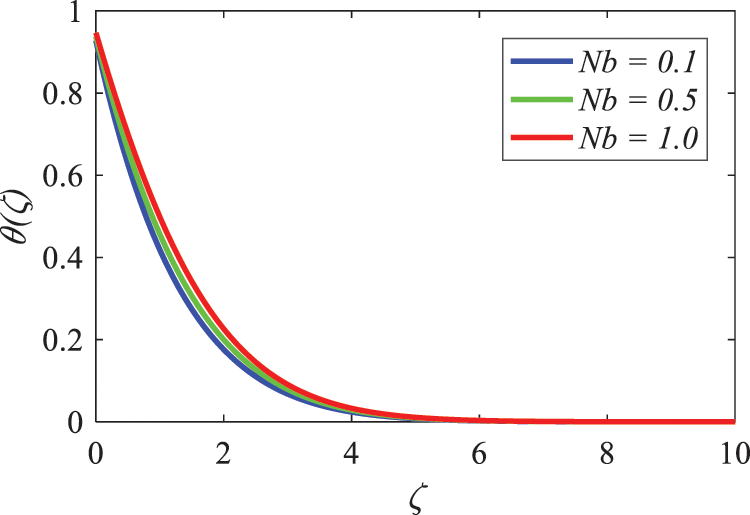
Figure 22: Nature of Brownian motion parameter on θ(ζ)

Figure 23: Nature of Brownian motion parameter on ϕ(ζ)

Both Figs. 24 and 25 are devoted to the objective of examining and revealing the influence that the thermophoresis Nt has on the data that pertain to the temperature and concentration within the system. Taking into account the information that is currently available, it is possible to draw the conclusion that the thermophoresis Nt signification is exhibiting an upward trend, which indicates that there is an increase in the distance between the boundaries of the thermal and concentration boundary layers.

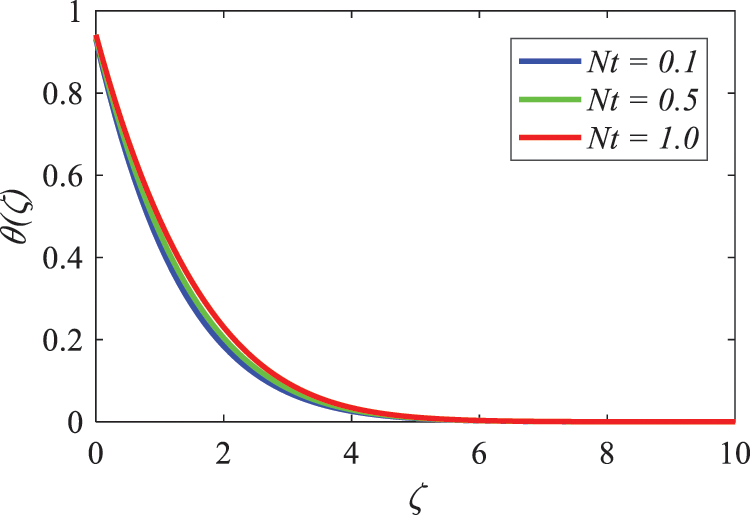
Figure 24: Nature of thermophoresis parameter on θ(ζ)

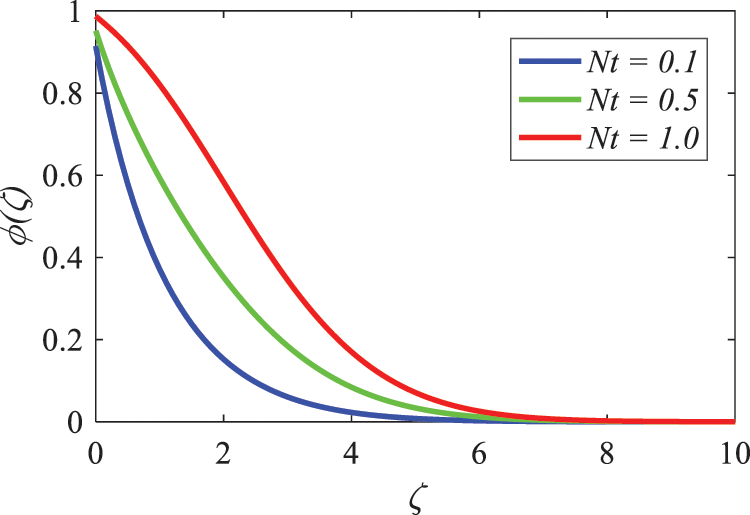
Figure 25: Nature of thermophoresis parameter on ϕ(ζ)

The influence that the Schmidt number Sc has on the concentration distribution is illustrated graphically in Fig. 26, which may be found here. Additionally, it has been widely seen and reported that the concentration profile gradually weakens and decreases as the numerical value constantly increases. This phenomenon has been known for quite some time. When the Schmidt number is larger, it shows that the mass diffusivity is declination in comparison to the momentum diffusivity during the experiment. This drop leads to a reduction in scalar diffusivity, which in turn leads to a reduction in the processes of spreading and more gradual changes in concentration within the fluid medium.

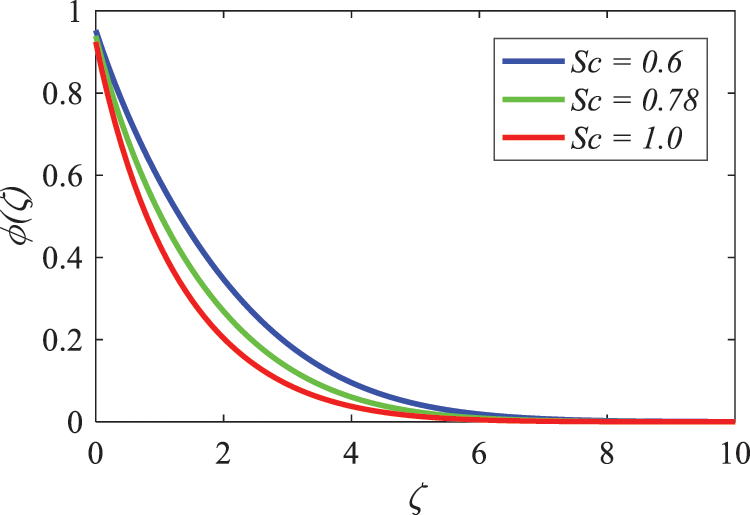
Figure 26: Nature of Schmidt number on ϕ(ζ)

Fig. 27 provides validation of the significant impact that a specific chemical reaction factor has on the dimensionless concentration profile ϕ(ζ). In processes involving mass transfer, such as diffusion or convection in fluid flow, a chemical reaction often acts to deplete the concentration of the reacting species. The reaction reduces the number of molecules of the reactant(s) in the system, resulting in a lower concentration over time.

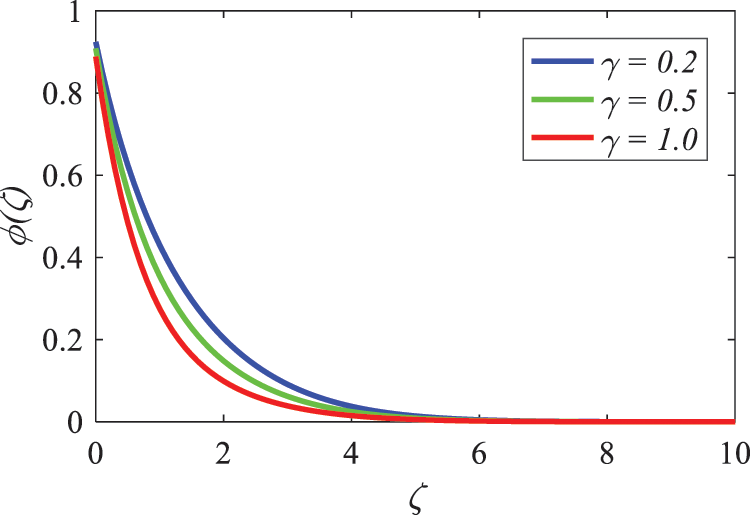
Figure 27: Nature of chemical parameter on ϕ(ζ)

Fig. 28 displays the coefficient of skin friction as a variant of velocity slip parameter δ1 and Williamson parameter λ. It is also observed an increase in λ and δ1 reduces the local skin friction coefficient. Fig. 29 shows that the local Nusselt number has a decreasing values as a function of δ2 and Ec. To increase in either Ec or δ2 decreases the local Nusselt number. Fig. 30 shows that local Sherwood number varies with Sc and δ3 and it is noted that local Sherwood number is an increasing function of Sc and decreases with an increases with δ3.

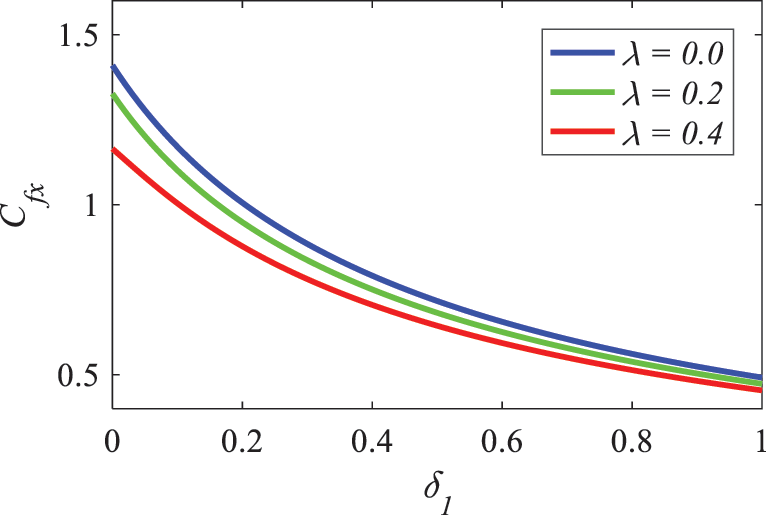
Figure 28: Nature of Williamson parameter and velocity slip factor on Cfx

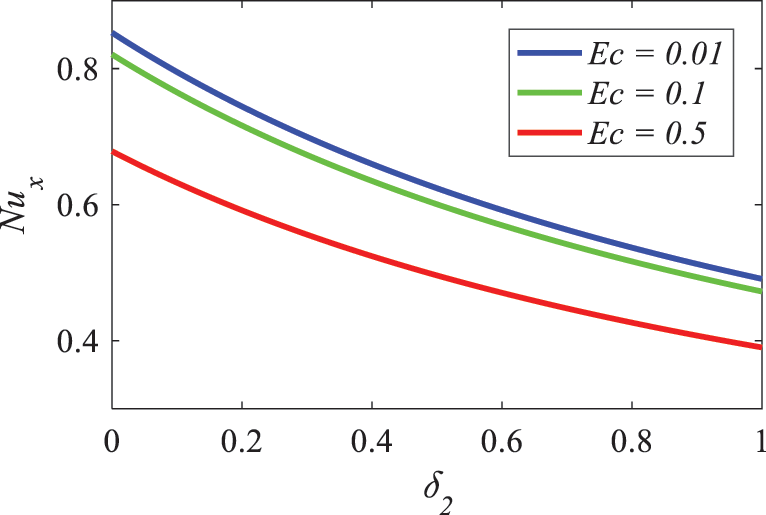
Figure 29: Nature of Eckert number and thermal slip factor on Nux

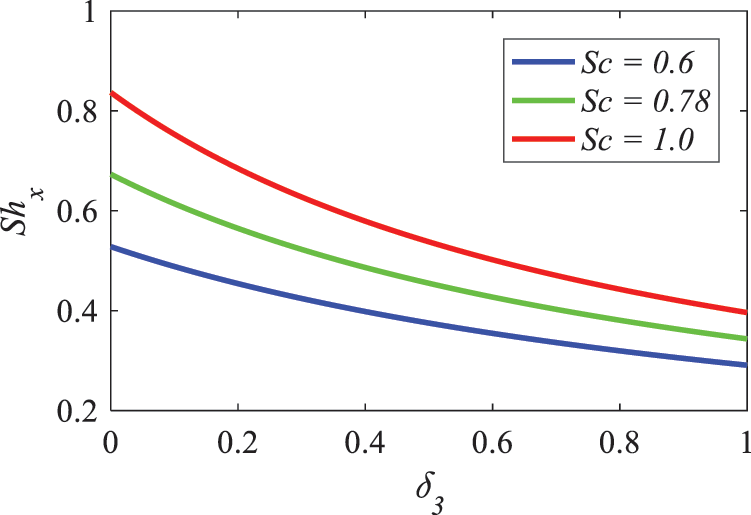
Figure 30: Nature of Schmidt number and concentration slip factor on Shx

4  Conclusions

This study used the HAM technique to analyze the chemically radiative viscous dissipation of a Williamson nanofluid at its stagnation point on an exponentially inclined stretching sheet. The following findings were reached:

➢   There is a decrease in the mobility of the fluid as the values of the Williamson nanofluid parameter increase.

➢   As the Prandtl number decreases, the thickness of the thermal boundary layer decreases. On the other hand, the radiation parameter generates the opposite outcome.

➢   The concentration profile decreases as the chemical reaction parameter increases, indicating a decrease in concentration.

➢   Temperature and concentration are both increased when the thermophoresis parameter is increased. In addition to this, the Brownian motion parameter has the effect of lowering the concentration while simultaneously raising the temperature.

➢   Examples of engineering coefficients that are depicted include Sherwood number, Nusselt number and skin friction. These coefficients behave differently depending on the values of numerous parameters. The skin friction factor can be reduced by increasing the values of the Williamson and velocity slip parameters. Additionally, the local Nusselt and Sherwood are functions that decrease as the slip parameters increase.

5  Future Research Study

The nature of various nanoparticle morphologies, such as spherical, cylindrical, and platelet, as well as their distribution in various non-Newtonian nanofluids could be the subject of research in the future. The understanding of the properties of heat and mass transfer in nanofluids under a variety of magnetic and radiative settings would be improved as a result of this.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: P. Saila Kumari, S. Mohammed Ibrahim, and Giulio Lorenzini are the authors who have confirmed their contributions to the work, which include the following: the conception and design of the study, the collecting of data, the analysis and interpretation of the results, and the creation of the draft text. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Requests for data can be made at any time.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Chiam TC. Stagnation-point flow towards a stretching plate. J Phy Soc Jpn. 1994;63(6):2443–4. doi:10.1143/JPSJ.63.2443. [Google Scholar] [CrossRef]

2. Khashi’ie NS, Arifin NM, Rashidi MM, Hafidzuddin EH, Wahi N. Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J Therm Anal Calorim. 2020;139:3635–48. doi:10.1007/s10973-019-08713-8. [Google Scholar] [CrossRef]

3. Baig MN, Salamat N, Duraihem FZ, Akhtar S, Nadeem S, Alzabut J, et al. Exact analytical solutions of stagnation point flow over a heated stretching cylinder: a phase flow nanofluid model. Chin J Phys. 2023;86:1. doi:10.1016/j.cjph.2023.03.017. [Google Scholar] [CrossRef]

4. Najib N, Bachok N, Arifin NM, Ishak A. Stagnation point flow and mass transfer with chemical reaction past a stretching/shrinking cylinder. Sci Rep. 2014;4(1):1–7. doi:10.1038/srep04178. [Google Scholar] [PubMed] [CrossRef]

5. Bano N, Singh BB, Sayyed SR. MHD stagnation-point flow and heat transfer over an exponentially stretching/shrinking vertical permeable cylinder. Diffus Found. 2020;26:23–38. doi:10.4028/www.scientific.net/DF.26.23. [Google Scholar] [CrossRef]

6. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne, IL, USA: Argonne National Lab. (ANL); 1995. [Google Scholar]

7. Lin YH, Kang SW, Chen HL. Effect of silver nano-fluid on pulsating heat pipe thermal performance. Appl Therm Eng. 2008;28(11–12):1312–7. [Google Scholar]

8. Kuznetsov AV, Nield DA. Natural convective boundary-layer flow of a nanofluid past a vertical plate: a revised model. Int J Therm Sci. 2014;77:126–9. doi:10.1016/j.ijthermalsci.2013.10.007. [Google Scholar] [CrossRef]

9. Buongiorno J. Convective transport in nanofluids. J Heat Transfer. 2006;128(3):240–50. doi:10.1115/1.2150834. [Google Scholar] [CrossRef]

10. Wong KV, De Leon O. Applications of nanofluids: current and future. Adv Mech Eng. 2010;2:519659. [Google Scholar]

11. Williamson RV. The flow of pseudoplastic materials. Ind Eng Chem. 1929;21(11):1108–11. [Google Scholar]

12. Taj M, Salahuddin TA. Three dimensional frictional flow study of Williamson fluid with chemical reaction. Mater Sci Eng B. 2023;291:116305. doi:10.1016/j.mseb.2023.116305. [Google Scholar] [CrossRef]

13. Shaheen S, Arain MB, Nisar KS, Albakri A, Shamshuddin MD, Mallawi FO. A case study of heat transmission in a Williamson fluid flow through a ciliated porous channel: a semi-numerical approach. Case Stud Therm Eng. 2023;41:102523. doi:10.1016/j.csite.2022.102523. [Google Scholar] [CrossRef]

14. Kada B, Hussain I, Pasha AA, Khan WA, Tabrez M, Juhany KA, et al. Significance of gyrotactic microorganism and bioconvection analysis for radiative Williamson fluid flow with ferromagnetic nanoparticles. Therm Sci Eng Prog. 2023;39:101732. doi:10.1016/j.tsep.2023.101732. [Google Scholar] [CrossRef]

15. Ahmed K, McCash LB, Akbar T, Nadeem S. Effective similarity variables for the computations of MHD flow of Williamson nanofluid over a non-linear stretching surface. Processes. 2022;10(6):1119. doi:10.3390/pr10061119. [Google Scholar] [CrossRef]

16. Vasudev C, Rao UR, Reddy MS, Rao GP. Peristaltic pumping of Williamson fluid through a porous medium in a horizontal channel with heat transfer. Am J Sci Ind Res. 2010;1(3):656–66. doi:10.5251/ajsir.2010.1.3.656.666. [Google Scholar] [CrossRef]

17. Chandel S, Sood S. Numerical analysis of Williamson-micropolar nanofluid flow through porous rotatory surface with slip boundary conditions. Int J Appl Comput Math. 2022;8(3):134–42. doi:10.1007/s40819-022-01337-x. [Google Scholar] [CrossRef]

18. Crane LJ. Flow past a stretching plate. Z Angew Math Phys. 1970;21:645–7. doi:10.1007/BF01587695. [Google Scholar] [CrossRef]

19. Magyari E, Ali ME, Keller B. Heat and mass transfer characteristics of the self-similar boundary-layer flows induced by continuous surfaces stretched with rapidly decreasing velocities. Heat Mass Transf. 2001;38:65–74. doi:10.1007/s002310000126. [Google Scholar] [CrossRef]

20. Bidin B, Nazar R. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur J Sci Res. 2009;33(4):710–7. [Google Scholar]

21. Kumar KA, Sugunamma V, Sandeep N, Reddy JR. Numerical examination of MHD nonlinear radiative slip motion of non-newtonian fluid across a stretching sheet in the presence of a porous medium. Heat Transf Res. 2019;50(12):1–9. doi:10.1615/HeatTransRes.2018026700. [Google Scholar] [CrossRef]

22. Saif RS, Muhammad T, Sadia H, Ellahi R. Boundary layer flow due to a nonlinear stretching curved surface with convective boundary condition and homogeneous-heterogeneous reactions. Physica A. 2020;551:123996. doi:10.1016/j.physa.2019.123996. [Google Scholar] [CrossRef]

23. Ishak A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malays. 2011;40(4):391–5. [Google Scholar]

24. Nayak MK, Shaw S, Chamkha AJ. 3D MHD free convective stretched flow of a radiative nanofluid inspired by variable magnetic field. Arab J Sci Eng. 2019;44:1269–82. doi:10.1007/s13369-018-3473-y. [Google Scholar] [CrossRef]

25. Megahed MA. Williamson fluid flow due to a nonlinearly stretching sheet with viscous dissipation and thermal radiation. J Egypt Math Soc. 2019;27(1):12. doi:10.1186/s42787-019-0016-y. [Google Scholar] [CrossRef]

26. Ahmed K, Akbar T. Numerical investigation of magnetohydrodynamics Williamson nanofluid flow over an exponentially stretching surface. Adv Mech Eng. 2021;13(5):16878140211019875. doi:10.1177/16878140211019875. [Google Scholar] [CrossRef]

27. Khan NA, Khan H. A boundary layer flows of non-Newtonian Williamson fluid. Nonlinear Eng. 2014;3(2):107–15. doi:10.1515/nleng-2014-0002. [Google Scholar] [CrossRef]

28. Nadeem S, Hussain ST, Lee C. Flow of a Williamson fluid over a stretching sheet. Braz J Chem Eng. 2013;30:619–25. doi:10.1590/S0104-66322013000300019. [Google Scholar] [CrossRef]

29. Hayat T, Khalid U, Qasim M. Steady flow of a Williamson fluid past a porous plate. Asia-Pac J Chem Eng. 2012;7(2):302–6. doi:10.1002/apj.496. [Google Scholar] [CrossRef]

30. Akbar NS, Hayat T, Nadeem S, Obaidat S. Peristaltic flow of a Williamson fluid in an inclined asymmetric channel with partial slip and heat transfer. Int J Heat Mass Transf. 2012;55(7–8):1855–62. doi:10.1016/j.ijheatmasstransfer.2011.11.038. [Google Scholar] [CrossRef]

31. Ibrahim W, Shankar B, Nandeppanavar MM. MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. Int J Heat Mass Transf. 2013;56(1–2):1–9. doi:10.1016/j.ijheatmasstransfer.2012.08.034. [Google Scholar] [CrossRef]

32. Ibrahim W, Shankar B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput Fluids. 2013;20(75):1–10. doi:10.1016/j.compfluid.2013.01.014. [Google Scholar] [CrossRef]

33. Nadeem S, Haq RU. Effect of thermal radiation for megnetohydrodynamic boundary layer flow of a nanofluid past a stretching sheet with convective boundary conditions. J Comput Theor Nanosci. 2014;11(1):32–40. doi:10.1166/jctn.2014.3313. [Google Scholar] [CrossRef]

34. Khan MR, Al-Johani AS, Elsiddieg AM, Saeed T, Abd Allah AM. The computational study of heat transfer and friction drag in an unsteady MHD radiated Casson fluid flow across a stretching/shrinking surface. Int Commun Heat Mass Transf. 2022;130:105832. doi:10.1016/j.icheatmasstransfer.2021.105832. [Google Scholar] [CrossRef]

35. Raza Q, Qureshi MZ, Khan BA, Kadhim Hussein A, Ali B, Shah NA, et al. Insight into dynamic of mono and hybrid nanofluids subject to binary chemical reaction, activation energy, and magnetic field through the porous surfaces. Mathematics. 2022;10(16):3013. doi:10.3390/math10163013. [Google Scholar] [CrossRef]

36. Koriko OK, Shah NA, Saleem S, Chung JD, Omowaye AJ, Oreyeni T. Exploration of bioconvection flow of MHD thixotropic nanofluid past a vertical surface coexisting with both nanoparticles and gyrotactic microorganisms. Sci Rep. 2021;11(1):16627. doi:10.1038/s41598-021-96185-y. [Google Scholar] [PubMed] [CrossRef]

37. Zhang XH, Abidi A, Ahmed AE, Khan MR, El-Shorbagy MA, Shutaywi M, et al. MHD stagnation point flow of nanofluid over a curved stretching/shrinking surface subject to the influence of Joule heating and convective condition. Case Stud Therm Eng. 2021;26:101184. doi:10.1016/j.csite.2021.101184. [Google Scholar] [CrossRef]

38. Rajendar P, Babu LA. MHD stagnation point flow of Williamson nanofluid over an exponentially inclined stretching surface with thermal radiation and viscous dissipation. J Nanofluids. 2018;7(4):683–93. doi:10.1166/jon.2018.1493. [Google Scholar] [CrossRef]