 Open Access
Open Access
ARTICLE
Simulations of the Boiling Process on a Porous Heater by Lattice Boltzmann Method
Laboratory of Rarified Gases, Institute of Thermophysics SB RAS, Novosibirsk, 630090, Russia
* Corresponding Author: Alexander Fedoseev. Email:
(This article belongs to the Special Issue: Heat and Mass Transfer in Energy Equipment)
Frontiers in Heat and Mass Transfer 2024, 22(6), 1679-1694. https://doi.org/10.32604/fhmt.2024.056999
Received 05 August 2024; Accepted 23 September 2024; Issue published 19 December 2024
Abstract
In order to research the process of boiling occurring on a porous surface, a model of multiple blocks was developed. The mathematical basis of these blocks is the lattice Boltzmann method in combination with heat transfer equation. The reported complex allows one to obtain the boiling curves for various wall superheats and to find the optimal parameters of a porous heater in terms of heat transfer enhancement. The porous heater structure is specified as a skeleton of square metal heaters located in the lower part of the computational domain. The calculations were performed for the following parameters of the porous heater structure: different number and size of the metal heaters, different distances between them in horizontal and vertical directions, regular and asymmetric packing of the heaters. Using the developed numerical model, parametric studies of the boiling process on porous heaters with different parameters of the porous skeleton were carried out and phase pictures of such a process were obtained. It was shown that the heat transfer coefficient on a porous heater is 3–7 times greater than that on a smooth heater, and depends on the number of heater elements, their size, and location. The results showed a significant advantage of the porous heaters with greater critical heat flux at higher wall superheats compared to that on the smooth surface.Graphic Abstract
Keywords
Nomenclature
| a, b, R, ω | Parameters in P–R equation of state |
| fi | Discrete distribution function of fluid particle velocity |
| fieq | Discrete equilibrium distribution function of fluid particle velocity |
| ci | Discrete lattice velocity vector |
| u | Velocity |
| uf | Physical velocity of fluid |
| Si | Force source term |
| cs | Lattice speed of sound |
| F | Total force acting on the fluid in cell |
| Fint | Force between particles |
| Fs | Force between particles and solid matter |
| Fg | Gravitational force |
| Pc | Critical point pressure |
| Zc | Critical point compressibility |
| Tc | Critical point Temperature |
| ∆t | Time step |
| h, ∆x | Spatial step |
| Greek Symbols | |
| Ω | Collision integral |
| ρ | Density |
| ρc | Critical point density |
| ρavg | Average density |
| τ | Relaxation time |
| ωi | Discrete lattice weight coefficients |
| θ | Contact angle |
| Ψ | Pseudopotential |
| Subscripts or Superscripts | |
| i | Discrete lattice velocity index |
| eq | Equilibrium value |
Boiling is one of the most efficient phase-change heat transfer processes compared to other single-phase processes, that is why it is widely used in the electronics industry characterized by high heat loads [1,2]. To date, the problem of heat transfer modification in the presence of boiling fluid has been the subject of excessive attention by multiple institutions [3,4]. There are many approaches to improve the boiling process by the modification of the heat exchange surface, such as mechanical machining, and texturing executed by laser or coating fabrication [5,6]. Surface modification could significantly increase the density of bubble nucleation centers, improve the liquid absorption ability of the surface enhance micro-convection and promote bubble departure, as well as increase the critical heat flux (CHF) avoiding crisis regimes. It is a known phenomenon, that the superhydrophilic coatings significantly enhance (up to 2–3 times) the CHF value [7].
Currently, nano- and micro-porous heat exchange surfaces attract increasing attention of researchers in the field of heat transfer at boiling due to their extreme performance [8–10]. The heat transfer coefficient on a porous heater can be several times greater than that on a smooth surface [10], which can be explained by an extensive surface area of heat exchange with the liquid, causing stronger mixing of flows. An example of the porous heater surface with micro- and macro-porous structures is the so-called “metal foam”, which permits to obtain even greater heat transfer coefficients [11–13]. Existing studies have shown that heat transfer coefficients could be 3–6 times larger than those on the microporous surface due to the large heated area and strong flow mixing [11]. They also received much attention in boiling heat transfer due to their high porosity, low weight, and high specific surface area [11–13].
Multiple parameters influence the heat transfer near the porous body, such as size, structural characteristics, surface wettability, liquid properties, and others. The structure of the metal foam is interconnected by a solid heat-conducting skeleton and transfers the heat from the heat source to its internal area, thus inducing boiling inside it. The greater the density of heat-conducting metal channels in the metal foam, the more active nucleation centers are formed. From the other hand, this also causes resistance to the movement of the vapor phase from the nucleation sites to the surface of the metal foam. To date, the extensive experimental and numerical studies of the influence of the metal foam parameters such as pore structure [13–15], thickness [16,17], and wettability [18–20] on the heat transfer enhancement at boiling on the metal foams have been performed. However, further many parametric research is needed to study the main mechanisms at boiling on the porous structures, to summarize relevant lows and to improve the heat transfer performance.
Finding the optimal pore arrangement to obtain extreme heat fluxes based on experimental study is a labor-intensive task. To investigate the influence of different structural parameters of the porous heaters there is a need to produce them and to perform a series of experimental researches. Different complex and precise experimental equipment is required to study the boiling process on the porous heaters. However, the boiling on a porous heater occurs not only on the surface of the heater but also inside the heater structure that substantially complicates the experimental measurements and visualization of such processes. With the advances in computer technologies, the numerical simulations become a promising alternative to experiment for studying the boiling process [21,22]. For modeling the two-phase flows, traditionally the Navier-Stokes equations are solved together with an additional method for tracking the two-phase interface. It includes the level set method [23,24], the volume of fluid method [25,26], and the VOSET method [27,28]. However, the nucleation process and the density of nucleation sites are implemented artificially in most of these methods. The process of nucleation should be simulated on a micro-nanoscale level, e.g., with the molecular dynamics (MD) method [29,30]. However, to study the heat transfer performance at boiling on the porous heaters and to obtain the boiling curves, a region with an ensemble of bubbles should be simulated during several vapor bubble life cycles, which makes the abovementioned methods practically inapplicable.
Lattice Boltzmann Method (LBM) is a mesoscopic method lying between the microscopic molecular dynamic method and the solution of Navier-Stokes equations for macroscopic parameters [31]. In LBM, the fluid is modeled by pseudoparticles. For said particles the kinetic Boltzmann equations are solved for the discretized time, space, and also velocity distribution. The discretization is performed in such a way that the pseudoparticles come strictly to the neighboring cells at each time step. These significant simplifications compared to the classical kinetic Boltzmann equation allow the LBM to model multi-phase flows [32,33]. The pseudopotential Shan-Chen method [33] is the so-called «bottom-up» approach postulating a microscopic interaction between fluid elements that eventually leads to the macroscopic separation of phases. In it, the bubble nucleation is determined by the equation of state, and the interface between the phases forms and evaluates automatically. The so-called «bounce-back» condition at the fluid-solid boundary [34] contains information about pseudoparticle angle velocity distribution and permits to setting of an arbitrary shape of the solid boundary with a prescribed wetting contact angle [35].
The abovementioned advantages make LBM suitable for modeling the pool boiling processes on smooth or micro-structured surfaces including porous structures. In [36,37], single bubble dynamics at boiling were considered using LBM. The bubble departure diameter and frequency depending on the wetting contact angle and the Jacob number were obtained. The boiling curves for the boiling on smooth surfaces were calculated in [35,38–40]. In [35,39,40], the boiling near the smooth body utilizing contrast wettability was simulated. It was found that the onset of nucleate boiling and the CHF sufficiently depends on the wetting contact angle in accordance with the experimental observations. The influence of various microstructures on the efficiency of heat exchange at boiling using LBM was studied in a large number of works, e.g., [41–43]. The increase of heat flux relative to a smooth surface was demonstrated. Numerical investigations on boiling in porous metals by LBM at a pore scale level are less represented in the literature [44–46]. In [44,45], it was shown that the use of a gradient pore structure promotes bubble detachment in flow boiling on metal foams. The pool boiling behavior on a multilayer skeleton surface was studied by LBM in a recent paper [46] at constant temperature boundary conditions. However, there is still no comprehensive understanding of the bubble behavior at boiling on the porous structures, and further experimental and numerical research is needed in the search for the optimal structural characteristics of the porous heaters.
The aim of this work is to study the boiling near a porous surface and to determine the optimal parameters for heat exchange intensification using a hybrid “thermo-LBM” model. In the model, the heater surface is specified as a skeleton of rectangular metal heaters located in the lower part of the computational domain. The number of such heaters, their size and location inside the porous heat-generating surface, as well as their temperature, are the subject of the parametric study of the present work. The model allows to calculate the boiling curves on various structures of the porous heaters for variuos wall superheats and to obtain optimal parameters of the porous heater in terms of heat transfer enhancement.
In this paper, a hybrid “thermo-LBM” model consisting of two Blocks is used to calculate the boiling process. In the first Block, the flow and interaction of the gas and the liquid phases are calculated using the lattice Boltzmann method. The second Block of this model calculates the temperature evolution using a finite-difference solution of a heat transfer equation. In LBM, the flow is described by discrete velocity distribution functions fi, which are also referred to as populations. The main equations of LBM are the flow-transfer equations for each such population. In general, the set of these equations can be described by the formula:
fi(→x+→ciΔt,t+Δt)=fi(→x,t)+Ωi(→x,t)+Si(→x,t),fi(→x+→ciΔt,t+Δt)=fi(→x,t)+Ωi(→x,t)+Si(→x,t),(1)
where →x→x is the coordinate, t is the time, →ci→ci is the discrete lattice velocity vector, Ωi is the collision integral, and Si is the coefficient describing the effect of external volume forces on the populations. For each individual LBM problem of dimension D, a suitable set of Q populations is selected. In this paper, the set of populations D2Q9 is used, for which the vector of discrete velocities was defined as |→ci→ci| = (0, 1, √2√2), i = {1, 2 ... 5, 6 ... 9}. According to the set of populations and the discrete velocity vectors at each point in space, the density and momentum of the fluid can be determined from the relations:
ρ(→x,t)=∑ifi(→x,t),ρ→u(→x,t)=∑i→cifi(→x,t).ρ(→x,t)=∑ifi(→x,t),ρ→u(→x,t)=∑i→cifi(→x,t).(2)
The collision integral Ωi defines the interactions of populations within a cell. Typically, this interaction defines the relaxation of the distribution function fi to its equilibrium state fieq. In this paper, standard collision approximation is used:
Ωi(→x,t)=−fi−fieqτ,Ωi(→x,t)=−fi−fieqτ,(3)
where τ is the relaxation time of the distribution function, which depends on the kinematic viscosity ν according to the relation τ=0.5+ν/c2sτ=0.5+ν/c2s, where cs2=(1/3)Δx2/Δt2cs2=(1/3)Δx2/Δt2 is the lattice speed of sound, in which Δx and Δt are steps in space and time.
The equilibrium distribution function is defined as:
feqi(ρ,→u)=ρwi[1+→ci→uc2s+(→ci→u)22c4s+→u22c2s],feqi(ρ,→u)=ρwi[1+→ci→uc2s+(→ci→u)22c4s+→u22c2s],(4)
where wi are weight coefficients with the values w1 = 4/9, w2–5 = 1/9, w6–9 = 1/36 for D2Q9 lattice.
The influence of the volume force on the distribution functions is given by the term Si of Eq. (1). In this paper, the exact difference method (EDM) is used, in which the force source term is defined by the formula [47]:
Si=fieq(ρ,→u+Δ→u)−fieq(ρ,→u),Si=fieq(ρ,→u+Δ→u)−fieq(ρ,→u),(5)
where Δ→uΔ→u = →F→F/ρ. The sum force →F→F influencing the fluid in the cell took into account the following terms:
→F(→x)=→Fint(→x)+→Fs(→x)+→Fg(→x),→F(→x)=→Fint(→x)+→Fs(→x)+→Fg(→x),(6)
where →Fint(→x)→Fint(→x) is the force of inter-particle interactions, →Fs(→x)→Fs(→x) is the interaction of the fluid with a solid surface, and →Fg(→x)=g(ρ−ρavg)→Fg(→x)=g(ρ−ρavg) is the force of gravity, in which ρavgρavg is the average density of the fluid in the working volume, g is the acceleration due to gravity. In this paper, we consider a neutral wetting surface with a contact angle θ = 90°, thus, Fs(x) = 0.
The pseudopotential Ψ(→x)Ψ(→x) defining interparticle force is then taken as follows [48]:
Ψ(→x)=√2(PEOS(→x)−ρ(→x)c2s)G.Ψ(→x)=√2(PEOS(→x)−ρ(→x)c2s)G.(7)
Following [47], we use isotropic finite difference approximation of the pseudopotential gradient to calculate force:
→Fint(→x)=−βΨ(→x)∑→x′G(→x,→x′)Ψ(→x′)(→x′−→x)−0.5(1−β)∑→x′G(→x,→x′)Ψ2(→x′)(→x′−→x),(8)
where
G(→x,→x′)={G,|→x′−→x|>00,|→x′−→x|<0
Free parameter β in Eq. (8) is used to adjust densities of liquid and vapor to match theoretical values on the binodal curve. We found β = 1.16 to give the most accurate results with the Peng-Robinson equation of state [49]:
PEOS(ρ,T)=ρTZc−bρ−aφ(T)ρ2Z2c+2bZcρ−b2ρ2,(9)
where φ(T)=(1+k(1−√T))2, k=0.37464+1.5422ω−0.26992ω2, a = 0.457235, b = 0.077796, Zc=PcVcRTc is the compressibility at the critical point, ω = 0.344 is the acentric factor.
The second Block of the hybrid model calculates the evolution of the heat transfer, which depends on diffusion, convection, the work of pressure forces, and phase transitions. In the paper, the following equation for temperature evolution is used, the detailed derivation of which is presented in the work [35]:
∂T∂t+→uf⋅→∇T=1ρcv→∇⋅(λ→∇T)−Tρcv(∂pEOS∂T)ρ→∇⋅→uf,(10)
where cv and λ are the heat capacity and thermal conductivity coefficient. The velocity →uf=→u+Δ→u/2 is the physical velocity of the continuum. If we represent this equation in units of Pc, Tc, and ρc, corresponding to the parameters of the liquid (pressure, temperature and density) at the critical point, then it takes the form:
∂T∂t+→uf⋅→∇T=1ρcρcv→∇⋅(λ→∇T)ΔtΔx2−TρcρcvPcTc(∂pEOS∂T)ρ→∇⋅→uf.(11)
Normalization of Eq. (10) to the critical parameters makes it possible to substitute the density and velocity fields obtained with the help of LBM Block. It should be emphasized that the latent heat of vaporization, which is responsible for the enhancement of the heat flux under onset of boiling, is implicitly accounted for by the last term of Eq. (11). Lax-Wendroff finite-difference method with cubic correction was used to solve numerically Eq. (11). Spatial derivatives were approximated by the isotropic central scheme [50]. This scheme shows more stable behavior compared to the classical fourth-order Runge–Kutta scheme, which was used in [35] to solve Eq. (10). The parameters used in the thermal part are chosen to match the properties of the water. It is worth mentioning that the latent heat of vaporization predicted by PR EOS matches quite well the experimental value [36].
To calculate the boiling curves on a porous heater, the computational domain was set with the resolution Nx = 600, Ny = 500 and filled with a fluid medium (liquid or vapor). For the simulation of the boiling process on a single square heater, the solution region with the resolution Nx = 400, Ny = 500 was used. The time and space steps were determined to be Δx = 30 × 10−6 m and Δt = 5 × 10−6 s, respectively. The choice of spatial and time steps as well as of the solution region scale is determined by the need to simulate simultaneously several bubbles at several bubble lifetimes to obtain the boiling curves for the process of boiling. At chosen parameters, each simulation is performed for the region of 18–15 mm within 10 s for each point of the boiling curve. It takes about 10 h of calculation time on a simple CPU. However, there are some limitations in the choice of spatial and time steps in LBM approach, which are described thoroughly in the book [31]. The limitations also are defined by the requirement of the minimum value of lattice viscosity and properties of the model fluid in Peng-Robinson equation of state.
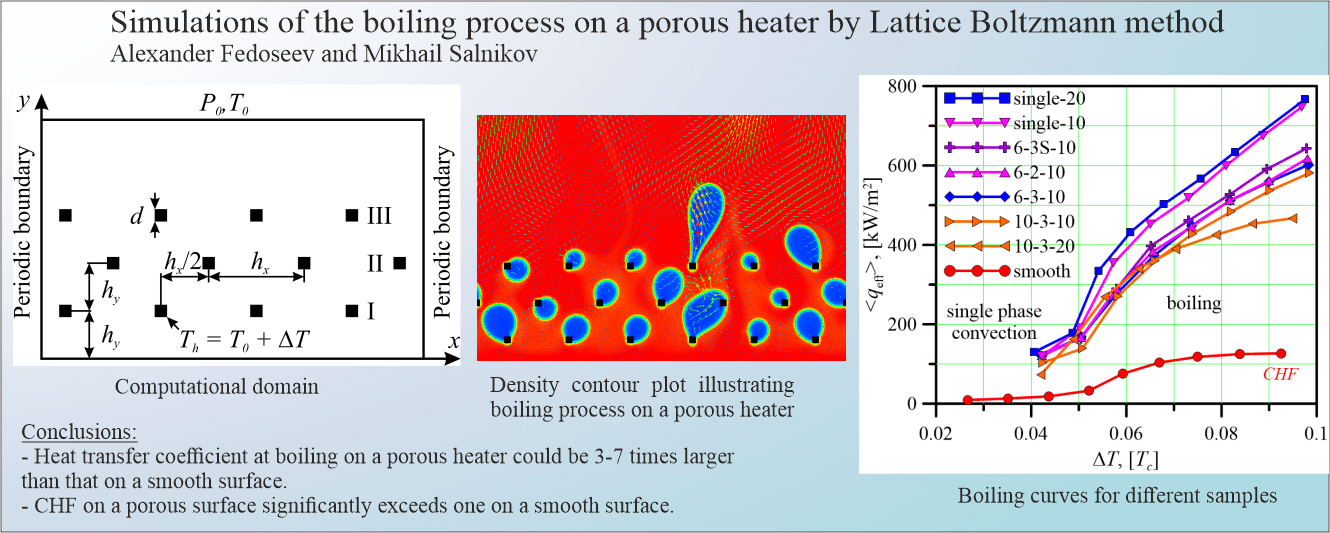
In the solution region, square solid metal heaters were placed at certain positions, which represent the skeleton of the porous material. They are denoted by the black squares in Fig. 1. In the solids, the fluid velocity was chosen to be zero, and for the nearest cells filled with the liquid the bounce-back condition was used assuming neutral surface wetting. Only heat diffusion Eq. (11) is solved inside the metal heaters with the given temperature Th in their centers. Thermal conductivity and heat capacity of the metal heaters are set to λh = 20 W/m/K and ch = 3 × 106 J/m3, respectively. Heat capacity, thermal conductivity, and viscosity are evaluated based on the current density of the fluid and are parametrized based on the properties of water and its vapor. The boundary conditions on the left and right boundaries were set to be periodic. A solid wall of temperature T0 = 0.9 Tc and pressure P0 was set on the upper boundary.
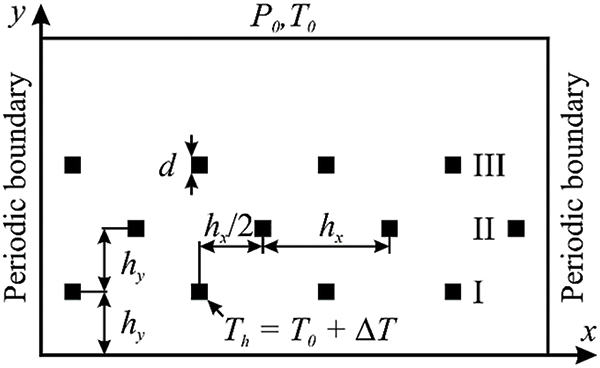
Figure 1: Domain of computation: d is the size of the square metal heaters, hx and hy are the distances between the layers of solids in horizontal and vertical directions
Different validation tests for the models based on LBM for the simulation of the boiling process can be performed [36,51–54]. The developed model was validated in the previous papers [37,39–41] on the following tests: 1) thermodynamic consistency test with Peng-Robinson EOS for the densities of liquid and vapor obtained from LBM compared with the Maxwell curves, 2) the obey of Laplace low for the surface tension, 3) the measurements of the contact angles for different surface wettability, 4) single bubble departure diameter and frequency, 5) the obtained boiling curves for a smooth surface with contrast wettability reflects to some extent the experimentally observed behavior at liquid boiling.
At the initial stage, the boiling process on a single square heater was investigated. In Fig. 2, the phase diagrams, the temperature fields and the velocity vectors are presented for different conditions. Several different superheats, Th = 0.95 Tc, 0.96 Tc and 0.98 Tc, are considered. Fig. 2a,e presents the single phase convection at low superheat, i.e., at the heater temperature Th = 0.95 Tc. It is worth noting that the convective heat transfer in this regime is pronounced due to free flow of liquid from the sides of the solution region to the bottom part of the heater and then up to the top of the solution region (see velocity vectors in Fig. 2). Fig. 2b,f denotes the moment before the bubble detachment from the heater, while Fig. 2c,g shows the moment just after the bubble detachment at Th = 0.96 Tc. At such wall superheat, the bubble growth and detachment occur in an infinite periodic regime that does not greatly disturb the liquid in the rest of the domain. The behavior of boiling on the single heater with large size d = 20 l.u. is approximately the same, but the heat fluxes are larger at the same conditions. The time between the bubble departures is td,10 = 8.25 s for the heater of size d = 10 l.u. and td,20 = 6 s for the heater of size d = 20 l.u. for the same heater temperature Th = 0.95 Tc. Less time td,20 = 6 s is explained by the fact that the heat necessary for the bubble growth and detachment achieves faster on the larger heater. Fig. 2d,h shows the boiling process at moderate heater temperature Th = 0.98 Tc. The vapor phase rises on the top and the bottom parts of the metal heater. Thus, the heat removal in this regime substantially exceeds one at lower superheats.
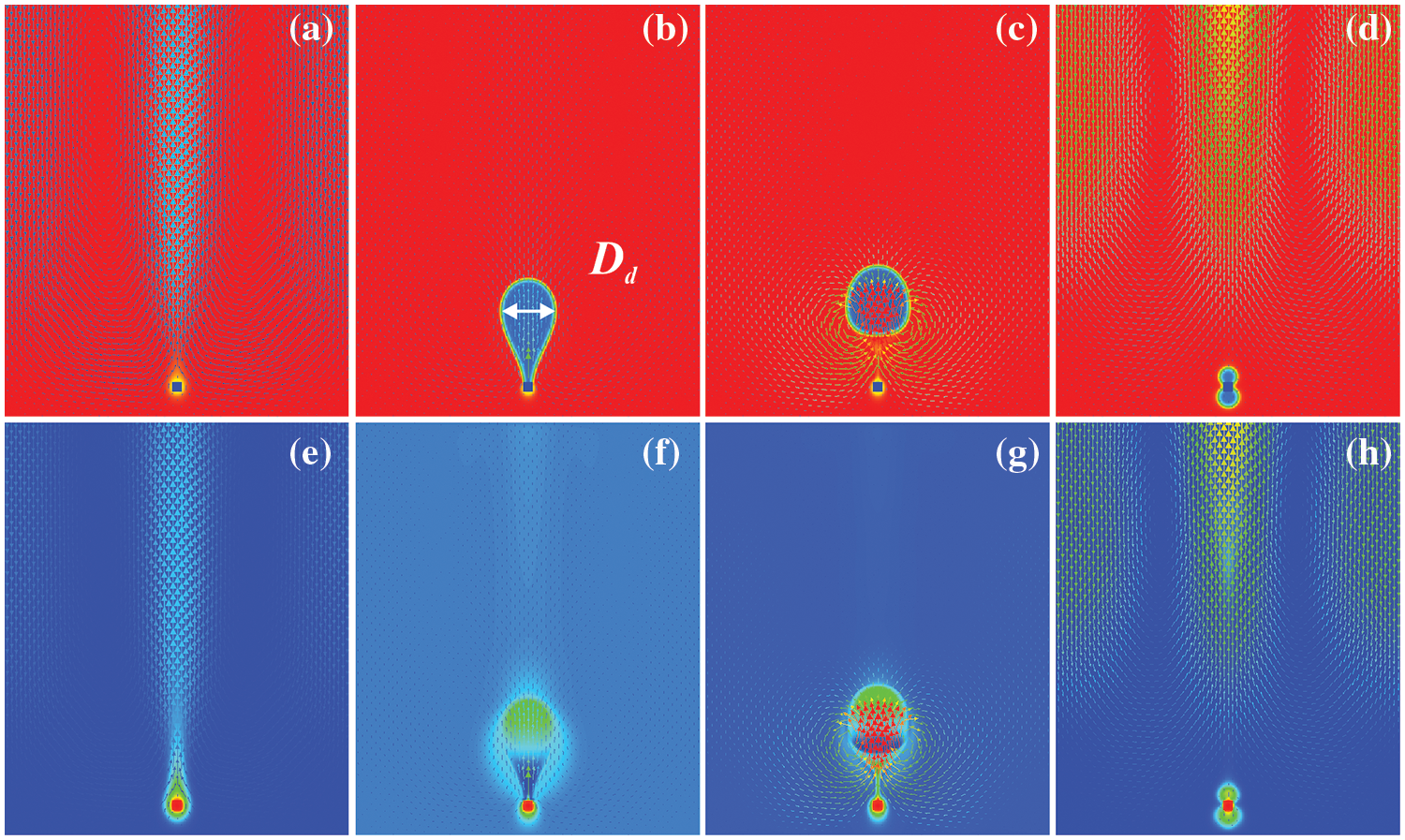
Figure 2: The density contour plots (a–d) and temperature fields (e–h) illustrating the boiling process on a single square heater of size d = 10 l.u. = 0.3 mm. (a) and (e) for Th = 0.95 Tc. (b) and (f) for Th = 0.96 Tc at moment t = 0.755 s. (c) and (g) for Th = 0.96 Tc at moment t = 0.76 s. (d) and (h) for Th = 0.98 Tc
To investigate the boiling process on the porous surfaces the following structures of the heaters were used in the simulations (see Table 1 and Fig. 1). Besides the samples with single square heaters of different sizes (“single-10” of size d = 10 l.u. = 0.3 mm and “single-20” of size d = 20 l.u. = 0.6 mm), the samples with Np = 2 and Np = 3 horizontal layers of square heaters were considered. The distance between the layers and the distance from the bottom surface of the solution region to the first layer were chosen to be equal to hy = 60 l.u. = 1.8 mm. Each layer consists of different number Nk = 6 and 10 of the heaters with equidistant separation hx = 100 and 60 l.u. in horizontal direction, respectively. All samples are assumed to be periodic in horizontal direction that is taken into account in the model by periodic boundary conditions.

The boiling processes on the samples with Nk = 6 heaters of size d = 10 l.u. in a layer are presented in Fig. 3 for the same heaters temperature Th = 0.99 Tc. The difference between the samples lies in the different number of layers in samples “6-2-10”, “6-3-10” and in asymmetric position of the second layer in sample “6-3S-10”. It is seen that in symmetric samples (Fig. 3b,c) the vapor phase rising from the bottom heaters envelopes upper heaters thus reducing the heat removing from the whole porous heater. At the same time, the asymmetric form of the sample “6-3S-10” leads to an increase in the vapor nucleation centers, and the bubble growth occurs almost on each heater. It leads to an increase in the effective heat flux from the heaters.

Figure 3: The spatial density distribution measured during the boiling: (a) “6-3S-10”, (b) “6-2-10”, (c) “6-3-10”. d = 10 l.u., Th = 0.99 Tc
Fig. 4 presents density contour plots with the velocity vectors and the corresponding temperature maps for some moments of the boiling process on the samples with a large number of heaters Nk = 10 in a layer. Due to the large total heat obtained from the larger number of heaters, the more vapor phase area is seen in Fig. 4 compared to that in Fig. 3. However, it is seen that the more heaters are surrounded by the vapor films, especially on the sample “10-3-20”. The temperature maps highlight the temperature distribution inside the solid heaters in the narrow range of a temperature difference of 0.01 Tc. The corresponding temperature maps show that the heaters, which are totally occupied by the vapor phase, are overheated compared to the heaters, which are in contact with the liquid phase. The heat removal from dry heaters surrounded by the vapor film is in crisis regime. The heat transfers from the heaters surrounded by the liquid due to single phase convection. Finally, the temperature of the heaters surface is much lower, where the vapor phase is produced in the process of phase transition. It means that the heat removal from such heaters is the most effective.
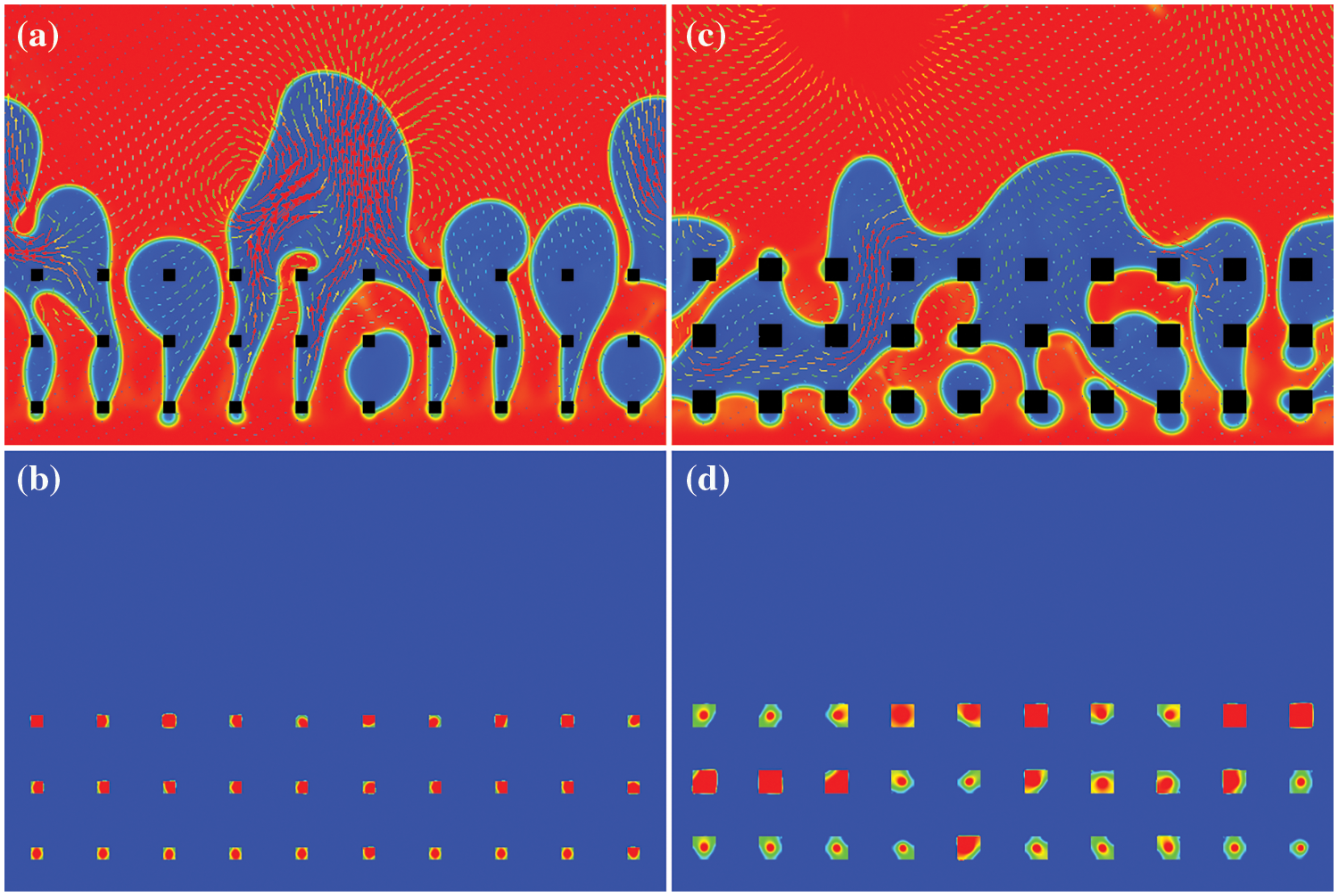
Figure 4: The density contour plots (up) and temperature maps (bottom) illustrating the boiling process on the samples: (a, b) “10-3-10”, d = 10 l.u., (c, d) “10-3-20”, d = 20 l.u. Th = 0.99 Tc
To calculate the boiling curves <qeff>(ΔT), a series of simulations of the boiling process were performed for each sample for different values of applied temperatures Th to the centers of each metal heaters. Here, ΔT = <Tw>-Tsat and Tsat = 0.9 Tc is the saturation temperature. Average heaters surface temperature <Tw> was obtained by averaging the temperature Tw(x,y,t) over time and over the whole surface area of all heaters. The heaters surface temperature Tw(x,y,t) depends on the heat transfer processes and evolves according to the Eq. (6). In calculations, to obtain each point of the dependence <qeff>(ΔT), the temperature value was set to be Th = const within the range of 0.94–1 Tc. The calculation for each value Th lasted 2·106 time steps to obtain sufficient statistics.
At low heaters temperature Th < 0.94 Tc, the heat removal from the smooth surface and from the single or multiple heaters occurs in the mode of single-phase natural convection. The heat loads are not sufficient to the onset of nucleate boiling (ONB). However, the effective heat fluxes from the single heater or from the porous structures substantially exceed one from the smooth surface. After the onset of boiling, the slope of the <qeff>(ΔT) curves sharply increases, which corresponds to an increase in the intensity of heat transfer with the transition from natural convection to nucleate boiling. It can be seen that the temperature corresponding to ONB (Th~0.94 Tc) is approximately the same for all samples. In the works [35,39,40], it was shown that the ONB could be reduced on lyophobic surfaces that will be studied for the porous structures in future research. At higher heaters temperatures Th > 0.94 Tc the process of boiling presented in Figs. 3 and 4 occurs. At the temperature Th~0.99 Tc of the heater with smooth surface, the boiling comes to a crisis regime when the whole surface is covered with the vapor film. The removal heat flux from the smooth surface substantially decreases in this regime.
As can be seen from the data presented in Fig. 5a,b, the highest effective heat fluxes were obtained for the single square heaters of size d = 20 l.u. It is surprising that the effective heat fluxes from the single heaters exceed ones from the other structured samples. The main reasons for that are 1) the small surface area of single heaters; 2) high convective heat transfer with free flow of liquid from the sides of the solution region to the bottom part of the heater and then up to the top of the solution region (see Fig. 2); and 3) the absence of other heaters that hinder convection and flows of the vapor and liquid phases. It should be noted that the heat flux from the single heater depends on the solution region size, and they are presented on Fig. 5 just for comparison between single heaters of sizes d = 10 and 20 l.u.
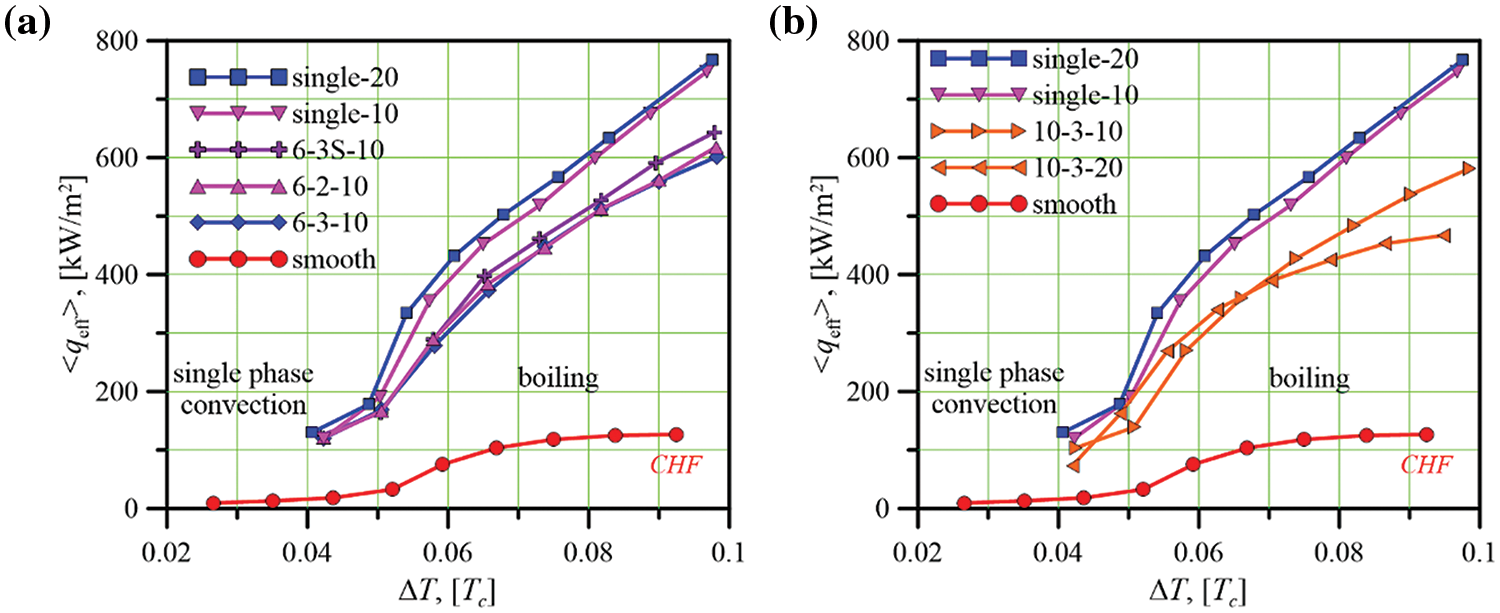
Figure 5: Boiling curves <qeff>(ΔT) for different samples
The results show that the highest effective heat fluxes from the structured porous heaters were obtained for the sample “6-3S-10” (see also Fig. 3). This is explained by the fact that the layers of heaters are not located strictly one under the other, but are shifted by half a step. As a result, it is easier for the vapor phase to rise up between the upper heaters. The heat transfer dependence on the number Np of the layers in the porous structure was studied by comparison between the two cases, Np = 2 and Np = 3. It is seen that, the samples “6-2-10” and “6-3-10” showed approximately the same heat transfer ability (see Fig. 5a). Moreover, the effective heat flux from the sample with two layers of the heaters slightly exceeds the heat flux from the sample with three layers. This is probably due to the fact that the vapor phase occupies top heaters in the sample “6-3-10” thus reducing the effective heat flux. The samples with Nk = 10 heaters in each layer show the lowest heat transfer at boiling (see Fig. 5b). The effective heat flux from the sample “10-3-20” is higher than that from sample “10-3-10” in the region of low superheat, while the opposite situation occurs at high superheats. This is explained by the fact that the initiation of the vapor phase easier occurs on larger heaters, but at high superheats, large heaters make it difficult for the vapor phase to be transferred up (see Fig. 4).
It should be noted that at present conditions, the boiling on the porous heaters does not go into a crisis regime even at the highest values of the heaters temperature Th > Tc. The vapor phase effectively removes from the heaters and does not occupy the whole region of the porous material as it happens in a crisis regime on a smooth or structured surface completely covered with a vapor film. Thus, in this paper we do not obtain the critical heat fluxes (CHF) from the porous surfaces, noting that they definitely exceed CHF at smooth or structured surfaces. The onset of nucleate boiling occurs at approximately the same wall superheats on all considered surfaces.
Finally, let us summarize the measurements of the heat transfer for smooth and porous surfaces. HTC/HTCsmooth is the heat transfer coefficient ratio (enhancement factor) for the specified cases, respectively, in the dependences of HTC/HTCsmooth on the temperature of the heater centers Th for different samples (Fig. 6). Evidently, in the case of Th < 0.97 Tc, HTC/HTCsmooth could reach the value of 7. The only exception is for the sample “10-3-20” at low heater temperature Th = 0.95 Tc. This is probably due to a large number of the heaters with a big size d = 20 l.u., which imped convective heat transfer and vapor phase movement. At high heaters temperatures, 0.97 < Th < 1 Tc, the enhancement factor on the porous surfaces is less and has values from 3 to 4. The results show that the highest values of the enhancement factor are for the sample “6-3S-10” in the whole range of the heaters temperatures. The lowest values of the enhancement factor HTC/HTCsmooth~3.3 are for the sample “10-3-20”, especially at high heater temperatures.
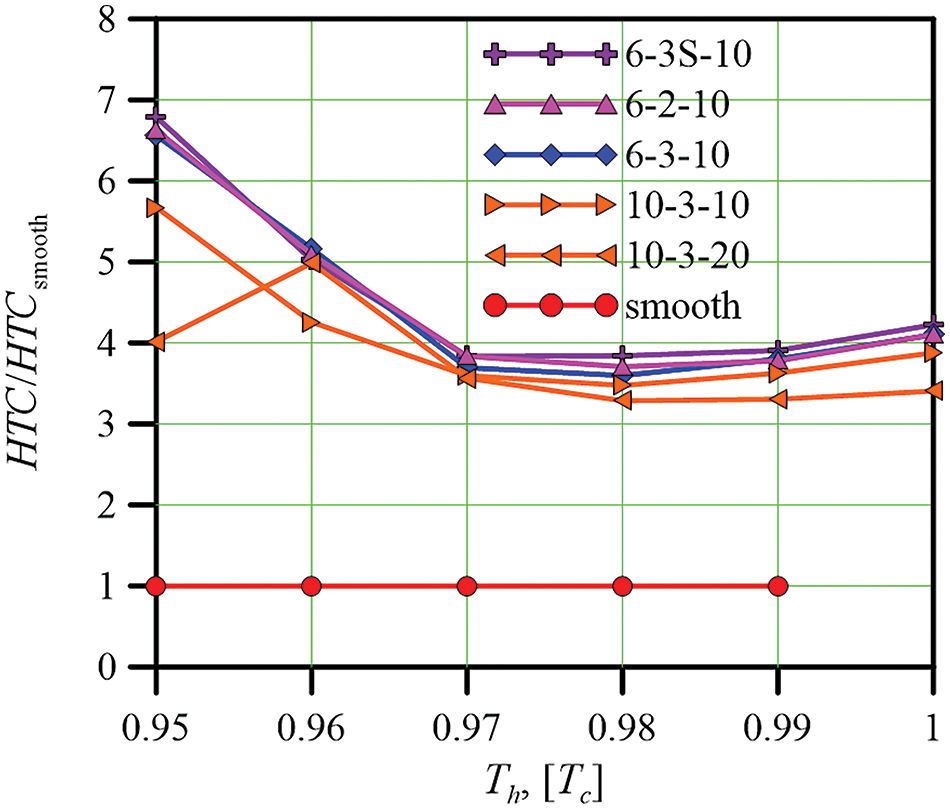
Figure 6: Enhancement factor for heat transfer on the porous surface relatively to that on the smooth surface
It should be noted that the multi-relaxation-time (MRT) approach is often used to avoid different numerical instabilities in calculations. However, it increases the computational time by about 30% compared to BGK. Our preliminary calculations showed that BGK and MRT approaches get almost identical numerical results for some particular regime of boiling on a porous heater. Besides, there were no instabilities for all considered in the paper cases using BGK. This is possible, in particular, because the exact difference method for the source of forces is used. Thus, the BGK approach was used in the paper to reduce the computational cost of the calculations of all considered porous samples.
The influence of the surface wetting properties on the boiling process was studied with the help of the present model in past studies [39–41]. The main conclusion is that the onset of nucleate boiling occurs at a lower temperature on a hydrophobic surface, while a more critical heat flux could be obtained on a hydrophilic surface. The optimum hydrophobic-to-hydrophilic area ratio in terms of heat transfer enhancement was found for a smooth surface with contrast wettability. The effect of the wetting properties on the boiling performance on spatially structured surfaces was studied in [41]. In the present work, only the spatial structure parameters of the porous heat exchange surfaces are under investigation as a first step, which makes it possible to highlight their influence on the heat transfer performance. The heater’s surface wettability will be taken into account in future studies considering the adhesive force Fs(x).
It should be noted that the presented hybrid “thermo-LBM” model has some limitations. In pseudopotential LBM, only a low liquid-to-vapor density ratio (ρl/ρv~25), i.e., close to the critical point, could be considered. There is very little experimental data for these conditions presented in the literature; thus, it is difficult to perform a direct quantitative comparison of the obtained results. However, the model describes quite well the following characteristics of the boiling process: calculated capillary constant, Bond number, departure frequency and diameter of a single bubble, the effect of the surface wetting properties on the evolution of individual vapor bubbles, as well as the behavior of the boiling curves at boiling on the smooth surface [39–41]. Though the parameters of the liquid correspond to that of the water, the results are viable for some model fluid. A valuable limitation of the 2D model is that the temperature of the centers of the solid heaters was set equal for all heaters, while the heat conduction through the metal wires of the metal foams occurs in 3D format. The abovementioned shortcomings will be improved in the model in the future.
A detailed parametric study of the boiling process on the porous surfaces was carried out. The phase pictures of the boiling process, the temperature and velocity fields, as well as the boiling curves on the porous heaters of different morphologies, were obtained. It was shown that:
- At low wall superheats in the regime of natural convection, the effective heat flux from the solid single heater and structured porous heaters substantially exceeds the heat flux from the smooth surface due to free liquid flow inside the porous heater.
- At moderate heater temperatures the enhancement factor of heat transfer on porous surfaces could reach the value of 7 compared to the smooth surface. At high heater temperatures, the enhancement factor on the porous surfaces is in the range of 3 to 4.
- The highest value of the enhancement factor was obtained for the sample with asymmetric placement of the heaters in the neighboring layers in the whole range of wall superheats.
- The increase in size and number of the heaters, as well as the increase in number of layers of the solid heaters, do not lead to the enhancement of the heat transfer; thus, the optimal parameters of the porous heaters must be carefully selected.
- The boiling on the porous heaters does not go into a crisis regime even at the highest value of the heaters temperature due to the effective convection of vapor and liquid phases inside the porous heaters. The results let us predict that the critical heat fluxes from the porous surfaces sufficiently exceed ones on the smooth or even modified surfaces.
The obtained results could be useful for scientists and engineers in the field of heat transfer enhancements developing various systems and devices operating at boiling. The obtained results can facilitate experimental studies of optimal configurations of porous surfaces designed to improve heat transfer. However, it is imperative to improve the model, to better control the surface wetting properties, morphological parameters, and liquid parameters.
Acknowledgement: The authors have no specific acknowledgements for this study.
Funding Statement: This research was funded by Russian Science Foundation grant number 24-29-00584.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Alexander Fedoseev; data collection: Alexander Fedoseev, Mikhail Salnikov; analysis and interpretation of results: Alexander Fedoseev, Mikhail Salnikov; draft manuscript preparation: Alexander Fedoseev, Mikhail Salnikov. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data are available from the authors.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Birbarah P, Gebrael T, Foulkes T, Stillwell A, Moore A, Pilawa-Podgurski R, et al. Water immersion cooling of high power density electronic. Int J Heat Mass Transf. 2020;147:118918. doi:10.1016/j.ijheatmasstransfer.2019.118918. [Google Scholar] [CrossRef]
2. Sefiane K, Koşar A. Prospects of heat transfer approaches to dissipate high heat fluxes: opportunities and challenges. Appl Therm Eng. 2022;215:118990. doi:10.1016/j.applthermaleng.2022.118990. [Google Scholar] [CrossRef]
3. Liang G, Mudawar I. Review of pool boiling enhancement by surface modification. Int J of Heat and Mass Transf. 2019;128:892–933. doi:10.1016/j.ijheatmasstransfer.2018.09.026. [Google Scholar] [CrossRef]
4. Mehralizadeh A, Shabanian S, Bakeri G. Effect of modified surfaces on bubble dynamics and pool boiling heat transfer enhancement: a review. Therm Sci and Eng Prog. 2019;15:100451–1–100451–25. doi:10.1016/j.tsep.2019.100451. [Google Scholar] [CrossRef]
5. Sun Y, Tang Y, Zhang S, Yuan W, Tang H. A review on fabrication and pool boiling enhancement of three-dimensional complex structures. Renew Sustain Energ Rev. 2022;162:112437. doi:10.1016/j.rser.2022.112437. [Google Scholar] [CrossRef]
6. Chu H, Xu N, Yu X, Jiang H, Ma W, Qiao F. Review of surface modification in pool boiling application: coating manufacturing process and heat transfer enhancement mechanism. Appl Therm Eng. 2022;215:119041. doi:10.1016/j.applthermaleng.2022.119041. [Google Scholar] [CrossRef]
7. Xie S, Beni MS, Cal J, Zhao J. Review of critical-heat-flux enhancement methods. Int J Heat Mass Transf. 2018;122:275–89. doi:10.1016/j.ijheatmasstransfer.2018.01.116. [Google Scholar] [CrossRef]
8. Lee CY, Bhuiya MMH, Kim KJ. Pool boiling heat transfer with nano-porous surface. Int J Heat Mass Transf. 2010;53(19–20):4274–9. doi:10.1016/j.ijheatmasstransfer.2010.05.054. [Google Scholar] [CrossRef]
9. Patil CM, Kandlikar SG. Pool boiling enhancement through microporous coatings selectively electrodeposited on fin tops of open microchannels. Int J Heat Mass Transf. 2014;79:816–28. doi:10.1016/j.ijheatmasstransfer.2014.08.063. [Google Scholar] [CrossRef]
10. Katarkar AS, Majumder B, Pingale AD, Belgamwar SU, Bhaumik S. A review on the effects of porous coating surfaces on boiling heat transfer. Mat Today: Proc. 2021;44(1):362–7. doi:10.1016/j.matpr.2020.09.744. [Google Scholar] [CrossRef]
11. Ha M, Graham S. Pool boiling characteristics and critical heat flux mechanisms of microporous surfaces and enhancement through structural modification. Appl Phys Lett. 2017;111(9):091601. doi:10.1063/1.4999158. [Google Scholar] [CrossRef]
12. Calati M, Righetti G, Doretti L, Zilio C, Longo GA, Hooman K, et al. Water pool boiling in metal foams: from experimental results to a generalized model based on artificial neural network. Int J Heat Mass Transf. 2021;176:121451. doi:10.1063/1.4999158. [Google Scholar] [CrossRef]
13. Yang Y, Ji X, Xu J. Pool boiling heat transfer on copper foam covers with water as working fluid. Int J Therm Sci. 2010;49:1227–37. doi:10.1016/j.ijthermalsci.2010.01.013. [Google Scholar] [CrossRef]
14. Zhou L, Li W, Ma T, Du X. Experimental study on boiling heat transfer of a self-rewetting fluid on copper foams with pore density gradient structures. Int J Heat Mass Transf. 2018;124:210–9. doi:10.1016/j.ijheatmasstransfer.2018.03.070. [Google Scholar] [CrossRef]
15. Xu ZG, Qin J, Qu GM. Numerical and experimental study of pool boiling heat transfer mechanisms in V-shaped grooved porous metals. Int J Therm Sci. 2022;173:107393. doi:10.1016/j.ijthermalsci.2021.107393. [Google Scholar] [CrossRef]
16. Xu ZG, Zhao CY. Thickness effect on pool boiling heat transfer of trapezoid-shaped copper foam fins. Appl Therm Eng. 2013;60(1–2):359–70. doi:10.1016/j.applthermaleng.2013.07.013. [Google Scholar] [CrossRef]
17. Manetti LL, Moita ASIH, Souza RR, Cardoso EM. Effect of copper foam thickness on pool boiling heat transfer of HFE-7100. Int J Heat Mass Transf. 2020;152(5):119547. doi:10.1016/j.ijheatmasstransfer.2020.119547. [Google Scholar] [CrossRef]
18. Hu H, Zhao Y, Lai Z, Hu C. Experimental investigation on nucleate pool boiling heat transfer characteristics on hydrophobic metal foam covers. Appl Therm Eng. 2020;179(25–26):115730. doi:10.1016/j.applthermaleng.2020.115730. [Google Scholar] [CrossRef]
19. Shi J, Jia X, Feng D, Chen Z, Dang C. Wettability effect on pool boiling heat transfer using a multiscale copper foam surface. Int J Heat Mass Transf. 2020;146(1–3):118726. doi:10.1016/j.ijheatmasstransfer.2019.118726. [Google Scholar] [CrossRef]
20. Yuan X, Du Y, Wang C. Experimental study on pool boiling enhancement by unique designing of porous media with a wettability gradient. Appl Therm Eng. 2023;231(11):120893. doi:10.1016/j.applthermaleng.2023.120893. [Google Scholar] [CrossRef]
21. Kharangate CR, Mudawar I. Review of computational studies on boiling and condensation. Int J Heat Mass Transf. 2017;108:1164–96. doi:10.1016/j.ijheatmasstransfer.2016.12.065. [Google Scholar] [CrossRef]
22. Enjadat SMJ. CFD Comparison of multiphase models in the pool boiling state. Curved Layered Struct. 2022;9(1):382–9. doi:10.1515/cls-2022-0029. [Google Scholar] [CrossRef]
23. Mukherjee A, Dhir VK. Study of lateral merger of vapor bubbles during nucleate pool boiling. J Heat Transfer. 2004;126(6):1023–39. doi:10.1115/1.1834614. [Google Scholar] [CrossRef]
24. Mukherjee A, Kandlikar SG. Numerical study of single bubbles with dynamic contact angle during nucleate pool boiling. Int J Heat Mass Transf. 2007;50(1–2):127–38. doi:10.1016/j.ijheatmasstransfer.2006.06.037. [Google Scholar] [CrossRef]
25. Kunkelmann C, Stephan P. CFD simulation of boiling flows using the volume of fluid method within OpenFOAM. Numer Heat Transf A: Appl. 2009;56(8):631–46. doi:10.1080/10407780903423908. [Google Scholar] [CrossRef]
26. Jiaqiang E, Zhang Z, Tu Z, Zuo W, Hu W, Han D, et al. Effect analysis on flow and boiling heat transfer performance of cooling water-jacket of bearing in the gasoline engine turbocharger. Appl Thermal Eng. 2018;130(3):754–66. doi:10.1016/j.applthermaleng.2017.11.070. [Google Scholar] [CrossRef]
27. Sun DL, Tao WQ. A coupled volume-of-fluid and level set (VOSET) method for computing incompressible two-phase flows. Int J Heat Mass Tran. 2010;53(4):645–55. doi:10.1016/j.ijheatmasstransfer.2009.10.030. [Google Scholar] [CrossRef]
28. Ling K, Li ZY, Tao WQ. A direct numerical simulation for nucleate boiling by the VOSET method. Numer Heat Tr A-Appl. 2014;65(10):949–71. doi:10.1080/10407782.2013.850971. [Google Scholar] [CrossRef]
29. Chen Y, Zou Y, Sun D, Wang Y, Yu B. Molecular dynamics simulation of bubble nucleation on nanostructure surface. Int J Heat Mass Transf. 2018;118(2):1143–51. doi:10.1016/j.ijheatmasstransfer.2017.11.079. [Google Scholar] [CrossRef]
30. Zhang L, Xu J, Liu G, Lei J. Nucleate boiling on nanostructured surfaces using molecular dynamics simulations. Int J Therm Scien. 2020;152(2015):106325. doi:10.1016/j.ijthermalsci.2020.106325. [Google Scholar] [CrossRef]
31. Krüger T, Kusumaatmaja H, Kuzmin A, Shardt O, Silva G, Viggen EM. The lattice boltzmann method: principles and practice. Switzerland: Springer International Publishing; 2017. doi:10.1007/978-3-319-44649-3. [Google Scholar] [CrossRef]
32. Pattnaik AC, Samanta R, Chattopadhy H. A brief on the application of multiphase lattice Boltzmann method for boiling and evaporation. J Therm Anal Calorim. 2023;148:2869–904. doi:10.1007/s10973-022-11820-8. [Google Scholar] [CrossRef]
33. Shan X, Chen H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys Rev E. 1993;47:1815–20. doi:10.1103/physreve.47.1815. [Google Scholar] [PubMed] [CrossRef]
34. Chen S, Martínez D. On boundary conditions in lattice Boltzmann methods. Phys Fluid. 1996;8:2527–36. doi:10.1063/1.869035. [Google Scholar] [CrossRef]
35. Li Q, Luo KH, Kang QJ, Chen Q. Lattice Boltzmann modeling of boiling heat transfer: the boiling curve and the effects of wettability. Int J Heat Mass Transf. 2015;85:053301.doi:10.1016/j.ijheatmasstransfer.2015.01.136. [Google Scholar] [CrossRef]
36. Gong S, Cheng P. Lattice Boltzmann simulation of periodic bubble nucleation, growth and departure from a heated surface in pool boiling. Int J Heat Mass Transf. 2013;64:122. doi:10.1016/j.ijheatmasstransfer.2013.03.058. [Google Scholar] [CrossRef]
37. Fedoseev AV, Salnikov MV, Ostapchenko AE. Modeling of a single bubble dynamics at boiling by lattice boltzmann method. J Appl Industrial Math. 2023;17(1):64–71. doi:10.1134/S1990478923010088. [Google Scholar] [CrossRef]
38. Zhang C, Cheng P. Mesoscale simulations of boiling curves and boiling hysteresis under constant wall temperature and constant heat flux conditions. Int J Heat Mass Transf. 2017;110(12):319–29. doi:10.1016/j.ijheatmasstransfer.2017.03.039. [Google Scholar] [CrossRef]
39. Moiseev MI, Fedoseev A, Shugaev MV, Surtaev AS. Hybrid thermal lattice Boltzmann model for boiling heat transfer on surfaces with different wettability. Int Phen Heat Tran. 2020;8(1):81–91. doi:10.1615/InterfacPhenomHeatTransfer.2020033929. [Google Scholar] [CrossRef]
40. Fedoseev AV, Salnikov MV, Ostapchenko AE, Surtaev AS. Lattice boltzmann simulation of optimal biphilic surface configuration to enhance boiling heat transfer. Energies. 2022;15(21):8204. doi:10.3390/en15218204. [Google Scholar] [CrossRef]
41. Fedoseev AV, Salnikov MV, Ostapchenko AE. Modelling of pool boiling on the structured surfaces using Lattice Boltzmann method. E3S Web Conf. 2023;459(2):05003. doi:10.1051/e3sconf/202345905003. [Google Scholar] [CrossRef]
42. Li WX, Li Q, Yu Y, Luo KH. Nucleate boiling enhancement by structured surfaces with distributed wettability-modified regions: a lattice Boltzmann study. Appl Therm Eng. 2021;194:117130. doi:10.1016/j.applthermaleng.2021.117130. [Google Scholar] [CrossRef]
43. Wang J, Liang G, Yin X, Shen S. Pool boiling on micro-structured surface with lattice Boltzmann method. Int J Therm Sci. 2023;187:108170. doi:10.1016/j.ijthermalsci.2023.108170. [Google Scholar] [CrossRef]
44. Qin J, Zhou X, Zhao CY, Xu ZG. Numerical investigation on boiling mechanism in porous metals by LBM at pore scale level. Int J Therm Sci. 2018;130:298–312. doi:10.1016/j.ijthermalsci.2018.05.004. [Google Scholar] [CrossRef]
45. Qin J, Xu ZY, Xu ZG. Pore-scale investigation on flow boiling heat transfer mechanisms in gradient open-cell metal foams by LBM. Int Commun Heat Mass Transf. 2020;119:104974. doi:10.1016/j.icheatmasstransfer.2020.104974. [Google Scholar] [CrossRef]
46. Shi J, Feng D, Chen Z, Ma Q. Numerical study of a hybrid thermal lattice Boltzmann method for pool boiling heat transfer on a modeled hydrophilic metal foam surface. Appl Therm Eng. 2023;229:120535. doi:10.1016/j.applthermaleng.2023.120535. [Google Scholar] [CrossRef]
47. Kupershtokh AL, Medvedev DA, Karpov DI. On equations of state in a lattice Boltzmann method. Comput Math Appl. 2009;58(5):965–74. doi:10.1016/j.camwa.2009.02.024. [Google Scholar] [CrossRef]
48. Zhang R, Chen H. Lattice Boltzmann method for simulations of liquid-vapor thermal flows. Phys Rev E. 2003;67(6):066711. doi:10.1103/PhysRevE.67.066711. [Google Scholar] [PubMed] [CrossRef]
49. Yuan P, Schaefer L. Equations of state in a lattice Boltzmann model. Phys Fluids. 2006;18(4):042101. doi:10.1063/1.2187070. [Google Scholar] [CrossRef]
50. Kumar A. Isotropic finite-differences. J Comput Phys. 2004;201(1):109–18. doi:10.1016/j.jcp.2004.05.005. [Google Scholar] [CrossRef]
51. Li Q, Luo KH, Kang QJ, He YL, Chen Q, Liu Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog Energy Combust. 2016;52:62–105. doi:10.1016/j.pecs.2015.10.001. [Google Scholar] [CrossRef]
52. Luo C, Tagawa T. Effect of heating wires with electric potential on pool-boiling heat transfer under an electric field. Appl Therm Eng. 2024;240:122327. doi:10.1016/j.applthermaleng.2023.122327. [Google Scholar] [CrossRef]
53. Channouf S, Jami M, Mezrhab A. Numerical study of the evolution of bubbles during nucleation and droplets during condensation on a surface of variable wettability using the pseudopotential MRT-LBM method. Numer Heat Trans Part B: Fund. 2023;85(2):131–58. doi:10.1080/10407790.2023.2229012. [Google Scholar] [CrossRef]
54. Channouf S, Jami M, Mezrhab A. Numerical hybrid thermal MRT-LBM for condensation and boiling phenomena on horizontal walls of different wettability. Fluid Dyn Res. 2022;54(2):025502. doi:10.1088/1873-7005/ac5d1e. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
